Modeling and Application of the Hydrus-2D Model for Simulating Preferential Flow in Loess Soil Under Various Scenarios
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Site
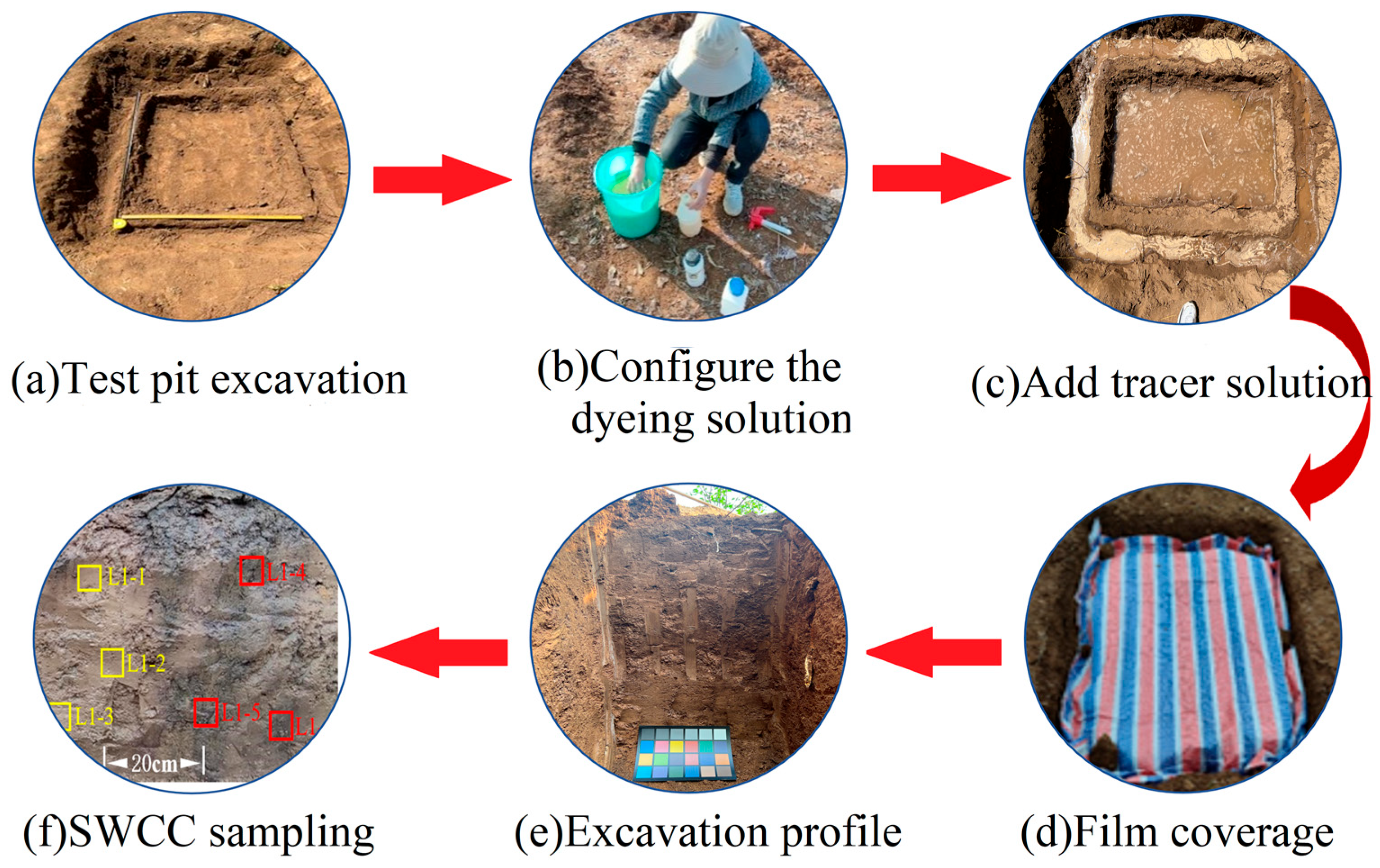
2.2. Dyeing Experiment
2.3. Model Establishment
2.3.1. Mathematical Equations
2.3.2. Establishment of Hydrus-2D/3D Model
2.4. Determining Conditions of Soil Macropore Flow Movement
2.4.1. Modelled Hydraulic Parameters
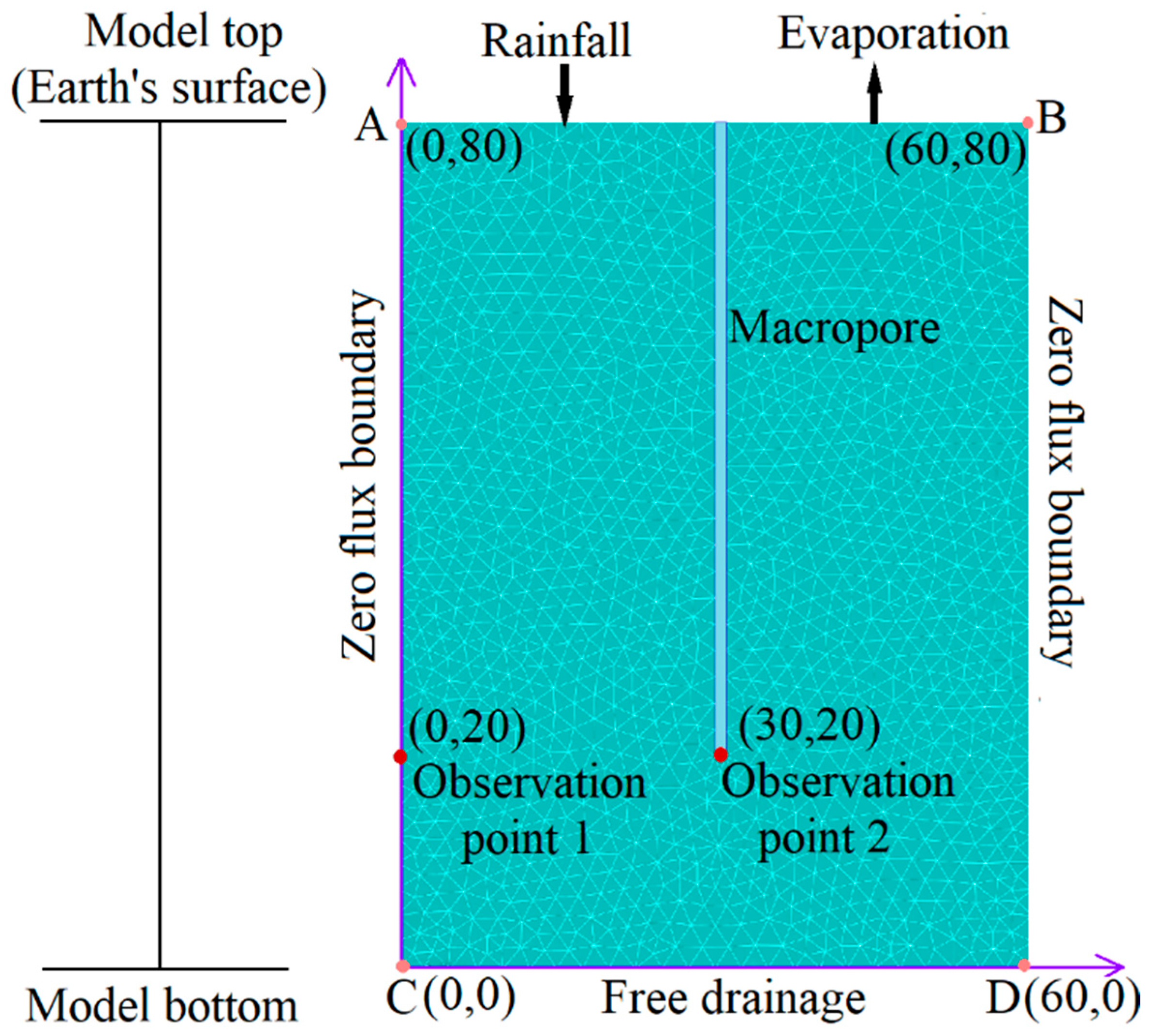
2.4.2. Boundary Conditions
2.4.3. Time Discretization
2.5. Simulation Scenario Setting
3. Results
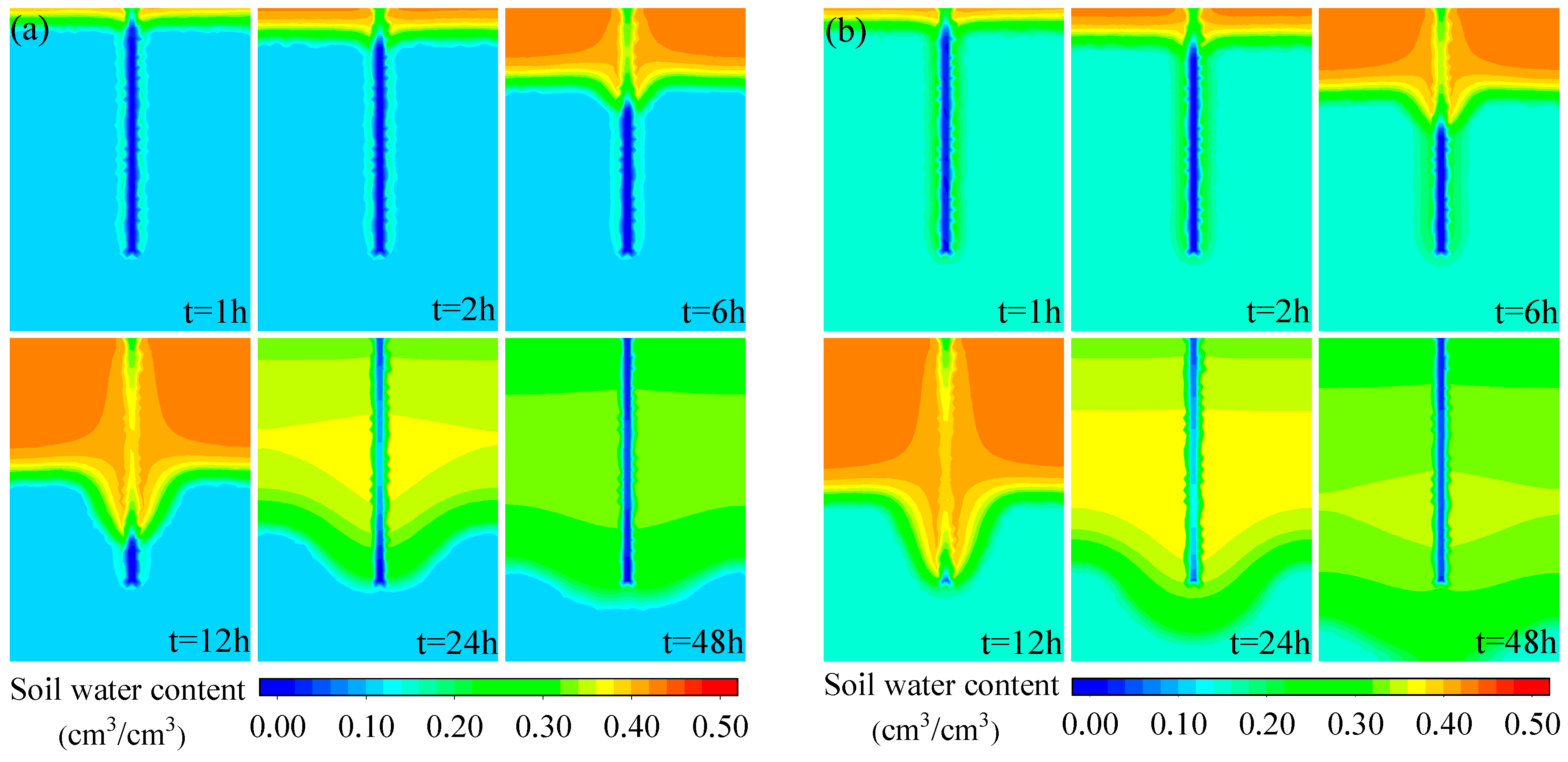
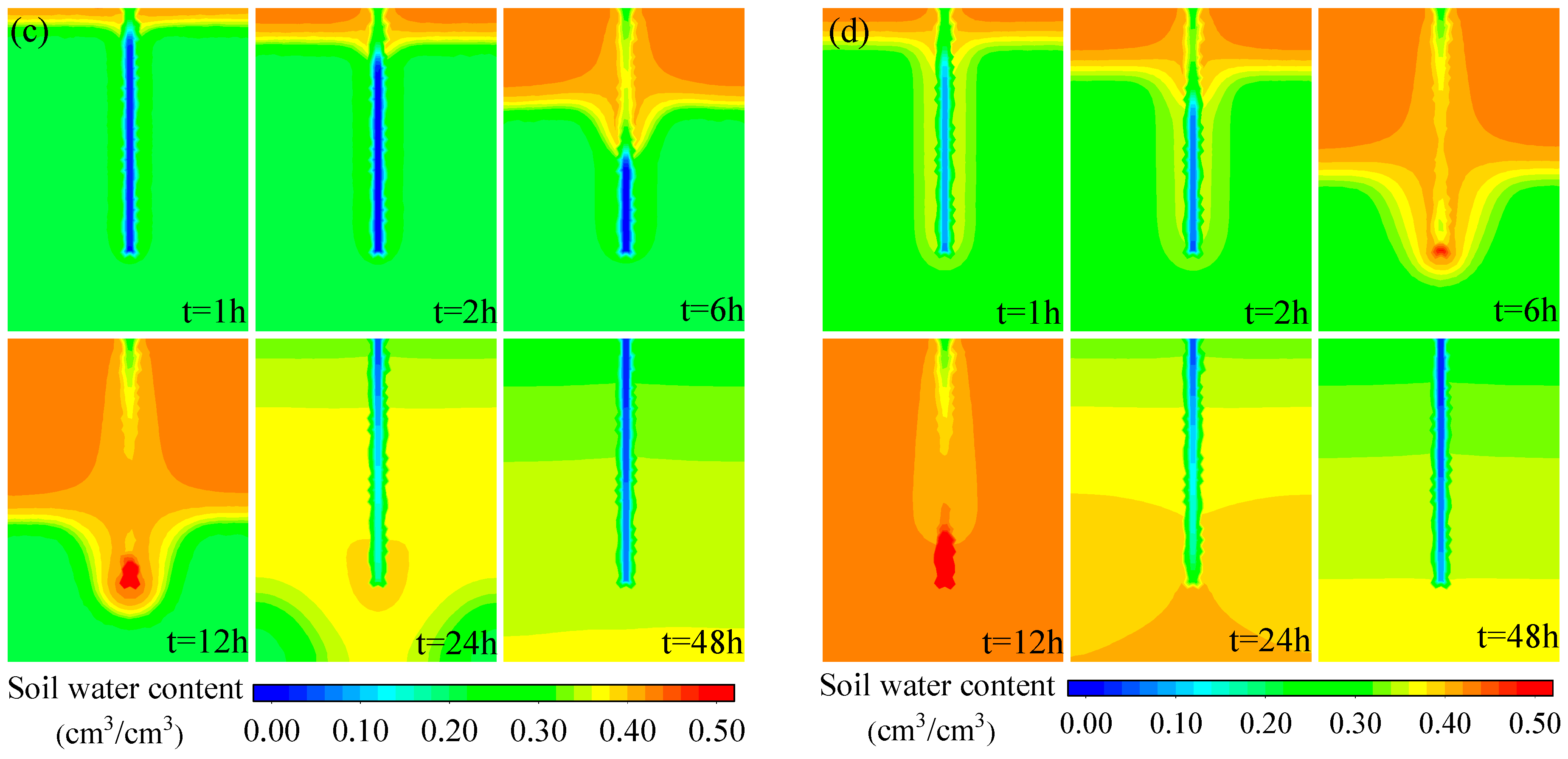
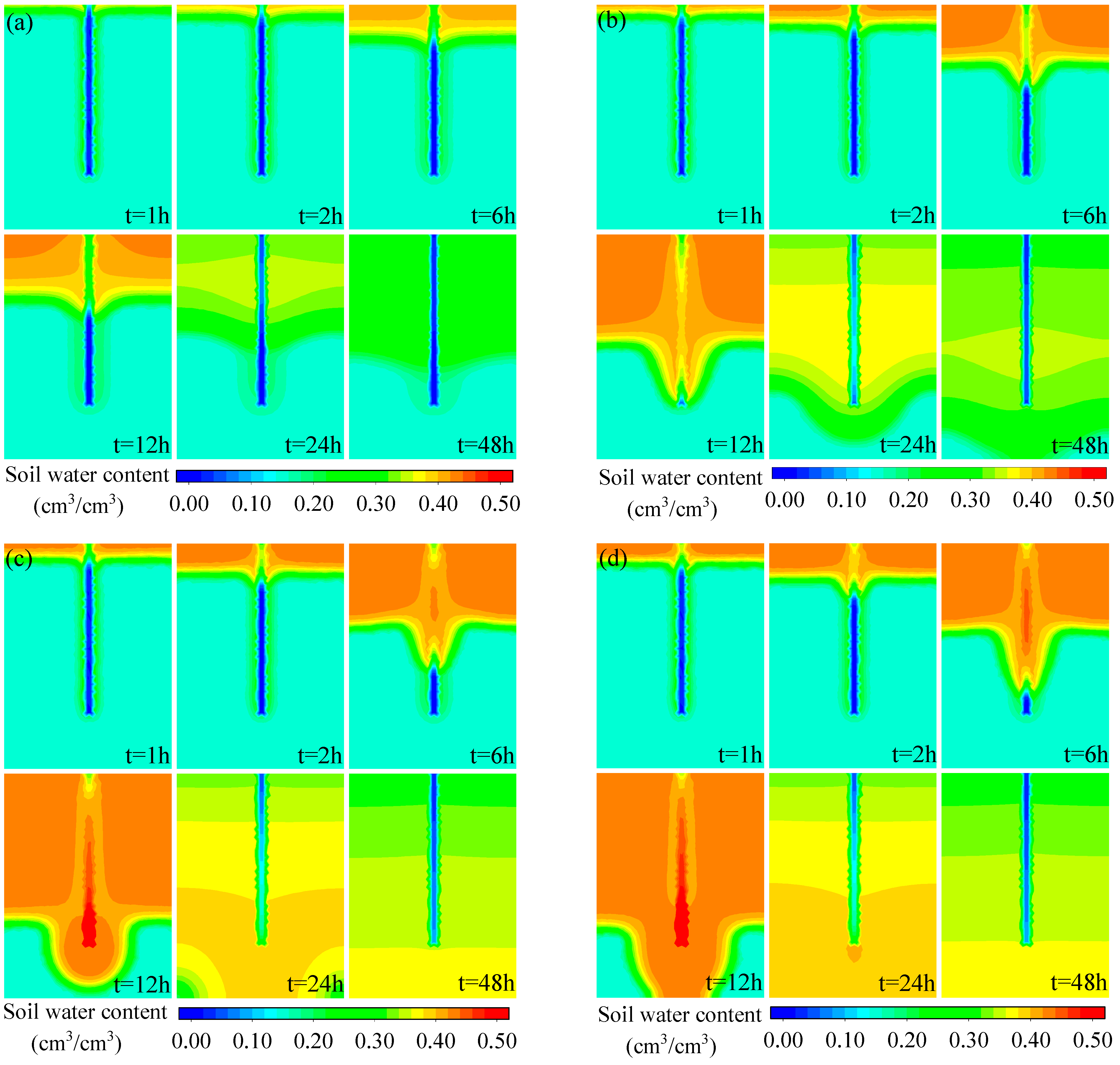
3.1. Response of Soil Water Content Variations to Different Scenarios
3.1.1. Different Initial Soil Water Content
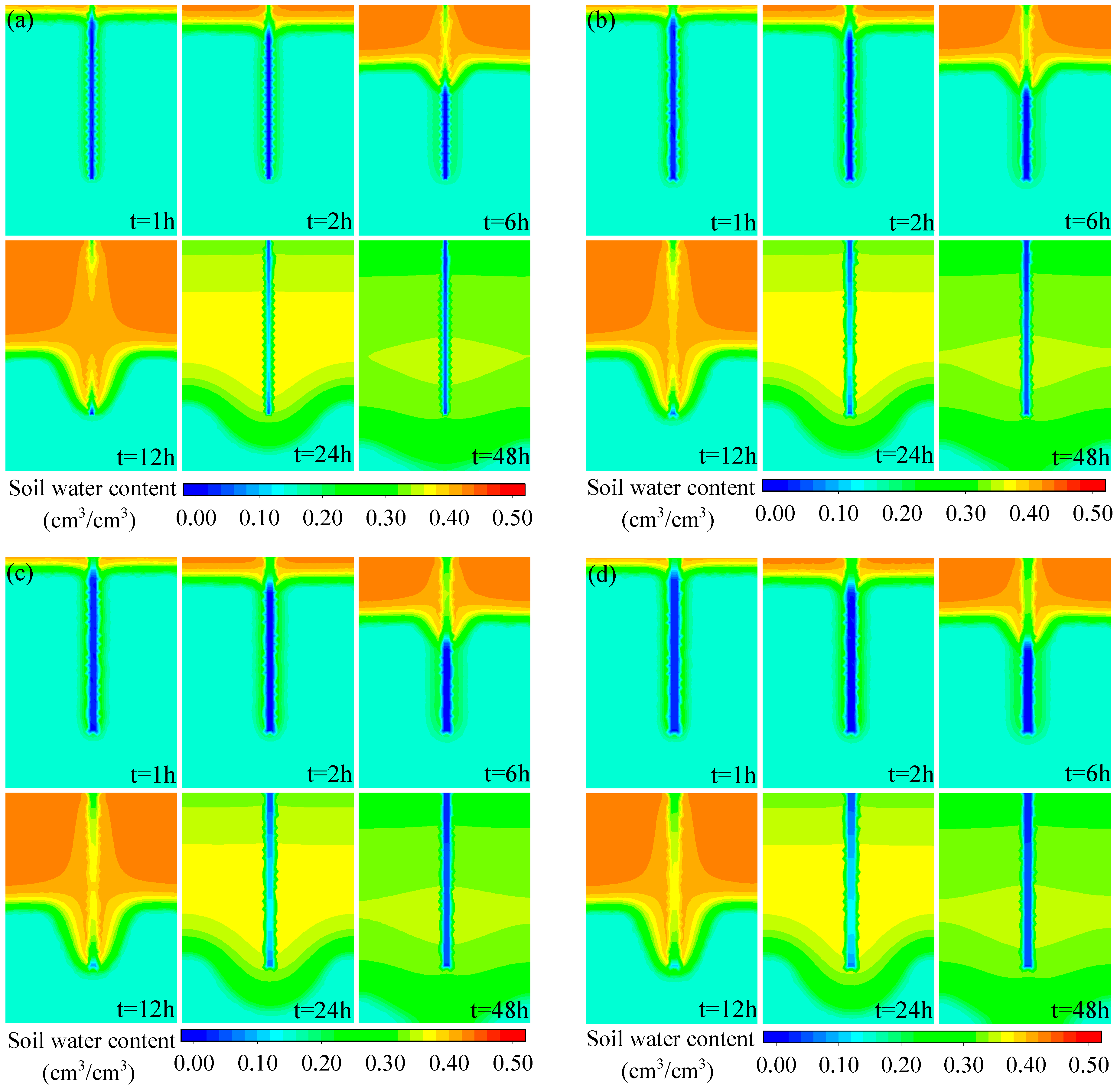
3.1.2. Different Rainfall Intensity
3.1.3. Different Cracks Width
3.2. Response of Maximum Water Content and Wetting Front Depth Variations to Different Scenarios
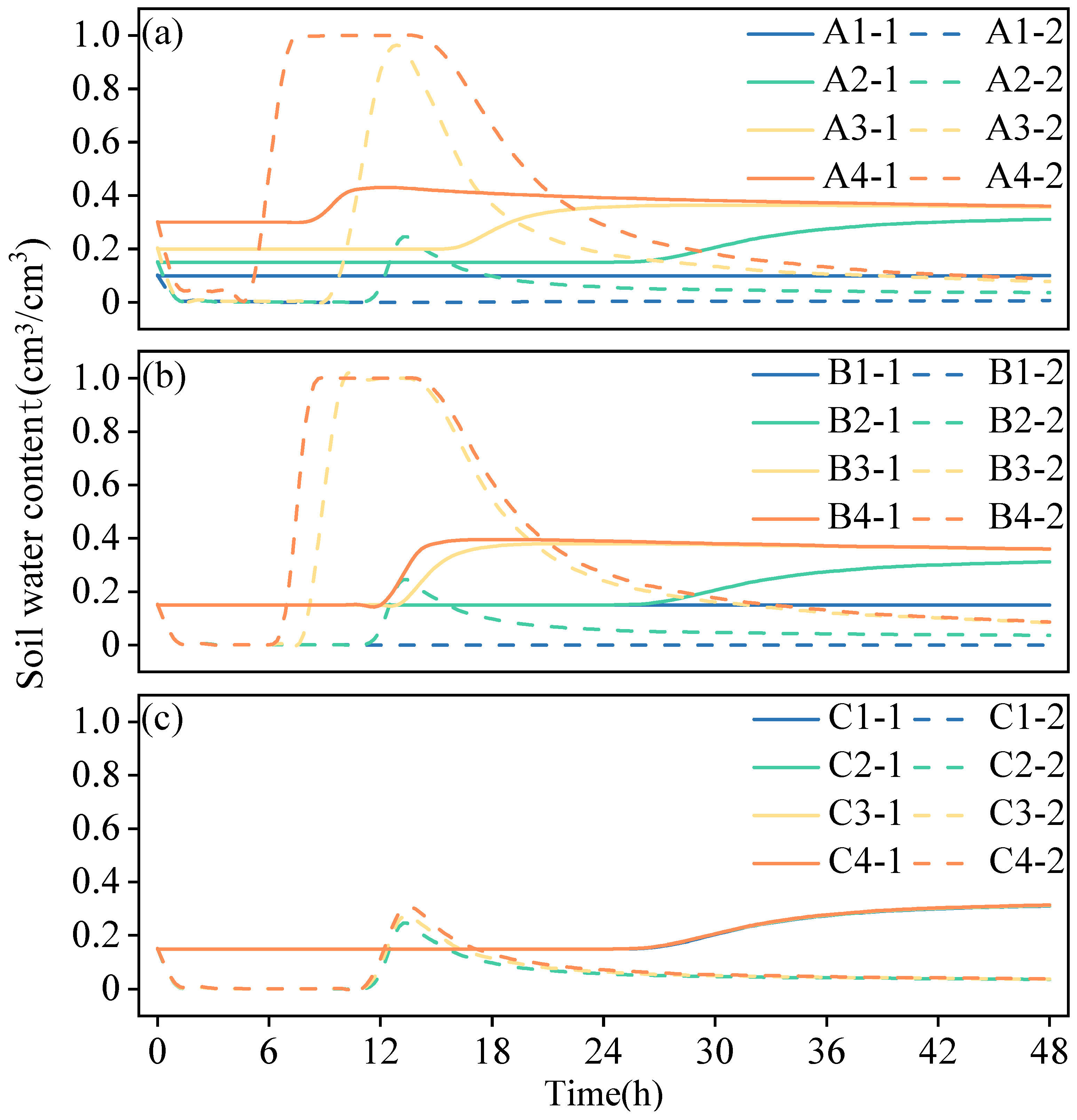
3.3. Response of Water Distribution Characteristics of Loess at Observation Points to Different Scenarios
3.3.1. Soil Water Content
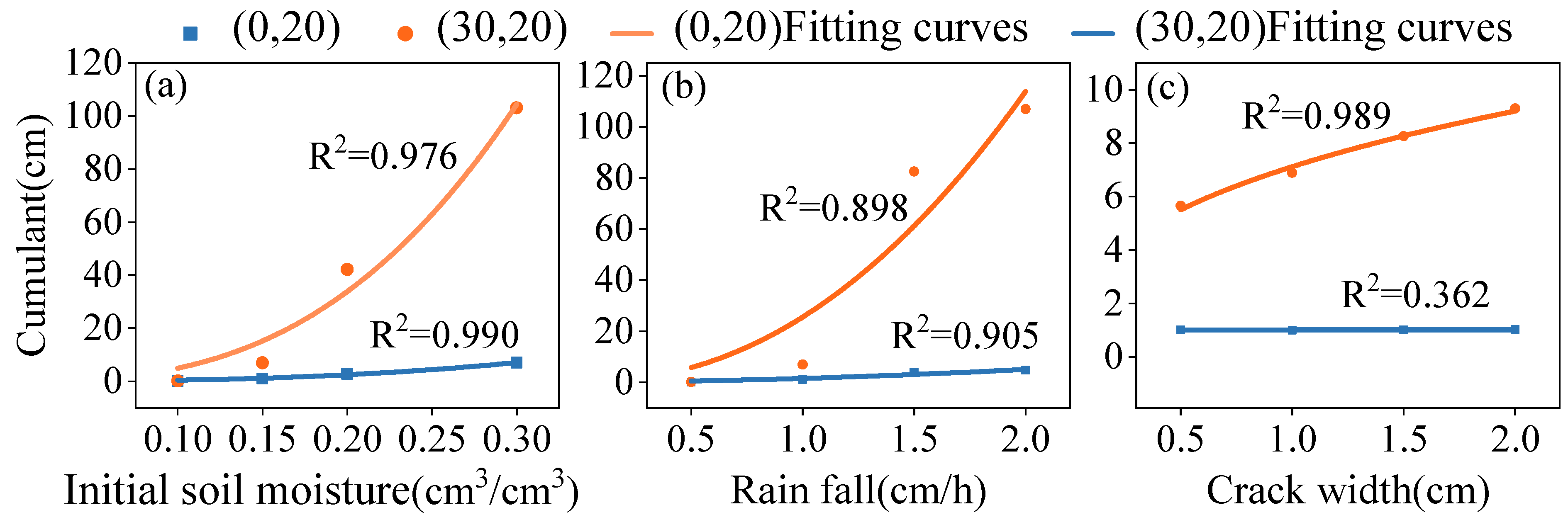
3.3.2. Cumulative Soil Water Flux
4. Discussion
4.1. Simulation and Verification of Preferential Flow Process
4.2. Improvement and Optimization of the Model
4.3. Regional Applicability and Future Research Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J.P.; Zhang, W.; Zuo, J.Q.; Bi, J.R.; Shi, J.S.; Wang, X.; Chang, Z.L.; Huang, Z.W.; Yang, S.; Zhang, B.D.; et al. An Overview of the Semi-arid Climate and Environment Research Observatory over the Loess Plateau. Adv. Atmos. Sci. 2008, 25, 906–921. [Google Scholar]
- Feng, S.; Fu, Q. Expansion of global drylands under a warming climate. Atmos. Chem. Phys. 2013, 13, 10081–10094. [Google Scholar] [CrossRef]
- Ravi, S.; Breshears, D.D.; Huxman, T.E.; D’Odorico, P. Land degradation in drylands: Interactions among hydrologic-aeolian erosion and vegetation dynamics. Geomorphology 2010, 116, 236–245. [Google Scholar]
- Torres, L.; Abraham, E.M.; Rubio, C.; Barbero-Sierra, C.; Ruiz-Pérez, M. Desertification Research in Argentina. Land Degrad. Dev. 2015, 26, 433–440. [Google Scholar]
- Belaroui, K.; Djediai, H.; Megdad, H. The influence of soil, hydrology, vegetation and climate on desertification in El-Bayadh region (Algeria). Desalin. Water Treat. 2014, 52, 2144–2150. [Google Scholar]
- D’Odorico, P.; Bhattachan, A.; Davis, K.F.; Ravi, S.; Runyan, C.W. Global desertification: Drivers and feedbacks. Adv. Water Resour. 2013, 51, 326–344. [Google Scholar]
- Kebre, M.B.; Cherblanc, F.; Ouedraogo, F.; Jamin, F.; Naon, B.; Zougmore, F.; Benet, J.C. Water flow in soil at small water contents: A simple approach to estimate the relative hydraulic conductivity in sandy soil. Eur. J. Soil Sci. 2017, 68, 167–176. [Google Scholar]
- Bayad, M.; Chau, H.W.; Trolove, S.; Moir, J.; Condron, L.; Bouray, M. The Relationship between Soil Moisture and Soil Water Repellency Persistence in Hydrophobic Soils. Water 2020, 12, 12. [Google Scholar] [CrossRef]
- Nakhaei, M.; Simunek, J. Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the HYDRUS-2D code. J. Hydrol. Hydromech. 2014, 62, 7–15. [Google Scholar]
- Beven, K.; Germann, P. Macropores and water flow in soils revisited. Water Resour. Res. 2013, 49, 3071–3092. [Google Scholar]
- Guan, N.; Cheng, J.H.; Shi, X.Q. Preferential Flow and Preferential Path Characteristics of the Typical Forests in the Karst Region of Southwest China. Forests 2023, 14, 17. [Google Scholar] [CrossRef]
- Weiler, M. Macropores and preferential flow-a love-hate relationship. Hydrol. Process. 2017, 31, 15–19. [Google Scholar] [CrossRef]
- Brunetti, G.F.A.; Maiolo, M.; Fallico, C.; Severino, G. Unraveling the complexities of a highly heterogeneous aquifer under convergent radial flow conditions. Eng. Comput. 2024, 40, 3115–3130. [Google Scholar]
- Yetbarek, E.; Kumar, S.; Ojha, R. Effects of soil heterogeneity on subsurface water movement in agricultural fields: A numerical study. J. Hydrol. 2020, 590, 15. [Google Scholar] [CrossRef]
- Bauser, H.H.; Kim, M.; Ng, W.R.; Bugaj, A.; Troch, P.A. Richards Equation at the Hillslope Scale: Can We Resolve the Heterogeneity of Soil Hydraulic Material Properties? Water Resour. Res. 2022, 58, 18. [Google Scholar]
- Peng, W.B.; Wang, Z.; Song, Y.G.; Pfaff, K.; Luo, Z.; Nie, J.S.; Chen, W.H. A comparison of heavy mineral assemblage between the loess and the Red Clay sequences on the Chinese Loess Plateau. Aeolian Res. 2016, 21, 87–91. [Google Scholar]
- Zhang, L.X.; Qi, S.W.; Yu, Y.T.; Zhang, Y.G.; Li, Z.Q.; Hou, X.K.; Ma, L.N.; Zou, Y.; Guo, S.F.; Peng, J.B. A comparative study on the physical properties of natural sedimentary loess and manual filling compacted loess. Environ. Earth Sci. 2021, 80, 17. [Google Scholar] [CrossRef]
- Qiu, D.X.; Xu, R.R.; Wu, C.X.; Mu, X.M.; Zhao, G.J.; Gao, P. Vegetation restoration improves soil hydrological properties by regulating soil physicochemical properties in the Loess Plateau, China. J. Hydrol. 2022, 609, 12. [Google Scholar]
- Morianou, G.; Kourgialas, N.N.; Karatzas, G.P. A Review of HYDRUS 2D/3D Applications for Simulations of Water Dynamics, Root Uptake and Solute Transport in Tree Crops under Drip Irrigation. Water 2023, 15, 23. [Google Scholar] [CrossRef]
- Deb, S.K.; Shukla, M.K.; Simunek, J.; Mexal, J.G. Evaluation of Spatial and Temporal Root Water Uptake Patterns of a Flood-Irrigated Pecan Tree Using the HYDRUS (2D/3D) Model. J. Irrig. Drainage Eng-ASCE 2013, 139, 599–611. [Google Scholar]
- Li, T.C.; Shao, M.A.; Jia, Y.H.; Jia, X.X.; Huang, L.M. Small-scale observation on the effects of the burrowing activities of mole crickets on soil erosion and hydrologic processes. Agric. Ecosyst. Environ. 2018, 261, 136–143. [Google Scholar] [CrossRef]
- Yin, M.S.; Xiao, K.; Xin, P.; Li, H.L.; Zheng, C.M.; Smith, E.; Wilson, A.M. Randomly Distributed Crab Burrows Enhance Groundwater Flow and Salt Transport in Creek-Marsh Systems. Water Resour. Res. 2023, 59, 15. [Google Scholar] [CrossRef]
- Barbosa, L.A.P.; Gerke, K.M.; Gerke, H.H. Modelling of soil mechanical stability and hydraulic permeability of the interface between coated biopore and matrix pore regions. Geoderma 2022, 410, 8. [Google Scholar] [CrossRef]
- Soltanmohammadi, R.; Iraji, S.; de Almeida, T.R.; Basso, M.; Munoz, E.R.; Vidal, A.C. Investigation of pore geometry influence on fluid flow in heterogeneous porous media: A pore-scale study. Energy Geosci. 2024, 5, 17. [Google Scholar] [CrossRef]
- Huber, C.; Su, Y. A pore-scale investigation of the dynamic response of saturated porous media to transient stresses. Geofluids 2015, 15, 11–23. [Google Scholar] [CrossRef]
- Tartakovsky, D.M.; Lu, Z.; Guadagnini, A.; Tartakovsky, A.M. Unsaturated flow in heterogeneous soils with spatially distributed uncertain hydraulic parameters. J. Hydrol. 2003, 275, 182–193. [Google Scholar] [CrossRef]
- Houben, G.J.; Stoeckl, L.; Mariner, K.E.; Choudhury, A.S. The influence of heterogeneity on coastal groundwater flow—Physical and numerical modeling of fringing reefs, dykes and structured conductivity fields. Adv. Water Resour. 2018, 113, 155–166. [Google Scholar] [CrossRef]
- Cui, P.F.; Xie, H.P.; Wang, Z.H.; Hao, H.C.; Li, C.B.; Gao, M.Z. Implications of Local-Scale Approximations on Describing Fluid Flow in Rock Fractures With Stress-Induced Void Heterogeneity. Water Resour. Res. 2022, 58, 19. [Google Scholar] [CrossRef]
- Severino, G.; Leveque, S.; Toraldo, G. Uncertainty quantification of unsteady source flows in heterogeneous porous media. J. Fluid Mech. 2019, 870, 5–26. [Google Scholar] [CrossRef]
- Tobella, A.B.; Reese, H.; Almaw, A.; Bayala, J.; Malmer, A.; Laudon, H.; Ilstedt, U. The effect of trees on preferential flow and soil infiltrability in an agroforestry parkland in semiarid Burkina Faso. Water Resour. Res. 2014, 50, 3342–3354. [Google Scholar] [CrossRef]
- Benegas, L.; Ilstedt, U.; Roupsard, O.; Jones, J.; Malmer, A. Effects of trees on infiltrability and preferential flow in two contrasting agroecosystems in Central America. Agric. Ecosyst. Environ. 2014, 183, 185–196. [Google Scholar] [CrossRef]
- Maples, S.R.; Fogg, G.E.; Maxwell, R.M. Modeling managed aquifer recharge processes in a highly heterogeneous, semi-confined aquifer system. Hydrogeol. J. 2019, 27, 2869–2888. [Google Scholar] [CrossRef]
- Autovino, D.; Rallo, G.; Provenzano, G. Predicting soil and plant water status dynamic in olive orchards under different irrigation systems with Hydrus-2D: Model performance and scenario analysis. Agric. Water Manage. 2018, 203, 225–235. [Google Scholar] [CrossRef]
- Zhu, X.A.; Chen, C.F.; Wu, J.N.; Yang, J.B.; Zhang, W.J.; Zou, X.; Liu, W.J.; Jiang, X.J. Can intercrops improve soil water infiltrability and preferential flow in rubber-based agroforestry system? Soil Tillage Res. 2019, 191, 327–339. [Google Scholar] [CrossRef]
- Nanda, A.; Sen, S.; Jirwan, V.; Sharma, A.; Kumar, V. Understanding plot-scale hydrology of Lesser Himalayan watershedA field study and HYDRUS-2D modelling approach. Hydrol. Process. 2018, 32, 1254–1266. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Noory, H. Modeling paddy field subsurface drainage using HYDRUS-2D. Paddy Water Environ. 2015, 13, 477–485. [Google Scholar] [CrossRef]
- Kadyampakeni, D.M.; Morgan, K.T.; Nkedi-Kizza, P.; Schumann, A.W.; Jawitz, J.W. Modeling Water and Nutrient Movement in Sandy Soils Using HYDRUS-2D. J. Environ. Qual. 2018, 47, 1546–1553. [Google Scholar] [CrossRef] [PubMed]
- Al-Salihi, Z.K.K.; Salim, S.B. Effect of lengthanddepthof thedriptapeon wetting front advance in the root zone of sunflowr using hydrus 2D/3D program. Iraqi J. Agric. Sci. 2023, 54, 768–776. [Google Scholar] [CrossRef]
- Trakal, L.; Kodesová, R.; Komárek, M. Modelling of Cd, Cu, Pb and Zn transport in metal contaminated soil and their uptake by willow (Salix × smithiana) using HYDRUS-2D program. Plant Soil 2013, 366, 433–451. [Google Scholar] [CrossRef]
- Varvaris, I.; Borgesen, C.D.; Kjærgaard, C.; Iversen, B.V. Three Two-Dimensional Approaches for Simulating the Water Flow Dynamics in a Heterogeneous Tile-Drained Agricultural Field in Denmark. Soil Sci. Soc. Am. J. 2018, 82, 1367–1383. [Google Scholar] [CrossRef]
- Selim, T.; Bouksila, F.; Hamed, Y.; Berndtsson, R.; Bahri, A.; Persson, M. Field experiment and numerical simulation of point source irrigation with multiple tracers. PLoS ONE 2018, 13, 15. [Google Scholar] [CrossRef]
- Latifi, M.; Etedali, H.R.; Soltani, M. Evaluation of the different soil management effects on salinity control in maize cropping by HYDRUS-2D. Soil Sci. Annu. 2023, 74, 11. [Google Scholar] [CrossRef]
- Geng, L.; Li, L.; Li, W.; Yang, C.F.; Meng, F.J. HYDRUS-2D simulations of water movement in a drip irrigation system under soilless substrate. Int. J. Agric. Biol. Eng. 2022, 15, 210–216. [Google Scholar] [CrossRef]
- Mguidiche, A.; Provenzano, G.; Douh, B.; Khila, S.; Rallo, G.; Boujelben, A. Assessing hydrus-2D to simulate soil water content (SWC) and salt accumulation under an SDI system: Application to a potato crop in a semi-arid area of central tunisia. Irrig. Drain. 2015, 64, 263–274. [Google Scholar] [CrossRef]
- Priya, R.Y.; Manjula, R. A review for comparing SWAT and SWAT coupled models and its applications. In Proceedings of the International Conference on Mechanical, Electronics and Computer Engineering (ICMECE)—Materials Science, Kancheepuram, India, 22 April 2020; Elsevier: Kancheepuram, India, 2021; pp. 7190–7194. [Google Scholar]
- Lagos, M.S.; Muñoz, J.F.; Suárez, F.I.; Fuenzalida, M.J.; Yáñez-Morroni, G.; Sanzana, P. Investigating the effects of channelization in the Silala River: A review of the implementation of a coupled MIKE-11 and MIKE-SHE modeling system. Wiley Interdiscip. Rev. Water 2024, 11, 17. [Google Scholar] [CrossRef]
- Yadav, B.; Krishnan, P.; Shafeeq, P.M.; Parihar, C.M.; Aggarwal, P. Modelling soil thermal regime in wheat using HYDRUS-2D under diversified maize-wheat-mungbean cropping system. Catena 2020, 194, 13. [Google Scholar] [CrossRef]
- Kan, X.Q.; Cheng, J.H.; Hu, X.J.; Zhu, F.F.; Li, M. Effects of Grass and Forests and the Infiltration Amount on Preferential Flow in Karst Regions of China. Water 2019, 11, 19. [Google Scholar] [CrossRef]
- Gerke, H.H.; Van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 2010, 29, 305–319. [Google Scholar] [CrossRef]
- Xu, X.X.; Kalhoro, S.A.; Chen, W.Y.; Raza, S. The evaluation/application of Hydrus-2D model for simulating macro-pores flow in loess soil. Int. Soil Water Conserv. Res. 2017, 5, 196–201. [Google Scholar] [CrossRef]
- Wei, H.; Yang, Y.F.; Wang, J.Y.; Meng, Q.M.; Deng, Y.S. A comparison of preferential flow characteristics and influencing factors between two soils developed in the karst region of Southwest China. Soil Tillage Res. 2024, 241, 17. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Erratum: Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 1026. [Google Scholar]
- Naglic, B.; Kechavarzi, C.; Coulon, F.; Pintar, M. Numerical investigation of the influence of texture, surface drip emitter discharge rate and initial soil moisture condition on wetting pattern size. Irrig. Sci. 2014, 32, 421–436. [Google Scholar]
- Fan, Y.W.; Yin, W.F.; Yang, Z.W.; Wang, Y.X.; Ma, L.J. Moisture content distribution model for the soil wetting body under moistube irrigation. Water SA 2023, 49, 73–91. [Google Scholar]
- Jiang, X.J.; Chen, C.F.; Zhu, X.A.; Zakari, S.; Singh, A.K.; Zhang, W.J.; Zeng, H.H.; Yuan, Z.Q.; He, C.G.; Yu, S.Q.; et al. Use of dye infiltration experiments and HYDRUS-3D to interpret preferential flow in soil in a rubber-based agroforestry systems in Xishuangbanna, China. Catena 2019, 178, 120–131. [Google Scholar]
- Zhao, Y.; De Maio, M.; Vidotto, F.; Sacco, D. Influence of wet-dry cycles on the temporal infiltration dynamic in temperate rice paddies. Soil Tillage Res. 2015, 154, 14–21. [Google Scholar] [CrossRef]
- Jordan, C.S.; Daniels, J.L.; Langley, W. The effects of temperature and wet-dry cycling on water-repellent soils. Environ. Geotech. 2017, 4, 299–307. [Google Scholar] [CrossRef]
- Hajjat, J.; Sánchez, M. Instrumented Plate to Study Soil Cracking Dynamics during Wetting-Drying Cycles. J. Geotech. Geoenviron. Eng. 2021, 147, 13. [Google Scholar]
- Luo, Y.; Zhang, J.M.; Zhou, Z.; Aguilar-Lopez, J.P.; Greco, R.; Bogaard, T. Effects of dynamic changes of desiccation cracks on preferential flow:experimental investigation and numerical modeling. Hydrol. Earth Syst. Sci. 2023, 27, 783–808. [Google Scholar]
- Pan, W.S.; Zhao, T.Y.; Li, X. Priority connectivity model of loess microstructure and its significance for preferential flow. Rock Soil Mech. 2024, 45, 1709–1719. [Google Scholar]
- Uhlemann, S.; Peruzzo, L.; Chou, C.; Williams, K.H.; Wielandt, S.; Wang, C.; Falco, N.; Wu, Y.; Carr, B.; Meldrum, P.; et al. Variations in Bedrock and Vegetation Cover Modulate Subsurface Water Flow Dynamics of a Mountainous Hillslope. Water Resour. Res. 2024, 60, 19. [Google Scholar] [CrossRef]
- Kodesová, R.; Nemecek, K.; Zigová, A.; Nikodem, A.; Fér, M. Using dye tracer for visualizing roots impact on soil structure and soil porous system. Biologia 2015, 70, 1439–1443. [Google Scholar]
- Cai, L.; Wang, F.; Lin, Y.Y.; Long, Q.; Zhao, Y.L.; Han, J.Q.; Ge, W.Y.; Chen, H. Changes in preferential flow caused by root effects in black locust plantations of different stand ages in the semi-arid region of the Loess Plateau. J. Hydrol. 2024, 634, 13. [Google Scholar] [CrossRef]
- Kan, X.Q.; Cheng, J.H.; Zheng, W.G.; Zhangzhong, L.L.; Li, J.; Liu, C.B.; Zhang, X. Interpretation of Soil Characteristics and Preferential Water Flow in Different Forest Covers of Karst Areas of China. Water 2024, 16, 20. [Google Scholar] [CrossRef]
| Loess Samples | θs(%) | θr(%) | α | n | m | R |
|---|---|---|---|---|---|---|
| L1-1 | 49.18 | - | 6.14 | 2.14 | 0.53 | 0.971 |
| L1-2 | 54.01 | - | 5.86 | 2.11 | 0.38 | 0.974 |
| L1-3 | 51.63 | - | 6.01 | 2.50 | 0.55 | 0.988 |
| Loess Samples | a1 | n1 | m1 | a2 | n2 | m2 |
|---|---|---|---|---|---|---|
| L1-4 | 11.26 | 2.91 | 0.82 | 482.37 | 2.79 | 1.12 |
| L1-5 | 13.18 | 3.23 | 0.47 | 378.75 | 3.22 | 1.41 |
| L1-6 | 12.94 | 3.88 | 0.38 | 681.40 | 3.44 | 1.53 |
| Scenario Setting | Treatment | Variable |
|---|---|---|
| Scenario A: different initial soil water content q0 (cm3/cm3) rainfall intensity P = 1 cm/h cracks width L = 1 cm | A1 | q0 = 0.1 cm3/cm3 |
| A2 | q0 = 0.15 cm3/cm3 | |
| A3 | q0 = 0.2 cm3/cm3 | |
| A4 | q0 = 0.3 cm3/cm3 | |
| Scenario B: different rainfall intensity P (cm/h) initial soil water content q0 = 0.15 cm3/cm3 cracks width L = 1 cm | B1 | P = 0.5 cm/h |
| B2 | P = 1 cm/h | |
| B3 | P = 1.5 cm/h | |
| B4 | P = 2 cm/h | |
| Scenario C: different cracks width L (cm) initial soil water content q0 = 0.15 cm3/cm3 rainfall intensity P = 1 cm/h | C1 | L = 0.5 cm |
| C2 | L = 1 cm | |
| C3 | L = 1.5 cm | |
| C4 | L = 2 cm | |
| Scenario A: different initial soil water content q0 (cm3/cm3) rainfall intensity P = 1 cm/h cracks width L = 1 cm | A1 | q0 = 0.1 cm3/cm3 |
| A2 | q0 = 0.15 cm3/cm3 | |
| A3 | q0 = 0.2 cm3/cm3 | |
| A4 | q0 = 0.3 cm3/cm3 |
| Scenario and q0 (cm3/cm3) | Time (h) | Maximum Soil Water Content in Substrate Area | Wetting Front Depth (cm) | ||
|---|---|---|---|---|---|
| Depth (cm) | Moisture Content (cm3/cm3) | Wetting Front Depth (cm) | Macropore Infiltration Depth (cm) | ||
| Scenario A1 q = 0.1 | 1 | 0 | 0.406 | 3 | 7 |
| 2 | 0 | 0.425 | 6 | 11 | |
| 6 | 0 | 0.436 | 16 | 27 | |
| 12 | 0 | 0.436 | 34 | 53 | |
| 24 | 32 | 0.366 | 40 | 64 | |
| 48 | 34 | 0.333 | 51 | 67 | |
| Scenario A2 q = 0.15 | 1 | 0 | 0.414 | 5 | 8 |
| 2 | 0 | 0.429 | 8 | 14 | |
| 6 | 0 | 0.436 | 22 | 32 | |
| 12 | 0 | 0.436 | 40 | 63 | |
| 24 | 42 | 0.373 | 53 | 75 | |
| 48 | 44 | 0.343 | 65 | >80 | |
| Scenario A3 q = 0.2 | 1 | 0 | 0.421 | 6 | 12 |
| 2 | 0 | 0.432 | 11 | 17 | |
| 6 | 0 | 0.436 | 27 | 39 | |
| 12 | 60 | 0.437 | 48 | 72 | |
| 24 | 62 | 0.388 | 58 | >80 | |
| 48 | 78 | 0.361 | >80 | >80 | |
| Scenario A4 q = 0.3 | 1 | 0 | 0.432 | 8 | 15 |
| 2 | 0 | 0.436 | 15 | 25 | |
| 6 | 60 | 0.437 | 42 | 69 | |
| 12 | 60 | 0.437 | >80 | >80 | |
| 24 | 63 | 0.405 | >80 | >80 | |
| 48 | 80 | 0.366 | >80 | >80 | |
| Scenario and q0 (cm3/cm3) | Time (h) | Maximum Soil Water Content in Substrate Area | Wetting Front Depth (cm) | ||
|---|---|---|---|---|---|
| Depth (cm) | Moisture Content (cm3/cm3) | Wetting Front Depth (cm) | Macropore Infiltration Depth (cm) | ||
| Scenario A1 q = 0.1 | 1 | 0 | 0.372 | 3 | 7 |
| 2 | 0 | 0.394 | 5 | 9 | |
| 6 | 0 | 0.419 | 13 | 18 | |
| 12 | 0 | 0.425 | 22 | 32 | |
| 24 | 19 | 0.349 | 26 | 58 | |
| 48 | 20 | 0.314 | 36 | 53 | |
| Scenario A2 q = 0.15 | 1 | 0 | 0.414 | 5 | 8 |
| 2 | 0 | 0.429 | 8 | 14 | |
| 6 | 0 | 0.436 | 22 | 32 | |
| 12 | 0 | 0.436 | 40 | 63 | |
| 24 | 42 | 0.373 | 53 | 75 | |
| 48 | 44 | 0.343 | 65 | >80 | |
| Scenario A3 q = 0.2 | 1 | 0 | 0.432 | 4 | 11 |
| 2 | 0 | 0.437 | 10 | 19 | |
| 6 | 0 | 0.437 | 29 | 61 | |
| 12 | 60 | 0.437 | 49 | 79 | |
| 24 | 62 | 0.399 | 68 | >80 | |
| 48 | 78 | 0.365 | >80 | >80 | |
| Scenario A4 q = 0.3 | 1 | 0 | 0.437 | 6 | 13 |
| 2 | 0 | 0.437 | 12 | 22 | |
| 6 | 25 | 0.437 | 30 | 61 | |
| 12 | 60 | 0.437 | 54 | >80 | |
| 24 | 63 | 0.403 | >80 | >80 | |
| 48 | 80 | 0.366 | >80 | >80 | |
| Scenario and q0 (cm3/cm3) | Time (h) | Maximum Soil Water Content in Substrate Area | Wetting Front Depth (cm) | ||
|---|---|---|---|---|---|
| Depth (cm) | Moisture Content (cm3/cm3) | Wetting Front Depth (cm) | Macropore Infiltration Depth (cm) | ||
| Scenario A1 q = 0.1 | 1 | 0 | 0.413 | 5 | 8 |
| 2 | 0 | 0.429 | 8 | 14 | |
| 6 | 0 | 0.436 | 21 | 32 | |
| 12 | 0 | 0.436 | 39 | 63 | |
| 24 | 42 | 0.372 | 50 | 75 | |
| 48 | 44 | 0.342 | 58 | >80 | |
| Scenario A2 q = 0.15 | 1 | 0 | 0.414 | 5 | 8 |
| 2 | 0 | 0.429 | 8 | 14 | |
| 6 | 0 | 0.436 | 22 | 32 | |
| 12 | 0 | 0.436 | 40 | 63 | |
| 24 | 42 | 0.373 | 53 | 75 | |
| 48 | 44 | 0.343 | 65 | >80 | |
| Scenario A3 q = 0.2 | 1 | 0 | 0.414 | 4 | 9 |
| 2 | 0 | 0.429 | 7 | 14 | |
| 6 | 0 | 0.436 | 20 | 32 | |
| 12 | 0 | 0.436 | 38 | 64 | |
| 24 | 42 | 0.373 | 50 | 75 | |
| 48 | 44 | 0.344 | 59 | >80 | |
| Scenario A4 q = 0.3 | 1 | 0 | 0.414 | 5 | 9 |
| 2 | 0 | 0.429 | 6 | 14 | |
| 6 | 0 | 0.436 | 20 | 34 | |
| 12 | 0 | 0.436 | 38 | 65 | |
| 24 | 42 | 0.373 | 50 | 77 | |
| 48 | 44 | 0.344 | 65 | >80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Lu, T.; Zhou, K.; Gu, Y.; Wang, B.; Lu, Y. Modeling and Application of the Hydrus-2D Model for Simulating Preferential Flow in Loess Soil Under Various Scenarios. Water 2024, 16, 3653. https://doi.org/10.3390/w16243653
Li S, Lu T, Zhou K, Gu Y, Wang B, Lu Y. Modeling and Application of the Hydrus-2D Model for Simulating Preferential Flow in Loess Soil Under Various Scenarios. Water. 2024; 16(24):3653. https://doi.org/10.3390/w16243653
Chicago/Turabian StyleLi, Shengnan, Ting Lu, Kexin Zhou, Yidong Gu, Bihui Wang, and Yudong Lu. 2024. "Modeling and Application of the Hydrus-2D Model for Simulating Preferential Flow in Loess Soil Under Various Scenarios" Water 16, no. 24: 3653. https://doi.org/10.3390/w16243653
APA StyleLi, S., Lu, T., Zhou, K., Gu, Y., Wang, B., & Lu, Y. (2024). Modeling and Application of the Hydrus-2D Model for Simulating Preferential Flow in Loess Soil Under Various Scenarios. Water, 16(24), 3653. https://doi.org/10.3390/w16243653







