Case Study of Contaminant Transport Using Lagrangian Particle Tracking Model in a Macro-Tidal Estuary
Abstract
:1. Introduction
2. Materials and Methods
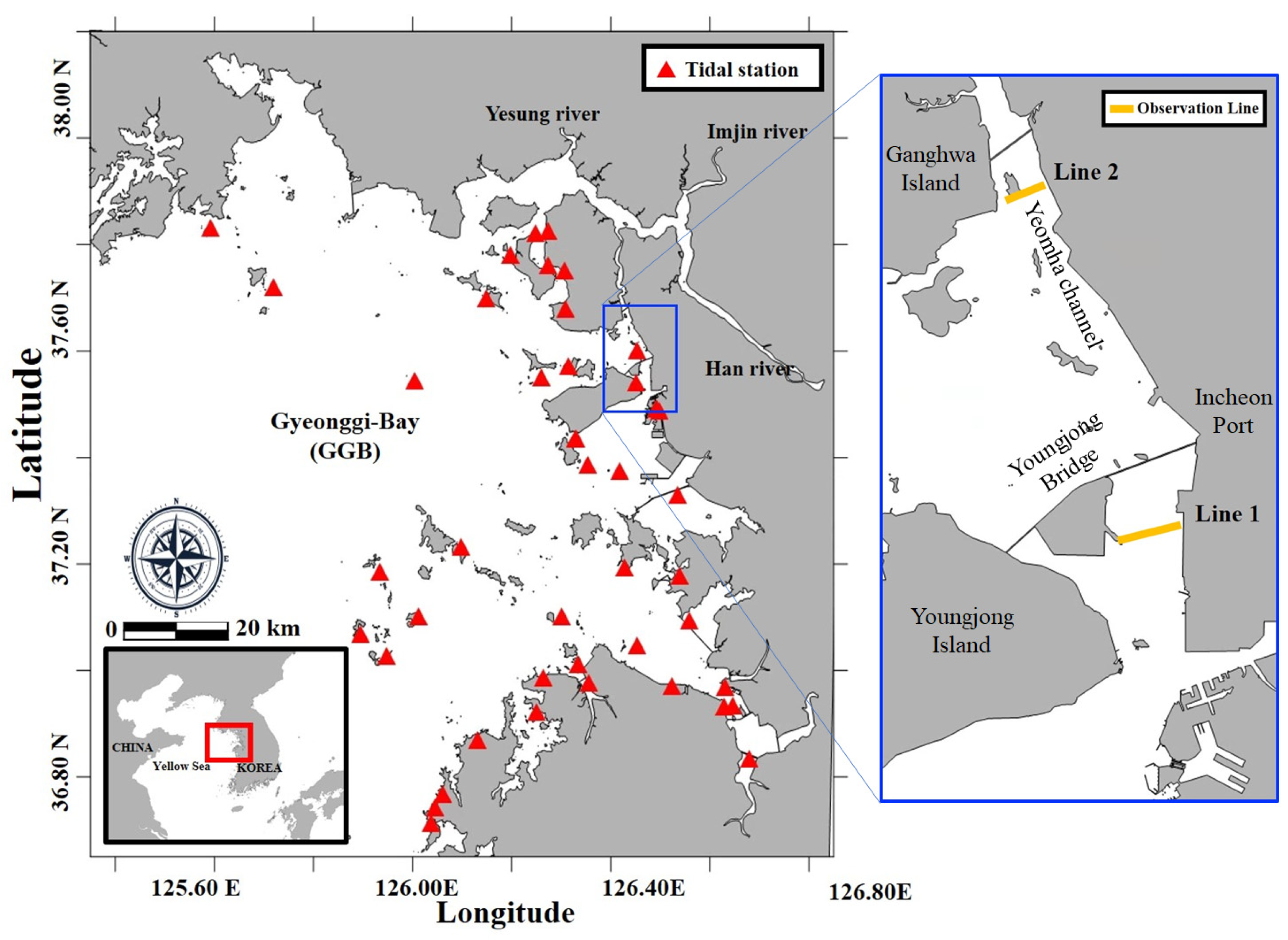
2.1. Study Area
2.2. Numerical Model
2.3. Field Measurements
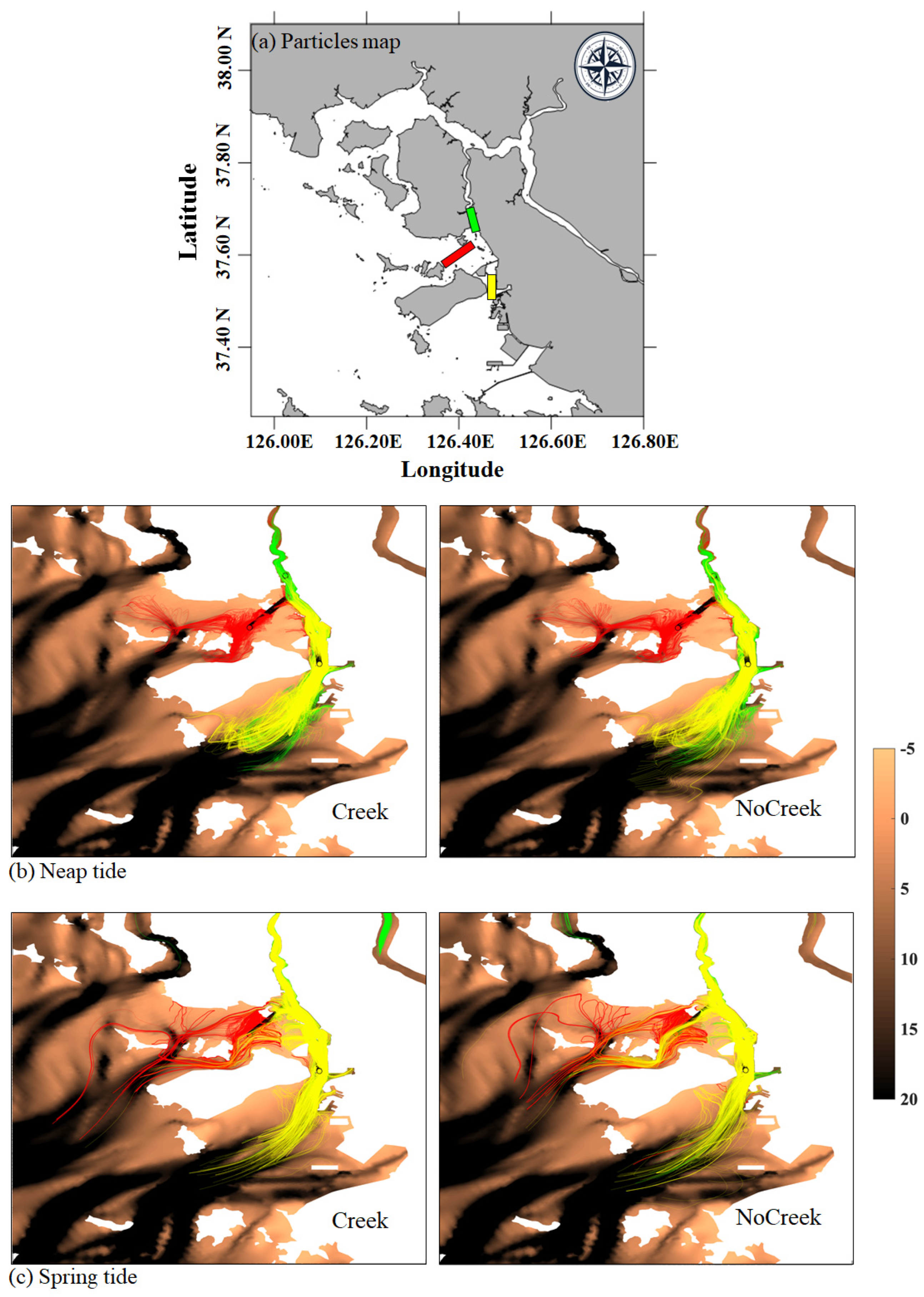
2.4. Experiment Design
3. Results
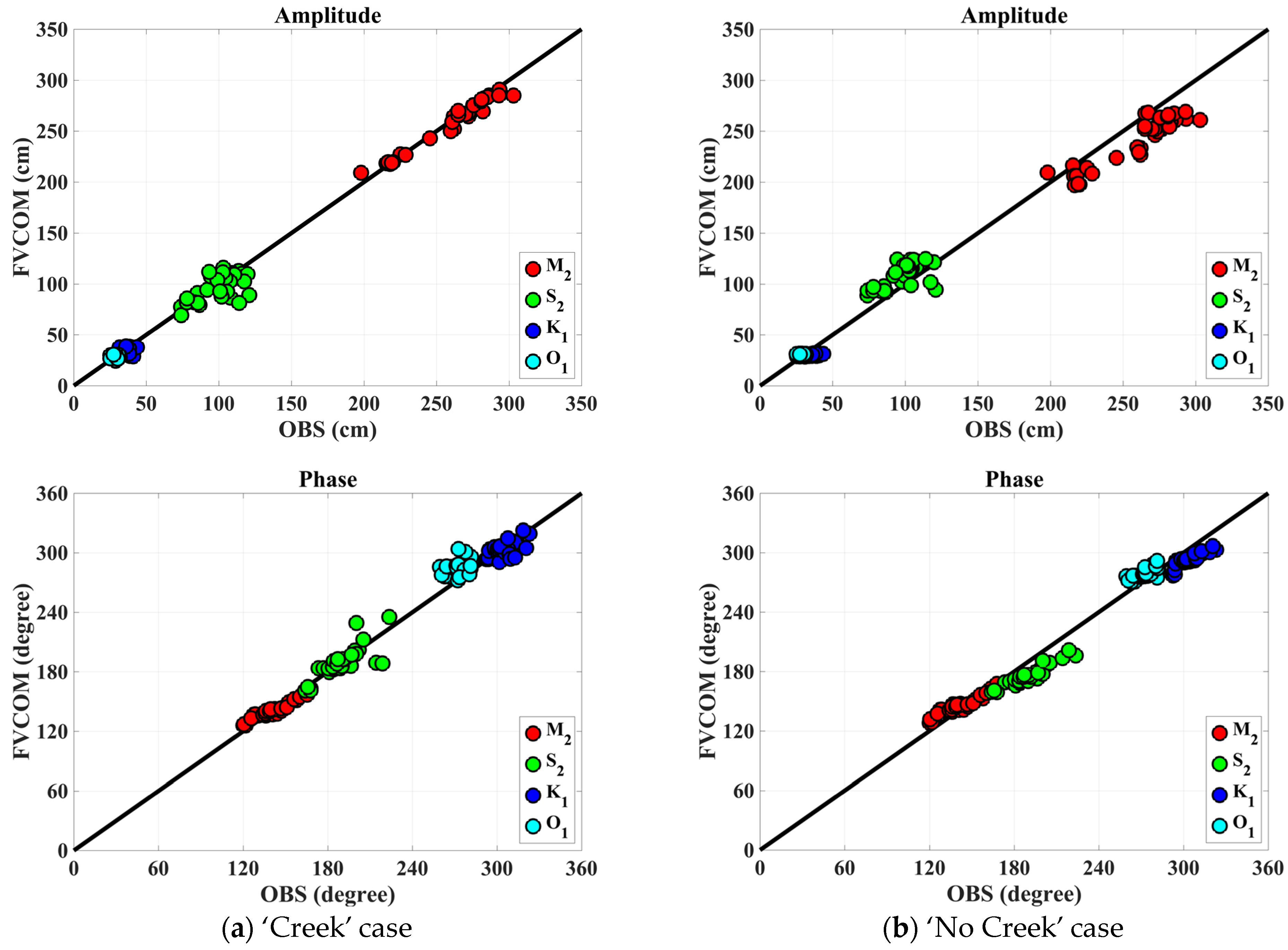
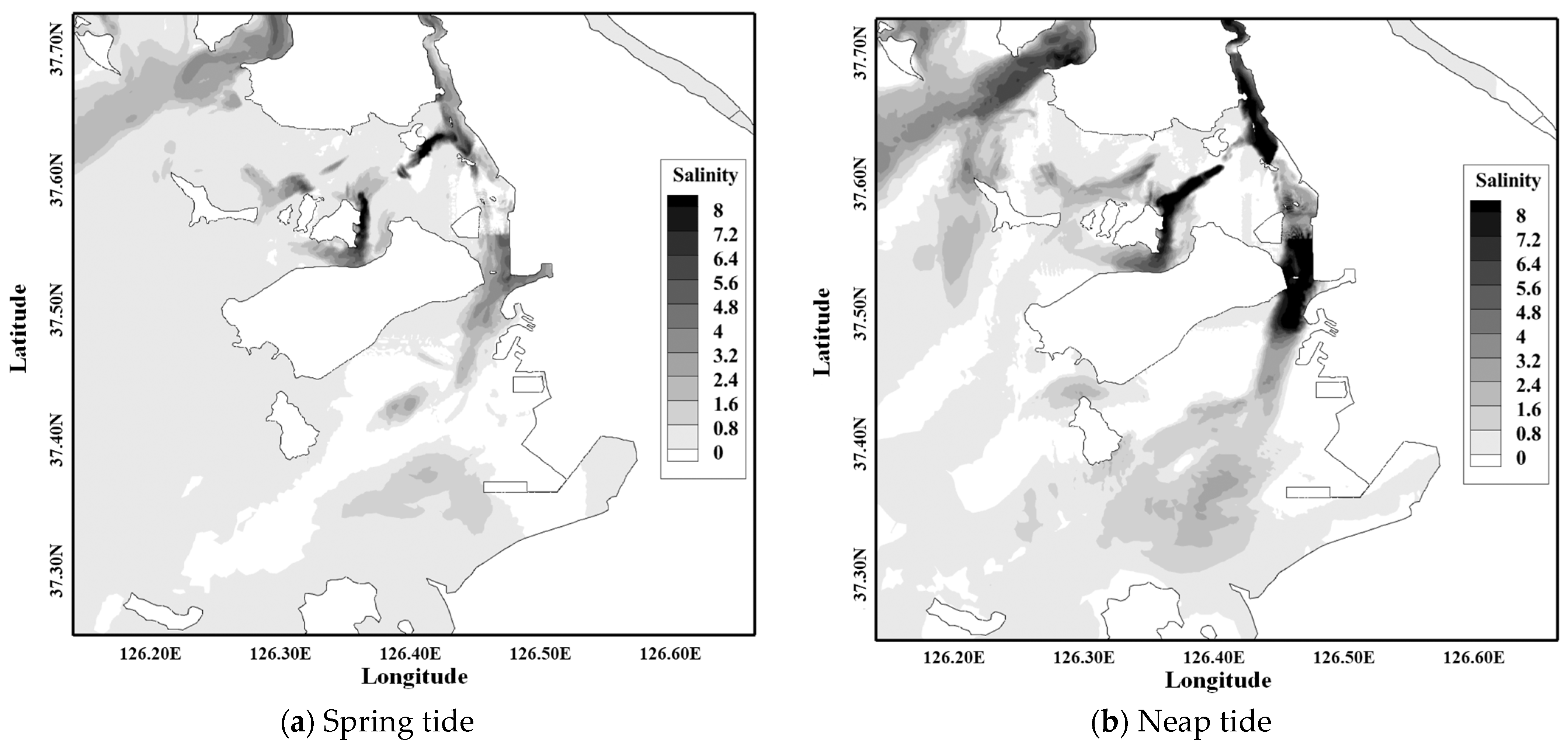
3.1. Model Validation
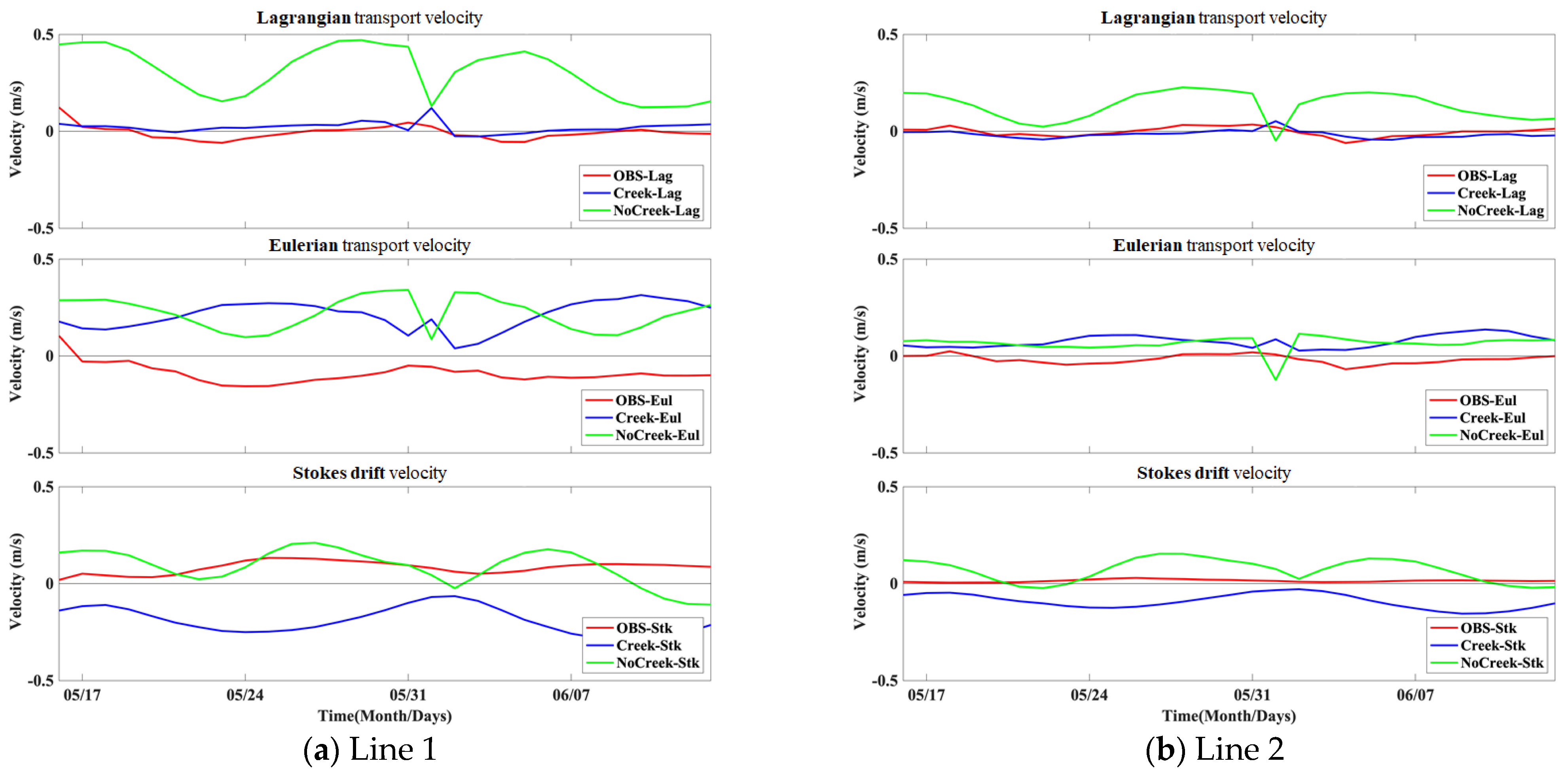
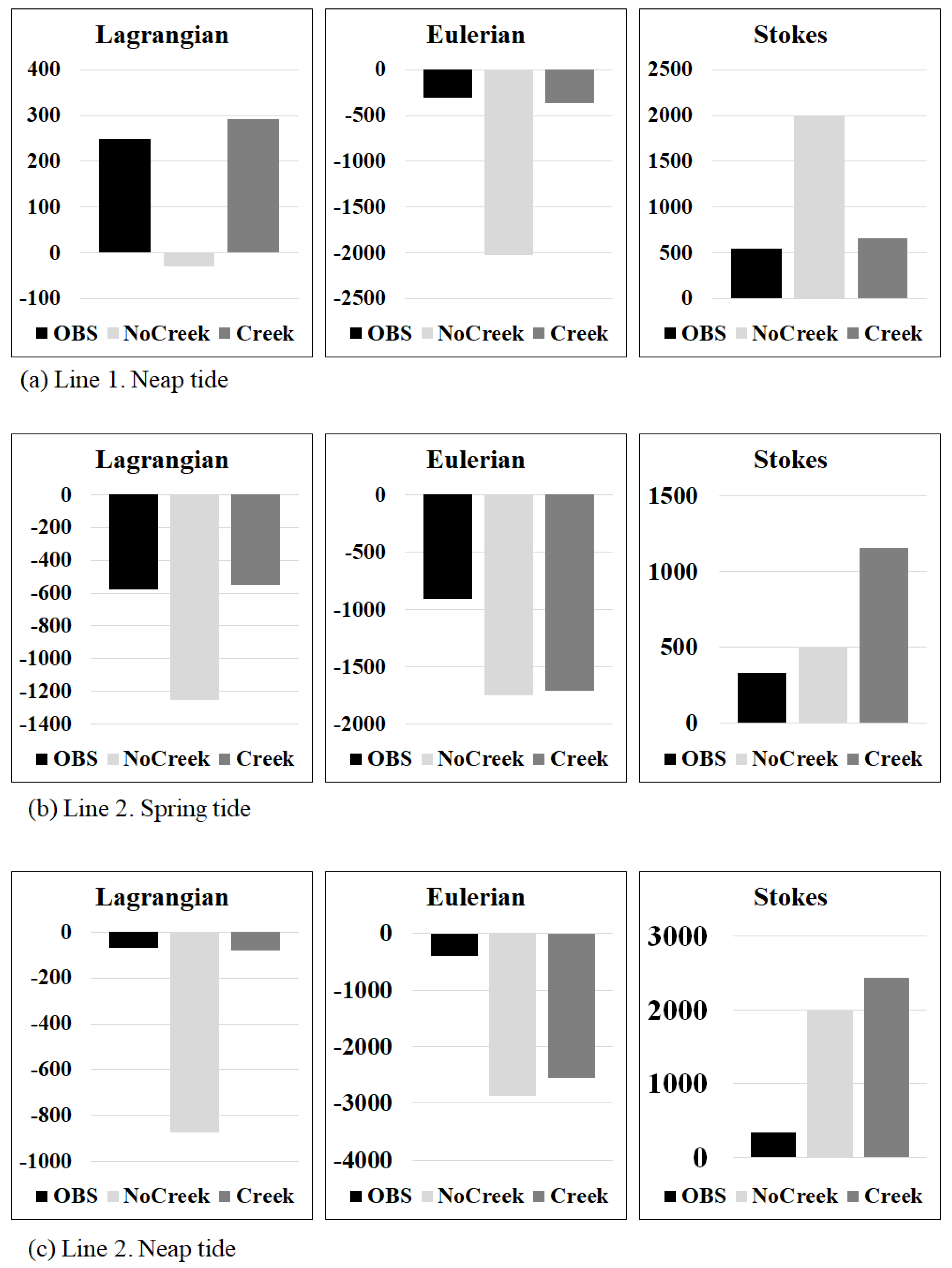
3.2. Residual Volume Transport
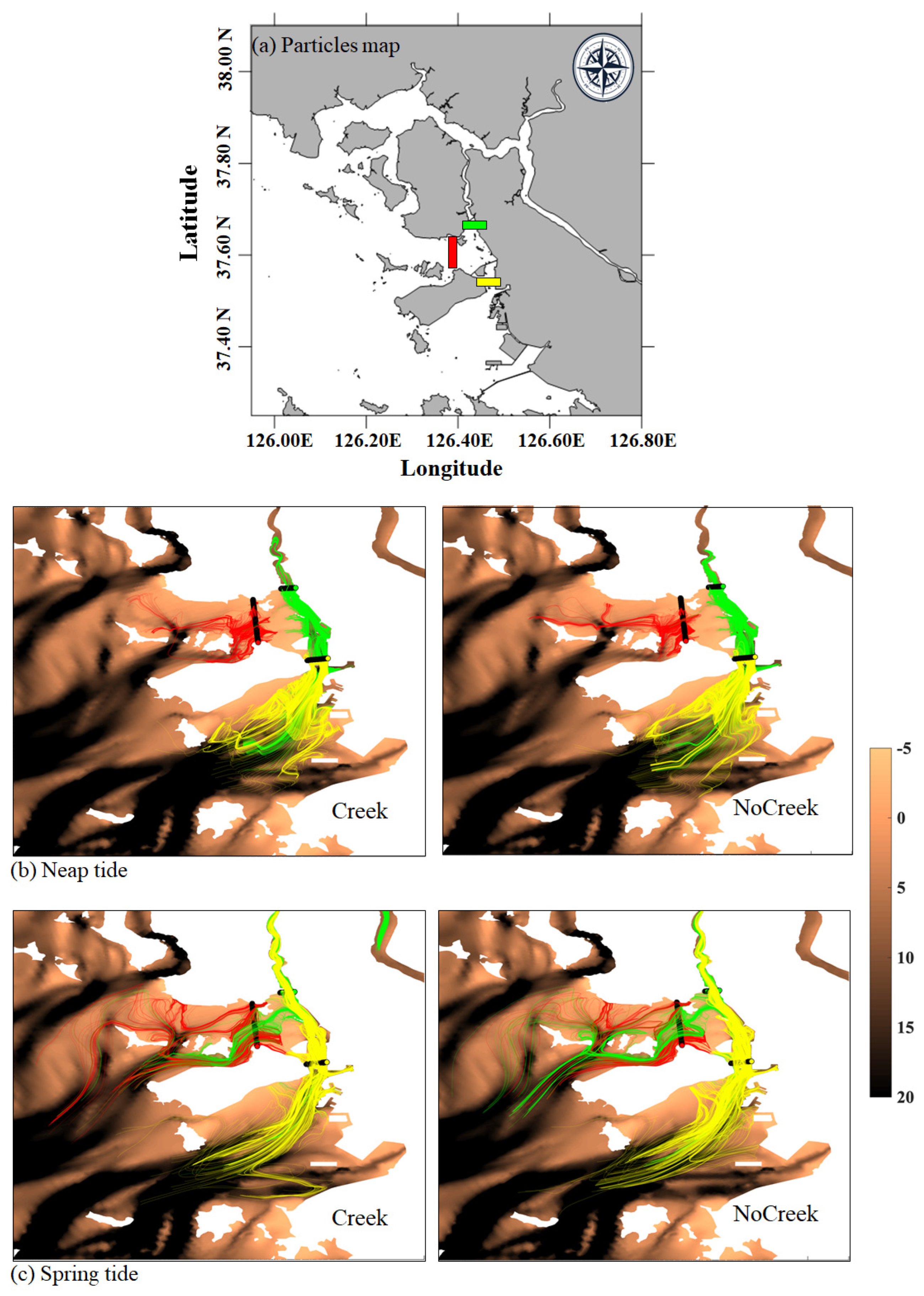
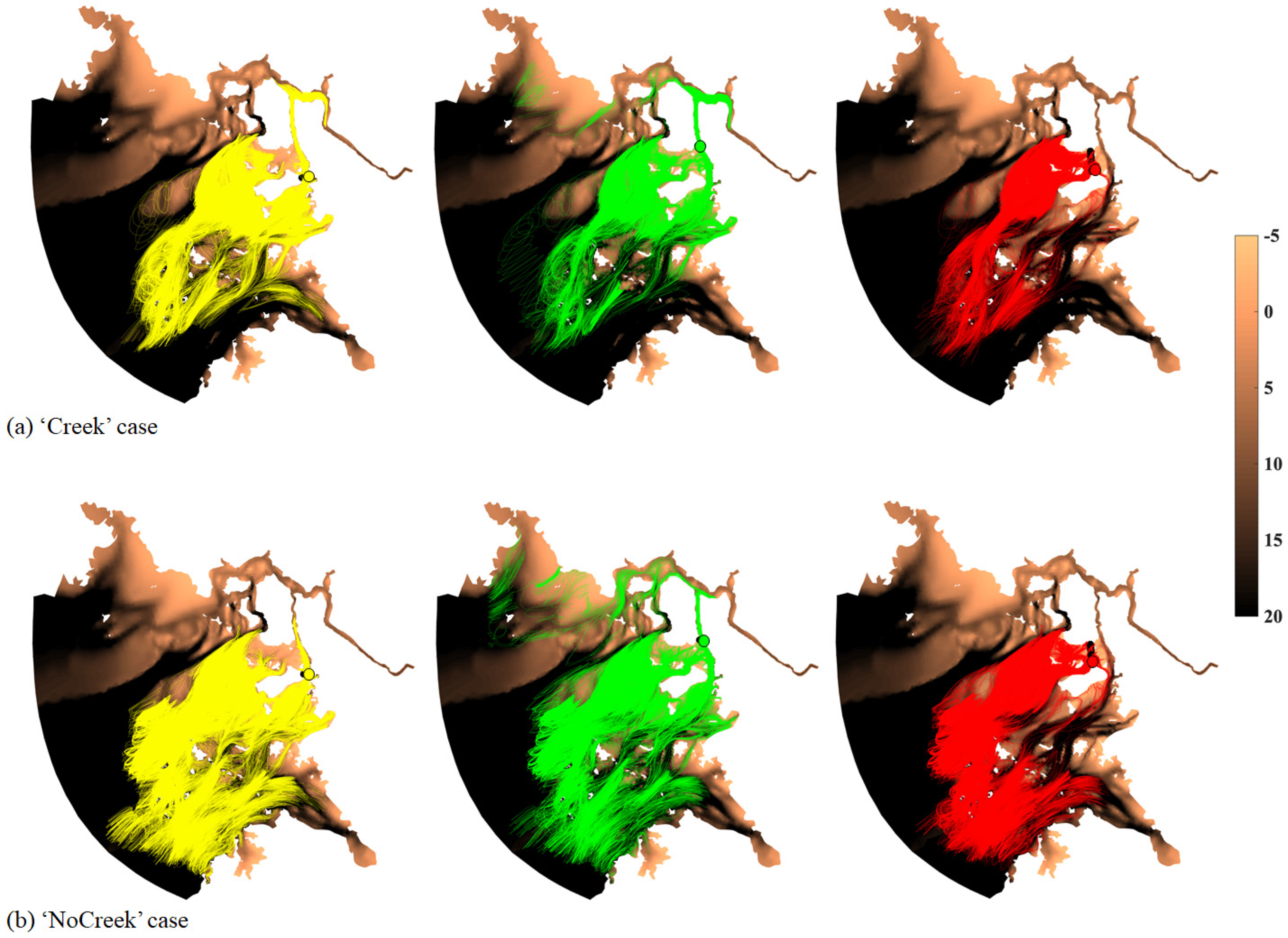
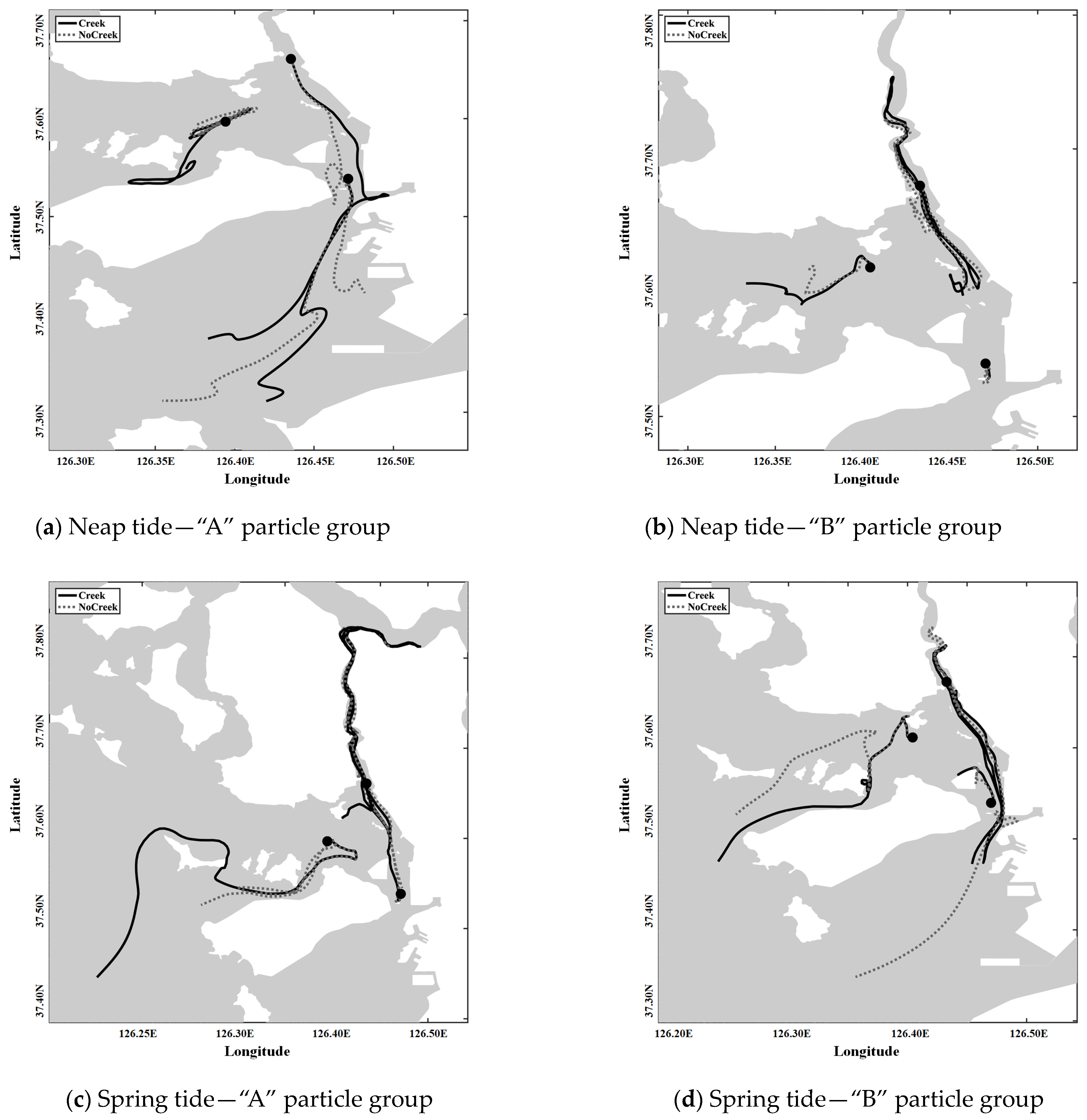
3.3. Lagrangian Particle Trajectory
4. Discussion
5. Conclusions
- This research highlights the importance of including the geometrical complexities of tidal creeks in contaminant transport models. The ‘Creek’ case demonstrated how these features substantially influence flow patterns, leading to enhanced retention of contaminants within the estuarine system. This enhanced retention can significantly affect the bioavailability and degradation rates of contaminants due to changes in exposure durations.
- The distinct dispersion behaviors in the ‘No Creek’ case suggest a risk related to the underestimation of contaminant retention within the estuary and the overestimation of their dispersion to coastal waters when such structural complexities are not considered. This insight is vital for precise contaminant budget assessments and the development of effective mitigation strategies in estuarine environments.
- The variation in the stratification during neap tides leads to the role of vertical mixing in contaminant distribution; this is an aspect which is crucial for the understanding of the vertical contaminant concentration profiles and their potential impacts across different trophic levels within the estuarine food web.
Appendix A
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aubrey, D.G.; Speer, P.E. A Study of Non-Linear Tidal Propagation in Shallow Inlet Estuarine Systems Part I: Observations. Estuar. Coast. Shelf Sci. 1985, 21, 185–205. [Google Scholar] [CrossRef]
- Speer, P.E.; Aubrey, D.G. A Study of Non-Linear Tidal Propagation in Shallow Inlet Estuarine Systems Part II: Theory. Estuar. Coast. Shelf Sci. 1985, 21, 207–224. [Google Scholar] [CrossRef]
- Murty, T.S. Nonlinear Tidal Distortion in Shallow Well-Mixed Estuaries. Estuar. Coast. Shelf Sci. 1990, 30, 321–322. [Google Scholar] [CrossRef]
- Lanzoni, S.; Seminara, G. On tide propagation in convergent estuaries. J. Geophys. Res.-Ocean. 1998, 103, 30793–30812. [Google Scholar] [CrossRef]
- Blanton, J.O.; Lin, G.Q.; Elston, S.A. Tidal current asymmetry in shallow estuaries and tidal creeks. Cont. Shelf Res. 2002, 22, 1731–1743. [Google Scholar] [CrossRef]
- Kim, C.S.; Lim, H.S.; Kim, J.; Kim, S.; Park, K.S.; Jung, K.T. Estimation of Tidal Residual Flow and Its Variability in Kyunggi Bay of Korea. J. Korean Soc. Mar. Environ. Energy 2010, 22, 353–360. [Google Scholar]
- Yoon, B.I.; Woo, S.-B. Study on Relationship Between Geographical Convergence and Bottom Friction at the Major Waterways in Han River Estuary using the Tidal Wave Propagation Characteristics. J. Korean Soc. Coast. Ocean Eng. 2011, 23, 383–392. [Google Scholar] [CrossRef]
- Park, K.; Oh, J.H.; Kim, H.S.; Im, H.H. Case study: Mass transport mechanism in Kyunggi Bay around Han River Mouth, Korea. J. Hydraul. Eng.-ASCE 2002, 128, 257–267. [Google Scholar] [CrossRef]
- Kang, J.W.; Park, S.J.; Kim, Y.S.; So, J.K. Tidal Flat Simulation Characteristics of the Hydrodynamic Models. J. Korean Soc. Coast. Ocean. Eng. 2009, 21, 357–370. [Google Scholar]
- Chen, C.S.; Liu, H.D.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Lee, D.H.; Yoon, B.I.; Woo, S.-B. The Cross-Sectional Characteristic and Spring-Neap Variation of Residual Current and Net Volume Transport at the Yeomha Channel. J. Korean Soc. Coast. Ocean. Eng. 2017, 29, 217–227. [Google Scholar] [CrossRef]
- Foreman, M.G.G.; Henry, R.F. The Harmonic-Analysis of Tidal Model Time-Series. Adv. Water Resour. 1989, 12, 109–120. [Google Scholar] [CrossRef]
- Sylaios, G.; Boxall, S.R. Residual currents and flux estimates in a partially-mixed estuary. Estuar. Coast. Shelf Sci. 1998, 46, 671–682. [Google Scholar] [CrossRef]
- Hwang, J.H.; Van, S.P.; Choi, B.-J.; Chang, Y.S.; Kim, Y.H. The physical processes in the Yellow Sea. Ocean. Coast. Manag. 2014, 102, 449–457. [Google Scholar] [CrossRef]
- Hwang, J.H.; Jang, D.; Kim, Y.H. Stratification and salt-wedge in the Seomjin river estuary under the idealized tidal influence. Ocean. Sci. J. 2017, 52, 469–487. [Google Scholar] [CrossRef]
- Xue, P.; Chen, C.; Ding, P.; Beardsley, R.C.; Lin, H.; Ge, J.; Kong, Y. Saltwater intrusion into the Changjiang River: A model-guided mechanism study. J. Geophys. Res. Ocean. 2009, 114, C02006. [Google Scholar] [CrossRef]
- Hache, I.; Niehüser, S.; Karius, V.; Arns, A.; von Eynatten, H. Assessing sediment accumulation at inundated anthropogenic marshland in the southeastern North Sea: Using particle tracking on modified coastal protection structures. Ocean Coast. Manag. 2021, 208, 105631. [Google Scholar] [CrossRef]
- Zhao, E.-J.; Mu, L.; Qu, K.; Shi, B.; Ren, X.-Y.; Jiang, C.-B. Numerical investigation of pollution transport and environmental improvement measures in a tidal bay based on a Lagrangian particle-tracking model. Water Sci. Eng. 2018, 11, 23–38. [Google Scholar] [CrossRef]
- Zhou, X.; Rowe, M.; Liu, Q.; Xue, P. Comparison of Eulerian and Lagrangian transport models for harmful algal bloom forecasts in Lake Erie. Environ. Model. Softw. 2023, 162, 105641. [Google Scholar] [CrossRef]
- Kuznetsov, I.; Androsov, A.; Fofonova, V.; Danilov, S.; Rakowsky, N.; Harig, S.; Wiltshire, K.H. Evaluation and Application of Newly Designed Finite Volume Coastal Model FESOM-C, Effect of Variable Resolution in the Southeastern North Sea. Water 2020, 12, 1412. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Zhou, Z.; Hu, Z. Transport of Contamination under the Influence of Sea Level Rise in Coastal Heterogeneous Aquifer. Sustainability 2020, 12, 9838. [Google Scholar] [CrossRef]
- Zhang, Q.; Volker, R.E.; Lockington, D.A. Experimental investigation of contaminant transport in coastal groundwater. Adv. Environ. Res. 2002, 6, 229–237. [Google Scholar] [CrossRef]
- Jones, J.E.; Davies, A.M. An intercomparison between finite difference and finite element (TELEMAC) approaches to modelling west coast of Britain tides. Ocean Dyn. 2005, 55, 178–198. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Tanaka, S.; Westerink, J.J.; Dawson, C.N.; Luettich, R.A.; Zijlema, M.; Holthuijsen, L.H.; Smith, J.M.; Westerink, L.G.; Westerink, H.J. Performance of the Unstructured-Mesh, SWAN+ADCIRC Model in Computing Hurricane Waves and Surge. J. Sci. Comput. 2011, 52, 468–497. [Google Scholar] [CrossRef]
- Xue, P.; Schwab, D.; Zhou, X.; Huang, C.; Kibler, R.; Ye, X. A Hybrid Lagrangian–Eulerian Particle Model for Ecosystem Simulation. J. Mar. Sci. Eng. 2018, 6, 109. [Google Scholar] [CrossRef]
- Pilechi, A.; Mohammadian, A.; Murphy, E. A numerical framework for modeling fate and transport of microplastics in inland and coastal waters. Mar. Pollut. Bull. 2022, 184, 114119. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Hwang, J.H.; Jeong, J.; Hong, Y.; Lee, M. Comprehensive modeling from watersheds to a bay and its validation with radar, drifters, and MVP methods. Reg. Stud. Mar. Sci. 2023, 68, 103262. [Google Scholar] [CrossRef]
- Oke, P.R.; Brassington, G.B.; Griffin, D.A.; Schiller, A. The Bluelink ocean data assimilation system (BODAS). Ocean Model. 2008, 21, 46–70. [Google Scholar] [CrossRef]
- Kim, N.-H.; Baek, D.; Kwon, J.-I.; Choi, J.-Y.; Heo, K.-Y. Strategy for additional buoy array installation in operational buoy-observation network in Korea. Ocean Eng. 2022, 266, 112746. [Google Scholar] [CrossRef]
- Oliveira, A.; Fortunato, A.B.; Rogeiro, J.; Teixeira, J.; Azevedo, A.; Lavaud, L.; Bertin, X.; Gomes, J.; David, M.; Pina, J.; et al. OPENCoastS: An open-access service for the automatic generation of coastal forecast systems. Environ. Model. Softw. 2020, 124, 104585. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, B.-H.; Woo, S.-B.; Kwon, J.-I.; Park, S.-H.; Kim, N.-H. Case Study of Contaminant Transport Using Lagrangian Particle Tracking Model in a Macro-Tidal Estuary. Water 2024, 16, 617. https://doi.org/10.3390/w16040617
Gu B-H, Woo S-B, Kwon J-I, Park S-H, Kim N-H. Case Study of Contaminant Transport Using Lagrangian Particle Tracking Model in a Macro-Tidal Estuary. Water. 2024; 16(4):617. https://doi.org/10.3390/w16040617
Chicago/Turabian StyleGu, Bon-Ho, Seung-Buhm Woo, Jae-Il Kwon, Sung-Hwan Park, and Nam-Hoon Kim. 2024. "Case Study of Contaminant Transport Using Lagrangian Particle Tracking Model in a Macro-Tidal Estuary" Water 16, no. 4: 617. https://doi.org/10.3390/w16040617
APA StyleGu, B.-H., Woo, S.-B., Kwon, J.-I., Park, S.-H., & Kim, N.-H. (2024). Case Study of Contaminant Transport Using Lagrangian Particle Tracking Model in a Macro-Tidal Estuary. Water, 16(4), 617. https://doi.org/10.3390/w16040617






