Numerical Simulation of Geophysical Models to Detect Mining Tailings’ Leachates within Tailing Storage Facilities
Abstract
1. Introduction
2. Literature Review
- (1)
- Research focus: choosing the published literature that is closely aligned with the research focus and objectives of this study;
- (2)
- Relevance: selecting articles that directly address similar or related research questions allows the authors to build upon existing knowledge and establish a coherent framework for their study;
- (3)
- Methodological compatibility: limiting the selected literature that uses the same electrode arrays and employs a similar or complementary methodologies
- (4)
- Limitations and scope: Because of limitations on space and the scope of the study, it is not feasible to include all the articles available on a particular topic. Thus, the authors had to make strategic choices to include representative studies that adequately cover the range of relevant perspectives and findings.
3. Methodology
3.1. ERT Technique and Data Collection
3.2. Synthetic ERT Model for MTL
3.3. Real Case of ERT Field Surveys for MTL
4. Results
4.1. Results of the Synthetic ERT Model for MTL
4.2. Results of the Real Case
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A

References
- Velásquez, J.R.; Schwartz, M.; Phipps, L.M.; Restrepo-Baena, O.J.; Lucena, J.; Smits, K.M. A review of the environmental and health implications of recycling mine tailings for construction purposes in artisanal and small-scale mining communities. Extr. Ind. Soc. 2022, 9, 101019. [Google Scholar] [CrossRef]
- Kinnunen, P.; Karhu, M.; Yli-Rantala, E.; Kivikytö-Reponen, P.; Mäkinen, J. A review of circular economy strategies for mine tailings. Clean. Eng. Technol. 2022, 8, 100499. [Google Scholar] [CrossRef]
- Adiansyah, J.S.; Rosano, M.; Vink, S.; Keir, G. A framework for a sustainable approach to mine tailings management: Disposal strategies. J. Clean. Prod. 2015, 108, 1050–1062. [Google Scholar] [CrossRef]
- Morrison, K.F. Tailings Management Handbook: A LifeCycle Approach; Society for Mining, Metallurgy & Exploration: Englewood, CO, USA, 2022. [Google Scholar]
- Mafra, C.; Bouzahzah, H.; Stamenov, L.; Gaydardzhiev, S. An integrated management strategy for acid mine drainage control of sulfidic tailings. Miner. Eng. 2022, 185, 107709. [Google Scholar] [CrossRef]
- Sarker, S.K.; Haque, N.; Bhuiyan, M.; Bruckard, W.; Pramanik, B.K. Recovery of strategically important critical minerals from mine tailings. J. Environ. Chem. Eng. 2022, 10, 107622. [Google Scholar] [CrossRef]
- Mewafy, F.M.; Werkema, D.D.; Atekwana, E.A.; Slater, L.D.; Abdel Aal, G.; Revil, A.; Ntarlagiannis, D. Evidence that bio-metallic mineral precipitation enhances the complex conductivity response at a hydrocarbon contaminated site. J. Appl. Geophys. 2013, 98, 113–123. [Google Scholar] [CrossRef]
- Mewafy, F.M.; Atekwana, E.A.; Werkema, D.D., Jr.; Slater, L.D.; Ntarlagiannis, D.; Revil, A.; Skold, M.; Delin, G.N. Magnetic susceptibility as a proxy for investigating microbially mediated iron reduction. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Maurya, P.K.; Rønde, V.K.; Fiandaca, G.; Balbarini, N.; Auken, E.; Bjerg, P.L.; Christiansen, A.V. Detailed landfill leachate plume mapping using 2D and 3D electrical resistivity tomography-with correlation to ionic strength measured in screens. J. Appl. Geophys. 2017, 138, 1–8. [Google Scholar] [CrossRef]
- Alam, M.I.; Katumwehe, A.; Atekwana, E. Geophysical characterization of a leachate plume from a former municipal solid waste disposal site: A case study on Norman landfill. Am. Assoc. Pet. Geol. Bull. 2022, 106, 1183–1195. [Google Scholar] [CrossRef]
- Zarif, F.; Isawi, H.; Elshenawy, A.; Eissa, M. Coupled geophysical and geochemical approach to detect the factors affecting the groundwater salinity in coastal aquifer at the area between Ras Sudr and Ras Matarma area, South Sinai, Egypt. Groundw. Sustain. Dev. 2021, 15, 100662. [Google Scholar] [CrossRef]
- Abdelfattah, M.; Abu-Bakr, H.A.-A.; Mewafy, F.M.; Hassan, T.M.; Geriesh, M.H.; Saber, M.; Gaber, A. Hydrogeophysical and hydrochemical assessment of the northeastern coastal aquifer of Egypt for desalination suitability. Water 2023, 15, 423. [Google Scholar] [CrossRef]
- Tavakoli, S.; Rasmussen, T.M. Geophysical tools to study the near-surface distribution of the tailings in the Smaltjärnen repository, south-central Sweden; a feasibility study. Acta Geophys. 2022, 70, 141–159. [Google Scholar] [CrossRef]
- Pierwoła, J.; Szuszkiewicz, M.; Cabala, J.; Jochymczyk, K.; Żogała, B.; Magiera, T. Integrated geophysical and geochemical methods applied for recognition of acid waste drainage (AWD) from Zn-Pb post-flotation tailing pile (Olkusz, southern Poland). Environ. Sci. Pollut. Res. 2020, 27, 16731–16744. [Google Scholar] [CrossRef] [PubMed]
- Binley, A.; Kemna, A. DC resistivity and induced polarization methods. In Hydrogeophysics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 129–156. [Google Scholar]
- Flores Orozco, A.; Ciampi, P.; Katona, T.; Censini, M.; Papini, M.P.; Deidda, G.P.; Cassiani, G. Delineation of hydrocarbon contaminants with multi-frequency complex conductivity imaging. Sci. Total Environ. 2021, 768, 144997. [Google Scholar] [CrossRef]
- Ciampi, P.; Esposito, C.; Cassiani, G.; Deidda, G.P.; Flores-Orozco, A.; Rizzetto, P.; Chiappa, A.; Bernabei, M.; Gardon, A.; Petrangeli Papini, M. Contamination presence and dynamics at a polluted site: Spatial analysis of integrated data and joint conceptual modeling approach. J. Contam. Hydrol. 2022, 248, 104026. [Google Scholar] [CrossRef] [PubMed]
- Gabarrón, M.; Martínez-Pagán, P.; Martínez-Segura, M.A.; Bueso, M.C.; Martínez-Martínez, S.; Faz, Á.; Acosta, J.A. Electrical resistivity tomography as a support tool for physicochemical properties assessment of near-surface waste materials in a mining tailing pond (El gorguel, SE Spain). Minerals 2020, 10, 559. [Google Scholar] [CrossRef]
- Yoram Rubin, S.S.H. Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 2005; Volume 50, ISBN 978-1-4020-3101-4. [Google Scholar]
- Radar, G.P. Ground Penetrating Radar Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 9780444533487. [Google Scholar]
- Baig, F.; Sherif, M.; Sefelnasr, A.; Faiz, M.A. Groundwater vulnerability to contamination in the gulf cooperation council region: A review. Groundw. Sustain. Dev. 2023, 23, 101023. [Google Scholar] [CrossRef]
- Chandnani, G.; Gandhi, P.; Kanpariya, D.; Parikh, D.; Shah, M. A comprehensive analysis of contaminated groundwater: Special emphasis on nature-ecosystem and socio-economic impacts. Groundw. Sustain. Dev. 2022, 19, 100813. [Google Scholar] [CrossRef]
- Meekes, J.A.C.; Goes, B.J.M. GeoPASS: A decision support system for selecting the optimal geophysical technique for shallow surveys. First Break 2005, 23. [Google Scholar] [CrossRef]
- Wang, Y.; Anderson, N.; Torgashov, E. Selection of geophysical methods based on matter-element analysis with analytic hierarchy process. Explor. Geophys. 2021, 52, 669–679. [Google Scholar] [CrossRef]
- Ducut, J.D.; Alipio, M.; Go, P.J.; Concepcion II, R.; Vicerra, R.R.; Bandala, A.; Dadios, E. A review of Electrical Resistivity Tomography applications in underground imaging and object detection. Displays 2022, 73, 102208. [Google Scholar] [CrossRef]
- Ali, M.; Sun, S.; Qian, W.; Bohari, A.D.; Claire, D.; Faruwa, A.R.; Zhang, Y. Borehole resistivity and induced polarization tomography at the Canadian Shield for Mineral Exploration in north-western Sudbury. E3S Web Conf. 2020, 168, 00002. [Google Scholar] [CrossRef]
- Wu, X.; Meng, Z.; Dang, X.; Wang, J. Effects of rock fragments on the water infiltration and hydraulic conductivity in the soils of the desert steppes of Inner Mongolia, China. Soil Water Res. 2021, 16, 151–163. [Google Scholar] [CrossRef]
- Skinner, D.; Heinson, G. A comparison of electrical and electromagnetic methods for the detection of hydraulic pathways in a fractured rock aquifer, Clare Valley, South Australia. Hydrogeol. J. 2004, 12, 576–590. [Google Scholar] [CrossRef]
- Ali, M.A.H.; Mewafy, F.M.; Qian, W.; Alshehri, F.; Almadani, S.; Aldawsri, M.; Aloufi, M.; Saleem, H.A. Mapping Leachate Pathways in Aging Mining Tailings Pond Using Electrical Resistivity Tomography. Minerals 2023, 13, 1437. [Google Scholar] [CrossRef]
- Booterbaugh, A.P.; Bentley, L.R.; Mendoza, C.A. Geophysical characterization of an undrained dyke containing an oil sands tailings pond, Alberta, Canada. J. Environ. Eng. Geophys. 2015, 20, 303–317. [Google Scholar] [CrossRef]
- Zhu, K.; Dou, M.; Lu, Y.; Zhang, Q.; Li, J.; Li, K.; Wang, H. Apparent conductivity-depth estimation of fixed-wing time-domain electromagnetic two-component data based on iterative lookup tables. J. Appl. Geophys. 2017, 140, 177–181. [Google Scholar] [CrossRef]
- Jekayinfa, S.M.; Oladunjoye, M.A.; Doro, K.O. Imaging the distribution of bitumen contaminants in shallow coastal plain sands in southwestern Nigeria using electrical resistivity. Environ. Earth Sci. 2023, 82, 55. [Google Scholar] [CrossRef]
- Bentley, L.R.; Gharibi, M. Two-and three-dimensional electrical resistivity imaging at a heterogeneous remediation site. Geophysics 2004, 69, 674–680. [Google Scholar] [CrossRef]
- Dong, L.; Jiang, F.; Wang, M.; Li, X. Fuzzy deep wavelet neural network with hybrid learning algorithm: Application to electrical resistivity imaging inversion. Knowl. Based Syst. 2022, 242, 108164. [Google Scholar] [CrossRef]
- Ali, M.A.H.; Sun, S.; Qian, W.; Abdou Dodo, B. Electrical resistivity imaging for detection of hydrogeological active zones in karst areas to identify the site of mining waste disposal. Environ. Sci. Pollut. Res. 2020, 27, 22486–22498. [Google Scholar] [CrossRef]
- Jiang, F.; Dong, L.; Dai, Q. Electrical resistivity imaging inversion: An ISFLA trained kernel principal component wavelet neural network approach. Neural Netw. 2018, 104, 114–123. [Google Scholar] [CrossRef]
- Park, J.-O.; You, Y.-J.; Kim, H.J. Electrical resistivity surveys for gold-bearing veins in the Yongjang mine, Korea. J. Geophys. Eng. 2009, 6, 73. [Google Scholar] [CrossRef]
- Martinez-Pagán, P.; Cano, Á.F.; Aracil, E.; Arocena, J.M. Electrical resistivity imaging revealed the spatial properties of mine tailing ponds in the Sierra Minera of southeast Spain. J. Environ. Eng. Geophys. 2009, 14, 63–76. [Google Scholar] [CrossRef]
- Dusabemariya, C.; Jiang, F.; Qian, W.; Faruwa, A.R.; Bagaragaza, R.; Ali, M. Water seepage detection using resistivity method around a pumped storage power station in China. J. Appl. Geophys. 2021, 188, 104320. [Google Scholar] [CrossRef]
- Ali, M.; Sun, S.; Qian, W.; Bohari, A.D.; Claire, D.; Zhang, Y. Application of Resistivity Method for Mining Tailings Site Selection in Karst Regions. E3S Web Conf. 2020, 144, 1002. [Google Scholar] [CrossRef]
- Irfan, M.; Hamza, S.; Azeem, M.W.; Mahmud, S.; Nawaz-ul-Huda, S.; Qadir, A. Groundwater Exploration and Salinity Intrusion Studies using Electrical Resistivity Survey (ERS)-Winder, Balochistan, Pakistan. Rud. Zb. 2022, 37. [Google Scholar] [CrossRef]
- Sasaki, Y. Resolution of resistivity tomography inferred from numerical simulation. Geophys. Prospect. 1992, 40, 453–463. [Google Scholar] [CrossRef]
- Loke, M.H.; Wilkinson, P.B.; Chambers, J.E.; Strutt, M. Optimized arrays for 2D cross-borehole electrical tomography surveys. Geophys. Prospect. 2014, 62, 172–189. [Google Scholar] [CrossRef]
- Dahlin, T. Short note on electrode charge-up effects in DC resistivity data acquisition using multi-electrode arrays. Geophys. Prospect. 2000, 48, 181–187. [Google Scholar] [CrossRef]
- Dahlin, T.; Zhou, B. A numerical comparison of 2D resistivity imaging with 10 electrode arrays. Geophys. Prospect. 2004, 52, 379–398. [Google Scholar] [CrossRef]
- Dahlin, T.; Zhou, B. Multiple-gradient array measurements for multichannel 2D resistivity imaging. Near Surf. Geophys. 2006, 4, 113–123. [Google Scholar] [CrossRef]
- Athanasiou, E.N.; Tsourlos, P.I.; Papazachos, C.B.; Tsokas, G.N. Combined weighted inversion of electrical resistivity data arising from different array types. J. Appl. Geophys. 2007, 62, 124–140. [Google Scholar] [CrossRef]
- Martorana, R.; Fiandaca, G.; Ponsati, A.C.; Cosentino, P.L. Comparative tests on different multi-electrode arrays using models in near-surface geophysics. J. Geophys. Eng. 2008, 6, 1. [Google Scholar] [CrossRef]
- Okpoli, C.C. Sensitivity and resolution capacity of electrode configurations. Int. J. Geophys. 2013, 2013, 608037. [Google Scholar] [CrossRef]
- Wilkinson, P.B.; Meldrum, P.I.; Chambers, J.E.; Kuras, O.; Ogilvy, R.D. Improved strategies for the automatic selection of optimized sets of electrical resistivity tomography measurement configurations. Geophys. J. Int. 2006, 167, 1119–1126. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P.; D’Alessandro, A.; Luzio, D. Comparison of different sets of array configurations for multichannel 2D ERT acquisition. J. Appl. Geophys. 2017, 137, 34–48. [Google Scholar] [CrossRef]
- Neyamadpour, A.; Wan Abdullah, W.A.T.; Taib, S.; Neyamadpour, B. Comparison of Wenner and dipole--dipole arrays in the study of an underground three-dimensional cavity. J. Geophys. Eng. 2010, 7, 30–40. [Google Scholar] [CrossRef]
- Loke, M.H.; Wilkinson, P.B.; Uhlemann, S.S.; Chambers, J.E.; Oxby, L.S. Computation of optimized arrays for 3-D electrical imaging surveys. Geophys. J. Int. 2014, 199, 1751–1764. [Google Scholar] [CrossRef]
- Szalai, S.; Szarka, L. On the classification of surface geoelectric arrays. Geophys. Prospect. 2008, 56, 159–175. [Google Scholar] [CrossRef]
- Ogilvy, R.D.; Kuras, O.; Palumbo-Roe, B.; Meldrum, P.I.; Wilkinson, P.B.; Chambers, J.E.; Klinck, B.A. The detection and tracking of mine-water pollution from abandoned mines using electrical tomography. Framework 2010, 917–925. Available online: https://nora.nerc.ac.uk/id/eprint/9313 (accessed on 2 January 2024).
- Martínez, J.; Mendoza, R.; Rey, J.; Sandoval, S.; Carmen Hidalgo, M. Characterization of tailings dams by electrical geophysical methods (Ert, ip): Federico mine (La Carolina, Southeastern Spain). Minerals 2021, 11, 145. [Google Scholar] [CrossRef]
- Rey, J.; Martínez, J.; Hidalgo, M.C.; Mendoza, R.; Sandoval, S. Assessment of Tailings Ponds by a Combination of Electrical (ERT and IP) and Hydrochemical Techniques (Linares, Southern Spain). Mine Water Environ. 2021, 40, 298–307. [Google Scholar] [CrossRef]
- Gabarrón, M.; Martínez-Pagán, P.; Martínez-Segura, M.A.; Martínez-Martínez, S.; Faz, Á.; Acosta, J.A. Electrical Resistivity Tomography as a Support Tool to Estimate Physicochemical Properties of Mining Tailings Pond. Preprints 2020, 2020010377. [Google Scholar] [CrossRef]
- do Nascimento, M.M.P.F.; Moreira, C.A.; Duz, B.G.; da Silveira, A.J.T. Geophysical Diagnosis of Diversion Channel Infiltration in a Uranium Waste Rock Pile. Mine Water Environ. 2022, 41, 704–720. [Google Scholar] [CrossRef]
- Yurkevich, N.V.; Abrosimova, N.A.; Bortnikova, S.B.; Karin, Y.G.; Saeva, O.P. Geophysical investigations for evaluation of environmental pollution in a mine tailings area. Toxicol. Environ. Chem. 2017, 99, 1328–1345. [Google Scholar] [CrossRef]
- Almeida, H.D.; Gomes Marques, M.C.; Sant’Ovaia, H.; Moura, R.; Espinha Marques, J. Environmental Impact Assessment of the Subsurface in a Former W-Sn Mine: Integration of Geophysical Methodologies. Minerals 2023, 13, 55. [Google Scholar] [CrossRef]
- Grissemann, C.; Furche, M.; Noell, U.; Rammlmair, D.; Günther, T.; Romero Baen, A.J. Geoelectrical observations at the mining dumps of the Peña de Hierro copper mine in the Rio Tinto mining district/Spain. In Proceedings of the 10th International Congress of the Brazilian Geophysical Society, Rio de Janeiro, Brazil, 19–23 November 2007; pp. 399–403. [Google Scholar] [CrossRef]
- Hudson, E.; Kulessa, B.; Edwards, P.; Williams, T.; Walsh, R. Integrated Hydrological and Geophysical Characterisation of Surface and Subsurface Water Contamination at Abandoned Metal Mines. Water. Air. Soil Pollut. 2018, 229, 256. [Google Scholar] [CrossRef]
- Gómez-Ortiz, D.; Martín-Velázquez, S.; Martín-Crespo, T.; De Ignacio-San José, C.; Lillo, J. Application of electrical resistivity tomography to the environmental characterization of abandoned massive sulphide mine ponds (Iberian Pyrite Belt, SW Spain). Near Surf. Geophys. 2010, 8, 65–74. [Google Scholar] [CrossRef]
- Acosta, J.A.; Martínez-Pagán, P.; Martínez-Martínez, S.; Faz, A.; Zornoza, R.; Carmona, D.M. Assessment of environmental risk of reclaimed mining ponds using geophysics and geochemical techniques. J. Geochem. Explor. 2014, 147, 80–90. [Google Scholar] [CrossRef]
- Banerjee, K.S.; Sharma, S.P.; Sarangi, A.K.; Sengupta, D. Delineation of subsurface structures using resistivity, VLF and radiometric measurement around a U-tailings pond and its hydrogeological implication. Phys. Chem. Earth 2011, 36, 1345–1352. [Google Scholar] [CrossRef]
- Kuranchie, F.A.; Shukla, S.K.; Habibi, D. Electrical resistivity of iron ore mine tailings produced in Western Australia. Int. J. Min. Reclam. Environ. 2015, 29, 191–200. [Google Scholar] [CrossRef]
- Loke, M.H. Tutorial: 2-D and 3-D Electrical Imaging Surveys; Geotomo Software: Gelugor, Malaysia, 2014; p. 127. [Google Scholar]
- Arisalwadi, M.; Sastrawan, F.D.; Sari, D.I. Analyzing of 2D resistivity data to determine the subsurface stratigraphy at Institut Teknologi Kalimantan (ITK) Balikpapan. J. Phys. Conf. Ser. 2021, 1763, 12014. [Google Scholar]
- Loke, M.H.; Chambers, J.E.; Rucker, D.F.; Kuras, O.; Wilkinson, P.B. Recent developments in the direct-current geoelectrical imaging method. J. Appl. Geophys. 2013, 95, 135–156. [Google Scholar] [CrossRef]
- Loke, M.H. RES2DMOD ver. 3.01: Rapid 2D resistivity forward modelling using the finite difference and finite-element methods. Softw. Man. 2002, 28, 29. [Google Scholar]
- Loke, M.H.; Acworth, I.; Dahlin, T. A comparison of smooth and blocky inversion methods in 2D electrical imaging surveys. Explor. Geophys. 2003, 34, 182–187. [Google Scholar] [CrossRef]
- Loke, M.H.; Dahlin, T. A comparison of the Gauss--Newton and quasi-Newton methods in resistivity imaging inversion. J. Appl. Geophys. 2002, 49, 149–162. [Google Scholar] [CrossRef]
- Loke, M.H.; Kiflu, H.; Wilkinson, P.B.; Harro, D.; Kruse, S. Optimized arrays for 2D resistivity surveys with combined surface and buried arrays. Near Surf. Geophys. 2015, 13, 505–518. [Google Scholar] [CrossRef]
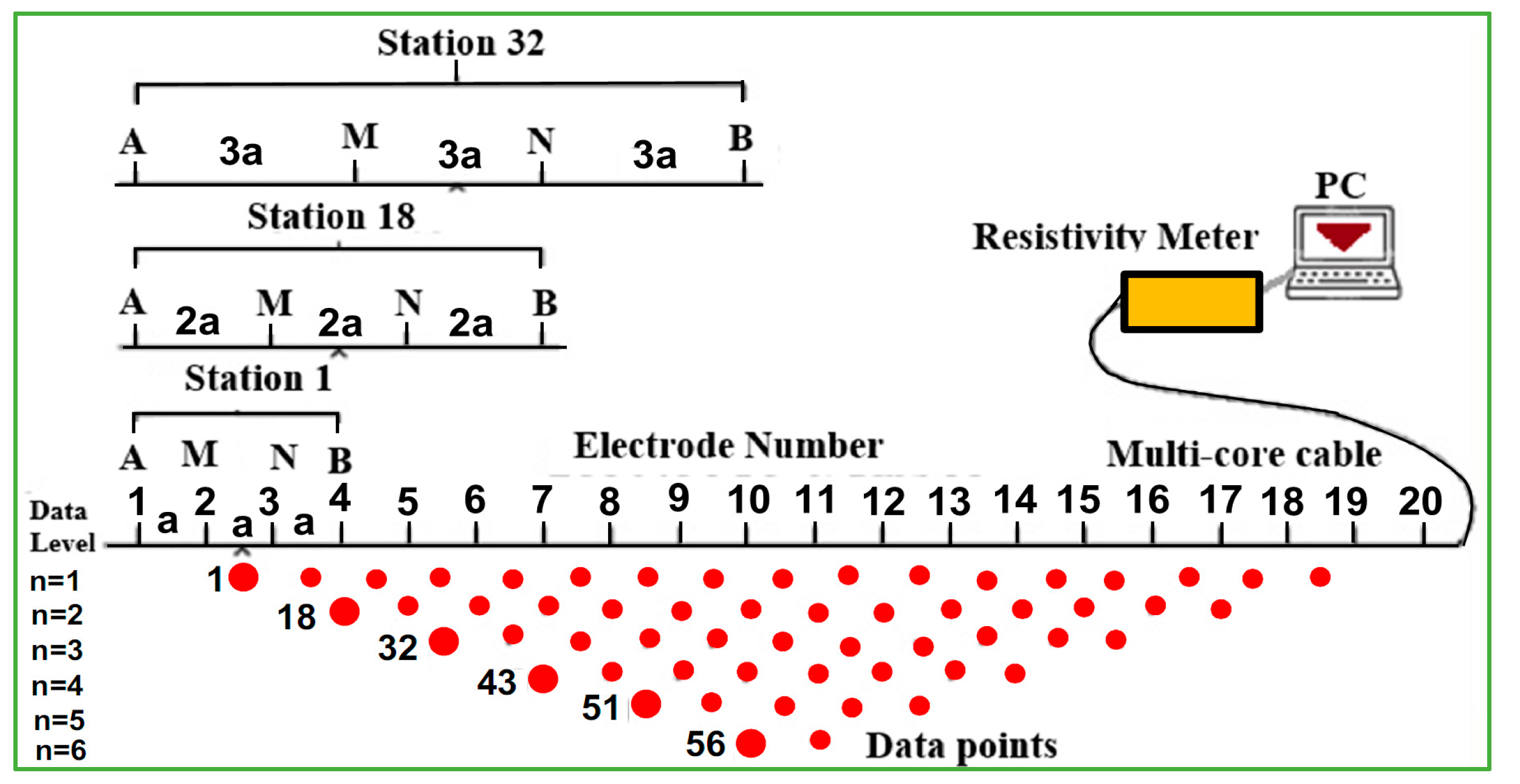


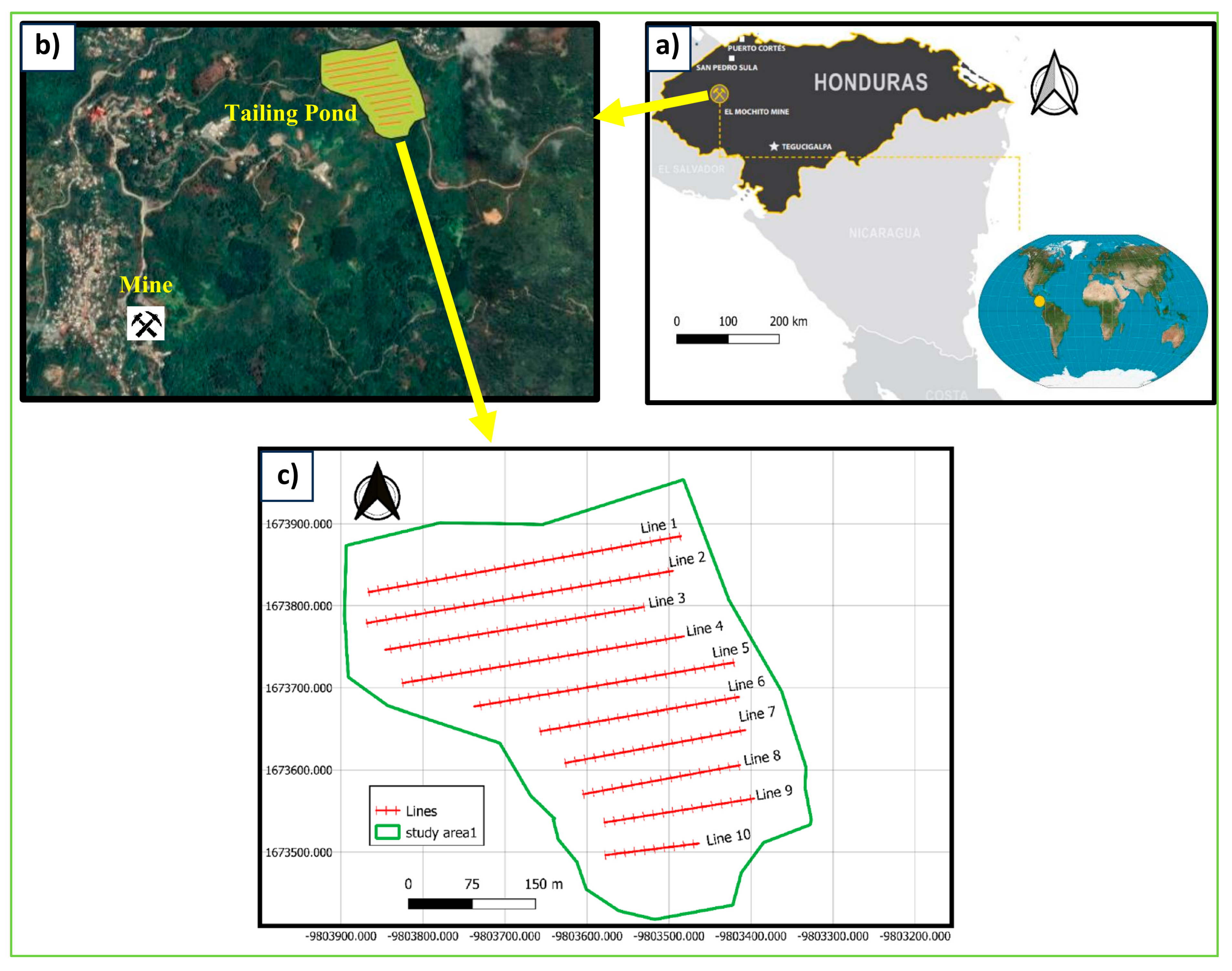



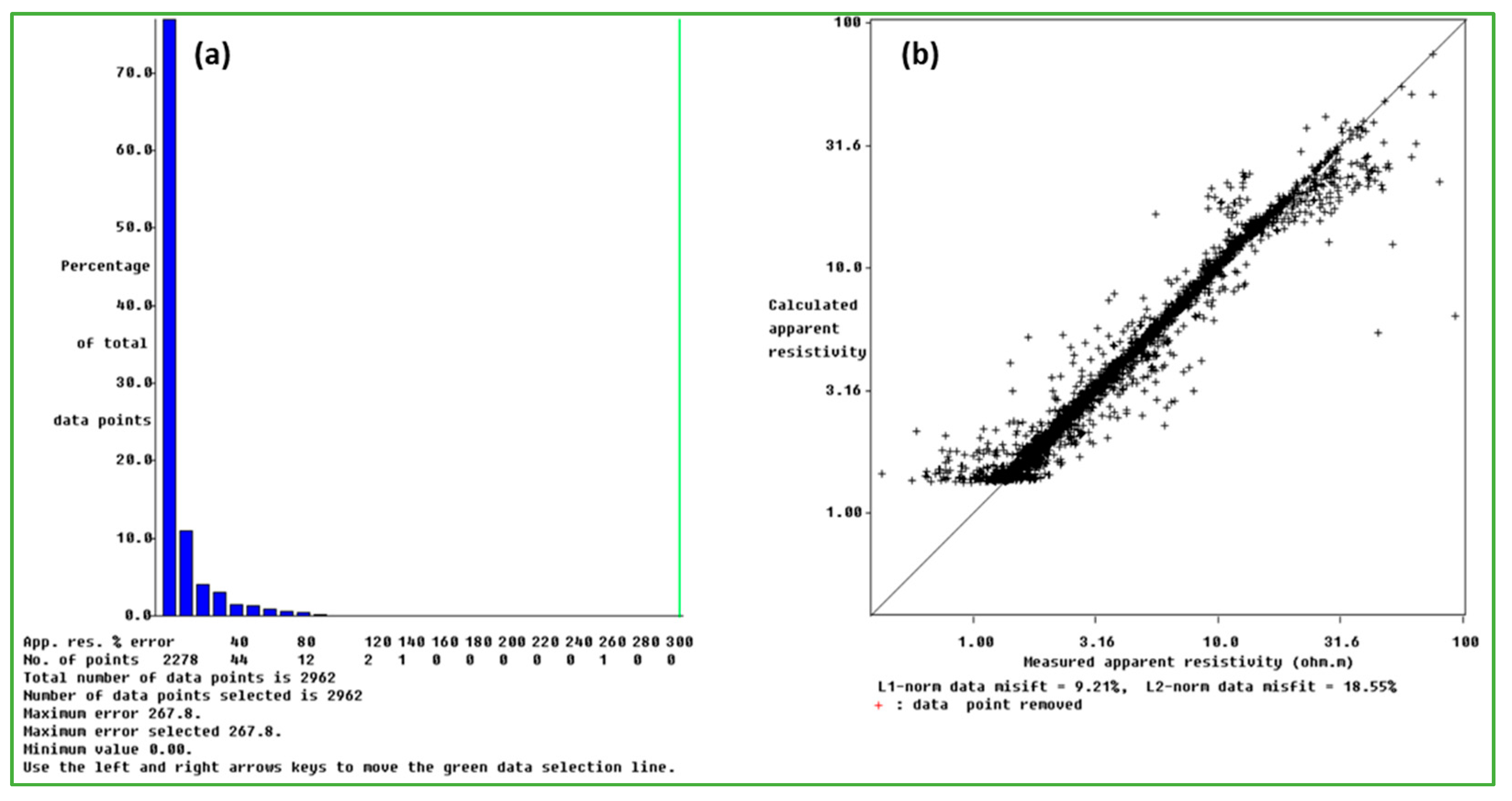
| Array | Survey Type | Ore | Mine | Country | Ref. |
|---|---|---|---|---|---|
| Wenner-Schlumberger | 2D | Lead (Pb) and Zinc (Zn) | Frongoch | UK | [36] |
| Wenner-Schlumberger | 2D/3D | Cadmium (Cd), Copper (Cu), Pb and Zn | Sierra Minera | Spain | [23] |
| Wenner- Schlumberger | 2D | Zn-Pb | Olkusz | Poland | [14] |
| Wenner–Schlumberger | 2D | Zn-Pb | Federico | Spain | [56] |
| Wenner-Schlumberger | 2D | Pb–Ag | Linares | Spain | [57] |
| Wenner-Schlumberger | 2D | Cu–Zn–Pb | Iberian | Spain | [64] |
| Wenner–Schlumberger | 2D | Pb-Cd- Zn | Cordillera Bética | Spain | [65] |
| Schlumberger | 1D/2D | Uranium | Jaduguda | India | [66] |
| Schlumberger | 2D/3D | Uranium | Osamu Utsumi | Brazil | [59] |
| Schlumberger | 2D | Gold | Komsomolsk | Russia | [60] |
| Wenner | 2D | Tungsten | Regoufe | Portugal | [59] |
| Wenner | 2D/3D | Cu | Peña de Hierro | Spain | [62] |
| Wenner | 2D | Oil | Fort McMurray | Canada | [30] |
| Wenner | 2D | Zn-Pb | EsgairMwyn | Ceredigion | [63] |
| Wenner | 2D | Iron | Mount Gibson | Australia | [67] |
| Wenner | 2D | Ag-Pb- Zn | El Mochito | Honduras | [35] |
| Dipole–dipole | 2D | Ni-Cd- Fe | Cartagena-La Union | Spain | [18] |
| Array Type | Geometric Factor (K) |
|---|---|
| Wenner-α | 2πa |
| Wenner-β | 6πa |
| Wenner-γ | 3πa |
| Dipole–dipole | πna(1 + n)(1 + 2n) |
| Schlumberger | πb(b + a)/a |
| Wenner-Schlumberger | πna(1 + n) |
| Array | Number of Data Points | Average Sensitivity | DOI | Resolution | Abs. Errors, % | RMS, % | |
|---|---|---|---|---|---|---|---|
| W-α | 335 | 2.831 | Moderate | Shallow | Moderate | 0.78 | 0.97 |
| W-β | 335 | 2.847 | Moderate | Shallow | Moderate | 0.81 | 1.04 |
| W-γ | 335 | 3.398 | Moderate | Shallow | Moderate | 0.7 | 0.87 |
| DD | 425 | 6.241 | High | Moderate | High | 0.87 | 1.1 |
| Sch | 520 | 4.231 | High | Moderate | High | 0.76 | 0.98 |
| WSC | 640 | 4.440 | High | Moderate/Deep | High | 0.79 | 1 |
| Sequence | Resistivity (Ωm) | Thickness (m) | Description |
|---|---|---|---|
| Upper (A) | >60 | ~2–5 | Dry tailings |
| Middle (B) | >30:60 | ~10–15 | Semi-saturated |
| Down (C) | <30 | ~>15 | Saturated layer |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.A.H.; Mewafy, F.M.; Qian, W.; Faruwa, A.R.; Shebl, A.; Dabaa, S.; Saleem, H.A. Numerical Simulation of Geophysical Models to Detect Mining Tailings’ Leachates within Tailing Storage Facilities. Water 2024, 16, 753. https://doi.org/10.3390/w16050753
Ali MAH, Mewafy FM, Qian W, Faruwa AR, Shebl A, Dabaa S, Saleem HA. Numerical Simulation of Geophysical Models to Detect Mining Tailings’ Leachates within Tailing Storage Facilities. Water. 2024; 16(5):753. https://doi.org/10.3390/w16050753
Chicago/Turabian StyleAli, Mosaad Ali Hussein, Farag M. Mewafy, Wei Qian, Ajibola Richard Faruwa, Ali Shebl, Saleh Dabaa, and Hussein A. Saleem. 2024. "Numerical Simulation of Geophysical Models to Detect Mining Tailings’ Leachates within Tailing Storage Facilities" Water 16, no. 5: 753. https://doi.org/10.3390/w16050753
APA StyleAli, M. A. H., Mewafy, F. M., Qian, W., Faruwa, A. R., Shebl, A., Dabaa, S., & Saleem, H. A. (2024). Numerical Simulation of Geophysical Models to Detect Mining Tailings’ Leachates within Tailing Storage Facilities. Water, 16(5), 753. https://doi.org/10.3390/w16050753








