Monitoring the Water Quality Distribution Characteristics in the Huaihe River Basin Based on the Sentinel-2 Satellite
Abstract
1. Introduction
2. Data and Methods
2.1. Research Areas
2.2. Data
2.2.1. Experimental Data
2.2.2. Satellite Data
2.3. Methods
2.3.1. Laboratory Measurements
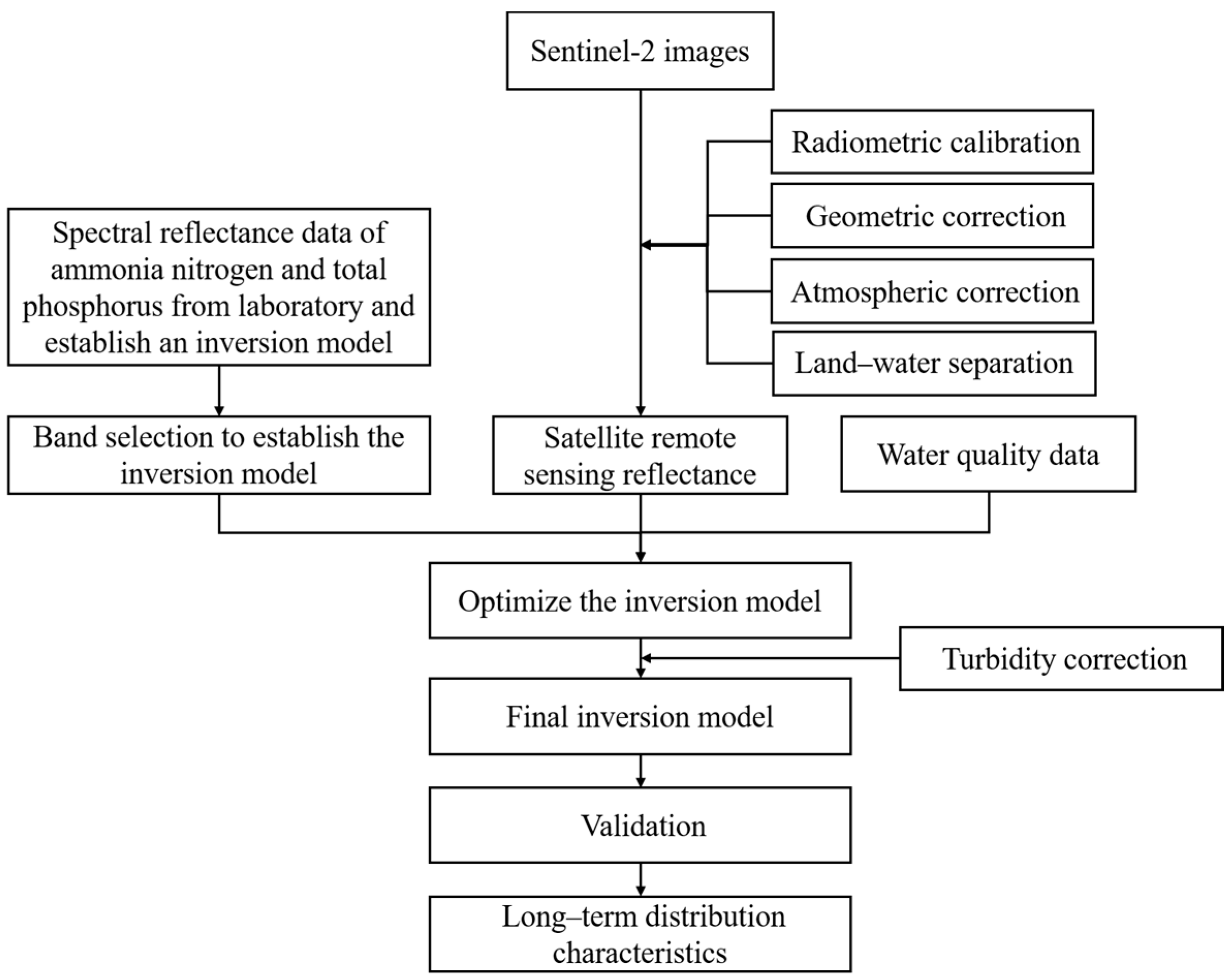
2.3.2. Pre-Processing of Satellite Data
2.3.3. Inversion Model
3. Results
3.1. Laboratory Measurement of Spectra and Selection of Characteristic Bands
3.2. Inversion Model for Total Phosphorus Concentration
3.2.1. Inversion Model from Laboratory Measurements
3.2.2. Inversion Model Optimized Using Matchup Datasets
3.2.3. Turbidity Correction
3.3. Inversion Model for Ammonia Nitrogen Concentration
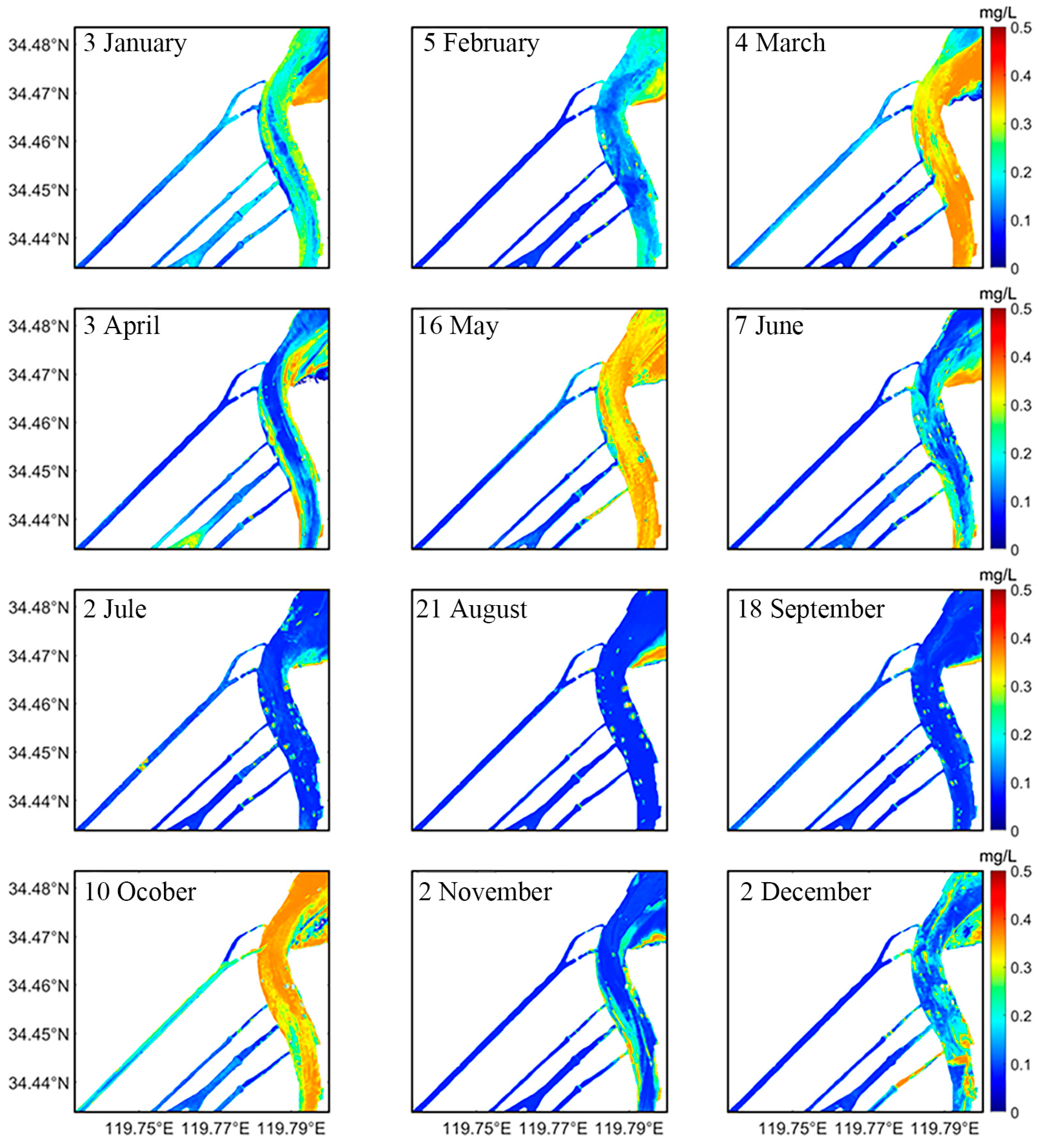
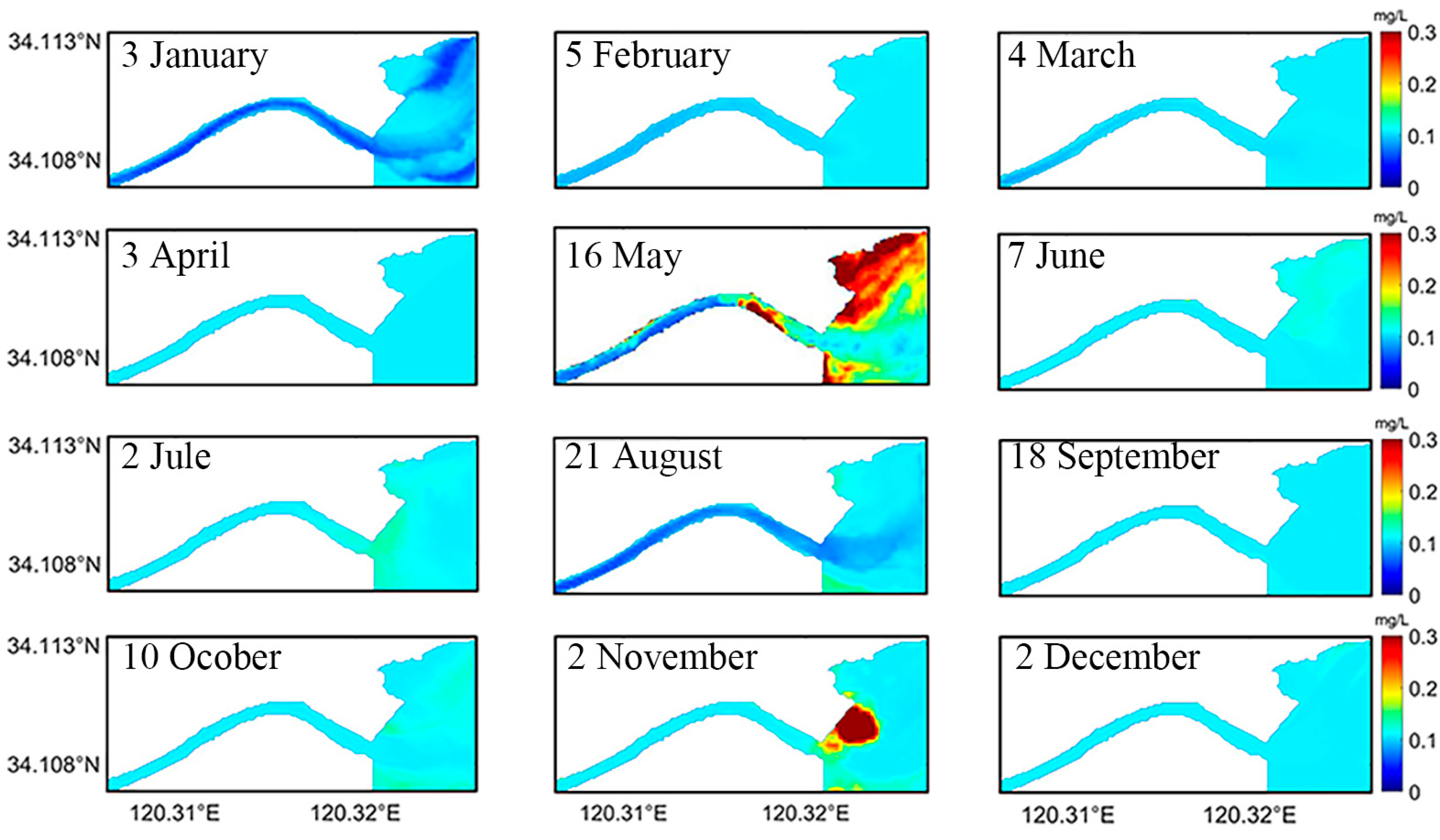
3.4. Temporal and Spatial Variation Characteristics of Total Phosphorus and Ammonia Nitrogen
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Deng, J.; Qin, B.; Zhu, G.; Zhang, Y.; Jeppesen, E.; Tong, Y. Importance and Vulnerability of Lakes and Reservoirs Supporting Drinking Water in China. Fundam. Res. 2023, 3, 265–273. [Google Scholar] [CrossRef]
- Wen, Z.; Song, K.; Liu, G.; Shang, Y.; Fang, C.; Du, J.; Lyu, L. Quantifying the Trophic Status of Lakes Using Total Light Absorption of Optically Active Components. Environ. Pollut. 2019, 245, 684–693. [Google Scholar] [CrossRef]
- Chen, K.; Wu, L.; Zhou, H. Assessment and Trend Analysis of Water Quality in the Huaihe River Basin. J. Hydroecol. (Chin. J. Engl. Abstr.) 2022, 43, 15–21. [Google Scholar] [CrossRef]
- Csathó, P.; Sisák, I.; Radimszky, L.; Lushaj, S.; Spiegel, H.; Nikolova, M. Agriculture as a source of phosphorus causing eutrophication in Central and Eastern Europe. Soil. Use Manag. 2009, 23, 36–56. [Google Scholar] [CrossRef]
- Zhao, J.; Fu, G.; Lei, K.; Li, Y. Multivariate analysis of surface water quality in the Three Gorges area of China and implications for water management. J. Environ. Sci. 2011, 23, 1460–1471. [Google Scholar] [CrossRef]
- Bangira, T.; Matongera, T.N.; Mabhaudhi, T.; Mutanga, O. Remote Sensing-Based Water Quality Monitoring in African Reservoirs, Potential and Limitations of Sensors and Algorithms: A Systematic Review. Phys. Chem. Earth Parts A/B/C 2024, 134, 103536. [Google Scholar] [CrossRef]
- Tian, D.; Zhao, X.; Gao, L.; Liang, Z.; Yang, Z.; Zhang, P.; Wu, Q.; Ren, K.; Li, R.; Yang, C.; et al. Estimation of Water Quality Variables Based on Machine Learning Model and Cluster Analysis-Based Empirical Model Using Multi-Source Remote Sensing Data in Inland Reservoirs, South China. Environ. Pollut. 2024, 342, 123104. [Google Scholar] [CrossRef]
- Lioumbas, J.; Christodoulou, A.; Katsiapi, M.; Xanthopoulou, N.; Stournara, P.; Spahos, T.; Seretoudi, G.; Mentes, A.; Theodoridou, N. Satellite Remote Sensing to Improve Source Water Quality Monitoring: A Water Utility’s Perspective. Remote Sens. Appl: Soc. Environ. 2023, 32, 101042. [Google Scholar] [CrossRef]
- Li, L.; Gu, M.; Gong, C.; Hu, Y.; Wang, X.; Yang, Z.; He, Z. An Advanced Remote Sensing Retrieval Method for Urban Non-Optically Active Water Quality Parameters: An Example from Shanghai. Sci. Total Environ. 2023, 880, 163389. [Google Scholar] [CrossRef]
- Yang, W.; Fu, B.; Li, S.; Lao, Z.; Deng, T.; He, W.; He, H.; Chen, Z. Monitoring Multi-Water Quality of Internationally Important Karst Wetland through Deep Learning, Multi-Sensor and Multi-Platform Remote Sensing Images: A Case Study of Guilin, China. Ecol. Indic. 2023, 154, 110755. [Google Scholar] [CrossRef]
- Rahat, S.H.; Steissberg, T.; Chang, W.; Chen, X.; Mandavya, G.; Tracy, J.; Wasti, A.; Atreya, G.; Saki, S.; Bhuiyan, M.A.E.; et al. Remote Sensing-Enabled Machine Learning for River Water Quality Modeling under Multidimensional Uncertainty. Sci. Total Environ. 2023, 898, 165504. [Google Scholar] [CrossRef]
- Kowe, P.; Ncube, E.; Magidi, J.; Ndambuki, J.M.; Rwasoka, D.T.; Gumindoga, W.; Maviza, A.; de jesus Paulo Mavaringana, M.; Kakanda, E.T. Spatial-Temporal Variability Analysis of Water Quality Using Remote Sensing Data: A Case Study of Lake Manyame. Sci. Afr. 2023, 21, e01877. [Google Scholar] [CrossRef]
- Chen, P.; Wang, B.; Wu, Y.; Wang, Q.; Huang, Z.; Wang, C. Urban River Water Quality Monitoring Based on Self-Optimizing Machine Learning Method Using Multi-Source Remote Sensing Data. Ecol. Indic. 2023, 146, 109750. [Google Scholar] [CrossRef]
- Wu, S.; Qi, J.; Yan, Z.; Lyu, F.; Lin, T.; Wang, Y.; Du, Z. Spatiotemporal Assessments of Nutrients and Water Quality in Coastal Areas Using Remote Sensing and a Spatiotemporal Deep Learning Model. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102897. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, H.; Huang, J.J.; Tian, S.; Xu, W.; Mai, Y. An Ensemble Machine Learning Model for Water Quality Estimation in Coastal Area Based on Remote Sensing Imagery. J. Environ. Manag. 2022, 323, 116187. [Google Scholar] [CrossRef]
- Sedighkia, M.; Abdoli, A. Linking Remote Sensing Analysis and Reservoir Operation Optimization for Improving Water Quality Management of Reservoirs. J. Hydrol. 2022, 613, 128445. [Google Scholar] [CrossRef]
- Mohseni, F.; Saba, F.; Mirmazloumi, S.M.; Amani, M.; Mokhtarzade, M.; Jamali, S.; Mahdavi, S. Ocean Water Quality Monitoring Using Remote Sensing Techniques: A Review. Mar. Environ. Res. 2022, 180, 105701. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Overview of the Application of Remote Sensing in Effective Monitoring of Water Quality Parameters. Remote Sens. 2023, 15, 1938. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Caballero, I.; Navarro, G. Monitoring cyanoHABs and Water Quality in Laguna Lake (Philippines) with Sentinel-2 Satellites during the 2020 Pacific Typhoon Season. Sci. Total Environ. 2021, 788, 147700. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q. Monitoring Dissolved Organic Carbon by Combining Landsat-8 and Sentinel-2 Satellites: Case Study in Saginaw River Estuary, Lake Huron. Sci. Total Environ. 2020, 718, 137374. [Google Scholar] [CrossRef]
- Cao, X.; Yang, S.; Wu, P.; Liu, S.; Liao, J. Coupling Stable Isotopes to Evaluate Sources and Transformations of Nitrate in Groundwater and Inflowing Rivers around the Caohai Karst Wetland, Southwest China. Environ. Sci. Pollut. Res. 2021, 28, 45826–45839. [Google Scholar] [CrossRef]
- Wei, L.; Wang, Z.; Huang, C.; Zhang, Y.; Wang, Z.; Xia, H.; Cao, L. Transparency Estimation of Narrow Rivers by UAV-Borne Hyperspectral Remote Sensing Imagery. IEEE Access 2020, 8, 168137–168153. [Google Scholar] [CrossRef]
- Li, S.; Song, K.; Wang, S.; Liu, G.; Wen, Z.; Shang, Y.; Lyu, L.; Chen, F.; Xu, S.; Tao, H.; et al. Quantification of Chlorophyll-a in Typical Lakes across China Using Sentinel-2 MSI Imagery with Machine Learning Algorithm. Sci. Total Environ. 2021, 778, 146271. [Google Scholar] [CrossRef]
- Moses, W.; Sterckx, S.; Montes, M.; De Keukelaere, L.; Knaeps, E. Chapter 3—Atmospheric correction for inland waters. Bio-optical modeling and remote sensing of inland waters. In Bio-Optical Modeling and Remote Sensing of Inland Waters; Elsevier: Amsterdam, The Netherlands, 2017; pp. 69–100. [Google Scholar] [CrossRef]
- Guanter, L.; Del Carmen González-Sanpedro, M.; Moreno, J. A method for the atmospheric correction of ENVISAT/MERIS data over land targets. Int. J. Remote Sens. 2007, 28, 709–728. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.; Acharya, P.; Bernstein, L.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.; Chetwynd, J.; Hoke, M.; et al. MODTRAN5: 2006 update. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XII; SPIE: Bellingham, WA, USA, 2006; Volume 6233. [Google Scholar] [CrossRef]
- Pereira-Sandoval, M.; Ruescas, A.; Urrego, P.; Ruiz-Verdú, A.; Delegido, J.; Tenjo, C.; Soria-Perpinyà, X.; Vicente, E.; Soria, J.; Moreno, J. Evaluation of atmospheric correction algorithms over Spanish inland waters for sentinel-2 multi spectral imagery data. Remote Sens. 2019, 11, 1469. [Google Scholar] [CrossRef]
- De Keukelaere, L.; Sterckx, S.; Adriaensen, S.; Knaeps, E.; Reusen, I.; Giardino, C.; Bresciani, M.; Hunter, P.; Neil, C.; Van der Zande, D.; et al. Atmospheric correction of Landsat-8/OLI and Sentinel-2/MSI data using iCOR algorithm: Validation for coastal and inland waters. Eur. J. Remote Sens. 2018, 51, 525–542. [Google Scholar] [CrossRef]
- Allam, M.; Meng, Q.; Elhag, M.; Giardino, C.; Ghirardi, N.; Su, Y.; Al-Hababi, M.; Menenti, M. Atmospheric Correction Algorithms Assessment for Sentinel-2A Imagery over Inland Waters of China: Case Study, Qiandao Lake. Earth Syst. Environ. 2024, 8, 105–119. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, C.; Ma, R.; Cao, Z. Remote sensing estimation of lake total phosphorus concentration based on MODIS: A case study of Lake Hongze. Remote Sens. 2019, 11, 2068. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Y.; Shi, K.; Zhang, Y.; Sun, X.; Wang, W.; Qian, H.; Yang, H.; Niu, Y. Real-Time and Continuous Tracking of Total Phosphorus Using a Ground-Based Hyperspectral Proximal Sensing System. Remote Sens. 2023, 15, 507. [Google Scholar] [CrossRef]
- Shang, W.; Jin, S.; He, Y.; Zhang, Y.; Li, J. Spatial–Temporal Variations of Total Nitrogen and Phosphorus in Poyang, Dongting and Taihu Lakes from Landsat-8 Data. Water 2021, 13, 1704. [Google Scholar] [CrossRef]
- Wu, C.; Wu, J.; Qi, J.; Zhang, L.; Huang, H.; Lou, L.; Chen, Y. Empirical estimation of total phosphorus concentration in the mainstream of the Qiantang River in China using Landsat TM data. Int. J. Remote Sens. 2010, 31, 2309–2324. [Google Scholar] [CrossRef]
- Du, C.; Li, Y.; Wang, Q.; Zhu, L.; Lü, H. Inversion Model and Daily Variation of Total Phosphorus Concentrations in Taihu Lake Based on GOCI Data. Environ. Sci. 2016, 37, 862–872. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Yuan, D.; Song, X. Empirical estimation of total nitrogen and total phosphorus concentration of urban water bodies in China using high resolution IKONOS multispectral imagery. Water 2015, 7, 6551–6573. [Google Scholar] [CrossRef]
- Cruz-Retana, A.; Becerril-Piña, R.; Fonseca, C.; Gómez-Albores, M.; Gaytán-Aguilar, S.; Hernández-Téllez, M.; Mastachi-Loza, C. Assessment of Regression Models for Surface Water Quality Modeling via Remote Sensing of a Water Body in the Mexican Highlands. Water 2023, 15, 3828. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, S.; Zhang, Y. Dynamic Water Quality Changes in the Main Stream of the Yangtze River from Multi-Source Remote Sensing Data. Remote Sens. 2023, 15, 2526. [Google Scholar] [CrossRef]
- Dong, G.; Hu, Z.; Liu, X.; Fu, Y.; Zhang, W. Spatio-temporal variation of total nitrogen and ammonia nitrogen in the water source of the middle route of the South-to-North Water Diversion Project. Water 2020, 12, 2615. [Google Scholar] [CrossRef]
- He, W.; Chen, S.; Liu, X.; Chen, J. Water quality monitoring in a slightly-polluted inland water body through remote sensing—Case study of the Guanting Reservoir in Beijing, China. Front. Environ. Sci. Eng. China 2008, 2, 163–171. [Google Scholar] [CrossRef]
- Ma, F.; Gao, Z.; Ye, B. Remote sensing inversion of Tangxun lake water quality based on high score remote sensing satellite image. Water Resour. Dev. Manag. 2021, 5, 69–75. [Google Scholar] [CrossRef]
- Wu, H.; Guo, Q.; Zang, J.; Qiao, Y.; Zhu, L.; He, Y. Study on Water Quality Parameter Inversion based on Landsat 8 and Measured Data. Remote Sens Technol. Appl. (Chin. J. Engl. Abstr.) 2021, 36, 898–907. [Google Scholar] [CrossRef]
- Al-Shaibah, B.; Liu, X.; Zhang, J.; Tong, Z.; Zhang, M.; El-Zeiny, A.; Faichia, C.; Hussain, M.; Tayyab, M. Modeling water quality parameters using landsat multispectral images: A case study of Erlong lake, northeast China. Remote Sens. 2021, 13, 1603. [Google Scholar] [CrossRef]
- Zhou, C.; Jiao, X.; Mao, C.; LÜ, Y.; Zhang, P. Present Marine Environment Situation Investigation in the Nearshore Area of Guanhe Estuary in Spring. J. Guangdong Ocean. Univ. (Chin. J. Engl. Abstr.) 2018, 38, 27–34. [Google Scholar] [CrossRef]


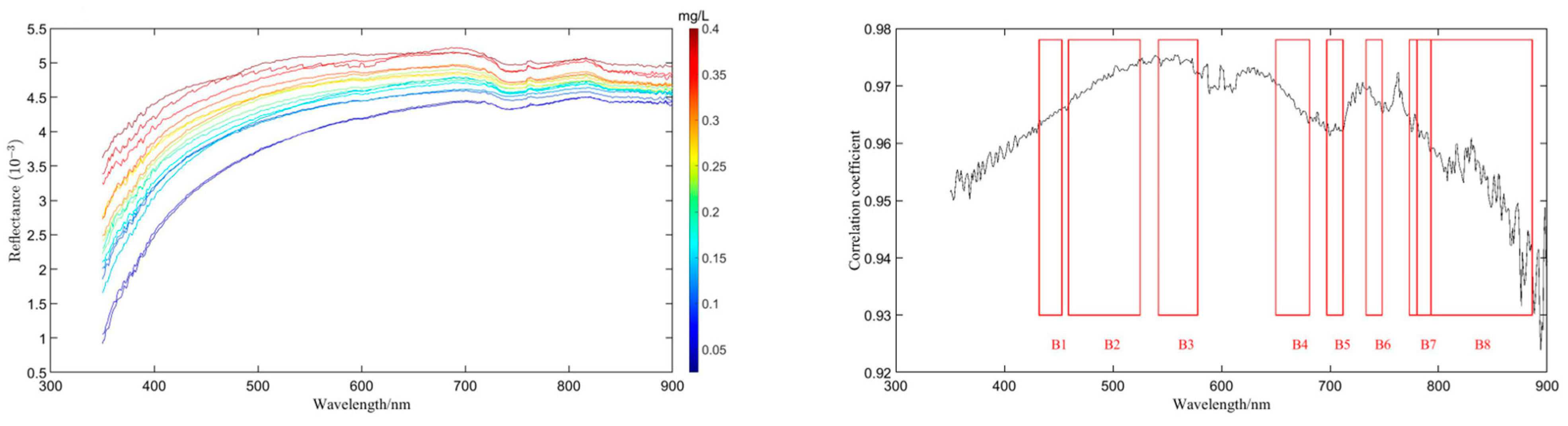


| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | |
|---|---|---|---|---|---|---|---|---|
| TP | 0.948 | 0.957 | 0.975 | 0.942 | 0.915 | 0.810 | 0.799 | 0.750 |
| Algorithms | R2 | RMSE |
|---|---|---|
| 0.8316 | 0.08117 | |
| 0.8374 | 0.08714 | |
| 0.8359 | 0.05684 | |
| 0.7865 | 0.08499 | |
| 0.8240 | 0.08183 | |
| 0.7674 | 0.08656 |
| Algorithms | R2 | RMSE |
|---|---|---|
| 0.6621 | 0.0223 | |
| 0.6713 | 0.02282 | |
| 0.6827 | 0.02334 | |
| 0.6725 | 0.02195 | |
| 0.6345 | 0.02319 | |
| 0.6955 | 0.02156 | |
| 0.6543 | 0.02436 | |
| 0.6099 | 0.02396 | |
| 0.6528 | 0.02216 | |
| 0.6481 | 0.02276 |
| Measured TP | Retrievals | Absolute Errors | Relative Errors | |
|---|---|---|---|---|
| 1 | 0.1878 | 0.1651 | 0.0227 | 12.08% |
| 2 | 0.0861 | 0.0999 | 0.0138 | 16.11% |
| 3 | 0.139 | 0.1647 | 0.0257 | 18.47% |
| 4 | 0.094 | 0.0823 | 0.0117 | 12.44% |
| 5 | 0.1182 | 0.0879 | 0.0303 | 25.61% |
| Measured TP | Results before TC | Relative Errors | Results after TC | Relative Errors | |
|---|---|---|---|---|---|
| 1 | 0.1878 | 0.1651 | 12.08% | 0.1946 | 3.64% |
| 2 | 0.0861 | 0.0999 | 16.11% | 0.0878 | 2.02% |
| 3 | 0.139 | 0.1647 | 18.47% | 0.1608 | 15.68% |
| 4 | 0.094 | 0.0823 | 12.44% | 0.097 | 3.23% |
| 5 | 0.1182 | 0.0879 | 25.61% | 0.1351 | 14.31% |
| Algorithms | R2 | RMSE |
|---|---|---|
| 0.7853 | 0.0465 | |
| 0.7476 | 0.05042 | |
| 0.8106 | 0.04545 | |
| 0.883 | 0.03732 | |
| 0.8143 | 0.04325 | |
| 0.8731 | 0.03721 | |
| 0.8736 | 0.03879 | |
| 0.8635 | 0.03708 | |
| 0.7344 | 0.05171 | |
| 0.8227 | 0.04398 | |
| 0.8997 | 0.03454 | |
| 0.7837 | 0.04667 | |
| 0.6717 | 0.0575 | |
| 0.7877 | 0.04624 |
| Measured NH3-N | Retrievals | Absolute Errors | Relative Errors | |
|---|---|---|---|---|
| 1 | 0.3547 | 0.3594 | 0.0047 | 1.33% |
| 2 | 0.0849 | 0.0880 | 0.0031 | 3.69% |
| 3 | 0.3501 | 0.3472 | 0.0030 | −0.84% |
| 4 | 0.1005 | 0.0853 | 0.0152 | −15.11% |
| 5 | 0.0769 | 0.0857 | 0.0088 | 11.49% |
| Algorithms | R2 | RMSE |
|---|---|---|
| 0.9514 | 0.02558 | |
| 0.9515 | 0.02659 | |
| 0.9574 | 0.02605 | |
| 0.8831 | 0.03966 | |
| 0.9277 | 0.03119 | |
| 0.9329 | 0.03006 |
| Measure NH3-N | Results before TC | Relative Errors | Results after TC | Relative Errors | |
|---|---|---|---|---|---|
| 1 | 0.3547 | 0.3594 | 1.33% | 0.3604 | 1.61% |
| 2 | 0.0849 | 0.0880 | 3.69% | 0.0800 | 5.73% |
| 3 | 0.3501 | 0.3472 | −0.84% | 0.3322 | 5.13% |
| 4 | 0.1005 | 0.0853 | −15.11% | 0.0847 | −15.69% |
| 5 | 0.0769 | 0.0857 | 11.49% | 0.0849 | 10.34% |
| Author | Inverse Model | Study Area | Sensor | Error |
|---|---|---|---|---|
| Xiong et al. [32] | TP = 0.2553 × (B2 − B5)/(B2 + B5) −0.0084 | Lake Hongze | MODIS | R2 = 0.607, RMSE = 0.031 mg/L, MRE = 37.584% |
| Li et al. [33] | TP = 0.1965 × R(740)/R(670)) + 0.027 | Lake Taihu, Fuchunjiang Reservoir, and Liangxi River | GHPS | R2 = 0.85, MAPE= 15.0% |
| Shang et al. [34] | TP = −5.3248 × ln(B4)/B4 + 0.0885 | Poyang lake | Landsat 8 | R2 = 0.7589, RMSE = 0.0048 mg/L |
| Wu et al. [35] | Ln(TP) = −21.45(B3/B2) − 14.42(B1/B3) +42.99(B1) + 27.1 | Qiantang River | Landsat TM | R2 = 0.77, RMSE = 0.77 mg/L |
| Du et al. [36] | TP= −6.739 × (B488 − B670) −0.217 × (B670 − B865)/(B670 + B865) + 0.303; | Lake Taihu | GOCI | R2 = 0.898 MAE = 33.642% |
| Liu et al. [37] | TP = −15.51 × B3+ 2.81 | Lake Cihu | IKONOS | R2 = 0.84, RMSE = 0.17 mg/L |
| Cruz-Retana et al. [38] | LogTP = 1.3544 + 0.1240 × (B5/B4) + 0.04610(B5/B6) | A water body in the Mexican highlands | Landsat 8 OLI | R2 = 0.79, RMSE = 9.63 mg/L |
| Zhao et al. [39] | TP = −33.64X3 + 19.39X2 − 1.79X + 0.08766, X= 1 − 3(B7 + B8A + B11) [min(B7, B8A, B11)] | Yangtze River | Sentinel-2A | R2 = 0.74, RMSE = 0.07 mg/L |
| Author | Inverse Model | Study Area | Sensor | Error |
|---|---|---|---|---|
| Dong et al. [40] | NH3-N = 0.474 × B550/B488 + 0.276; | Danjiangkou Reservoir | Sentinel-2 | R2 = 0.739, RMSE = 0.0107 mg/L |
| He et al. [41] | ln(NH3-N) = −7.177 + 1.93ln(B7) + 0.1323(B6) −2.185(B6/B3)−0.07648B1 | Guanting Reservoir | Landsat 5 TM | R2 = 0.806, MRE = 28% |
| Ma et al. [42] | NH3-N =1.7313((B3 + B4)/B1) − 3.9968 | Tangxun lake | GF-2, GF-6 | R2 = 0.8497, MRE = 21.53% |
| Wu et al. [43] | NH3-N =0.219 + 0.001(B5 + B7) | Haihe River | Landsat 8 OLI | R2 = 0.611, MAD = 0.404 |
| Al-Shaibah et al. [44] | NH3-N= 0.8 × (Bred + BNIR) + (Bblue/BNIR) × (Bblue + BNIR)+ (Bblue/BNIR) × 0.099 | Erlong Lake | Landsat TM5, ETM7, and OLI8 | R2 = 0.862, RMSE = 0.645 mg/L |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Qiu, Z.; Hu, Y.; Zhao, D.; Zhao, A.; Lin, H.; Zhan, Y.; Wang, Y.; Zhang, Y. Monitoring the Water Quality Distribution Characteristics in the Huaihe River Basin Based on the Sentinel-2 Satellite. Water 2024, 16, 860. https://doi.org/10.3390/w16060860
Shi X, Qiu Z, Hu Y, Zhao D, Zhao A, Lin H, Zhan Y, Wang Y, Zhang Y. Monitoring the Water Quality Distribution Characteristics in the Huaihe River Basin Based on the Sentinel-2 Satellite. Water. 2024; 16(6):860. https://doi.org/10.3390/w16060860
Chicago/Turabian StyleShi, Xuanshuo, Zhongfeng Qiu, Yunjian Hu, Dongzhi Zhao, Aibo Zhao, Hui Lin, Yating Zhan, Yu Wang, and Yuanzhi Zhang. 2024. "Monitoring the Water Quality Distribution Characteristics in the Huaihe River Basin Based on the Sentinel-2 Satellite" Water 16, no. 6: 860. https://doi.org/10.3390/w16060860
APA StyleShi, X., Qiu, Z., Hu, Y., Zhao, D., Zhao, A., Lin, H., Zhan, Y., Wang, Y., & Zhang, Y. (2024). Monitoring the Water Quality Distribution Characteristics in the Huaihe River Basin Based on the Sentinel-2 Satellite. Water, 16(6), 860. https://doi.org/10.3390/w16060860







