Study on Multi-Measures Joint Optimization Regulation of Temperature Control and Ice Melting for Water Conveyance Projects in Cold Regions
Abstract
:1. Introduction
2. Method
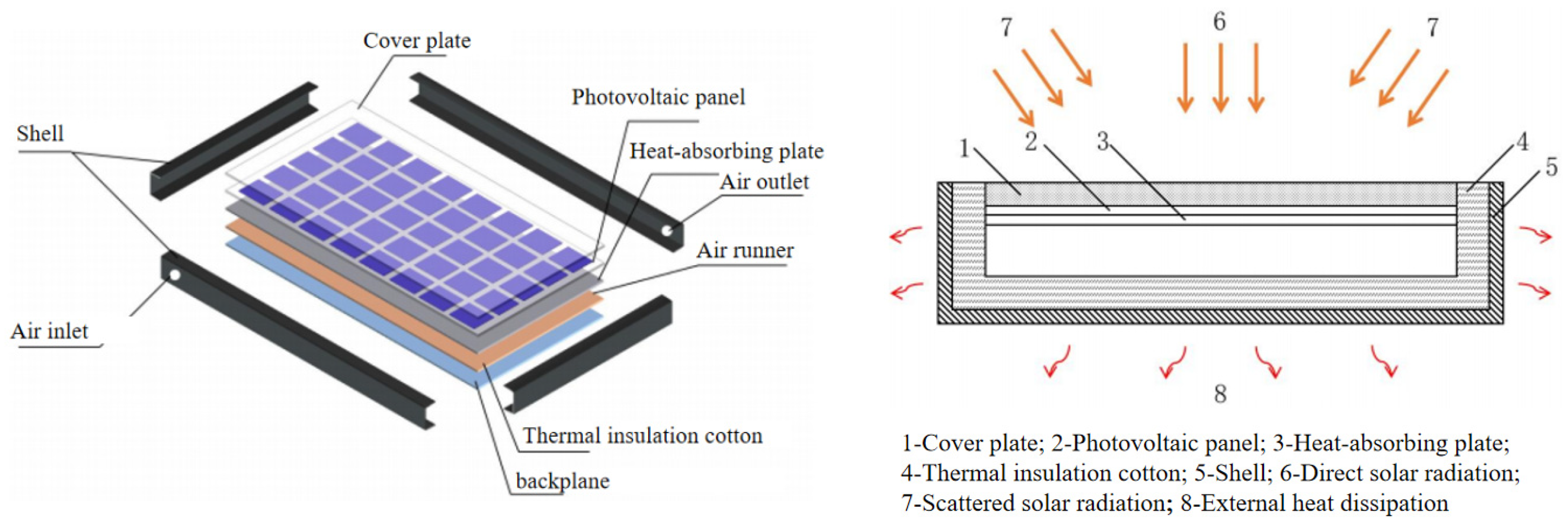
2.1. Basic Principles of Ice-Melting Measures
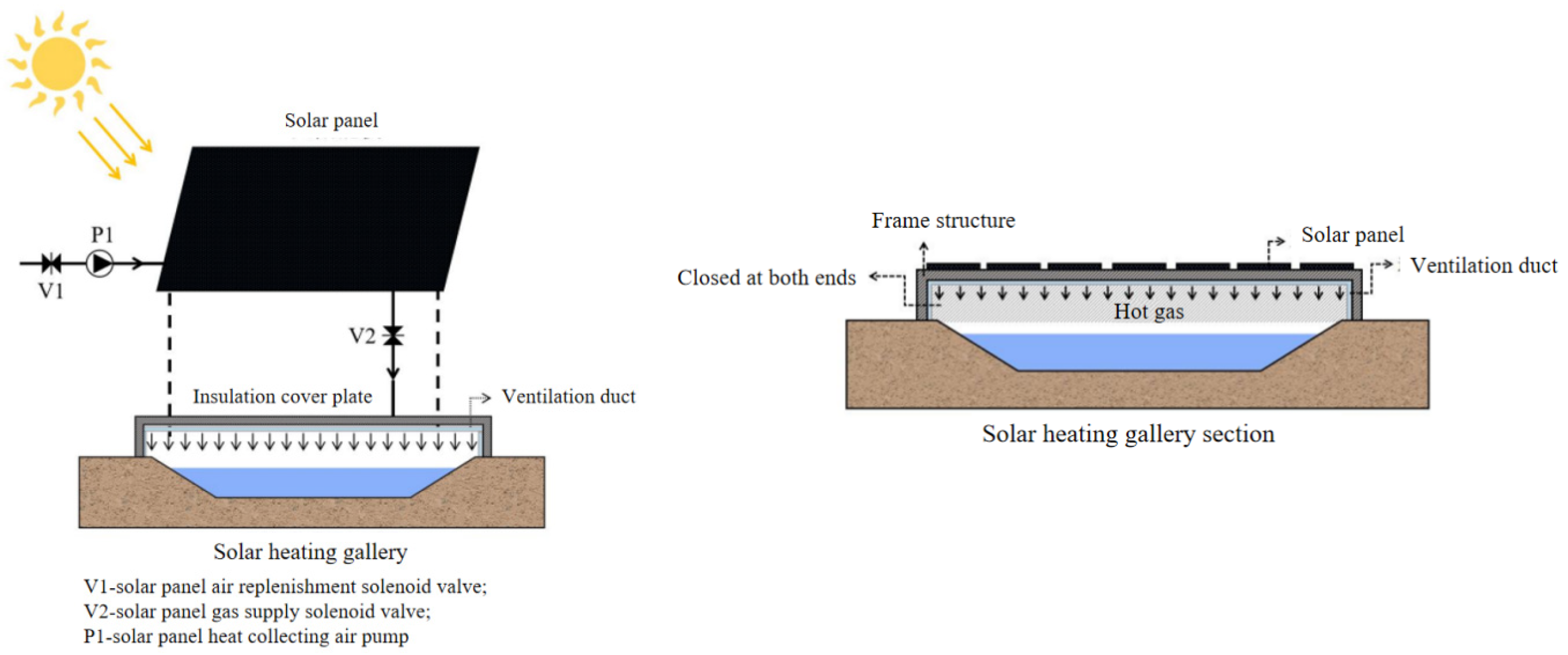
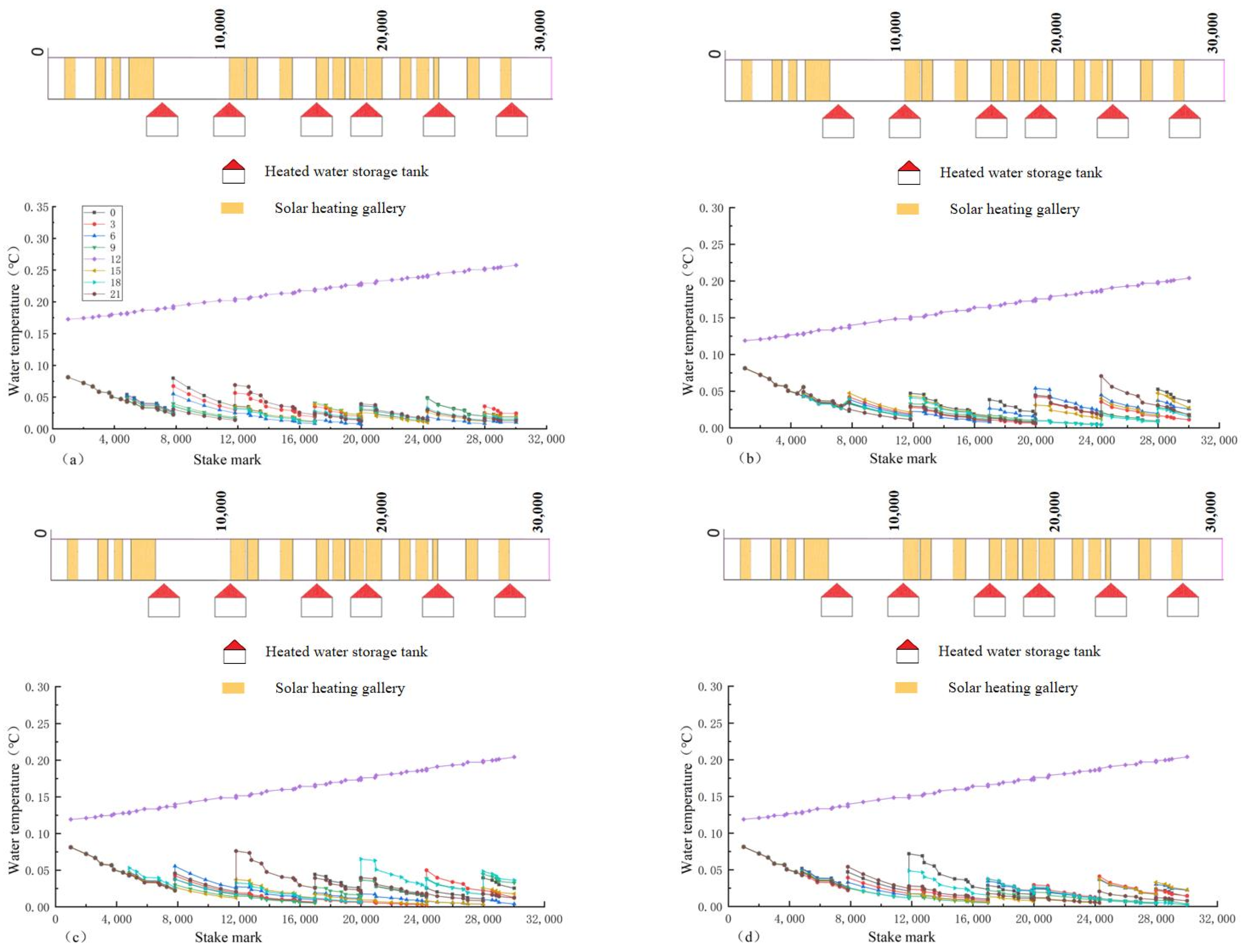
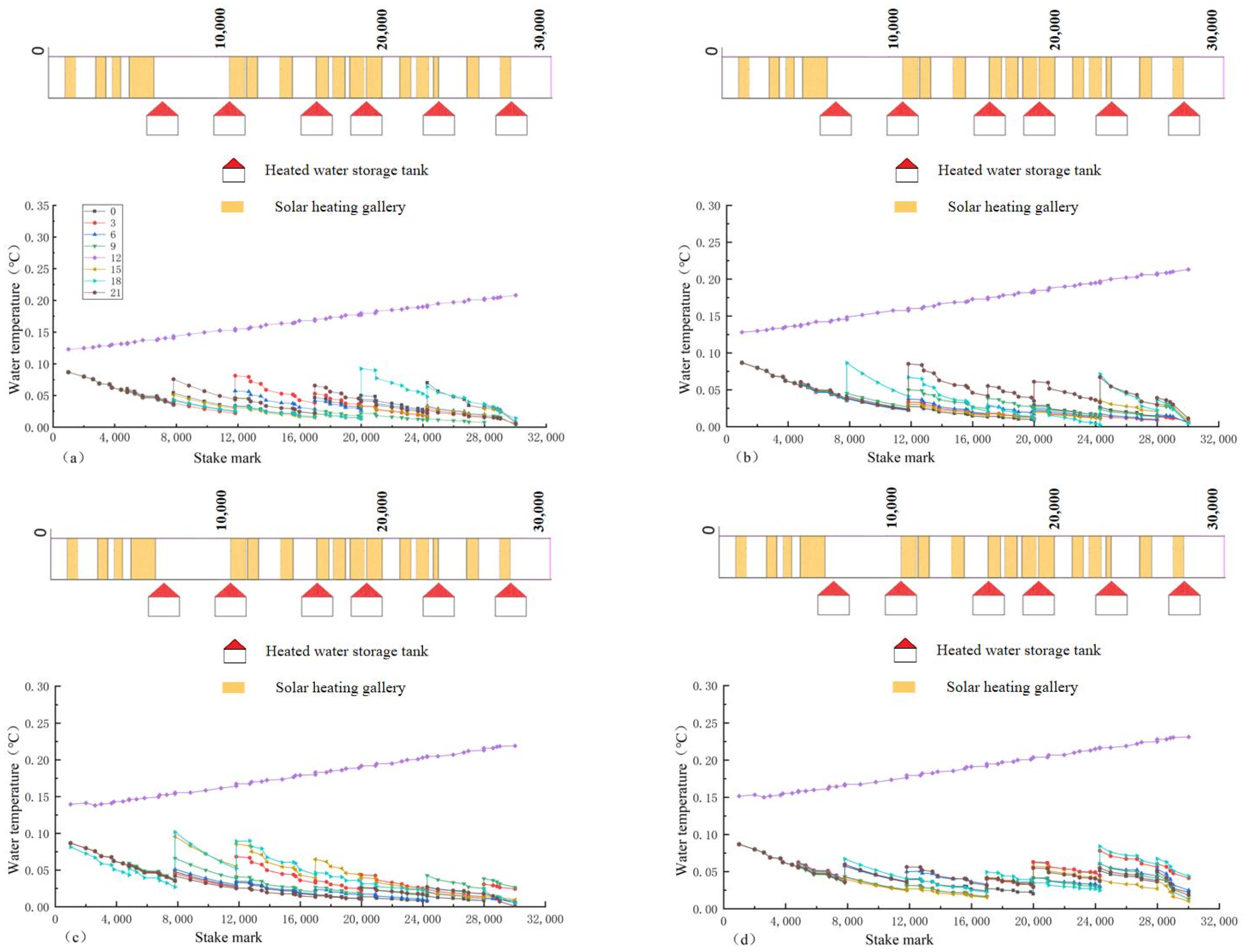
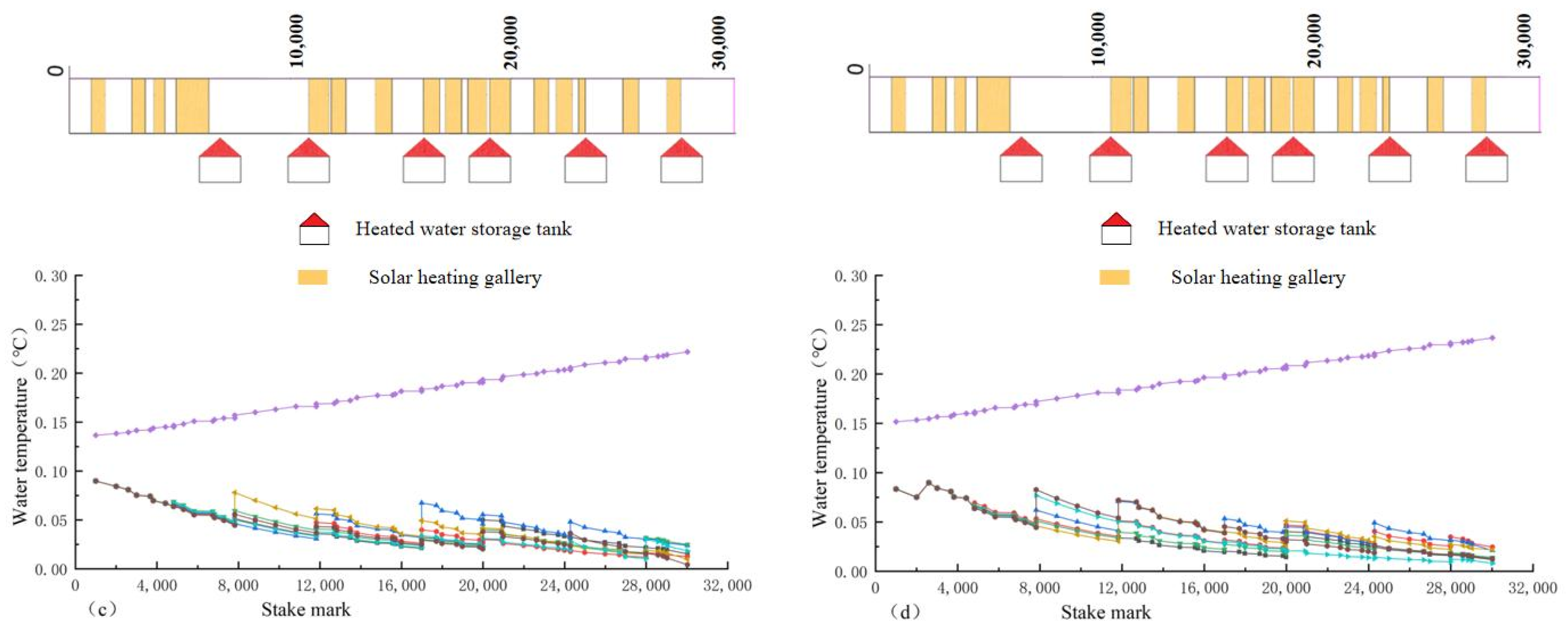
2.1.1. Solar Heating Gallery
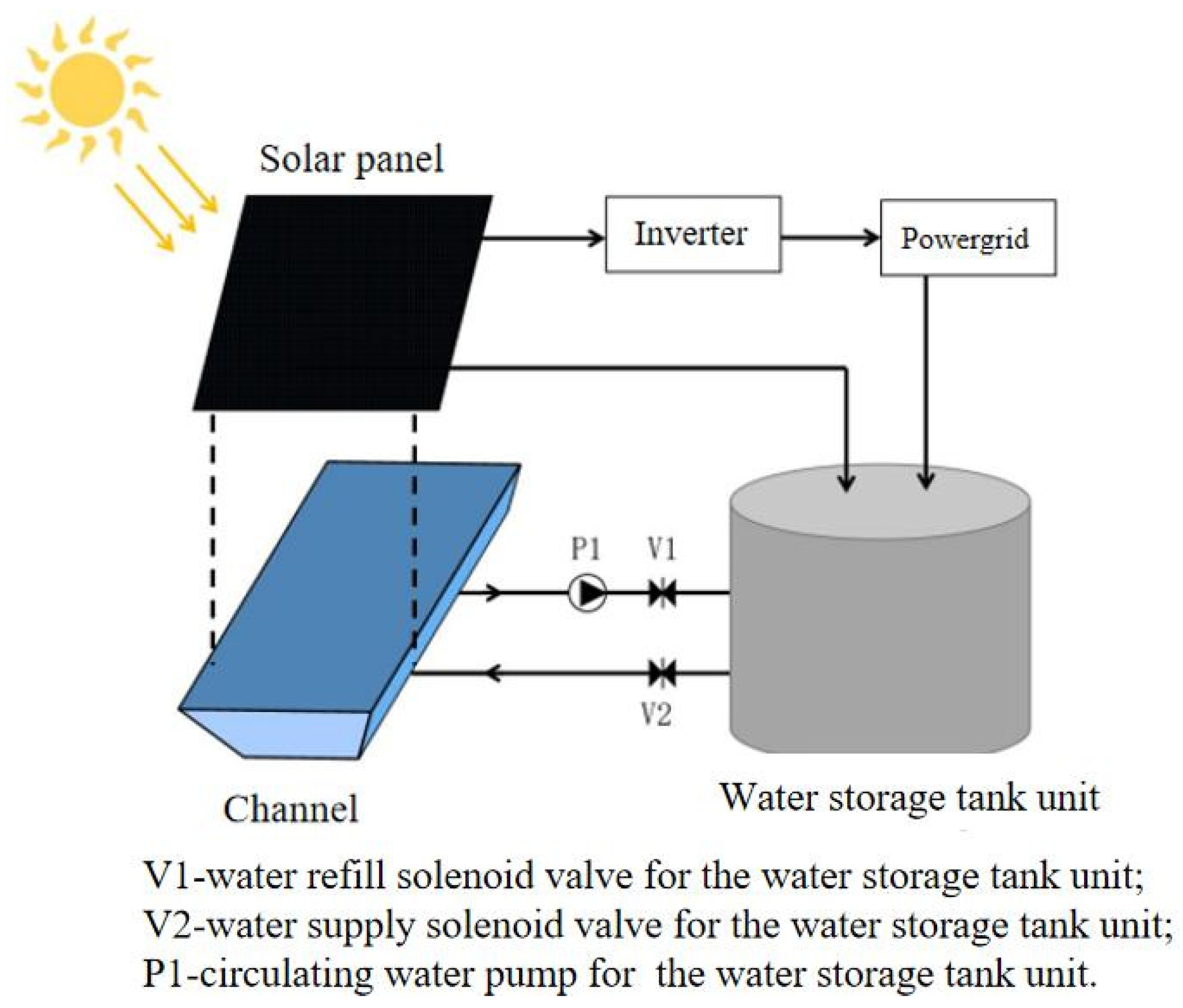
2.1.2. Heated Water Storage Tank
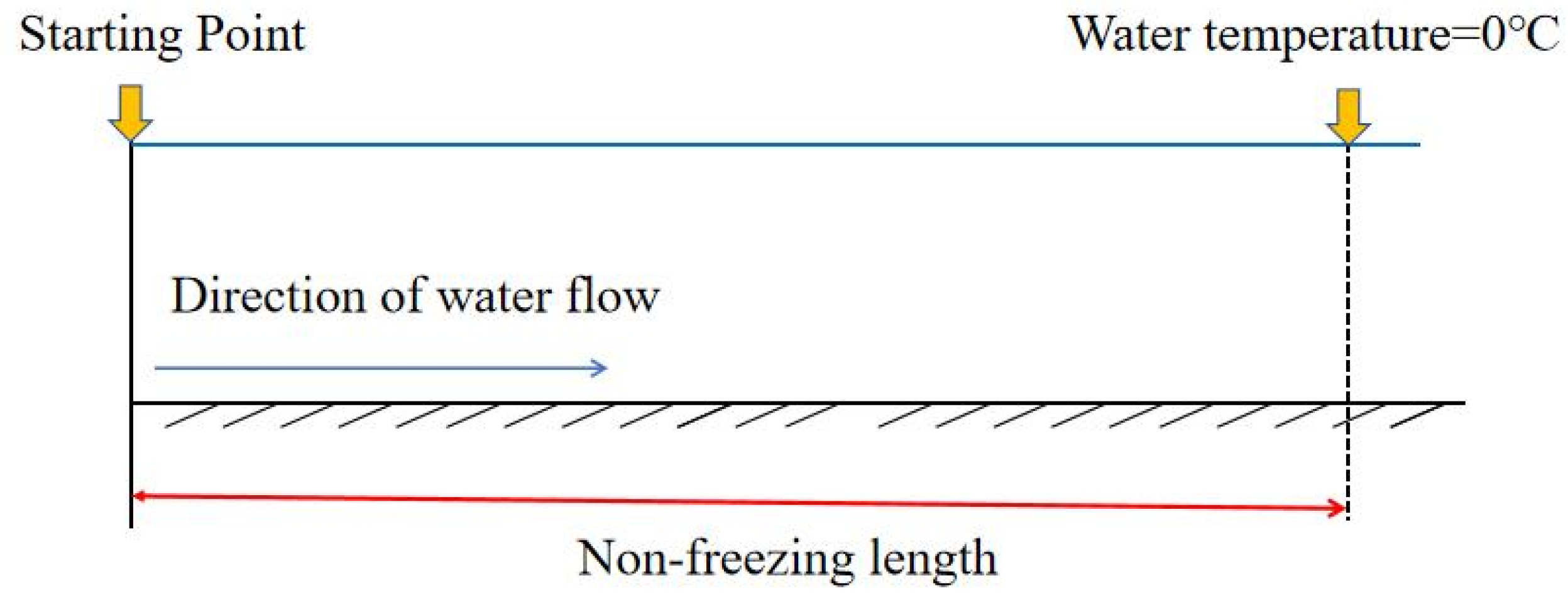
2.1.3. Ice Melting in Water Conveyance Channels
2.2. Single-Objective Function
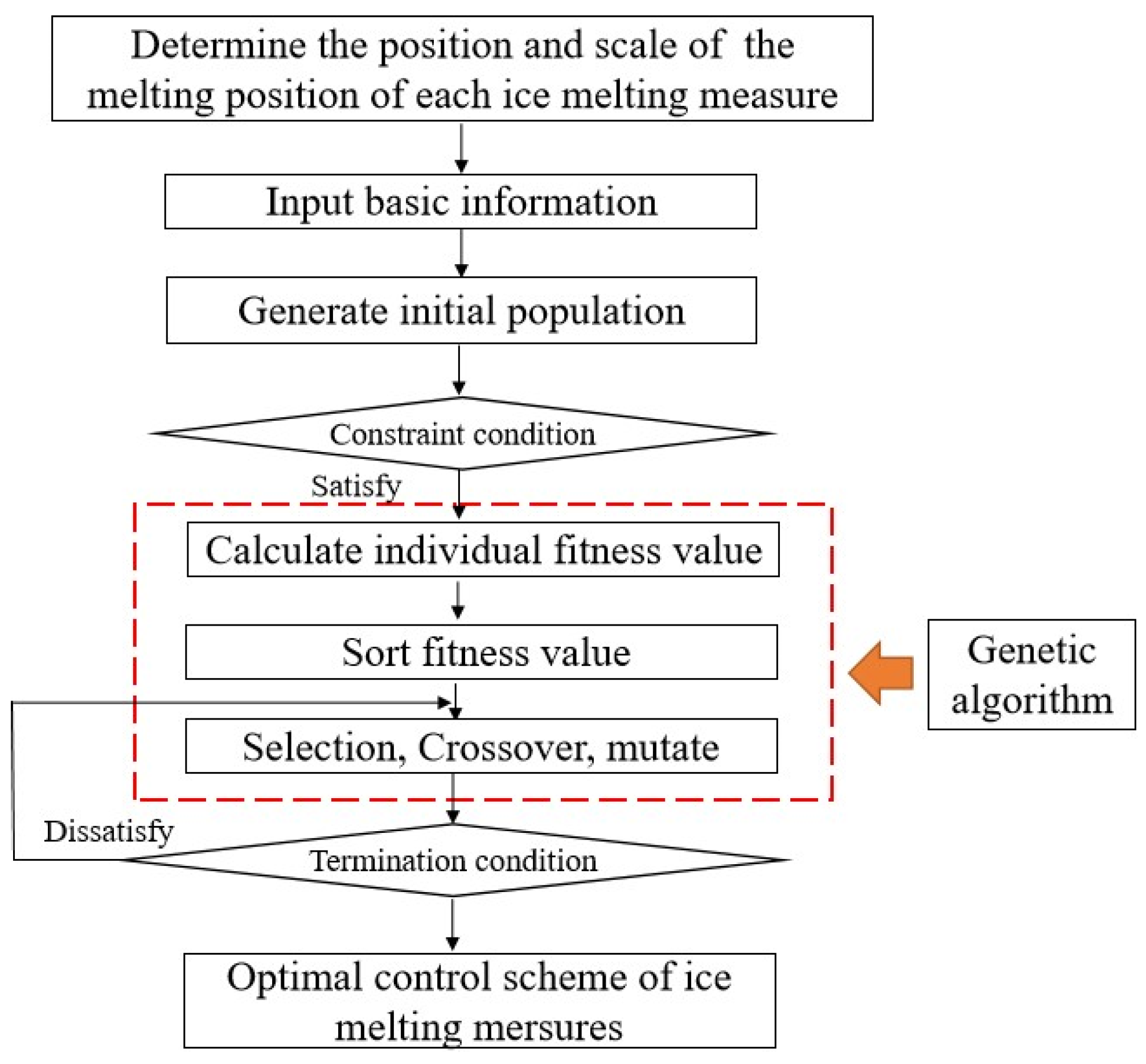
2.3. Genetic Algorithm
3. A Case Study
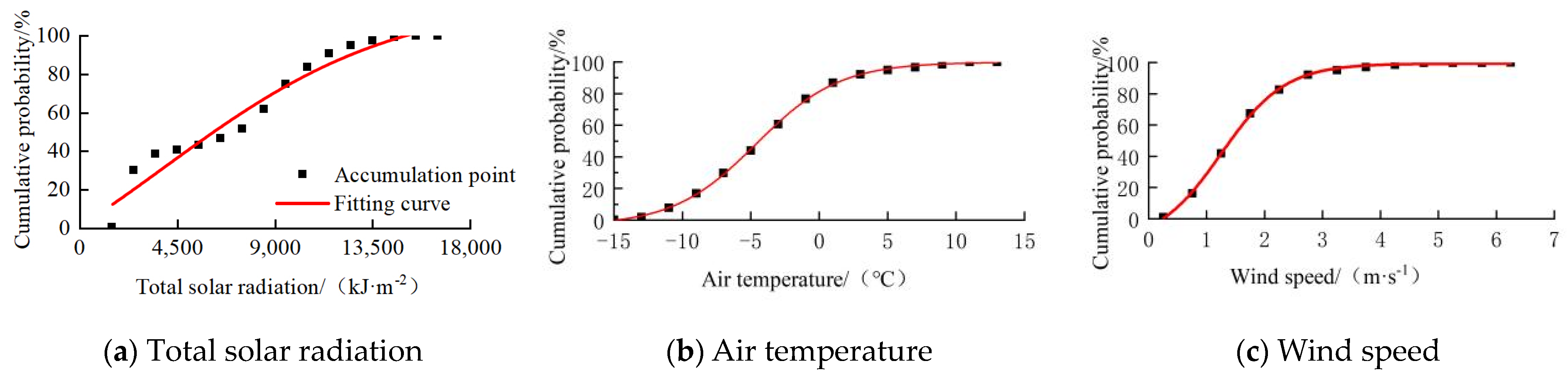
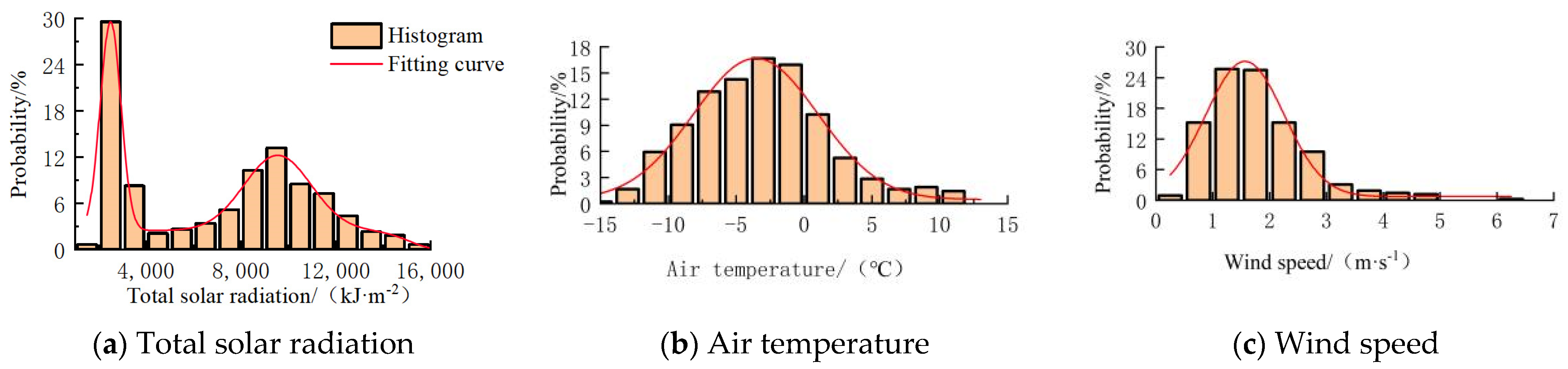
3.1. Basic Data Description
3.2. Objective Functions and Decision Variables
3.2.1. Objective Functions
3.2.2. Decision Variables
3.2.3. Constraint Conditions
- (1)
- Constraints on the injection flow:
- (2)
- Constraints on the injection water temperature:
- (3)
- Constraints on the non-freezing length of each channel:
- (4)
- Equation (3) is used to calculate the non-freezing length and node water temperature, so that the length of each redivided channel meets the conditions, then the time–history change curve of the water temperature of the whole channel can be obtained. The constraints on the heating power of the heated water storage tank are as follows:
3.3. Model Solving Procedure
3.4. Setting of the GA Optimization
4. Result and Discussion
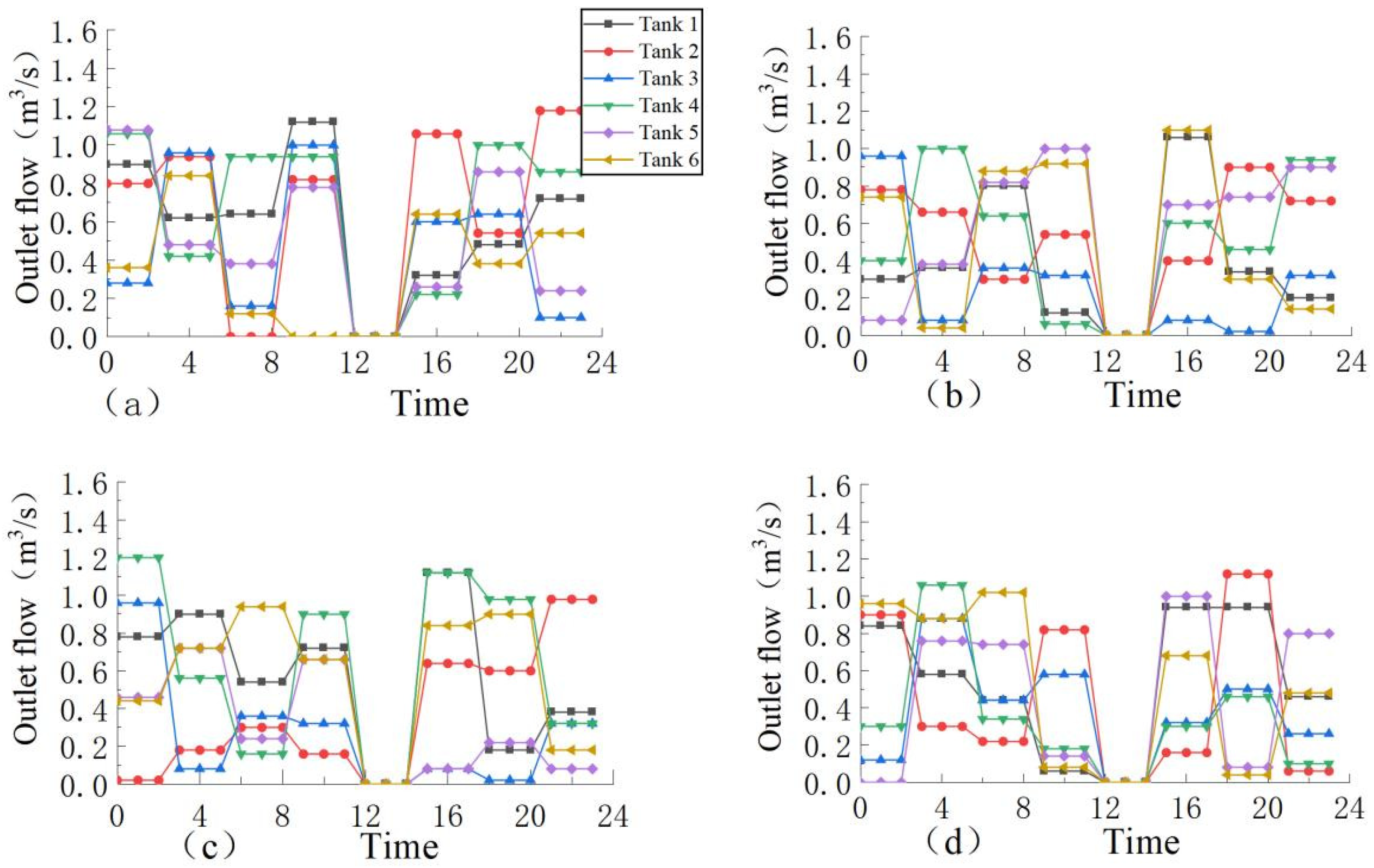
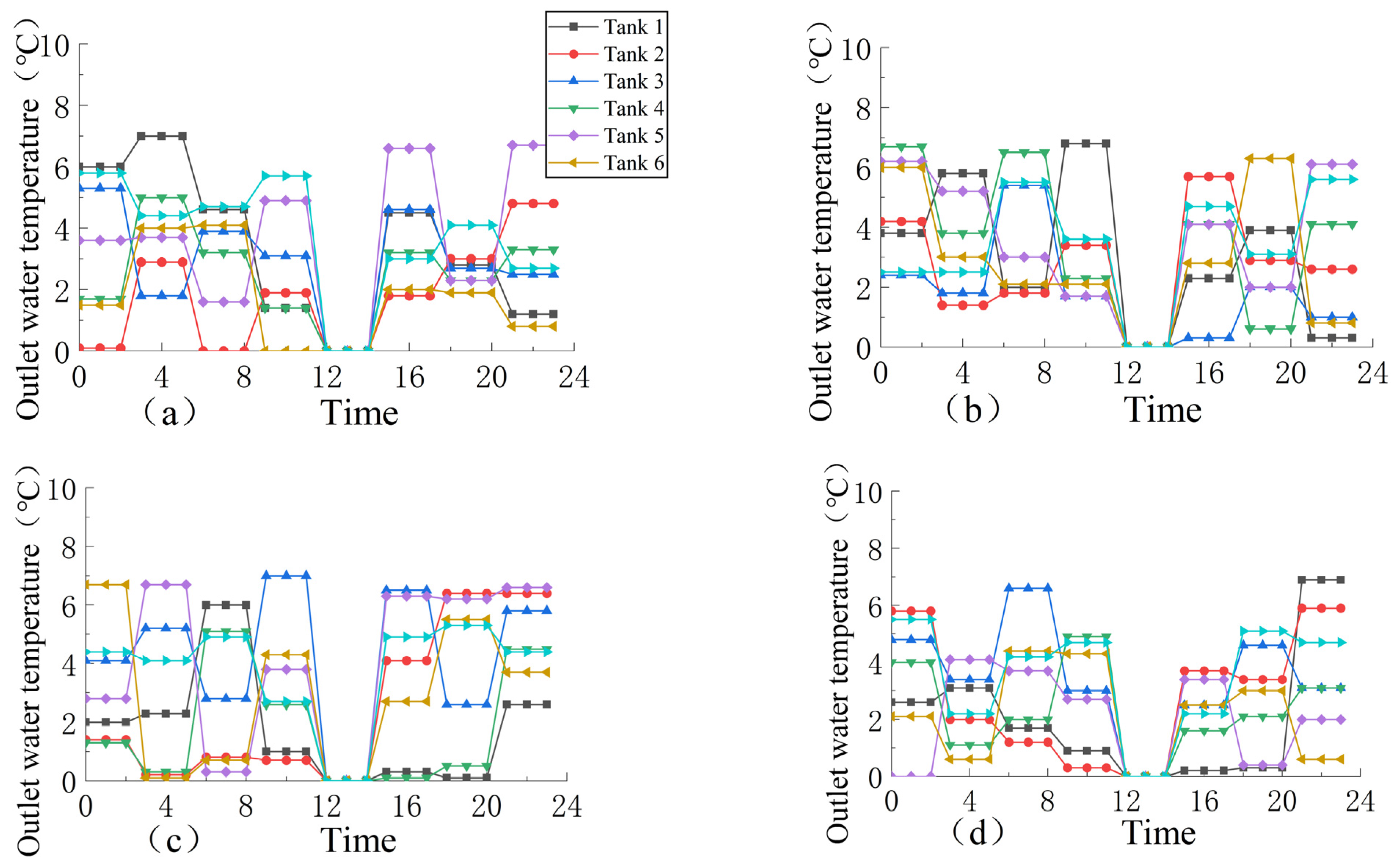
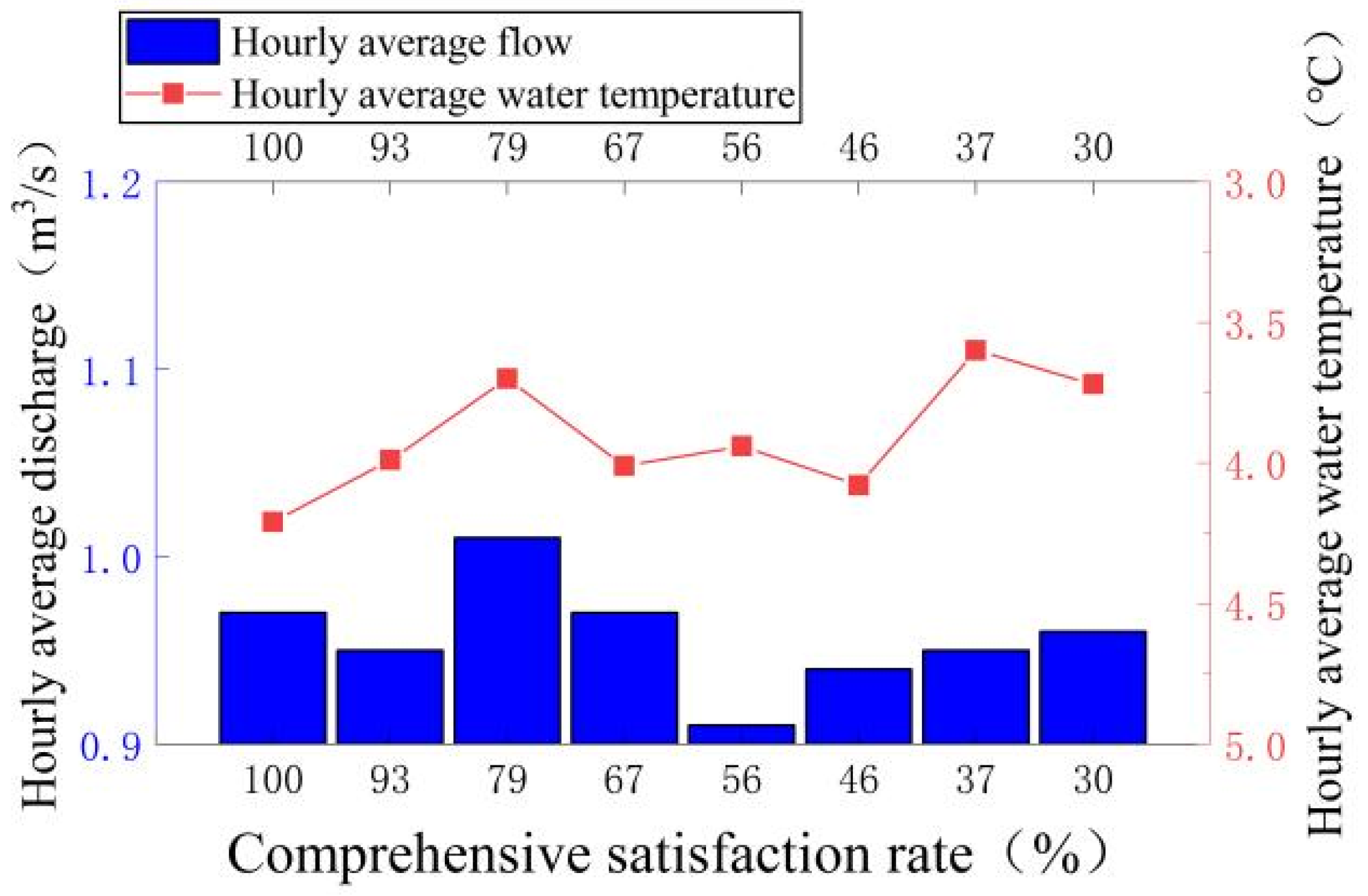
4.1. Analysis of Results of Different Comprehensive Satisfaction Rates
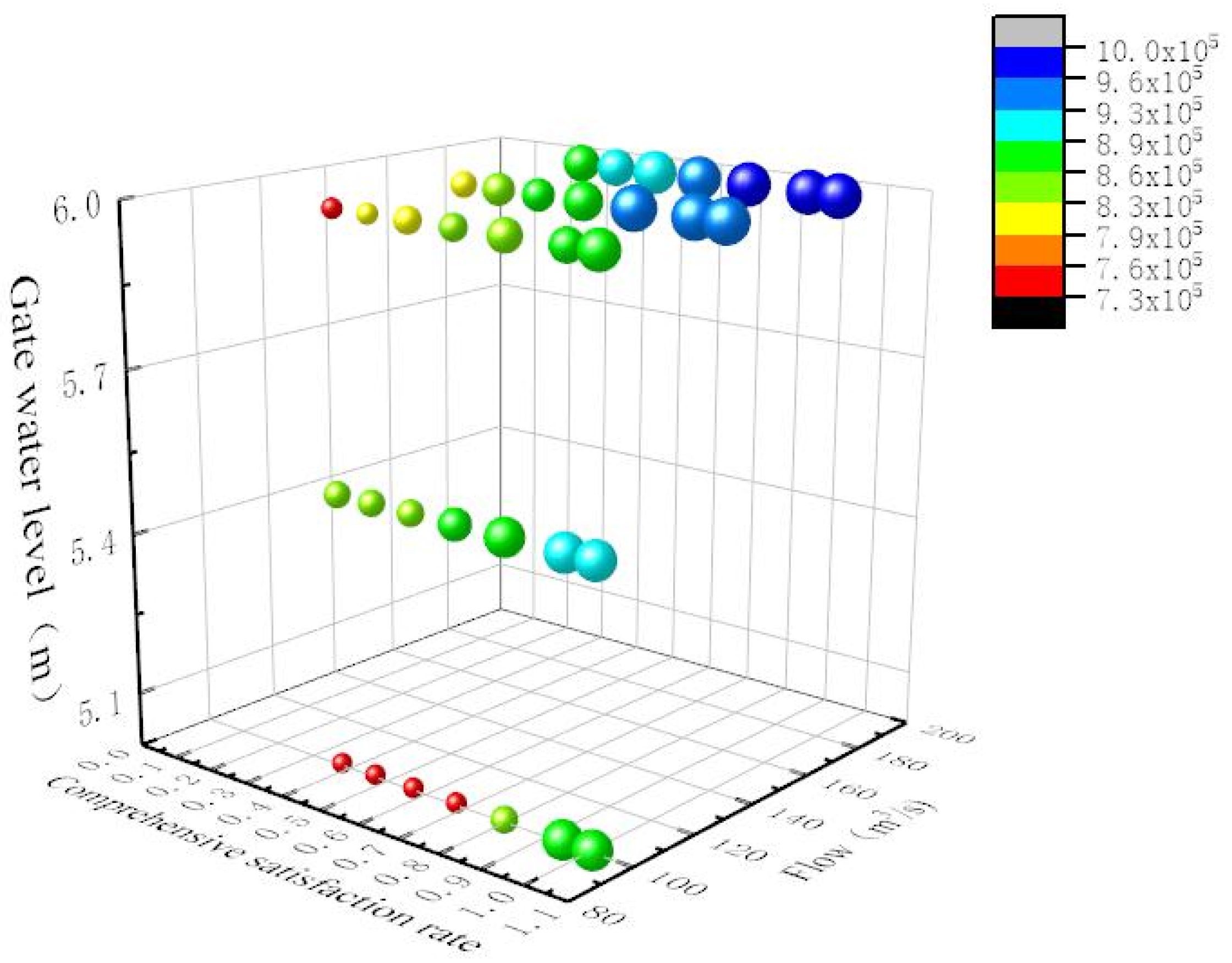
4.2. Analysis of the Influence of Water Flow
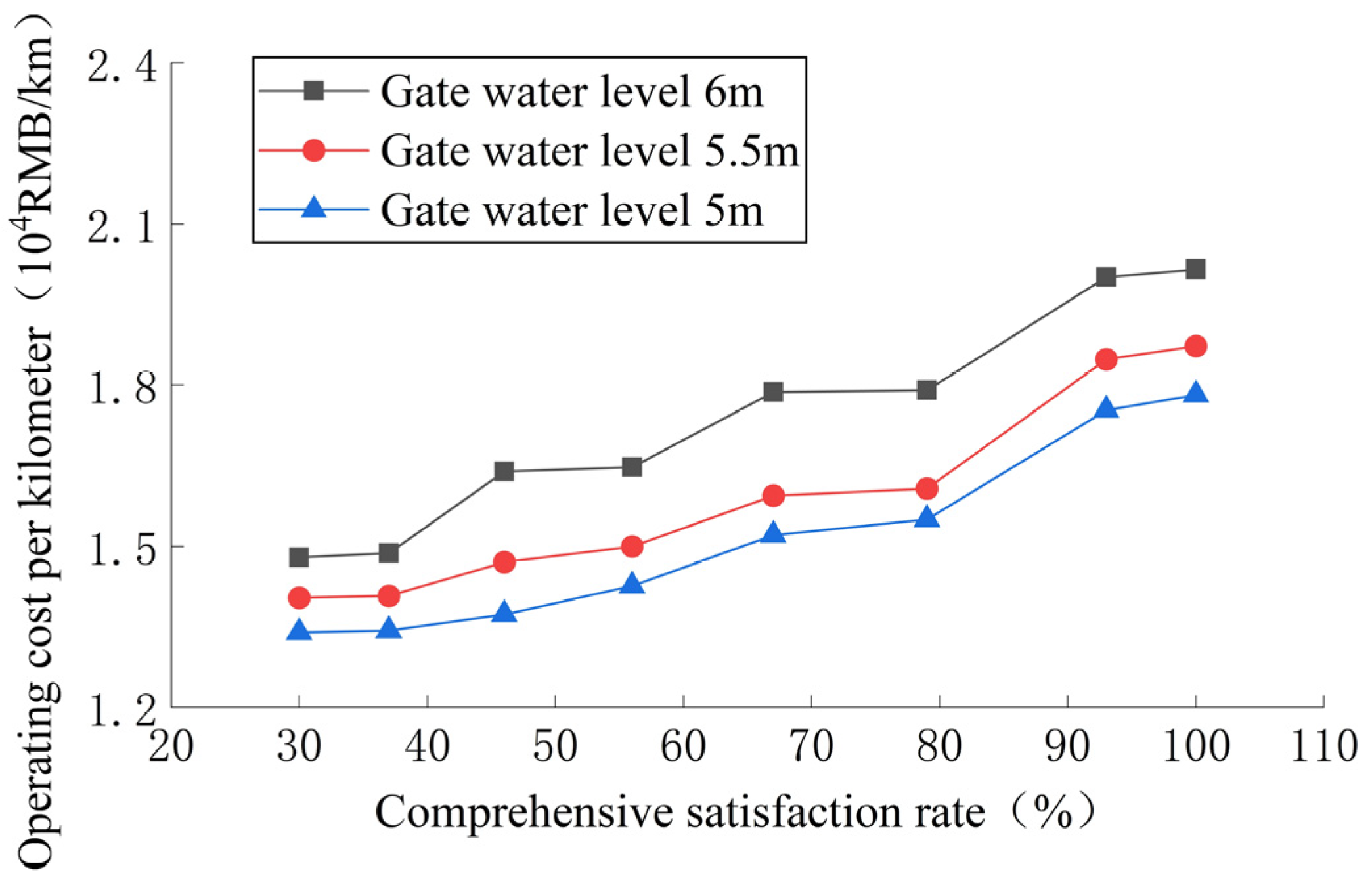
4.3. Analysis of the Influence of Downstream Depth before the Gate
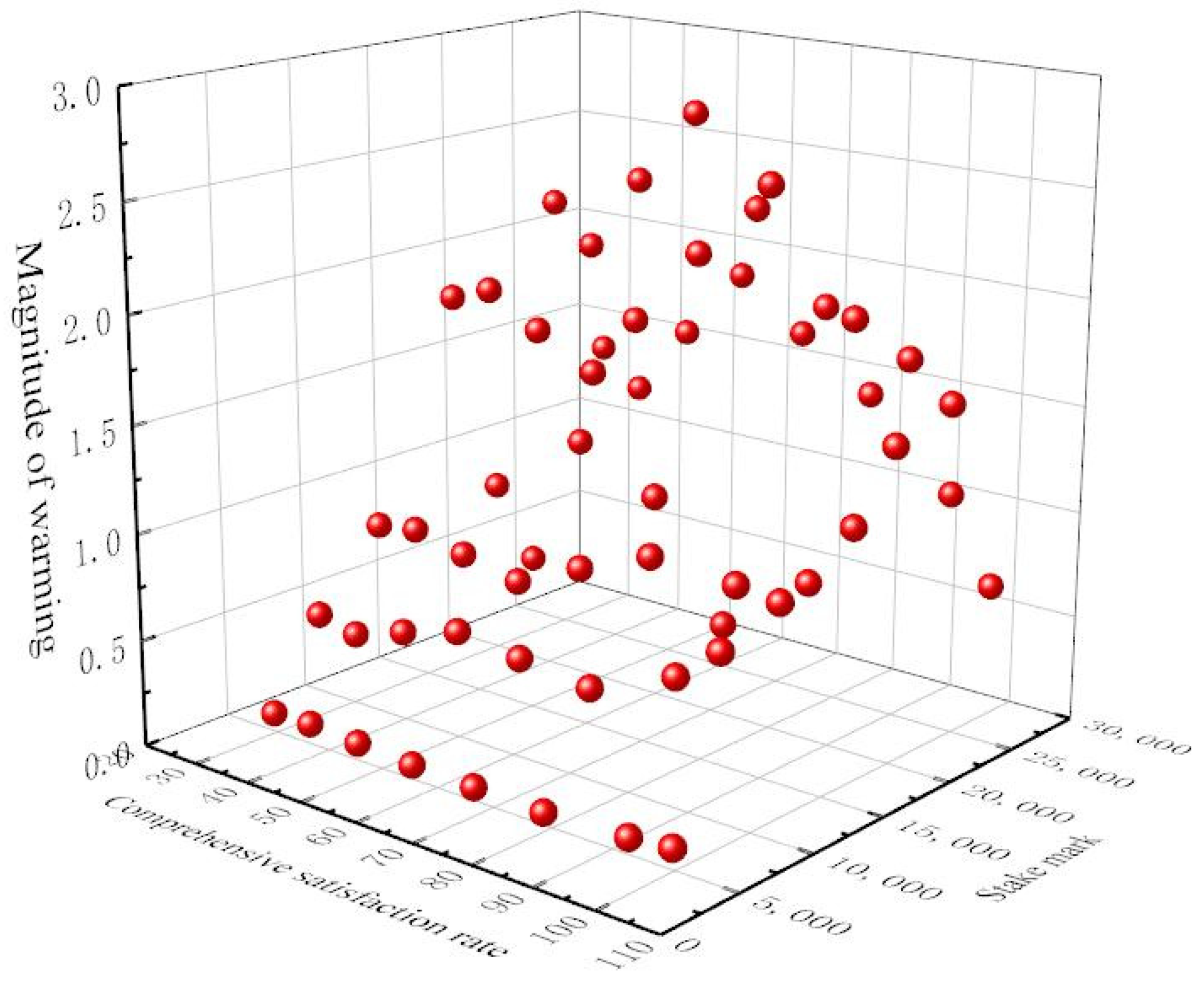
4.4. Multi-Factor Relationship Fitting
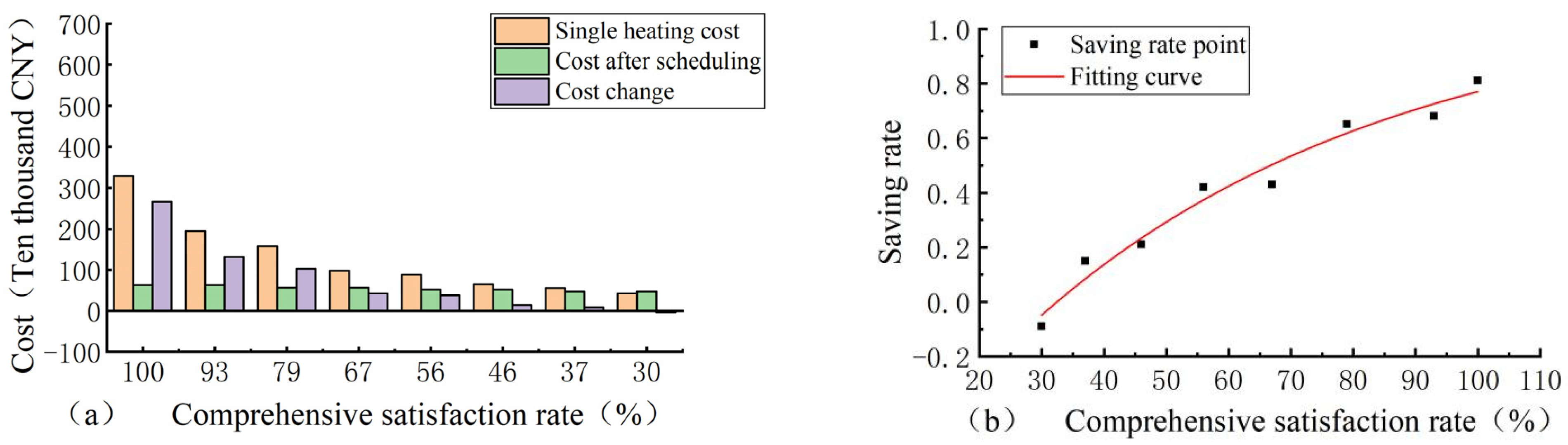
4.5. Cost and Benefit Analysis
4.5.1. Cost Comparison
4.5.2. Benefit Analysis
5. Conclusions
- (i)
- Under the optimal regulation of the two ice-melting measures, the overall water temperature along the lines presents a “ladder shape”, and the average hourly flow and water temperature have the characteristics of overall unity and local complementarity. The higher the comprehensive satisfaction rate, the greater the average hourly operating cost, but when the comprehensive satisfaction rate is less than 56%, the change range of the operating cost slows down and has no obvious change. The decreasing trend in the water temperature of the channel with the heating gallery is much slower than that without the heating gallery, and the decrease range is 15%.
- (ii)
- With an increase in the water flow, the operating cost also increases, but under the strong control of the velocity of the flow, its growth rate slows down to a certain extent, and the average growth rate decreases from 18.3% to 13.1% when the water flow rate increases by 40 . With a decrease in the downstream depth in front of the gate, the velocity of the flow increases, the heat transfer efficiency increases, and the operating cost decreases.
- (iii)
- Through the analysis of the costs and benefits of the ice-melting measures, with the decrease in the comprehensive satisfaction rate, their operating costs gradually becomes smaller, and the cost advantages of the ice-melting measures compared with other methods gradually diminish. In addition, the benefits of water transfer flow, power generation, and water saving are very considerable, far exceeding the operating costs, which shows that the ice-melting measures have broad prospects.
- (iv)
- The change in the operating costs of the ice-melting measures is a relatively dynamic process, which will vary with the change in the location and scale of the ice-melting measures. The research conclusions in this paper are only applicable to the research object in this paper, but the research method in this paper can be extended to other similar projects and has a good guiding significance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PV | photovoltaic |
| PV/T | photovoltaic–solar-thermal |
| ITC | investment tax credit |
| PTC | production tax credit |
| WSPV | water surface photovoltaic |
| PHS | pumped hydro storage |
| CSA | crow search algorithm |
| CSAAC-AP | CSA with an adaptive chaotic awareness probability |
| GA | genetic algorithm |
| PSO | particle swarm optimization |
| IRPG | independent regional power grid |
| NPV | net present value |
References
- Wang, L.Z. Status and Prospect of Green Energy. World Sci. Technol. Res. Dev. 2003, 5, 49–53. [Google Scholar] [CrossRef]
- Makkonen, L.; Tikanmäki, M. Modelling Frazil and Anchor Ice on Submerged Objects. Cold Reg. Sci. Technol. 2018, 151, 64–74. [Google Scholar] [CrossRef]
- Wazney, L.; Clark, S.P.; Malenchak, J.; Knack, I.; Shen, H.T. Numerical Simulation of River Ice Cover Formation and Consolidation at Freeze-Up. Cold Reg. Sci. Technol. 2019, 168, 102884. [Google Scholar] [CrossRef]
- Zhao, X. Research on Water Delivery Capacity and Ice Hazard Control of Large-Scale Water Conveyance Project in the Ice Period; Tianjin University: Tianjin, China, 2011. [Google Scholar]
- Liu, G.; Guan, G.; Wang, C. Transition Mode of Long Distance Water Delivery Project before Freezing in Winter. J. Hydroinform. 2013, 15, 306–320. [Google Scholar] [CrossRef]
- Mu, X.P.; Chen, W.X.; Liu, S.; Zhong, H.R.; Zhang, X.Y. Study on hydraulic control conditions of main canal in South-to-North Water Diversion Middle Route Project. J. Chin. Inst. Water Resour. Hydropower Res. 2018, 16, 90–97. [Google Scholar] [CrossRef]
- Mu, X.P.; Chen, W.X.; Guo, X.C.; Cui, W. Study on long-distance water transfer channel with thermal insulation cover in winter. J. Hydraul. Eng. 2013, 44, 1071–1079. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Wang, Z.; Zhu, X.; Cai, Z.; Jiang, H. Research on Film Insulation Technology for Artificial, Open Water Delivery Canals Based on Solar Heat Radiation Utilization. Sustainability 2022, 14, 5720. [Google Scholar] [CrossRef]
- Dehghan, A.A.; Dehghani, A.R. Experimental and Theoretical Investigation of Thermal Performance of Underground Cold-Water Reservoirs. Int. J. Therm. Sci. 2011, 50, 816–824. [Google Scholar] [CrossRef]
- Liu, L.; Sun, Q.; Li, H.; Yin, H.; Ren, X.; Wennersten, R. Evaluating the Benefits of Integrating Floating Photovoltaic and Pumped Storage Power System. Energy Convers. Manag. 2019, 194, 173–185. [Google Scholar] [CrossRef]
- Zeng, M.; Li, C.; Zhou, L. Progress and Prospective on the Police System of Renewable Energy in China. Renew. Sustain. Energy Rev. 2013, 20, 36–44. [Google Scholar] [CrossRef]
- Bird, L.; Lew, D.; Milligan, M.; Carlini, E.M.; Estanqueiro, A.; Flynn, D.; Gomez-Lazaro, E.; Holttinen, H.; Menemenlis, N.; Orths, A.; et al. Wind and Solar Energy Curtailment: A Review of International Experience. Renew. Sustain. Energy Rev. 2016, 65, 577–586. [Google Scholar] [CrossRef]
- Michael, S. Global Market Outlook for Solar Power 2021–2025; Solar Power Europe: Brussels, Belgium, 2021; Volume 7, pp. 1–68. [Google Scholar]
- Colmenar-Santos, A.; Buendia-Esparcia, Á.; de Palacio-Rodríguez, C.; Borge-Diez, D. Water Canal Use for the Implementation and Efficiency Optimization of Photovoltaic Facilities: Tajo-Segura Transfer Scenario. Sol. Energy 2016, 126, 168–194. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Zhuo, R.; Wang, X. Optimal Operation of Independent Regional Power Grid with Multiple Wind-Solar-Hydro-Battery Power. Appl. Energy 2019, 235, 1541–1550. [Google Scholar] [CrossRef]
- Ma, C.; Liu, Z.; He, W. Water Surface Photovoltaic along Long-Distance Water Diversion Projects and Its Co-Benefits. J. Clean. Prod. 2022, 331, 129924. [Google Scholar] [CrossRef]
- Blake, M. The long read: Canal-top solar solutions. PV Magazine, 11 June 2022. [Google Scholar]
- Wolf, M. Performance Analyses of Combined Heating and Photovoltaic Power Systems for Residences. Energy Convers. 1976, 16, 79–90. [Google Scholar] [CrossRef]
- Chow, T.T.; He, W.; Ji, J. An Experimental Study of Façade-Integrated Photovoltaic/Water-Heating System. Appl. Therm. Eng. 2007, 27, 37–45. [Google Scholar] [CrossRef]
- Rounis, E.D.; Athienitis, A.K.; Stathopoulos, T. Multiple-inlet Building Integrated Photovoltaic/Thermal system modelling under varying wind and temperature conditions. Sol. Energy 2016, 139, 157–170. [Google Scholar] [CrossRef]
- Ji, Y.S. Research on Solar Energy Temperature Increasing and Temperature Control Device for Long Distance Water Conveying Channel; Tianjin University: Tianjin, China, 2022. [Google Scholar]
- BanJiu, C.R.; Cao, S.Y.; Li, R.; Liu, X.N. New Exploration on Solar Energy Deice Hydropower Plant in Tibet. China Rural Water Hydropower 2003, 6, 22–24. [Google Scholar]
- Carbonell, D.; Philippen, D.; Haller, M.Y.; Frank, E. Modeling of an Ice Storage Based on a De-Icing Concept for Solar Heating Applications. Sol. Energy 2015, 121, 2–16. [Google Scholar] [CrossRef]
- Zhang, Y.N. Study on the Influence of Recharge and Pumping on Water Temperature of Baiquan Underground Reservoir and the Optimization Operation Mode of Multiple Wells; Tianjin University: Tianjin, China, 2022. [Google Scholar]
- Spencer, R.S.; Macknick, J.; Aznar, A.; Warren, A.; Reese, M.O. Floating Photovoltaic Systems: Assessing the Technical Potential of Photovoltaic Systems on Man-Made Water Bodies in the Continental United States. Environ. Sci. Technol. 2019, 53, 1680–1689. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. Performance Assessment of Different Photovoltaic Technologies for Canal-Top and Reservoir Applications in Subtropical Humid Climate. IEEE J. Photovolt. 2019, 9, 722–732. [Google Scholar] [CrossRef]
- McKuin, B.; Zumkehr, A.; Ta, J.; Bales, R.; Viers, J.H.; Pathak, T.; Campbell, J.E. Energy and Water Co-Benefits from Covering Canals with Solar Panels. Nat. Sustain. 2021, 4, 609–617. [Google Scholar] [CrossRef]
- Zhang, N.; Chen, G.; Xu, Y.; Xu, X.; Yu, L. Power Generation, Evaporation Mitigation, and Thermal Insulation of Semitransparent Polymer Solar Cells: A Potential for Floating Photovoltaic Applications. ACS Appl. Energy Mater. 2019, 2, 6060–6070. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.J.; Chang, L.C.; Lee, W.D.; Huang, A.; Xu, C.Y.; Guo, S. An Advanced Complementary Scheme of Floating Photovoltaic and Hydropower Generation Flourishing Water-Food-Energy Nexus Synergies. Appl. Energy 2020, 275, 115389. [Google Scholar] [CrossRef]
- Ye, B.; Jiang, J.; Liu, J. Feasibility of Coupling Pv System with Long-Distance Water Transfer: A Case Study of China’s “South-to-North Water Diversion”. Resour. Conserv. Recycl. 2021, 164, 105194. [Google Scholar] [CrossRef]
- Wang, G.Z. Optimization distribution model for groundwater and water diverted from the Yellow river. J. Water Resour. Water Eng. 2004, 15, 44–48. [Google Scholar]
- Yang, L.L.; Wang, Y.X.; Xie, X.M.; Ye, Y.; Ding, F. Study on Water Resources Allocation Model Based on Joint Operation of Surface Water and Ground Water. Water Resour. Power 2010, 28, 23–26. [Google Scholar]
- Makhdoomi, S.; Askarzadeh, A. Optimizing Operation of a Photovoltaic/Diesel Generator Hybrid Energy System with Pumped Hydro Storage by a Modified Crow Search Algorithm. J. Energy Storage 2020, 27, 101040. [Google Scholar] [CrossRef]
- Edwards, K.C.; Finn, D.P. Generalised Water Flow Rate Control Strategy for Optimal Part Load Operation of Ground Source Heat Pump Systems. Appl. Energy 2015, 150, 50–60. [Google Scholar] [CrossRef]
- Das, B.K.; Zaman, F. Performance Analysis of a PV/Diesel Hybrid System for a Remote Area in Bangladesh: Effects of Dispatch Strategies, Batteries, and Generator Selection. Energy 2019, 169, 263–276. [Google Scholar] [CrossRef]
- Kusakana, K. Hybrid DG-PV with Groundwater Pumped Hydro Storage for Sustainable Energy Supply in Arid Areas. J. Energy Storage 2018, 18, 84–89. [Google Scholar] [CrossRef]
- Zhang, Y. Research on Water Temperature Prediction and Water Temperature Control for Ice-Damage-Free Water Delivery in the Middle Route o South-to-North Water Transfer Project Trunk Canal; Tianjin University: Tianjin, China, 2022. [Google Scholar]
- Fang, S.; Mao, K.; Xia, X.; Wang, P.; Shi, J.; Bateni, S.M.; Xu, T.; Cao, M.; Heggy, E.; Qin, Z. Dataset of Daily Near-Surface Air Temperature in China from 1979 to 2018. Earth Syst. Sci. Data 2022, 14, 1413–1432. [Google Scholar] [CrossRef]
- Feng, F.; Wang, K. Merging Ground-Based Sunshine Duration Observations with Satellite Cloud and Aerosol Retrievals to Produce High-Resolution Long-Term Surface Solar Radiation over China. Earth Syst. Sci. Data 2021, 13, 907–922. [Google Scholar] [CrossRef]



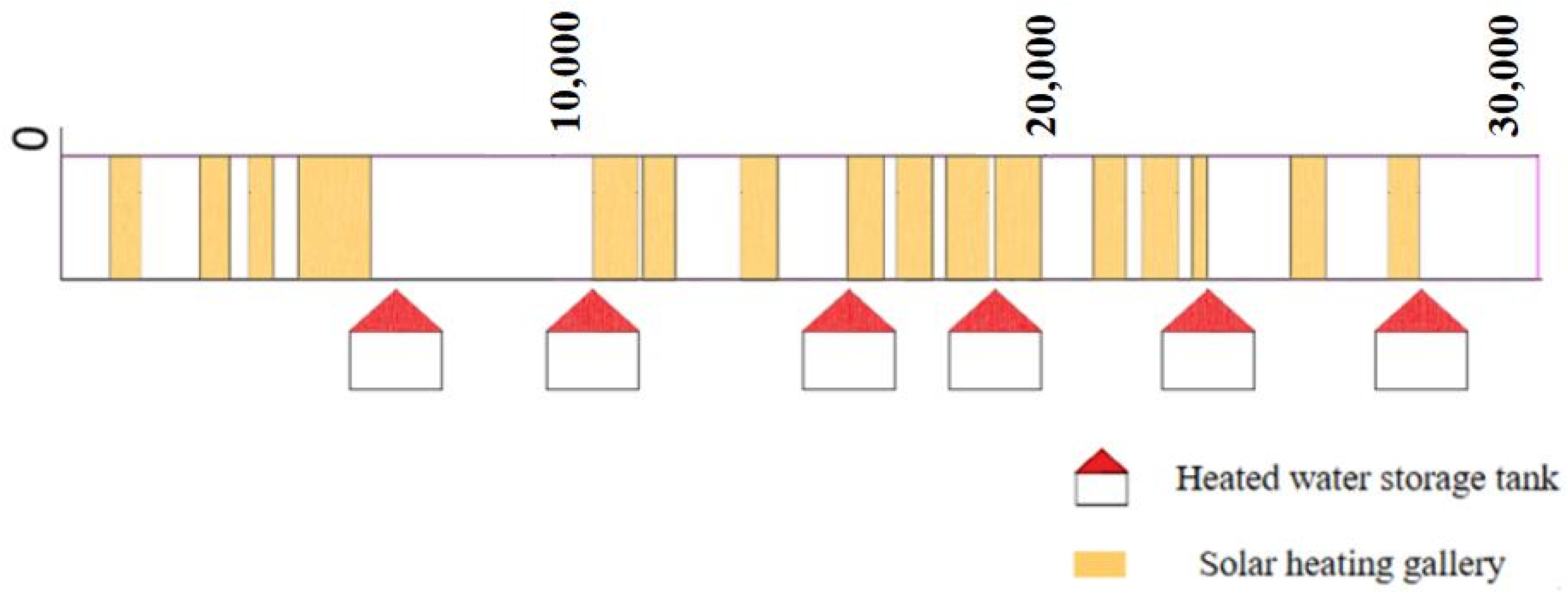


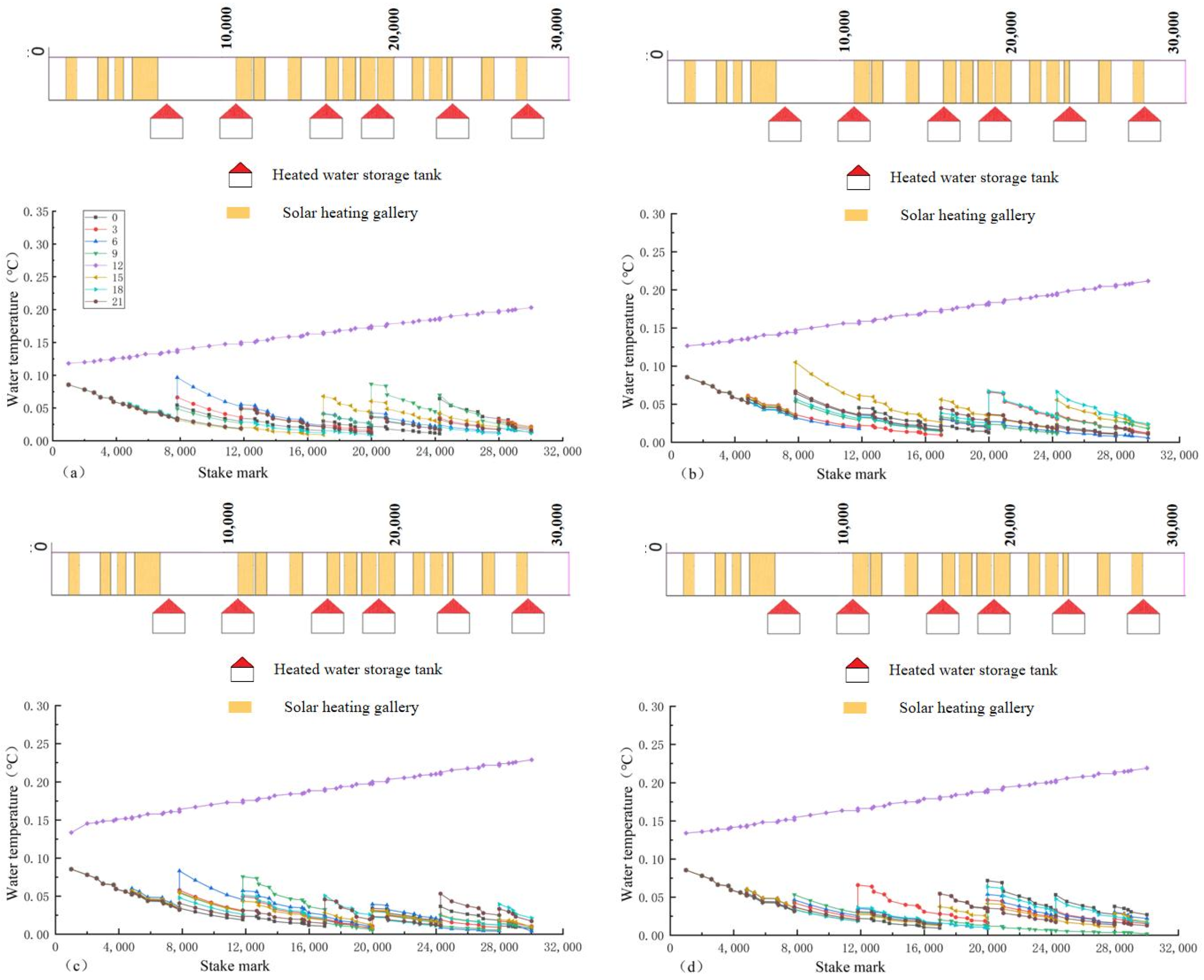
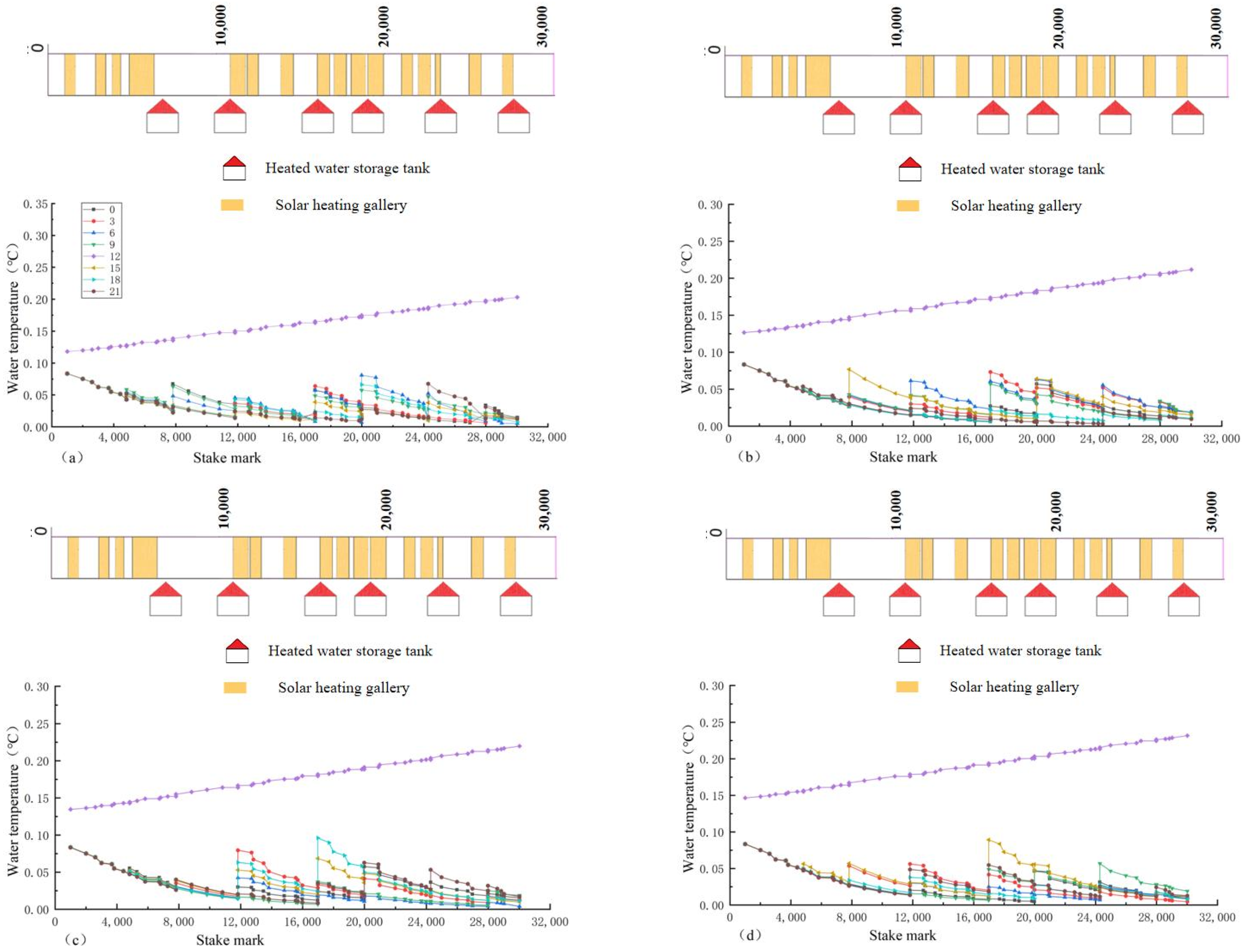

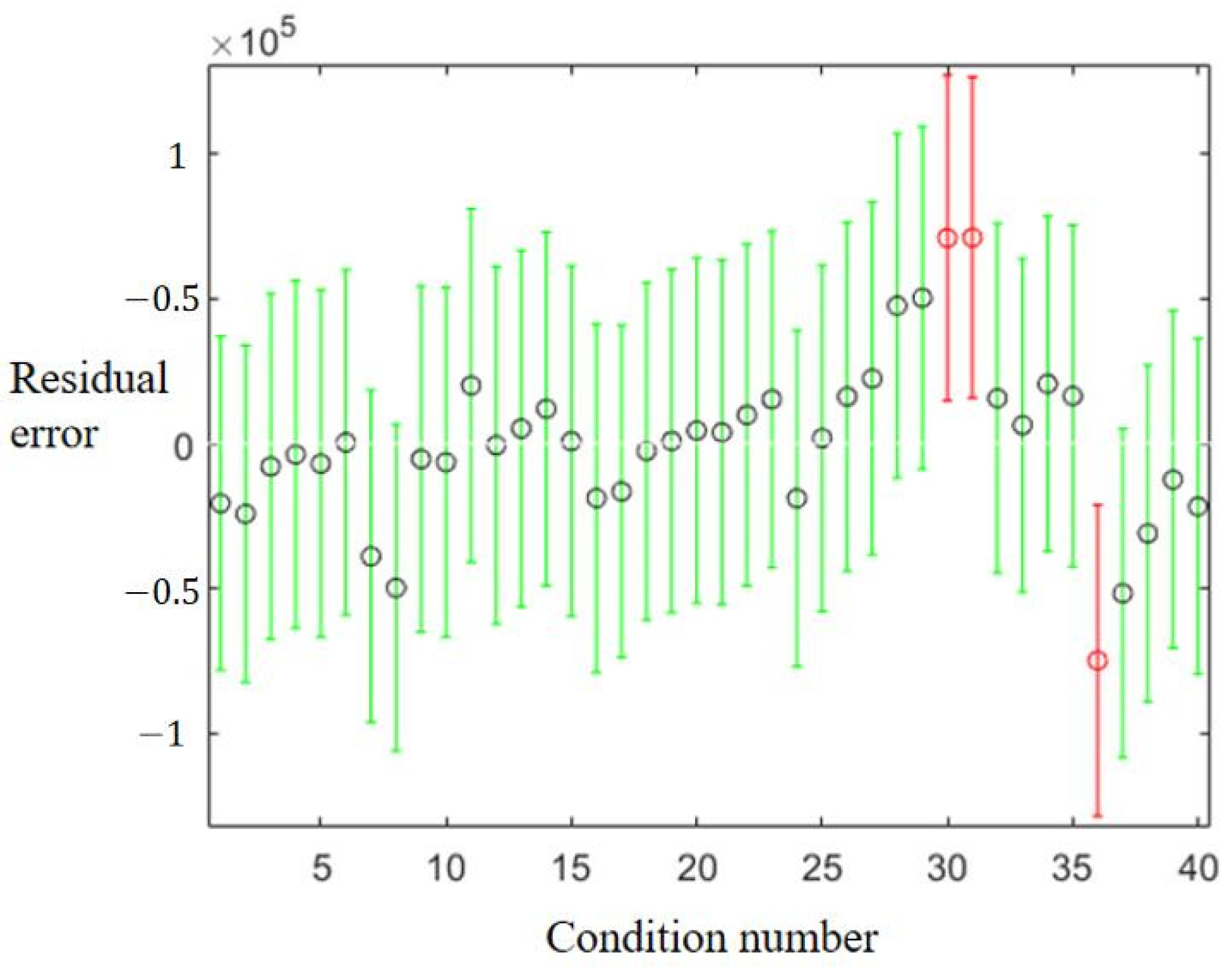
| Design Flow for Ice Cover Operation | Velocity | Slope Coefficient | Water Depth | Bottom Width | Canal Length |
|---|---|---|---|---|---|
| 78 m3/s | 0.4 m/s | 2 | 6 m | 23.5 m | 30.4 m |
| Name | Collector | Photovoltaic Panel | ||||
|---|---|---|---|---|---|---|
| Structure Parameters | Size/m | Efficiency | Air hole diameter/m | Heat collection efficiency | Temperature coefficient | Power generation efficiency |
| Value | 2 × 1 × 0.22 | 65% | 0.18 | 65% | 0.4 | 17% |
| Name | Water tank | Electric heating rod | ||||
| Structure Parameters | Radius/m | Height/m | Number of coils | Height/m | Diameter/m | Total length/m |
| Value | 3 | 6 | 8 | 3.6 | 0.3 | 75.48 |
| City Name | Temperature Probability Density Function | Fit Degree | Wind Speed Probability Density Function | Fit Degree |
|---|---|---|---|---|
| Handan | 0.97 | 0.96 |
| Cumulative Probability (%) | 100 | 95 | 90 | 85 | 80 | 75 | 70 | 65 |
|---|---|---|---|---|---|---|---|---|
| −15 | −13.4 | −11.8 | −10.6 | −9.4 | −8.2 | −7 | −6.3 | |
| ) | 6.3 | 4.5 | 2.6 | 2.4 | 2.2 | 2.0 | 1.8 | 1.6 |
| ) | 1788 | 1788 | 1788 | 2039 | 2281 | 2523 | 2765 | 4234 |
| Comprehensive satisfaction rate (%) | 100 | 93 | 79 | 67 | 56 | 46 | 37 | 30 |
| Ice-Melting Measures | Comprehensive Satisfaction Rates (%) | Average Hourly Flow ) | Average Hourly Water Temperature ) | Average Hourly Operating Cost ) |
|---|---|---|---|---|
| Heating gallery + heated water storage tank | 100 | 0.57 | 3.42 | 24,262 |
| 93 | 0.58 | 3.16 | 24,068 | |
| 79 | 0.47 | 3.46 | 21,325 | |
| 67 | 0.54 | 3.34 | 21,272 | |
| 56 | 0.45 | 3.58 | 19,449 | |
| 46 | 0.49 | 3.37 | 19,343 | |
| 37 | 0.48 | 3.22 | 17,363 | |
| 30 | 0.44 | 3.23 | 17,257 |
| Comprehensive Satisfaction Rate (%) | 79 | 37 | ||||
|---|---|---|---|---|---|---|
| Flow () | 101 | 140 | 180 | 101 | 140 | 180 |
| Velocity of flow ) | 0.47 | 0.66 | 0.83 | 0.47 | 0.66 | 0.83 |
| Operating cost ) | 5.62 | 6.61 | 7.39 | 4.67 | 5.64 | 6.61 |
| Number | (%) | ) | ) | Actual Value ) | Predicted Value ) | Error Rate (%) |
|---|---|---|---|---|---|---|
| 1 | 62 | 167 | 5.8 | 9.12 | 9.04 | 0.9 |
| 2 | 76 | 147 | 5.8 | 9.53 | 9.09 | 4.9 |
| 3 | 80 | 144 | 5.4 | 8.58 | 9.01 | 4.8 |
| 4 | 84 | 174 | 5.6 | 9.25 | 9.53 | 2.9 |
| 5 | 48 | 123 | 5 | 7.57 | 7.95 | 4.8 |
| Comprehensive Satisfaction Rate (%) | Single Heating Charge CNY/Day) | Cost after Regulating CNY/Day) | Cost Change CNY/Day) | Saving Rate |
|---|---|---|---|---|
| 100 | 32.90 | 6.32 | 26.57 | 0.81 |
| 93 | 19.47 | 6.28 | 13.19 | 0.68 |
| 79 | 15.83 | 5.62 | 10.21 | 0.65 |
| 67 | 9.78 | 5.61 | 4.18 | 0.43 |
| 56 | 8.88 | 5.17 | 3.71 | 0.42 |
| 46 | 6.51 | 5.14 | 1.37 | 0.21 |
| 37 | 5.52 | 4.67 | 0.85 | 0.15 |
| 30 | 4.25 | 4.64 | −0.39 | −0.09 |
| Flow (m3/s) | Flow Benefit CNY/Day) | Power Generation Benefit CNY/Year) | Water Saving Benefit CNY/Year) |
|---|---|---|---|
| 101 | 0.31 | 4.84 | 4.07 |
| 140 | 0.84 | 4.84 | 4.33 |
| 180 | 1.38 | 4.84 | 4.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Lian, J.; Zhao, X.; Chen, Y. Study on Multi-Measures Joint Optimization Regulation of Temperature Control and Ice Melting for Water Conveyance Projects in Cold Regions. Water 2024, 16, 1039. https://doi.org/10.3390/w16071039
Yang D, Lian J, Zhao X, Chen Y. Study on Multi-Measures Joint Optimization Regulation of Temperature Control and Ice Melting for Water Conveyance Projects in Cold Regions. Water. 2024; 16(7):1039. https://doi.org/10.3390/w16071039
Chicago/Turabian StyleYang, Deming, Jijian Lian, Xin Zhao, and Yunfei Chen. 2024. "Study on Multi-Measures Joint Optimization Regulation of Temperature Control and Ice Melting for Water Conveyance Projects in Cold Regions" Water 16, no. 7: 1039. https://doi.org/10.3390/w16071039
APA StyleYang, D., Lian, J., Zhao, X., & Chen, Y. (2024). Study on Multi-Measures Joint Optimization Regulation of Temperature Control and Ice Melting for Water Conveyance Projects in Cold Regions. Water, 16(7), 1039. https://doi.org/10.3390/w16071039







