Combining Crop and Water Decisions to Manage Groundwater Overdraft over Decadal and Longer Timescales
Abstract
:1. Introduction
2. Materials and Methods
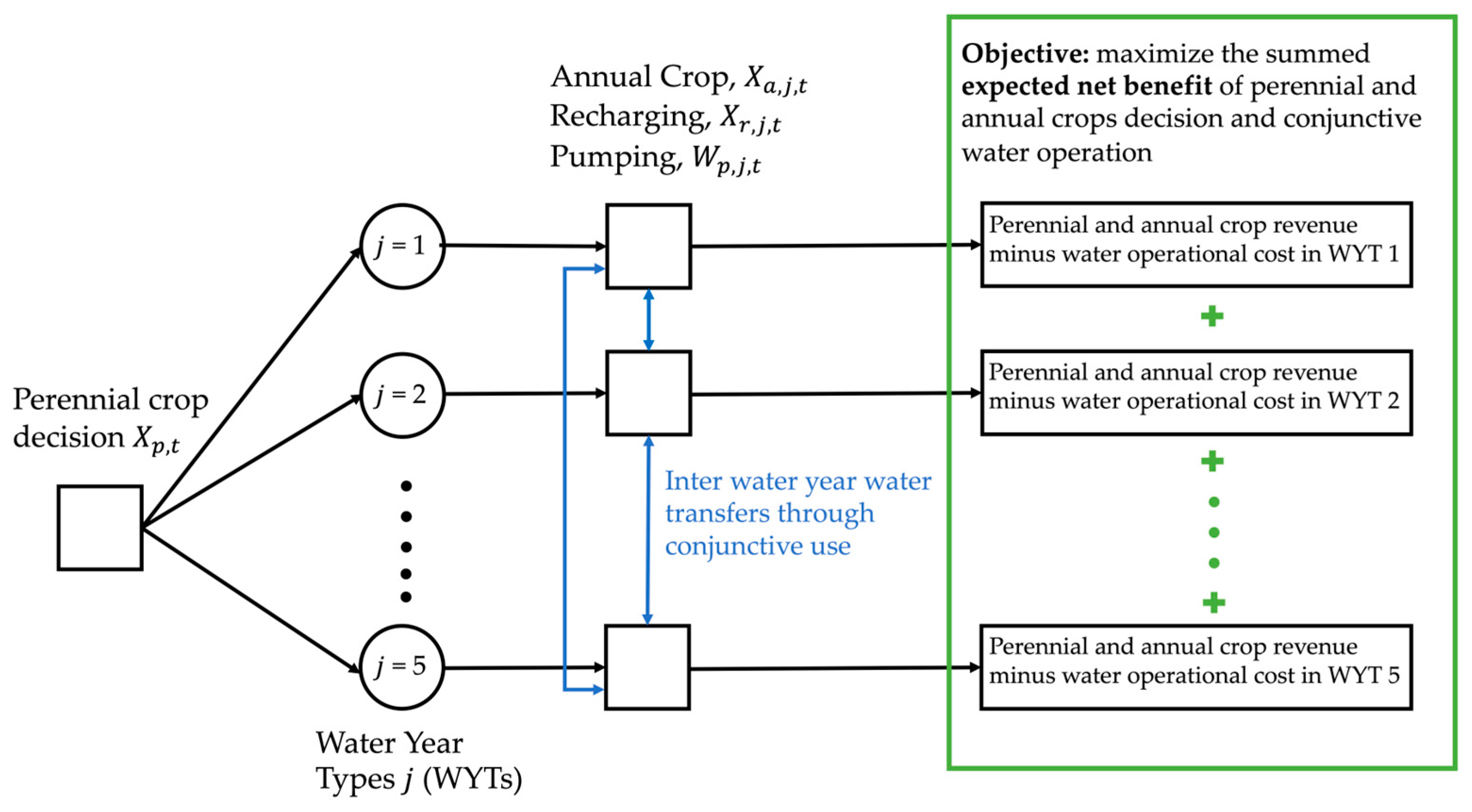
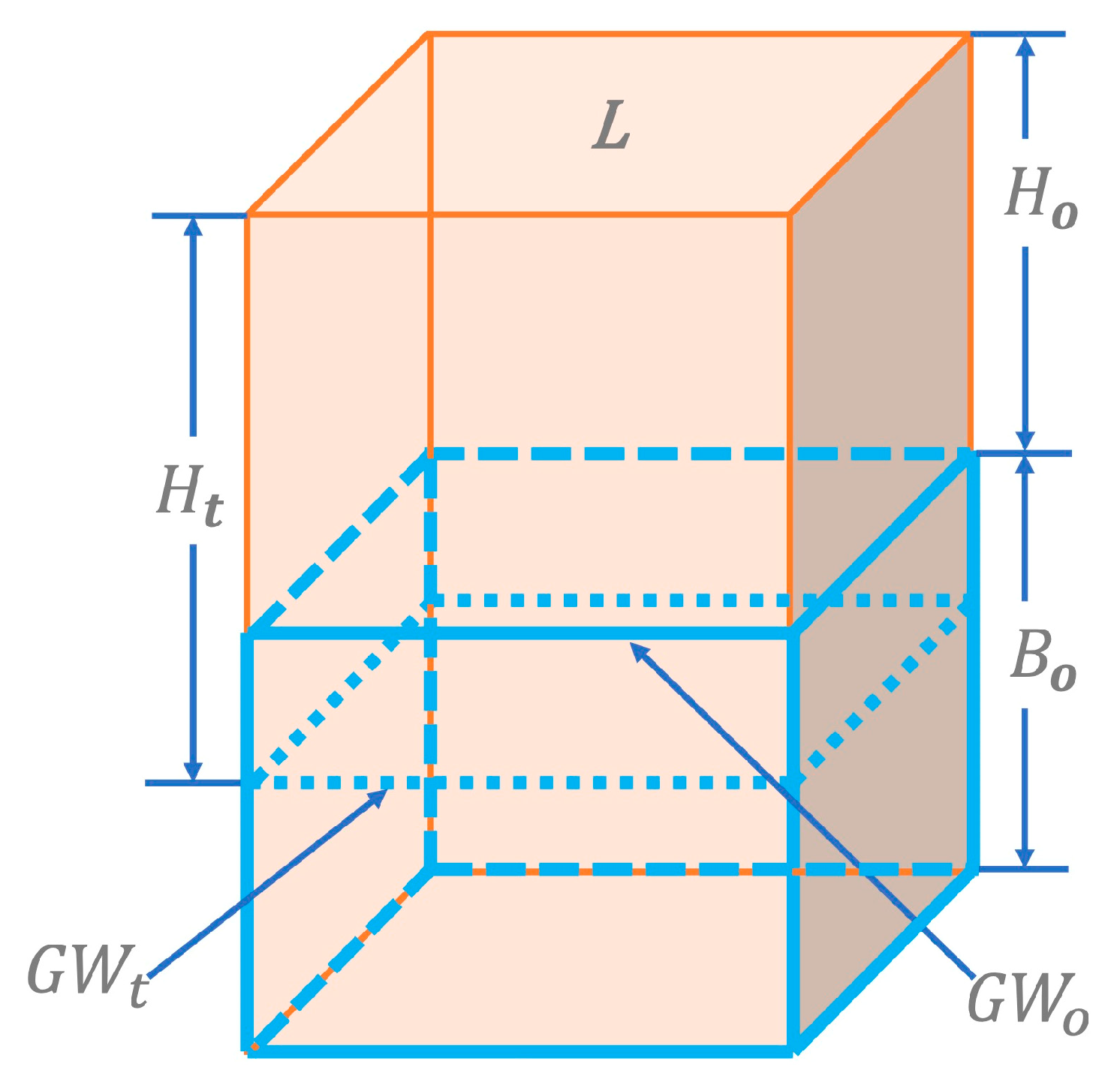
2.1. Inner Model Formulation
2.2. Outer Model Formulation
2.3. Model Assumptions and Limitations
2.4. Case Example
3. Results
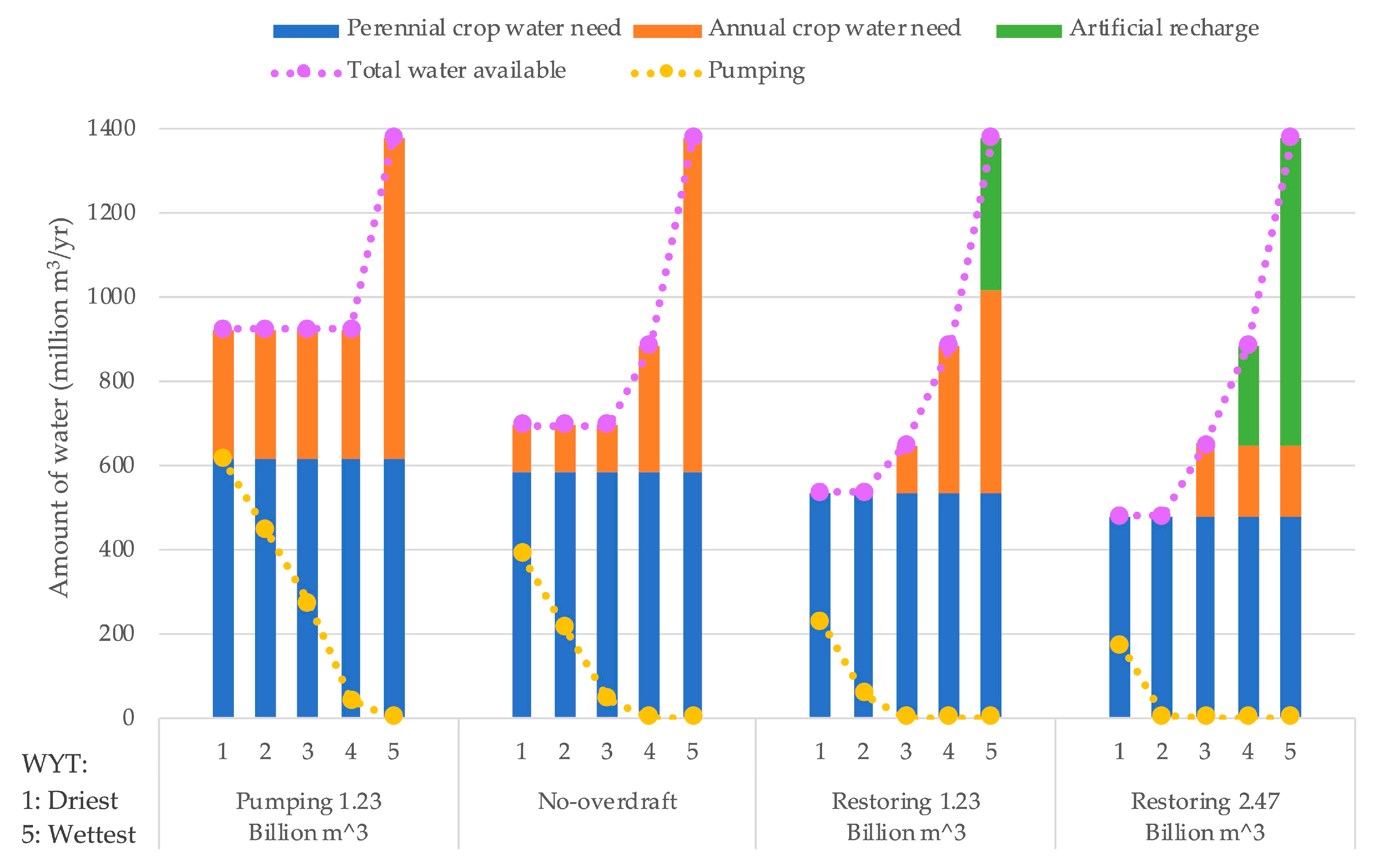
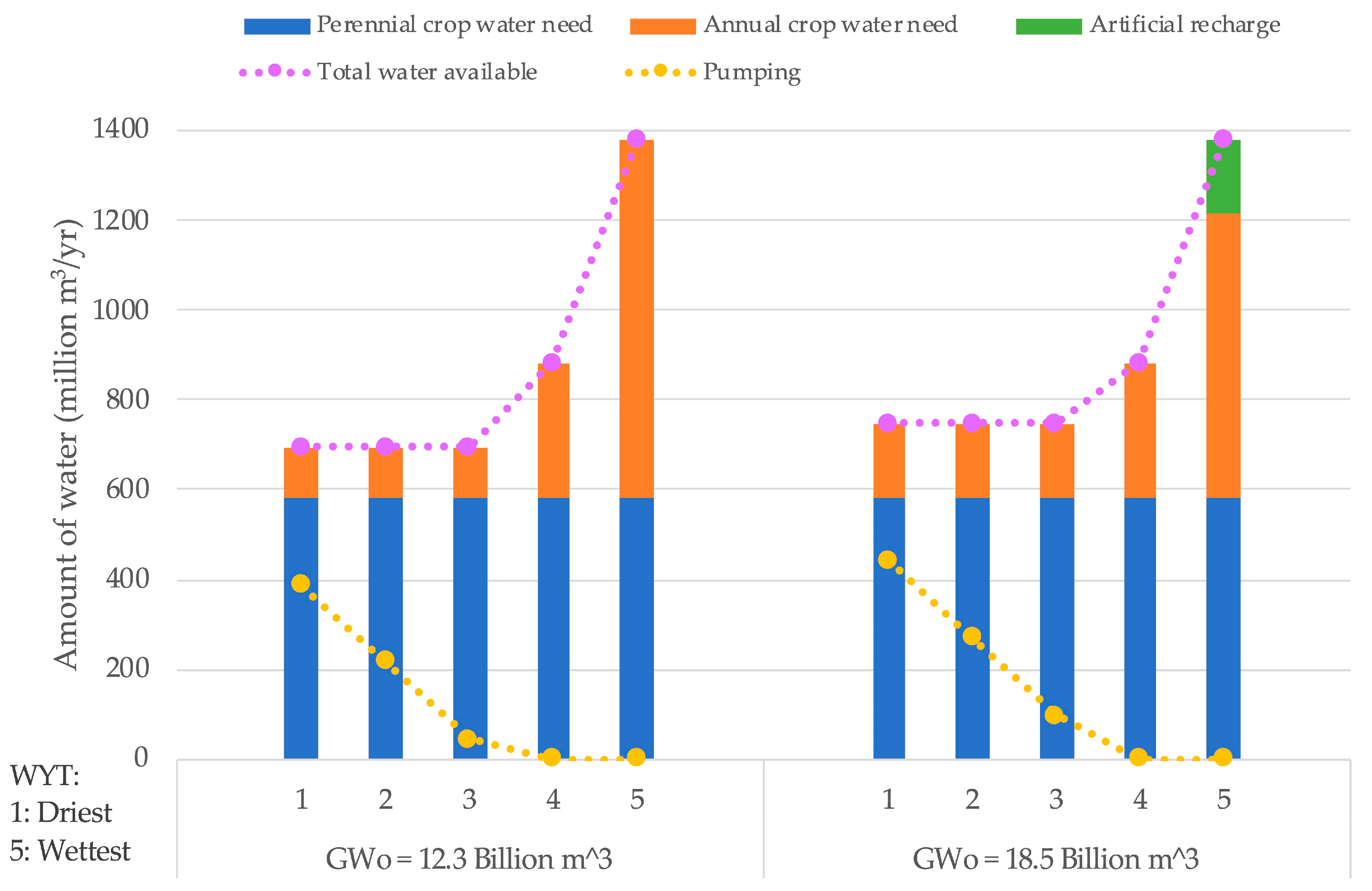
3.1. Conjunctive Use and Cropping for Within-decade Timescales
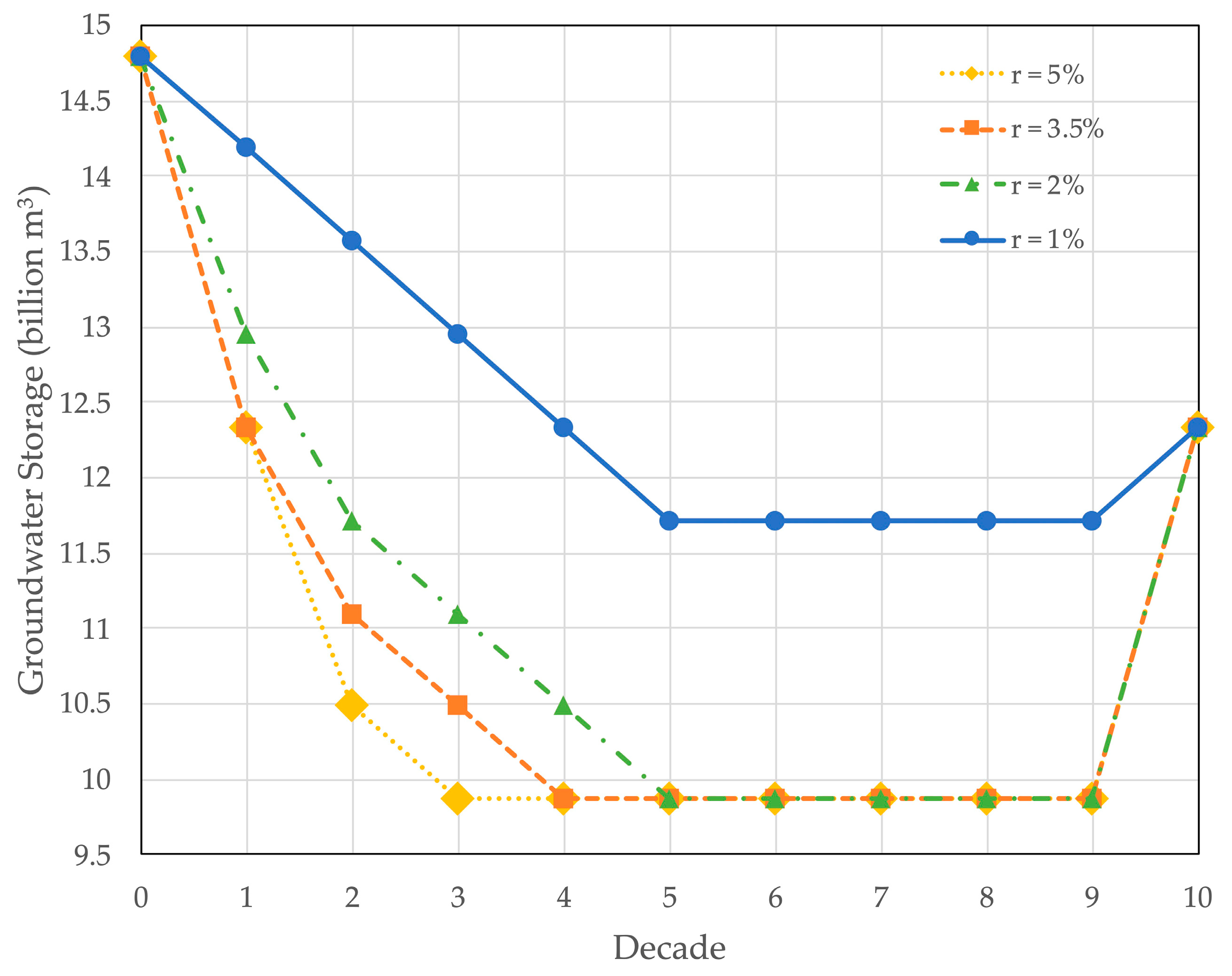
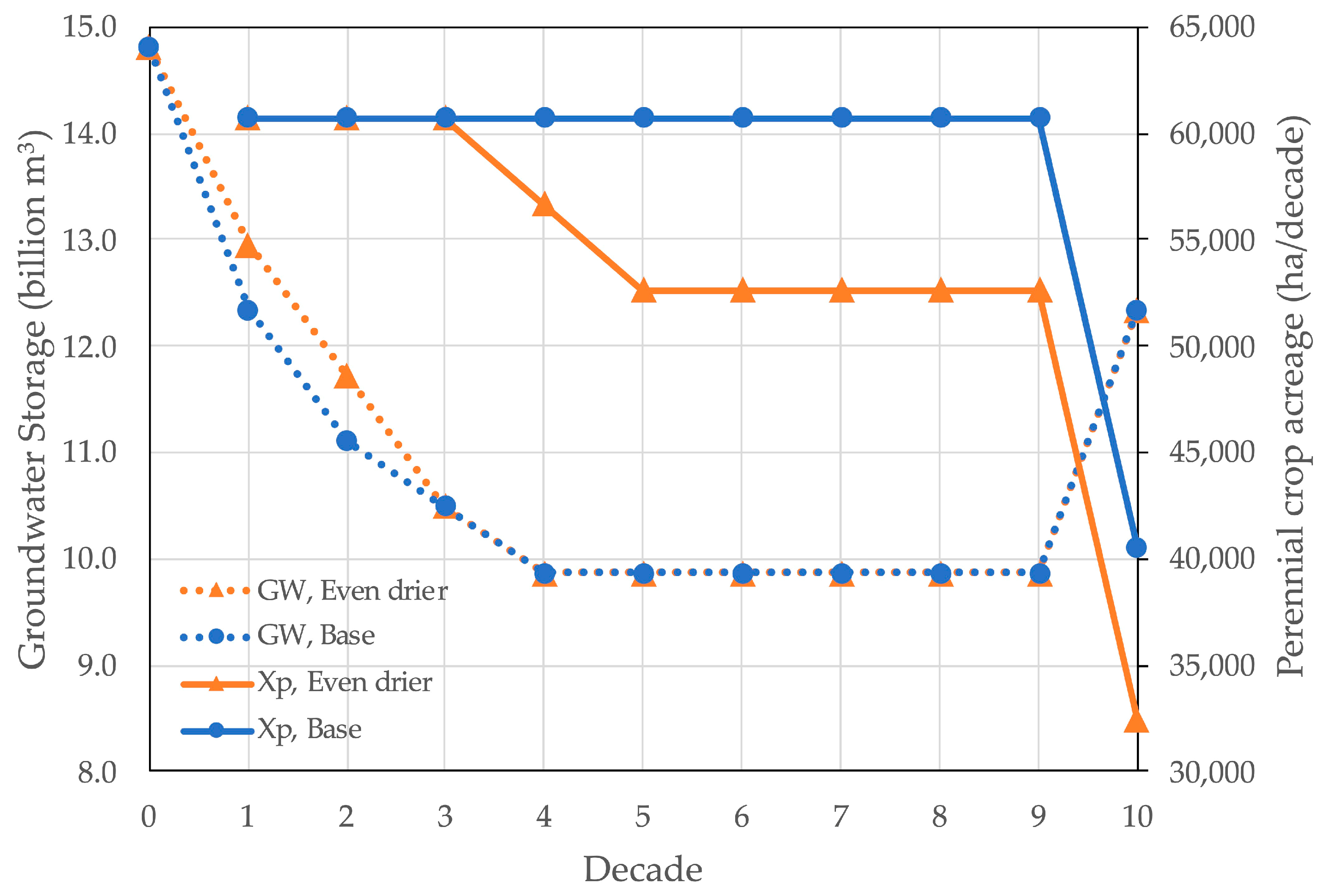
3.2. Groundwater Management and Cropping for Long-Term Timescales
3.3. Sensitivity Analyses
3.3.1. Different Discount Rates
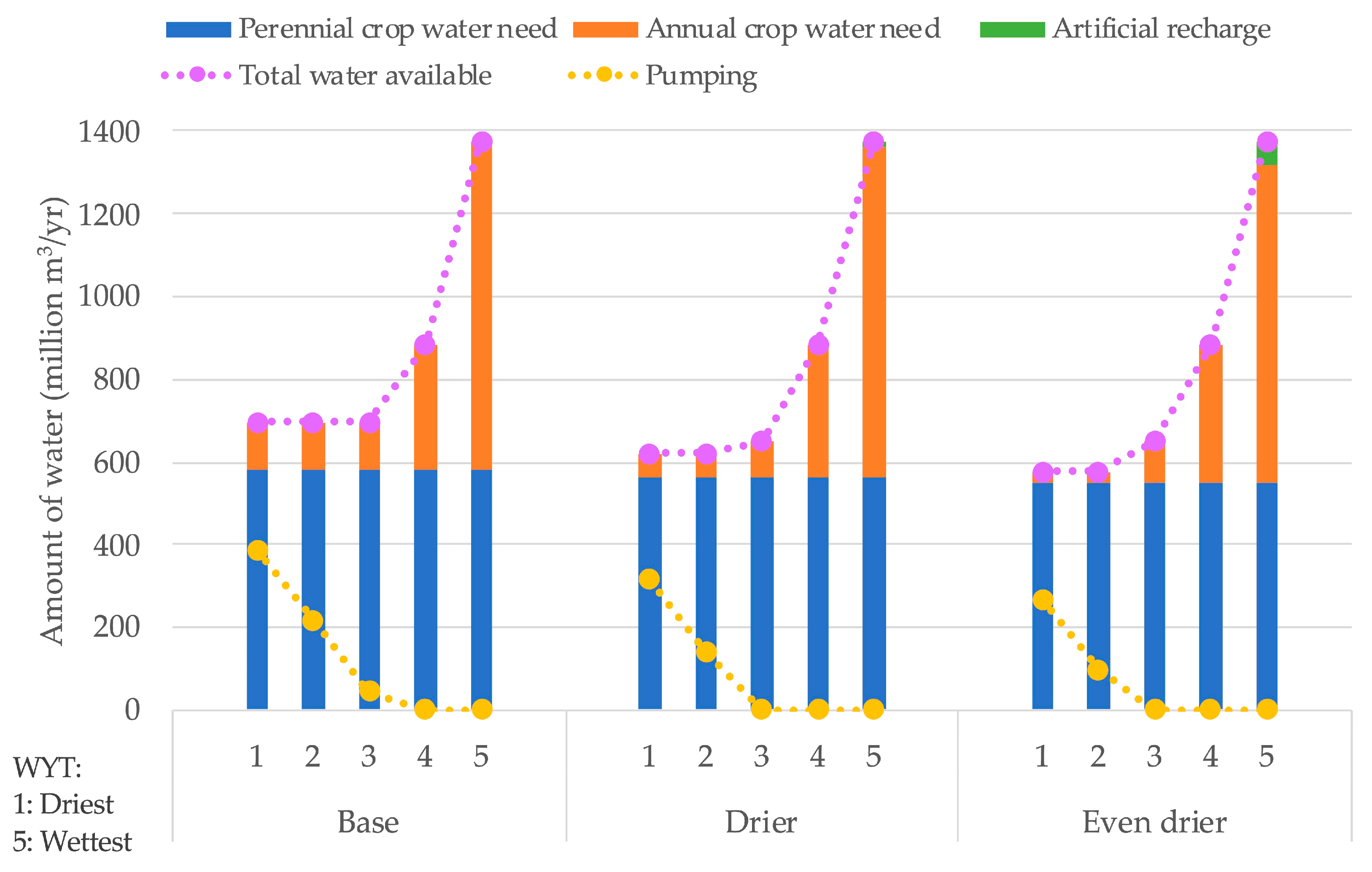
3.3.2. Climate Effects
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter (Unit) | Perennial Crop (Similar to Almonds) | Annual Crop (Similar to Alfalfa) | |
|---|---|---|---|
| Base year observations | (ha) | 132,874 | 67,724 |
| (kg/ha) | 2242 | 17,934 | |
| ($/kg) | 4.66 | 0.173 | |
| (m/ha) | 3.07 | 3.65 | |
| Land cost ($/ha) | 2006 | 783 | |
| Other supply cost ($/ha) | 4146 | 1344 | |
| Labor cost ($/ha) | 786 | 52 | |
| Total cost ($/ha) | 6939 | 2179 | |
| PMP cost function | ($/ha) | 3713.62 | 1571.37 |
| ($/ha2) | 0.0485 | 0.0180 |
References
- Reilly, T.E.; Dennehy, K.F.; Alley, W.M.; Cunningham, W.L. Ground-Water Availability in the United States; Geological Survey (US): Reston, VA, USA, 2008; ISBN 1-4113-2183-9.
- Faunt, C. Groundwater Availability of the Central Valley Aquifer. U.S. Geol. Surv. Prof. Pap. 2009, 1766, 225. [Google Scholar]
- Lund, J.; Medellin-Azuara, J.; Durand, J.; Stone, K. Lessons from California’s 2012–2016 Drought. J. Water Resour. Plann. Manag. 2018, 144, 04018067. [Google Scholar] [CrossRef]
- Escriva-Bou, A.; Hui, R.; Maples, S.; Medellín-Azuara, J.; Harter, T.; Lund, J.R. Planning for Groundwater Sustainability Accounting for Uncertainty and Costs: An Application to California’s Central Valley. J. Environ. Manag. 2020, 264, 110426. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Hu, Q. Groundwater Influences on Soil Moisture and Surface Evaporation. J. Hydrol. 2004, 297, 285–300. [Google Scholar] [CrossRef]
- Pauloo, R.A.; Fogg, G.E.; Guo, Z.; Harter, T. Anthropogenic Basin Closure and Groundwater Salinization (ABCSAL). J. Hydrol. 2021, 593, 125787. [Google Scholar] [CrossRef]
- Yao, Y.; Lund, J.R.; Harter, T. Conjunctive Water Management for Agriculture with Groundwater Salinity. Water Resour. Res. 2022, 58, e2021WR031058. [Google Scholar] [CrossRef]
- Romero, E. Friant-Kern Canal Slows By 60 Percent, Subsidence To Blame. Available online: https://www.kvpr.org/environment/2017-08-03/friant-kern-canal-slows-by-60-percent-subsidence-to-blame (accessed on 22 April 2024).
- California Department of Water Resources California Aqueduct Subsidence Study. Available online: https://cawaterlibrary.net/wp-content/uploads/2017/11/Aqueduct_Subsidence_Study-FINAL-2017.pdf (accessed on 22 April 2024).
- Harou, J.J.; Lund, J.R. Ending Groundwater Overdraft in Hydrologic-Economic Systems. Hydrogeol. J. 2008, 16, 1039. [Google Scholar] [CrossRef]
- Dogan, M.S.; Buck, I.; Medellin-Azuara, J.; Lund, J.R. Statewide Effects of Ending Long-Term Groundwater Overdraft in California. J. Water Resour. Plan. Manag. 2019, 145, 04019035. [Google Scholar] [CrossRef]
- Alam, S.; Gebremichael, M.; Li, R.; Dozier, J.; Lettenmaier, D.P. Can Managed Aquifer Recharge Mitigate the Groundwater Overdraft in California’s Central Valley? Water Resour. Res. 2020, 56, e2020WR027244. [Google Scholar] [CrossRef]
- Buras, N. Conjunctive Operation of Dams and Aquifers. J. Hydraul. Div. 1963, 89, 111–131. [Google Scholar] [CrossRef]
- Burt, O.R. The Economics of Conjunctive Use of Ground and Surface Water. Hilg 1964, 36, 31–111. [Google Scholar] [CrossRef]
- Burt, O.R. Economic Control of Groundwater Reserves. Am. J. Agric. Econ. 1966, 48, 632–647. [Google Scholar] [CrossRef]
- Bredehoeft, J.D.; Young, R.A. Conjunctive Use of Groundwater and Surface Water for Irrigated Agriculture: Risk Aversion. Water Resour. Res. 1983, 19, 1111–1121. [Google Scholar] [CrossRef]
- Fredericks, J.W.; Labadie, J.W.; Altenhofen, J.M. Decision Support System for Conjunctive Stream-Aquifer Management. J. Water Resour. Plan. Manag. 1998, 124, 69–78. [Google Scholar] [CrossRef]
- Pulido-Velázquez, M.; Andreu, J.; Sahuquillo, A. Economic Optimization of Conjunctive Use of Surface Water and Groundwater at the Basin Scale. J. Water Resour. Plan. Manag. 2006, 132, 454–467. [Google Scholar] [CrossRef]
- Gorelick, S.M. A Review of Distributed Parameter Groundwater Management Modeling Methods. Water Resour. Res. 1983, 19, 305–319. [Google Scholar] [CrossRef]
- Bazargan-Lari, M.R.; Kerachian, R.; Mansoori, A. A Conflict-Resolution Model for the Conjunctive Use of Surface and Groundwater Resources That Considers Water-Quality Issues: A Case Study. Environ. Manag. 2009, 43, 470–482. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Soltani, J. Multi-Objective Optimal Model for Conjunctive Use Management Using SGAs and NSGA-II Models. Water Resour. Manag. 2013, 27, 37–53. [Google Scholar] [CrossRef]
- Naghdi, S.; Bozorg-Haddad, O.; Khorsandi, M.; Chu, X. Multi-Objective Optimization for Allocation of Surface Water and Groundwater Resources. Sci. Total Environ. 2021, 776, 146026. [Google Scholar] [CrossRef]
- Varela-Ortega, C.; Blanco-Gutiérrez, I.; Swartz, C.H.; Downing, T.E. Balancing Groundwater Conservation and Rural Livelihoods under Water and Climate Uncertainties: An Integrated Hydro-Economic Modeling Framework. Glob. Environ. Change 2011, 21, 604–619. [Google Scholar] [CrossRef]
- Rouhi Rad, M.; Haacker, E.M.K.; Sharda, V.; Nozari, S.; Xiang, Z.; Araya, A.; Uddameri, V.; Suter, J.F.; Gowda, P. MOD$$AT: A Hydro-Economic Modeling Framework for Aquifer Management in Irrigated Agricultural Regions. Agric. Water Manag. 2020, 238, 106194. [Google Scholar] [CrossRef]
- Ali, A.A.; Tran, D.Q.; Kovacs, K.F.; Dahlke, H.E. Hydro-economic Modeling of Managed Aquifer Recharge in the Lower Mississippi. J. Am. Water Resour. Assoc. 2023, 59, 1413–1434. [Google Scholar] [CrossRef]
- Marques, G.F.; Lund, J.R.; Howitt, R.E. Modeling Conjunctive Use Operations and Farm Decisions with Two-Stage Stochastic Quadratic Programming. J. Water Resour. Plan. Manag. 2010, 136, 386–394. [Google Scholar] [CrossRef]
- Gorelick, S.M.; Voss, C.I.; Gill, P.E.; Murray, W.; Saunders, M.A.; Wright, M.H. Aquifer Reclamation Design: The Use of Contaminant Transport Simulation Combined With Nonlinear Programing. Water Resour. Res. 1984, 20, 415–427. [Google Scholar] [CrossRef]
- Sedki, A.; Ouazar, D. Simulation-Optimization Modeling for Sustainable Groundwater Development: A Moroccan Coastal Aquifer Case Study. Water Resour. Manag. 2011, 25, 2855–2875. [Google Scholar] [CrossRef]
- Singh, A. Conjunctive Use of Water Resources for Sustainable Irrigated Agriculture. J. Hydrol. 2014, 519, 1688–1697. [Google Scholar] [CrossRef]
- Hazell, P.; Norton, R. Mathematical Programming for Economic Analysis in Agriculture; Macmillan Publishing Company: New York, NY, USA, 1986; ISBN 978-0-02-947930-8. [Google Scholar]
- Howitt, R.E. Positive Mathematical Programming. Am. J. Agric. Econ. 1995, 77, 329–342. [Google Scholar] [CrossRef]
- Yeh, W.W.-G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Shang, S.; Mao, X. Application of a Simulation Based Optimization Model for Winter Wheat Irrigation Scheduling in North China. Agric. Water Manag. 2006, 85, 314–322. [Google Scholar] [CrossRef]
- Kuwayama, Y.; Brozović, N. The Regulation of a Spatially Heterogeneous Externality: Tradable Groundwater Permits to Protect Streams. J. Environ. Econ. Manag. 2013, 66, 364–382. [Google Scholar] [CrossRef]
- Yakowitz, S. Dynamic Programming Applications in Water Resources. Water Resour. Res. 1982, 18, 673–696. [Google Scholar] [CrossRef]
- Philbrick, C.R.; Kitanidis, P.K. Optimal Conjunctive-Use Operations and Plans. Water Resour. Res. 1998, 34, 1307–1316. [Google Scholar] [CrossRef]
- Karamouz, M.; Kerachian, R.; Zahraie, B. Monthly Water Resources and Irrigation Planning: Case Study of Conjunctive Use of Surface and Groundwater Resources. J. Irrig. Drain. Eng. 2004, 130, 391–402. [Google Scholar] [CrossRef]
- Azaiez, M.N.; Hariga, M.; Al-Harkan, I. A Chance-Constrained Multi-Period Model for a Special Multi-Reservoir System. Comput. Oper. Res. 2005, 32, 1337–1351. [Google Scholar] [CrossRef]
- Yaron, D.; Dinar, A. Optimal Allocation of Farm Irrigation Water during Peak Seasons. Am. J. Agric. Econ. 1982, 64, 681–689. [Google Scholar] [CrossRef]
- Dudley, N.J.; Howell, D.T.; Musgrave, W.F. Optimal Intraseasonal Irrigation Water Allocation. Water Resour. Res. 1971, 7, 770–788. [Google Scholar] [CrossRef]
- Dudley, N.J.; Burt, O.R. Stochastic Reservoir Management and System Design for Irrigation. Water Resour. Res. 1973, 9, 507–522. [Google Scholar] [CrossRef]
- Gupta, R.K.; Chauhan, H.S. Stochastic Modeling of Irrigation Requirements. J. Irrig. Drain. Eng. 1986, 112, 65–76. [Google Scholar] [CrossRef]
- Davidsen, C.; Pereira-Cardenal, S.J.; Liu, S.; Mo, X.; Rosbjerg, D.; Bauer-Gottwein, P. Using Stochastic Dynamic Programming to Support Water Resources Management in the Ziya River Basin, China. J. Water Resour. Plan. Manag. 2015, 141, 04014086. [Google Scholar] [CrossRef]
- Soleimani, S.; Bozorg-Haddad, O.; Loáiciga, H.A. Reservoir Operation Rules with Uncertainties in Reservoir Inflow and Agricultural Demand Derived with Stochastic Dynamic Programming. J. Irrig. Drain. Eng. 2016, 142, 04016046. [Google Scholar] [CrossRef]
- Anvari, S.; Mousavi, S.J.; Morid, S. Stochastic Dynamic Programming-Based Approach for Optimal Irrigation Scheduling under Restricted Water Availability Conditions. Irrig. Drain. 2017, 66, 492–500. [Google Scholar] [CrossRef]
- Safavi, H.R.; Alijanian, M.A. Optimal Crop Planning and Conjunctive Use of Surface Water and Groundwater Resources Using Fuzzy Dynamic Programming. J. Irrig. Drain. Eng. 2011, 137, 383–397. [Google Scholar] [CrossRef]
- Franklin, B.; Schwabe, K.; Levers, L. Perennial Crop Dynamics May Affect Long-Run Groundwater Levels. Land 2021, 10, 971. [Google Scholar] [CrossRef]
- Zhu, T.; Marques, G.F.; Lund, J.R. Hydroeconomic Optimization of Integrated Water Management and Transfers under Stochastic Surface Water Supply. Water Resour. Res. 2015, 51, 3568–3587. [Google Scholar] [CrossRef]
- Yao, Y. Managing Groundwater for Agriculture, with Hydrologic Uncertainty and Salinity; University of California: Davis, CA, USA, 2021. [Google Scholar]
- Rao, N.H.; Sarma, P.B.S.; Chander, S. Optimal Multicrop Allocation of Seasonal and Intraseasonal Irrigation Water. Water Resour. Res. 1990, 26, 551–559. [Google Scholar] [CrossRef]
- Paul, S.; Panda, S.N.; Kumar, D.N. Optimal Irrigation Allocation: A Multilevel Approach. J. Irrig. Drain. Eng. 2000, 126, 149–156. [Google Scholar] [CrossRef]
- Ghahraman, B.; Sepaskhah, A.-R. Optimal Allocation of Water from a Single Purpose Reservoir to an Irrigation Project with Pre-Determined Multiple Cropping Patterns. Irrig. Sci. 2002, 21, 127–137. [Google Scholar] [CrossRef]
- CH2MHILL DRAFT Agricultural Economics Technical Appendix. Available online: https://web.archive.org/web/20170711215918/http://water.ca.gov/economics/downloads/Models/SWAP_TechAppendix_080612_Draft.pdf (accessed on 22 April 2024).

| Symbol | Parameter | Value (Unit) |
|---|---|---|
| T | Length of planning horizon | 10 (yr) |
| L | Total available area | 202,343 ha (500,000 acre) |
| Ho | Initial pump head | 60.96 m (200 ft) |
| Bo | Initial thickness of the aquifer | 60.96 m (200 ft) |
| sy | Aquifer specific yield | 0.1 |
| r | Constant discount rate for inner model | 3.5% |
| inip | Perennial crop initial establishment cost | $29,653/ha ($12,000/acre) |
| cland | Unit price of land for recharging | $741/ha ($300/acre) |
| cclass1 | Unit price of class 1 (firm contract) water | $0.034/m3 ($42/AF) |
| cclass2 | Unit price of class 2 (surplus) water | $0.024/m3 ($30/AF) |
| class1 | Amount of firm contract water | 617 million m3/yr (500 TAF/yr) |
| ce | Unit price of energy | $0.189/kWh |
| ηp | Pumping efficiency | 0.7 |
| cap | Capacity of land for recharging | 4.572 m/yr (15 ft/yr) |
| 1 − φ | Irrigation efficiency | 0.85 |
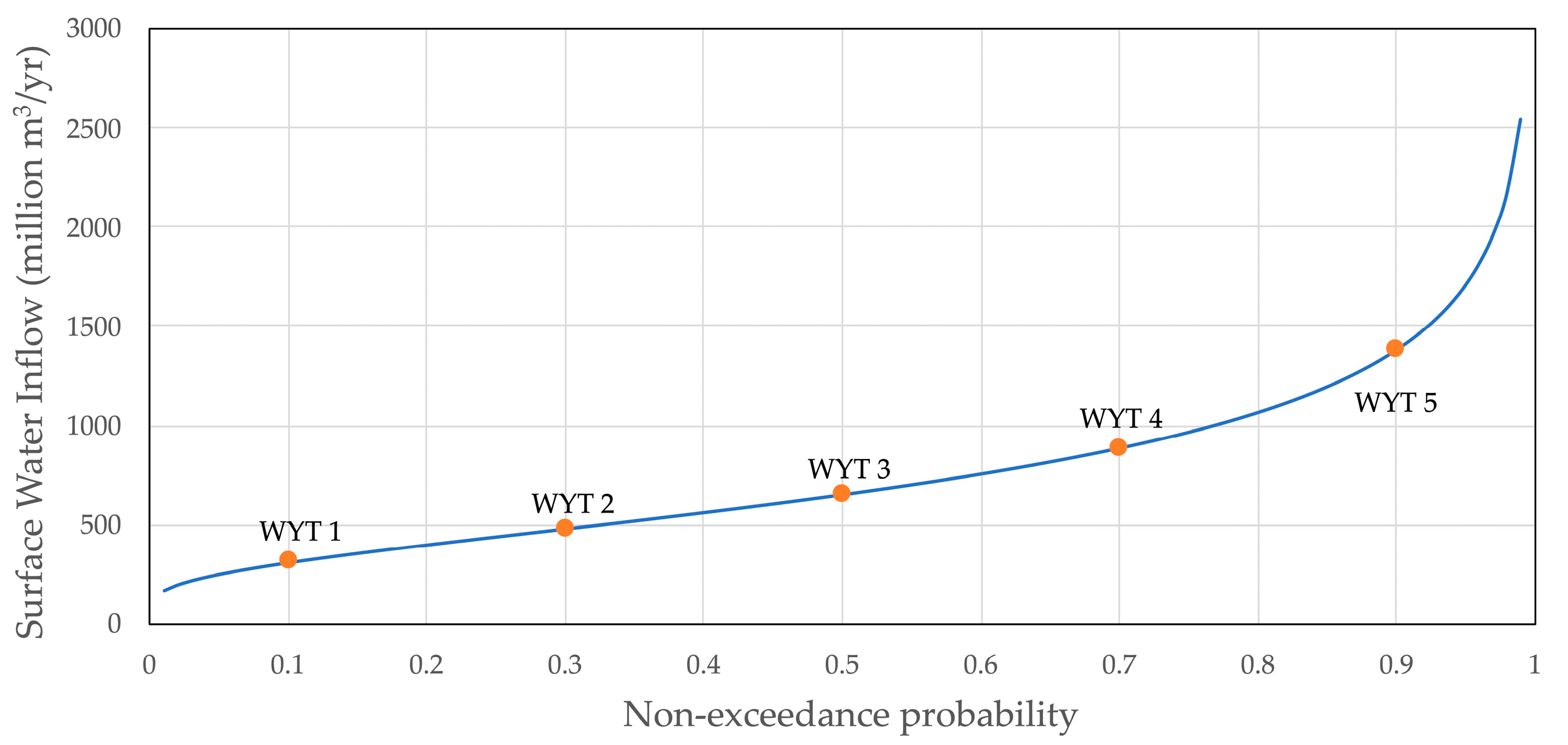
| WYT j | Percentile | swj (Million m3/yr) | pj |
|---|---|---|---|
| 1 (Dry) | 10th | 306 | 0.2 |
| 2 | 30th | 478 | 0.2 |
| 3 | Median | 649 | 0.2 |
| 4 | 70th | 883 | 0.2 |
| 5 (Wet) | 90th | 1376 | 0.2 |
| ∆GW (Billion m3) | Economic Values of Water ($/m3) | |||||
|---|---|---|---|---|---|---|
| Dry | Surface Water | Wet | Groundwater | |||
| WYT 1 | WYT 2 | WYT 3 | WYT 4 | WYT 5 | ||
| −1.23 | 0.14 | 0.14 | 0.14 | 0.14 | 0.078 | 0.031 |
| 0 | 0.17 | 0.17 | 0.17 | 0.15 | 0.079 | 0.049 |
| 1.23 | 0.23 | 0.23 | 0.18 | 0.15 | 0.13 | 0.079 |
| 2.47 | 0.28 | 0.28 | 0.182 | 0.182 | 0.182 | 0.105 |
| Xa (ha/yr) | Xr (ha/yr) | Wp (Million m3/yr) | |||||
|---|---|---|---|---|---|---|---|
| GWt − 1 (Billion m3) | 12.3 | 18.5 | 12.3 | 18.5 | 12.3 | 18.5 | |
| WYT j | 1 (Dry) | 7537 | 11,140 | 0 | 0 | 389 | 442 |
| 2 | 7537 | 11,140 | 0 | 0 | 217 | 271 | |
| 3 | 7537 | 11,140 | 0 | 0 | 46 | 99 | |
| 4 | 20,276 | 20,276 | 0 | 0 | 0 | 0 | |
| 5 (Wet) | 53,692 | 42,883 | 0 | 3488 | 0 | 0 | |
| WYT j | Climates | ||
|---|---|---|---|
| Even Drier | Drier | Base | |
| 1 (Dry) | 0.3 | 0.25 | 0.2 |
| 2 | 0.3 | 0.25 | 0.2 |
| 3 | 0.2 | 0.2 | 0.2 |
| 4 | 0.1 | 0.2 | 0.2 |
| 5 (Wet) | 0.1 | 0.1 | 0.2 |
| Expected incoming surface water (million m3/yr) | 591 (−20%) | 640 (−13%) | 739 |
| Climates | Even Drier | Drier | Base | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Xp (ha/Decade) | 44,158 | 45,123 | 47,058 | ||||||
| Second Stage Decisions | Xa | Xr | Wp | Xa | Xr | Wp | Xa | Wp | |
| (ha/yr) | (ha/yr) | (m3/yr) | (ha/yr) | (ha/yr) | (m3/yr) | (ha/yr) | (m3/yr) | ||
| WYT j | 1 (Dry) | 1899 | 0 | 269 × 106 | 4142 | 0 | 314 × 106 | 7537 | 389 × 106 |
| 2 | 1899 | 0 | 98 × 106 | 4142 | 0 | 143 × 106 | 7537 | 217 × 106 | |
| 3 | 6882 | 0 | 0 | 6071 | 0 | 0 | 7537 | 46 × 106 | |
| 4 | 22,715 | 0 | 0 | 21,903 | 0 | 0 | 20,276 | 0 | |
| 5 (Wet) | 52,064 | 1312 | 0 | 54,307 | 327 | 0 | 53,692 | 0 | |
| Climates | Economic Values of Water ($/m3) | |||||
|---|---|---|---|---|---|---|
| Dry | Surface Water | Wet | Groundwater | |||
| WYT 1 | WYT 2 | WYT 3 | WYT 4 | WYT 5 | ||
| Base | 0.17 | 0.17 | 0.17 | 0.147 | 0.079 | 0.049 |
| Drier | 0.23 | 0.23 | 0.177 | 0.145 | 0.040 | 0.053 |
| Even drier | 0.28 | 0.28 | 0.184 | 0.072 | 0.042 | 0.056 |
| Initial Groundwater Storage GWo (Billion m3) | Climate Change | |
|---|---|---|
| Even Drier to Drier | Drier to Base | |
| 9.87 | 0.36 | 0.28 |
| 11.1 | 0.34 | 0.24 |
| 12.3 | 0.30 | 0.22 |
| 13.6 | 0.28 | 0.21 |
| 14.8 | 0.27 | 0.20 |
| Groundwater Storage Change (Billion m3) | Climates | ||
|---|---|---|---|
| Even Drier | Drier | Base | |
| 9.87 to 11.1 | 0.095 | 0.087 | 0.057 |
| 11.1 to 12.3 | 0.075 | 0.060 | 0.046 |
| 12.3 to 13.6 | 0.062 | 0.051 | 0.044 |
| 13.6 to 14.8 | 0.057 | 0.051 | 0.043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Lund, J.R.; Medellín-Azuara, J. Combining Crop and Water Decisions to Manage Groundwater Overdraft over Decadal and Longer Timescales. Water 2024, 16, 1223. https://doi.org/10.3390/w16091223
Yao Y, Lund JR, Medellín-Azuara J. Combining Crop and Water Decisions to Manage Groundwater Overdraft over Decadal and Longer Timescales. Water. 2024; 16(9):1223. https://doi.org/10.3390/w16091223
Chicago/Turabian StyleYao, Yiqing, Jay R. Lund, and Josué Medellín-Azuara. 2024. "Combining Crop and Water Decisions to Manage Groundwater Overdraft over Decadal and Longer Timescales" Water 16, no. 9: 1223. https://doi.org/10.3390/w16091223
APA StyleYao, Y., Lund, J. R., & Medellín-Azuara, J. (2024). Combining Crop and Water Decisions to Manage Groundwater Overdraft over Decadal and Longer Timescales. Water, 16(9), 1223. https://doi.org/10.3390/w16091223









