Forecasting the River Water Discharge by Artificial Intelligence Methods
Abstract
:1. Introduction
- Modeling the rivers’ discharge. A wide range of techniques have been employed for this purpose:
- (a)
- (b)
- (c)
- Artificial intelligence (AI) methods [17,18,19], such as support vector machines (SVM), artificial neural networks (ANN) [12,20,21,22], radial basis (RB) neural networks, multi-layer perceptron (MLP) [12], generalized regression neural network, least-square support vector regression [23], long short-term memory (LSTM) [24,25].
- (d)
- Hybrid models [10,26], integrating AI and non-linear time series models [27], k-nearest neighbor regression [23], Particle Swarm Optimization–support vector machine (PSO-SVM) [28], Particle Swarm Optimization–long short-term memory PSO-LSTM [29], CEEMDAN-PSO-ELM [30], support vector machine–Particle Swarm Optimization (SVM-PSO) [31], wavelet–autoregressive models [32], wavelet–LSTM [33], etc.;
- Testing statistical hypotheses [34];
- Time series decomposition and forecast [38].
- Providing alternative models for the Buzău River discharge before and after building the dam using AI algorithms;
- Pointing out the modification of the river flow alteration after the dam apparition;
- Exploring the BPNN, LSTM, and ELM capacity for modeling the water river discharge on series with high variability and outliers. These techniques were selected due to their advantages in modeling time series from various research fields [42,43,44,45,46,47,48]. Moreover, we aimed to prove their performances in hydrological modeling (where they were less used compared to other approaches).
- Comparing the single and hybrid AI techniques in hydrological modeling.
2. Study Area and Data Series
3. Methods
3.1. BPNN
3.2. LSTM
3.3. ELM
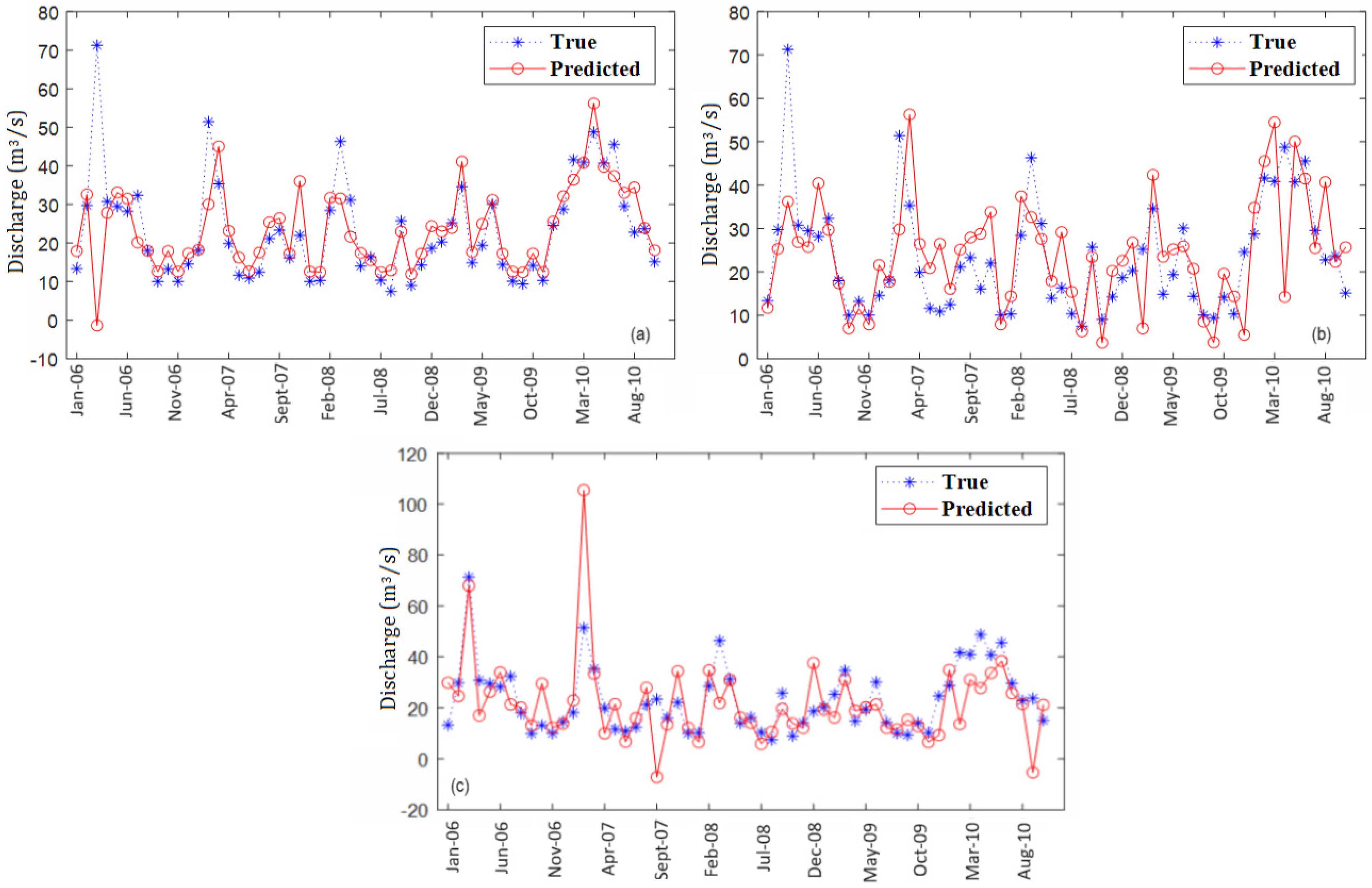
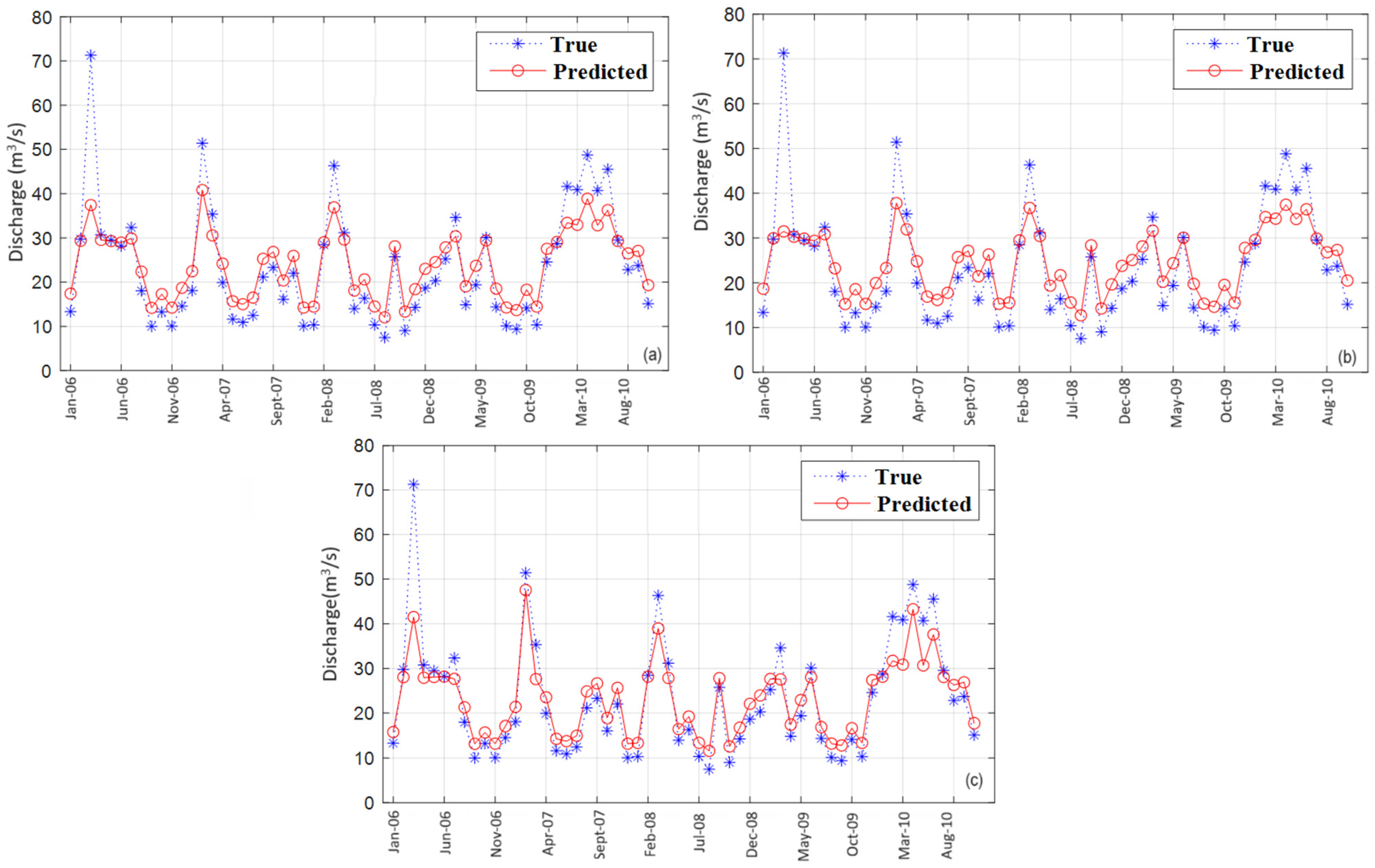
4. Results and Discussion
- ELM and PSO-ELM perform similarly with respect to all goodness-of-fit indicators. The run time is significantly lower for ELM than that of PSO-ELM (358.07 s for S, 56.43 s for S1, and 50.13 (or S2).
- LSTM was more accurate than CNN-LSTM in terms of R2 and MSE for S and S2. The run time for LSTM was 2.35 (1.63) times lower than that of CNN-LSTM for S (S2).
- All algorithms perform better than multi-layer perceptron (MLP) and the Box–Jenkins (ARIMA) models for S, S1, and S2.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van De Wiel, M.J.; Coulthard, T.J.; Macklin, M.G.; Lewin, J. Modelling the response of river systems to environmental change: Progress, problems and prospects for palaeo-environmental reconstructions. Earth Sci. Rev. 2011, 104, 167–185. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Barbeş, L.; Dumitriu, C.Ş. Statistical Assessment of the Water Quality Using Water Quality Indicators—Case Study from India. In Water Safety, Security and Sustainability. Advanced Sciences and Technologies for Security Applications; Vaseashta, A., Maftei, C., Eds.; Springer: Cham, Switzerland, 2021; pp. 599–613. [Google Scholar]
- Bărbulescu, A.; Maftei, C.E. Evaluating the Probable Maximum Precipitation. Case study from the Dobrogea region, Romania. Rom. Rep. Phys. 2023, 75, 704. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Dumitriu, C.S.; Maftei, C. On the Probable Maximum Precipitation Method. Rom. J. Phys. 2022, 67, 801. [Google Scholar]
- Crăciun, A.; Costache, R.; Bărbulescu, A.; Chandra Pal, S.; Costache, I.; Dumitriu, C.S. Modern techniques for flood susceptibility estimation across the Deltaic Region (Danube Delta) from the Black Sea’s Romanian Sector. J. Marine Sci. Eng. 2022, 10, 1149. [Google Scholar] [CrossRef]
- Popescu, C.; Bărbulescu, A. On the Flash Flood Susceptibility and Accessibility in the Vărbilău Catchment (Romania). Rom. J. Phys. 2022, 67, 811. [Google Scholar]
- Popescu, C.; Bărbulescu, A.; Dumitriu, C.S. Modeling Road Accessibility in a Flood-Prone Area in Romania. Eng. Proc. 2023, 39, 22. [Google Scholar] [CrossRef]
- Ahmadpour, A.; Mirhashemi, S.H.; Haghighatjou, P.; Foroughi, F. Comparison of the monthly streamflow forecasting in Maroon dam using HEC-HMS and SARIMA models. Sustain. Water Resour. Manag. 2022, 8, 158. [Google Scholar] [CrossRef]
- Ghimire, B.N. Application of ARIMA Model for River Discharges Analysis. J. Nepal Phys. Soc. 2017, 4, 27–32. [Google Scholar] [CrossRef]
- Phan, T.-T.-H.; Nguyen, X.H. Combining statistical machine learning models with ARIMA for water level forecasting: The case of the Red river. Adv. Water Resour. 2020, 142, 103656. [Google Scholar] [CrossRef]
- Subha, J.; Saudia, S. Robust Flood Prediction Approaches Using Exponential Smoothing and ARIMA Models. In Artificial Intelligence and Sustainable Computing; Pandit, M., Gaur, M.K., Kumar, S., Eds.; Springer: Singapore, 2023; pp. 457–470. [Google Scholar]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X.; Zhu, G.; Lu, X.; Wang, K. A seasonal ARIMA model based on the gravitational search algorithm (GSA) for runoff prediction. Water Supply 2022, 22, 6959–6977. [Google Scholar] [CrossRef]
- Yürekli, K.; Kurunc, A.; Ozturk, F. Application of Linear Stochastic Models to Monthly Flow Data of Kelkit Stream. Ecol. Model. 2005, 183, 67–75. [Google Scholar] [CrossRef]
- Uca; Toriman, E.; Jaafar, O.; Maru, R.; Arfan, A.; Ahmar, A.S. Daily Suspended Sediment Discharge Prediction Using Multiple Linear Regression and Artificial Neural Network. J. Phys. Conf. Ser. 2018, 954, 012030. [Google Scholar] [CrossRef]
- Chaibandit, K.; Konyai, S. Using Statistics in Hydrology for Analyzing the Discharge of Yom River. APCBEE Procedia 2012, 1, 356–362. [Google Scholar] [CrossRef]
- Dumitriu, C.S.; Bărbulescu, A. Artificial intelligence models for the mass loss of copper-based alloys under the cavitation. Materials 2022, 15, 6695. [Google Scholar] [CrossRef] [PubMed]
- Bărbulescu, A.; Dumitriu, C.S. Modeling the Voltage Produced by Ultrasound in Seawater by Stochastic and Artificial Intelligence Methods. Sensors 2022, 22, 1089. [Google Scholar] [CrossRef]
- Dumitriu, C.Ş.; Dragomir, F.-L. Modeling the Signals Collected in Cavitation Field by Stochastic and Artificial Intelligence Methods. In Proceedings of the 2021 13th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Pitesti, Romania, 1–3 July 2021; pp. 1–4. [Google Scholar]
- Alquraish, M.M.; Khadr, M. Remote-Sensing-Based Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models. Remote Sens. 2021, 13, 4147. [Google Scholar] [CrossRef]
- Kisi, Ö.; Cobaner, M. Modeling River Stage-Discharge Relationships Using Different Neural Network Computing Techniques. Clean 2009, 37, 160–169. [Google Scholar] [CrossRef]
- Tanty, R.; Desmukh, T.S. Application of Artificial Neural Network in Hydrology—A Review. Int.J. Eng. Resear. Technol. 2015, 4, 184–188. [Google Scholar]
- Modaresi, F.; Araghinejad, S.; Ebrahimi, K. A comparative assessment of artificial neural network, least-square support vector regression, and K-nearest neighbor regression for monthly streamflow forecasting in linear and nonlinear conditions. Water Resour. Manag. 2018, 32, 243–258. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Sys. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2019, 583, 124296. [Google Scholar] [CrossRef]
- Xu, H.; Song, S.; Li, J.; Guo, T. Hybrid model for daily runoff interval predictions based on Bayesian inference. Hydrol. Sci. J. 2022, 68, 62–75. [Google Scholar] [CrossRef]
- Fathian, F.; Mehdizadeh, S.; Sales, A.K.; Safari, M.J.S. Hybrid models to improve the monthly river flow prediction: Integrating artificial intelligence and non-linear time series models. J. Hydrol. 2019, 575, 1200–1213. [Google Scholar] [CrossRef]
- Samantaray, S.; Sahoo, A.; Agnihotri, A. Prediction of Flood Discharge Using Hybrid PSO-SVM Algorithm in Barak River Basin. MethodsX 2023, 10, 102060. [Google Scholar] [CrossRef]
- Ruma, J.F.; Adnan, M.S.G.; Dewan, A.; Rahman, M.R. Particle swarm optimization based LSTM networks for water level forecasting: A case study on Bangladesh river network. Result Eng. 2023, 17, 100951. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Zhao, D.; Wang, T.; Wu, X.L.; Duan, B.S. A novel rainfall prediction model based on CEEMDAN-PSO-ELM coupled model. Water Supply 2023, 22, 4531–4543. [Google Scholar] [CrossRef]
- Zaini, N.; Malek, M.A.; Yusoff, M.; Mardi, N.H.; Norhisham, S. Daily River Flow Forecasting with Hybrid Support Vector Machine—Particle Swarm Optimization. IOP Conf. Ser. Earth Environ. Sci. 2018, 140, 012035. [Google Scholar] [CrossRef]
- Tantanee, S.; Patamatammakul, S.; Oki, T.; Sriboonlue, V.; Prempree, T. Coupled Wavelet-Autoregressive Model for Annual Rainfall Prediction. J. Environ. Hydrol. 2005, 13, 1–8. [Google Scholar]
- Liang, Z.; Liu, Y.; Hu, H.; Li, H.; Ma, Y.; Khan, M.Y.A. Combined Wavelet Transform with Long Short-Term Memory Neural Network for Water Table Depth Prediction in Baoding City, North China Plain. Front. Environ. Sci. 2021, 9, 7804. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Dumitriu, C.Ș. Assessing the water quality by statistical methods. Water 2021, 13, 1026. [Google Scholar] [CrossRef]
- Pang, Y.-H.; Wang, H.-B.; Zhao, J.-J.; Shang, D.-Y. Analysis and Prediction of Hydraulic Support Load Based on Time Series Data Modeling. Geofluids 2020, 2020, 8851475. [Google Scholar] [CrossRef]
- Kapoor, A.; Pathiraja, S.; Marshall, L.; Chandra, R. DeepGR4J: A deep learning hybridization approach for conceptual rainfall-runoff modelling. Environ. Modell. Softw. 2023, 169, 105831. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Towards Improved Predictions in Ungauged Basins: LSTM Networks for Rainfall-Runoff Modeling. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Alonso Brito, G.R.; Rivero Villaverde, A.; Lau Quan, A.; Ruíz Pérez, M.E. Comparison between SARIMA and Holt–Winters models for forecasting monthly streamflow in the western region of Cuba. SN Appl. Sci. 2021, 3, 671. [Google Scholar] [CrossRef]
- Abrahart, R.J.; See, L. Comparing Neural Network and Autoregressive Moving Average Techniques for the Provision of Continuous River Flow Forecasts in Two Contrasting Catchments. Hydrol. Process. 2000, 14, 2157–2172. [Google Scholar] [CrossRef]
- Khan, F.; Pilz, J. Modelling and sensitivity analysis of river flow in the Upper Indus Basin, Pakistan. Int. J. Water 2018, 12, 1–21. [Google Scholar] [CrossRef]
- Birikundavyi, S.; Labib, R.; Trung, H.T.; Rousselle, J. Performance of Neural Networks in Daily Streamflow Forecasting. J. Hydrol. Eng. 2002, 7, 392. [Google Scholar] [CrossRef]
- Huang, G.-B. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Ahuja, B.; Vishwakarma, V.P. Deterministic Multi-kernel based extreme learning machine for pattern classification. Expert Syst. Appl. 2021, 183, 115308. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Ghose, D.K. Measuring Discharge Using Back-Propagation Neural Network: A Case Study on Brahmani River Basin. In Intelligent Engineering Informatics; Bhateja, V., Coello, C.A.C., Satapathy, S.C., Pattnaik, P.K., Eds.; Springer: Singapore, 2018; pp. 591–598. [Google Scholar]
- Khan, M.Y.A.; Hasan, F.; Panwar, S.; Chakrapani, G.J. Neural network model for discharge and water-level prediction for Ramganga River catchment of Ganga Basin, India. Hydrol. Sci. J. 2016, 61, 2084–2095. [Google Scholar] [CrossRef]
- Magilligan, F.J.; Nislow, K.H. Changes in hydrologic regime by dams. Geomorphology 2005, 71, 61–78. [Google Scholar] [CrossRef]
- Nislow, K.H.; Magilligen; Fassnacht, H.; Becgtel, D.; Ruesink, A. Effects of Dam Impoundment on the Flood Regime of Natural Floodplain Communities in the Upper Connecticut River. JAWRA J. Am. Water Res. Assoc. 2002, 38, 1533–1548. [Google Scholar] [CrossRef]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A method for assessing hydrologic alteration within ecosystems. Conserv. Biol. 1996, 10, 1163–1174. [Google Scholar] [CrossRef]
- Bisoyi, N.; Gupta, N.; Padhy, N.P.; Chakrapani, G.J. Prediction of daily sediment discharge using a back propagation neural network training algorithm: A case study of the Narmada River, India. Int. J. Sedim. Resear. 2019, 34, 125–135. [Google Scholar] [CrossRef]
- Minea, G.; Bărbulescu, A. Statistical assessing of hydrological alteration of Buzău River induced by Siriu dam (Romania). Forum Geogr. 2014, 13, 50–58. [Google Scholar] [CrossRef]
- Mocanu-Vargancsik, C.; Tudor, G. On the linear trends of a water discharge data under temporal variation. Case study: The upper sector of the Buzău river (Romania). Forum Geogr. 2020, 19, 37–44. [Google Scholar] [CrossRef]
- Chendeş, V. Water Resources in Curvature Subcarpathians. Geospatial Assessments; Editura Academiei Române: Bucureşti, Romania, 2011; (In Romanian with English Abstract). [Google Scholar]
- The Arrangement of the Buzău River. Available online: https://www.hidroconstructia.com/dyn/2pub/proiecte_det.php?id=110&pg=1 (accessed on 17 October 2023). (In Romanian).
- Difference between Training Data and Testing Data. Available online: https://edupepper.com/difference-between-training-data-and-testing-data/ (accessed on 17 April 2024).
- Fausett, L. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Wang, W.; Du, Y.; Chau, K.; Chen, H.; Liu, C.; Ma, Q. A Comparison of BPNN, GMDH, and ARIMA for Monthly Rainfall Forecasting Based on Wavelet Packet Decomposition. Water 2021, 13, 2871. [Google Scholar] [CrossRef]
- Saxena, S. What is LSTM? Introduction to Long Short-Term Memory. Available online: https://www.analyticsvidhya.com/blog/2021/03/introduction-to-long-short-term-memory-lstm/ (accessed on 17 March 2024).
- Zhen, L.; Bărbulescu, A. Comparative Analysis of Convolutional Neural Network-Long Short-Term Memory, Sparrow Search Algorithm-Backpropagation Neural Network, and Particle Swarm Optimization-Extreme Learning Machine for the Water Discharge of the Buzău River, Romania. Water 2024, 16, 289. [Google Scholar] [CrossRef]
- Deep Learning|Introduction to Long Short Term Memory. Available online: https://www.geeksforgeeks.org/deep-learning-introduction-to-long-short-term-memory/ (accessed on 17 March 2024).
- Understanding LSTM Networks. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 17 March 2024).
- Extreme Learning Machine. Available online: https://www.geeksforgeeks.org/extreme-learning-machine/ (accessed on 17 March 2024).
- Zhu, H.; Tsang, E.C.C.; Zhu, J. Training an extreme learning machine by localized generalization error model. Soft Comput. 2018, 22, 3477–3485. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, L. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agr. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Tsironi, E.; Barros, P.; Weber, C.; Wermter, S. An analysis of Convolutional Long Short-Term Memory Recurrent Neural Networks for gesture recognition. Neurocomputing 2017, 268, 76–86. [Google Scholar] [CrossRef]
- Zhang, R.; Pan, Z.; Yin, Y.; Cai, Z. A Model of Network Security Situation Assessment Based on BPNN Optimized by SAA-SSA. Int. J. Digital Crime Forens. 2022, 14, 1–18. [Google Scholar] [CrossRef]
- Karlsson, V.; Rosvall, E. Extreme Kernel Machine. Available online: https://www.diva-portal.org/smash/get/diva2:1130092/FULLTEXT01.pdf (accessed on 6 January 2024).
- Ouma, Y.O.; Cheruyot, R.; Wachera, A.N. Rainfall and runoff time-series trend analysis using LSTM recurrent neural network and wavelet neural network with satellite-based meteorological data: Case study of Nzoia hydrologic basin. Complex Intell. Syst. 2022, 2022, 213–236. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, M.; Nedjah, N.; Xu, D.; Ye, F. A Hydrological Data Prediction Model Based on LSTM with Attention Mechanism. Water 2023, 15, 670. [Google Scholar] [CrossRef]
- Liu, T.; Ding, Y.; Cai, X.; Zhu, Y.; Zhang, X. Extreme learning machine based on particle swarm optimization for estimation of reference evapotranspiration. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 4567–4572. [Google Scholar]
- Anupam, S.; Pani, P. Flood forecasting using a hybrid extreme learning machine-particle swarm optimization algorithm (ELM-PSO) model. Model. Earth Syst. Environ. 2020, 6, 341–347. [Google Scholar] [CrossRef]



| Model | Full Data Range | Training Data Range | Test Data Range |
|---|---|---|---|
| S | January 1955–December 2010 | January 1955–December 2005 | January 2006–December 2010 |
| S1 | January 1955–December 1983 | January 1955–December 1983 | January 2006–December 2010 |
| S2 | January 1984–December 2010 | January 1984–December 2005 | January 2006–December 2010 |
| Parameter | Value |
|---|---|
| Number of Input Nodes | 1 (Water discharge series) |
| Number of Hidden Nodes | 300 |
| Number of Output Nodes | 1 (Water discharge series) |
| Learning Rate | 0.01 |
| Max Iterations | 100 |
| Optimization Algorithm | Momentum Gradient Descent |
| Loss Function | MSE |
| Shuffle Data Every Epoch | Yes |
| Parameter | Value |
|---|---|
| Number of Train Samples | 612 |
| Number of Test Samples | 131 |
| Max Epochs | 100 |
| Initial Learning Rate | 0.01 |
| Learning Rate Schedule | Piecewise |
| Learning Rate Drop Factor | 0.1 |
| Learning Rate Drop Period | 80% of Max Epochs |
| Optimization Algorithm | Adam |
| Shuffle Data Every Epoch | Yes |
| Parameter | Value |
|---|---|
| Number of Input Nodes | 1 (Water discharge series) |
| Number of Hidden Nodes | 300 |
| Number of Output Nodes | 1 (Water discharge series) |
| Activation Function of Hidden Layer | Sigmoid |
| Input Layer Weight Initialization | Uniform distribution (−1 to 1) |
| Hidden Layer Weight Initialization | Randomly generated |
| Input Layer Bias Initialization | 0 |
| Hidden Layer Bias Initialization | Random number between 0 and 1 |
| Max Epochs | 100 |
| Optimization Algorithm | None |
| Loss Function | MSE |
| Indicator | Model | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|---|
| S | S1 | S2 | S | S1 | S2 | ||
| MAE (m3/s) | BPNN | 6.96 | 11.00 | 8.14 | 5.52 | 7.94 | 8.29 |
| LSTM | 6.78 | 10.50 | 5.72 | 4.92 | 7.64 | 4.49 | |
| ELM | 6.01 | 6.79 | 5.02 | 4.60 | 5.21 | 4.01 | |
| MSE ((m3/s)2) | BPNN | 152.44 | 326.62 | 145.38 | 125.06 | 116.36 | 158.55 |
| LSTM | 87.69 | 213.22 | 60.07 | 41.48 | 98.74 | 35.65 | |
| ELM | 98.12 | 126.33 | 78.63 | 41.29 | 54.54 | 32.21 | |
| R2 (%) | BPNN | 52.89 | 18.30 | 0.50 | 31.07 | 40.80 | 42.17 |
| LSTM | 99.39 | 98.99 | 99.92 | 99.83 | 99.74 | 99.97 | |
| ELM | 83.05 | 76.14 | 79.71 | 88.70 | 81.84 | 89.71 | |
| Algorithm | S | S1 | S2 |
|---|---|---|---|
| BPNN | 1.3154 | 1.2271 | 1.1639 |
| LSTM | 4.3335 | 3.5738 | 3.5890 |
| ELM | 0.6996 | 0.7449 | 0.6467 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bărbulescu, A.; Zhen, L. Forecasting the River Water Discharge by Artificial Intelligence Methods. Water 2024, 16, 1248. https://doi.org/10.3390/w16091248
Bărbulescu A, Zhen L. Forecasting the River Water Discharge by Artificial Intelligence Methods. Water. 2024; 16(9):1248. https://doi.org/10.3390/w16091248
Chicago/Turabian StyleBărbulescu, Alina, and Liu Zhen. 2024. "Forecasting the River Water Discharge by Artificial Intelligence Methods" Water 16, no. 9: 1248. https://doi.org/10.3390/w16091248
APA StyleBărbulescu, A., & Zhen, L. (2024). Forecasting the River Water Discharge by Artificial Intelligence Methods. Water, 16(9), 1248. https://doi.org/10.3390/w16091248








