Long-Term Changes in Water and Ion Flows of the Pechora River, the Longest Full-Water European Arctic River

Abstract

Long-term series of annual and seasonal water flow and major ions in the Pechora River were analyzed. Long-term phases of increased and decreased water flow were identified, ranging in duration from 11 to 49 years, and the major characteristics of these phases were determined. Changes in the sequence and boundaries of contrast phases in the annual and snowmelt spring–summer flood runoff were found to coincide. The difference between the mean seasonal water runoff during the phases of increased and decreased flow varied from 12 to 41%. The ion flow values of contrast phases typically differed by 9 to 36%, which is less than for water flow. This is due to the inverse dependence between ion concentrations and water discharge. Such peculiar negative feedback stabilizes the rates of chemical denudation in the river catchments to some extent and, thus, the discharge of major ions into seas, even during significant variations in water.

1. Introduction

Because of the recent period of global warming, which began in the 1970s–1980s [1], considerable attention has been paid to studies of long-term variations in the geoflow of Arctic rivers. This article considers long-term phases of increased or decreased annual and seasonal water flow, with a focus on the accompanying flow of major ions in the Pechora River, one of the largest Arctic rivers in Europe.

The term ‘global warming’ is not an entirely accurate characterization of the global changes that are currently occurring. Indeed, changes were first detected in global (i.e., integrated over a hemisphere or the globe) surface air temperature [2], and interpreted as a manifestation of the discernable impact of anthropogenic activity on the chemical composition of greenhouse gases in the atmosphere [3]. These changes have now been observed in most components of the Earth System, i.e., in the atmosphere, hydrosphere, cryosphere, world ocean, and biosphere [4,5], and interact via numerous negative and positive feedbacks. One such feedback is the impact of the geoflow of Arctic rivers into the Arctic Ocean. The Arctic Ocean is relatively shallow, has unstable seasonal ice cover, and contains sensitive chemical and thermal regimes. Due to large freshwater influxes, its salinity is much lower than that of the world ocean (approximately 30 psu versus 34.7 psu). Due to its unstable heat balance regulated by variable inflow and outflow oceanic streams, sea ice area, and depth decreases [6,7], the Arctic Ocean generates phenomena that act as feedbacks to the surrounding areas, extending as far as the tropics [8,9,10].

According to Muraveiskii [11], geoflow includes flows of water, heat, sediments, and chemicals, which are very sensitive to contemporary climate change [12,13,14,15,16,17,18]. Long-term variations in the geoflow components of Arctic rivers (as well as rivers in other regions) include periods (or phases, according to the terminology accepted in Russia [19]) of increased or decreased values with different durations. Synchronous long phases of increase or decrease may extend over vast areas. These contrast phases have a specific and relatively stable water regime in rivers, and influence the state of riverine, lake, and marine ecosystems [20,21].

Multiannual variations in water flow include long periods, which may last from 10–15 years to many decades [16,22,23]. Alternating periods are an important feature of the long-term dynamics of hydrological characteristics. They can be caused by climate change, and the resulting differences between runoff values in successive contrast phases are usually statistically significant. The annual and seasonal water runoff of rivers in the Arctic (and other regions of the world) have already been studied [24,25].

The long contrast phases of other geoflux components have received much less attention, although it is obvious that changes in water flow should influence each geoflux component. In general, the more distinct the components are, the more closely they are related to the water flow [26]. Furthermore, a significant number of studies have been conducted since the onset of global warming, including field studies examining a wide range of both dissolved and suspended particle chemicals [24,26,27,28,29,30,31,32,33,34,35]. It is expected that an increase in the water flow in rivers of the Arctic Ocean Basin can contribute to an increase in the input of dissolved organic matter, inorganic nutrients, and major ions [26,36,37].

There were assumptions that, with climatic warming, the demise of permafrost and the deepening of the so-called “active soil layer” will lead to an increasing impact of more mineralized soil waters on the ion runoff of the arctic rivers. Frey and McClelland [36] suggested that “… one of the most profound changes to occur with future arctic warming may be the transition of the Arctic System from a surface water-dominated system to a groundwater-dominated system, with resulting cascading impacts on hydrology, ecosystems, and biogeochemical cycling”. However, our findings for the Pechora River Basin show that, so far, the currently observed water runoff increases and resulting dilution effects somewhat mitigated the expected (and ongoing) increases in major ion concentrations occurring from permafrost degradation and enhanced upper layer water interaction with deep mineral horizons.

1.1. Characteristics of the Pechora River Basin

The Pechora River Basin lies in the northeastern portion of European Russia between 61° and 66° N. It has an area of 322,000 km² with a maximal size of 755 km from south to north and 763 km from west to east. The natural boundaries of the Pechora River Basin are the Timanskii Ridge in the west, the Ural Mountains in the east, the uplands of the Bol’shezemel’skaya Tundra in the north, and the Volga–Pechora water section in the south. The relief of the Pechora basin is mostly flat, except for the easternmost foothills of the Ural Mountains.

For our analysis, we used hydrological measurements at the Ust’-Tsil’ma Village hydrometric observation station on the Pechora River. This station is 425 km from the mouth of the river and gauges a watershed area of 248,000 km² (approximately 77% of the entire area of the basin). A hydrometric station, Oksino, is positioned in the delta of the river. However, for our goal of accurately reporting the ion fluxes of the river, measurements at this site cannot be used. They are partially contaminated by the Barents Sea confluence.

The Pechora River catchment lies in the northern taiga and tundra ecological zones. Permafrost is common in the north and northeast of the basin [38]. The mean annual air temperature is −3.3 °C, and the annual precipitation is 534 mm. A schematic map of the basin is given in Figure 1.

Table 1. The three typical hydrological seasons in the Pechora River Basin and their associations with the major sources of the river recharge.

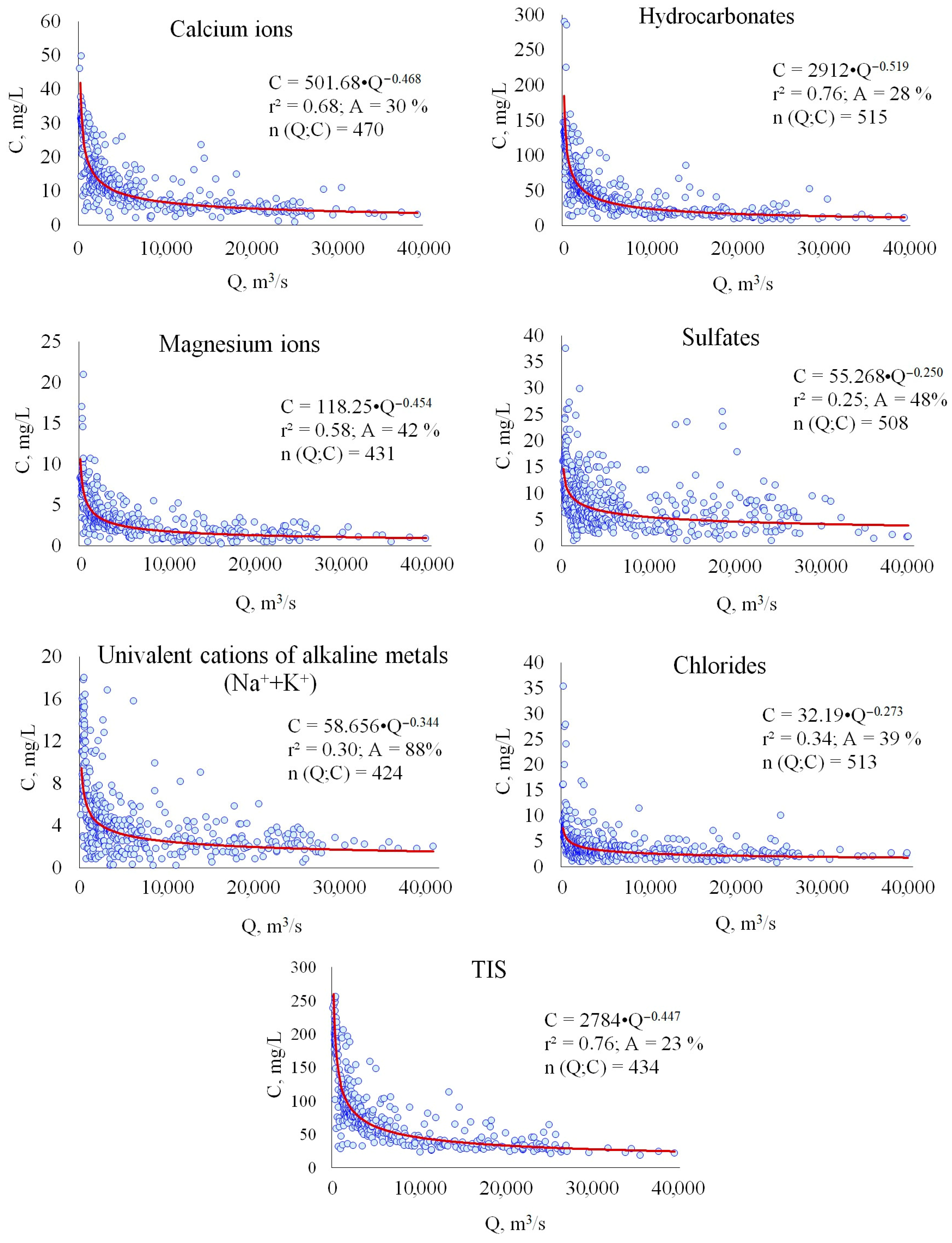
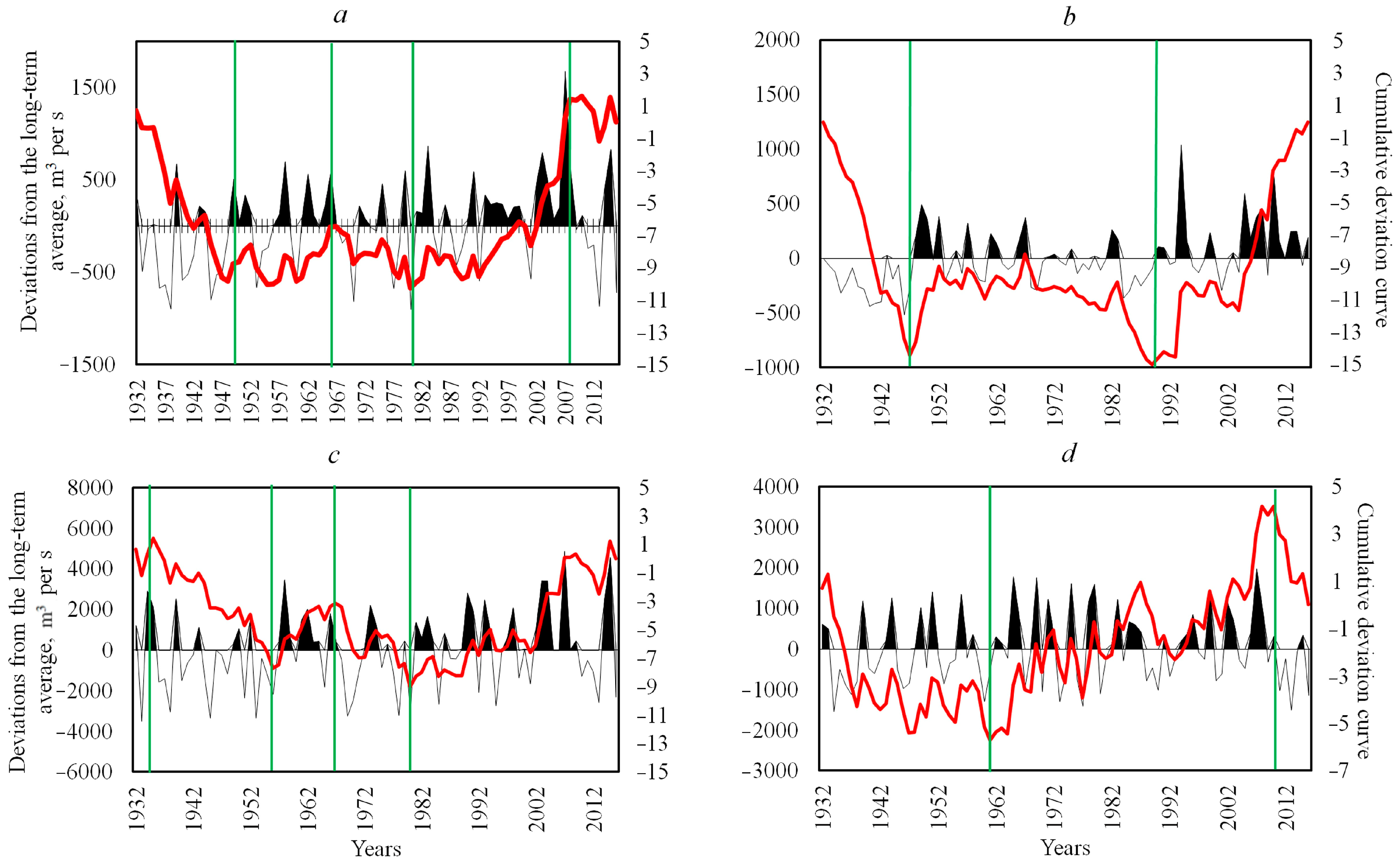
Period/Months	River Flow	Dominant Source of Runoff
November–April	Winter low flow	Groundwater
May–June	Spring–summer high flow	Snowmelt water, overland flow
July–October	Summer–autumn low flow	Soil–subsoil water and overland flow during rainfall

describes three major hydrological seasons of the river.

The recharge of the river is strongly influenced by snow contributions. The mean long-term water runoff at Ust’-Tsil’ma Village hydrometric station is 3305 m³/s. During the spring–summer snowmelt flood period (May–June, hereafter, the snowmelt flood period) the runoff reaches 11,593 m³/s. Over summer and autumn (July–October), it is close to the mean annual flow, i.e., 3285 m³/s. During the winter low-water season (November–April), it decreases to 905 m³/s.

More than one-third of the Pechora basin area is covered by insular, discontinuous, and continuous permafrost (mostly in the northeastern piedmont and mountain parts of the basin). The southern boundary of the permafrost is located approximately along the Arctic Circle, and shifts far to the south, reaching 61° N in the Ural Mountains. More than half of the territory occupied by permafrost in the Pechora River Basin lies in the Usa River Basin, which is its largest right tributary. The permafrost depth in Northern European Russia is relatively small, varying from 10–15 to 500–700 m. Because this permafrost is “warm” (ranging from −0.5 to −20 °C), it is sensitive to climate change and anthropogenic impacts [39].

1.2. Hydrochemical Characteristics of the Pechora River at Ust’-Tsil’ma Village

The water chemistry of the Pechora River and its largest tributaries have been well studied. Its chemical runoff into the Barents Sea has been estimated for different time intervals over a long instrumental period [40,41,42,43,44,45]. Much research has focused on the flow of dissolved substances as key contributors to the salt balance of seas and as a characteristic arising from the chemical denudation of continental surfaces. We define chemical denudation here as an amount of solved material per time unit brought from the surface and the soil interior. The ion river runoff characterizes an intensity of this process. Dissolved components include ion runoff and major ion runoff (approximately 80% of the total volume of dissolved matter runoff), the runoff of mineral colloids, inorganic biogenic elements, microelements, and organic matter. The ion flow has been particularly well characterized [38].

Hydrochemical observations and estimates of dissolved matter runoff and unit area discharge were mostly made at the Naryan-Mar City outlet station (Oksino Village), which gauges a greater portion of the Pechora River Basin (312,000 out of 322,000 km²) than the Ust’-Tsil’ma Village station. However, despite the requirement that the positive and negative setup phenomena should have no effect on water chemistry observations at the outlet station, the water in the reach near Naryan-Mar City sometimes shows chloride–sodium water chemistry, which is not typical for the Pechora River. This, instead, indicates the effect of tidal waves [29]. Estimates at the Naryan-Mar City and Ust’-Tsil’ma Village observation sites are different because several large tributaries (the Pizhma, Tsilma, and Shapkina rivers) discharge into the Pechora River downstream of the latter. In addition, some differences between estimates can arise due to the different procedures used to calculate dissolved matter runoff (for example, different basic periods of observations, etc.).

The chemistry of total inorganic solutes (TIS) in Pechora River water is primarily controlled by soils and underlying deposits, which mostly include podzol soils on glacial and fluvio-glacial deposits, represented by boulder loam and sandy loam. These soils do not contain highly soluble chlorides and sulfates and, among other soluble compounds, contain mostly carbonate calcium compounds [38]. Due to its ion-salt composition, the Pechora River water is characterized as in the hydrocarbonate class and the calcium group (relative equivalent content: HCO₃⁻ < Ca²⁺ + Mg²⁺ < HCO₃⁻ + SO₄²⁻). This means that it is genetically related to underlying sedimentary rocks and their weathering products [46].

The predominant effect of the dissolution of carbonate minerals in the underlying rocks on the ion-salt composition of the Pechora River water is confirmed by the proportions of the equivalent amounts of the sum of calcium/magnesium and hydrocarbonates. These proportions are close to 1:1, which is consistent with the hydrolysis of carbonate minerals in the presence of carbonic acid [37]. On the other hand, sulfates in river water under natural conditions form during the dissolution of gypsum. The left tributaries of the river flow in or through the gypsum karst areas. In this case, magnesium sulfates (as well as univalent cations of alkaline metals) are formed because of cation exchanges between dissolved gypsum and rocks containing magnesium as absorbing bases [47]. The presence of a gypsum sulfate source is confirmed by the correspondence between the equivalent amounts of sulfates and the sum of calcium and magnesium ions. The closeness of this correlation is much weaker than that for hydrocarbonates, and may indicate an additional source of sulfate inflow into the river water [43]. This inflow can be caused by atmospheric precipitation, during which ions enter the Pechora River channel, along with soil-surface water. Atmospheric precipitation can account for approximately one-tenth of the mean TIS value of soil–surface water. In terms of their ion composition, these processes lead to considerable increases in the concentrations of sulfates and sodium cations [38].

The main features of water chemical composition in the Pechora River are similar across all seasons; however, their appearances and TIS values differ between low- and high-water seasons. These differences are due to the predominance of groundwater during river recharge in the winter low-water season and soil–subsoil water in the summer low-water season instead of the predominance of overland water flow (soil–surface water) in the periods of snowmelt and rain floods [38]. Within a single year, TIS may vary from 18 to 256 mg/L with an average of 85 mg/L. However, even in the winter low-water season, when the major ion concentrations reach their maximum values, the water of the Pechora River maintains a low TIS: 27–256 mg/L (on average, 170 mg/L). During the spring flood period, the concentration of major ions decreases to 18–157 mg/L (on average, 43 mg/L), and in summer, it varies within the range of 32–153 mg/L (on average, 82 mg/L).

The unit area discharge of the Pechora River is approximately 30 t/km² per year [48]. This is greater than that of Siberian rivers, e.g., the Ob or Lena (about 20 t/km² per year) but less than that of other rivers in the European North of Russia (about 40 t/km² per year; for example, the Northern Dvina and Onega). This intermediate position is due to both the presence of permafrost rocks in the Pechora River Basin (unlike the Northern Dvina) and the specific effect of its tributaries. The right and left tributaries of the Pechora differ considerably in their water TIS. The mountain right tributaries have low-TIS water with a stable hydrocarbonate composition. The lowland left tributaries contain waters with a higher TIS due to the instability of the predominant anion composition resulting from the presence of gypsum karst in their basins (for example, the Northern Mylva, Vel’yu, and Izhma). The left tributaries, thus, have a minor effect on the ion composition of the Pechora, except for areas immediately downstream of those tributaries. The main control of the ion composition of the Pechora River is provided by the more water-abundant right tributaries [38].

2. Materials and Methods

Variations in the water and ion flow of the Pechora River were studied using observational data on water discharges and hydrochemical substances collected by the State Observation Network, part of the Federal Service for Hydrometeorology and Environmental Monitoring (Roshydromet). Observations of water chemistry in the Pechora River at Ust’-Tsil’ma Village station began in 1938, and observations of water discharges began in 1932. The hydrochemical data analyzed in this article were collected by procedures developed by the FGBU Hydrochemical Institute [49].

Analyzing long phases within the long-term variations in annual and seasonal water flow, caused by climate change, uses cumulative deviation curves, the criteria of statistical homogeneity of the mean runoff values, and estimates of the characteristics of identified phases of contrast water abundance. The cumulative deviation curves represent the increasing sum of deviations of a characteristic from its long-term average value, and are calculated over the entire observation period [16,19]. These curves allow us to identify long phases, within which the values of characteristics are below or above their long-term mean values.

The boundaries of the hydrological seasons (in Table 1) were determined using runoff hydrographs constructed for the entire observation period. Data corresponding to normal annual dates of the start and end of the spring flood and freeze-up periods were also used.

The time boundaries of the change in long-term phases (with a duration of 10 years or more) of increased and decreased water flow were determined by identifying the minimal and maximal values of coordinates in cumulative deviation curves; such methods have been widely used [19,22,50,51].

The cumulative deviation curve (CDC) represents the cumulative sum of deviations of a certain characteristic (variable) from its long-term annual average value, and it calculated over the entire observation period. Deviations are frequently normalized to the coefficient of variation such that the temporal variability of dissimilar characteristics can be compared. Normalized CDCs were calculated using the following formulas:

$$CD{C}_{\tau }=\frac{1}{C_v}{\displaystyle \sum _{i=1}^{\tau }}\left(K_i-1\right)$$

$$K_i=E_i/E_m$$

$$C_v=\frac{\sigma }{E_m}$$

$$\sigma =\sqrt{\frac{1}{n-1}{\sum }_{i=1}^n{\left(E_i-E_m\right)}^2},$$

where CDC_τ is the coordinate value of the cumulative deviation curve at time τ, E_i is the value of the i-th term of the series (i = 1, 2, …, n), n is the number of terms in the time series, E_m is the long-term annual mean of the time series, K_i is the modular coefficient of the i-th term of the time series, C_v is the coefficient of variation in the time series, and σ is the standard deviation of the time series.

The same boundaries of contrast phases were used to calculate the normal annual values of ion flow because its variations are closely related to those of the water regime of the river.

Several main approaches are used to calculate the runoff of dissolved substances based on a limited set of hydrochemical data, which are heterogeneous in terms of sampling frequency and observation times during long periods. The simplest method to determine these characteristics is direct calculation because it is based on linear interpolation of the measured values of dissolved matter concentrations for each day of the calculation period [40]. This method provides a reliable result only when a river exhibits no correlation between the concentration of dissolved matter and water discharge [48].

However, for major ions, a statistically significant relationship can be often found between water discharge and ion concentrations. This manifests itself in a rapid TIS drop during the spring flood and freshet periods, and in an increase in TIS throughout the low-water seasons. Figure 2 shows that this relationship can be represented by hyperbolic curves. Branches of these curves asymptotically approach the coordinate axes due to the dilution of winter water by meltwater, which has a lower TIS [46]. In this case, in the authors’ opinion, it is better to use the correlation–regression method to assess chemical runoff. This method is based on identifying correlation relationships between the concentrations of dissolved substances and water discharges. These correlations, along with the values of mean daily water discharges, can then be used to evaluate the mean daily concentrations of dissolved substances [52].

For pairs of water flow (Q) and the concentration of an individual ion (C), functional approximations were chosen to describe the relationship between the hydrochemical and water regimes (Figure 2). Note that, in low-flow phases, especially during the winter low-water season when the groundwater recharge of the river dominates, correlations between the concentrations of major ions and water discharge become much weaker. This contributes to an increase in the data approximation error inherent to chosen functions. Furthermore, during periods of lower water, the approximation error can be high because the water discharge is unchanged, but water TIS may vary widely due to the presence of waters with different genetic histories. At the initiation of water level rise, the river channel is still mostly filled by subsoil water; subsequently, most of the channel water is formed by surface recharge. Hydrocarbonates and calcium are the key ions that determine the Pechora chemical runoff and, hence, the integral characteristic of river water TIS. For these key ions, the determination indices at a level of 0.68–0.76 allow the determination of relationships between the mean daily water discharge rate (Q, m³/s) and the measured concentration values (C) to be stated the form C = f(Q). These can be considered as smoothing functions that reduce, to some extent, calculation errors due to errors in sampling, laboratory measurements, and input of results into databases, as well as other possible errors. The use of a unified approach for evaluating the runoff of major ions enables the identification of general regularities in variation during changes in long-term phases of water flow.

Using the daily water discharge data as an argument of the functions in Figure 2, we obtained a time series of calculated daily concentrations of dissolved chemicals, which were used to calculate the daily ion runoff (G) and its individual components according to the following formula:

$$G={\displaystyle \sum _{i=1}^n}{W}_i\times C_i$$

where W_i is water runoff over a day (km³), C_i is the mean daily concentration of the substance (t/km³), n is the number of days in the year, and i is the ordinal number of a day in the year.

To calculate the ion runoff for one year or one season, the values of daily chemical runoff in the appropriate calculation periods were summed. The seasonal ion runoff was calculated by rounding to one month.

3. Results and Discussion

The boundaries of the contrast phases of snowmelt flood and annual runoff in the Pechora show a strong coincidence (Figure 3 and

Table 2. Characteristics of phases of decreased and increased water flow in the Pechora River at Ust’-Tsil’ma Village. Boundaries of the phases, their duration (years), and average water flow, m³/s.

River Water Flow Phases	Snowmelt Flood Flow	Summer–Autumn Flow	Winter Flow	Annual Flow
Decreased flow	1936–1956 (21) 10,767 m3/s	1933–1961 (29) 3094 m3/s	1933–1949 (17) 736 m3/s	1932–1948 (17) 3204 m3/s
	1969–1980 (12) 10,708 m3/s	–	–	1967–1980 (24) 3349 m3/s
Increased flow	1957–1967 (11) 12,271 m3/s	1962–2010 (49) 3460 m3/s	1989–2016 (28) 1036 m3/s	1949–1966 (18) 3564 m3/s
	1981–2015 (25) 12,148 m3/s	–	–	1981–2008 (28) 3673 m3/s
Phases of water flow close to the long-term mean	–	–	1950–1988 (39) 885 m3/s	–

). The order of changes and the boundaries of contrast phases of winter runoff differ considerably from the runoff phase dynamics both of other seasons and of annual runoff.

There are only two long periods in which the phases of winter runoff and annual and snowmelt spring–summer flood runoff have the same signs. These occurred in 1932–1947 (when both runoffs decreased) and in 1989–2008 during an increased runoff phase. During a period of almost forty years (1950–1988), the winter flow did not show any long periods with an average flow differing significantly from its mean value over the entire observation period. Additionally, the long-term dynamics of the contrast phases of summer–autumn runoff differed from the dynamics of runoff phases in other seasons of the year and from the annual runoff. The runoff of the summer–autumn season first showed a phase of decreased flow which, in 1962, changed to a long phase of increased flow. In this case, long phases of water flow with the same sign over the summer–autumn period, the snowmelt flood period, and the annual period were observed only in the phase of their increased flow in 1981–2008. The summer–autumn and winter flows have the same phase sign (increased) only in 1989–2009. In both the Pechora and Northern Dvina rivers (the basin of the latter is located westward adjacent to the Pechora River Basin), phases with the same sign for the snowmelt flood runoff were observed within relatively long periods in 1935–1945, 1967–1980, and 1989–2004. For the winter flow, phases with the same sign were observed in 1936–1947 and 1989–2016 and, for the summer–autumn flow, in 1935–1961 and 2009–2016. For the annual runoff, such synchronicity was observed only in 1934–1947 [26].

The durations of contrast phases in the Pechora River vary within a range of 11–25 years for the snowmelt flood runoff, 29–49 years for the summer–autumn runoff, 17–28 years for the winter runoff, and 17–28 years for the annual runoff.

The differences between the mean water flow for long-term phases of increased and decreased values (relative to the values of phases of decreased flow) in the Pechora River are 11% for the annual runoff, 41% for the winter runoff, 12% for the summer–autumn runoff, and 13% for the snowmelt flood runoff (

Table 3. Mean water discharges in the Pechora River at Ust’-Tsil’ma Village for contrast phases (m³/s), and their absolute and relative differences.

River Water Flow Phases	Snowmelt Flood Flow	Summer–Autumn Flow	Winter Flow	Annual Flow
I	12,179	3460	1036	3631
D	10,745	3094	736	3270
I − D, m3/s	1434	367	300	361
(I − D)/D × 100, %	13	12	41	11

Notes: I, increased river runoff; D, decreased river runoff. Here, as well as in the following Table 4 and Table 5, all calculations were made with long mantissas, while the results of relative changes are presented rounded to a whole percent. Some minor discrepancies may be expected when the presented table values are used for percent recalculations.

).

The relationship between the hydrochemical and water regimes of the Pechora River suggests that the alternation of the periods of increased and decreased water flow could influence both the total volume of ion flow and the flow of its components over different seasons of the annual cycle (

Table 4. Ion runoff (G) in the Pechora River at Ust’-Tsil’ma Village hydrometric station during contrast phases of decreased and increased water flow (the table gives the average value of G ± standard deviation σ of the sample data).

Water Flow Phase	Ion Runoff (Gaverage ± σ), Million ton Per Year
	Ca2+	Mg2+	Na+ + K+	HCO3−	SO42−	Cl−	TIS
Year as a whole
I	1.11 ± 0.08	0.29 ± 0.02	0.44 ± 0.04	4.17 ± 0.29	0.76 ± 0.08	0.34 ± 0.03	7.33 ± 0.58
D	0.99 ± 0.10	0.25 ± 0.03	0.38 ± 0.04	3.73 ± 0.39	0.66 ± 0.08	0.29 ± 0.03	6.51 ± 0.69
I − D	0.12	0.04	0.06	0.44	0.1	0.05	0.82
(I − D)/D × 100, %	12	13	14	12	15	15	13
Snowmelt flood period
I	0.38 ± 0.03	0.10 ± 0.01	0.17 ± 0.02	1.36 ± 0.10	0.34 ± 0.04	0.15 ± 0.02	2.59 ± 0.22
D	0.34 ± 0.04	0.09 ± 0.01	0.15 ± 0.02	1.23 ± 0.13	0.29 ± 0.04	0.13 ± 0.02	2.32 ± 0.27
I − D	0.04	0.01	0.02	0.13	0.05	0.02	0.27
(I − D)/D × 100, %	11	12	13	11	15	15	12
Summer–autumn period
I	0.42 ± 0.06	0.11 ± 0.02	0.16 ± 0.03	1.57 ± 0.21	0.27 ± 0.06	0.12 ± 0.03	2.75 ± 0.42
D	0.38 ± 0.05	0.10 ± 0.01	0.14 ± 0.02	1.44 ± 0.19	0.24 ± 0.05	0.11 ± 0.02	2.49 ± 0.37
I − D	0.04	0.01	0.02	0.13	0.03	0.01	0.26
(I − D)/D × 100, %	10	11	12	9	14	14	10
Winter low-water season
I	0.33 ± 0.02	0.08 ± 0.01	0.11 ± 0.01	1.29 ± 0.08	0.16 ± 0.02	0.07 ± 0.01	2.08 ± 0.16
D	0.26 ± 0.03	0.06 ± 0.01	0.08 ± 0.01	1.06 ± 0.11	0.12 ± 0.02	0.05 ± 0.01	1.66 ± 0.20
I − D	0.07	0.02	0.03	0.23	0.04	0.02	0.42
(I − D)/D × 100, %	24	27	30	22	36	35	25
The phase of water flow close to its long-term mean value	0.30 ± 0.02	0.07 ± 0.01	0.10 ± 0.01	1.20 ± 0.09	0.14 ± 0.02	0.07 ± 0.01	1.92 ± 0.16

Note: D, I—ion runoff for decreased and increased water flow phases, accordingly.

).

Variations in ion runoff during changes in water phases are pronounced and are most visible during the winter low-water season, following the tendencies typical for water flow. However, the differences in ion runoff between the contrast phases are weaker than those in water runoff. The increase in the runoff of major ions during phases of increased flow was 24–36%, depending on the ion, and the water discharge in the same periods increased by 41%. During other hydrological seasons, the differences between contrast phases were smoothed. Thus, an increase in water discharge by approximately 12% in the summer–autumn season and by 13% in the snowmelt flood period was accompanied by an increase in the flow of major ions by 10–14 and 11–15%, respectively. The weaker response of ion runoff compared to water runoff may be due to the inverse character of the dependence of ion concentrations on water discharge.

On the other hand, seasonal runoff anomalies of opposite sign to the annual runoff anomalies may level out changes in the annual chemical runoff. For example, in 1958, which is generally considered as a phase of increased runoff, the spring runoff also increased, whereas the summer–autumn runoff decreased, and the winter runoff remained close to its long-term average value.

The intrannual distribution of the volume of Pechora River ion runoff between phases of decreased and increased water flow changes only slightly. According to [38], the ion runoff, determined over the observation period between 1939 to 1966, amounts to approximately 6.61 million tons per year. Twenty three percent of this ion runoff occurs between December and March, 36% occurs during the period of snowmelt flood, 25% occurs during the summer–autumn from July to September, and 15% occurs in October and November. We obtained similar estimates of the interannual ion runoff distribution.

The proportion of the ion runoff of lithogenic cations and anions (hydrocarbonate, calcium and magnesium ions) is largest in the summer–autumn low-water season, accounting for 38–39% of total runoff during the phase of decreased water flow. This decreases to 37% in the phase of increased water flow. Snowmelt flood causes the flux of lithogenic ions to be somewhat lower. It is 33–37% in the phase of decreased water flow and 32–36% in the phase of increased water flow. The lowest fluxes of hydrocarbonates, calcium, and magnesium are observed during the winter low-water season (25–28%). However, in the phase of higher water content, unlike other hydrological seasons, the corresponding proportion increases (27–31%).

The largest proportion of sulfates, chlorides, and univalent cations of alkaline metals were observed during the snowmelt flood period (40–45% in the phase of decreased water flow and 39–44% in the phase of increased water flow). These values are somewhat lower in the summer–autumn low-water season (37–38%) under a general decreasing trend in runoff and during the passage from phase of decreased water runoff to that of increased water runoff (36–37%). During the winter low-water season, which corresponds to the smallest portion of ionic runoff, the ion proportion also increases from 18–22% to 21–25% at the change between the phases of decreased and increased water runoff.

The variations in ionic runoff consist of two components: variations in water runoff and concentrations of dissolved matter. To evaluate the effect of the change in long-period contrast phases of water flow, we calculated the typical mean concentrations for those periods.

Table 5. Mean concentrations (C) of major ions in the Pechora River at Ust’-Tsil’ma Village in contrast phases of decreased and increased water flow (the table gives the average value C_average ± standard deviation σ of the sample data).

Water Flow Phase	Concentrations (Caverage ± σ), mg/L
	Ca2+	Mg2+	Na+ + K+	HCO3−	SO42−	Cl−	TIS
Year as a whole
I	16.14 ± 7.17	4.19 ± 1.81	4.60 ± 1.56	65.03 ± 31.59	8.55 ± 2.17	4.23 ± 1.16	103.82 ± 44.33
D	17.95 ± 8.29	4.64 ± 2.09	4.96 ± 1.75	73.25 ± 37.03	9.03 ± 2.38	4.49 ± 1.28	114.88 ± 51.03
I − D	−1.81	−0.45	−0.37	−8.21	−0.48	−0.26	−11.06
(I − D)/D × 100, %	−10	−10	−7	−11	−5	−6	−10
Snowmelt Spring-Summer flood period
I	7.87 ± 4.89	2.08 ± 1.25	2.69 ± 1.13	29.46 ± 21.04	5.78 ± 1.65	2.76 ± 0.87	52.15 ± 30.56
D	9.02 ± 6.00	2.38 ± 1.52	2.96 ± 1.35	34.39 ± 26.08	6.18 ± 1.94	2.97 ± 1.03	59.35 ± 37.34
I − D	−1.15	−0.29	−0.27	−4.93	−0.40	−0.21	−7.21
(I − D)/D×100, %	−13	−12	−9	−14	−6	−7	−12
Summer–autumn period
I	11.89 ± 2.87	3.12 ± 0.73	3.73 ± 0.66	45.90 ± 12.30	7.40 ± 0.97	3.61 ± 0.51	77.75 ± 17.95
D	13.05 ± 3.53	3.41 ± 0.90	3.99 ± 0.79	50.93 ± 15.35	7.77 ± 1.11	3.80 ± 0.59	84.95 ± 21.95
I − D	−1.16	−0.29	−0.26	−5.03	−0.37	−0.20	−7.20
(I − D)/D×100, %	−9	−9	−6	−10	−5	−5	−8
Winter low-water season
I	21.02 ± 4.19	5.43 ± 1.05	5.68 ± 0.86	86.34 ± 18.86	10.06 ± 1.14	5.04 ± 0.62	134.11 ± 25.68
D	26.13 ± 6.25	6.70 ± 1.56	6.65 ± 1.20	110.01 ± 28.90	11.28 ± 1.52	5.71 ± 0.83	165.00 ± 37.90
I − D	−5.10	−1.27	−0.97	−23.67	−1.22	−0.67	−30.89
(I − D)/D×100, %	−20	−19	−15	−22	−11	−12	−19
The phase of water flow close to its long-term mean value	22.49 ± 4.66	5.79 ± 1.17	5.96 ± 0.93	93.07 ± 21.21	10.43 ± 1.21	5.24 ± 0.66	143.04 ± 28.43

Note: D, I—ion concentration for decreased and increased water flow phases, accordingly.

presents normal annual and seasonal concentrations, together with standard deviations, showing considerable variability in the data. The scatter in the samples does not allow the changes to be considered statistically significant. However, some general characteristics are observed in the variations in major ion concentrations during changes from decreased to increased water flow, and vice versa. The chemistry of major ions in Pechora Rover water is primarily controlled by soils and underlying deposits.

An increase in the annual volume of ion runoff during the transition from the phase of decreased water flow to the phase of increased water flow is accompanied by a decrease in the average concentrations of major ions, particularly sulfates and chlorides. Both the flushing of soils and the low content of these ions in soils suggests that in the phase of increased water flow, the recharge of the river is facilitated by overland flow water depleted in ions enlarges in comparison with groundwater. During the snowmelt flood, a decrease in the average TIS values is observed along with an increase in water runoff due to dilution processes. The increase in ion runoff during this period occurs primarily due to an increase in water flow. No significant changes in the average concentrations of the main ions were observed during the summer–autumn period. Changes in these ions are mostly consistent with annual changes. During the winter low-water season, the effect of dilution during the transition to the phase of increased water flow is most pronounced for bicarbonates, calcium, and magnesium cations. In general, the dynamics of average concentrations indicate that, under observed global warming conditions accompanied by an increase in water flow, increased recharge by groundwater is compensated by processes of dilution of ions and a general increase in river water flow.

4. Conclusions

Analysis of long-term time series of annual and seasonal water flow in the Pechora River at Ust’-Tsil’ma Village, covering the period from 1932 to 2016, revealed long-term phases of increased and decreased values. The ordering and boundaries of the contrast phases of the annual and the spring snowmelt flood runoff were practically identical. The dynamics of the phases of winter and summer–autumn runoff differed significantly from the long-term variations in the annual and snowmelt flood runoff seasons. Over a period of almost forty years (1950–1988), winter runoff variations did not feature any long periods in which the mean runoff differed significantly from the average value calculated over the entire observation period.

The duration of contrast phases varied in the range of 11–25 years for snowmelt flood runoff, 29–49 years for summer–autumn runoff, 17–28 years for winter runoff, and 17–28 years for annual runoff.

The difference between the average water flow for long-term phases of increased and decreased values (relative to the values typical of decreased runoff phases) amounts to 11% for annual runoff, 41% for winter runoff, 12% for summer–autumn runoff, and 13% for snowmelt flood runoff.

The largest difference between ion and water runoff in the Pechora River in contrast phases of water flow occurs during winter low-water season. However, it is generally less than the differences in water runoff due to the inverse dependence of ion concentration on water discharge. This results in negative feedback that stabilizes the rate of ion runoff in the Pechora River Basin and into the Barents Sea, even during periods characterized by significant variations in water flow.

The dynamics of the mean concentrations of major ions in the contrast phases suggest that these phases are accompanied by a redistribution of the roles of surface and ground flow river recharge. During phases of increased water flow, this increase is likely caused by soil-surface water and ions that enter the catchment surface due to atmospheric precipitation. During the period of snowmelt flood, an increase in river water flow leads to dilution and hence to a decrease in TIS relative to the decreased water flow phase.

Throughout the summer–autumn low-water season, the ionic composition of the Pechora River water shows an increased contribution of its left tributaries flowing in or through gypsum karst areas (i.e., through the regions with higher TIS, such as, for example, the Northern Mylva, Vel’yu, and Izhma Rivers). During phases of increased water flow in the winter low-water season, the TIS increases. In this case, the processes of dilution are less significant than the increase in the availability of water of subsoil origin with higher TIS.

Overall, we conclude that climate change causing appreciable transformations in water flow has a limited effect on the runoff of ions. Some relative dynamic stability of the geochemical load into the Barents Sea is provided by Pechora River water, irrespective of the amplitude of river water flow variations in contrast phases.