Numerical Study on the Formation Mechanism of Plume Bulge in the Pearl River Estuary under the Influence of River Discharge
Abstract
:1. Introduction
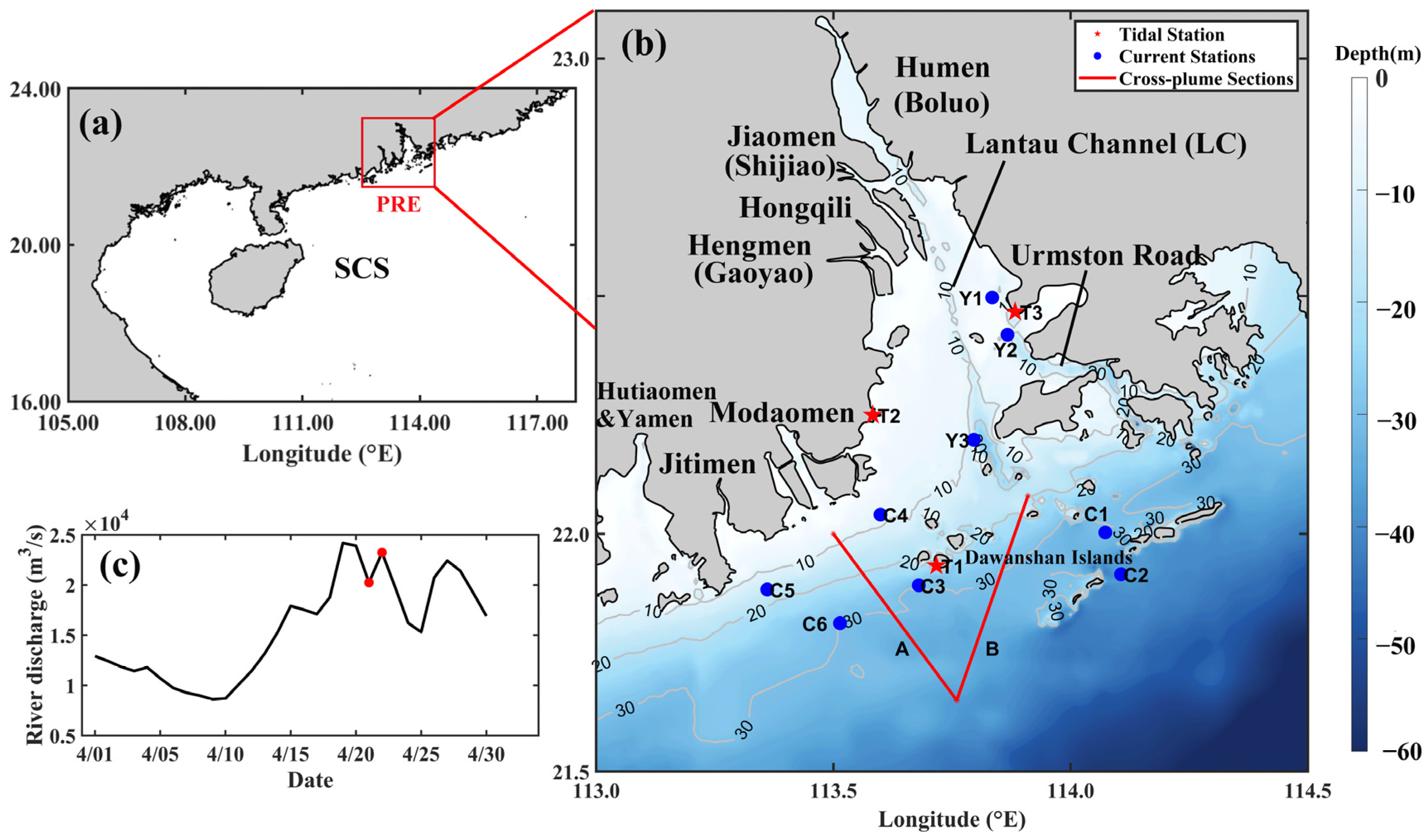
2. Study Area
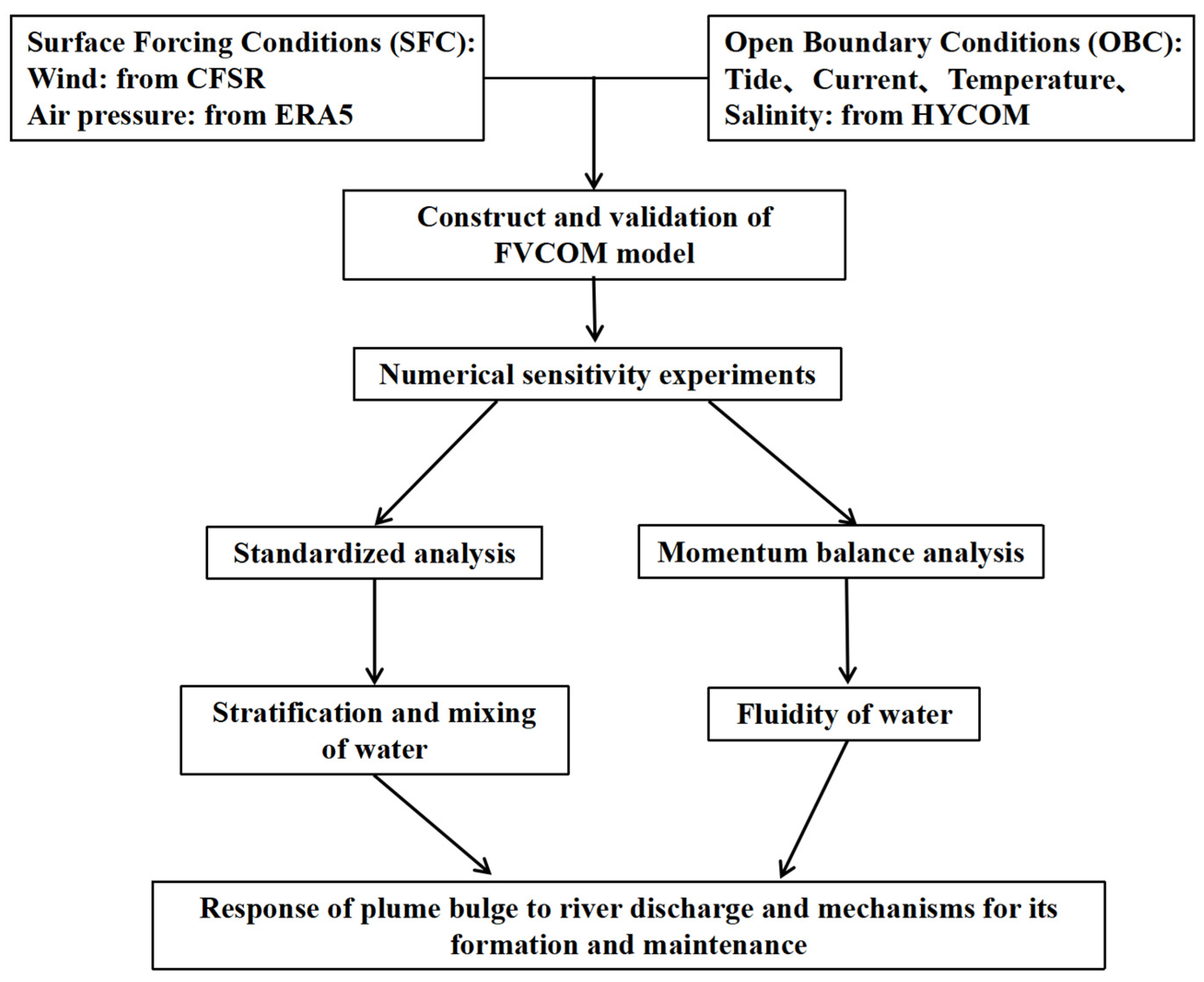
3. Materials and Methods
3.1. Observation Data
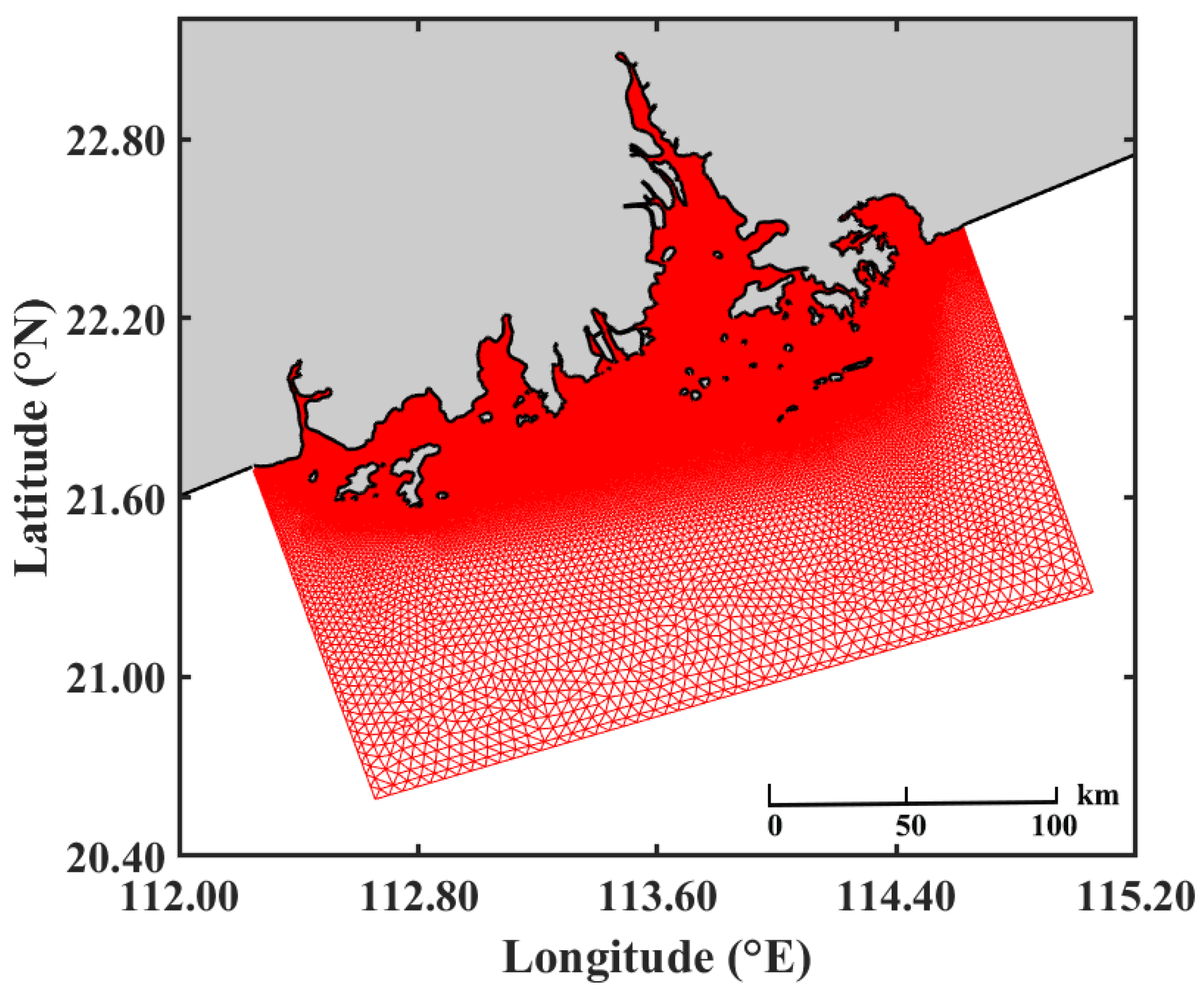
3.2. Model Configuration
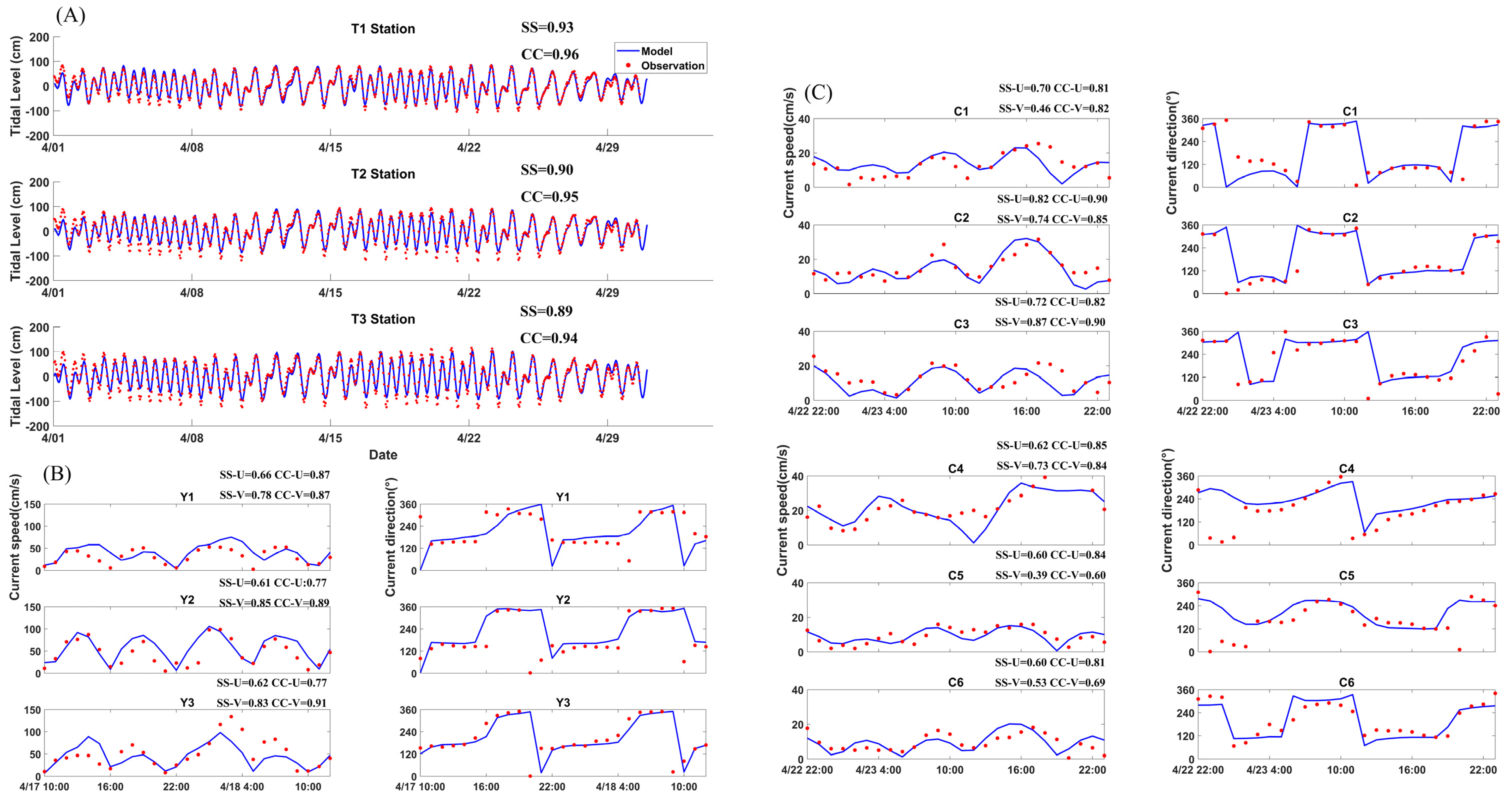
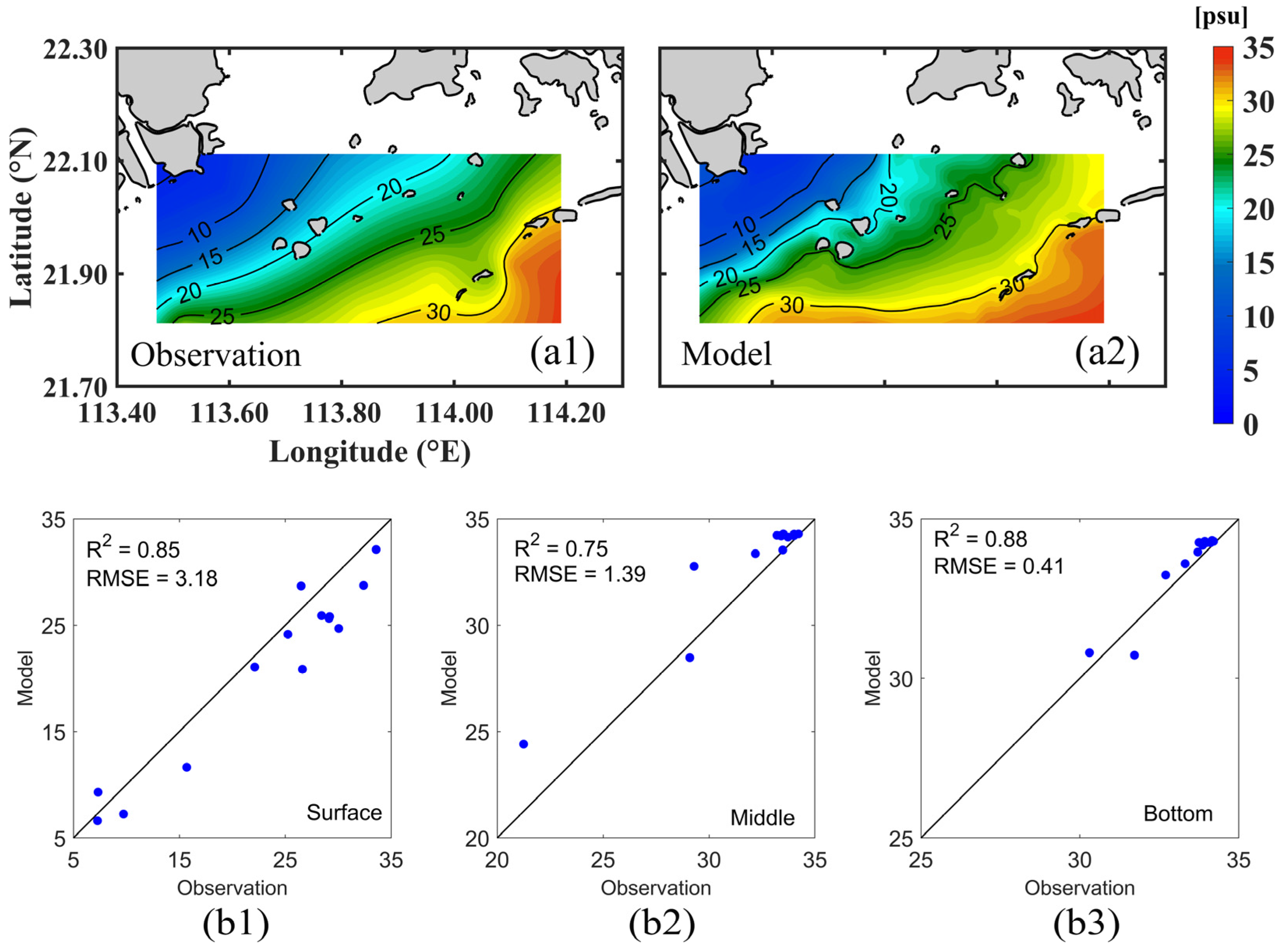
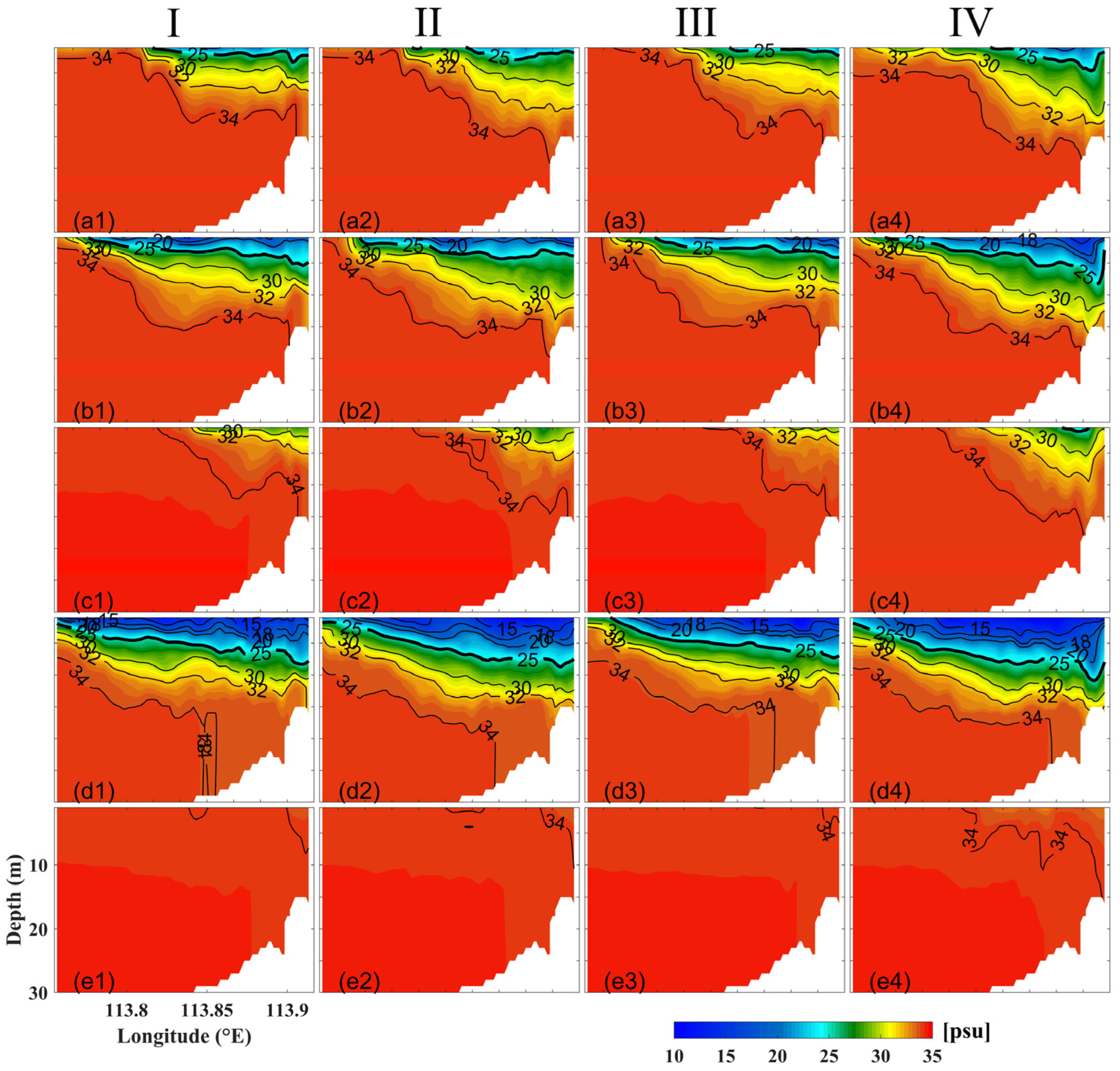
3.3. Model Validation
3.4. Model Setting
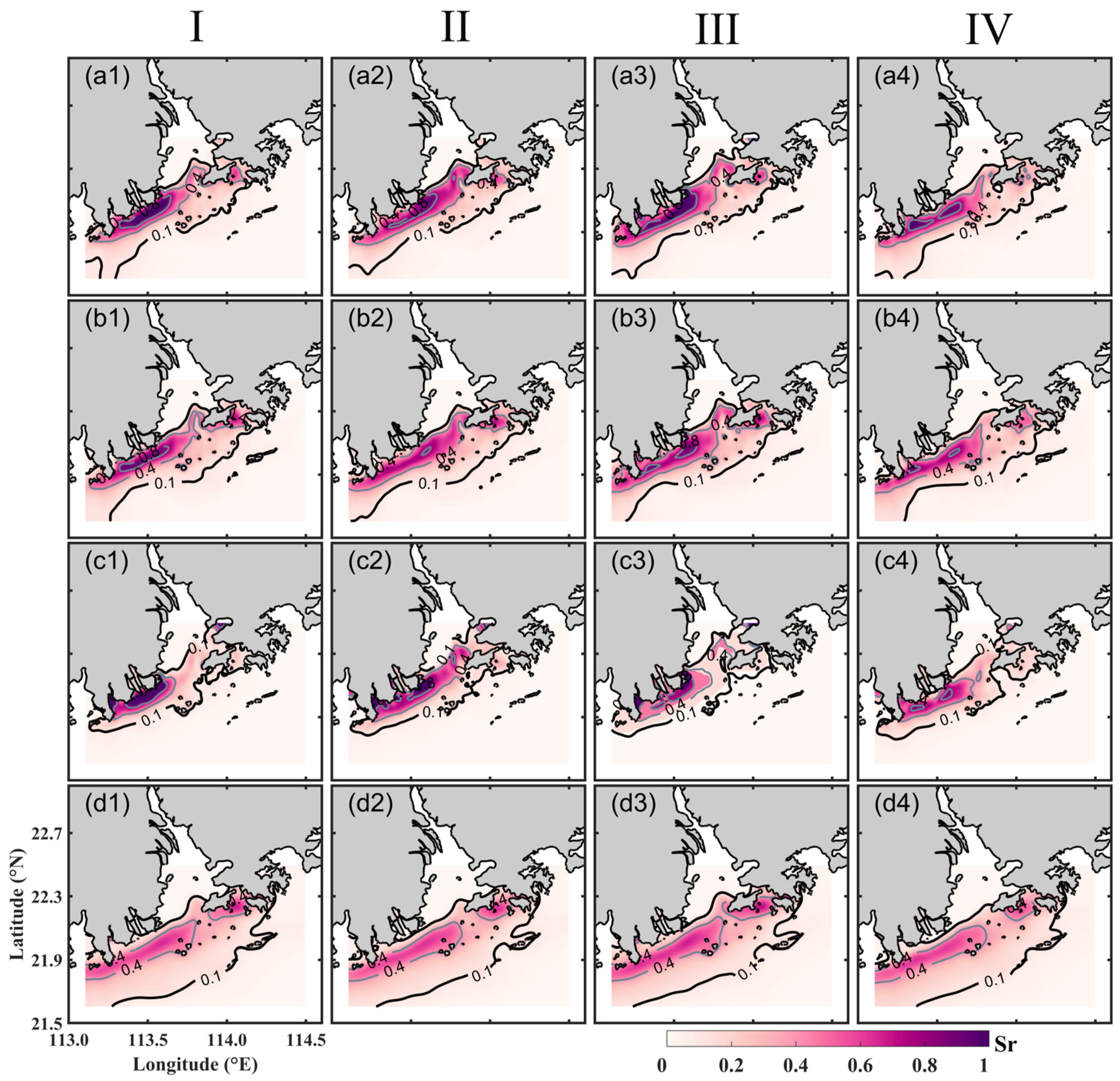
3.5. Salinity Standardization Stratification Coefficient
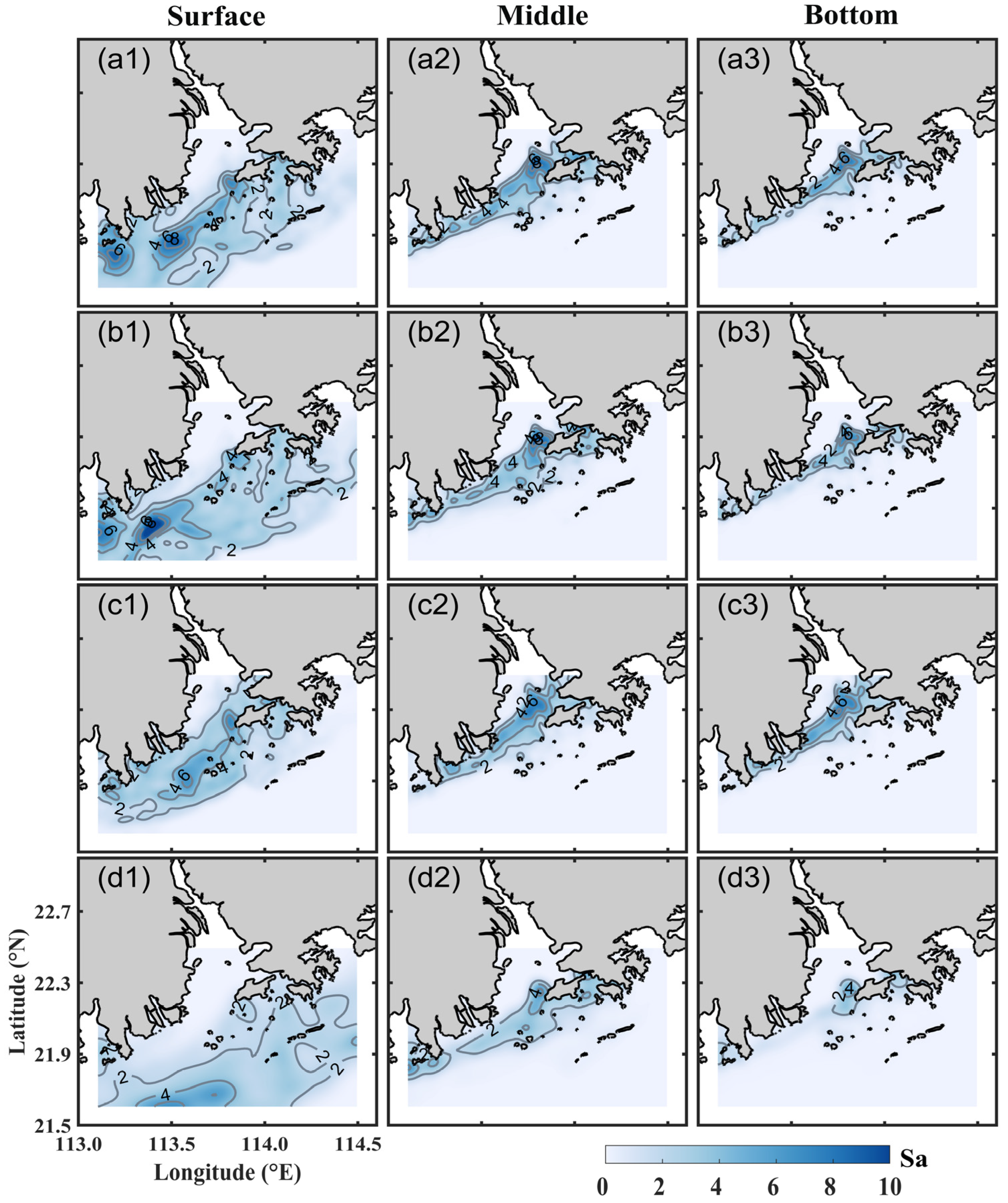
3.6. Amplitude of Tidal Salinity Variation
4. Results
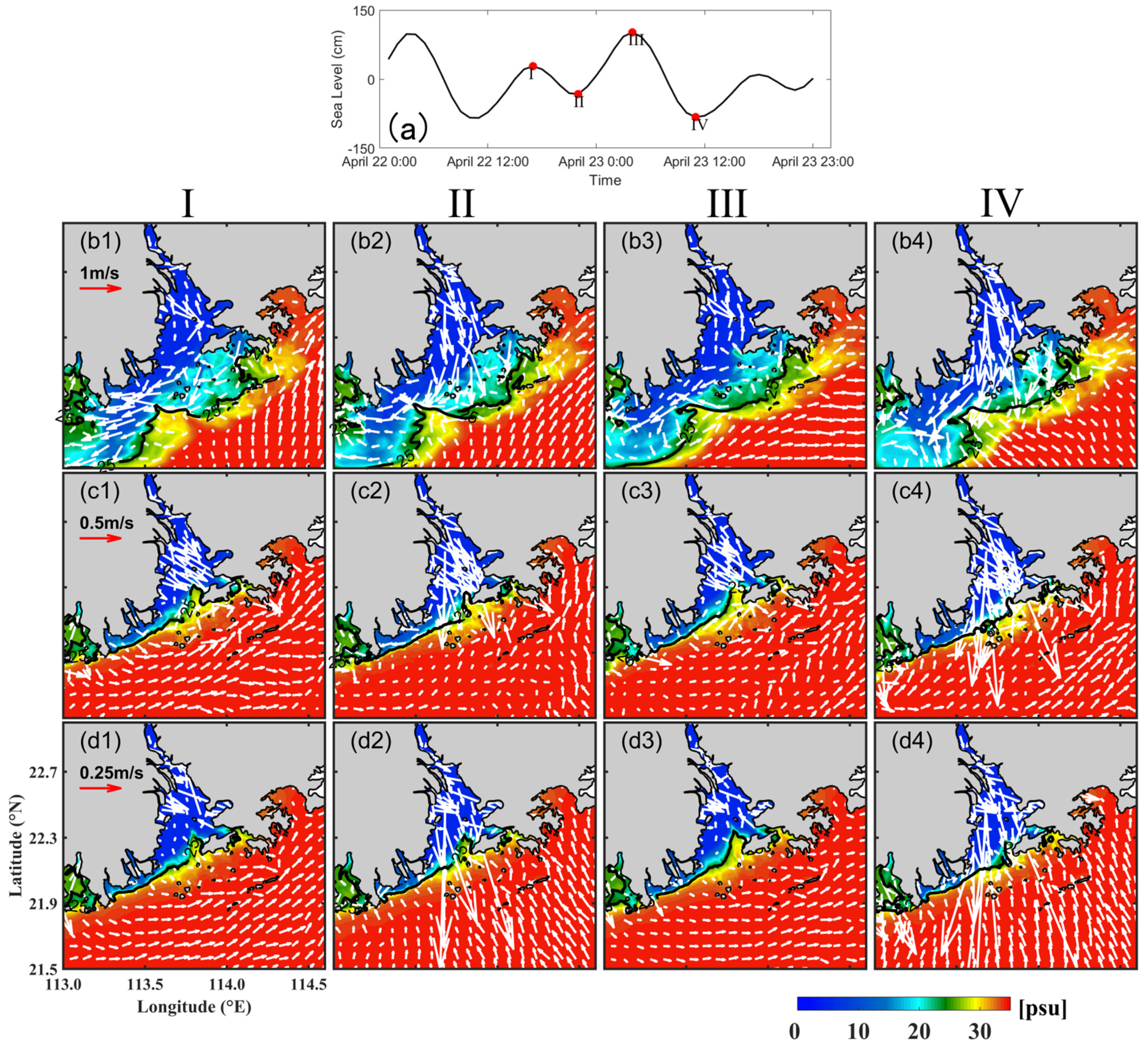
4.1. Spatial and Temporal Evolution of the Plume Bulge in PRE
4.2. Horizontal Distribution of the Plume Bulge in PRE after River Discharge Changes
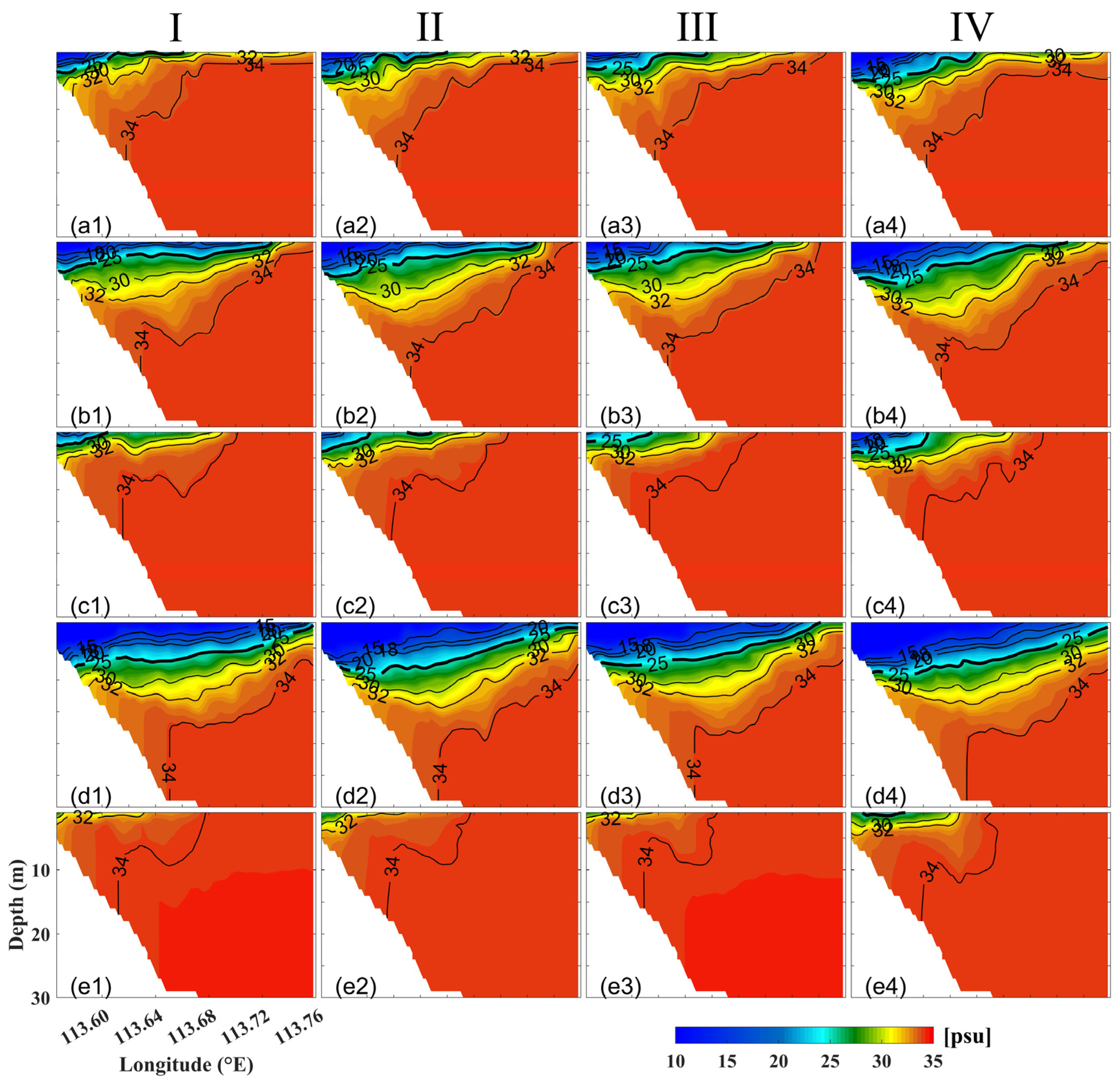
4.3. Vertical Distribution of the Plume Bulge in PRE
4.4. Standardized Analysis
4.4.1. Salinity Standardization Stratification Coefficient
4.4.2. Amplitude of Tidal Salinity Variation
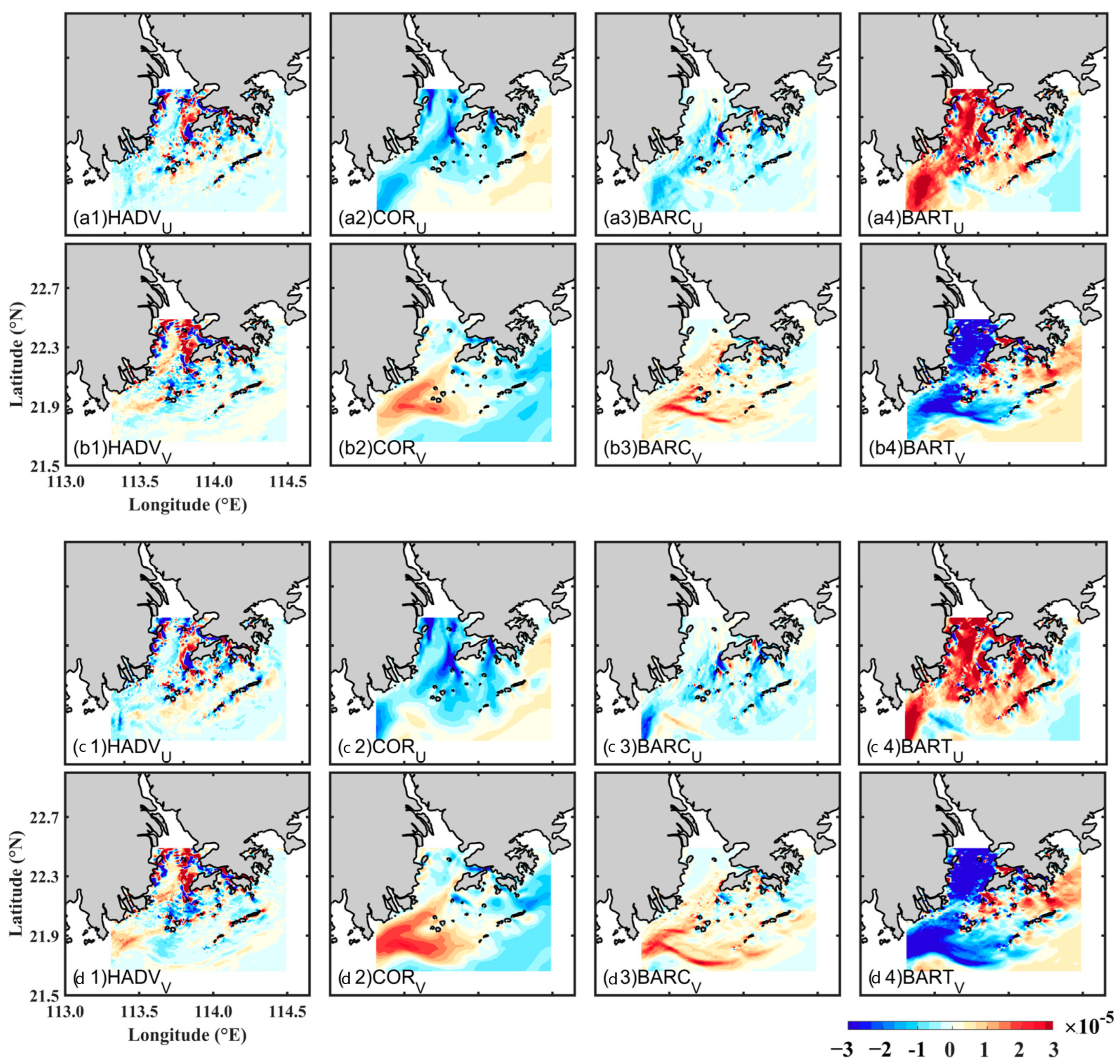
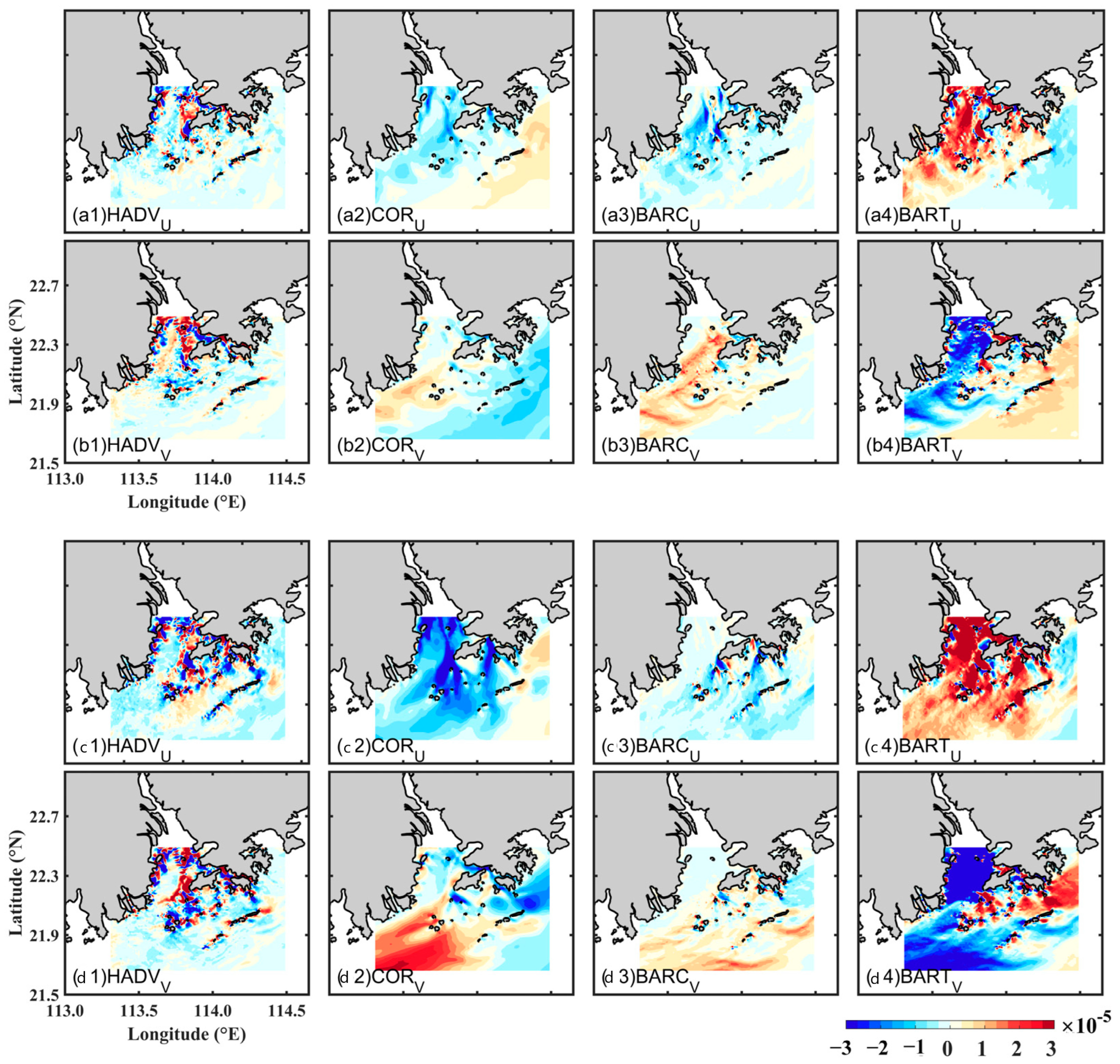
4.5. Momentum Balance Analysis
5. Discussion: The Mechanisms of Plume Bulge Formation and Maintenance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Horner-Devine, A.R.; Hetland, R.D.; MacDonald, D.G. Mixing and Transport in Coastal River Plumes. Annu. Rev. Fluid Mech. 2015, 47, 569–594. [Google Scholar] [CrossRef]
- Yankovsky, A.E.; Chapman, D.C. A Simple Theory for the Fate of Buoyant Coastal Discharges. J. Phys. Oceanogr. 1997, 27, 1386–1401. [Google Scholar] [CrossRef]
- Garvine, R.W. A steady state model for buoyant surface plume hydrodynamics in coastal waters. Tellus. 1982, 24, 293–306. [Google Scholar] [CrossRef]
- Lentz, S.J.; Helfrich, K.R. Buoyant gravity currents along a sloping bottom in a rotating Fluid. J. Fluid Mech. 2002, 464, 251–278. [Google Scholar] [CrossRef]
- Hetland, R.D. Relating river plume structure to vertical mixing. J. Phys. Oceanogr. 2005, 35, 1667–1688. [Google Scholar] [CrossRef]
- Hetland, R.D. The effects of mixing and spreading on density in near-field river plumes. Dyn. Atmos. Ocean. 2010, 49, 37–53. [Google Scholar] [CrossRef]
- McCabe, R.M.; MacCready, P.; Hickey, B.M. Ebb tide dynamics and spreading of a large river plume. J. Phys. Oceanogr. 2009, 39, 2839–2856. [Google Scholar] [CrossRef]
- Lohan, M.C.; Bruland, K.W. Importance of vertical mixing for additional sources of nitrate and iron to surface waters of the Columbia River plume: Implications for biology. Mar. Chem. 2006, 98, 260–273. [Google Scholar] [CrossRef]
- Bormans, M.; Garrett, C. A Simple Criterion for Gyre Formation by the Surface Outflow from a Strait, With Application to the Alboran Sea. J. Geophys. Res. 1989, 94, 12637–12644. [Google Scholar] [CrossRef]
- Wiseman, J.W.J.; Garvine, R.W. Plumes and Coastal Currents Near Large River Mouths. Estuaries 1995, 18, 509–517. [Google Scholar] [CrossRef]
- Yu, L.; Gan, J.; Dai, M.; Hui, C.R.; Lu, Z.; Li, D. Modeling the role of riverine organic matter in hypoxia formation within the coastal transition zone off the Pearl River Estuary. Limnol. Oceanogr. 2021, 66, 452–468. [Google Scholar] [CrossRef]
- Li, D.; Gan, J.; Hui, C.; Yu, L.; Liu, Z.; Lu, Z.; Kao, S.J.; Dai, M. Spatiotemporal Development and Dissipation of Hypoxia Induced by Variable Wind-Driven Shelf Circulation Off the Pearl River Estuary: Observational and Modeling Studies. J. Geophys. Res. Ocean. 2021, 126. [Google Scholar] [CrossRef]
- Masse, A.K.; Murthy, C.R. Analysis of the Niagara River Plume Dynamics. J. Geophys. Res. 1992, 97, 2403–2420. [Google Scholar] [CrossRef]
- Chant, R.J.; Glenn, S.M.; Hunter, E.; Kohut, J.; Chen, R.F.; Houghton, R.W.; Bosch, J.; Schofield, O. Bulge Formation of a Buoyant River Outflow. J. Geophys. Res.Ocean. 2008, 113. [Google Scholar] [CrossRef]
- Horner-Devine, A.R. The Bulge Circulation in the Columbia River Plume. Cont. Shelf Res. 2009, 29, 234–251. [Google Scholar] [CrossRef]
- Horner-Devine, A.R.; Jay, D.A.; Orton, P.M.; Spahn, E.Y. A conceptual model of the strongly tidal Columbia River Plume. J. Mar. Syst. 2009, 78, 460–475. [Google Scholar] [CrossRef]
- Rong, Z.; Li, M. Tidal effects on the bulge region of Changjiang River Plume. Estuar. Coast Shelf Sci. 2012, 97, 149–160. [Google Scholar] [CrossRef]
- Münchow, A.; Garvine, R.W. Dynamical Properties of a Buoyancy-Driven Coastal Current. J. Geophys. Res. 1993, 98, 20063–20077. [Google Scholar] [CrossRef]
- Simpson, J.H.; Bos, W.G.; Schirmer, F.; Souza, A.J.; Rippeth, T.P.; Jones, S.E.; Hydes, D. Periodic Stratification in the Rhine ROFI in the North Sea. Oceanol. Acta 1993, 16, 23–32. [Google Scholar]
- Huq, P. The Role of Kelvin Number on Bulge Formation from Estuarine Buoyant Outflows. Estuaries Coasts 2009, 32, 709–719. [Google Scholar] [CrossRef]
- Gu, Y.; Li, P.; Li, M. Numerical modeling and theoretical analysis of the existence of the Pearl River plume bulge. Ocean Dyn. 2019, 69, 1155–1163. [Google Scholar] [CrossRef]
- Xia, M.; Xie, L.; Pietrafesa, L.J.; Whitney, M.M. The ideal response of a Gulf of Mexico estuary plume to wind forcing; Its connection with salt flux and a Lgrangian View. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Pan, J.; Gu, Y.; Wang, D. Observations and numerical modeling of the Pearl River plume in summer season. J. Geophys. Res. Ocean. 2014, 119, 2480–2500. [Google Scholar] [CrossRef]
- Pan, J.; Gu, Y. Cruise observation and numerical modeling of turbulent mixing in the Pearl River estuary in summer. Cont. Shelf Res. 2016, 120, 122–138. [Google Scholar] [CrossRef]
- Liu, X.; Gu, Y.; Li, P.; Liu, Z.; Zhai, F.; Wu, K. A tidally dependent plume bulge at the Pearl River Estuary mouth. Estuar. Coast Shelf Sci. 2020, 243, 106867. [Google Scholar] [CrossRef]
- Isobe, A. Ballooning of River-Plume Bulge and its Stabilization by Tidal Currents. J. Phys. Oceanogr. 2005, 35, 2337–2351. [Google Scholar] [CrossRef]
- Garvine, R.W. The impact of model configuration in studies of buoyant coastal discharge. J. Mar. Res. 2001, 59, 193–225. [Google Scholar] [CrossRef]
- Xia, M. Cape Fear River Estuary Modeling System; North Carolina State University: Raleigh, NC, USA, 2006. [Google Scholar]
- Bai, P.; Gu, Y.; Luo, L.; Zhang, W.; Fan, K. Observation of the supercritical Pearl River plume front under the downwelling-favorable winds. Sci. China Earth Sci. 2015, 58, 2059–2066. [Google Scholar] [CrossRef]
- Li, M.; Wang, N.; Li, G.; Song, D.; Gu, Y.; Bao, X.; Liu, S.; Zhang, L. Plume bulge observed in the Pearl River Estuary in summer: Spatiotemporal characteristics and influencing factors. Estuar. Coast Shelf Sci. 2023, 282, 108242. [Google Scholar] [CrossRef]
- Simpson, J.H.; Allen, C.M.; Morris, N.C.G. Fronts on the continental shelf. J. Geophys. Res. Ocean. 1978, 83, 4607–4614. [Google Scholar] [CrossRef]
- Yao, Z. The Characteristics and Warnings of the “June 2005” Storm Flood in the Pearl River Basin (in Chinese). Exp. Water Res. Hydropower Inf. 2008, 29, 68–74. [Google Scholar]
- Zu, T.; Wang, D.; Gan, J.; Guan, W. On the role of wind and tide in generating variability of Pearl River plume during summer in a coupled wide estuary and shelf system. J. Mar. Syst. 2014, 136, 65–79. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An Unstructured Grid, Finite-Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Lin, S.; Liu, G.; Niu, J.; Wei, X.; Cai, S. Responses of hydrodynamics to changes in shoreline and bathymetry in the Pearl River Estuary, China. Cont. Shelf Res. 2021, 229, 104556. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Bleck, R. An Oceanic General Circulation Model Framed in Hybrid Isopycnic-Cartesian Coordinates. Ocean Model. 2001, 37, 55–88. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The Hycom (Hybrid Coordinate Ocean Model) Data Assimilative System. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The Era5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Schneider, D.P.; Deser, C.; Fasullo, J.; Trenberth, K.E. Climate Data Guide Spurs Discovery and Understanding. Eos Trans. Am. Geophys. Union. 2013, 94, 121–122. [Google Scholar] [CrossRef]
- Gao, G.D.; Wang, X.H.; Song, D.; Bao, X.; Yin, B.S.; Yang, D.Z.; Ding, Y.; Li, H.; Hou, F.; Ren, Z. Effects of Wave–Current Interactions on Suspended-Sediment Dynamics During Strong Wave Events in Jiaozhou Bay, Qingdao, China. J. Phys. Oceanogr. 2018, 48, 1053–1078. [Google Scholar] [CrossRef]
- Zhi, H.; Wu, H.; Wu, J.; Zhang, W.; Wang, Y. River Plume Rooted on the Sea-Floor: Seasonal and Spring-Neap Variability of the Pearl River Plume Front. Front. Mar. Sci. 2022, 9, 791948. [Google Scholar] [CrossRef]
- Simpson, J.H.; Bowers, D. Models of stratification and frontal movement in shelf seas. Deep-Sea Res. Pt I 1981, 28A, 727–738. [Google Scholar] [CrossRef]
- Chen, C.; Beardsley, R.C. A Numerical Study of Stratified Tidal Rectification over Finite-Amplitude Banks. Part I: Symmetric Banks. J. Phys. Oceanogr. 1995, 25, 2090–2110. [Google Scholar] [CrossRef]
- Ryan, H.F.; Noble, M.A.; Williams, E.A.; Schroeder, W.W.; Pennock, J.R.; Gelfenbaum, G. Tidal current shear in a broad, shallow, river-dominated estuary. Cont. Shelf Res. 1997, 17, 665–688. [Google Scholar] [CrossRef]
| Tide | River Discharge | Wind | |
|---|---|---|---|
| Exp1 (Control) | Spring | 23,440 m3/s | × |
| Exp2 | Spring | 35,160 m3/s (1.5× Control) | × |
| Exp3 | Spring | 11,720 m3/s (0.5× Control) | × |
| Exp4 | Spring | 70,320 m3/s (3× Control) | × |
| Exp5 | Spring | 5860 m3/s (0.25× Control) | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Wang, N.; Ding, Y.; Song, D.; Li, J.; Li, M.; Zhou, L.; Yu, H.; Chen, Y.; Bao, X. Numerical Study on the Formation Mechanism of Plume Bulge in the Pearl River Estuary under the Influence of River Discharge. Water 2024, 16, 1296. https://doi.org/10.3390/w16091296
Zhao C, Wang N, Ding Y, Song D, Li J, Li M, Zhou L, Yu H, Chen Y, Bao X. Numerical Study on the Formation Mechanism of Plume Bulge in the Pearl River Estuary under the Influence of River Discharge. Water. 2024; 16(9):1296. https://doi.org/10.3390/w16091296
Chicago/Turabian StyleZhao, Chenyu, Nan Wang, Yang Ding, Dehai Song, Junmin Li, Mengqi Li, Lingling Zhou, Hang Yu, Yanyu Chen, and Xianwen Bao. 2024. "Numerical Study on the Formation Mechanism of Plume Bulge in the Pearl River Estuary under the Influence of River Discharge" Water 16, no. 9: 1296. https://doi.org/10.3390/w16091296
APA StyleZhao, C., Wang, N., Ding, Y., Song, D., Li, J., Li, M., Zhou, L., Yu, H., Chen, Y., & Bao, X. (2024). Numerical Study on the Formation Mechanism of Plume Bulge in the Pearl River Estuary under the Influence of River Discharge. Water, 16(9), 1296. https://doi.org/10.3390/w16091296







