Reliability Analysis of the Bearing Performance of Corroded Piles Subjected to Scour Action
Abstract
:1. Introduction
2. Modeling Chloride Corrosion
2.1. Chloride Diffusion Model
2.2. Modeling Reinforcement Corrosion
2.3. Pile Stiffness Reduction
2.4. Modeling the Scour Depth
3. Probabilistic Analysis
3.1. Performance Functions
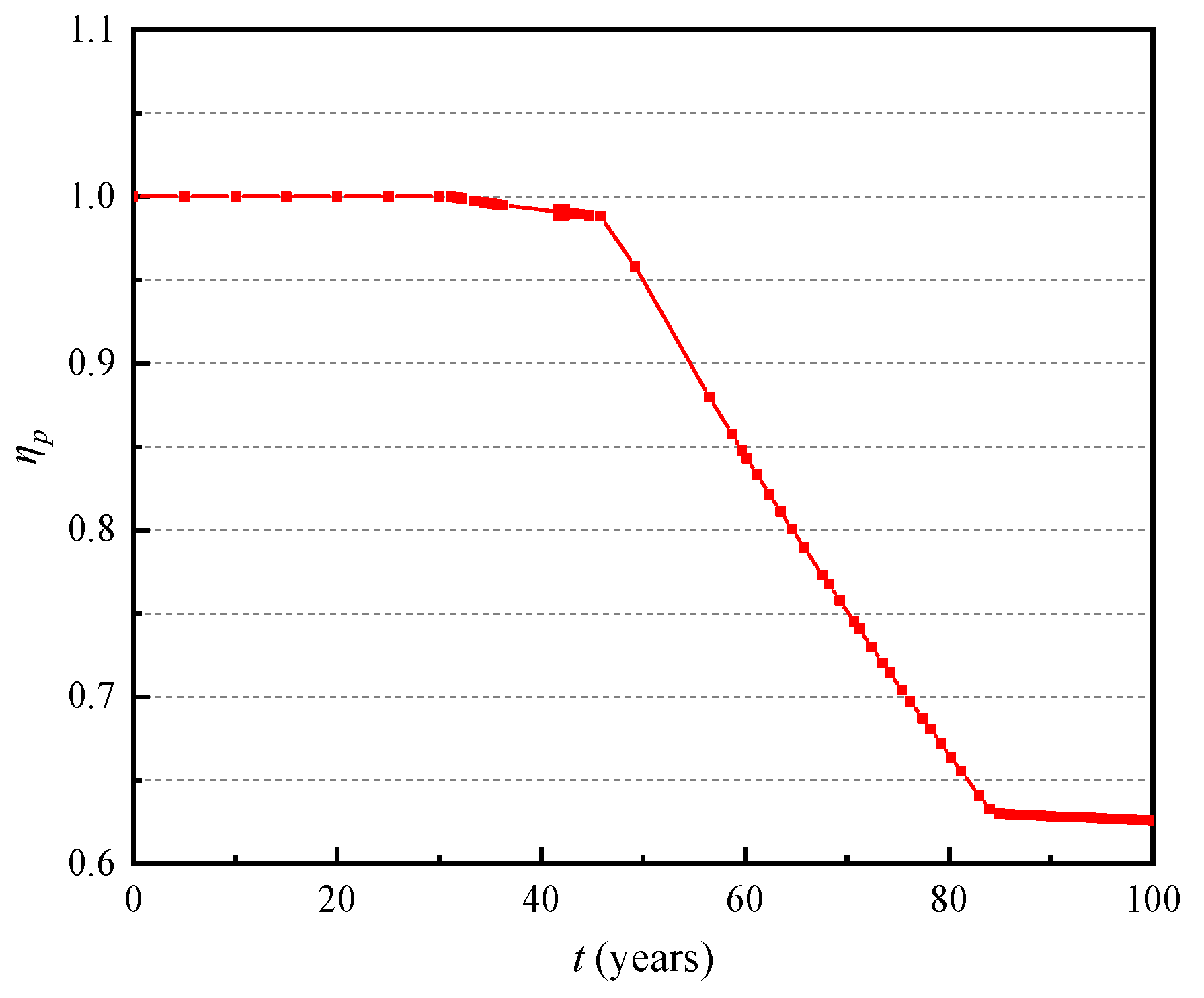
3.2. Stiffness Reduction Coefficient
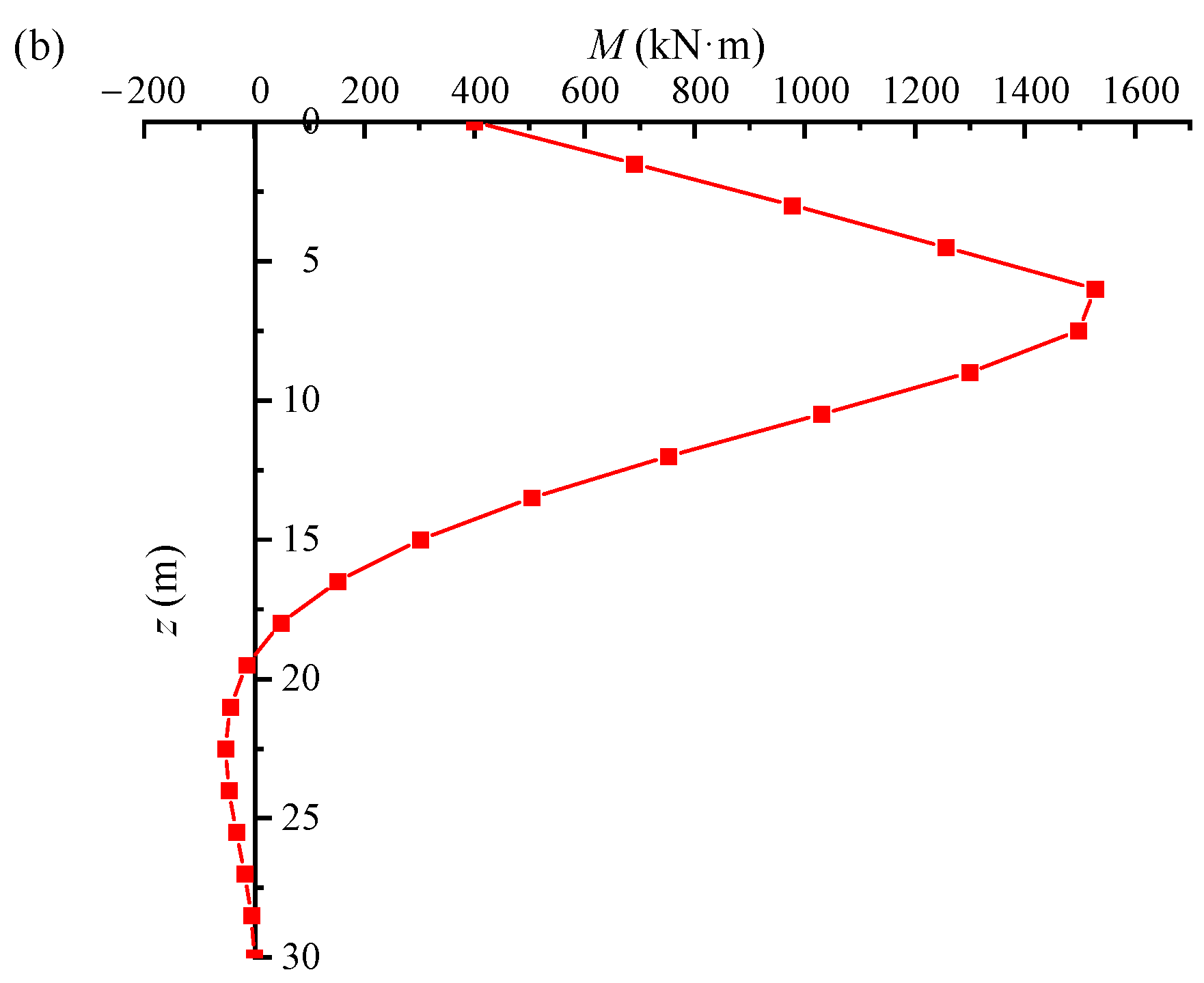
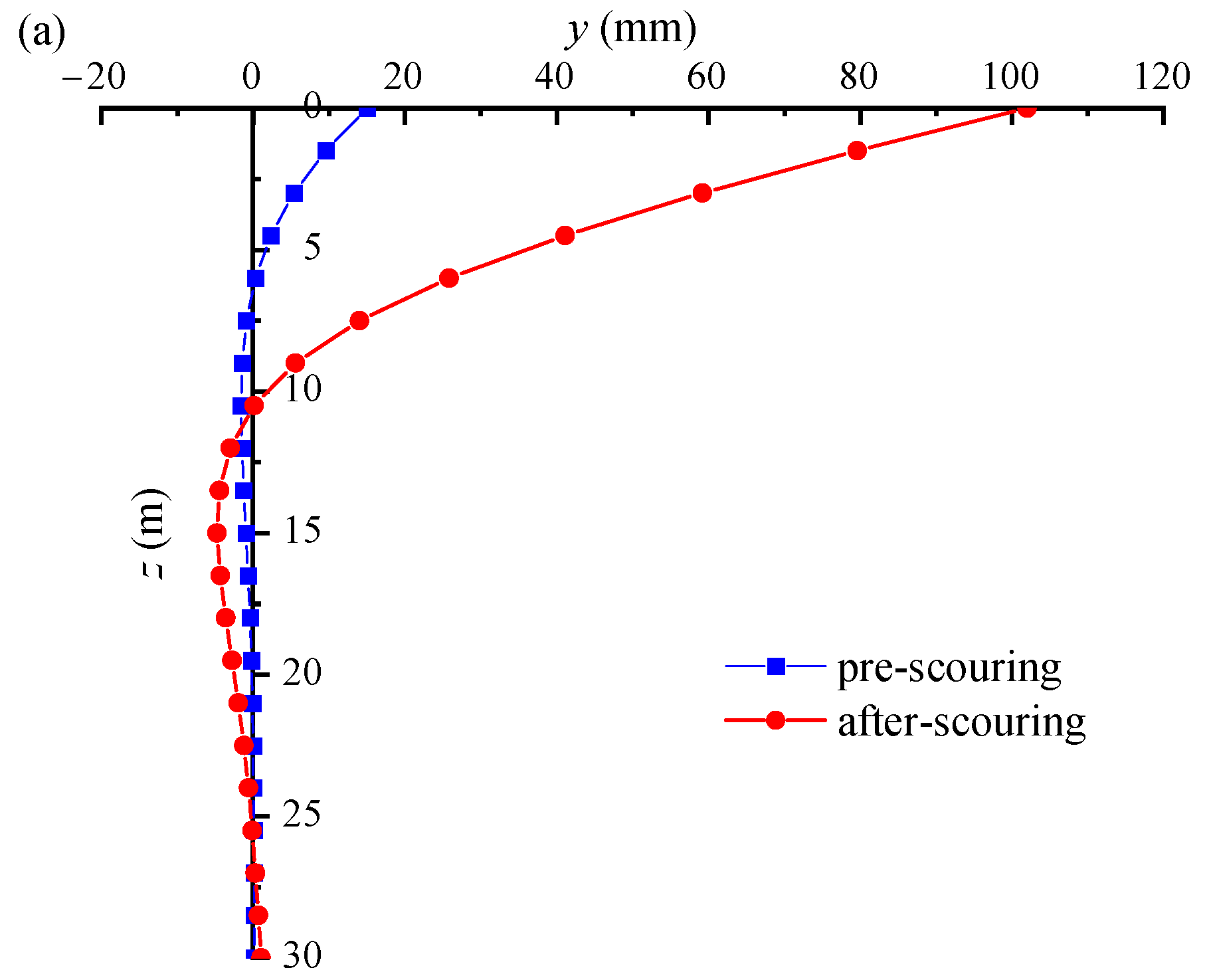
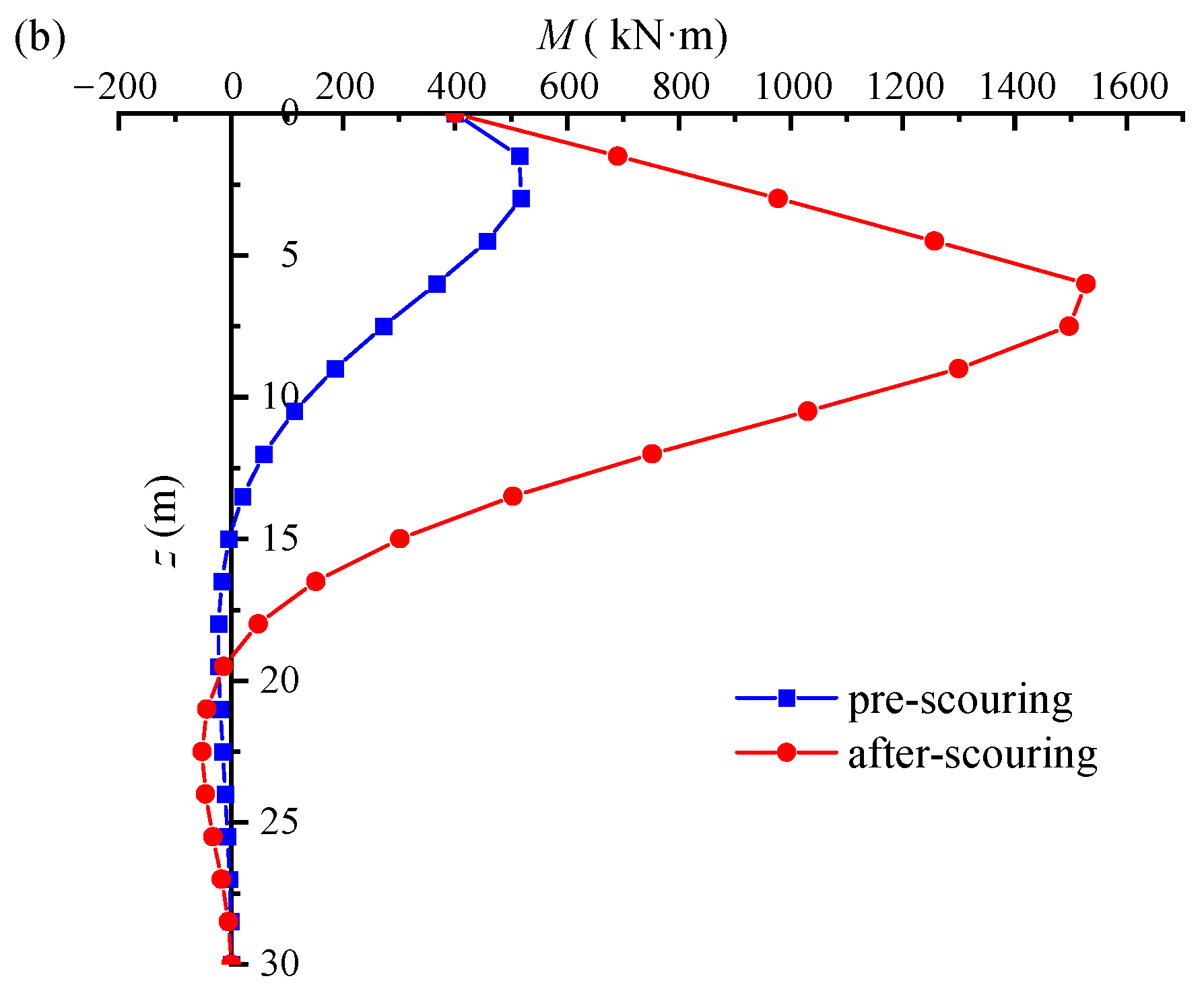
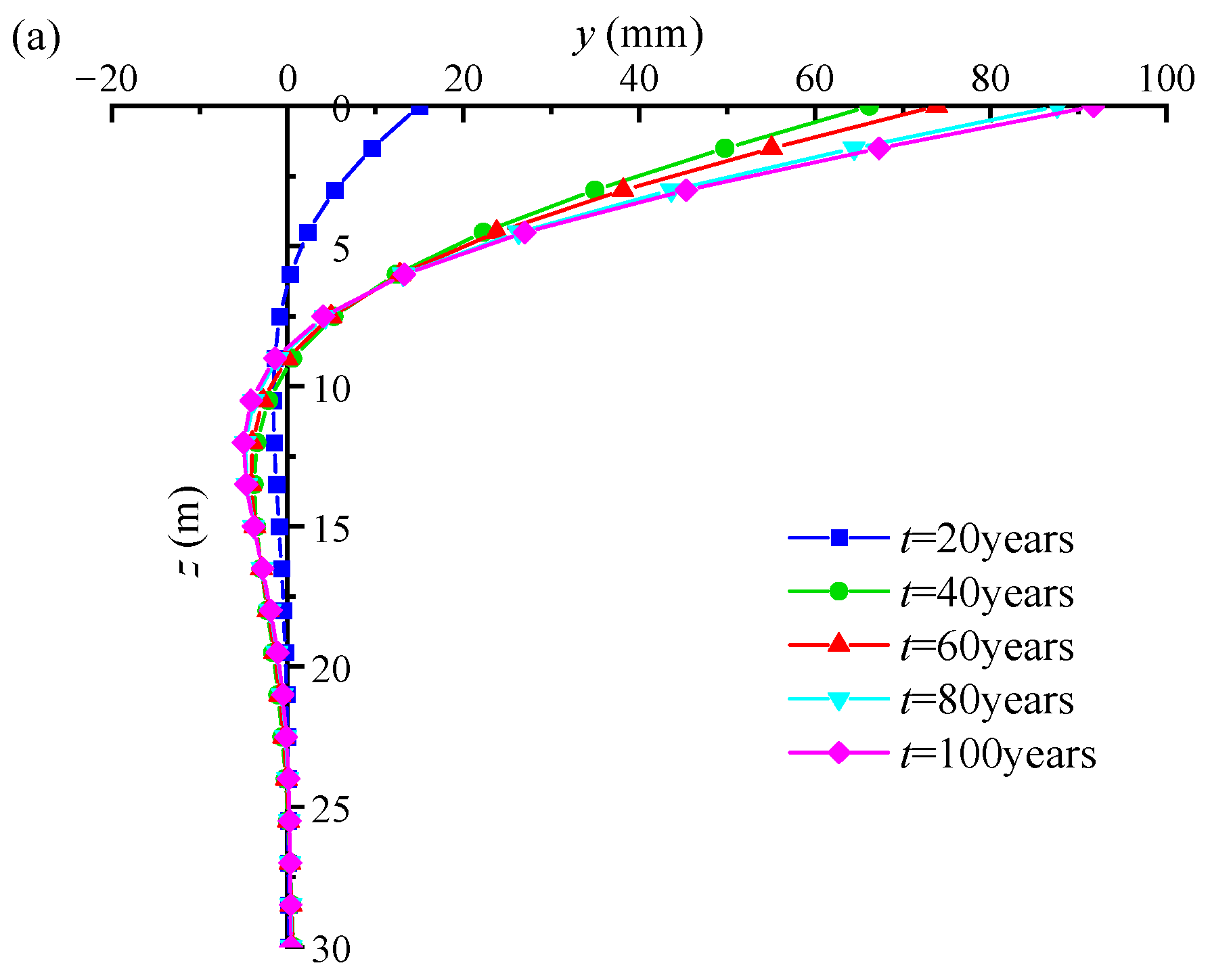
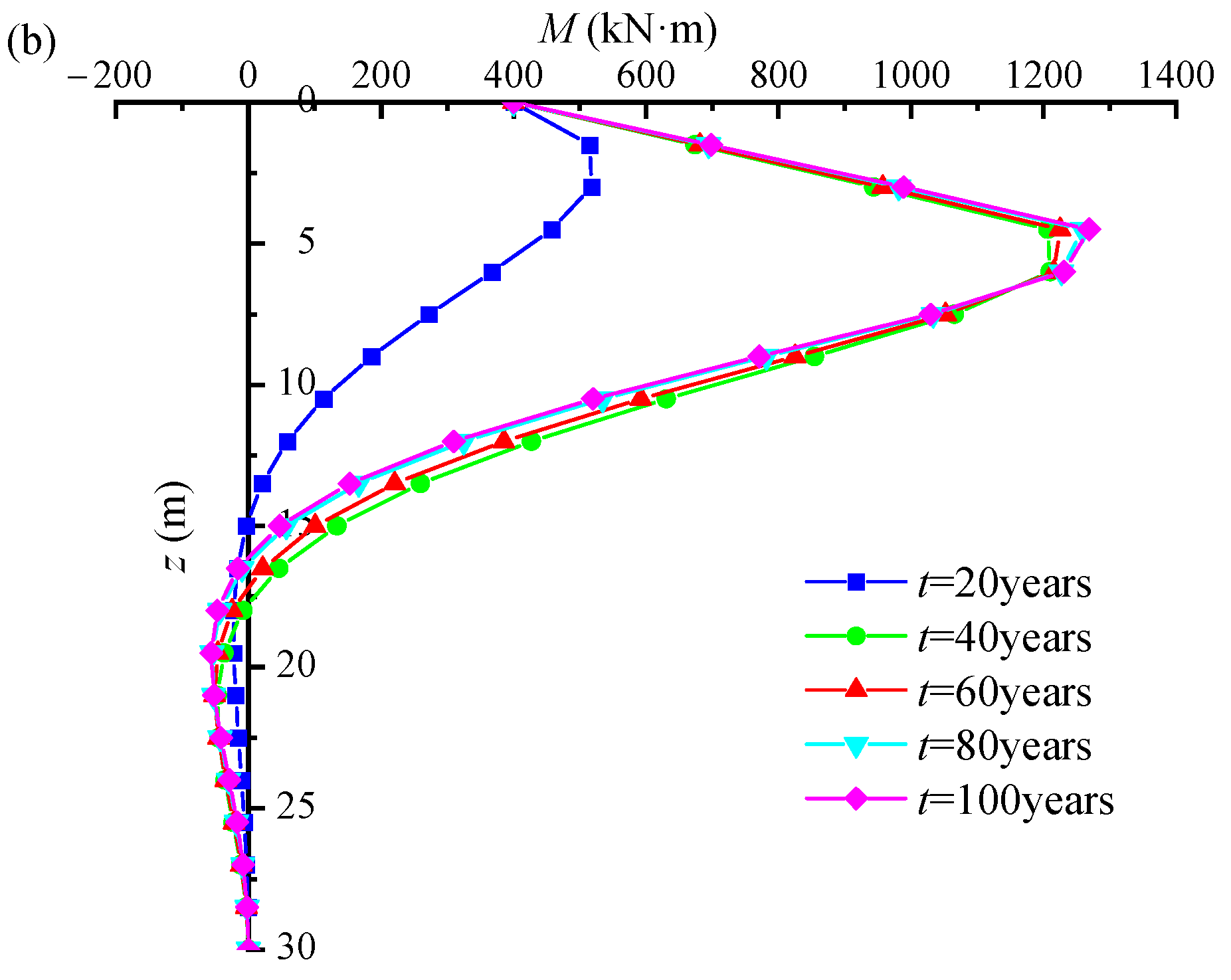
3.3. Time-Varying Characterization of Bending Moment and Lateral Displacement
3.4. Scour Depth Probability Prediction
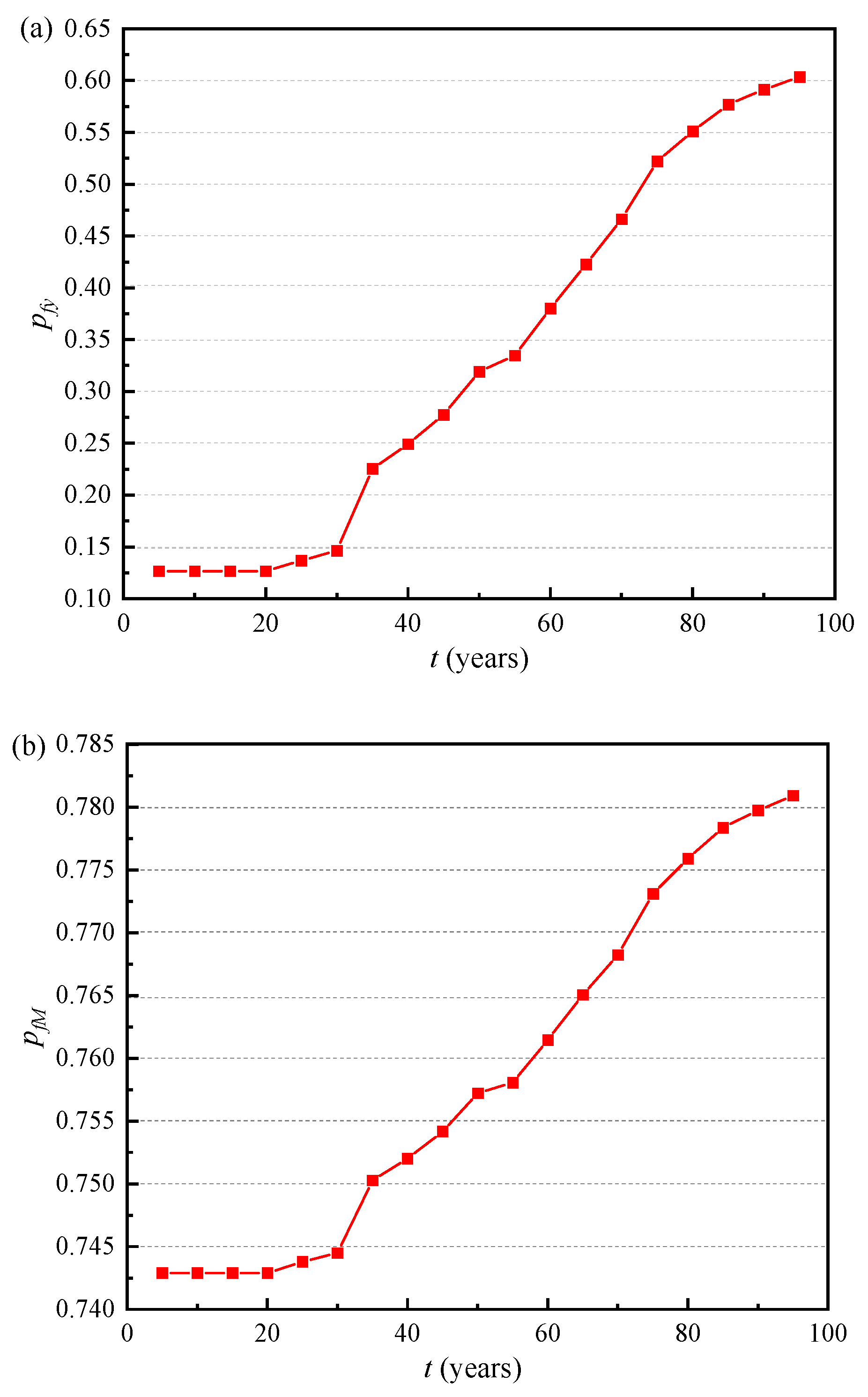
3.5. Time-Varying Failure Probability
3.6. Parametric Analysis
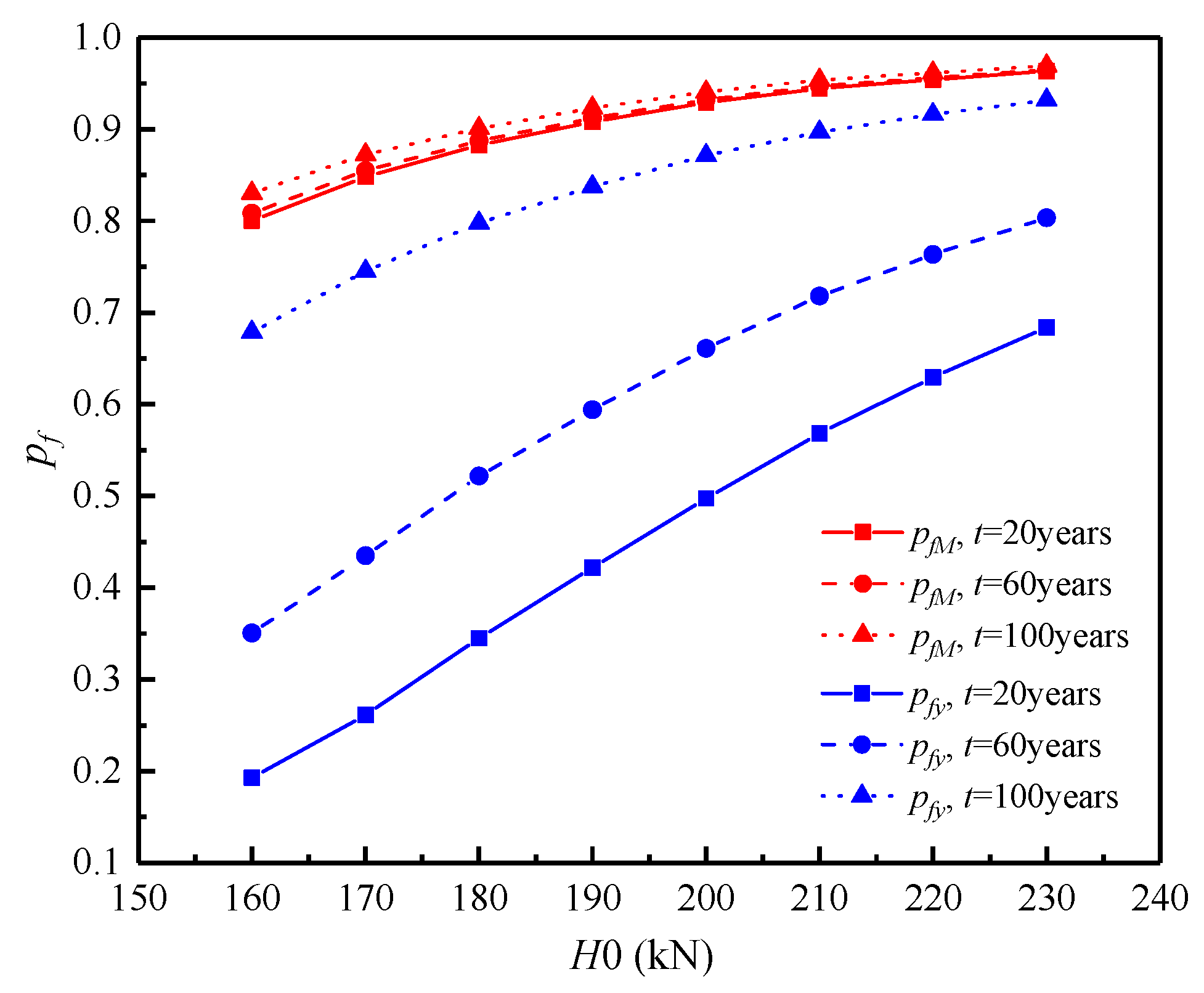
3.6.1. Bending Moment at Top of Pile
3.6.2. Lateral Load at Top of Pile
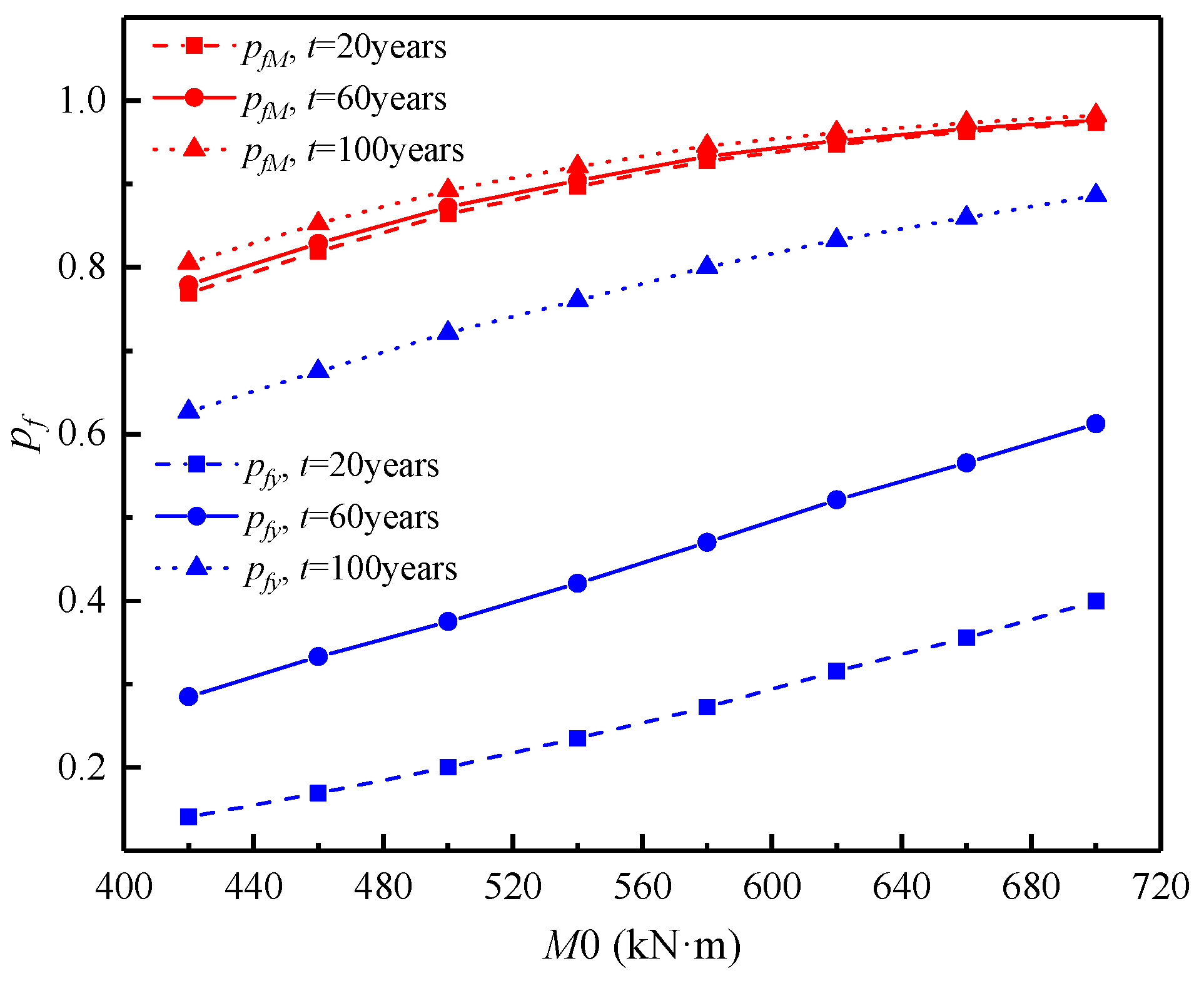
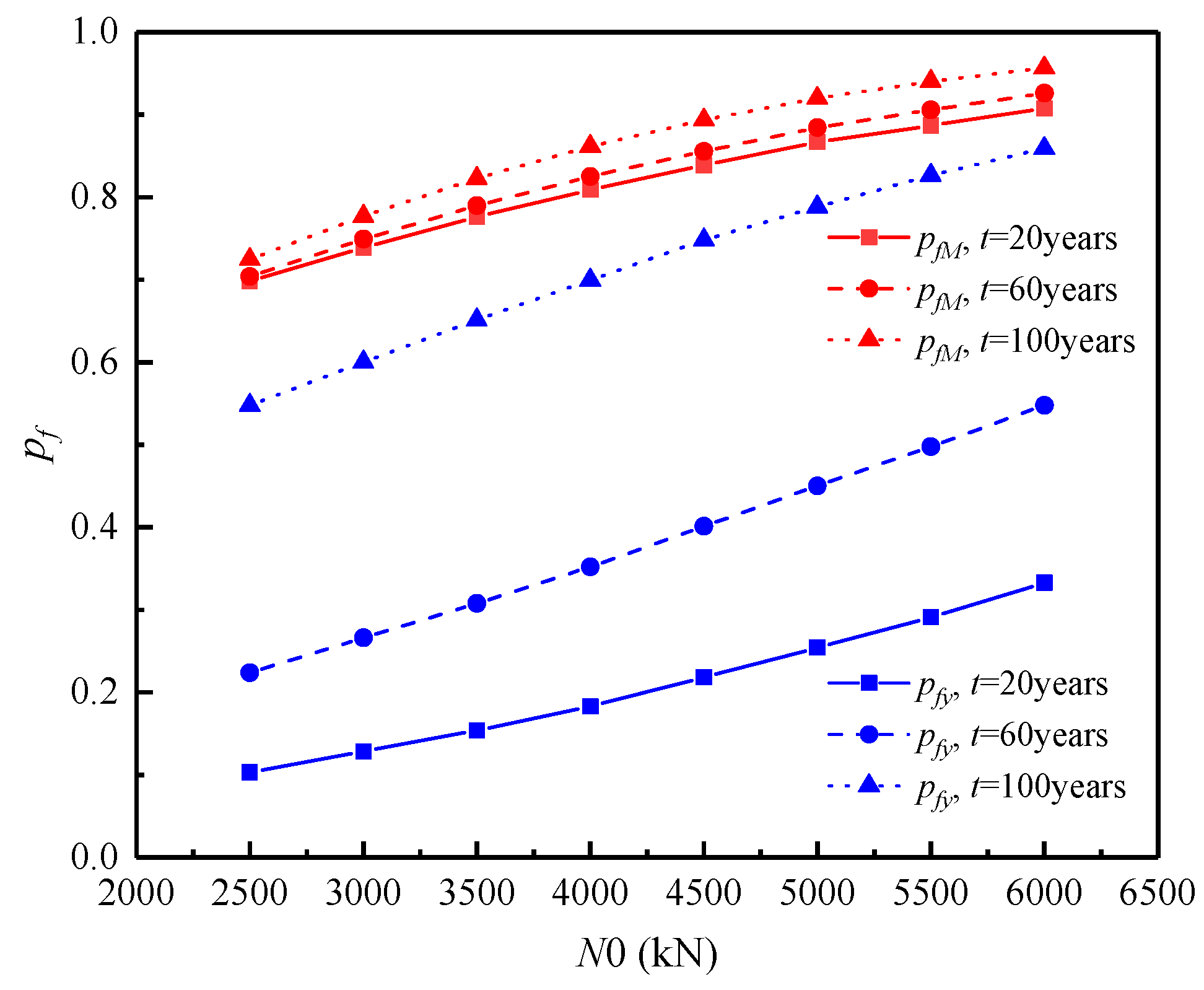
3.6.3. Vertical Load at Top of Pile
3.6.4. Time-Varying Properties Under the Influence of Seawater Velocity
4. Conclusions
- (1)
- The stiffness reduction coefficient of the pile foundation decreases gradually with increasing exposure time. When the scour depth reaches a critical value, it has a large effect on both the lateral displacement and the bending moment. With increasing exposure time, the lateral displacement and bending moment generated by the pile also increase. As the seawater velocity increases, the probability of exceeding the reference value of scour depth around the pile base also increases.
- (2)
- Under the two failure criteria, the lateral displacement and bending moment of the piles remain constant until the initial corrosion time, but then gradually increase with the increase in exposure time. Comparing the failure probability of lateral displacement and bending moment, it can be found that the failure probability of lateral displacement is more sensitive to the exposure time. At the same exposure period, the pile foundation’s failure probability increases as the average values of bending moment, lateral load, and vertical load rise.
- (3)
- Increasing seawater velocity increases the likelihood of pile foundation failures, including that of the lateral displacement and bending moment. And the sensitivity of the lateral displacement failure probability is still greater than the bending moment failure probability. Therefore, the lateral displacement failure criterion is more suitable as the determination criterion of lateral bearing pile failure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.Q. Initiation of chloride-induced reinforcement corrosion in concrete structural members-prediction. ACI Struct. J. 2002, 99, 133–141. [Google Scholar] [CrossRef]
- Zhou, L.; Alam, M.S.; Dong, Y.; Ruiwei, F. Seismic resilience assessment of extended pile shaft supported coastal bridges considering scour and uniform corrosion effects. Eng. Struct. 2024, 304, 117643. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, S.; Liu, K.; Li, T.; Yang, H. Research on the critical chloride content of reinforcement corrosion in marine concrete—A review. J. Build. Eng. 2023, 79, 107838. [Google Scholar] [CrossRef]
- Li, J.P.; Shao, W. The effect of chloride binding on the predicted service life of RC pipe piles exposed to marine environments. Ocean Eng. 2014, 88, 55–62. [Google Scholar] [CrossRef]
- Shao, W.; Shi, D.; Jiang, J.; Chen, Y. Time-dependent lateral bearing behavior of corrosion-damaged RC pipe piles in marine environments. Constr. Build. Mater. 2017, 157, 676–684. [Google Scholar] [CrossRef]
- Jiang, C.; Guo, S.; Shao, X. A time-variant non-probabilistic reliability assessment strategy for laterally loaded offshore monopiles under scour and corrosion. Ocean. Eng. 2024, 310, 118714. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Bressolette, P.; Chateauneuf, A. Probabilistic lifetime assessment of RC structures under coupled corrosion-fatigue deterioration processes. Struct. Saf. 2008, 31, 84–96. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, X.; Zhang, Y. Randomness of bidirectional chloride corrosion of sluice gate and time to corrosion initiation of reinforcement in a strong tidal environment. Constr. Build. Mater. 2019, 227, 116707. [Google Scholar] [CrossRef]
- Kioumarsi, M.M.; Hendriks, M.A.N.; Kohler, J.; Geiker, M.R. The effect of interference of corrosion pits on the failure probability of a reinforced concrete beam. Eng. Struct. 2016, 114, 113–121. [Google Scholar] [CrossRef]
- Firouzi, A.; Abdolhosseini, M.; Ayazian, R. Service life prediction of corrosion-affected reinforced concrete columns based on time-dependent reliability analysis. Eng. Fail. Anal. 2020, 117, 104944. [Google Scholar] [CrossRef]
- Homaei, F.; Mohammad, N. Failure analysis of scouring at pile groups exposed to steady-state flow: On the assessment of reliability-based probabilistic methodology. Ocean Eng. 2022, 266, 112707. [Google Scholar] [CrossRef]
- Khalid, M.; Mohd, M.; Javed, A. A reliability-based assessment of live bed scour at bridge piers. J. Hydraul. Eng. 2019, 27, 105–112. [Google Scholar] [CrossRef]
- Homaei, F.; Najafzadeh, M.A. Reliability-based probabilistic evaluation of the wave-induced scour depth around marine structure piles. Ocean Eng. 2020, 196, 106818. [Google Scholar] [CrossRef]
- Jafari-Asl, J.; Ben Seghier, M.E.A.; Ohadi, S.; Dong, Y.; Plevris, V. A comparative study on the efficiency of reliability methods for the probabilistic analysis of local scour at a bridge pier in clay-sand-mixed sediments. Modeling 2021, 2, 63–77. [Google Scholar] [CrossRef]
- Wu, M.; Vasiliki, S.; Tiago, F.-F. Experimental uncertainty analysis of monopile scour protection stability test. Renew. Energy 2023, 210, 174–187. [Google Scholar] [CrossRef]
- Shao, W.; Nie, Y.; Liang, F. A novel comprehensive evaluation method for the corrosion initiation life of RC hollow piles in chloride environments. Constr. Build. Mater. 2020, 249, 118801. [Google Scholar] [CrossRef]
- Maeda, S.; Takewaka, K.; Yamaguchi, T. Quantification of chloride diffusion process into concrete under marine environment. Proc. Jpn. Soc. Civ. Eng. 2004, 63, 109–120. [Google Scholar]
- Shao, W.; Zhang, W.; Shi, D.D.; Xu, Y.Z.; Liu, E.L. Time-varying characteristics of the durability and lateral bearing behaviour of FRP bar-reinforced concrete piles in marine environments. Constr. Build. Mater. 2021, 302, 124192. [Google Scholar] [CrossRef]
- Maaddawy, E.T.; Soudki, K. A model for prediction of time from corrosion initiation to corrosion cracking. Cem. Concr. Compos. 2007, 29, 168–175. [Google Scholar] [CrossRef]
- Papakonstantinou, K.G.; Shinozuka, M. Probabilistic model for steel corrosion in reinforced concrete structures of large dimensions considering crack effects. Eng. Struct. 2013, 57, 306–326. [Google Scholar] [CrossRef]
- Lu, C.; Jin, W.; Liu, R. Reinforcement corrosion-induced cover cracking and its time prediction for reinforced concrete structures. Corros. Sci. 2011, 53, 1337–1347. [Google Scholar] [CrossRef]
- Vu, K.A.T.; Stewart, M.G. Structural reliability of concrete bridges including improved chloride-induced corrosion models. Structures 2000, 22, 313–333. [Google Scholar] [CrossRef]
- Shao, W.; Huang, T.; Shi, D. Time-varying behavior of corrosion-damaged piles under cyclic lateral loading in marine environments. Mar. Georesources Geotechnol. 2022, 40, 856–868. [Google Scholar] [CrossRef]
- Phanikanth, V.; Choudhury, D.; Reddy, R. Response of single pile under lateral loads in cohesionless soils. Electron. J. Geotech. Eng. 2020, 15, 813–830. [Google Scholar]
- Durability Evaluation Criteria for Concrete Structures; Architecture & Building Press: Beijing, China, 2007.
- Li, T.; Lin, J.; Liu, J. Analysis of time-dependent seismic fragility of the offshore bridge under the action of scour and chloride ion corrosion. Structures 2020, 28, 1785–1801. [Google Scholar] [CrossRef]
- Briaud, J.L.; Ting, F.C.; Chen, H.C.; Gudavalli, R.; Perugu, S.; Wei, G. SRICOS: Prediction of scour rate in cohesive soils at bridge piers. J. Geotech. Geoenvironmental Eng. 1999, 125, 237–246. [Google Scholar] [CrossRef]
- Shao, W.; Nie, Y.; Shi, D. Probabilistic analysis of the behaviour of laterally loaded piles in chloride environments. Ocean Eng. 2020, 27, 107872. [Google Scholar] [CrossRef]
- Haldar, S.; Sivakumar Babu, G.L. Effect of soil spatial variability on the response of laterally loaded pile in undrained clay. Comput. Geotech. 2008, 35, 537–547. [Google Scholar] [CrossRef]
- Chan, C.L.; Low, B.K. Reliability analysis of laterally loaded piles involving nonlinear soil and pile behavior. J. Geotech. Geoenvironmental Eng. 2009, 135, 431–443. [Google Scholar] [CrossRef]
- Shao, W.; Li, J.P.; Chen, H.B.; Li, L. Time-dependant behavior analysis of laterally loaded corrosion damaged RC pipe piles. J. Harbin Inst. Technol. 2015, 47, 77. [Google Scholar]
- Chen, D.; Mahadevan, S. Chloride-induced reinforcement corrosion and concrete cracking simulation. Cem. Concr. Compos. 2008, 30, 227–238. [Google Scholar] [CrossRef]
- Reale, T.; O’Connor, A. A review and comparative analysis of corrosion-induced time to first crack models. Constr. Build. Mater. 2012, 36, 475–483. [Google Scholar] [CrossRef]
- Su, D.; Huang, J.J.; Yan, W.M. Parametric investigation on the responses of laterally loaded piles in over-consolidated clay using nondimensional solutions addressing nonlinear soil-pile interaction. Comput. Geotech. 2018, 96, 203–214. [Google Scholar] [CrossRef]
- Collepardi, M.; Marcialis, A.; Turriziani, R. Penetration of chloride ions into cement pastes and concrete. J. Am. Ceram. Soc. 1972, 55, 534–535. [Google Scholar] [CrossRef]



| Variables | Unit | Meaning | Value | Reference |
|---|---|---|---|---|
| Da | m2/s | Chloride diffusion coefficient | 1.0 × 10−12 | [31] |
| Cs | kg/m3 | Surface chloride concentration | 8 | |
| w/b | - | Water–binder ratio | 0.35 | |
| Cth | kg/m3 | Chloride threshold concentration | 1.2 | [5] |
| d0 | mm | Reinforcement diameter | 32 | |
| ρs | g/cm3 | Density of the reinforcing steel | 7.85 | [32] |
| δ0 | μm | Porous layer thickness | 12 | |
| νc | - | Poisson’s ratio of concrete cover | 0.20 | [32] |
| φc | - | Concrete creep coefficient | 2.0 | [33] |
| αv | - | Volume expansion rate of corrosion products | 3.0 | [31] |
| fct | MPa | Tensile strength of the concrete | 2.0 | |
| Ec | GPa | Elastic modulus of the pile concrete | 38 | [31] |
| a | mm | Internal radius of the hollow pile | 360 | |
| b | mm | External radius of the hollow pile | 500 | |
| D | mm | Pile diameter | 1000 | |
| c | mm | Thickness of the concrete cover | 55 |
| Variables | Unit | Meaning | Value |
|---|---|---|---|
| M | kN·m | Bending moment at pile top | 400 |
| H | kN | Lateral load at pile top | 150 |
| N | kN | Vertical load at pile top | 3000 |
| Es | kN/m2 | Elastic modulus of the soil | 5000 |
| L | m | Length of the pile embedded in the soil | 30 |
| n | - | Number of elements | 100 |
| Variables | Unit | Probability Distribution | Mean | COV | Reference |
|---|---|---|---|---|---|
| Mth | kN·m | Constant (non-random) | 1088 | - | [29] |
| yth | mm | Constant (non-random) | 100 | - | |
| H0 | kN | Normal | 150 | 0.25 | [28] |
| N0 | kN | Constant (non-random) | 3000 | - | |
| M0 | kN·m | Normal | 400 | 0.15 | [28] |
| Es | kN/m2 | Lognormal | 5000 | 0.10 | [34] |
| Ec | GPa | Normal | 38 | 0.15 | [35] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Wu, C.; Zhang, W.; Fan, S.; Dai, J.; Zhang, W. Reliability Analysis of the Bearing Performance of Corroded Piles Subjected to Scour Action. Water 2025, 17, 84. https://doi.org/10.3390/w17010084
Chen B, Wu C, Zhang W, Fan S, Dai J, Zhang W. Reliability Analysis of the Bearing Performance of Corroded Piles Subjected to Scour Action. Water. 2025; 17(1):84. https://doi.org/10.3390/w17010084
Chicago/Turabian StyleChen, Bo, Caihong Wu, Wei Zhang, Shenghua Fan, Jialin Dai, and Wenbing Zhang. 2025. "Reliability Analysis of the Bearing Performance of Corroded Piles Subjected to Scour Action" Water 17, no. 1: 84. https://doi.org/10.3390/w17010084
APA StyleChen, B., Wu, C., Zhang, W., Fan, S., Dai, J., & Zhang, W. (2025). Reliability Analysis of the Bearing Performance of Corroded Piles Subjected to Scour Action. Water, 17(1), 84. https://doi.org/10.3390/w17010084







