Experimental Assessment of Vegetation Density and Orientation Effects on Flood-Induced Pressure Forces and Structural Accelerations
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Vegetation Configurations
3. Results
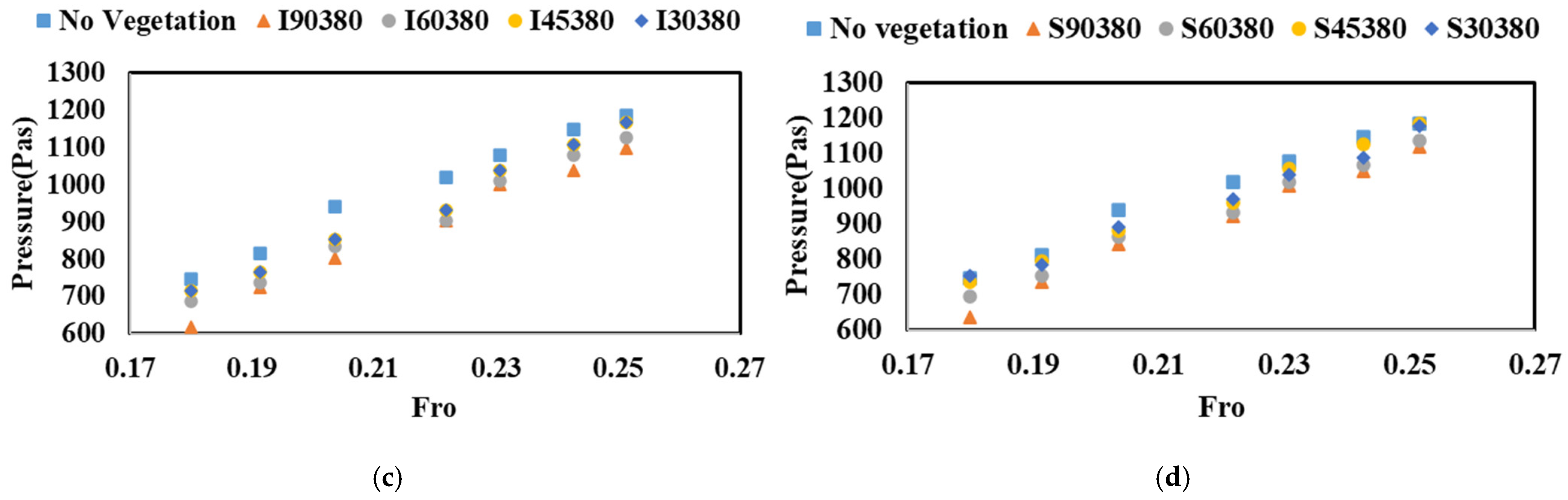
3.1. Flow-Induced Pressure
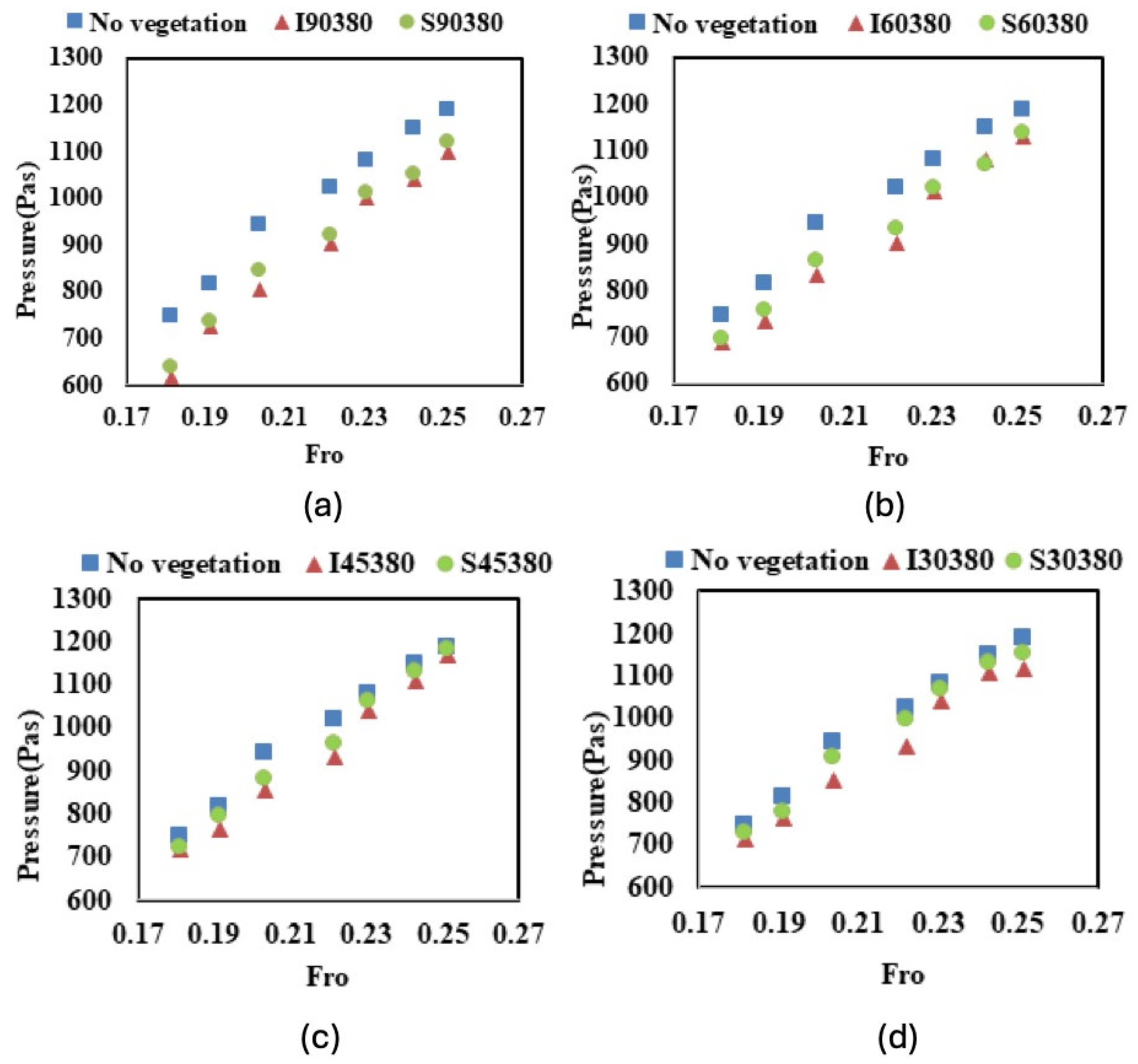
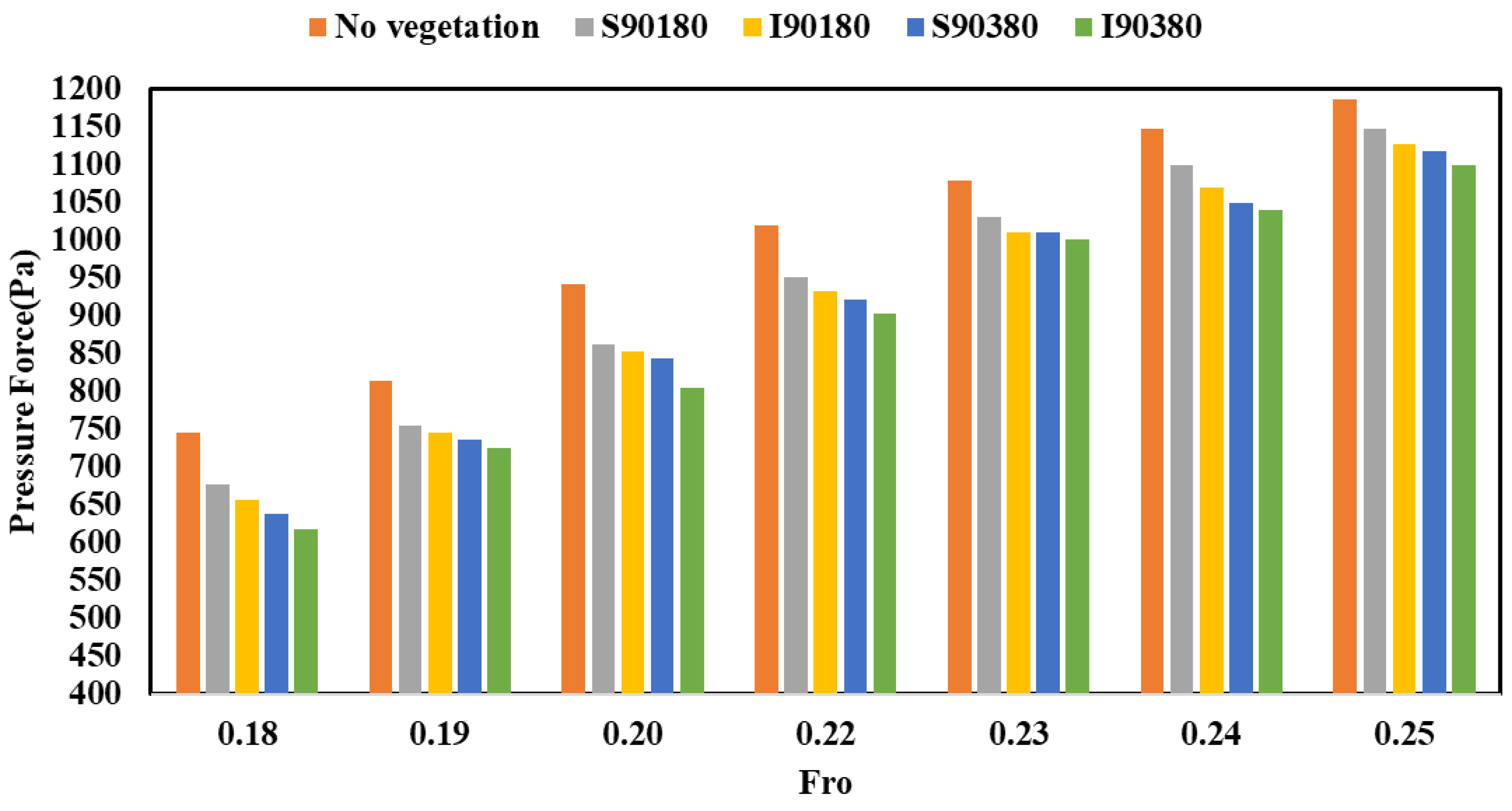
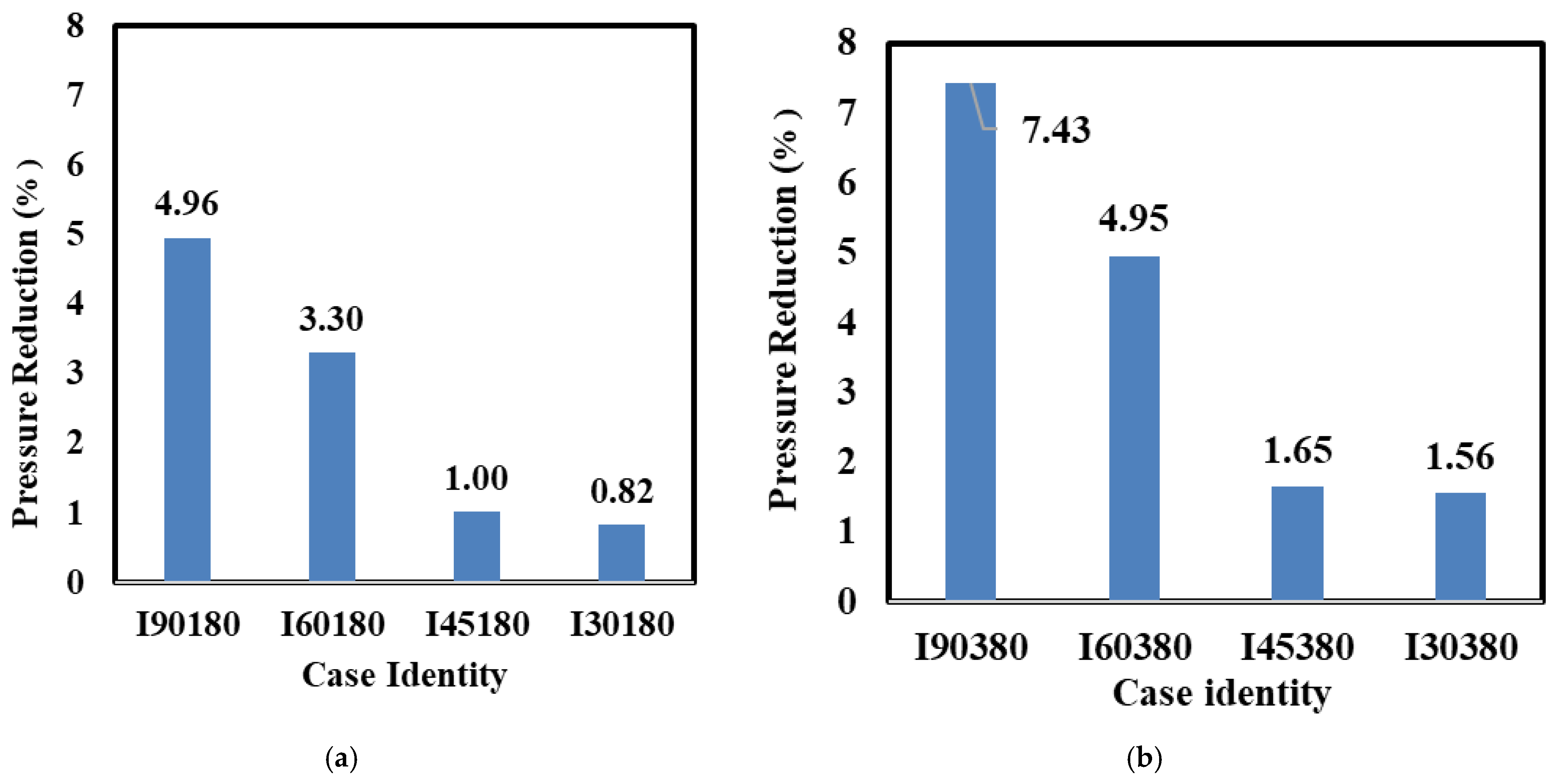
3.1.1. Effects of Vegetation Patch Density and Thickness
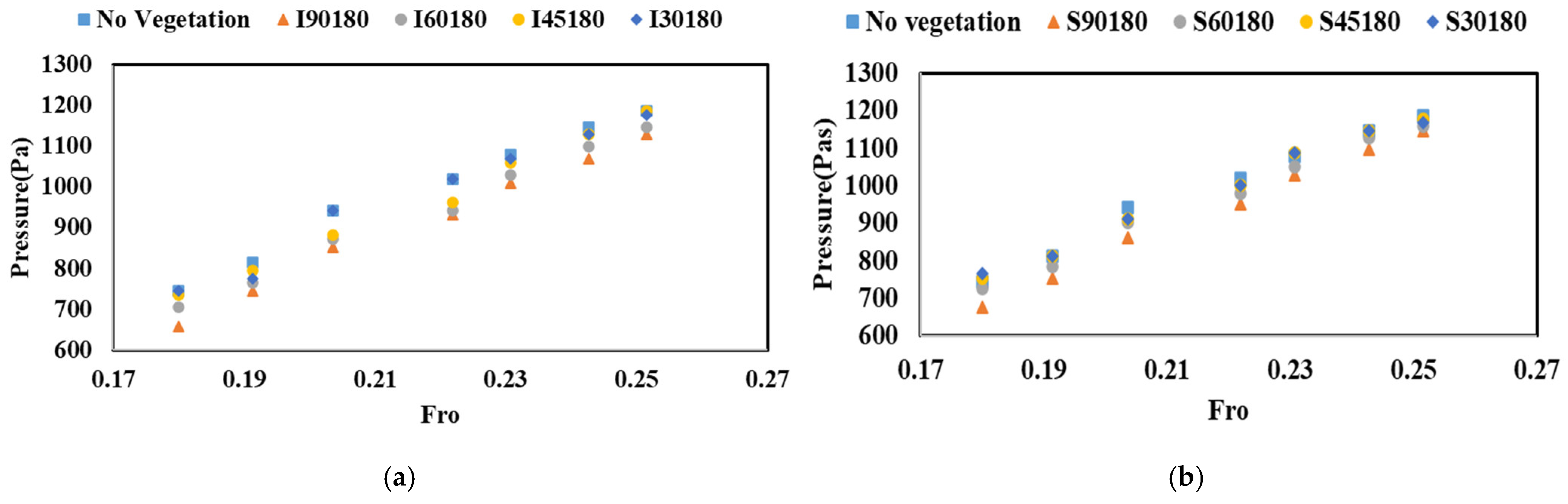
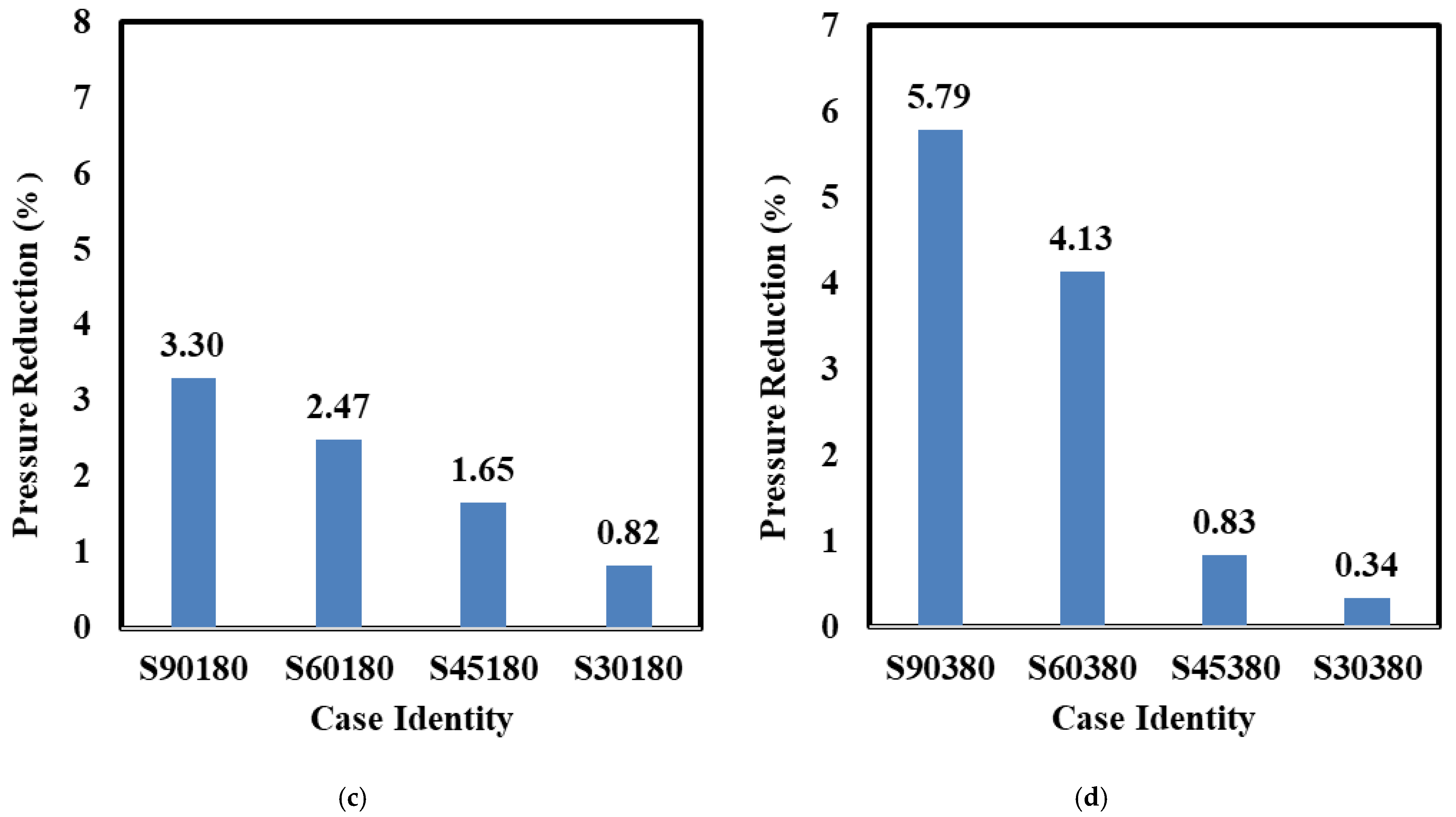
3.1.2. Effect of Angles and Staggered Arrangement
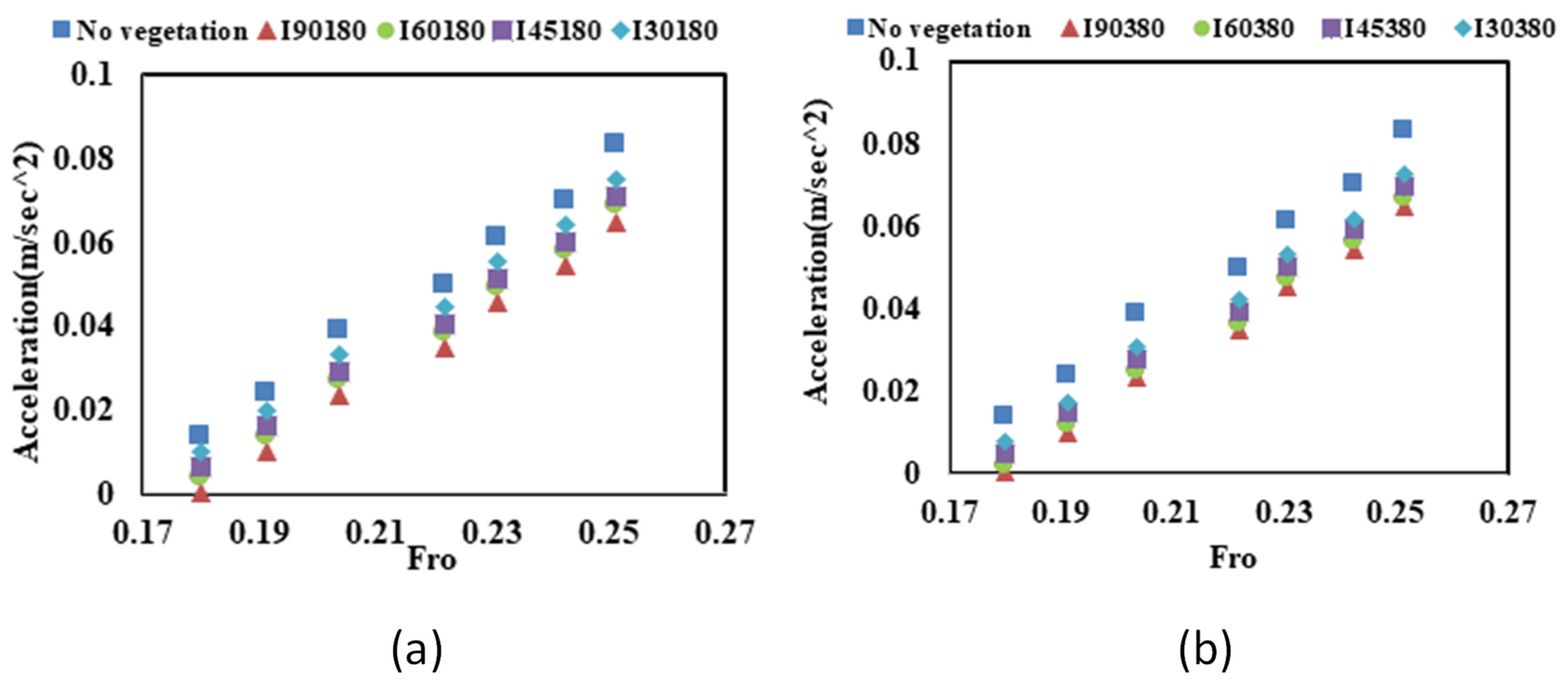
3.2. Acceleration of the Physical Model
3.2.1. Effect of Vegetation Density and Thickness
3.2.2. Significance of Vegetation Orientations in Physical Model Structure Acceleration
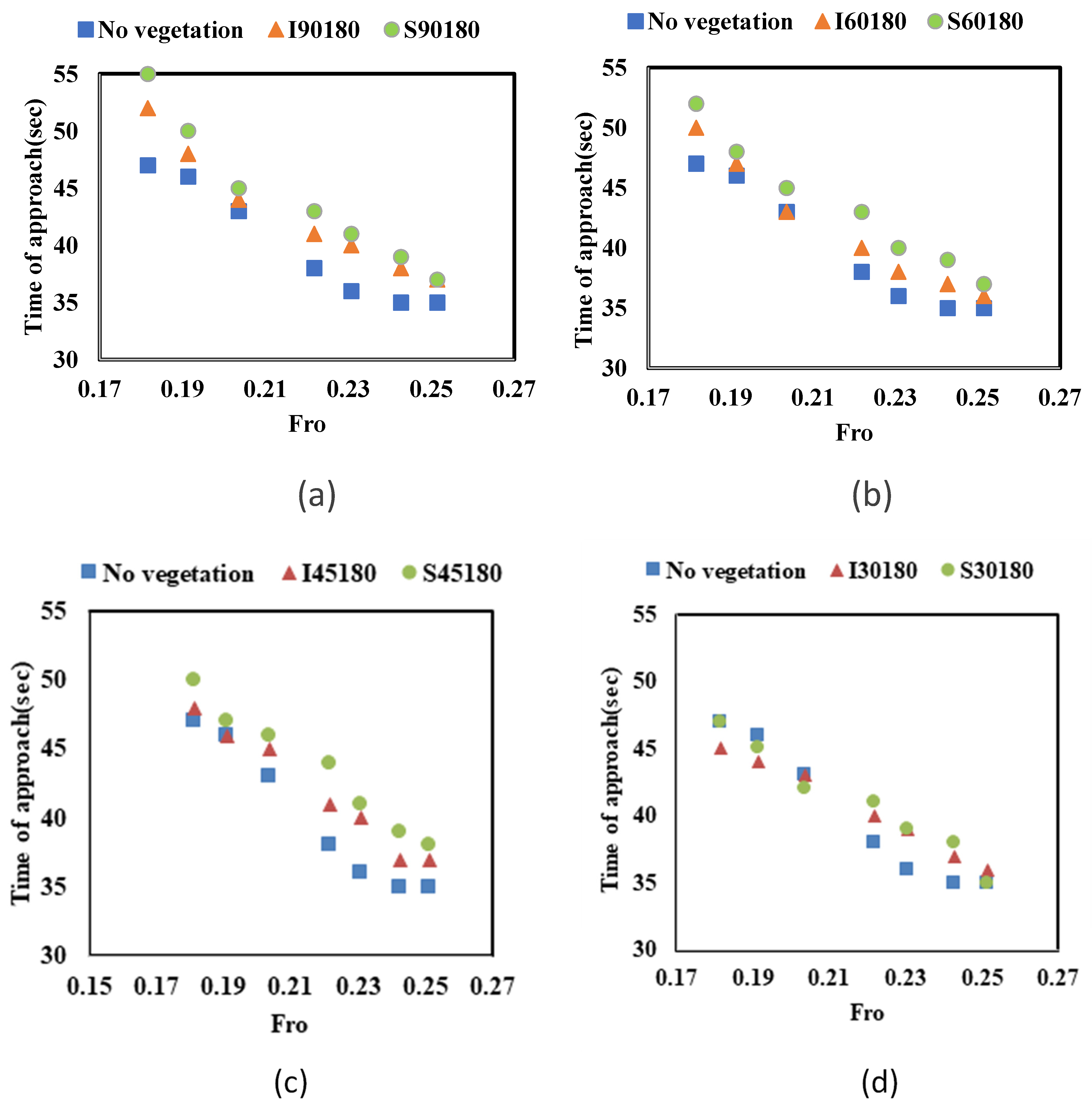
3.3. Time of Approach
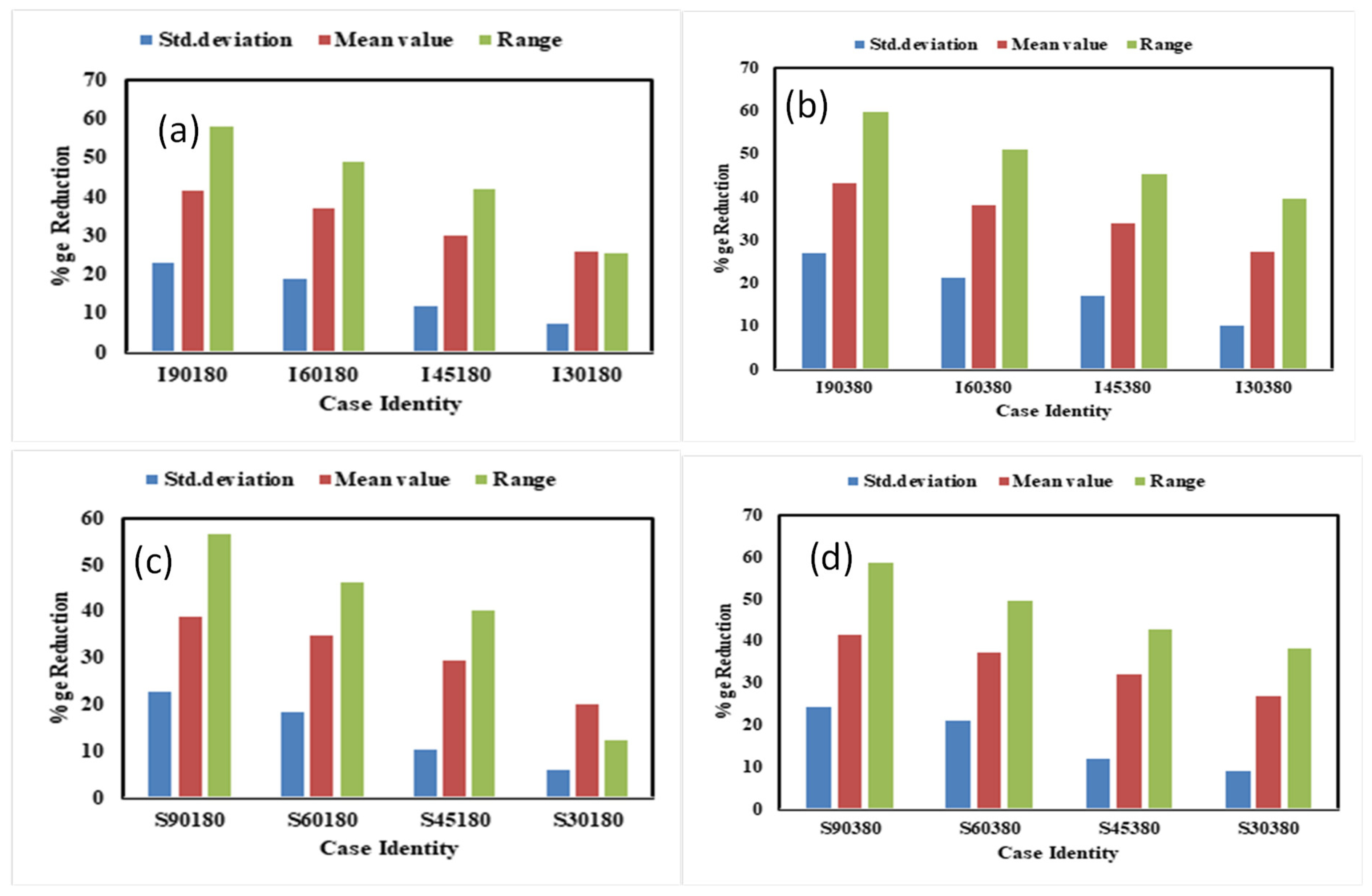
3.4. Statistical Analysis
4. Discussion
5. Conclusions and Recommendations
5.1. Conclusions
- Experimental results indicate that the reduction in hydraulic pressure increases with increasing vegetation thickness and decreasing vegetation orientation relative to the main flow, reaching a maximum at an intermediate vegetation density, with dn = 380. Thus, intermediate vegetation density (G/d = 1.09) emerges as the optimal configuration, achieving superior hydrostatic pressure and acceleration reduction compared to sparse arrangements while remaining practically implementable.
- Perpendicular vegetation alignment provides measurably superior flood force mitigation compared to oblique arrangements, supporting design recommendations for nature-based flood defences.
- The results show that vegetation plays a significant role in influencing fluid pressure forces and the dissipation of acceleration in model building. The X2-2 accelerometer methodology successfully quantified structural response under flood conditions, providing a replicable framework for evaluating vegetation-based mitigation strategies. The physical model’s structural acceleration reduction increases with the vegetation patch orientation changing from 30° to 90°. The hydraulic pressure and maximum model building acceleration reduction for the case of sparse vegetation patch arrangement with a vegetation patch thickness of dn = 180 and 90° orientation were 3.3% and 20.8%, respectively.
- The hydraulic pressure and maximum model building acceleration dissipation in the intermediate arrangement, with a vegetation patch thickness of dn = 380 and orientation at 90° relative to the flow direction, were 7.4% and 22.1%, respectively.
- The time of approach within the vegetation depends upon the resistance offered by the vegetation. The findings demonstrated that, in all cases considered, the time of approach decreased linearly as the Fr value increased. The value of approaching time for I90 is higher than for S90. The maximum value of approaching time is seen to increase by 21.7% and 14.5%, respectively.
- The results show maximum depth of water against the highest Froude number, i.e., 0.25. Therefore, the statistical parameters are at their maximum without vegetation at Fro = 0.25. The standard deviation, mean, and range values dissipated to a maximum in intermediate cases. The values of statistical analysis I90 are higher than S90. The maximum values of standard deviation, mean, and range dissipation were 26.1%, 43.5%, and 59.8%, respectively. These findings support the integration of strategically configured vegetation into flood risk management systems, offering sustainable alternatives to traditional hard infrastructure while providing quantifiable protection benefits.
5.2. Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lacerna, K.C.; Dalugdog, W.D. Disaster Preparedness among Selected Beach Resorts in San Juan Batangas. Int. J. Multidiscip. Appl. Bus. Educ. Res. 2025, 6, 3208–3230. [Google Scholar] [CrossRef]
- Smith, K. Environmental Hazards: Assessing Risk and Reducing Disaster; Routledge: New York, NY, USA, 2003. [Google Scholar]
- United Nations Office for Disaster Risk Reduction. Global Assessment Report on Disaster Risk Reduction 2025: Resilience Pays: Financing and Investing for Our Future; Stylus Publishing, LLC: New York, NY, USA, 2025. [Google Scholar]
- Zaha, T.; Tanaka, N.; Kimiwada, Y. Flume Experiments on Optimal Arrangement of Hybrid Defence System Comprising an Embankment, Moat, and Emergent Vegetation to Mitigate Inundating Tsunami Current. Ocean Eng. 2019, 173, 45–57. [Google Scholar] [CrossRef]
- Feizbahr, M.; Tonekaboni, N.; Jiang, G.J.; Chen, H.X. Optimized Vegetation Density to Dissipate Energy of Flood Flow in Open Canals. Math. Probl. Eng. 2021, 2021, 9048808. [Google Scholar] [CrossRef]
- Rezzoug, A.; Khan, A.; Murtaza, N.; Rizvi, S.A.S. Predicting Flood Energy Reduction in Vegetated Open Channel: Comparative Assessment of Hybrid Artificial Intelligence Techniques. Eng. Appl. Artif. Intell. 2025, 159, 111756. [Google Scholar] [CrossRef]
- Ahmed, A.; Ghumman, A.R. Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defence Systems. Water 2019, 11, 1971. [Google Scholar] [CrossRef]
- Ahmed, A.; Valyrakis, M.; Ghumman, A.R.; Pasha, G.A.; Farooq, R. Experimental Investigation of Flood Energy Reduction through Vegetation at Various Angles. River Res. Appl. 2021, 37, 644–655. [Google Scholar] [CrossRef]
- Rehman, S.U.; Ahmed, A.; Gilja, G.; Valyrakis, M.; Ghumman, A.R.; Pasha, G.A.; Farooq, R. A Laboratory Study of the Role of Nature-Based Solutions in Improving Flash Flooding Resilience in Hilly Terrains. Water 2023, 16, 124. [Google Scholar] [CrossRef]
- Merz, B.; Hall, J.; Disse, M.; Schumann, A. Fluvial Flood Risk Management in a Changing World. Nat. Hazards Earth Syst. Sci. 2010, 10, 509–527. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of Vegetated Channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Vundavilli, V.S.S.R.H. The Interaction of Buoyant River Plumes with Vegetation and Consequences for Sediment Transport and Deposition in Coastal Regions. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 2023. [Google Scholar]
- van Zelst, V.T.M.; Dijkstra, J.T.; van Wesenbeeck, B.K.; Eilander, D.; Morris, E.P.; Winsemius, H.C.; Ward, P.J. Cutting the Costs of Coastal Protection by Integrating Vegetation in Flood Defences. Nat. Commun. 2021, 12, 6533. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Undular Hydraulic Jump Formation and Energy Loss in a Flow through Emergent Vegetation of Varying Thickness and Density. Ocean Eng. 2017, 141, 308–325. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, C.; Wang, Z.; Zhu, N.; Du, N.; Xu, J.; Li, Y. Experimental Investigation on Effect of Vegetation Distribution Pattern on Hydraulic Characteristics of Overland Flow. Hydrol. Process. 2025, 39, e70234. [Google Scholar] [CrossRef]
- Tanaka, N. Effectiveness and Limitations of Coastal Forest in Large Tsunami. Annu. J. Hydraul. Eng. JSCE 2012, 56, 127–132. [Google Scholar]
- Tiggeloven, T.; de Moel, H.; Winsemius, H.C.; Eilander, D.; Erkens, G.; Gebremedhin, E.; Ward, P.J. The Benefits of Coastal Adaptation through Conservation of Foreshore Vegetation. J. Flood Risk Manag. 2022, 15, e12790. [Google Scholar] [CrossRef]
- Kumar Yadav, P.; Thapa, S.; Han, X.; Richmond, C.; Zhang, N. Investigation of the Effects of Wetland Vegetation on Coastal Flood Reduction Using Hydrodynamic Simulation. In Proceedings of the ASME 2015 Fluids Engineering Division Summer Meeting, Seoul, Republic of Korea, 26–31 July 2015. [Google Scholar] [CrossRef]
- Dissanayaka, K.D.C.R.; Tanaka, N.; Vinodh, T.L.C. Integration of Eco-DRR and Hybrid Defense System on Mitigation of Natural Disasters (Tsunami and Coastal Flooding): A Review. Nat. Hazards 2022, 110, 1–30. [Google Scholar] [CrossRef]
- Ali, A.; Pasha, G.A.; Ghani, U.; Ahmed, A.; Abbas, F.M. Investigating Role of Vegetation in Protection of Houses during Floods. Civ. Eng. J. 2019, 5, 2598–2613. [Google Scholar] [CrossRef]
- Varanis, M.; Silva, A.; Mereles, A.; Pederiva, R. MEMS Accelerometers for Mechanical Vibrations Analysis: A Comprehensive Review with Applications. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 527. [Google Scholar] [CrossRef]
- Martínez-Castro, R.E.; Jang, S.; Christenson, R.E. Rapid Cable Tension Estimation Using Dynamic and Mechanical Properties. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2016, Las Vegas, NV, USA, 21–24 March 2016; SPIE: Washington, DC, USA, 2016; Volume 9803. [Google Scholar] [CrossRef]
- Tanaka, N. Vegetation Bioshields for Tsunami Mitigation: Review of Effectiveness, Limitations, Construction, and Sustainable Management. Landsc. Ecol. Eng. 2009, 5, 71–79. [Google Scholar] [CrossRef]
- Jennings, P.C. Distant Motions from a Building Vibration Test. Bull. Seismol. Soc. Am. 1970, 60, 2037–2043. [Google Scholar] [CrossRef]
- Alhusban, Z.; Valyrakis, M. Assessing Sediment Transport Dynamics from Energy Perspective by Using the Instrumented Particle. Int. J. Sediment Res. 2022, 37, 833–846. [Google Scholar] [CrossRef]
- Al-Obaidi, K.; Xu, Y.; Valyrakis, M. The Design and Calibration of Instrumented Particles for Assessing Water Infrastructure Hazards. J. Sens. Actuator Netw. 2020, 9, 36. [Google Scholar] [CrossRef]
- Al-Obaidi, K.; Valyrakis, M. A Sensory Instrumented Particle for Environmental Monitoring Applications: Development and Calibration. IEEE Sens. J. 2021, 21, 10153–10166. [Google Scholar] [CrossRef]
- Al-Obaidi, K.; Valyrakis, M. Linking the Explicit Probability of Entrainment of Instrumented Particles to Flow Hydrodynamics. Earth Surf. Process. Landf. 2021, 46, 2448–2465. [Google Scholar] [CrossRef]
- Hott, J.W. The Design and Implementation of an Underfloor Accelerometer-Based Local Structural Dynamics Monitoring System for the Ashraf Islam Engineering Building. Master’s Thesis, Tennessee Technological University, Cookeville, TN, USA, 2024. [Google Scholar]
- Chitsaz, N.; Banihabib, M.E. Comparison of Different Multi-Criteria Decision-Making Models in Prioritizing Flood Management Alternatives. Water Resour. Manag. 2015, 29, 2503–2525. [Google Scholar] [CrossRef]
- Mita, A.; Yokoi, I. Fiber Bragg Grating Accelerometer for Buildings and Civil Infrastructures. Proc. SPIE 2001, 4330, 479–486. [Google Scholar] [CrossRef]
- Sanjou, M.; Okamoto, T.; Nezu, I. Experimental Study on Fluid Energy Reduction through a Flood Protection Forest. J. Flood Risk Manag. 2018, 11, e12339. [Google Scholar] [CrossRef]
- Valyrakis, M.; Liu, D.; Turker, U.; Yagci, O. The Role of Increasing Riverbank Vegetation Density on Flow Dynamics across an Asymmetrical Channel. Environ. Fluid Mech. 2021, 21, 643–666. [Google Scholar] [CrossRef]
- Williams, C.J.; Pierson, F.B.; Kormos, P.R.; Al-Hamdan, O.Z.; Hardegree, S.P. Vegetation, Ground Cover, Soil, Rainfall Simulation, and Overland-Flow Experiments before and after Tree Removal in Woodland-Encroached Sagebrush Steppe. Earth Syst. Sci. Data 2020, 12, 1347–1365. [Google Scholar] [CrossRef]
- Siniscalchi, F.; Nikora, V.I.; Aberle, J. Plant Patch Hydrodynamics in Flows: Results from a Laboratory Study. Water Resour. Res. 2012, 48, W10533. [Google Scholar] [CrossRef]
- Liu, C.; Tang, H.; Zhou, J. Effects of Patch Properties of Submerged Vegetation on Sediment Scouring and Deposition. Water 2022, 14, 4025. [Google Scholar]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S.J. Effects of Vegetation on Flow and Sediment Transport: Comparative Analyses and Validation of Predicting Models. Earth Surf. Process. Landf. 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Zong, L.; Nepf, H. Flow and Deposition in and Around a Finite Patch of Vegetation. Geomorphology 2010, 110, 363–372. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An Experimental Study of Flow through Rigid Vegetation. J. Geophys. Res. Earth Surf. 2008, 113, F04015. [Google Scholar] [CrossRef]
- Tang, C.; Yi, Y.; Zhang, S. Flow and Turbulence in Unevenly Obstructed Channels with Rigid and Flexible Vegetation. J. Environ. Manage. 2022, 323, 116736. [Google Scholar] [CrossRef]
- Yagci, O.; Tafarojnoruz, A.; Celik, M.F.; Kitsikoudis, V.; Duran, Z.; Kirca, V.S.O. Scour Patterns around Isolated Vegetation Elements. Adv. Water Resour. 2016, 97, 251–265. [Google Scholar] [CrossRef]
- Van Dijk, W.M.; Teske, R.; Van de Lageweg, W.I.; Kleinhans, M.G. Effects of Vegetation Distribution on Experimental River Channel Dynamics. Water Resour. Res. 2013, 49, 7558–7574. [Google Scholar] [CrossRef]
- Ram, N.H.; Sriram, V. Energy Dissipation Characteristics of Vegetation Belt for the Tsunami-like Bore. Phys. Fluids 2025, 37, 037172. [Google Scholar] [CrossRef]
- Borghei, S.M.; Jalili, M.R.; Ghodsian, M. Discharge Coefficient for Sharp-Crested Side Weir in Subcritical Flow. J. Hydraul. Eng. 1999, 125, 1051–1056. [Google Scholar] [CrossRef]
- Ali, S.; Uijttewaal, W.S.J. Flow Resistance of Vegetated Oblique Weirlike Obstacles during High Water Stages. Hydrol. Earth Syst. Sci. 2014, 18, 1–14. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Ball, J.E. Discharge Coefficient of Sharp-Crested Side Weir in Trapezoidal Channel with Different Side-Wall Slopes under Subcritical Flow Conditions. Irrig. Drain. 2014, 63, 40–50. [Google Scholar] [CrossRef]
- Azimi, A.H.; Rajaratnam, N.; Zhu, D.Z. Submerged Flows over Rectangular Weirs of Finite Crest Length. J. Irrig. Drain. Eng. 2014, 140, 04014008. [Google Scholar] [CrossRef]
- Cheng, N.-S.; Nguyen, H.T. Hydraulic Radius for Evaluating Resistance Induced by Simulated Emergent Vegetation in Open-Channel Flows. J. Hydraul. Eng. 2011, 137, 995–1004. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent Flow Through Idealized Emergent Vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Tinoco, R.O.; San Juan, J.E.; Mullarney, J.C. Simplification bias: Lessons from laboratory and field experiments on flow through aquatic vegetation. Earth Surf. Process. Landf. 2020, 45, 121–143. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the Blade Scale to the Reach Scale: A Characterization of Aquatic Vegetation Drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Folkard, A.M. Hydrodynamics of Model Posidonia Oceanica Patches in Shallow Water. Limnol. Oceanogr. 2005, 50, 1592–1600. [Google Scholar] [CrossRef]
- Marjoribanks, T.I.; Hardy, R.J.; Lane, S.N.; Parsons, D.R. High-Resolution Numerical Modelling of Flow—Vegetation Interactions. J. Hydraul. Res. 2014, 52, 775–793. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Stoesser, T.; Bates, P.D.; Pinzen, A.B. Open Channel Flow through Different Forms of Submerged Flexible Vegetation. J. Hydraul. Eng. 2003, 129, 847–853. [Google Scholar] [CrossRef]
- Al-Obaidi, K.; Valyrakis, M. Coherent Flow Structures Linked to the Impulse Criterion for Incipient Motion of Coarse Sediment. Appl. Sci. 2023, 13, 10656. [Google Scholar] [CrossRef]


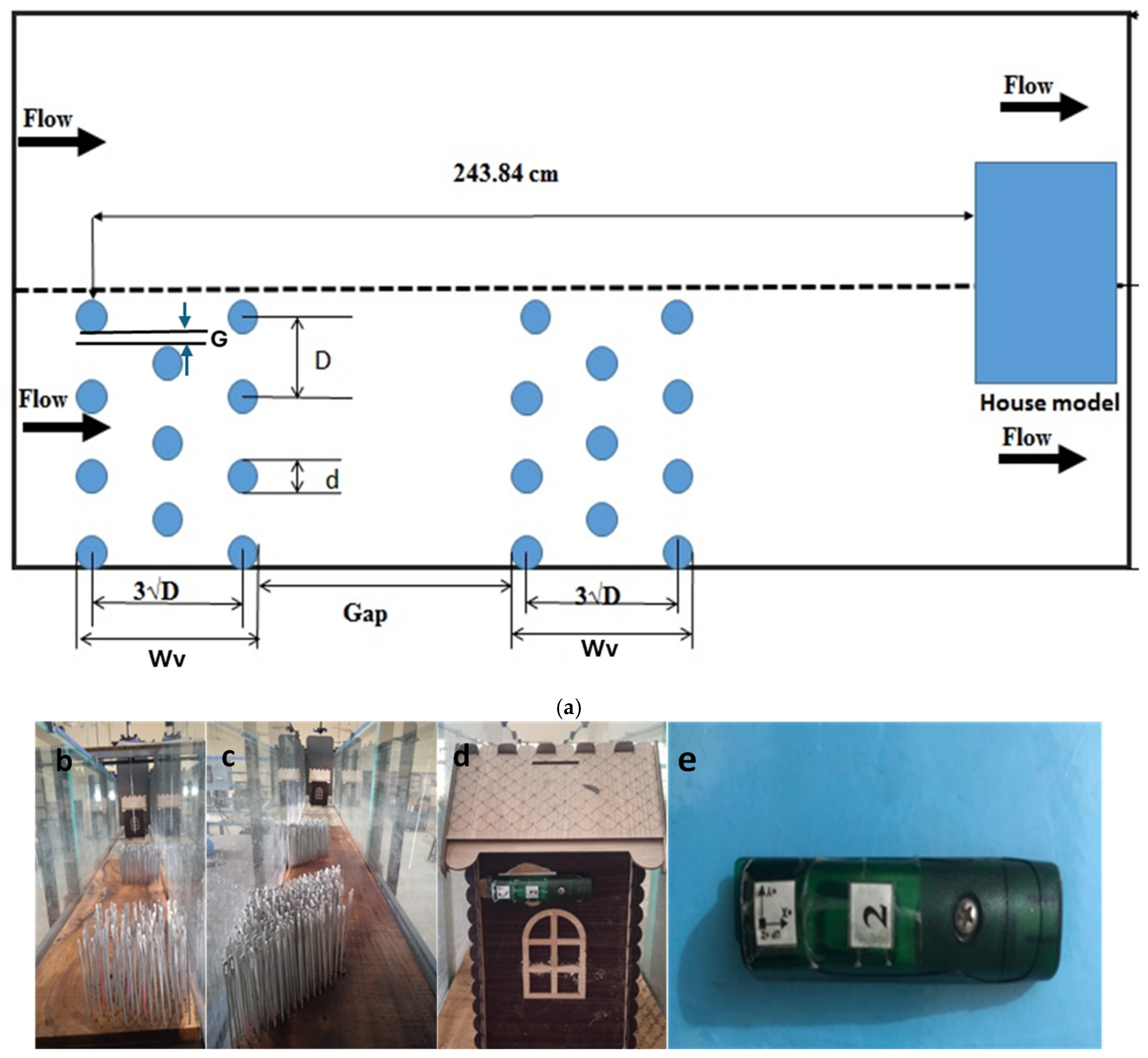



| Case # | Angle of Vegetation | Initial Froude No. (Fro) | d (cm) | Vegetation Type | Vegetation Thickness (dn) |
|---|---|---|---|---|---|
| 1 | No vegetation | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | 180,380 | |
| 2 | 90 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Intermediate | 180,380 |
| 3 | 90 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Sparse | 180,380 |
| 4 | 60 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Intermediate | 180,380 |
| 5 | 60 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Sparse | 180,380 |
| 6 | 45 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Intermediate | 180,380 |
| 7 | 45 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Sparse | 180,380 |
| 8 | 30 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Intermediate | 180,380 |
| 9 | 30 | 0.18, 0.19, 0.20, 0.22, 0.23, 0.24, and 0.25 | 0.3 | Sparse | 180,380 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qadir, I.; Ahmed, A.; Ghumman, A.R.; Valyrakis, M.; Mehboob, S.S.; Pasha, G.A.; Abbas, F.M.; Qadir, I. Experimental Assessment of Vegetation Density and Orientation Effects on Flood-Induced Pressure Forces and Structural Accelerations. Water 2025, 17, 2879. https://doi.org/10.3390/w17192879
Qadir I, Ahmed A, Ghumman AR, Valyrakis M, Mehboob SS, Pasha GA, Abbas FM, Qadir I. Experimental Assessment of Vegetation Density and Orientation Effects on Flood-Induced Pressure Forces and Structural Accelerations. Water. 2025; 17(19):2879. https://doi.org/10.3390/w17192879
Chicago/Turabian StyleQadir, Imran, Afzal Ahmed, Abdul Razzaq Ghumman, Manousos Valyrakis, Syed Saqib Mehboob, Ghufran Ahmed Pasha, Fakhar Muhammad Abbas, and Irfan Qadir. 2025. "Experimental Assessment of Vegetation Density and Orientation Effects on Flood-Induced Pressure Forces and Structural Accelerations" Water 17, no. 19: 2879. https://doi.org/10.3390/w17192879
APA StyleQadir, I., Ahmed, A., Ghumman, A. R., Valyrakis, M., Mehboob, S. S., Pasha, G. A., Abbas, F. M., & Qadir, I. (2025). Experimental Assessment of Vegetation Density and Orientation Effects on Flood-Induced Pressure Forces and Structural Accelerations. Water, 17(19), 2879. https://doi.org/10.3390/w17192879







