When Are Models Useful? Revisiting the Quantification of Reality Checks
Abstract
:All models are wrong but some are useful(George E. P. Box) [1]
1. Introduction
2. Revisiting the Existing Framework
2.1. Nash–Sutcliffe Efficiency
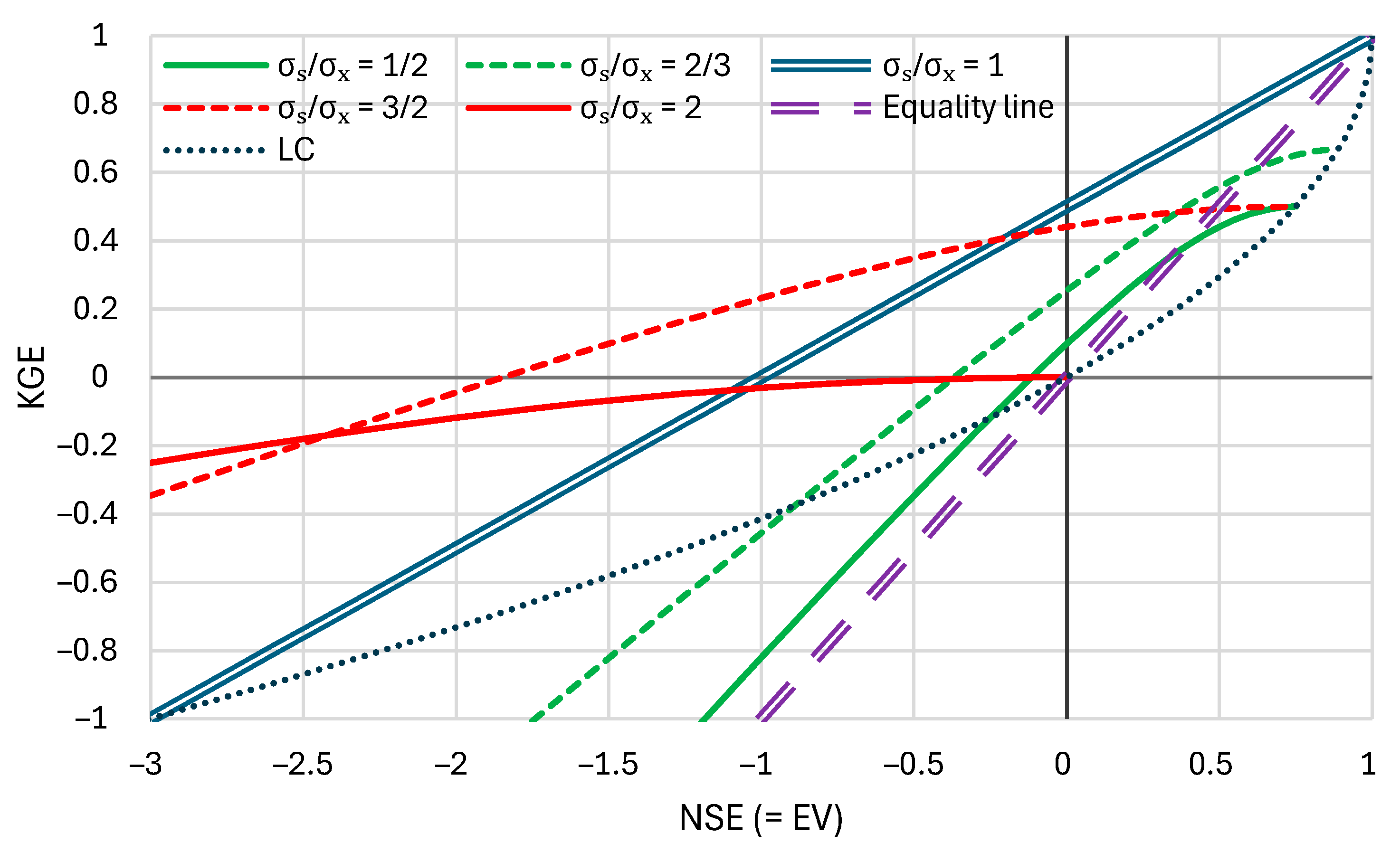
2.2. Kling–Gupta Efficiency and Its Relationship with the Nash–Sutcliffe Efficiency
3. Proposed Framework
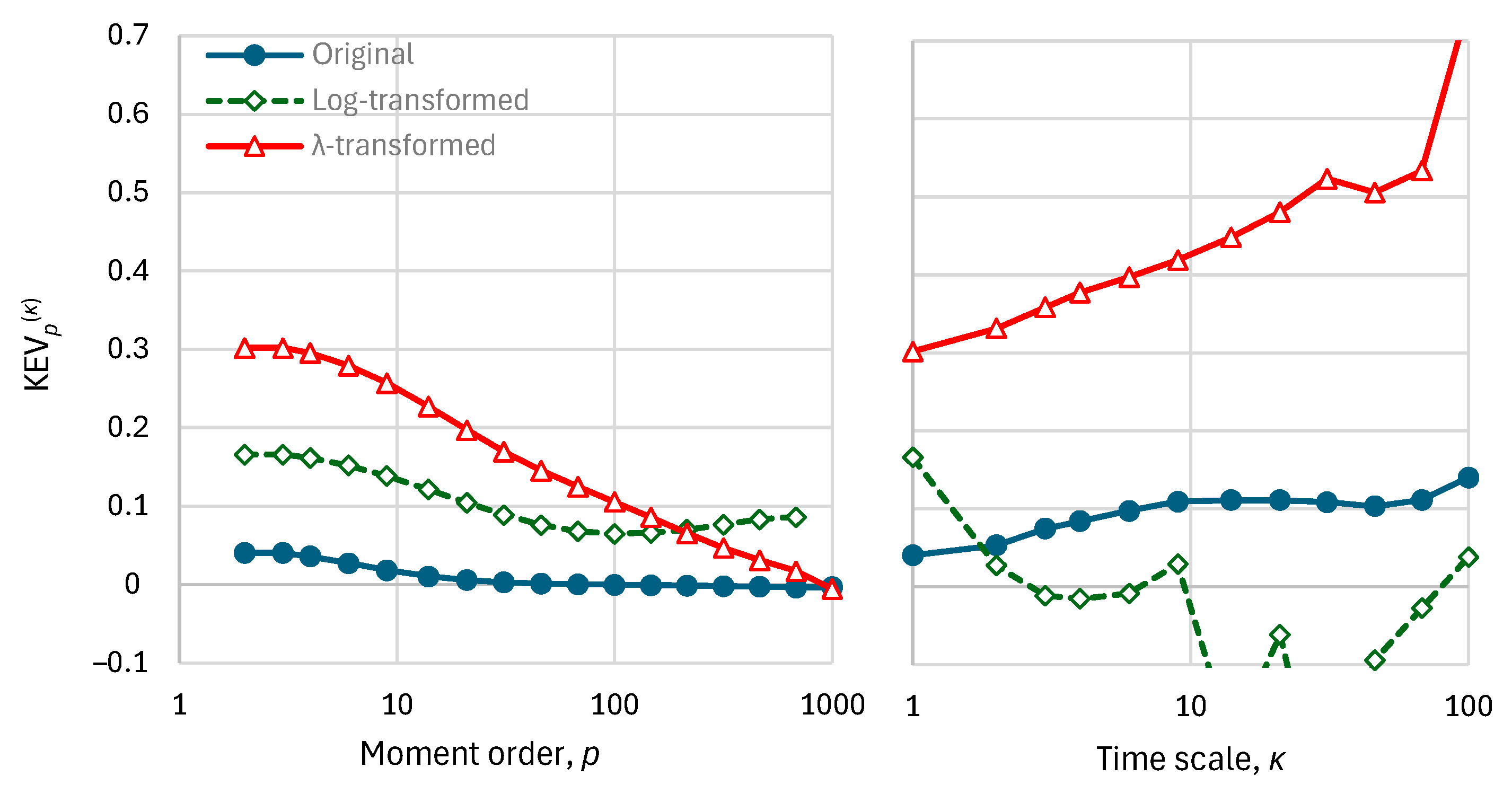
3.1. A Summary of K-Moments
3.2. K-Moments Based Metrics of Efficiency
3.3. Possible Transformations of Data
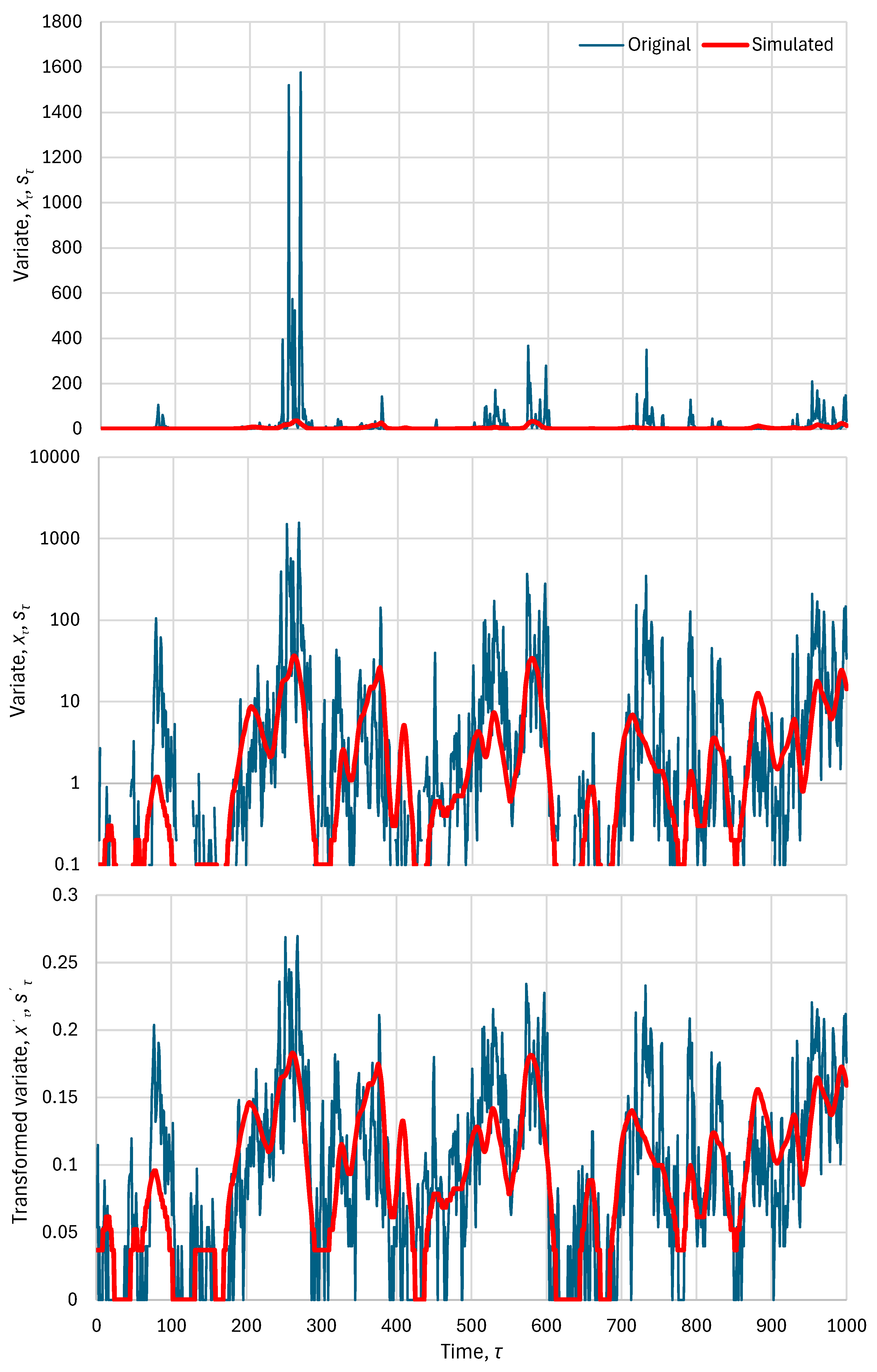
4. Real-World Case Study
5. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Box, G.E.P. Robustness in the Strategy of Scientific Model Building. In Robustness in Statistics; Launer, R.L., Wilkinson, G.N., Eds.; Academic Press: New York, NY, USA, 1979; pp. 201–236. ISBN 978-0-12-438150-6. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Negligent killing of scientific concepts: The stationarity case. Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
- Kurshan, R. Computer-Aided Verification of Coordinating Processes: The Automata-Theoretic Approach; Princeton University Press: Princeton, NJ, USA, 1994; ISBN 0-691-03436-2. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kundzewicz, Z.W. Editorial—Quantifying the impact of hydrological studies. Hydrol. Sci. J. 2007, 52, 3–17. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Ocean. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Wu, J. Detecting, extracting, and monitoring surface water from space using optical sensors: A review. Rev. Geophys. 2018, 56, 333–360. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Zurell, D.; Franklin, J.; König, C.; Bouchet, P.J.; Dormann, C.F.; Elith, J.; Fandos, G.; Feng, X.; Guillera-Arroita, G.; Guisan, A.; et al. A standard protocol for reporting species distribution models. Ecography 2020, 43, 1261–1277. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Hassani, A.; Azapagic, A.; Shokri, N. Predicting long-term dynamics of soil salinity and sodicity on a global scale. Proc. Natl. Acad. Sci. USA 2020, 117, 33017–33027. [Google Scholar] [CrossRef] [PubMed]
- Hassani, A.; Azapagic, A.; Shokri, N. Global predictions of primary soil salinization under changing climate in the 21st century. Nat. Commun. 2021, 12, 6663. [Google Scholar] [CrossRef] [PubMed]
- Yaseen, Z.M. An insight into machine learning models era in simulating soil, water bodies and adsorption heavy metals: Review, challenges and solutions. Chemosphere 2021, 277, 130126. [Google Scholar] [CrossRef] [PubMed]
- Naser, M.Z.; Alavi, A.H. Error metrics and performance fitness indicators for artificial intelligence and machine learning in engineering and sciences. Archit. Struct. Constr. 2023, 3, 499–517. [Google Scholar] [CrossRef]
- Martinho, A.D.; Hippert, H.S.; Goliatt, L. Short-term streamflow modeling using data-intelligence evolutionary machine learning models. Sci. Rep. 2023, 13, 13824. [Google Scholar] [CrossRef] [PubMed]
- O’Connell, P.E.; Koutsoyiannis, D.; Lins, H.F.; Markonis, Y.; Montanari, A.; Cohn, T.A. The scientific legacy of Harold Edwin Hurst (1880–1978). Hydrol. Sci. J. 2016, 61, 1571–1590. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H. On typical range, sensitivity, and normalization of Mean Squared Error and Nash-Sutcliffe Efficiency type metrics. Water Resour. Res. 2011, 47, W10601. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Lombardo, F.; Volpi, E.; Koutsoyiannis, D.; Papalexiou, S.M. Just two moments! A cautionary note against use of high-order moments in multifractal models in hydrology. Hydrol. Earth Syst. Sci. 2014, 18, 243–255. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Knowable moments for high-order stochastic characterization and modelling of hydrological processes. Hydrol. Sci. J. 2019, 64, 19–33. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Replacing histogram with smooth empirical probability density function estimated by K-moments. Sci 2022, 4, 50. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Knowable moments in stochastics: Knowing their advantages. Axioms 2023, 12, 590. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Stochastics of Hydroclimatic Extremes—A Cool Look at Risk, 3rd ed.; Kallipos Open Academic Editions: Athens, Greece, 2023; 391p, ISBN 978-618-85370-0-2. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Yao, H.; Georgakakos, A. Medium-range flow prediction for the Nile: A comparison of stochastic and deterministic methods. Hydrol. Sci. J. 2008, 53, 142–164. [Google Scholar] [CrossRef]
- Trouet, V.; Van Oldenborgh, G.J. KNMI Climate Explorer: A web-based research tool for high-resolution paleoclimatology. Tree-Ring Res. 2013, 69, 3–13. [Google Scholar] [CrossRef]
- The KNMI Climate Explorer. Available online: https://climexp.knmi.nl/start.cgi (accessed on 19 August 2024).
- ERA5: Data Documentation—Copernicus Knowledge Base—ECMWF Confluence Wiki. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation (accessed on 25 March 2023).
- Soci, C.; Hersbach, H.; Simmons, A.; Poli, P.; Bell, B.; Berrisford, P.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Radu, R.; et al. The ERA5 global reanalysis from 1940 to 2022. Q. J. R. Meteorol. Soc. 2024, 150, 4014–4048. [Google Scholar] [CrossRef]
- Web-Based Reanalyses Intercomparison Tools. Available online: https://psl.noaa.gov/data/atmoswrit/timeseries/index.html (accessed on 19 August 2024).
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Hassler, B.; Lauer, A. comparison of reanalysis and observational precipitation datasets including ERA5 and WFDE5. Atmosphere 2021, 12, 1462. [Google Scholar] [CrossRef]
- Bandhauer, M.; Isotta, F.; Lakatos, M.; Lussana, C.; Båserud, L.; Izsák, B.; Szentes, O.; Tveito, O.E.; Frei, C. Evaluation of daily precipitation analyses in E-OBS (v19. 0e) and ERA5 by comparison to regional high-resolution datasets in European regions. Int. J. Climatol. 2022, 42, 727–747. [Google Scholar] [CrossRef]
- Longo-Minnolo, G.; Vanella, D.; Consoli, S.; Pappalardo, S.; Ramírez-Cuesta, J.M. Assessing the use of ERA5-Land reanalysis and spatial interpolation methods for retrieving precipitation estimates at basin scale. Atmos. Res. 2022, 271, 106131. [Google Scholar] [CrossRef]
- Cavalleri, F.; Lussana, C.; Viterbo, F.; Brunetti, M.; Bonanno, R.; Manara, V.; Lacavalla, M.; Sperati, S.; Raffa, M.; Capecchi, V.; et al. Multi-scale assessment of high-resolution reanalysis precipitation fields over Italy. Atmos. Res. 2024, 312, 107734. [Google Scholar] [CrossRef]
- Lavers, D.A.; Hersbach, H.; Rodwell, M.J.; Simmons, A. An improved estimate of daily precipitation from the ERA5 reanalysis. Atmos. Sci. Lett. 2024, 25, e1200. [Google Scholar] [CrossRef]


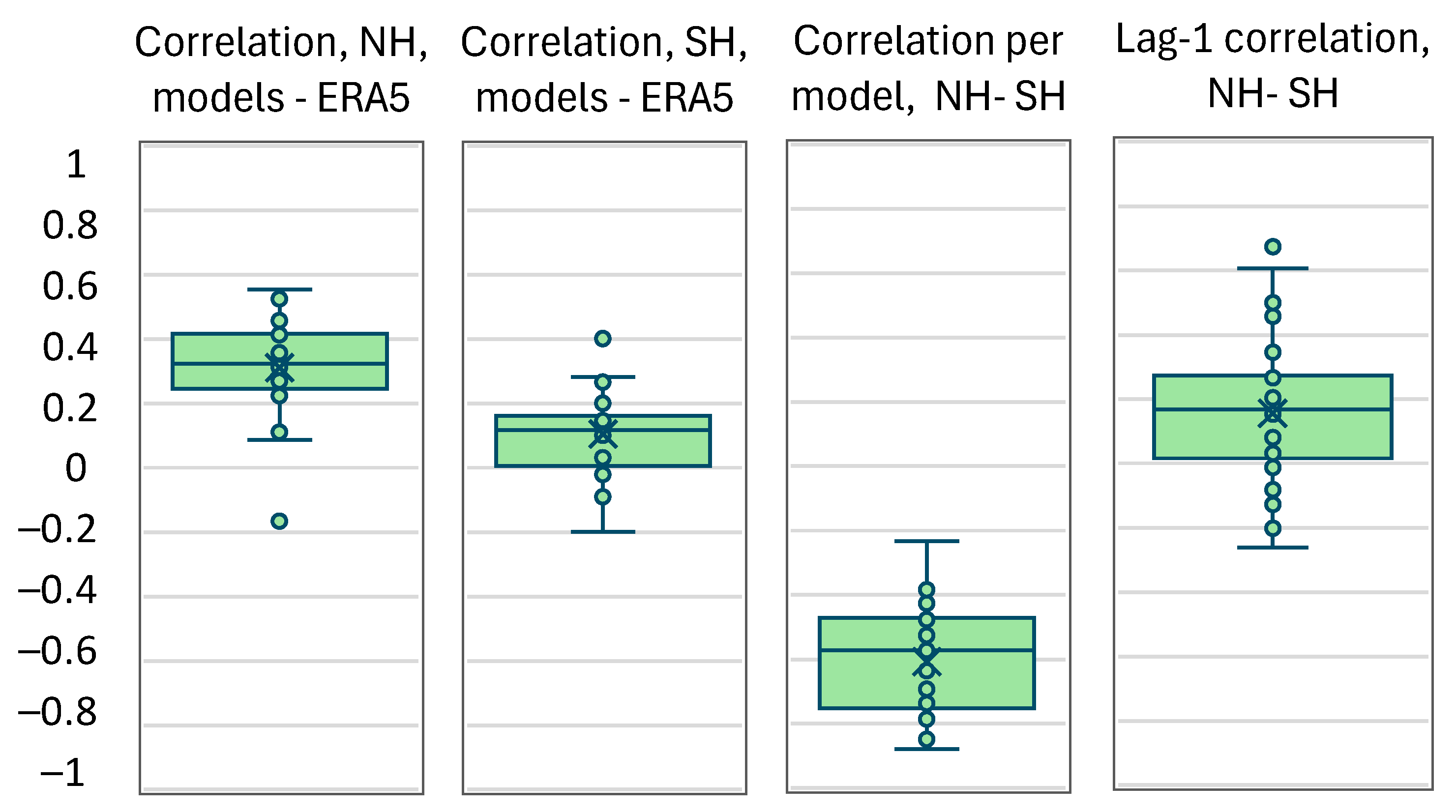
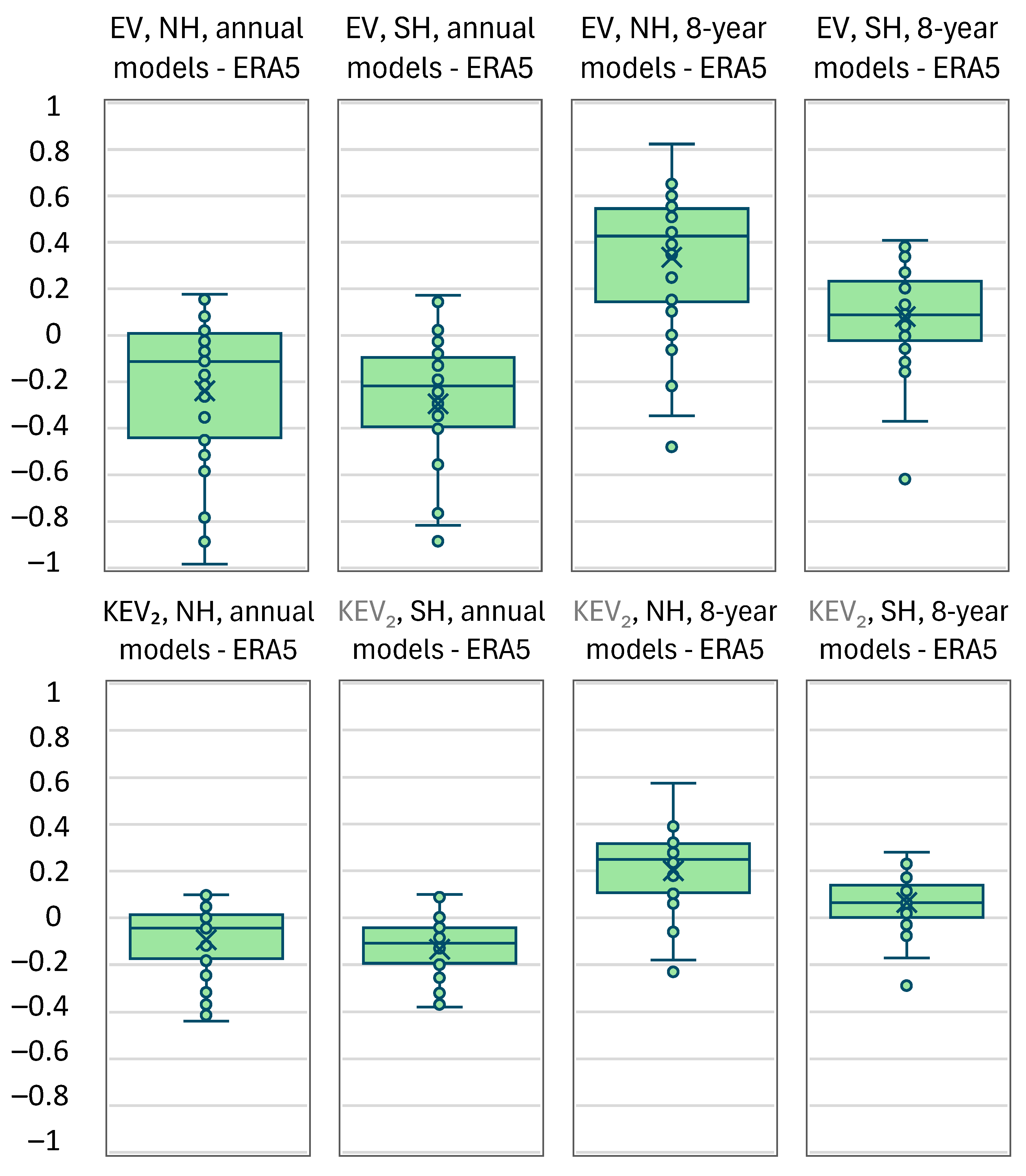
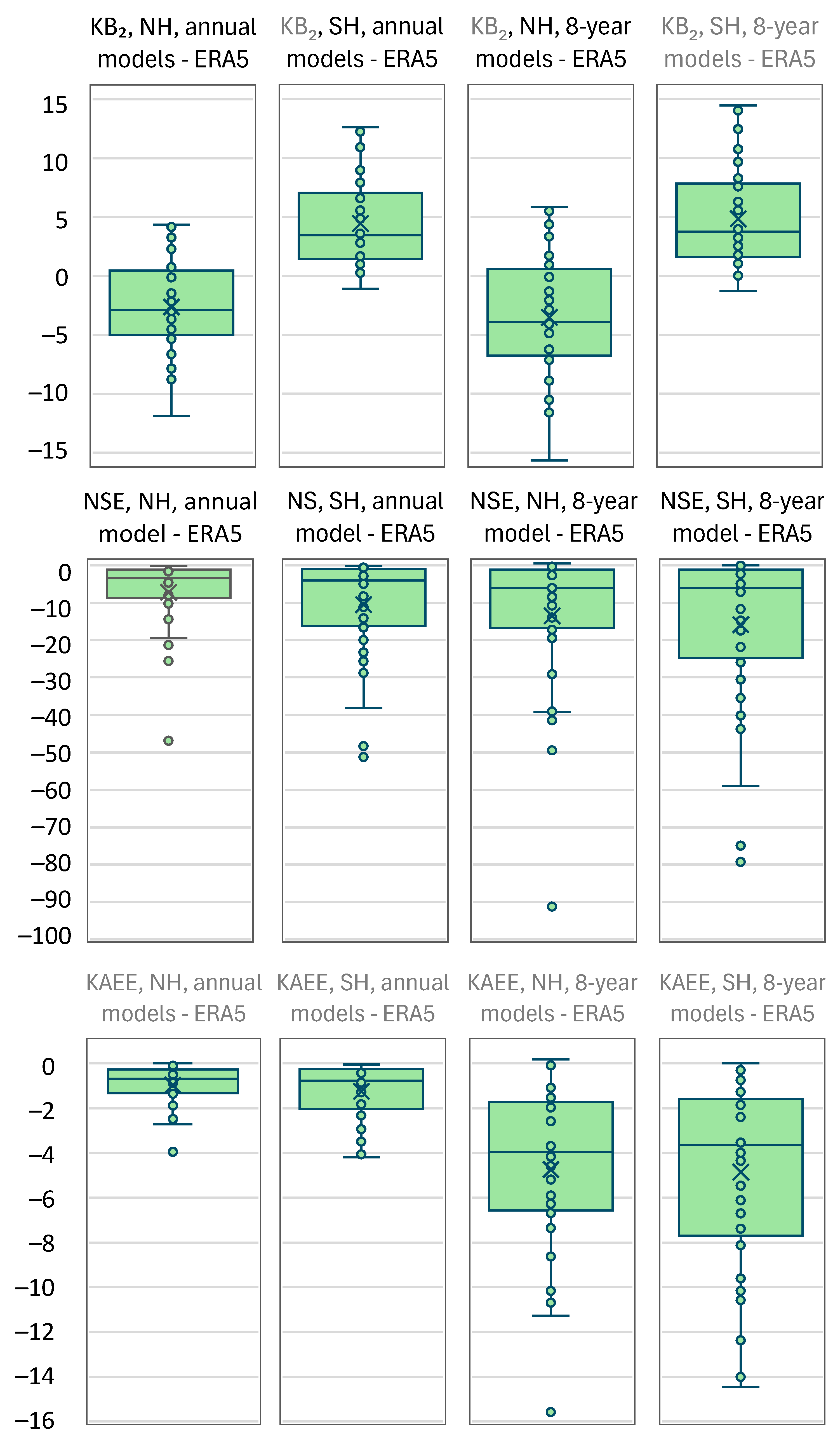
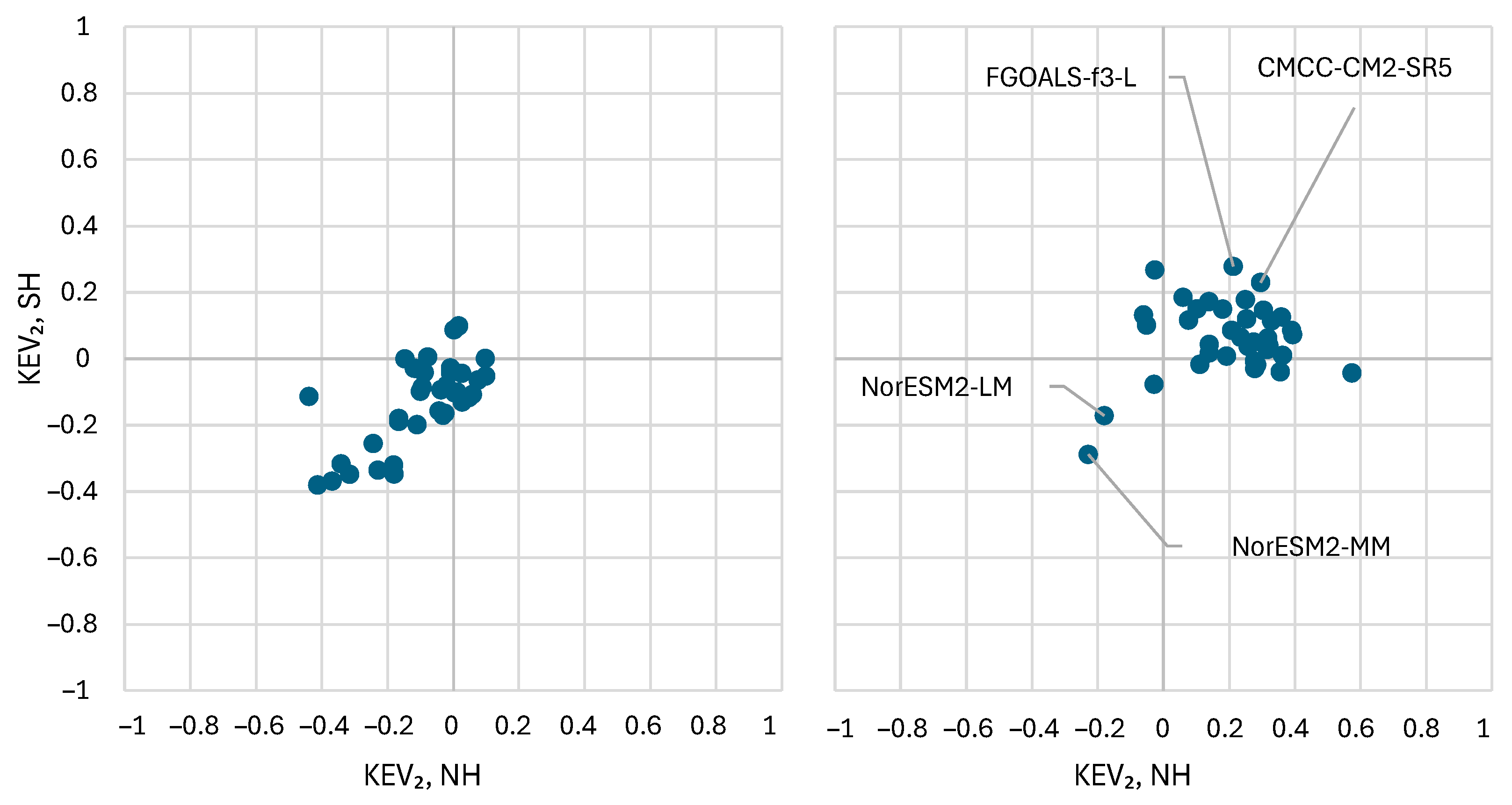
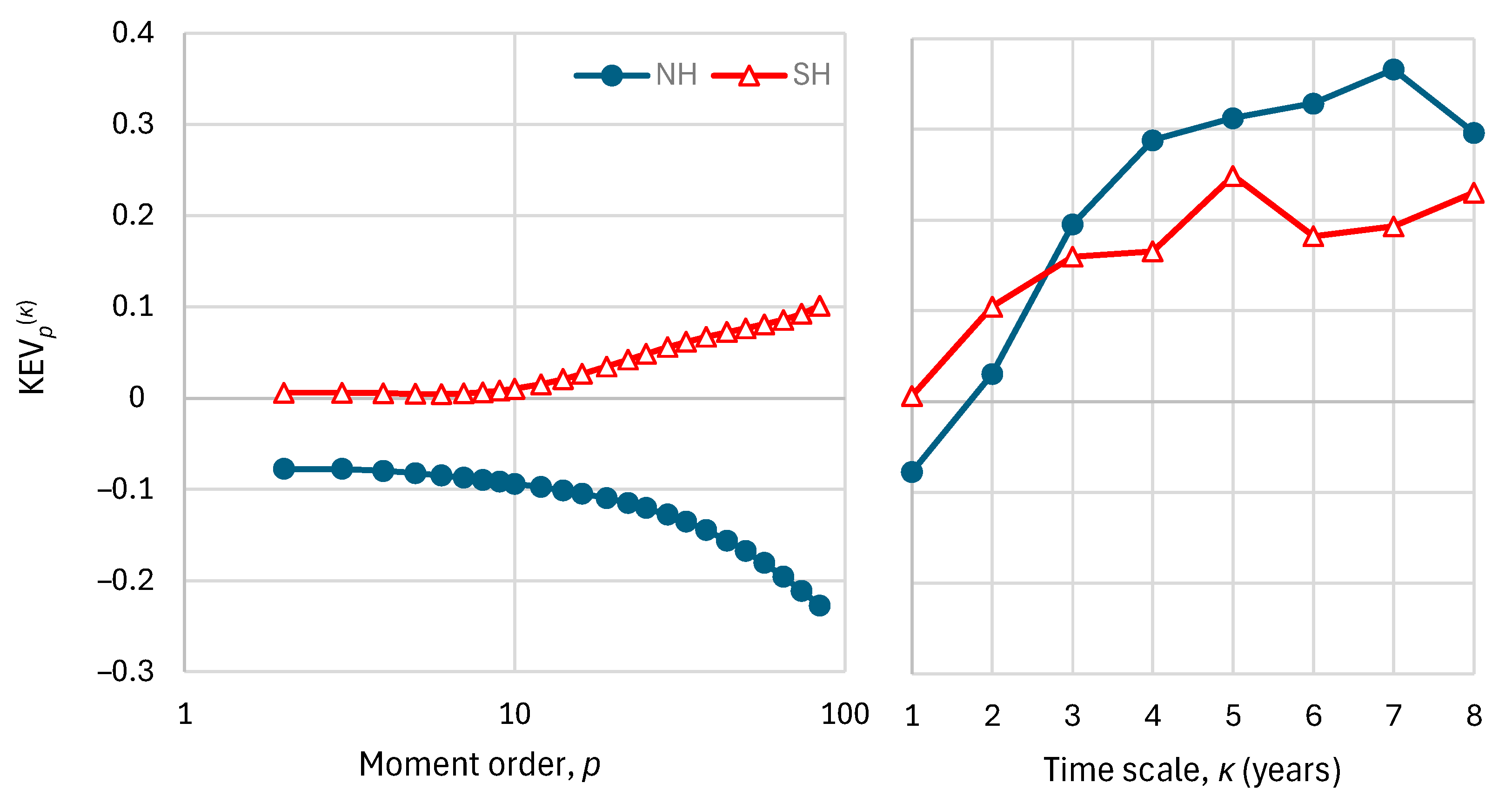


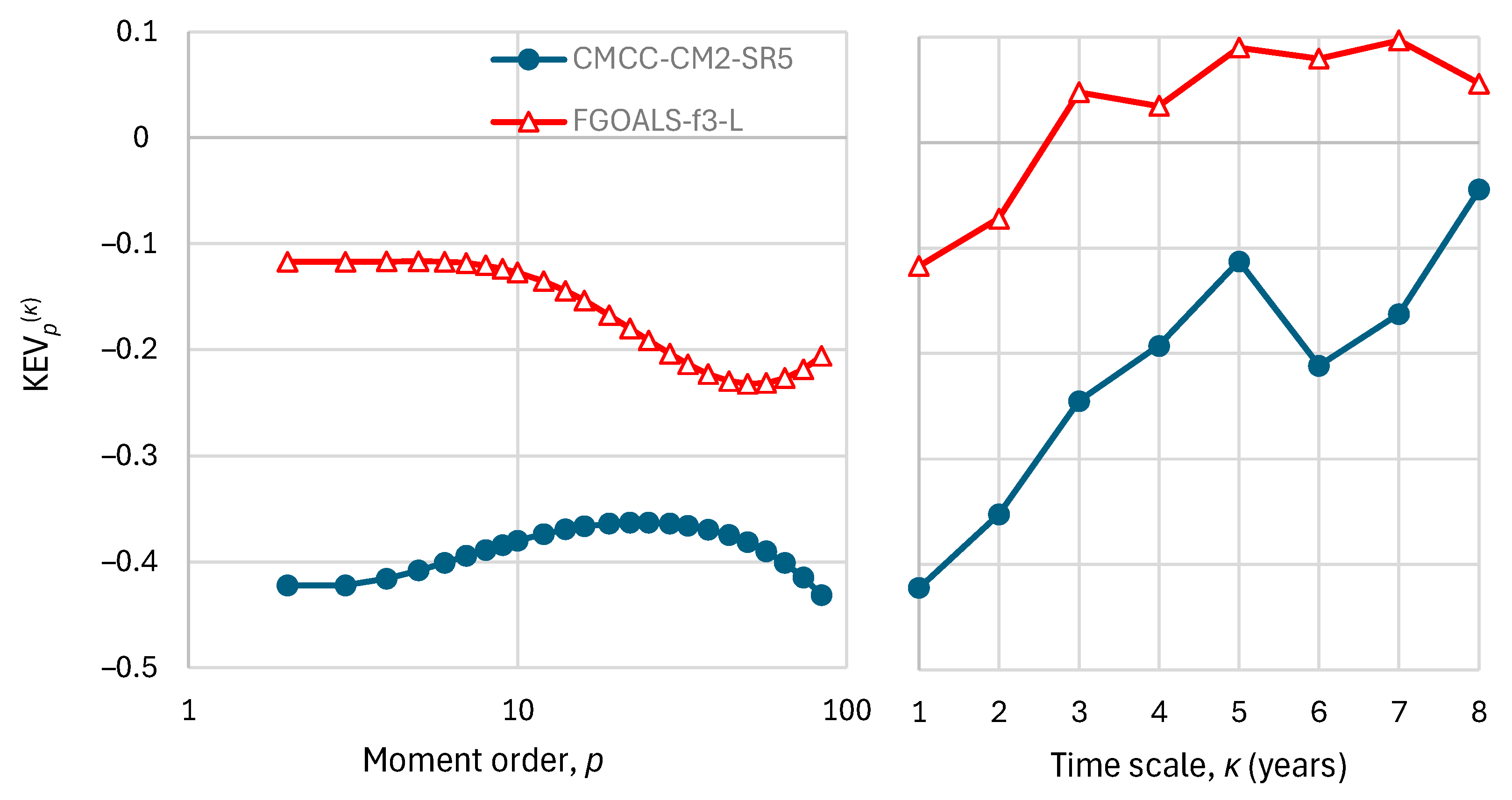
| # | Euclidean Distance | Logarithmic Distance | λ Distance for λ = 1 | |
|---|---|---|---|---|
| 1 | = 0 = 0.1 | 0.1 − 0 = 0.1 | ln 0.1 − ln 0 = ∞ | ln 1.1 − ln 1 = 0.10 |
| 2 | = 0.1 = 0.2 | 0.2 − 0.1 = 0.1 | ln 0.2 − ln 0.1 = 0.69 | ln 1.2 − ln 1.1 = 0.09 |
| 3 | = 100 = 100.1 | 100.1 − 100 = 0.1 | ln 100.1 − ln 100 = 0.001 | ln 101.1 − ln 101 = 0.001 |
| 4 | = 100 = 110 | 110 − 100 = 10 | ln 110 − ln 100 = 0.10 | ln 111 − ln 101 = 0.09 |
| 5 | = 100 = 200 | 200 − 100 = 100 | ln 200 − ln 100 = 0.69 | ln 201 − ln 101 = 0.69 |
| Site | λ | α | β | r | EV | RB | NSE | KGE | KEV2 | KB2 | AEE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Untransformed | 0.364 | 0.049 | −0.167 | 0.022 | −0.371 | 0.040 | −0.921 | −0.160 | |||
| Log-transformed | 0.571 | 0.299 | −0.179 | 0.277 | 0.398 | 0.165 | −0.315 | 0.136 | |||
| λ-transformed | 0.044 | 0 | 1 | 0.708 | 0.486 | −0.131 | 0.477 | 0.656 | 0.292 | −0.233 | 0.273 |
| λ-transformed | 0.024 | −0.005 | 1.057 | 0.714 | 0.504 | −0.019 | 0.504 | 0.649 | 0.302 | −0.033 | 0.301 |
| # | CMIP6 GCM | # | CMIP6 GCM | # | CMIP6 GCM | # | CMIP6 GCM |
|---|---|---|---|---|---|---|---|
| 1 | ACCESS-CM2 | 11 | CIESM | 21 | GFDL-CM4 | 31 | MPI-ESM1-2-HR |
| 2 | ACCESS-ESM1-5 | 12 | CMCC-CM2-SR5 | 22 | GFDL-ESM4 | 32 | MPI-ESM1-2-LR |
| 3 | AWI-CM-1-1-MR | 13 | CNRM-CM6-1 f2 | 23 | GISS-E2-1-G-p3 | 33 | MRI-ESM2-0 |
| 4 | BCC-CSM2-MR | 14 | CNRM-CM6-1-HR f2 | 24 | HadGEM3-GC31-LL f3 | 34 | NESM3 |
| 5 | CAMS-CSM1-0 | 15 | CNRM-ESM2-1-f2 | 25 | INM-CM4-8 | 35 | NorESM2-LM |
| 6 | CanESM5 p2 | 16 | EC-Earth3 | 26 | INM-CM5-0 | 36 | NorESM2-MM |
| 7 | CanESM5-CanOE p2 | 17 | EC-Earth3-Veg | 27 | IPSL-CM6A-LR | 37 | UKESM1-0-LL f2 |
| 8 | CanESM5-p1 | 18 | FGOALS-f3-L | 28 | KACE-1-0-G | ||
| 9 | CESM2 | 19 | FGOALS-g3 | 29 | MIROC6 | ||
| 10 | CESM2-WACCM | 20 | FIO-ESM-2-0 | 30 | MIROC-ES2L f2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsoyiannis, D. When Are Models Useful? Revisiting the Quantification of Reality Checks. Water 2025, 17, 264. https://doi.org/10.3390/w17020264
Koutsoyiannis D. When Are Models Useful? Revisiting the Quantification of Reality Checks. Water. 2025; 17(2):264. https://doi.org/10.3390/w17020264
Chicago/Turabian StyleKoutsoyiannis, Demetris. 2025. "When Are Models Useful? Revisiting the Quantification of Reality Checks" Water 17, no. 2: 264. https://doi.org/10.3390/w17020264
APA StyleKoutsoyiannis, D. (2025). When Are Models Useful? Revisiting the Quantification of Reality Checks. Water, 17(2), 264. https://doi.org/10.3390/w17020264





