The Theoretical Basis of qPCR and ddPCR Copy Number Estimates: A Critical Review and Exposition
Abstract
:1. Introduction
- How does qPCR make it possible to estimate the initial copy number in an environmental sample by monitoring, in real-time, the increasing fluorescence during successive PCR cycles, using additional information derived from a standard curve?
- How does ddPCR make it possible to estimate the initial copy number in a sample by determining the proportion of droplets that do not fluoresce above background at the reaction endpoint, without requiring a standard curve?
2. Real-Time Quantitative PCR
2.1. A Brief Overview of qPCR
2.2. Basic Equations of the qPCR Process
2.2.1. Number of Target Sequence Copies
- Denaturation of DNA at 95 °C;
- Annealing of target-specific forward and reverse primers and probes to the target sequence at 50 °C;
- Extension of primers by DNA polymerase and concomitant cleavage of probes at 72 °C to yield free reporters that fluoresce when excited with the appropriate wavelength of light.
2.2.2. Number of Free Reporters
2.2.3. Fluorescence
2.3. Adapting the Basic Equations for Use in the Laboratory
2.3.1. Accounting for Background Fluorescence and Well Effects
2.3.2. An Equation for the Threshold Cycle
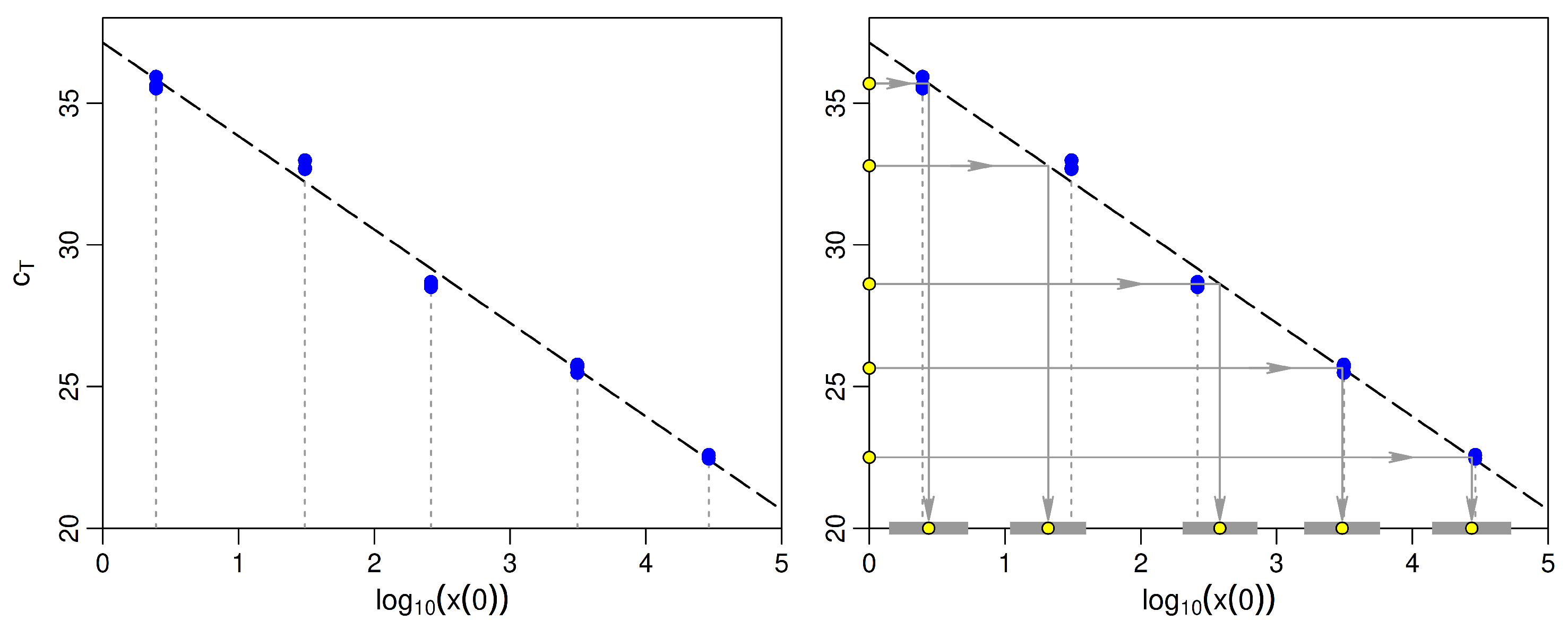
2.3.3. Estimating the Initial Copy Number
2.3.4. Accounting for and Minimizing Sample Interference
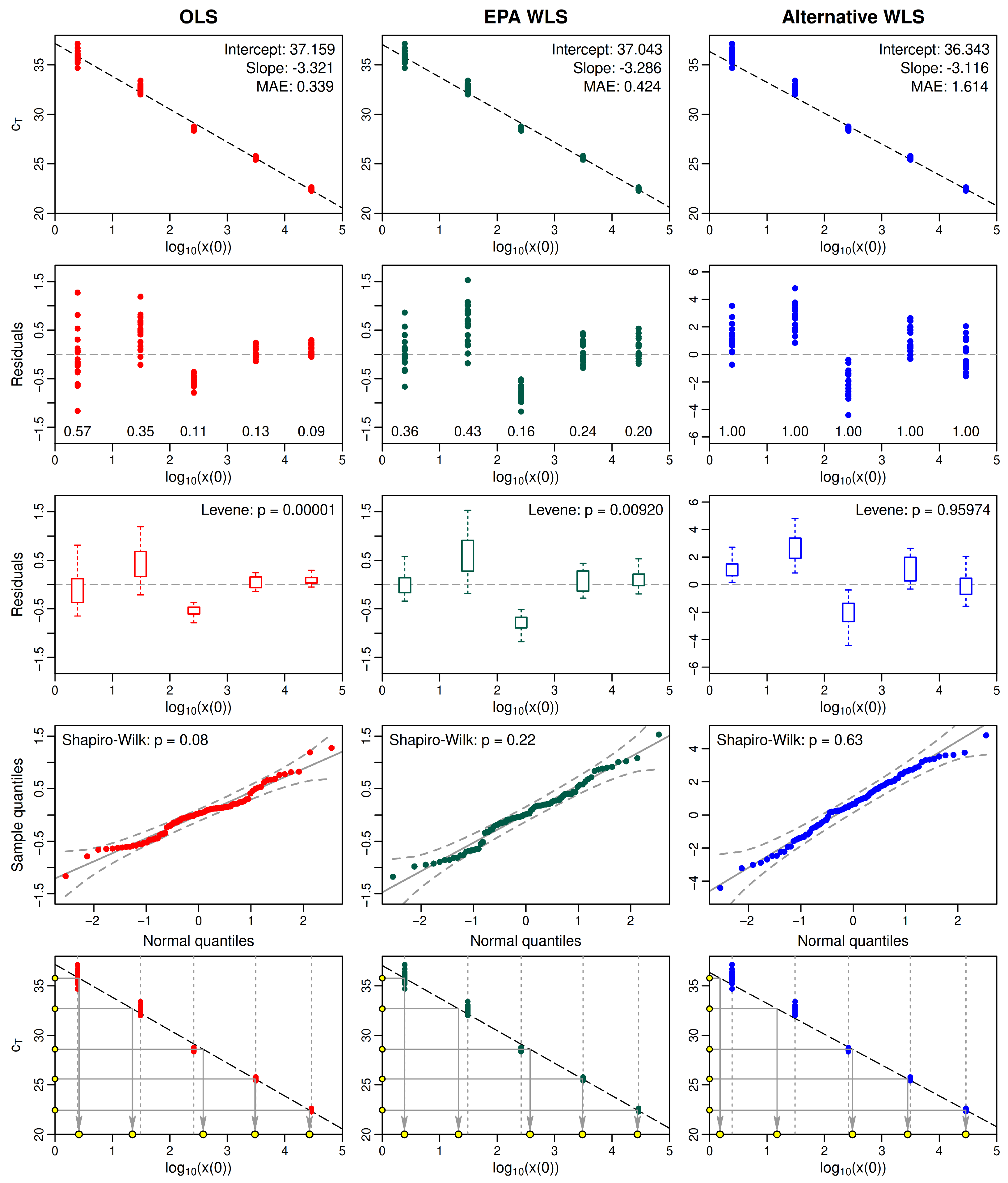
2.4. Fitting the Regression Model to Calibration Data
2.5. Example: Comparing Statistical Properties of Fitted OLS and WLS Standard Curves
- Simple OLS regression;
- WLS regression using the EPA Draft Method C weights;
- WLS regression using alternative weights based on the data.
3. Droplet Digital PCR
3.1. A Brief Overview of ddPCR
3.2. Basic Equations of the ddPCR Process
3.2.1. Estimating the TSC Concentration
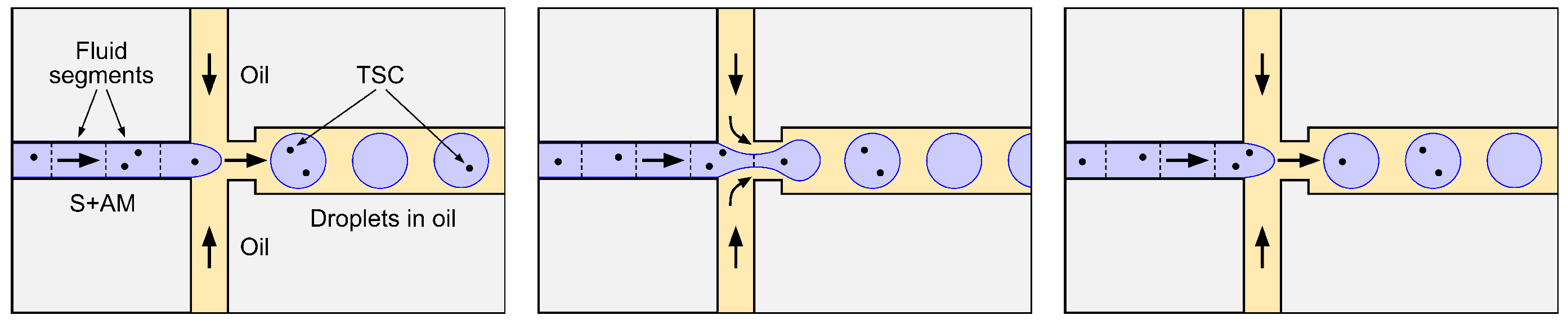
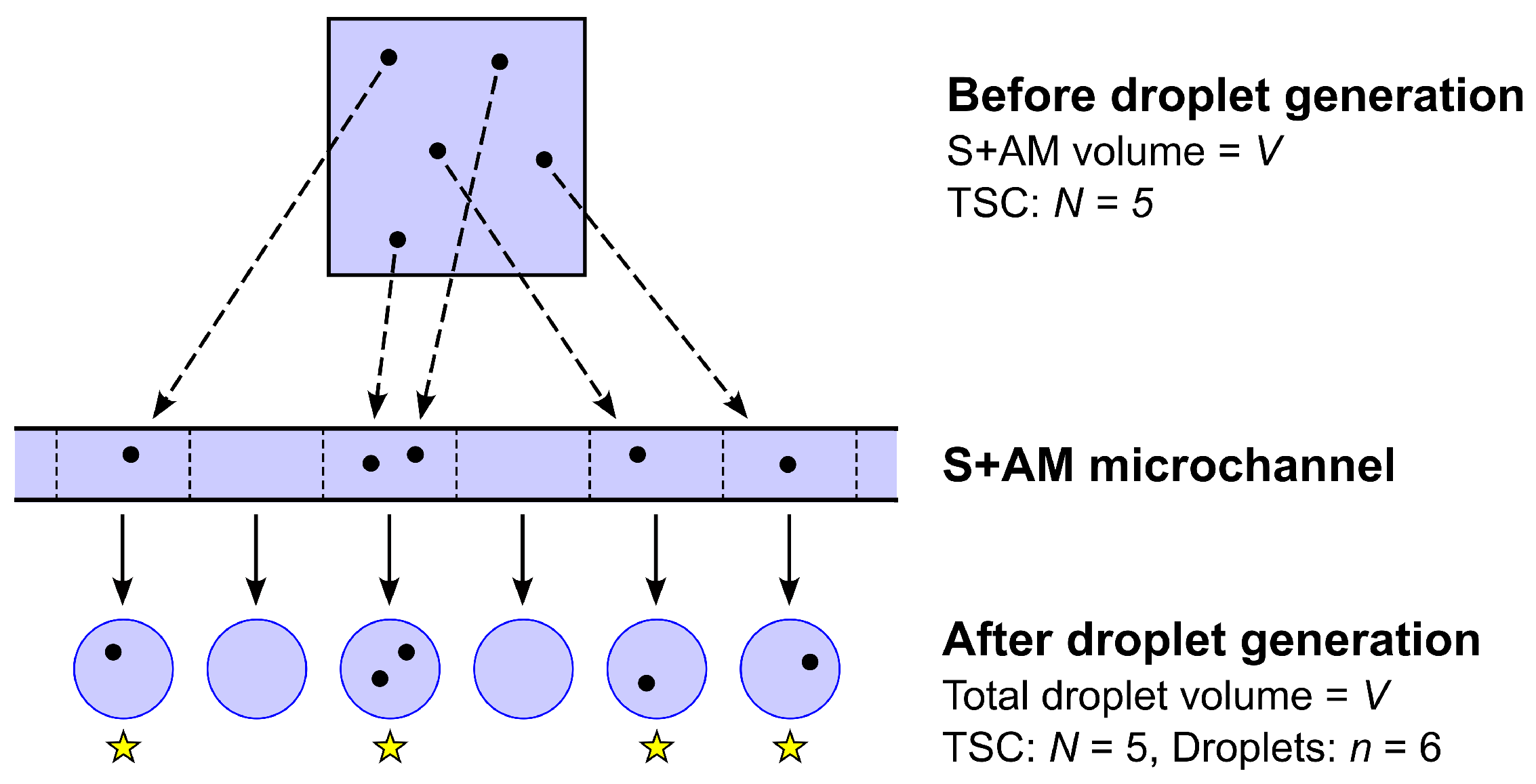
- Before being drawn into the sample microchannel, the S+AM is homogeneous (well mixed) in the sense that any given TSC that was present in the original sample is equally likely to be contained in any subset of the S+AM of fixed volume , where V is the total S+AM volume (≈20 μL).
- The droplet generator partitions the entire S+AM volume V (or nearly so) into a large number n of droplets ( is typically assumed) of variable but similar volumes.
- The process by which the N TSC present in the S+AM are allocated to the n disjoint segments of S+AM flowing through the sample microchannel, and, hence, to the n resulting droplets, is a stochastic partition process equivalent to independent random allocation of N objects (the TSC) to n boxes (the segments or droplets) labeled , where each object has probability of being allocated to box j (Figure 7).
- The probability that any given TSC is allocated to S+AM segment or droplet j is simply the fraction of S+AM volume V that the segment or droplet contains, so that
- In order to arrive at the simple standard formula for TSC concentration C in the S+AM stated in Equation (38), we must make the additional assumption that the volumes of different droplets are similar enough so the approximation,is adequate, in which case, it follows that
- The probability that a randomly chosen droplet from the m scanned and accepted droplets contains no TSC is the same as the probability that a randomly chosen droplet from the full set of n droplets contains no TSC. That is,
- The ratio of TSC to droplets in the m scanned and accepted droplets is the same as the ratio in the full set of n droplets. That is, .
- The mean droplet volume in the m scanned and accepted droplets is the same as the mean droplet volume in the full set of n droplets. That is, .
- It follows from properties 1 and 2 that, to a very good approximation, the ratio of the cumulative number of TSC in the m scanned and accepted droplets to the cumulative volume of those droplets is the same as the ratio of the cumulative number N of TSC in the total number n of droplets (and in the S+AM) to the total volume V of those droplets (and of the S+AM). That is,where C is the TSC concentration in the combined n droplets (and in the S+AM) and is the combined TSC concentration in the m droplets scanned and accepted by the droplet reader.
3.2.2. Estimating the Probability That a Droplet Has No TSC
3.2.3. Estimating the Mean Droplet Volume
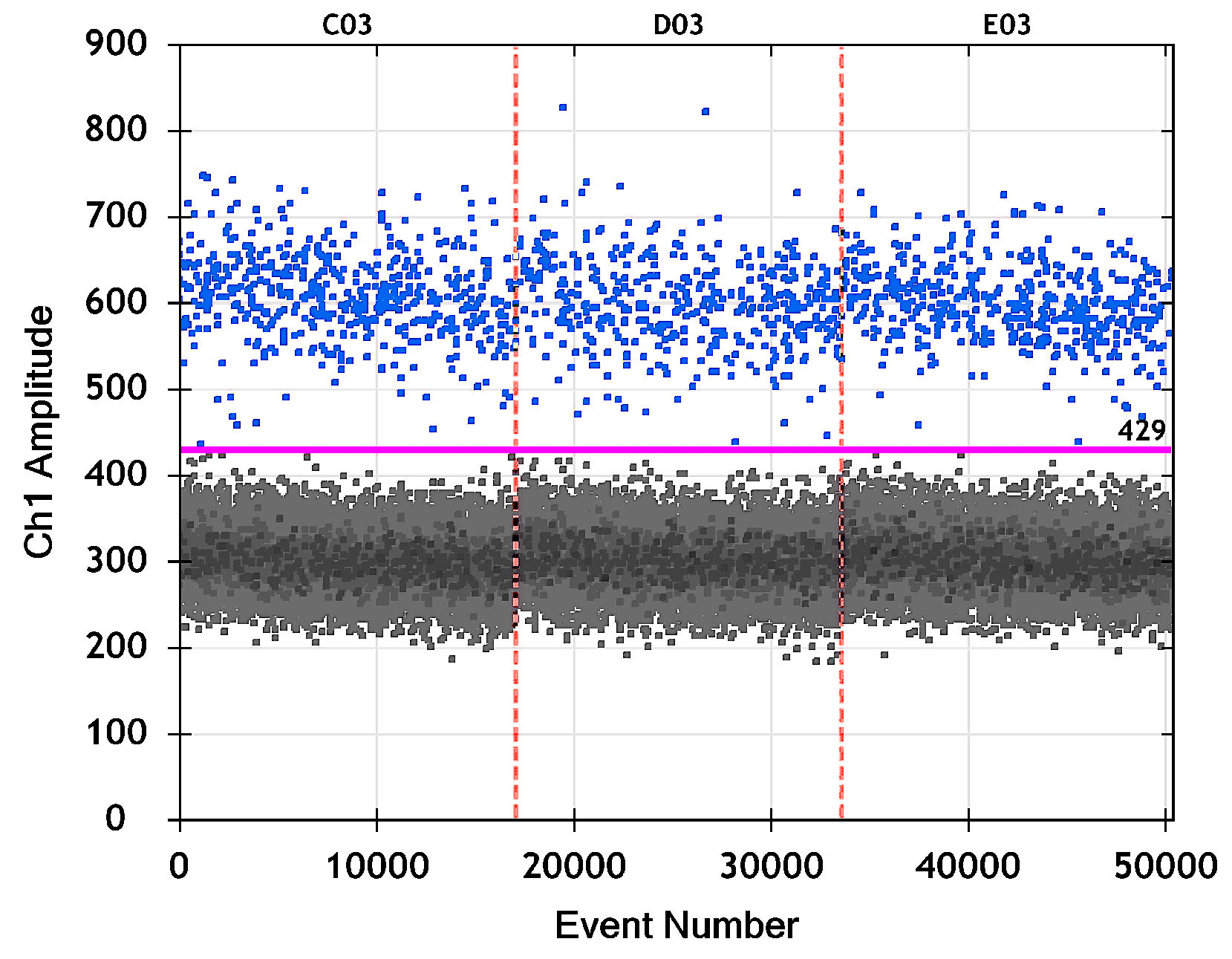
3.2.4. Example: Droplet Classification and Estimating the TSC Concentration
4. Discussion
- Over the range of standards typically required for analysis of water samples, the variance of measured values often differs markedly for different standards, meaning that the values are heteroskedastic. In such cases, the variance homogeneity assumption of classical OLS regression is not tenable.
- One way to address heteroskedasticity is by employing WLS regression. However, any choice of weights must be carefully assessed to ensure it succeeds in homogenizing the variance in residuals.
- Even if weights can be found so that WLS regression successfully homogenizes the variance of residuals, the resulting intercept and slope parameters may exaggerate errors in predicted sample copy numbers at low concentrations, due to heavier weighting of residuals for high concentrations, where values typically are less variable.
5. Conclusions
- The theoretical basis of mathematical and statistical methods commonly used for estimating target sequence copy numbers and concentrations with qPCR and ddPCR is sound.
- The reliance of qPCR on a standard curve creates both complications and uncertainties in fitting and assessing the standard curve, because the calibration data, typically, are heteroskedastic.
- Compared to ddPCR, the method for estimating copy numbers and concentrations with qPCR is more sensitive to sample properties that interfere with fluorescence intensity or reduce amplification efficiency, making the use of effective methods to reduce interference particularly important.
- Estimating copy numbers and concentrations with ddPCR does not rely on a standard curve and, therefore, avoids statistical complications and uncertainties regarding the proper fitting and assessment of standard curves when the calibration data are heteroskedastic.
- The accuracy of ddPCR copy number and concentration estimates is sensitive to the mean droplet volume, which differs meaningfully for different combinations of droplet generator and master mix. Therefore, the mean droplet volume should be determined empirically for the particular combination of droplet generator and master mix used in a given analysis instead of relying on a rough universal estimate (e.g., one coded into software supplied by the instrument manufacturer).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
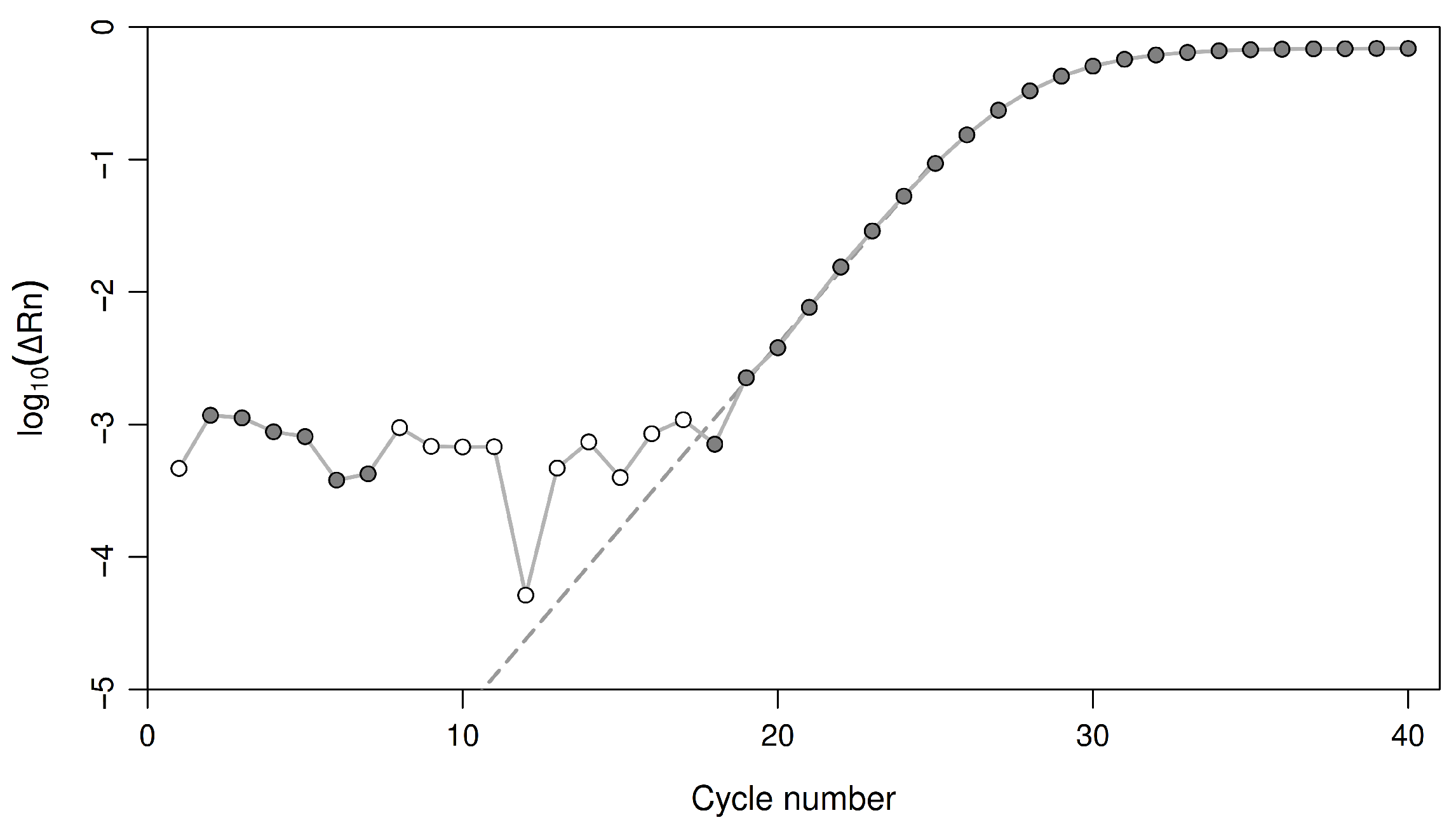
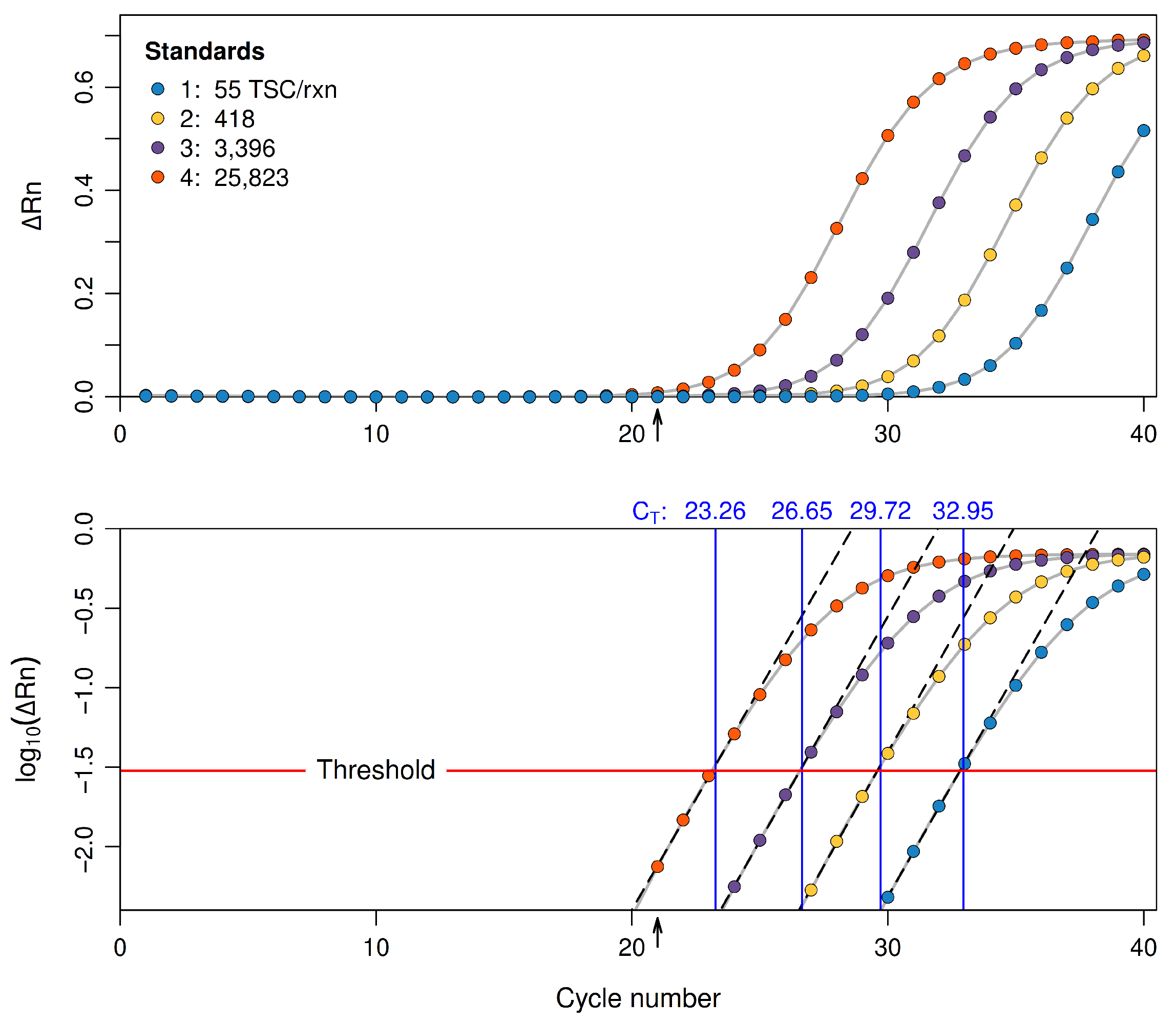
Appendix A. Example of a qPCR Workflow
Appendix B. Justification of an Approximation
Appendix C. Example of a ddPCR Workflow
Appendix D. Justification of an Upper Bound Based on Chebychev’s Inequality
References
- Kleppe, K.; Ohtsuka, E.; Kleppe, R.; Molineux, I.; Khorana, H. Studies on polynucleotides: XCVI. Repair replication of short synthetic DNA’s as catalyzed by DNA polymerases. J. Mol. Biol. 1971, 56, 341–361. [Google Scholar] [CrossRef] [PubMed]
- Saiki, R.K.; Scharf, S.; Faloona, F.; Mullis, K.B.; Horn, G.T.; Erlich, H.A.; Arnheim, N. Enzymatic amplification of β-globin genomic sequences and restriction site analysis for diagnosis of sickle cell anemia. Science 1985, 230, 1350–1354. [Google Scholar] [CrossRef] [PubMed]
- Mullis, K.; Faloona, F.; Scharf, S.; Saiki, R.; Horn, G.; Erlich, H. Specific enzymatic amplification of DNA in vitro: The polymerase chain reaction. In Proceedings of the Cold Spring Harbor Symposia on Quantitative Biology; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 1986; Volume 51, pp. 263–273. [Google Scholar]
- Mullis, K.B.; Faloona, F.A. Specific synthesis of DNA in vitro via a polymerase-catalyzed chain reaction. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 1987; Volume 155, pp. 335–350. [Google Scholar]
- Shanks, O.C.; White, K.; Kelty, C.A.; Hayes, S.; Sivaganesan, M.; Jenkins, M.; Varma, M.; Haugland, R.A. Performance assessment PCR-based assays targeting Bacteroidales genetic markers of bovine fecal pollution. Appl. Environ. Microbiol. 2010, 76, 1359–1366. [Google Scholar] [CrossRef] [PubMed]
- Shanks, O.C.; Kelty, C.A.; Peed, L.; Sivaganesan, M.; Mooney, T.; Jenkins, M. Age-related shifts in the density and distribution of genetic marker water quality indicators in cow and calf feces. Appl. Environ. Microbiol. 2014, 80, 1588–1594. [Google Scholar] [CrossRef]
- USEPA. Recreational Water Quality Criteria; Technical Report 820-F-12-058; U.S. Environmental Protection Agency: Washington, DC, USA, 2012.
- Higuchi, R.; Fockler, C.; Dollinger, G.; Watson, R. Kinetic PCR analysis: Real-time monitoring of DNA amplification reactions. Bio/technology 1993, 11, 1026–1030. [Google Scholar] [CrossRef]
- Basu, A.S. Digital assays part I: Partitioning statistics and digital PCR. SLAS Technol. Transl. Life Sci. Innov. 2017, 22, 369–386. [Google Scholar] [CrossRef]
- Sykes, P.; Neoh, S.; Brisco, M.; Hughes, E.; Condon, J.; Morley, A. Quantitation of targets for PCR by use of limiting dilution. Biotechniques 1992, 13, 444–449. [Google Scholar]
- Vogelstein, B.; Kinzler, K.W. Digital PCR. Proc. Natl. Acad. Sci. USA 1999, 96, 9236–9241. [Google Scholar] [CrossRef]
- Burns, M.A.; Mastrangelo, C.H.; Sammarco, T.S.; Man, F.P.; Webster, J.R.; Johnsons, B.; Foerster, B.; Jones, D.; Fields, Y.; Kaiser, A.R.; et al. Microfabricated structures for integrated DNA analysis. Proc. Natl. Acad. Sci. USA 1996, 93, 5556–5561. [Google Scholar] [CrossRef]
- Burns, M.A.; Johnson, B.N.; Brahmasandra, S.N.; Handique, K.; Webster, J.R.; Krishnan, M.; Sammarco, T.S.; Man, P.M.; Jones, D.; Heldsinger, D.; et al. An integrated nanoliter DNA analysis device. Science 1998, 282, 484–487. [Google Scholar] [CrossRef]
- Ferrance, J.P.; Giordano, B.; Landers, J.P. Toward effective PCR-based amplification of DNA on microfabricated chips. In Capillary Electrophoresis of Nucleic Acids: Volume II: Practical Applications of Capillary Electrophoresis; Humana Press: Totowa, NJ, USA, 2001; pp. 191–204. [Google Scholar]
- Hindson, B.J.; Ness, K.D.; Masquelier, D.A.; Belgrader, P.; Heredia, N.J.; Makarewicz, A.J.; Bright, I.J.; Lucero, M.Y.; Hiddessen, A.L.; Legler, T.C.; et al. High-throughput droplet digital PCR system for absolute quantitation of DNA copy number. Anal. Chem. 2011, 83, 8604–8610. [Google Scholar] [CrossRef] [PubMed]
- Sekar, R.; Jin, X.; Liu, S.; Lu, J.; Shen, J.; Zhou, Y.; Gong, Z.; Feng, X.; Guo, S.; Li, W. Fecal contamination and high nutrient levels pollute the watersheds of Wujiang, China. Water 2021, 13, 457. [Google Scholar] [CrossRef]
- McNair, J.N.; Lane, M.J.; Hart, J.J.; Porter, A.M.; Briggs, S.; Southwell, B.; Sivy, T.; Szlag, D.C.; Scull, B.T.; Pike, S.; et al. Validity assessment of Michigan’s proposed qPCR threshold value for rapid water-quality monitoring of E. coli contamination. Water Res. 2022, 226, 119235. [Google Scholar] [CrossRef] [PubMed]
- McNair, J.N.; Rediske, R.R.; Hart, J.J.; Jamison, M.N.; Briggs, S. Performance of Colilert-18 and qPCR for monitoring E. coli contamination at freshwater beaches in Michigan. Environments 2025, 12, 21. [Google Scholar] [CrossRef]
- Ballesté, E.; Demeter, K.; Masterson, B.; Timoneda, N.; Sala-Comorera, L.; Meijer, W.G. Implementation and integration of microbial source tracking in a river watershed monitoring plan. Sci. Total Environ. 2020, 736, 139573. [Google Scholar] [CrossRef]
- Cao, Y.; Raith, M.R.; Griffith, J.F. Droplet digital PCR for simultaneous quantification of general and human-associated fecal indicators for water quality assessment. Water Res. 2015, 70, 337–349. [Google Scholar] [CrossRef]
- Frick, C.; Vierheilig, J.; Nadiotis-Tsaka, T.; Ixenmaier, S.; Linke, R.; Reischer, G.H.; Komma, J.; Kirschner, A.K.; Mach, R.L.; Savio, D.; et al. Elucidating fecal pollution patterns in alluvial water resources by linking standard fecal indicator bacteria to river connectivity and genetic microbial source tracking. Water Res. 2020, 184, 116132. [Google Scholar] [CrossRef]
- Flood, M.T.; Hernandez-Suarez, J.S.; Nejadhashemi, A.P.; Martin, S.L.; Hyndman, D.; Rose, J.B. Connecting microbial, nutrient, physiochemical, and land use variables for the evaluation of water quality within mixed use watersheds. Water Res. 2022, 219, 118526. [Google Scholar] [CrossRef]
- Hart, J.J.; Jamison, M.N.; McNair, J.N.; Woznicki, S.A.; Jordan, B.; Rediske, R.R. Using watershed characteristics to enhance fecal source identification. J. Environ. Manag. 2023, 336, 117642. [Google Scholar] [CrossRef]
- Jamison, M.N.; Hart, J.J.; Szlag, D.C. Improving the identification of fecal contamination in recreational water through the standardization and normalization of microbial source tracking. Environ. Sci. Technol. Water 2022, 2, 2305–2311. [Google Scholar] [CrossRef]
- Pendergraph, D.P.; Ranieri, J.; Ermatinger, L.; Baumann, A.; Metcalf, A.L.; DeLuca, T.H.; Church, M.J. Differentiating sources of fecal contamination to wilderness waters using droplet digital PCR and fecal indicator bacteria methods. Wilderness Environ. Med. 2021, 32, 332–339. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, A.; Kelty, C.A.; Sivaganesan, M.; Shanks, O.C.; Dorevitch, S. Fecal pollution source characterization at non-point source impacted beaches under dry and wet weather conditions. Water Res. 2020, 182, 116014. [Google Scholar] [CrossRef] [PubMed]
- Steinbacher, S.; Savio, D.F.; Demeter, K.; Karl, M.; Kandler, W.; Kirschner, A.K.; Reischer, G.H.; Ixenmaier, S.K.; Mayer, R.; Mach, R.L.; et al. Genetic microbial faecal source tracking: Rising technology to support future water quality testing and safety management. Österreichische Wasser-Abfallwirtsch. 2021, 73, 468–481. [Google Scholar] [CrossRef]
- Doi, H.; Takahara, T.; Minamoto, T.; Matsuhashi, S.; Uchii, K.; Yamanaka, H. Droplet digital polymerase chain reaction (PCR) outperforms real-time PCR in the detection of environmental DNA from an invasive fish species. Environ. Sci. Technol. 2015, 49, 5601–5608. [Google Scholar] [CrossRef]
- Doi, H.; Uchii, K.; Takahara, T.; Matsuhashi, S.; Yamanaka, H.; Minamoto, T. Use of droplet digital PCR for estimation of fish abundance and biomass in environmental DNA surveys. PLoS ONE 2015, 10, e0122763. [Google Scholar] [CrossRef]
- Te, S.H.; Chen, E.Y.; Gin, K.Y.H. Comparison of quantitative PCR and droplet digital PCR multiplex assays for two genera of bloom-forming cyanobacteria, Cylindrospermopsis and Microcystis. Appl. Environ. Microbiol. 2015, 81, 5203–5211. [Google Scholar] [CrossRef]
- Flood, M.T.; D’Souza, N.; Rose, J.B.; Aw, T.G. Methods evaluation for rapid concentration and quantification of SARS-CoV-2 in raw wastewater using droplet digital and quantitative RT-PCR. Food Environ. Virol. 2021, 13, 303–315. [Google Scholar] [CrossRef]
- Schmitz, B.W.; Innes, G.K.; Prasek, S.M.; Betancourt, W.Q.; Stark, E.R.; Foster, A.R.; Abraham, A.G.; Gerba, C.P.; Pepper, I.L. Enumerating asymptomatic COVID-19 cases and estimating SARS-CoV-2 fecal shedding rates via wastewater-based epidemiology. Sci. Total Environ. 2021, 801, 149794. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Lin, Y.; Zhang, L.; Chen, J.; Li, P.; Liu, W.; Wang, Y.; Yao, C.; Yang, K. Technical framework for wastewater-based epidemiology of SARS-CoV-2. Sci. Total Environ. 2021, 791, 148271. [Google Scholar] [CrossRef]
- Ciesielski, M.; Blackwood, D.; Clerkin, T.; Gonzalez, R.; Thompson, H.; Larson, A.; Noble, R. Assessing sensitivity and reproducibility of RT-ddPCR and RT-qPCR for the quantification of SARS-CoV-2 in wastewater. J. Virol. Methods 2021, 297, 114230. [Google Scholar] [CrossRef]
- Hart, J.J.; Jamison, M.N.; McNair, J.N.; Szlag, D.C. Frequency and degradation of SARS-CoV-2 markers N1, N2, and E in sewage. J. Water Health 2023, 21, 514–524. [Google Scholar] [CrossRef] [PubMed]
- Raeymaekers, L. Basic principles of quantitative PCR. Mol. Biotechnol. 2000, 15, 115–122. [Google Scholar] [CrossRef] [PubMed]
- Rutledge, R.; Cote, C. Mathematics of quantitative kinetic PCR and the application of standard curves. Nucleic Acids Res. 2003, 31, e93. [Google Scholar] [CrossRef] [PubMed]
- Stephenson, F.H. Calculations for Molecular Biology and Biotechnology; Academic Press: New York, NY, USA, 2016. [Google Scholar]
- Thermo-Fisher. Real-Time PCR Handbook; Technical report; Thermo Fisher Scientific Inc.: Waltham, MA, USA, 2016. [Google Scholar]
- Bio-Rad. Droplet Digital PCR Applications Guide; Technical Report Bulletin 6407 B; Bio-Rad Laboratories, Inc.: Hercules, CA, USA, 2018. [Google Scholar]
- Vadde, K.K.; Moghadam, S.V.; Jafarzadeh, A.; Matta, A.; Phan, D.C.; Johnson, D.; Kapoor, V. Precipitation impacts the physicochemical water quality and abundance of microbial source tracking markers in urban Texas watersheds. PLoS Water 2024, 3, e0000209. [Google Scholar] [CrossRef]
- Kaltenboeck, B.; Wang, C. Advances in real-time PCR: Application to clinical laboratory diagnostics. Adv. Clin. Chem. 2005, 40, 219. [Google Scholar]
- Arya, M.; Shergill, I.S.; Williamson, M.; Gommersall, L.; Arya, N.; Patel, H.R. Basic principles of real-time quantitative PCR. Expert Rev. Mol. Diagn. 2005, 5, 209–219. [Google Scholar] [CrossRef]
- Aw, T.G.; Sivaganesan, M.; Briggs, S.; Dreelin, E.; Aslan, A.; Dorevitch, S.; Shrestha, A.; Isaacs, N.; Kinzelman, J.; Kleinheinz, G.; et al. Evaluation of multiple laboratory performance and variability in analysis of recreational freshwaters by a rapid Escherichia coli qPCR method (Draft Method C). Water Res. 2019, 156, 465–474. [Google Scholar] [CrossRef]
- Sivaganesan, M.; Aw, T.G.; Briggs, S.; Dreelin, E.; Aslan, A.; Dorevitch, S.; Shrestha, A.; Isaacs, N.; Kinzelman, J.; Kleinheinz, G.; et al. Standardized data quality acceptance criteria for a rapid Escherichia coli qPCR method (Draft Method C) for water quality monitoring at recreational beaches. Water Res. 2019, 156, 456–464. [Google Scholar] [CrossRef]
- Thermo-Fisher. Application Note: Understanding Ct; Technical report; Thermo Fisher Scientific Inc.: Waltham, MA, USA, 2016. [Google Scholar]
- Thermo-Fisher. Application Note: ROX Passive Reference Dye for Troubleshooting Real-Time PCR; Technical report; Thermo Fisher Scientific Inc.: Waltham, MA, USA, 2015. [Google Scholar]
- Bio-Rad. Real-Time PCR Applications Guide; Technical Report Bulletin 5279; Bio-Rad Laboratories, Inc.: Hercules, CA, USA, 2006. [Google Scholar]
- Parker, P.A.; Vining, G.G.; Wilson, S.R.; Szarka, J.L., III; Johnson, N.G. The prediction properties of classical and inverse regression for the simple linear calibration problem. J. Qual. Technol. 2010, 42, 332–347. [Google Scholar] [CrossRef]
- Nappier, S.P.; Ichida, A.; Jaglo, K.; Haugland, R.; Jones, K.R. Advancements in mitigating interference in quantitative polymerase chain reaction (qPCR) for microbial water quality monitoring. Sci. Total Environ. 2019, 671, 732–740. [Google Scholar] [CrossRef]
- Sidstedt, M.; Rådström, P.; Hedman, J. PCR inhibition in qPCR, dPCR and MPS—Mechanisms and solutions. Anal. Bioanal. Chem. 2020, 412, 2009–2023. [Google Scholar] [CrossRef] [PubMed]
- Sivaganesan, M.; Varma, M.; Siefring, S.; Haugland, R. Quantification of plasmid DNA standards for US EPA fecal indicator bacteria qPCR methods by droplet digital PCR analysis. J. Microbiol. Methods 2018, 152, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Corbisier, P.; Pinheiro, L.; Mazoua, S.; Kortekaas, A.M.; Chung, P.Y.J.; Gerganova, T.; Roebben, G.; Emons, H.; Emslie, K. DNA copy number concentration measured by digital and droplet digital quantitative PCR using certified reference materials. Anal. Bioanal. Chem. 2015, 407, 1831–1840. [Google Scholar] [CrossRef]
- Dagata, J.A.; Farkas, N.; Kramer, J. Method for measuring the volume of nominally 100 μm diameter spherical water-in-oil emulsion droplets. NIST Spec. Publ. 2016, 260, 260-184. [Google Scholar]
- Košir, A.B.; Divieto, C.; Pavšič, J.; Pavarelli, S.; Dobnik, D.; Dreo, T.; Bellotti, R.; Sassi, M.P.; Žel, J. Droplet volume variability as a critical factor for accuracy of absolute quantification using droplet digital PCR. Anal. Bioanal. Chem. 2017, 409, 6689–6697. [Google Scholar] [CrossRef] [PubMed]
- Ryan, T. Modern Regression Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Kokkoris, V.; Vukicevich, E.; Richards, A.; Thomsen, C.; Hart, M.M. Challenges using droplet digital PCR for environmental samples. Appl. Microbiol. 2021, 1, 74–88. [Google Scholar] [CrossRef]
- Pinheiro, L.B.; Coleman, V.A.; Hindson, C.M.; Herrmann, J.; Hindson, B.J.; Bhat, S.; Emslie, K.R. Evaluation of a droplet digital polymerase chain reaction format for DNA copy number quantification. Anal. Chem. 2012, 84, 1003–1011. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Nevzorov, V.B. A Primer on Statistical Distributions; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Forbes, C.; Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Brown, L.D.; Cai, T.T.; DasGupta, A. Interval estimation for a binomial proportion. Stat. Sci. 2001, 16, 101–133. [Google Scholar] [CrossRef]
- Agresti, A.; Coull, B.A. Approximate is better than “exact” for interval estimation of binomial proportions. Am. Stat. 1998, 52, 119–126. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1994. [Google Scholar]
- Dorai-Raj, S. binom: Binomial Confidence Intervals for Several Parameterizations; R Package Version 1.1-1.1. 2022. [Google Scholar]
- Canty, A.; Ripley, B. boot: Bootstrap R (S-Plus) Functions; R Package Version 1.1-1.1. 2024. [Google Scholar]
- Tibshirani, R.; Leisch, F. bootstrap: Functions for the Book “An Introduction to the Bootstrap”; R Package Version 2019.6. 2019. [Google Scholar]
- Dingle, T.C.; Sedlak, R.H.; Cook, L.; Jerome, K.R. Tolerance of droplet-digital PCR vs real-time quantitative PCR to inhibitory substances. Clin. Chem. 2013, 59, 1670–1672. [Google Scholar] [CrossRef]
- Verhaegen, B.; De Reu, K.; De Zutter, L.; Verstraete, K.; Heyndrickx, M.; Van Coillie, E. Comparison of droplet digital PCR and qPCR for the quantification of Shiga toxin-producing Escherichia coli in bovine feces. Toxins 2016, 8, 157. [Google Scholar] [CrossRef] [PubMed]
- Sze, M.A.; Abbasi, M.; Hogg, J.C.; Sin, D.D. A comparison between droplet digital and quantitative PCR in the analysis of bacterial 16S load in lung tissue samples from control and COPD GOLD 2. PLoS ONE 2014, 9, e110351. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.H.; Kim, E.; Yang, S.M.; Kim, D.S.; Suh, S.M.; Lee, G.Y.; Kim, H.Y. Comparison of real-time PCR and droplet digital PCR for the quantitative detection of Lactiplantibacillus plantarum subsp. plantarum. Foods 2022, 11, 1331. [Google Scholar] [CrossRef]
- Chandler, D. Redefining relativity: Quantitative PCR at low template concentrations for industrial and environmental microbiology. J. Ind. Microbiol. Biotechnol. 1998, 21, 128–140. [Google Scholar] [CrossRef]
- Lane, M.J.; McNair, J.N.; Rediske, R.R.; Briggs, S.; Sivaganesan, M.; Haugland, R. Simplified analysis of measurement data from a rapid E. coli qPCR method (EPA Draft Method C) using a standardized Excel workbook. Water 2020, 12, 775. [Google Scholar] [CrossRef] [PubMed]
- Çinlar, E. Introduction to Stochastic Processes; Dover Publications, Inc.: Mineola, NY, USA, 2013. [Google Scholar]

| Symbol | Dimension | Meaning |
|---|---|---|
| – | Proportional amplification efficiency, | |
| – | Amplification factor, | |
| J | Fluorescence intensity per free reporter | |
| – | Well effect factor | |
| J | Background fluorescence intensity | |
| J | Passive dye fluorescence intensity | |
| – | Threshold level of | |
| c | – | DAE cycle number |
| – | Threshold cycle number | |
| – | Number of TSC per reaction at the end of cycle c | |
| – | Initial number of TSC per reaction, | |
| – | Number of free reporters per reaction | |
| J | Notional S+AM fluorescence with no background or well effect | |
| J | Notional S+AM fluorescence with background but no well effect | |
| J | Measured S+AM fluorescence with background and well effect | |
| J | Measured reference dye fluorescence with well effect | |
| – | Normalized S+AM fluorescence with well effect removed | |
| – * | Normalized S+AM fluorescence with background and well effects removed | |
| – | Random variable representing the value of in sample i | |
| – | Measured value of in sample i | |
| – | intercept of a linear standard curve | |
| – | Slope of a linear standard curve | |
| – | Random error in the measured value of in sample i | |
| – | Log10-transformed value of in sample i | |
| – | Weight applied to the residual for sample i in WLS regression | |
| – | Sum of squared residuals, with or without weighting | |
| – | Re-scaled random variable in WLS regression | |
| – | Re-scaled measured value in WLS regression | |
| – | Re-scaled measured value in WLS regression. |
| New | Predicted | 95% LCL | 95% UCL | Standard |
|---|---|---|---|---|
| 35.69 | 0.44 | 0.15 | 0.73 | 0.39 |
| 32.79 | 1.32 | 1.04 | 1.60 | 1.49 |
| 28.62 | 2.58 | 2.31 | 2.86 | 2.42 |
| 25.65 | 3.48 | 3.20 | 3.76 | 3.49 |
| 22.50 | 4.44 | 4.15 | 4.73 | 4.46 |
| Symbol | Dimension | Meaning |
|---|---|---|
| L3 | Volume of droplet j | |
| L3 | Average droplet volume | |
| V | L3 | S+AM volume |
| n | – | Number of droplets |
| N | – | Number of TSC |
| – | Probability that any given TSC in S+AM is allocated to droplet j | |
| – | Average of over all droplets | |
| – | Random variable representing number of TSC allocated to droplet j | |
| – | Realized number of TSC allocated to droplet j | |
| – | Probability that any given droplet contains no TSC | |
| m | – | Total number of droplets counted by the droplet reader |
| – | Number of negative droplets counted by the droplet reader | |
| C | L−3 | Estimated number of TSC per unit volume of S+AM. |
| Well | m | C | CI Type | LCL | UCL | C LCL | C UCL | ||
|---|---|---|---|---|---|---|---|---|---|
| C03 | 16,563 | 17,073 | 0.97013 | 35.7 | Wilson | 0.96747 | 0.97258 | 32.7 | 38.9 |
| Agresti–Coull | 0.96746 | 0.97258 | 32.7 | 38.9 | |||||
| Wald | 0.96757 | 0.97268 | 32.6 | 38.8 | |||||
| Percentile (boot) | — | — | 32.7 | 38.7 | |||||
| (boot) | — | — | 32.8 | 38.9 | |||||
| QuantaSoft | — | — | 34.1 | 38.8 | |||||
| D03 | 16,072 | 16,513 | 0.97329 | 31.8 | Wilson | 0.97072 | 0.97564 | 29.0 | 35.0 |
| Agresti–Coull | 0.97072 | 0.97565 | 29.0 | 35.0 | |||||
| Wald | 0.97083 | 0.97575 | 28.9 | 34.8 | |||||
| Percentile (boot) | — | — | 28.8 | 34.9 | |||||
| (boot) | — | — | 28.8 | 34.9 | |||||
| QuantaSoft | — | — | 30.3 | 34.8 | |||||
| E03 | 16,325 | 16,809 | 0.97121 | 34.4 | Wilson | 0.96857 | 0.97363 | 31.4 | 37.6 |
| Agresti–Coull | 0.96857 | 0.97363 | 31.4 | 37.6 | |||||
| Wald | 0.96868 | 0.97373 | 31.3 | 37.4 | |||||
| Percentile (boot) | — | — | 31.3 | 37.4 | |||||
| (boot) | — | — | 31.3 | 37.9 | |||||
| QuantaSoft | — | — | 32.8 | 37.4 |
| Property | Factor | qPCR | ddPCR |
|---|---|---|---|
| Cost | Instrumentation cost | Lower | Higher |
| Per-sample cost | Lower | Higher | |
| Sample turnaround time | Sample preparation and analysis time | Shorter | Longer |
| Calibration | Standard curve required? | Yes | No |
| Other calibration required or advisable? | Yes | Yes | |
| Inhibition | Sensitivity to PCR inhibition | Higher | Lower |
| Limits of quantification | Upper limit of quantification | Higher | Lower |
| Lower limit of quantification | Higher | Lower | |
| Dynamic range | Wider | Narrower | |
| Simplicity | Simplicity of laboratory analysis | Higher | Lower |
| Simplicity of proper data analysis | Lower | Higher | |
| Simplicity of the underlying theory | Lower | Higher |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McNair, J.N.; Frobish, D.; Rediske, R.R.; Hart, J.J.; Jamison, M.N.; Szlag, D.C. The Theoretical Basis of qPCR and ddPCR Copy Number Estimates: A Critical Review and Exposition. Water 2025, 17, 381. https://doi.org/10.3390/w17030381
McNair JN, Frobish D, Rediske RR, Hart JJ, Jamison MN, Szlag DC. The Theoretical Basis of qPCR and ddPCR Copy Number Estimates: A Critical Review and Exposition. Water. 2025; 17(3):381. https://doi.org/10.3390/w17030381
Chicago/Turabian StyleMcNair, James N., Daniel Frobish, Richard R. Rediske, John J. Hart, Megan N. Jamison, and David C. Szlag. 2025. "The Theoretical Basis of qPCR and ddPCR Copy Number Estimates: A Critical Review and Exposition" Water 17, no. 3: 381. https://doi.org/10.3390/w17030381
APA StyleMcNair, J. N., Frobish, D., Rediske, R. R., Hart, J. J., Jamison, M. N., & Szlag, D. C. (2025). The Theoretical Basis of qPCR and ddPCR Copy Number Estimates: A Critical Review and Exposition. Water, 17(3), 381. https://doi.org/10.3390/w17030381






