Next Article in Journal
Comprehensive Assessment of the Jebel Zaghouan Karst Aquifer (Northeastern Tunisia): Availability, Quality, and Vulnerability, in the Context of Overexploitation and Global Change
Next Article in Special Issue
Multi-Scale Debris Flow Warning Technology Combining GNSS and InSAR Technology
Previous Article in Journal
Response of Trichoptera and Oligochaeta Communities to Modifications of Mountain River Channels with Low-Head Barriers
Previous Article in Special Issue
Numerical Simulations of a Permeability Test on Non-Cohesive Soil Under an Increasing Water Level
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 3
10.3390/w17030406
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Case Study of the Debris Flows Event in the Chalk Cliffs Basin, Colorado, USA: Numerical Simulations Based on a Multi-Phase Flow Model

by
Mohammad Wasif Naqvi
†,
Diwakar KC
‡ and
Liangbo Hu
*
Department of Civil and Environmental Engineering, University of Toledo, Toledo, OH 43606, USA
*
Author to whom correspondence should be addressed.
†
Current address: Highway Technology Partners LLC, Turner Fairbank Highway Research Center, 6300 Georgetown Pike, McLean, VA 22101, USA.
‡
Current address: Universal Engineering Sciences (UES), Sharonville, OH 45241, USA.
Water 2025, 17(3), 406; https://doi.org/10.3390/w17030406
Submission received: 31 October 2024 / Revised: 20 January 2025 / Accepted: 27 January 2025 / Published: 1 February 2025
(This article belongs to the Special Issue Flowing Mechanism of Debris Flow and Engineering Mitigation)
Browse Figures
Versions Notes

Abstract

:
Debris flows are among the severe gravity-driven mass phenomena that pose a significant threat to the environment and communities. Recent events and studies in the Chalk Cliffs basin in Colorado suggest that it is very susceptible to debris flow incidents that initiate from surface run-off, which involves significant entrainment of material along the hill slope and channel sediments. The entrainment of material along the flow makes these events destructive, with large travel distances s well as high velocity, flow pressure, kinetic energy, etc. This paper presents a case study of a debris flow event on 15 September 2009 based on a multi-phase flow model. The model provides the ability to investigate the effect of fluid and solid phases individually. Three sensitivity analyses are presented investigating the effect of bed roughness on solid and fluid phases separately, and also the effect of the entrainment of bed material. The findings demonstrate that the numerical model effectively replicates the observed field data, with the simulated peak discharge and runout distance closely aligning with the observed measurements. The analysis reveals that lower bed roughness promotes higher flow mobility and longer runout distances, while entrainment significantly influences flow height, velocity, and deposition pattern. Furthermore, the analysis highlights the dominant role of entrainment in debris flow evolution and emphasizes its importance in determining deposition and erosion patterns. These findings provide critical insights into the key processes of debris flows and could contribute to the development of accurate numerical models for debris flow events.

1. Introduction

Debris flows are rapidly moving mass flows that can be triggered by rainfall, snow melting, wildfire, volcanic eruptions, earthquakes, and events induced by human activities. A debris flow can contain a variety of rock or soil sediments with diverse sizes and a significant amount of water, and it has the potential to carry objects removed or entrained along its travel path, such as sediments, trees, vegetation, and other types of debris material. With their high destructive potential, debris flows have gained recognition as a serious geological hazard that may occur frequently in steep, rocky, and sparsely vegetated terrains. The physical and mechanical processes of debris flows involve complex interactions between solid and fluid phases. Early studies laid the groundwork for understanding these processes, with foundational research emphasizing the geomorphological characteristics and destructive potential of debris flows [1]. Subsequent investigations developed conceptual frameworks for their physical dynamics, focusing on the role of material–fluid interactions and flow resistance in shaping debris flow behavior [2,3]. These efforts highlighted key mechanisms, such as erosion or entrainment, which significantly influence flow evolution and deposition patterns. Later advancements introduced two-phase modeling approaches, simulating the coupling between solid and fluid phases to improve the prediction of flow behavior [4]. Further work on the rheological classifications and mechanical properties of debris flows linked material composition to flow dynamics, establishing a strong foundation for hazard prediction and mitigation strategies [5,6,7,8].
Experimental and theoretical studies have provided valuable insights into debris flow mechanics, forming the basis for modern numerical modeling [9]. Pioneering experiments on the dispersion of solids in fluids under shear [10] and methods of interpreting geological processes [11] enhanced our understanding of flow resistance and entrainment. These studies are complemented by advanced rheological models, including generalized viscoplastic frameworks and macro-viscous perspectives that capture large-scale flow dynamics [12,13,14]. More recent developments, such as two-fluid models integrating fluid–solid interactions, have significantly improved the accuracy of debris flow simulations, enabling realistic predictions of flow characteristics and deposition patterns [15]. Collectively, these contributions have shaped our current understanding of debris flow processes, guiding both theoretical advancements and practical applications.
Numerical simulations have become indispensable tools for analyzing geological disasters due to their ability to replicate complex processes in a controlled virtual environment [16,17,18,19]. In the context of debris flows, numerical models allow for the evaluation of critical parameters such as flow height, velocity, and deposition patterns under varying conditions. Their applications extend to hazard prediction, mitigation planning, and assessing the impact of different environmental or anthropogenic factors on debris flow dynamics [3,20,21]. Numerical simulations provide the advantage of cost-effectiveness and safety over physical experiments, especially in hazardous or inaccessible terrains [7]. However, it is also important to recognize the limitations of this approach, such as the need for high-resolution topographic data, the accurate representation of material properties, and the computational resources needed to reduce uncertainties [22]. Recent advancements in sensor technology have significantly enhanced the input data available for numerical models [23,24]. For example, the studies by Huang et al. [25] and Navratil et al. [26] utilized high-frequency ground vibration monitoring and real-time flow propagation measurements to improve simulation accuracy. Kean et al. [27] and Comiti et al. [28] demonstrated the importance of integrating rainfall and soil moisture conditions in simulations to predict debris flow initiation and propagation more accurately. Furthermore, Schimmel et al. [29] highlighted the use of infrasound sensors to identify mass movements, providing critical real-time data for validation. Despite these advancements, challenges remain in simulating multi-phase interactions and entrainment processes, which are pivotal in debris flow dynamics. Continued efforts are still needed to incorporate the findings of laboratory and field studies to refine these numerical models, particularly in terms of their ability to capture dynamic entrainment and deposition processes under varied geological conditions.
In the present study an active site with frequent occurrence of run-off type debris flows, the Chalk Cliffs in Colorado (USA), is investigated. This region is highly susceptible to debris flows, mainly due to the abundance of steep, sparsely vegetated slopes with exposed bedrock that is often mantled by loose debris [23,30,31,32,33,34,35,36]. Run-off-generated debris flows typically contain a significant amount of water. The debris flows rapidly entrain and concentrate large quantities of fine sediments and debris into hazardous flow fronts [37]. The wildfire-burned areas and the formerly glaciated flanks of the valleys are most susceptible to run-off-initiated debris flow events in the region [38]. The residents of the Chalk Cliffs region often refer to the primary channel that drained the debris flow originating at the cliffs as “the Ditch”.
The present study begins by briefly summarizing the reported findings of the event of debris flow that occurred on the 15th of September, 2009, at the Chalk Cliffs basin in Colorado. The Chalk Cliffs Basin is a natural debris flow laboratory, experiencing frequent rainfall-induced debris flows. This high activity, coupled with extensive monitoring data, makes it a representative and unique site for studying debris flow dynamics and assessing numerical models. The summary of this event is followed by the presentation of numerical simulations of this event based on a multi-phase flow model. The adopted model [39] is capable of treating the different material phases with appropriate rheology and is suitable for modeling various mass-driven geological processes, including mud flows, debris flows, and rock and snow avalanches [40,41]. After calibration of the parameters based on the back-calculation of the event, the sensitivity of important parameters to the physical characteristics is further investigated, focusing on the simulated runout distance, velocity, flow height, and deposition pattern. The present study shows that the numerical simulations have promising potential to predict the characteristics of potential future events.

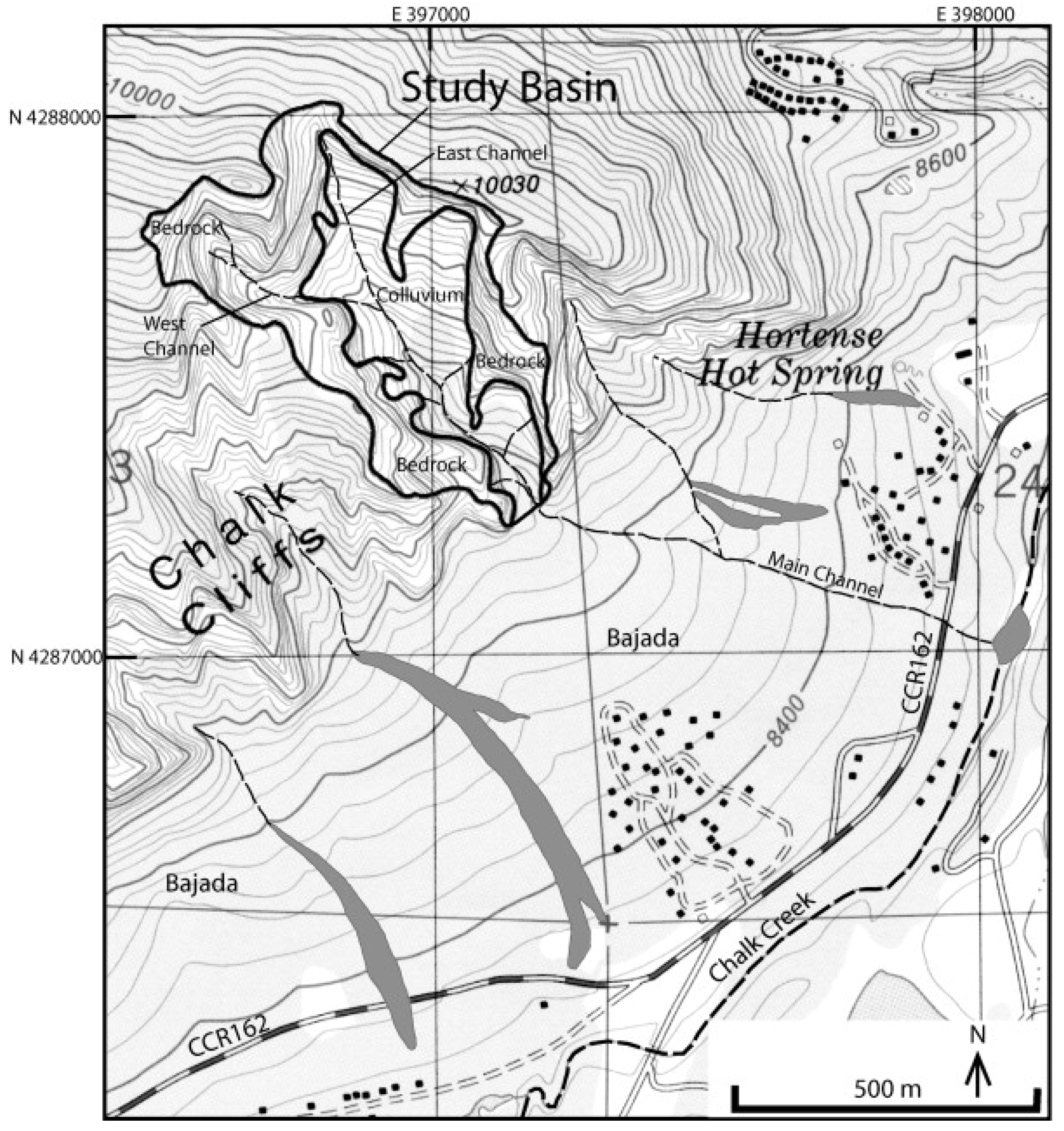
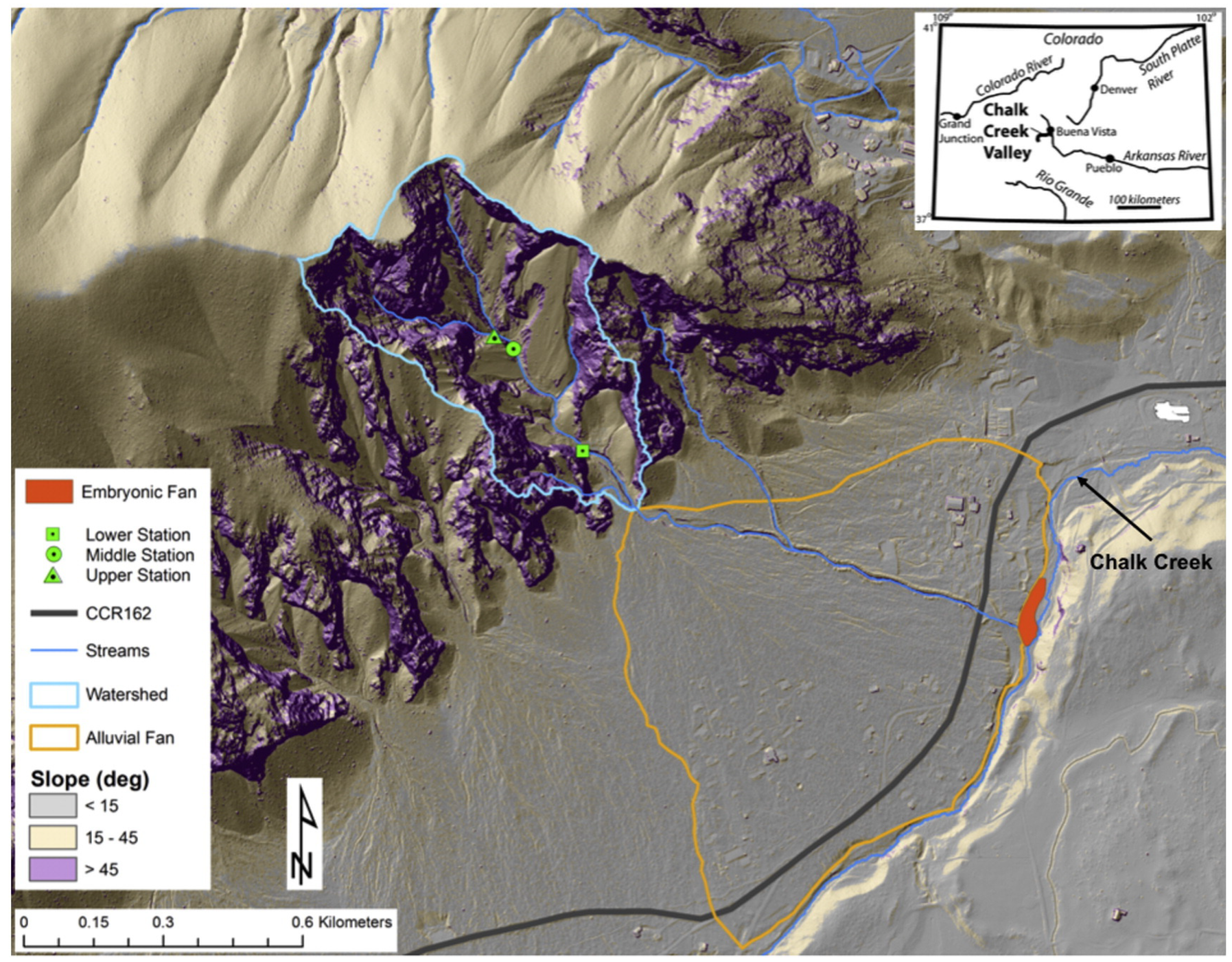
2. Study Area

The Chalk Cliffs are located in the southern portion of the Mount Princeton Batholith on the northern extent of the Rio Grande Rift. The region is on the eastern flank of the Sawatch Mountain Range of Central Colorado, USA, and its geographic coordinates are 38°43′55″ N and 106°11′8″ W (E 396,953 and N 4,287,698) [42], as shown in Figure 1. It consists mainly of a highly fractured, friable, and hydrothermally altered quartz monzonite [37,43]. Some of the basic characteristics of the deposited materials, including their particle size distribution, are reported in Coe et al. [38]. The name “Chalk Cliffs” is derived from the white color of the laumontite and leonhardite minerals (a calcium zeolite variety of laumontite) which are found abundantly in the area. The basin’s steep slopes, sparse vegetation, and hydrothermally altered quartz monzonite create ideal conditions for debris flow initiation and propagation. These characteristics, combined with comprehensive historical data, provide a robust foundation for numerical modeling.
An alluvial fan basin has been formed around the source area of a semiarid drainage basin of approximately 0.3 km 2 . The large alluvial fan basin has an area of 0.69 km 2 . The basin has a steep slope of greater than 50 degrees with colluvial toe slopes. The main channel that drains the basin extends 940 m from the mouth of the basin, across the bajada of a very gentle slope and Chaffee County road (known as and hereafter referred to as CCR162), to a fan formed in Chalk Creek. The Chalk Creek Valley drains into the north–south-trending upper Arkansas River Valley, which is part of the northern Rio Grande Rift [44,45]. The Chalk Cliffs Valley consists of colluvial, glacial till, and debris fan deposits. Channels in the upper half of the basin consist of bedrock steps, bedrock-constrained channels with a thin layer of colluvium or debris flow deposits, or thick deposits of colluvium. Channels in the lower half of the basin are all composed of thicker deposits of colluvium, alluvium, and debris flow material [46].
Between 2004 and 2009, seventeen debris flow or flood events occurred in the basin. All flows were initiated by the surface run-off during rainfall events between May and October. Typically, one to four debris flow incidents within the basin are reported per year [37]. The debris flow in the upper portion of the basin usually creates a fire-hosing effect and carries material via progressive bulking or entrainment along the channel in the drainage basin [23,47,48]. The debris flow incidents varied in their travel distance; while some traveled to the bajada and arrived at the embryonic fan surface from the basin, others stayed in the upper and middle sections of the channel above the alluvial fan.
The infrastructure and buildings on the northern side of the channelized section of the bajada are in danger from the impact of debris flows. To protect the overflow, the residents have engineered a channel by excavating along the majority of the alluvial fan portion to avert the risk. This has been carried out with the aim of constraining the debris flow and forcing it to travel through the concrete channel crossing in CCR162, which is situated around 50 m from behind the embryonic alluvial fan. Road signs warning motorists against driving through the crossing during flow events are posted on both sides of the roads. According to the county maintenance record, cleaning of the debris material on the road is required once a year on average. The embryonic fan area shown in Figure 2 had an area of 2848 m 2 with a slope of 0.10 m/m in the year 2009 [46].
The high frequency of debris flows initiated by rainfall incidents has made this location an ideal site for long-term monitoring; it has been used in a number of research efforts led by the United States Geological Survey [47,48]. An automated monitoring system was installed at three locations (upper, middle, and lower) in the basin, as shown in Figure 2. Two video cameras at the middle and upper stations were also installed. The upper station (US) is located 38 m above the east–west channel junction on the west channel. The middle station (MS) is located at 92 m and 54 m downstream from the upper station and east–west junction, respectively. The final lower station (LS) is located at 220 m from the mouth of the basin and 319 m downstream from the middle station. These three stations are hereafter referred to as US, MS, and LS in the following discussion. In 2009, the stations were upgraded with the addition of an ultrasonic stage sensor with an accuracy of ±1 cm, one or two unvented pressure transducers with an accuracy of ±3 mm, a siphonage rain gauge with an accuracy of ±2%, and a temperature sensor. This upgrade was part of a monitoring effort to measure the flow height, pore fluid pressure, total rainfall, and temperature during mass flow events.

3. Method

3.1. The Studied Debris Flow Event

The incident on 15 September 2009 was a massive debris flow event. Large debris flowed in the east, west, and other channels in the basin and traveled along the length of the main channel; it eventually crossed CCC162 and finally deposited at the large fan in Chalk Creek. The material volume calculated at the upper station was found to be 822 m 3 . A cumulative rainfall of 24.6 mm and a rainstorm duration of 115 min were recorded. The high percentage of water during this event caused significant erosion in the reach of the channel between the upper and middle stations. The post-event observation showed that 33% of the fan surface underwent elevation change after the debris flow event. Debris flow deposition increased the fan dimension from 3192.2 m 2 (on 29 May) to 3501.4 m 2 (on 27 September 2009) [47]. The peak discharge observed at the upper station was 13.5 m 3 / s . Table 1 summarizes the relevant observations during the debris event reported by McCoy et al. [47].
In the present study, the afore-mentioned debris flow event is investigated numerically with a multi-phase continuum flow model developed by Pudasaini and Mergili [39], which is implemented in the numerical simulation package r.avaflow [22]. It is a Geographic Information System (GIS)-supported software tool for complex simulations of multi-phase mass flows over arbitrary topographies [49]. It can operate as a module of the Geographic Resources Analysis Support System (Grass) GIS software. It follows the Eulerian frame of the reference system and uses the non-oscillatory total variation diminishing numerical scheme (TVD-NOC).
The multi-phase mass flow model is derived from the universal phase-averaged mass and momentum conservation equations, each of which is established for each individual phase [39]. It defines the three phases most conveniently. The fluid phase consists of a mixture of water and very fine particles such as silt, colloids, and clay, which are modeled as a shear rate-dependent Herschel–Bulkley viscoplastic fluid. The second phase is known as the fine solid phase, consisting of fine gravel and particles larger than clay and silt. The rheology of the fine solid phase is modeled with shear and pressure-dependent Coulomb viscoplasticity. The solid phase, the last of the three phases, includes boulders and coarser particles such as cobbles and gravel and is modeled with shear rate-independent Mohr–Coulomb plastic rheology. For the present study, only the fluid and solid phases are considered. The post-event investigation suggested the dominant presence of large cobbles and boulder-sized particles along the event flow path. In addition, the event occurred during rainfall. Hence, the two phases adopted to represent the flow rheology are the solid and fluid phase, as the rheology of large boulder-sized particles and the rheology of water are defined by the solid and fluid phases, respectively.

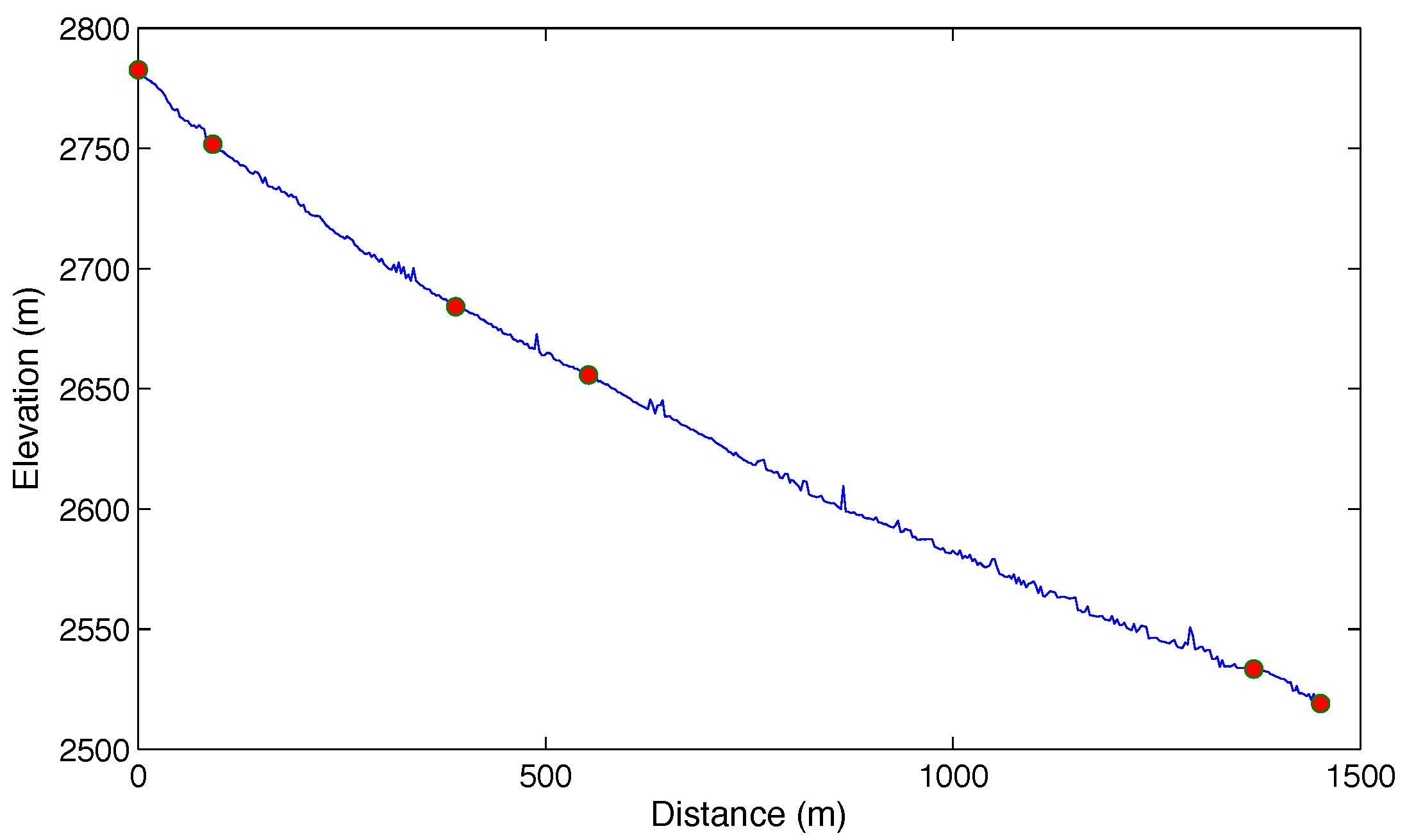
3.2. Input Parameters

In typical mass flow simulation, the uncertainties are not only associated with the choices of flow parameters, but can also be caused by the unavailability of appropriate event data as well as a lack of GIS data for accurate topographic presentation. These complexities are further compounded by the computational power and storage space available for extensive result generation. The model performance and the results obtained can significantly vary due to these factors. In the present study, our best efforts are made to replicate the past event and to reproduce the general overall characteristics of the event; however there always remains an element of improvisation and uncertainty. For the present study, Airborne Lidar data obtained from Open Topography with a point density of 5.74 pts / m 2 are used [50]. To reduce the computational time and susceptibility of numerical instabilities, a grid of 2 m resolution is used for all the simulations. The area of interest is extracted from the LIDAR data using ArcGIS software [51].
As an initial condition, a block release of source material of a predefined volume of 900 m 3 is provided in both the east and west channels, as shown in Figure 3. This initial volume is selected based on the afore-mentioned observation of 822 m 3 of the event volume mentioned in Section 3.1 and validated through multiple simulation trials, achieving the observed total runout distance. The total height of the initial release is kept at 0.35 m with a solid-to-fluid ratio of 0.75 (Table 2). Multiple simulations modifying the parameters are run to replicate the 15 September Debris flow event by comparing the peak discharge at US and the runout distance of the simulated one with the real event data. The entrainment of sediment along the flow is considered [52]. The final parameters used in the simulation are summarized in Table 2, resulting from the calibration with the flow characteristics reported in McCoy et al. [47]. The time step for output result generation is kept at 10 s.
Six important locations useful for numerical examinations are shown in Figure 3, including the three monitoring stations previously mentioned, US, MS and LS, as well as three more locations: the basin mouth (hereafter referred to as BM), CCR 162 crossing (CC), and fan apex (FA) along the flow direction. At these six locations, different entities, such as frontal velocity, are computed during the numerical simulations. The elevation profile along the observed flow is shown in Figure 4, where the six locations are also highlighted. The quantities associated with these six locations and other relevant results are simulated in the retrospective analysis of the actual event.

3.3. Sensitivity Analysis

A sensitivity analysis is carried out focusing on three important parameters that play a critical role in the debris flow process [53]. They are the basal friction angle, the fluid friction coefficient, and the entrainment coefficient. The selection of these three parameters is based on their critical influence on debris flow dynamics and their importance for modeling similar phenomena, as discussed in the literature. These parameters are fundamental in capturing the mechanics of debris flows, including flow mobility, deposition patterns, and the interaction between flow and the bed material [54]. The basal friction angle directly represents the bed roughness, which significantly impacts the mobility of the solid phase in debris flows. It quantifies the resistance offered by the bed material to the solid phase during flow, influencing runout distance, velocity, and deposition patterns [54,55]. The fluid friction coefficient determines the resistance of the fluid phase to flow and is critical in events with a significant water component. While its influence may be more prominent in flows with a higher fluid-to-solid ratio, it remains essential for understanding the dynamics of water-rich debris flows [55]. Entrainment plays a central role in debris flow evolution by incorporating bed material into the flow, increasing its volume and altering its energy and momentum. The entrainment coefficient controls the rate of material incorporation and significantly impacts flow height, runout distance, and deposition [52,54,56].
The first parameter studied reflects the effect of bed roughness on the mobility of the solid phase in the debris flow; it is represented by a basal friction angle ( δ ) and, thus, the basal roughness can be readily calculated as tan δ . It is evident that the higher the bed roughness, the greater the resistance of solid propagation. At the fundamental level, the basal roughness is believed to depend upon characteristics of the bed material (size and shape), vegetation, the concentration of sediments, and temperature [57]. The second parameter examined is the fluid friction coefficient ( μ ). Similarly, this coefficient reflects the effect of basal roughness on the mobility of the fluid phase. The coefficient is multiplied by the flow velocity at every time step to calculate the resistance to flow in the numerical simulation.
Finally, the effect of the entrainment coefficient as the third parameter is also investigated, which controls the volume of entrained material. The bed entrainment or erosion is a very complex phenomenon and depends on a number of factors. A detailed discussion about possible approaches to dynamically simulate the entrainment of material can be found in Pudasaini and Fisher [20]. An empirical approach is adopted in the present model to compute the entrainment of basal material [56]. The potential solid and fluid entrainment rates are characterized by an empirical coefficient, C E . The coefficient is multiplied by the total kinetic energy (or total flow momentum) to calculate the entrainment rate of the basal material, defined as the rate of the change in bed depth, at every time step. It is worth noting that this forms a coupled process, as the entrained bed material enters the mass and momentum balance equation. In turn, the additional mass and momentum production terms will affect the subsequent kinetic energy and entrainment. Evidently, a higher value of C E represents greater entrainment of the material. In the numerical simulations, it is also necessary to specify the material domain where the entrainment occurs along the flow path on the bed surface. In the present study, the maximum entrainment depth of the material is confined to be 1.1 m below and 0.25 m below the bed surface for solid and fluid phases, respectively. This is based on the field observation of [47], where a maximum bed height decrease of approximately 1.1 m was found after the event. A very low value of 0.25 m is also assumed for the maximum allowable entrainment depth for the fluid phase, since the contribution of entrainment is generally negligible for this phase, and this event was largely dominated by the solid phase fraction.

4. Results

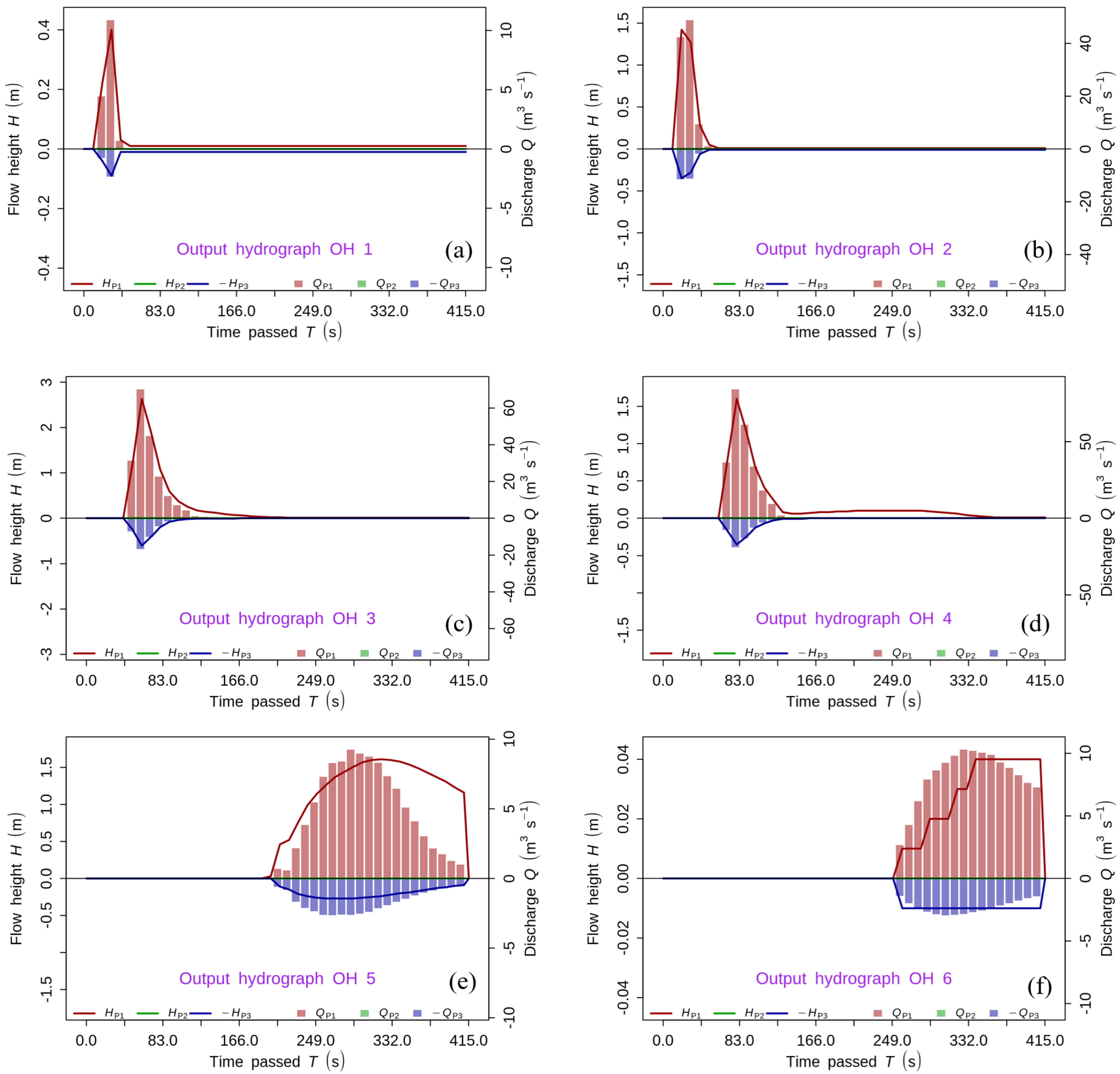
4.1. Analysis of the 15 September 2009 Event

The numerical results of the time evolution of the flow height and discharge at the six selected locations are shown in Figure 5. It clearly shows the progression of the traveling flow that passes through these locations; it reaches the upper station (US) at around 10 s, then proceeds to the middle station (MS) and lower station (LS) at around 15 s and 40 s, respectively. Subsequently it reaches the basin mouth (BM) at around 70 s, and it takes approximately 190 s for the flow to reach the CCR 162 crossing (CC), and about an additional 50 s to arrive at the fan apex (FA). The results also include the contributions of both the solid phase (red) and fluid phase (blue) in the flow height indicated by the solid line, as well as in the discharge indicated by the bar height. It should be noted that the values of these two phases are plotted together on opposite axes in each sub-figure for comparison purposes, the negative sign for the fluid phase has no bearing, and the sum of the magnitudes of both phases represents the total flow height or discharge.
The present simulation attempts to replicate the total runout distance as observed from the post-event investigation, and the peak discharge (13.5 m 3 / s ) measured at the upper station (US). As shown in Figure 5a, the simulated peak discharge at the upper station (US) is 13.2 m 3 / s , which is reasonably close to that measured in the field. A maximum peak discharge of 102.88 m 3 / s is found in the basin mouth (BM), whereas a minimum peak discharge of 11.88 m 3 / s is found at CCR162 crossing (CC). It is worth noting that the values of both quantities evolve considerably in the process, spanning almost 3 orders of magnitude, especially for flow height, and thus have to be plotted at different scales across Figure 5a–f. Clearly, the flow grows significantly from US to MS and LS in terms of both height and discharge, then gradually subsides from BM to CC and FA. Due to high fractions of the initial solid volume, the height of the solid phase is substantially higher than the height of the fluid phase at all selected locations. The maximum height of the individual phases, as well as the total height of the flow, is found at LS with magnitudes of 3.17 m, 0.71 m, and 3.88 m, respectively.
Figure 6a shows the frontal velocity of each phase along the flow path, while the maximum velocity of each phase is presented in Figure 6b. Both of the figures show the velocity of the flow front entering at any specific location along its path. The velocity of individual phases is reasonably close; the fluid phase velocity is slightly higher than the solid phase for most of the path. Overall, the velocity gradually declines after passing the upper station (US) and middle station (MS) and decreases considerably around the CCR162 crossing (CC). CC is right at the center of the crossing, located at the embryonic fan, which provides a large area for material to deposit; hence, the velocity around CC is reduced when the material traveling in a narrow channel enters the fan and spreads material over a large area. The debris flow continues toward the fan apex (FA) and still possesses some momentum and velocity, as it can still entrain a certain amount of material downward along the narrow channel before it reaches FA, which is right at the apex of the fan opening and essentially the exit point from the channel. Figure 6b shows the maximum velocity of the flow passing through each selected location. The highest magnitude of the velocity of 10.62 m / s among these locations is found in the fluid phase at the middle station (MS) due to the steep slope.
Figure 7 shows the maximum entrained depth at the selected locations. Since the entrainment coefficient is formulated to depend on the kinetic energy which is affected by both the velocity and the mass of the flow, the maximum entrained depth of 0.73 m occurs at the basin mouth (BM), where the flow retains significant mass and high velocity, whereas the minimum entrained depth occurs at the embryonic fan apex (FA) as the mass has gradually deposited and the velocity has significantly declined before reaching FA.
The maximum total flow height, as well as the height of the individual phases during the total simulated flow, are shown in Figure 8a–c. In addition, the final change in the basal topography after the event is shown in Figure 8d. The maximum flow heights for the individual phases, as well as the combined flow height, are 4.58 m, 1.04 m, and 5.60 m, respectively. It is evident that the high-depth flow concentrates on the narrow channel; the highest magnitude of flow height is found near the lower station (LS) and around the CCR162 crossing (CC). The final basechange results from the entrainment (negative) and the deposition (positive) of the material. The maximum ground depletion is approximately −1.1 m along the channel in the alluvial fan; it is noted that this value matches well with the measured basal change in the actual debris flow event. The maximum ground deposition of up to 1.94 m occurs at the CCR162 crossing (CC) and embryonic fan.
Figure 9 shows the maximum velocity of the solid and fluid phases during the simulated debris flow event. When closely compared, the magnitude of the maximum flow velocity for the fluid phase is generally higher than for the solid phase in most of the primary channel. However, some very high values of the maximum velocity of the solid phase occur near the initial release area. This may be due to the toppling of large boulder particles because of the steep slopes causing significantly higher velocity at the start of the event. The maximum kinetic energy and flow pressure along the flow are shown in Figure 10. The maximum kinetic energy and flow pressure are 397 kJ and 993 kPa, respectively. Higher values of both of these parameters occur in the upstream mountain region of the primary channel.

4.2. Sensitivity Analysis

A sensitivity analysis was also carried out to explore the effects of three parameters on the flow characteristics, including flow height, deposition pattern, runout distance, and final basechange. The first parameter investigated was the basal friction angle ( δ ) of the solid phase, which describes the effect of bed roughness on the mobility of the solid phase in the debris flow. The angle, originally set up to be 15 ∘ in the back-analysis of the preceding simulation, was varied between 10 ∘ and 20 ∘ , with all the other parameters kept the same. The major effect of bed roughness is found in the runout distance and deposition pattern, as shown in Figure 11. With a low roughness, the flow travels at a higher velocity and over a longer distance compared to the case of higher bed roughness. The maximum flow height is shown in Figure 12, which indicates a smaller flow height overall in the case of lower bed roughness. With a 20 ∘ bed friction angle, the material essentially stops at the CCR162 crossing and does not reach the embryonic fan (Figure 11b). However, with a 10 ∘ friction angle, the flow is able to reach the embryonic fan in 170 s, which is considerably shorter than the 260 s needed in the case of a 15 ∘ friction angle. In addition, the bed friction angle significantly affects the deposition pattern of the mass flow. The material spreads laterally in the bajada under the lower bed roughness, while it remains confined in the channel under the higher roughness, as shown in Figure 11. The peak discharge obtained at BM, CC, and FA increases substantially with the decrease in bed roughness. The increase in the peak discharge is 1.9 times, 7.1 times, and 4.7 times at BM, CC, and FA, respectively, with the lower basal friction angle.
The second sensitivity analysis evaluated the effect of bed roughness on the mobility of the fluid phase, which is represented by the fluid friction coefficient ( μ ). The values of parameters were changed from 0.1 as in the back-analysis to 0.05 and 0.15. The results obtained show that the effect is not as significant as that of the bed friction angle of the solid phase. The various quantities, such as peak discharge, flow height, and velocity, increase only slightly as the fluid friction coefficient decreases. The flow deposition pattern also changes slightly. The primary reason for the modest influence of the fluid friction coefficient is related to the small fluid fraction in the initial material, and the variation in fluid phase properties does not cause considerable differences in the flow behavior. For example, the maximum deposition varies from 2.0 m at μ = 0.15 to 1.9 m at μ = 0.05 . The material is able to reach the apex of the fan even with a low value of the fluid friction coefficient. However, the time taken to reach that distance is 220 s when μ = 0.05 , compared to 260 s when μ = 0.10 , and it extends to 280 s when μ is raised to 0.15.
The third sensitivity analysis assessed the effect of the entrainment of material along the flow path. The initial simulations indicate that the mass flow is very sensitive to the value of the entrainment coefficient, C E and can significantly influence the behavior of the flow. The higher value of C E indicates greater erosion of material from the bed which joins in the volume of flow, thus significantly affecting the physics and mechanics of the flow. The value is typically input with an exponent of base-10 in the simulation. As discussed previously, C E = 10 − 6.65 is used for the back-analysis to match certain key field observations. When the entrainment coefficient is decreased to 10 − 6.75 , Figure 13b shows a significantly reduced area of spread material around the primary flow channel compared with Figure 8d. Whereas with a greater coefficient, C E = 10 − 6.55 , Figure 13c shows an expanded area of material spread around the primary flow channel, especially near its exit. It is also noted that overall, the maximum basal change is somewhat reduced with greater C E , since more material is entrained, thus enhancing the bed depletion or reducing the basal increase. If the entrainment is completely ignored in the simulation, C E = 0 is adopted, and the result in Figure 13a shows that the flow would practically run out shortly after entering the basin mouth (BM) of the fan. In this case, there is not enough material to continue, and all material deposits in the flow path, as indicated by the entire area of positive basal change. Indeed, the (horizontal) runout distance would only be around 930 m, as opposed to the 1518 m full distance from the initiation location to the eventual fan apex (FA), as simulated with higher values of the entrainment coefficient. Figure 14 shows the results of the maximum flow height of all cases. Evidently, the increase in C E causes more material to flow and increases the flow height.

5. Discussion

This retrospective analysis of the 15 September 2009 event simulation offers matching results for the runout distance, height of flow, and peak discharge at the upper station (US), and also for deposition behavior. Overall, the back-calibration of the event gives high priority to the runout distance and overall deposition pattern. Similarly to the actual event, the material travels all the way to the fan, with significant deposition at the crossing and at the embryonic fan. The height of flow and peak discharge obtained at US are 0.87 m and 13.2 m 3 / s , respectively, which are comparable to the actual observed values shown in Table 1. However, the flow depths calculated at the other two stations are at very high levels compared to their actual values. The higher values of parameters such as bed height change and flow depth obtained at other stations can be mainly attributed to the entrainment mechanics adopted by the model. As discussed in the preceding section, the simulation is very sensitive to the entrainment coefficient and works in a forward manner in relation to the kinetic energy of the flow. As the flow proceeds, the material is entrained, and the volume of the event is increased substantially, leading to high values of the height of flow and entrainment depth.
The flow height increases from US to LS due to an increment in the volume of material because of entrainment, and also because of the narrow channels in the upstream mountain region. As the material enters the basin mouth, it spreads slightly, thus reducing the height of flow. Similar behavior is observed for peak discharge. However, the highest value of peak discharge is obtained at the basin mouth due to a very high velocity of flow and the increase in the debris volume as a result of entrainment. The maximum flow heights are observed in the main channel. The large deposition of material in the CCR162 crossing and the fan can be attributed to the relatively flat slope and large area available for the material to spread out laterally. Some of the inconsistencies in these results can be attributed to the cell size of 2 m; however, this is dictated by the available source data for the digital elevation model (DEM) of the study area. In addition, the generation of results at the time interval of 10 s may sometimes inaccurately represent some flow characteristics.
The sensitivity analysis results indicate that both the basal friction angle and the entrainment coefficient have a significant effect on the outcome of the results. The fluid friction coefficient may have a greater effect on the events with a higher fluid ratio. The areas with a low basal friction angle, i.e., low bed roughness, will have a large deposition area and a long runout distance affected by debris flow events, thus posing a greater threat to the local community. Low bed roughness may also contribute to large entrainment of material along the flow path in many cases. Properly vegetated terrain will provide higher bed roughness, which will restrict the affected area of debris flow events. The sensitivity analysis considering the entrainment of material has the greatest effect on flow characteristics. The flow height, travel distance, and deposition pattern are primarily affected by the entrainment of material during the flow. The case with no entrainment has the smallest travel distance, flow height, and deposition area, signifying the major effect of entrainment compared with other potential causal factors. It is also noted that more statistically sophisticated methods [58] could be explored in future investigations to improve our understanding of the uncertainty of model performance. Overall, the main causes of the discrepancies between the numerical predictions and field observations can be attributed to several factors, including limitations in available field data and modeling assumptions. The lack of precise information on initial failure volume, the exact location of debris flow initiation, and transient flow properties introduces uncertainties that propagate through the simulations. Computational limitations, such as simplified representations of complex entrainment processes and transient flow dynamics, further constrain the accuracy of the numerical predictions.
Overall, several limitations of the modeling approach in the present study should be noted. The model relies on assumptions regarding the initial material volume, which, while validated through simulation trials, may not fully capture the variability in real-world conditions. Additionally, the use of a moderate resolution in the digital elevation model (DEM) and the simplified treatment of entrainment processes could affect the accuracy of the results. The model also assumes uniform material properties and does not account for potential spatial variability in the geotechnical characteristics of the bed material. At the fundamental level, the adopted approach focuses on the overall characteristics of each phase of the debris material, and the discrete nature of debris particles in motion is not directly considered. The particle sizes and their distribution may have an important influence on the growth of the debris material and the entrainment. In addition, recent advancements in debris flow research emphasize the critical role of entrainment in flow dynamics and runout modeling, highlighting its influence on debris flow initiation mechanisms, enlargement processes, and sediment bulking. Studies incorporating suitable entrainment models have demonstrated improved accuracy in replicating real-world events [54,59,60]. Future studies could address these limitations by incorporating higher-resolution DEMs, advanced field data, and more sophisticated entrainment mechanisms to further improve the numerical predictions.

6. Concluding Remarks

A significant debris flow event which occurred in the Chalk Cliff region of Colorado on the 15 of September 2009 was back-calculated based on a multi-phase flow model. The model parameters were calibrated to replicate the real event observation. The results of the numerical simulations are reasonably consistent with the actual observed data, albeit with some overestimation of certain parameters. Overall, the numerical model was able to effectively replicate the observed field data, with the simulated peak discharge and runout distance closely aligning with the observed measurements. The results show that lower bed roughness promotes higher flow mobility and longer runout distances, while entrainment significantly influences flow height, velocity, and deposition pattern. In particular, the sensitivity analysis highlights the dominant role of entrainment in debris flow evolution and demonstrates its importance in determining deposition and erosion patterns. These findings could provide critical insights into the governing parameters of debris flows and contribute to the development of accurate numerical models for evaluating debris flow events. Improved prediction of debris runout distance and deposition is beneficial for assessing the risk impact and supporting more effective mitigation strategies. The inconsistencies can be minimized by analyzing expanded ranges of field data of actual flow events and high-resolution GIS data, the accurate calibration of material properties, etc. Additional simulations are needed to establish guiding parameter sets for further studies. Statistical methods to systematize the variations in key modeling parameters could be incorporated into sensitivity analyses to improve our understanding of the intricacies of model performance in future studies. Overall, the present study demonstrates the potential applications of advanced simulation tools for engineering hazard assessment. These tools are capable of simulating complex mass flow events and are able to address the very complex processes involved in the multi-phase interactions of debris material.

Author Contributions

Conceptualization, M.W.N.; methodology, M.W.N. and L.H.; software, M.W.N. and D.K.; formal analysis, M.W.N.; investigation, M.W.N.; resources, L.H.; data curation, M.W.N. and D.K.; writing—original draft preparation, M.W.N. and L.H.; writing—review and editing, M.W.N. and L.H.; visualization, M.W.N. and D.K.; supervision, L.H.; project administration, L.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Costa, J.E. Physical geomorphology of debris flows. In Developments and Applications of Geomorphology; Springer: Berlin/Heidelberg, Germany, 1984; pp. 268–317. [Google Scholar]
  2. Iverson, R.M.; Denlinger, R.P. The physics of debris flows—A conceptual assessment. In Proceedings of the International Symposium on Erosion and Sedimentation in the Pacific Rim, Corvallis, OR, USA, 3–7 August 1987; p. 165. [Google Scholar]
  3. Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
  4. Bozhinskiy, A.N.; Nazarov, A.N. Two-phase model of debris-flow. In Proceedings of the 2nd International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, Taipei, Taiwan, 16–18 August 2000; pp. 263–269. [Google Scholar]
  5. Coussot, P. Mudflow rheology and dynamics. In Mudflow Rheology and Dynamics; A.A. Balkema: Rotterdam, The Netherlands, 1997. [Google Scholar]
  6. Julien, P.; Leon, C. Mud floods, mudflows and debris flows. Classification, rheology and structural design. Jornadas Investig. JIFI 2000, 33, 1–15. [Google Scholar]
  7. Takahashi, T. Debris Flow: Mechanics, Prediction and Countermeasures; Taylor & Francis: London, UK, 2007. [Google Scholar]
  8. Iverson, R.M. Debris-flow mechanics. In Debris-flow Hazards and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2007; pp. 105–134. [Google Scholar]
  9. Trujillo-Vela, M.G.; Ramos-Canon, A.M.; Escobar-Vargas, J.A.; Galindo-Torres, S.A. An overview of debris-flow mathematical modelling. Earth Sci. Rev. 2022, 232, 104135. [Google Scholar] [CrossRef]
  10. Bagnold, R.A. Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1954, 225, 49–63. [Google Scholar]
  11. Johnson, A.M. Physical Processes in Geology: A Method for Interpretation of Natural Physical Processes in Geology Phenomena; Freeman Cooper: San Francisco, CA, USA, 1970. [Google Scholar]
  12. Takahashi, T. Debris Flow. Annu. Rev. Fluid Mech. 1981, 13, 57–77. [Google Scholar] [CrossRef]
  13. Davies, T.R.H. Large debris flows: A macro-viscous phenomenon. Acta Mech. 1986, 63, 161–178. [Google Scholar] [CrossRef]
  14. Chen, C. Generalized viscoplastic modeling of debris flow. J. Hydraul. Eng. 1988, 114, 237–258. [Google Scholar] [CrossRef]
  15. Pitman, E.B.; Le, L. A two-fluid model for avalanche and debris flows. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2005, 363, 1573–1601. [Google Scholar] [CrossRef]
  16. Mousavi Tayebi, S.A.; Moussavi Tayyebi, S.; Pastor, M. Depth-Integrated Two-Phase Modeling of Two Real Cases: A Comparison between r.avaflow and GeoFlow-SPH Codes. Appl. Sci. 2021, 11, 5751. [Google Scholar] [CrossRef]
  17. Zhang, X.; Tang, C.; Yu, Y.; Tang, C.; Li, N.; Xiong, J.; Chen, M. Some Considerations for Using Numerical Methods to Simulate Possible Debris Flows: The Case of the 2013 and 2020 Wayao Debris Flows (Sichuan, China). Water 2022, 14, 1050. [Google Scholar] [CrossRef]
  18. KC, D.; Naqvi, M.W.; Hu, L. A Case Study and Numerical Modeling of Post-Wildfire Debris Flows in Montecito, California. Water 2024, 16, 1285. [Google Scholar] [CrossRef]
  19. Abraham, M.T.; Satyam, N.; Kowalski, J. Numerical Modelling of Debris Flows for Simulation-Based Decision Support: An Indian Perspective. Indian Geotech. J. 2024. [Google Scholar] [CrossRef]
  20. Pudasaini, S.P.; Fischer, J.T. A mechanical erosion model for two-phase mass flows. Int. J. Multiphase Flow 2020, 132, 103416. [Google Scholar] [CrossRef]
  21. Somos-Valenzuela, M.A.; Oyarzun-Ulloa, J.E.; Fustos-Toribio, I.J.; Garrido-Urzua, N.; Chen, N. The mudflow disaster at Villa Santa Lucia in Chilean Patagonia: Understandings and insights derived from numerical simulation and postevent field surveys. Nat. Hazards Earth Syst. Sci. 2020, 20, 2319–2333. [Google Scholar] [CrossRef]
  22. Mergili, M. Simulation of geomorphic mass flows: Recent advances of the open-source simulation framework r.avaflow. In Proceedings of the 84th EAGE Annual Conference & Exhibition, Vienna, Austria, 5–8 June 2023; pp. 1–3. [Google Scholar]
  23. McCoy, S.W.; Kean, J.W.; Coe, J.A.; Staley, D.M.; Wasklewicz, T.A.; Tucker, G.E. Evolution of a natural debris flow: In situ measurements of flow dynamics, video imagery, and terrestrial laser scanning. Geology 2010, 38, 735–738. [Google Scholar] [CrossRef]
  24. Marcel, H.; Claudia, A.; Jose, M. Debris-Flow Monitoring at the Rebaixader Torrent, Central Pyrenees, Spain. Results on Initiation, Volume and Dynamic Behaviour. Eng. Geol. Soc. Territ. 2015, 2, 469–472. [Google Scholar]
  25. Huang, C.J.; Yin, H.Y.; Chen, C.Y.; Yeh, C.H.; Wang, C.L. Ground vibrations produced by rock motions and debris flows. J. Geophys. Res. Earth Surf. 2007, 112, F02014. [Google Scholar] [CrossRef]
  26. Navratil, O.; Liébault, F.; Bellot, H.; Travaglini, E.; Theule, J.; Chambon, G.; Laigle, D. High-frequency monitoring of debris-flow propagation along the Real Torrent, Southern French Prealps. Geomorphology 2013, 201, 157–171. [Google Scholar] [CrossRef]
  27. Kean, J.W.; Staley, D.M.; Cannon, S.H. In situ measurements of post-fire debris flows in southern California: Comparisons of the timing and magnitude of 24 debris-flow events with rainfall and soil moisture conditions. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
  28. Comiti, F.; Marchi, L.; Macconi, P.; Arattano, M.; Bertoldi, G.; Borga, M.; Brardinoni, F.; Cavalli, M.; D’Agostino, V.; Penna, D. A new monitoring station for debris flows in the European Alps: First observations in the Gadria basin. Nat. Hazards 2014, 7, 1175–1198. [Google Scholar] [CrossRef]
  29. Schimmel, A.; Hubl, J.; McArdell, B.W.; Walter, F. Automatic Identification of Alpine Mass Movements by a Combination of Seismic and Infrasound Sensors. Sensors 2018, 18, 1658. [Google Scholar] [CrossRef] [PubMed]
  30. Jochim, C.L. Debris-Flow Hazard in the Immediate Vicinity of Ouray, Colorado; Colorado Geological Survey: Denver, CO, USA, 1986. [Google Scholar]
  31. Cannon, S.H.; Powers, P.S.; Savage, W.Z. Fire-related hyperconcentrated and debris flows on Storm King Mountain, Glenwood Springs, Colorado, USA. Environ. Geol. 1998, 35, 210–218. [Google Scholar] [CrossRef]
  32. Cannon, S.H.; Kirkham, R.M.; Parise, M. Wildfire-related debris-flow initiation processes, Storm King Mountain, Colorado. Geomorphology 2001, 39, 171–188. [Google Scholar] [CrossRef]
  33. Coe, J.A.; Godt, J.W.; Henceroth, A.J. Debris Flows Along the Interstate 70 Corridor, Floyd Hill to the Arapahoe Basin Ski Area, Central Colorado; a Field Trip Guidebook; Geological Survey (U.S.): Reston, VA, USA, 2002. [Google Scholar]
  34. Coe, J.A.; Bigio, E.R.; Blair, R.W., Jr.; Burke, M.; Cannon, S.H.; de Wolfe, V.G.; Ey, J.; Gartner, J.E.; Gillam, M.L.; Knowlton, N.D.; et al. Mass Wasting Following the 2002 Missionary Ridge Fire near Durango, Colorado, a Field Trip Guidebook; Geological Survey (U.S.): Reston, VA, USA, 2007. [Google Scholar]
  35. Coe, J.A.; Godt, J.W.; Wait, T.C.; Kean, J.W. Field Reconnaissance of Debris Flows Triggered by a July 21, 2007, Thunderstorm in Alpine, Colorado, and Vicinity; Geological Survey (U.S.): Reston, VA, USA, 2007. [Google Scholar]
  36. Godt, J.W.; Coe, J.A. Alpine debris flows triggered by a 28 July 1999 thunderstorm in the central Front Range, Colorado. Geomorphology 2007, 84, 80–97. [Google Scholar] [CrossRef]
  37. Coe, J.A.; Kinner, D.A.; Godt, J.W. Initiation conditions for debris flows generated by run-off at Chalk Cliffs, central Colorado. Geomorphology 2008, 96, 270–297. [Google Scholar] [CrossRef]
  38. Coe, J.A.; Kean, J.W.; McCoy, S.W.; Staley, D.M.; Wasklewicz, T.A. Chalk Creek Valley: Colorado’s natural debris-flow laboratory. In Geological Society of America Field Guide 18 (June 2014); Geological Society of America: Boulder, CO, USA, 2010; pp. 95–117. [Google Scholar]
  39. Pudasaini, S.P.; Mergili, M. A Multi-Phase Mass Flow Model. J. Geophys. Res. Earth Surf. 2019, 124, 2920–2942. [Google Scholar] [CrossRef]
  40. Naqvi, M.W.; KC, D.; Hu, L. Numerical modeling and a parametric study of various mass flows based on a multi-phase computational framework. Geotechnics 2022, 2, 506–522. [Google Scholar] [CrossRef]
  41. Naqvi, M.W.; KC, D.; Hu, L. Numerical modelling and sensitivity analysis of the Pitztal Valley debris flow event. Geosciences 2024, 13, 378. [Google Scholar] [CrossRef]
  42. Colman, S.M.; McCalpin, J.P.; Ostenaa, D.A.; Kirkham, R.M. Map Showing Upper Cenozoic Rocks and Deposits and Quaternary Faults, Rio Grande Rift, South-Central Colorado; U.S. Geological Survey: Reston, VA, USA, 1985. [Google Scholar]
  43. Miller, M.G. Active breaching of a geometric segment boundary in the Sawatch Range normal fault, Colorado, USA. J. Struct. Geol. 1999, 21, 769–776. [Google Scholar] [CrossRef]
  44. Tweto, O. Guidebook to the Rio Grande Rift, Circular 163; New Mexico Bureau of Mines and Mineral Resources: Socorro, NM, USA, 1978. [Google Scholar]
  45. Kellogg, K.S. Neogene basins of the northern Rio Grande rift: Partitioning and asymmetry inherited from Laramide and older uplifts. Tectonophysics 1999, 305, 141–152. [Google Scholar] [CrossRef]
  46. Wasklewicz, T.; Scheinert, C. Development and maintenance of a telescoping debris flow fan in response to human-induced fan surface channelization, Chalk Creek Valley Natural Debris Flow Laboratory, Colorado, USA. Geomorphology 2016, 252, 51–65. [Google Scholar] [CrossRef]
  47. McCoy, S.W.; Coe, J.A.; Kean, J.W.; Tucker, G.E.; Staley, D.M.; Wasklewicz, T.A. Observations of debris flows at Chalk Cliffs, Colorado, USA: Part 1, in-situ measurements of flow dynamics, tracer particle movement and video imagery from the summer of 2009. Ital. J. Eng. Geol. Environ. 2011, 1, 65–75. [Google Scholar]
  48. Staley, D.M.; Wasklewicz, T.A.; Coe, J.A.; Kean, J.W.; McCoy, S.W.; Tucker, G.E. Observations of debris flows at Chalk Cliffs, Colorado, USA: Part 2, changes in surface morphometry from terrestrial laser scanning in the summer of 2009. Ital. J. Eng. Geol. Environ. 2011, 759–768. [Google Scholar] [CrossRef]
  49. Pandey, N.K.; Satyam, N.; Gupta, K. Landslide-induced debris flows and its investigation using r.avaflow: A case study from Kotrupi, India. J. Earth Syst. Sci. 2024, 133, 93. [Google Scholar] [CrossRef]
  50. McCoy, S. San Isabel NF, CO: Debris Flow Mechanics and Landscape Evolution Airborne Lidar; Open Topography: San Diego, CA, USA, 2012. [Google Scholar] [CrossRef]
  51. ESRI, ArcGIS Desktop. Environmental Systems Research Institute (ESRI). Available online: https://www.esri.com/en-us/arcgis/geospatial-platform/overview (accessed on 22 January 2020).
  52. Qiao, Z.; Li, T.; Simoni, A.; Gregoretti, C.; Bernard, M.; Wu, S.; Shen, W.; Berti, M. Numerical modelling of an alpine debris flow by considering bed entrainment. Front. Earth Sci. 2023, 10, 1059525. [Google Scholar] [CrossRef]
  53. Mikos, M.; Bezak, B.N. Debris Flow Modelling Using RAMMS Model in the Alpine Environment With Focus on the Model Parameters and Main Characteristics. Front. Earth Sci. 2021, 8, 605061. [Google Scholar] [CrossRef]
  54. Frank, F.; McArdell, B.W.; Huggel, C.; Vieli, A. The importance of entrainment and bulking on debris flow runout modeling: Examples from the Swiss Alps. Nat. Hazards Earth Syst. Sci. 2015, 15, 2569–2583. [Google Scholar] [CrossRef]
  55. Rinzin, S.; Dunning, S.; Carr, R.; Sattar, A.; Mergili, M. Exploring implications of input parameter uncertainties on GLOF modelling results using the state-of-the-art modelling code, r.avaflow. EGUsphere 2024. [Google Scholar] [CrossRef]
  56. Mergili, M.; Fischer, J.T.; Krenn, J.; Pudasaini, S.P. R.avaflow v1, an advanced open-source computational framework for the propagation and interaction of two-phase mass flows. Geosci. Model Dev. 2017, 10, 553–565. [Google Scholar] [CrossRef]
  57. Simons, D.B.; Richardson, E.V. The effect of bed roughness on depth-discharge relations in alluvial channels. In Geological Survey Water-Supply Paper 1498-E; US Department of the Interior: Washington, DC, USA, 1962. [Google Scholar]
  58. Zhang, J.; Lin, C.; Tang, H.; Wen, T.; Tannant, D.D.; Zhang, B. Input-parameter optimization using a SVR based ensemble model to predict landslide displacements in a reservoir area—A comparative study. Appl. Soft Comput. 2024, 150, 111107. [Google Scholar] [CrossRef]
  59. Shen, P.; Zhang, L.; Wong, H.F.; Peng, D.; Zhou, S.; Zhang, S.; Chen, C. Debris flow enlargement from entrainment: A case study for comparison of three entrainment models. Eng. Geol. 2020, 270, 105581. [Google Scholar] [CrossRef]
  60. Du, J.; Fan, Z.-J.; Xu, W.-T.; Dong, L.-Y. Research Progress of Initial Mechanism on Debris Flow and Related Discrimination Methods: A Review. Front. Earth Sci. 2021, 9, 629567. [Google Scholar] [CrossRef]
Water 17 00406 g001
Figure 1. Topographic Map of Chalk Cliffs, Colorado, USA [37] (reproduced with the permission of Geomorphology).
Figure 1. Topographic Map of Chalk Cliffs, Colorado, USA [37] (reproduced with the permission of Geomorphology).
Water 17 00406 g001
Water 17 00406 g002
Figure 2. A map of the Chalk Creek Valley and the alluvial fan (from Wasklewicz and Scheinert [46], reproduced with the permission of Geomorphology).
Figure 2. A map of the Chalk Creek Valley and the alluvial fan (from Wasklewicz and Scheinert [46], reproduced with the permission of Geomorphology).
Water 17 00406 g002
Water 17 00406 g003
Figure 3. Hill shade view with the initial release (marked with yellow blocks), station points (green dots, indicating US, MS, and LS), and other control points (yellow dots, indicating BM, CC, and FA).
Figure 3. Hill shade view with the initial release (marked with yellow blocks), station points (green dots, indicating US, MS, and LS), and other control points (yellow dots, indicating BM, CC, and FA).
Water 17 00406 g003
Water 17 00406 g004
Figure 4. The elevation profile along the flow path; markers indicate the six observation locations in descending order of US, MS, LS, BM, CC, and FA.
Figure 4. The elevation profile along the flow path; markers indicate the six observation locations in descending order of US, MS, LS, BM, CC, and FA.
Water 17 00406 g004
Water 17 00406 g005
Figure 5. Flow height and discharge at six selected locations: (a) US, (b) MS, (c) LS, (d) BM, (e) CC, and (f) FA; solid line indicates flow height, and bar indicates discharge, including both solid phase (red) and fluid phase (blue), which are plotted together for comparison purposes, note that the negative sign has no physical meaning.
Figure 5. Flow height and discharge at six selected locations: (a) US, (b) MS, (c) LS, (d) BM, (e) CC, and (f) FA; solid line indicates flow height, and bar indicates discharge, including both solid phase (red) and fluid phase (blue), which are plotted together for comparison purposes, note that the negative sign has no physical meaning.
Water 17 00406 g005
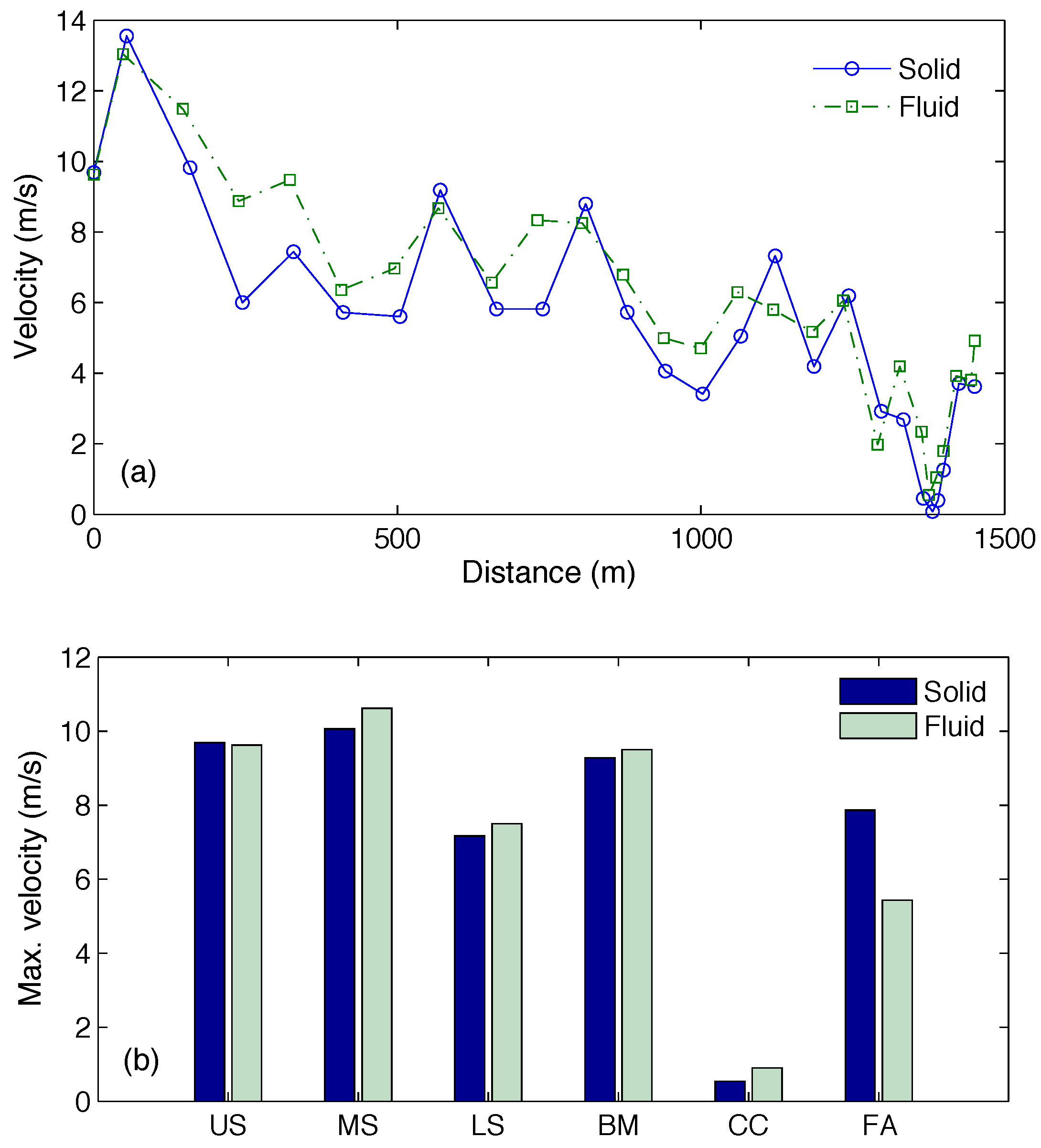
Water 17 00406 g006
Figure 6. (a) Frontal velocity along the flow path; (b) maximum velocity at selected locations.
Figure 6. (a) Frontal velocity along the flow path; (b) maximum velocity at selected locations.
Water 17 00406 g006
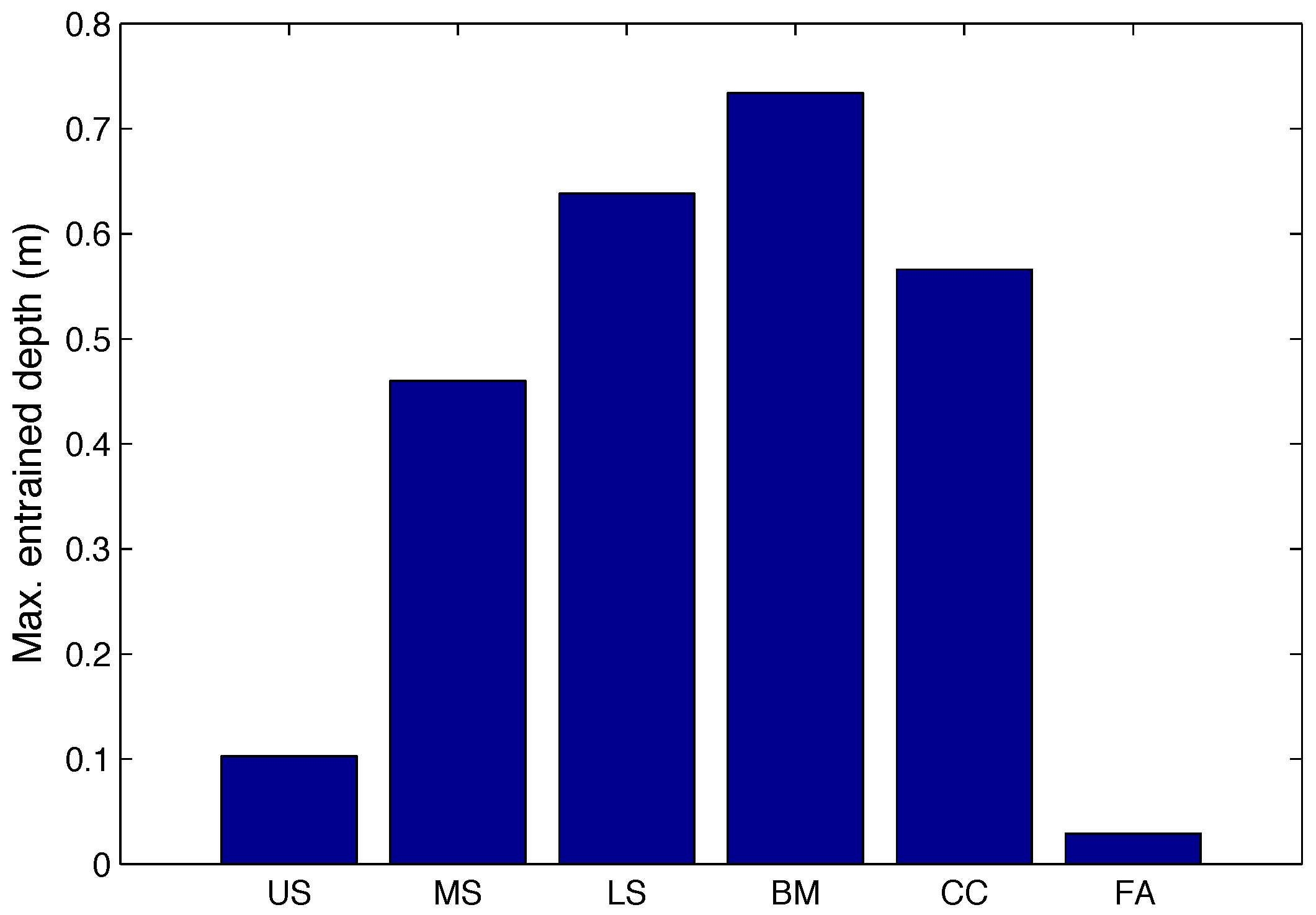
Water 17 00406 g007
Figure 7. Maximum entrained depth at selected locations.
Figure 7. Maximum entrained depth at selected locations.
Water 17 00406 g007
Water 17 00406 g008
Figure 8. Flow height for (a) solid, (b) fluid, (c) total (combined solid and fluid), and (d) final basechange.
Figure 8. Flow height for (a) solid, (b) fluid, (c) total (combined solid and fluid), and (d) final basechange.
Water 17 00406 g008
Water 17 00406 g009
Figure 9. Maximum velocity for the (a) solid and (b) fluid phases during the simulated debris flow.
Figure 9. Maximum velocity for the (a) solid and (b) fluid phases during the simulated debris flow.
Water 17 00406 g009
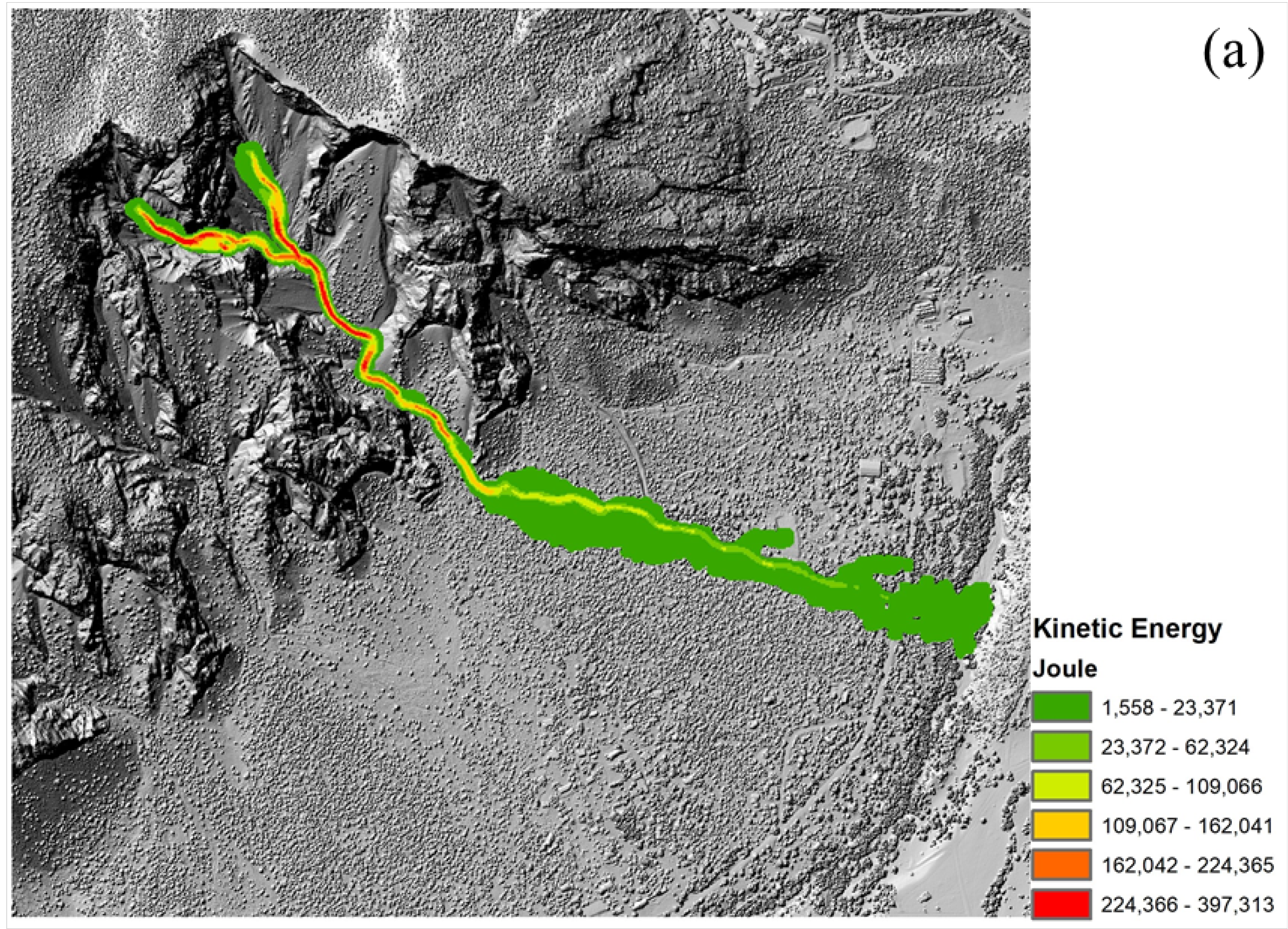
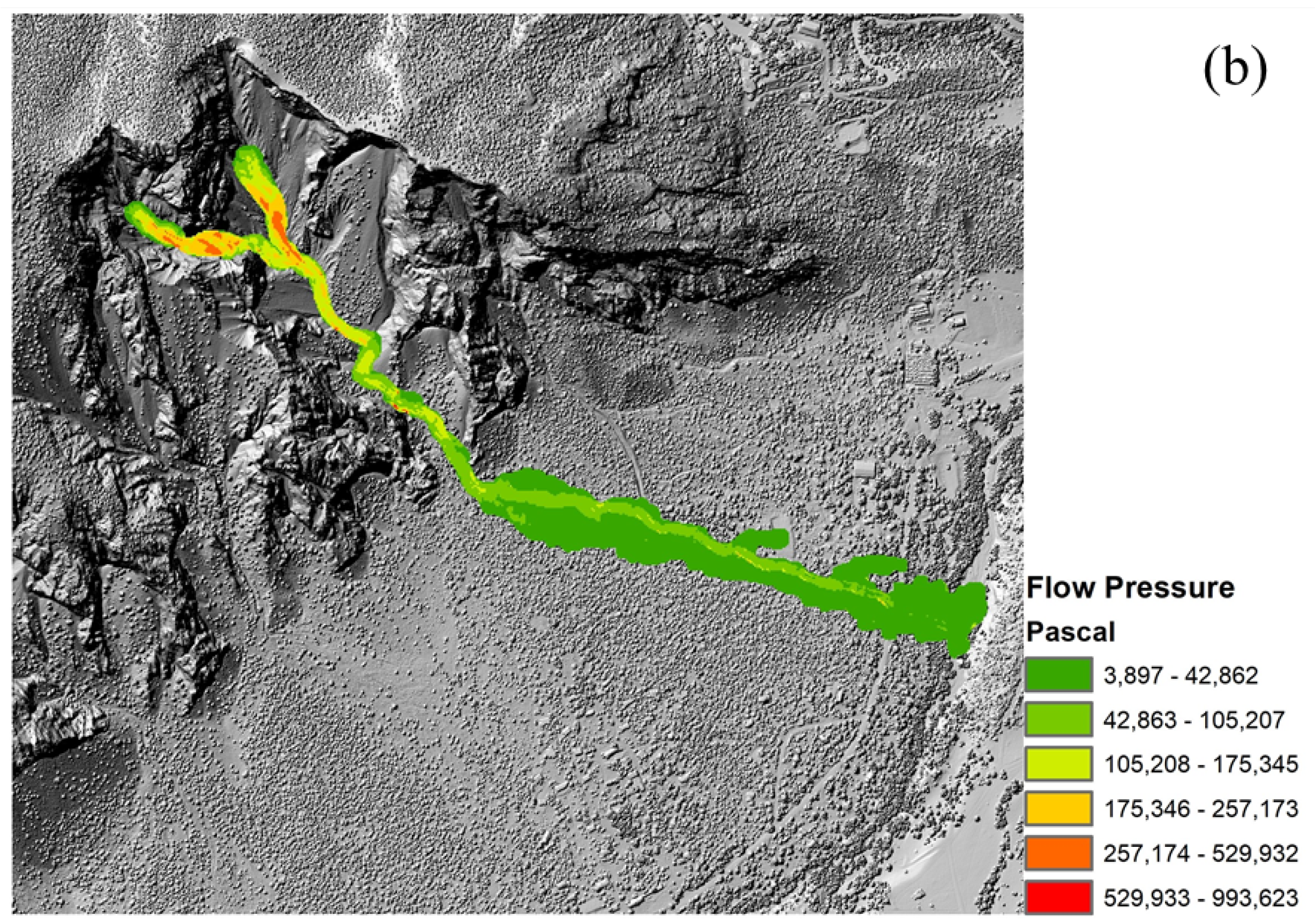
Water 17 00406 g010aWater 17 00406 g010b
Figure 10. (a) Maximum kinetic energy and (b) maximum flow pressure during the simulated debris flow.
Figure 10. (a) Maximum kinetic energy and (b) maximum flow pressure during the simulated debris flow.
Water 17 00406 g010aWater 17 00406 g010b
Water 17 00406 g011
Figure 11. Final Basechange with a basal solid friction angle of (a) 10 ∘ and (b) 20 ∘ .
Figure 11. Final Basechange with a basal solid friction angle of (a) 10 ∘ and (b) 20 ∘ .
Water 17 00406 g011
Water 17 00406 g012
Figure 12. Maximum flow height with a basal solid friction angle of (a) 10 ∘ and (b) 20 ∘ .
Figure 12. Maximum flow height with a basal solid friction angle of (a) 10 ∘ and (b) 20 ∘ .
Water 17 00406 g012
Water 17 00406 g013
Figure 13. Final basechange with an entrainment coefficient of (a) C E = 0 , (b) C E = 10 − 6.75 , and (c) C E = 10 − 6.55 .
Figure 13. Final basechange with an entrainment coefficient of (a) C E = 0 , (b) C E = 10 − 6.75 , and (c) C E = 10 − 6.55 .
Water 17 00406 g013
Water 17 00406 g014
Figure 14. Maximum flow height with an entrainment coefficient of (a) C E = 0 , (b) C E = 10 − 6.75 , and (c) C E = 10 − 6.55 .
Figure 14. Maximum flow height with an entrainment coefficient of (a) C E = 0 , (b) C E = 10 − 6.75 , and (c) C E = 10 − 6.55 .
Water 17 00406 g014
Table 1. A summary of the characteristics of the debris flow event on 15 September 2009 [47].
Table 1. A summary of the characteristics of the debris flow event on 15 September 2009 [47].
ObservationValue
Cumulative rainfall24.6 mm
Rainstorm duration115 min
Event volume at US822 m 3
Peak discharge at US13.5 m 3 / s
Max frontal velocity V u s , V t t 3.7, 1.2 m / s
Max flow depth at US, MS, and LS1.1, 0.45, 1.02 m
Basal change at US, MS, and LS−1.1, −0.28, +0.14 m
Table 2. Parameters used in the simulation.
Table 2. Parameters used in the simulation.
ParameterValue
Density of solid1750 kg / m 3
Density of fluid1000 kg / m 3
Internal friction angle 35 ∘
Basal friction angle ( δ ) 15 ∘
Fluid friction coefficient ( μ )0.1
Ambient drag coefficient0.01
Kinematic viscosity 10 − 3 kg / ( m s )
Entrainment coefficient ( C E ) 10 − 6.65
Solid–fluid ratio0.75:0.25
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Naqvi, M.W.; KC, D.; Hu, L. A Case Study of the Debris Flows Event in the Chalk Cliffs Basin, Colorado, USA: Numerical Simulations Based on a Multi-Phase Flow Model. Water 2025, 17, 406. https://doi.org/10.3390/w17030406

AMA Style

Naqvi MW, KC D, Hu L. A Case Study of the Debris Flows Event in the Chalk Cliffs Basin, Colorado, USA: Numerical Simulations Based on a Multi-Phase Flow Model. Water. 2025; 17(3):406. https://doi.org/10.3390/w17030406

Chicago/Turabian Style

Naqvi, Mohammad Wasif, Diwakar KC, and Liangbo Hu. 2025. "A Case Study of the Debris Flows Event in the Chalk Cliffs Basin, Colorado, USA: Numerical Simulations Based on a Multi-Phase Flow Model" Water 17, no. 3: 406. https://doi.org/10.3390/w17030406

APA Style

Naqvi, M. W., KC, D., & Hu, L. (2025). A Case Study of the Debris Flows Event in the Chalk Cliffs Basin, Colorado, USA: Numerical Simulations Based on a Multi-Phase Flow Model. Water, 17(3), 406. https://doi.org/10.3390/w17030406

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop