Spatiotemporal Drought Analysis Using the Composite Drought Index (CDI) over Dobrogea, Romania
Abstract
1. Introduction
2. Materials and Methods
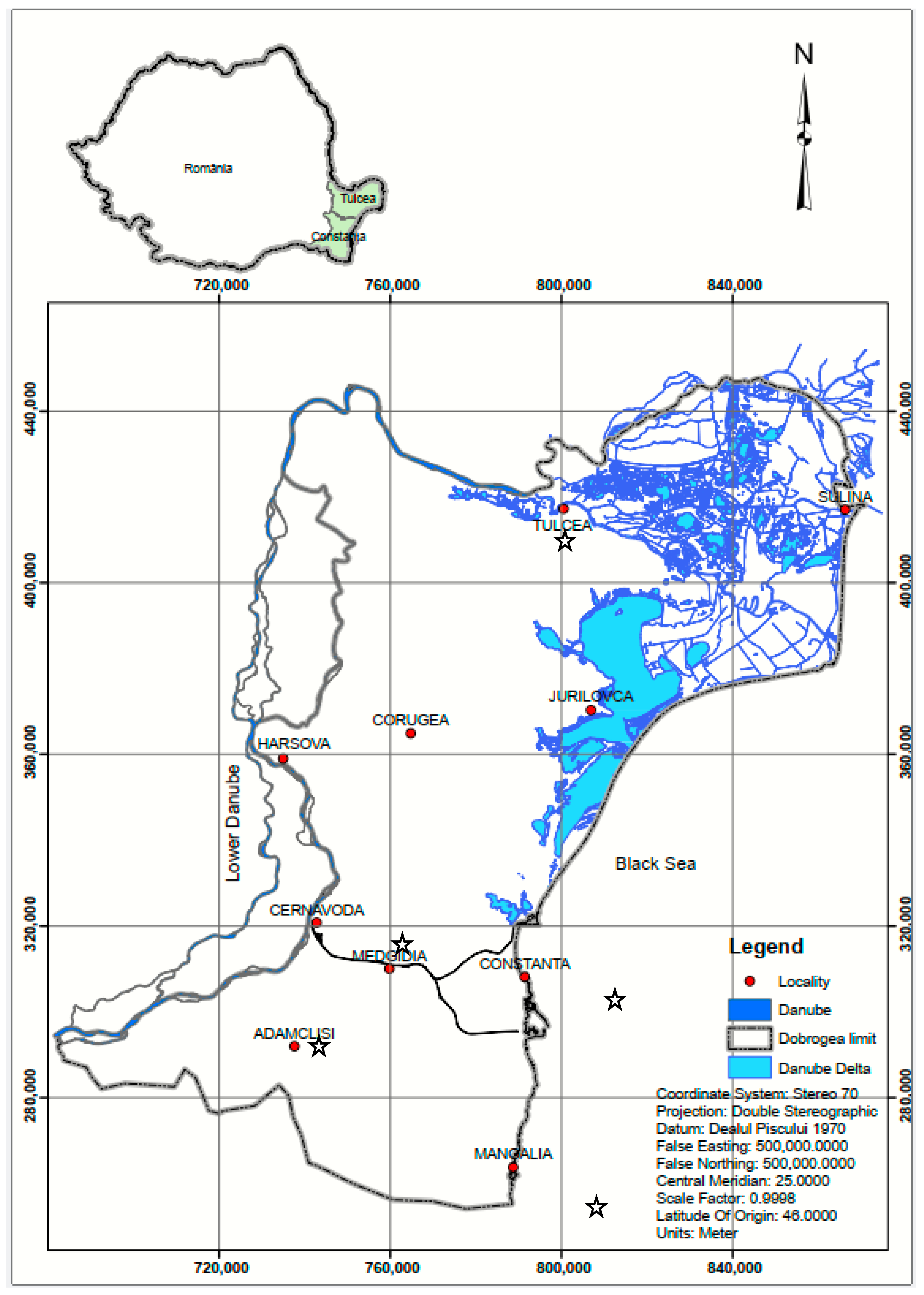
2.1. Study Area
2.2. Datasets
| Station Used | Longitude/Latitude |
|---|---|
| Constanta | 28.64/44.21 |
| Tulcea | 28.82/45.19 |
| Medgidia | 28.25/44.24 |
| Mangalia | 28.58/43.82 |
| Adamclisi | 27.96/44.09 |
2.2.1. NDVI and LST Datasets
2.2.2. Precipitation Datasets
2.2.3. SPEI Dataset
2.2.4. Ground Stations Datasets
2.3. Methods
2.3.1. Composite Drought Index (CDI)
2.3.2. Standardized Precipitation Index (SPI)
2.3.3. Drought Severity, Duration, Frequency, Intensity, and Probability of Occurrence
2.3.4. Validation of High-Resolution Rainfall Products
2.3.5. Performance Evaluation of Satellite Precipitation Products
2.3.6. Correlation Between the SPI and CDI
2.3.7. Correlation Between the SPEI and CDI
3. Results
3.1. Annual Precipitation Evaluation of Two High-Resolution Precipitation Products at the Regional Scale
3.2. Correlation Between 1-Month SPI-1 and In Situ SPI-1
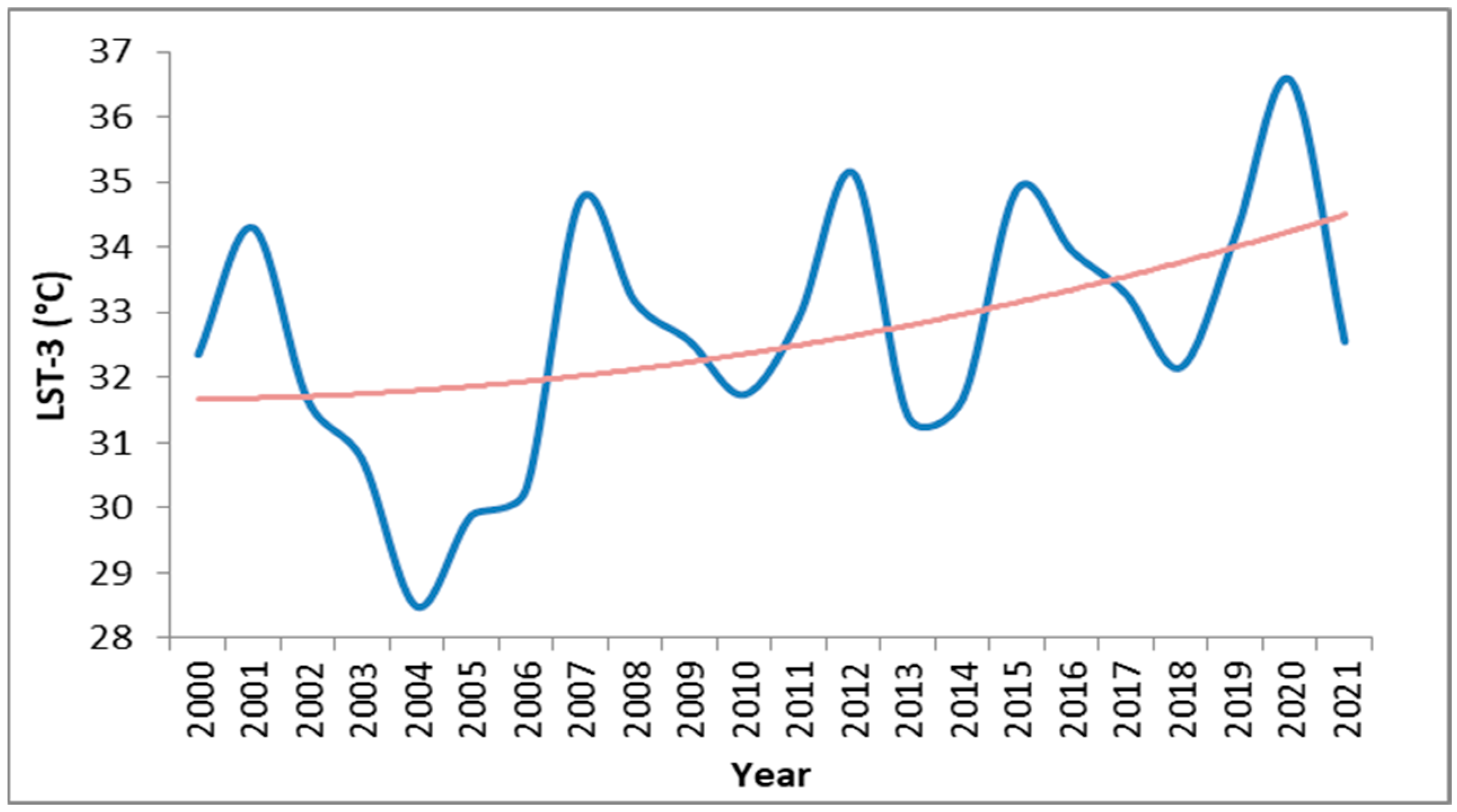
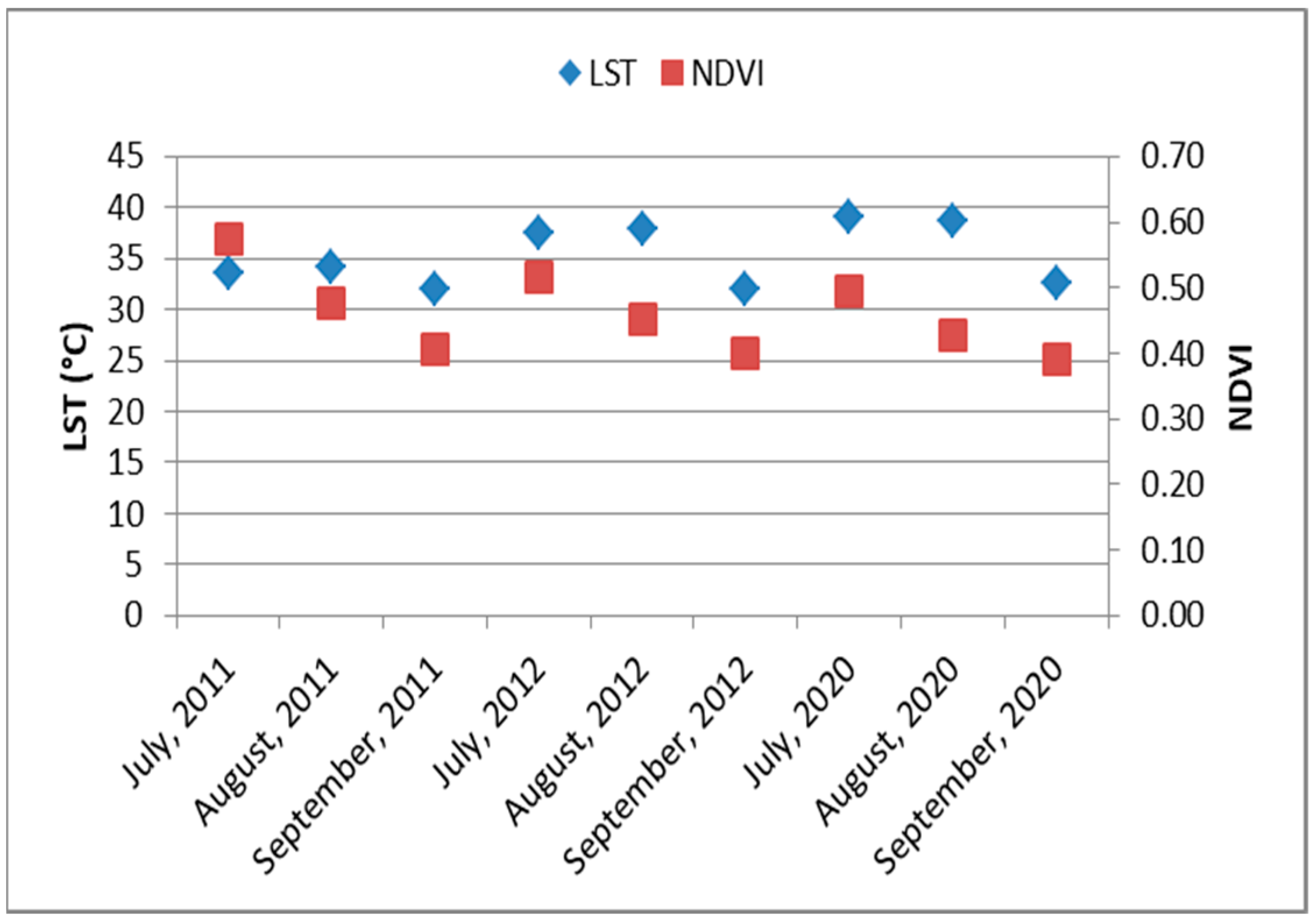
3.3. Temporal Dynamics of LST and the NDVI During the Dry Season
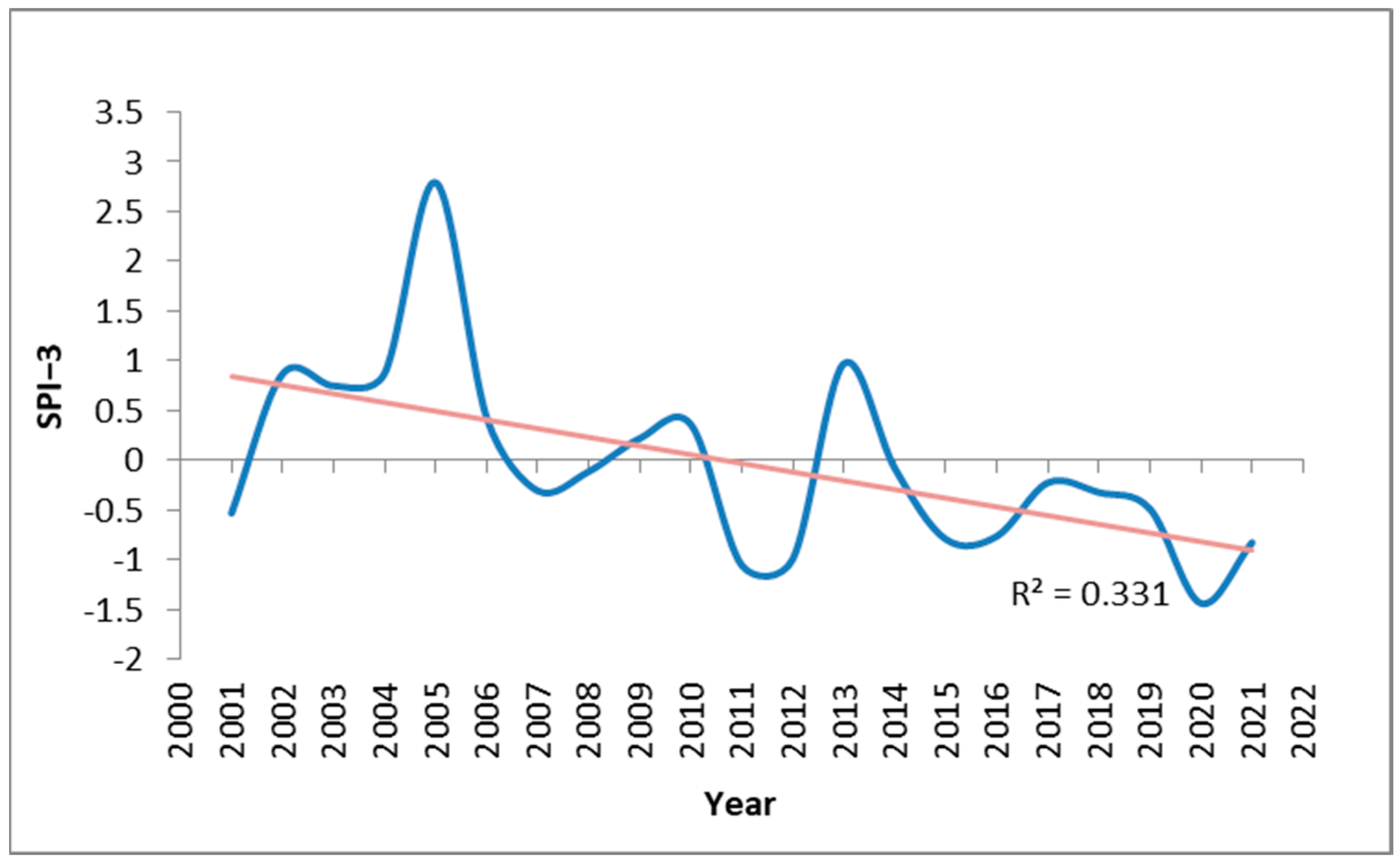
3.4. Spatiotemporal Dynamics of 3-Month SPI During the Dry Season
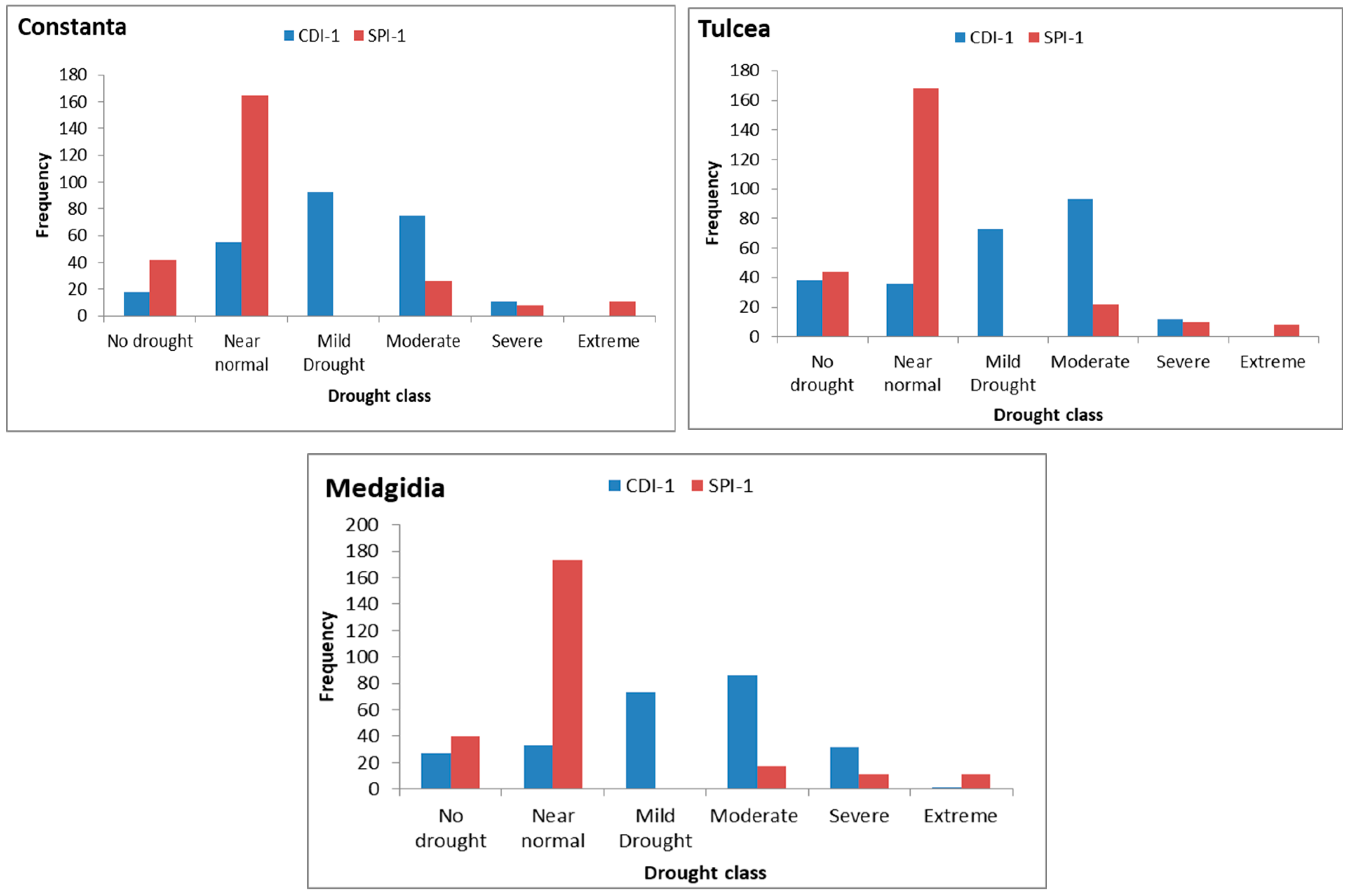
3.5. Spatiotemporal Dynamics of the CDI During the Dry Season
3.6. Correlation Between the CDI and SPI
3.7. Correlation Between the SPEI and SPI
3.8. Correlation Between the CDI and SPEI
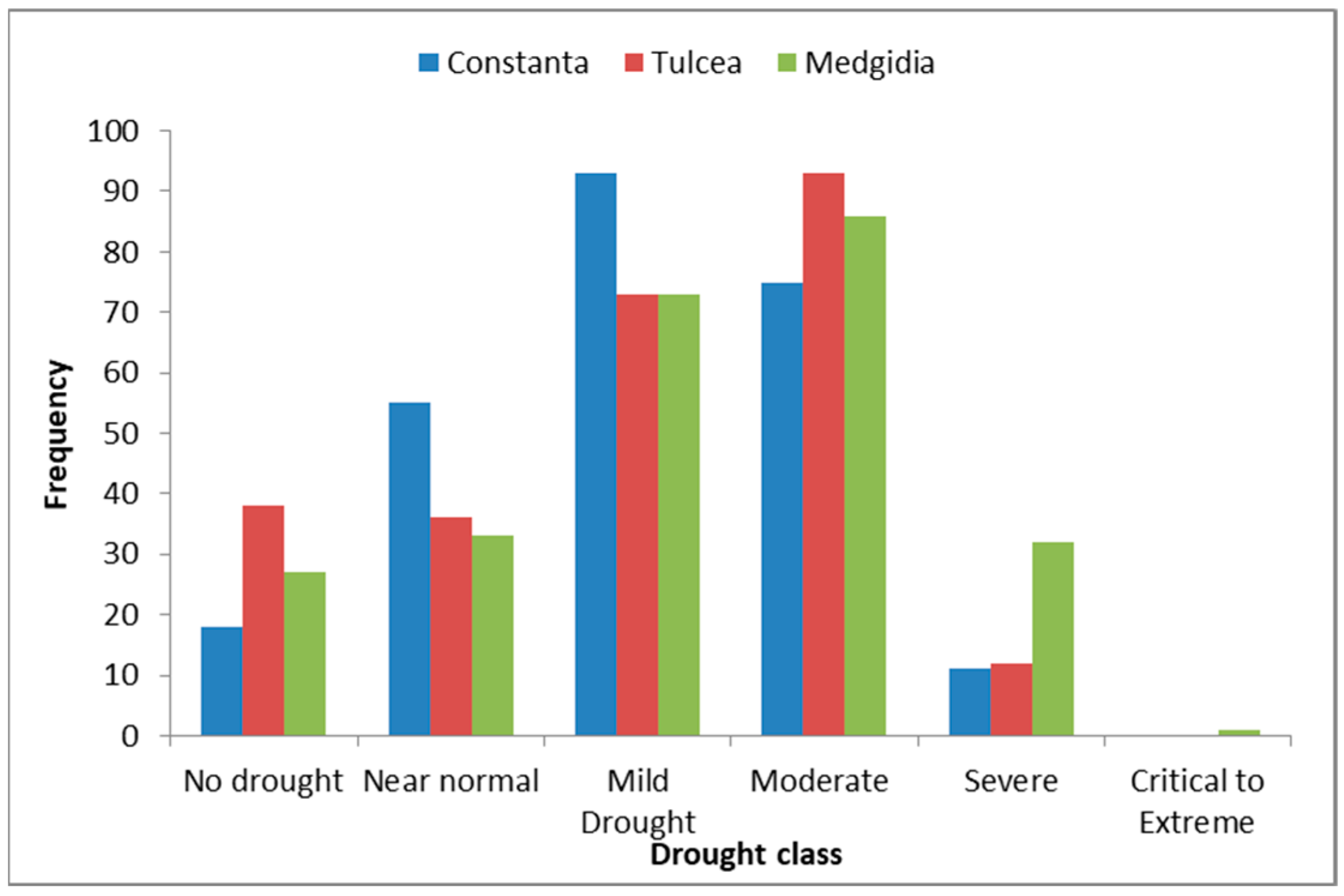
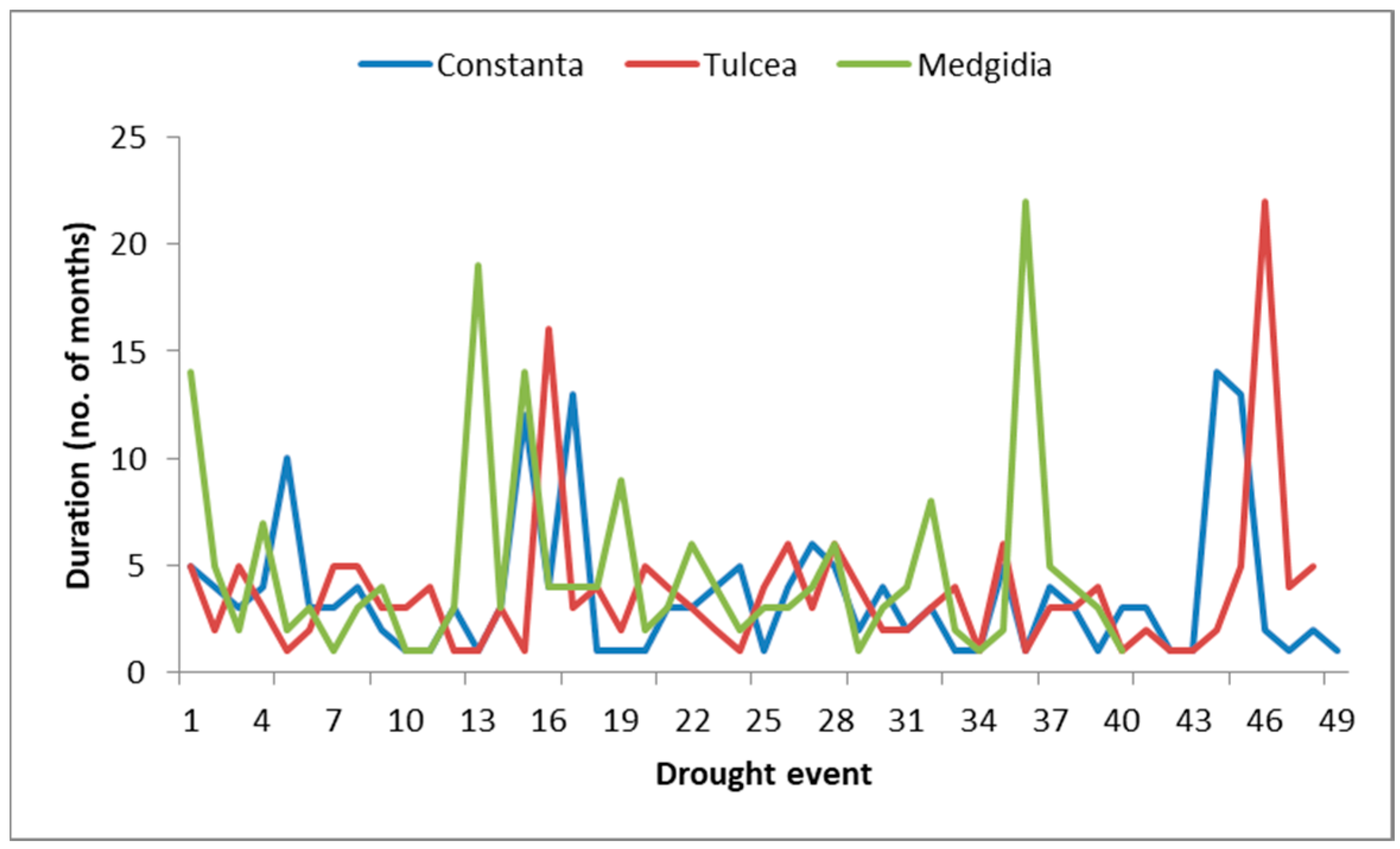
3.9. CDI-Based Drought Characteristics
4. Discussion
4.1. Assessment of Drought Based on the CDI in Dobrogea Area and Practical Implication
4.2. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bokal, S.; Müller, R. Integrated Drought Management in Central and Eastern Europe; WMO: Geneva, Switzerland, 2018. [Google Scholar]
- Maftei, C.E.; Bărbulescu, A.; Osman, A. Assessment of the Drought Risk in Constanta County, Romania. Atmosphere 2024, 15, 1281. [Google Scholar] [CrossRef]
- Maftei, C.; Dobrica, G.; Cerneaga, C.; Buzgaru, N. Drought Land Degradation and Desertification—Case Study of Nuntasi-Tuzla Lake in Romania. In Water Safety, Security and Sustainability: Threat Detection and Mitigation; Vaseashta, A., Maftei, C., Eds.; Advanced Sciences and Technologies for Security Applications; Springer International Publishing: Cham, Switzerland, 2021; pp. 583–597. ISBN 978-3-030-76008-3. [Google Scholar]
- CE. COM (2007) 414—Addressing the Challenge of Water Scarcity and Droughts in the EU—EU Monitor; CE: Brussels, Belgium, 2007. [Google Scholar]
- CE. COM (2012) 673—Blueprint to Safeguard Europe’s Water Resources—EU Monitor; CE: Brussels, Belgium, 2012. [Google Scholar]
- Stein, U.; Özerol, G.; Tröltzsch, J.; Landgrebe, R.; Szendrenyi, A.; Vidaurre, R. European Drought and Water Scarcity Policies. In Governance for Drought Resilience: Land and Water Drought Management in Europe; Bressers, H., Bressers, N., Larrue, C., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 17–43. ISBN 978-3-319-29671-5. [Google Scholar]
- Fatulová, E.; Majerčáková, O.; Houšková, B.; Bardarska, G.; Alexandrov, V.; Kulířová, P.; Gayer, J.; Molnár, P.; Fiala, K.; Tamás, J.; et al. Guidelines for Preparation of the Drought Management Plans: Development and Implementation of Risk-Based Drought Management Plans in the Context of the EU Water Framework Directive—As Part of the River Basin Management Plans; Global Water Partnership Central and Eastern Europe: Bratislava, Slovakia, 2015; ISBN 978-80-972060-1-7. [Google Scholar]
- United Nations Office for Disaster Risk Reduction (UNDRR). Available online: https://www.undrr.org/terminology/hazard (accessed on 15 October 2024).
- Kogan, F.N. Droughts of the Late 1980s in the United States as Derived from NOAA Polar-Orbiting Satellite Data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Haied, N.; Foufou, A.; Khadri, S.; Boussaid, A.; Azlaoui, M.; Bougherira, N. Spatial and Temporal Assessment of Drought Hazard, Vulnerability and Risk in Three Different Climatic Zones in Algeria Using Two Commonly Used Meteorological Indices. Sustainability 2023, 15, 10. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- WMO; GWP. Handbook of Drought Indicators and Indices; Svoboda, M., Fuchs, B., Eds.; WMO: Geneva, Switzerland, 2016; ISBN 978-92-63-11173-9. [Google Scholar]
- Palmer, W.C. Meteorological Drought. Weather. Bur. Res. Pap. 1965, 45, 1–58. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. Eighth Conf. Appl. Climatol. 1993, 22, 174–184. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln Declaration on Drought Indices: Universal Meteorological Drought Index Recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef]
- Alahacoon, N.; Edirisinghe, M.A. Comprehensive Assessment of Remote Sensing and Traditional Based Drought Monitoring Indices at Global and Regional Scale. Geomat. Nat. Hazards Risk 2022, 13, 762–799. [Google Scholar] [CrossRef]
- European Drought Observatory|Copernicu. Available online: https://www.copernicus.eu/en/european-drought-observatory (accessed on 23 October 2024).
- EDO. Available online: https://www.copernicus.eu/ro/node/8534 (accessed on 15 October 2024).
- Mateescu, E.; Smarandache, M.; Jeler, N.; Apostol, V. Drought Conditions and Management Strategies in Romania (Capacity Development to Support National Drought Management Policy) [Country Report]. Available online: https://www.droughtmanagement.info/literature/UNW-DPC_NDMP_Country_Report_Romania_2013.pdf (accessed on 1 July 2015).
- Maftei, C.; Barbulescu, A. Statistical Analysis of Climate Evolution in Dobrudja Region. In Proceedings of the World Congress on Engineering, WCE, London, UK, 2–4 July2008; Volume 2, pp. 2–4. [Google Scholar]
- Dobrica, G. Evaluarea Secetei Hidrologice în Bazinul Hidrografic al Lacului Nuntași-Tuzla, Județul Constanța (Assessment of the Hydrological Drought in the Nuntași-Tuzla Lake Watershed, Constanța County). Ph.D. Thesis, Unpublished. Ovidius University of Constanta, Constanta, Romania, 2023. [Google Scholar]
- Croitoru, A.-E.; Piticar, A.; Imbroane, A.M.; Burada, D.C. Spatiotemporal distribution of aridity indices based on temperature and precipitation in the extra-Carpathian regions of Romania. Theor. Appl. Climatol. 2013, 112, 597–607. [Google Scholar] [CrossRef]
- Dascălu, S.I.; Gothard, M.; Bojariu, R.; Birsan, M.-V.; Cică, R.; Vintilă, R.; Adler, M.-J.; Chendeș, V.; Mic, R.-P. Drought-related variables over the Bârlad basin (Eastern Romania) under climate change scenarios. CATENA 2016, 141, 92–99. [Google Scholar] [CrossRef]
- Ionita, M.; Scholz, P.; Chelcea, S. Assessment of droughts in Romania using the Standardized Precipitation Index. Nat. Hazards 2016, 81, 1483–1498. [Google Scholar] [CrossRef]
- Paltineanu, C.; Mihailescu, I.F.; Prefac, Z.; Dragota, C.; Vasenciuc, F.; Claudia, N. Combining the standardized precipitation index and climatic water deficit in characterizing droughts: A case study in Romania. Theor. Appl. Climatol. 2009, 97, 219–233. [Google Scholar] [CrossRef]
- Stefan, S.; Ghioca, M.; Rimbu, N.; Boroneant, C. Study of meteorological and hydrological drought in southern Romania from observational data. Int. J. Climatol. 2004, 24, 871–881. [Google Scholar] [CrossRef]
- Chelcea, S.M.; Aldea, A.A.; Trifu, M.C. An Assessment of Low Flow and Water Deficits on the Danube and Romanian Rivers During 1980–2020. In Modeling and Monitoring Extreme Hydrometeorological Events; IGI Global Scientific Publishing: Hershey, PA, USA, 2024; pp. 185–229. [Google Scholar] [CrossRef]
- Drobot, R.; Draghia, A.F.; Sîrbu, N.; Dinu, C. Synthetic Drought Hydrograph. Hydrology 2023, 10, 10. [Google Scholar] [CrossRef]
- Pravalie, R.; Sîrodoev, I.; Peptenatu, D. Changes in the forest ecosystems in areas impacted by aridization in south-western Romania. J. Environ. Health Sci. Eng. 2014, 12, 2. [Google Scholar] [CrossRef]
- Nasiri, V.; Sadeghi, S.M.M.; Moradi, F.; Afshari, S.; Deljouei, A.; Griess, V.C.; Maftei, C.; Borz, S.A. The Influence of Data Density and Integration on Forest Canopy Cover Mapping Using Sentinel-1 and Sentinel-2 Time Series in Mediterranean Oak Forests. ISPRS Int. J. Geo-Inf. 2022, 11, 423. [Google Scholar] [CrossRef]
- Cheval, S.; Dumitrescu, A. The summer surface urban heat island of Bucharest (Romania) retrieved from MODIS images. Theor. Appl. Climatol. 2015, 121, 631–640. [Google Scholar] [CrossRef]
- Vorovencii, I. Assessing and monitoring the risk of desertification in Dobrogea, Romania, using Landsat data and decision tree classifier. Environ. Monit. Assess. 2015, 187, 204. [Google Scholar] [CrossRef]
- Angearu, C.-V.; Ontel, I.; Boldeanu, G.; Mihailescu, D.; Nertan, A.; Craciunescu, V.; Catana, S.; Irimescu, A. Multi-Temporal Analysis and Trends of the Drought Based on MODIS Data in Agricultural Areas, Romania. Remote Sens. 2020, 12, 23. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Juez, C.; Potopová, V.; Boincean, B.; Murphy, C.; Domínguez-Castro, F.; Eklundh, L.; Peña-Angulo, D.; Noguera, I.; Jin, H.; et al. Drought Risk in Moldova under Global Warming and Possible Crop Adaptation Strategies. Ann. N. Y. Acad. Sci. 2024, 1538, 144–161. [Google Scholar] [CrossRef]
- Páscoa, P.; Gouveia, C.M.; Russo, A.C.; Bojariu, R.; Vicente-Serrano, S.M.; Trigo, R.M. Drought Impacts on Vegetation in Southeastern Europe. Remote Sens. 2020, 12, 2156. [Google Scholar] [CrossRef]
- Badaluta, C.A.; Haliuc, A.; Badaluta, G.; Scriban, R.E. Spatiotemporal variability of drought in Romania during 1901-2021 using the Standardized Precipitation Evapotranspiration Index (SPEI). Analele Univ. Din Oradea Ser. Geogr. 2024, 1, 33–43. [Google Scholar] [CrossRef]
- Angearu, C.V.; Irimescu, A.; Mihailescu, D.; Virsta, A. Evaluation of droughts and fires in the Dobrogea region, using Modis satellite data, Agriculture for Life Life for Agriculture. Conf. Proc. 2018, 1, 336–345. [Google Scholar]
- Abdourahamane, Z.S.; Garba, I.; Gambo Boukary, A.; Mirzabaev, A. Spatiotemporal Characterization of Agricultural Drought in the Sahel Region Using a Composite Drought Index. J. Arid. Environ. 2022, 204, 104789. [Google Scholar] [CrossRef]
- Maftei, C.; Barbulescu, A. Statistical Analysis of Precipitation Time Series in the Dobrudja Region. Mausam 2012, 63, 553–564. [Google Scholar] [CrossRef]
- Roşu, L.; Macarov, L.I. Management of Drought and Floods in the Dobrogea Region. In Extreme Weather and Impacts of Climate Change on Water Resources in the Dobrogea Region; IGI Global: Hershey, PA, USA, 2015; pp. 403–443. ISBN 978-1-4666-8438-6. [Google Scholar]
- Ciulache, S.; Torica, V. Dobrudja ’s climate (in Romanian), Annals of the University of Bucharest. Geogr. Ser. 2003, 17, 83–105. [Google Scholar]
- Posea, G.; Bogdan, O.; Zăvoianu, I. (Eds.) Geography of Romania. In The Romanian Plain, Danube, Dobrudja Platou, The Romanian Black Sea Seaside and the Continental Platform (in Romanian); Romanian Academy Printing House: Bucharest, Romania, 2005; Volume 5. [Google Scholar]
- Bandoc, G.; Pravalie, R. Climatic water balancedynamics over the last five decades in Romania’smost arid region, Dobrogea. J. Geogr. Sci. 2015, 25, 1307–1327. [Google Scholar] [CrossRef]
- Mitrică, B.; Mateescu, E.; Dragotă, C.S.; Grigorescu, I.; Dumitraşcu, M.; Popovici, E.A. Climatechange impacts on agricultural crops in the Timiş Plain, Romania. Rom. Agric. Res. 2015, 32, 93–101. [Google Scholar]
- Lup, A.; Miron, L. Drought Management in the Agriculture of Dobrogea Province, MPRA Paper 53403; University Library of Munich: Munich, Germany, 2013. [Google Scholar]
- Chelcea, S.; Ionita, M.; Adler, M.-J. Identification of Dry Periods in the Dobrogea Region. In Extreme Weather and Impacts of Climate Change on Water Resources in the Dobrogea Region; IGI Global: Hershey, PA, USA, 2015; pp. 52–72. ISBN 978-1-4666-8438-6. [Google Scholar]
- Ionita, M.; Chelcea, S. Spatio-Temporal Variability of Seasonal Drought over the Dobrogea Region. In Extreme Weather and Impacts of Climate Change on Water Resources in the Dobrogea Region; IGI Global: Hershey, PA, USA, 2015; pp. 17–51. ISBN 978-1-4666-8438-6. [Google Scholar]
- Maftei, C.; Buta, C.; Carazeanu Popovici, I. The Impact of Human Interventions and Changes in Climate on the Hydro-Chemical Composition of Techirghiol Lake (Romania). Water 2020, 12, 2261. [Google Scholar] [CrossRef]
- Balteanu, D.; Șerban, M. Global environmental changes. In An Interdisciplinary Evaluation of Uncertainties; Coresi Printing House: Bucharest, Romania, 2005. (In Romanian) [Google Scholar]
- Google Earth Engine (GEE) Platform. Available online: https://developers.google.com/earth-engine/datasets/ (accessed on 10 May 2024).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Javed, T.; Li, Y.; Rashid, S.; Li, F.; Hu, Q.; Feng, H.; Chen, X.; Ahmad, S.; Liu, F.; Pulatov, B. Performance and relationship of four different agricultural drought indices for drought monitoring in China’s mainland using remote sensing data. Sci. Total Environ 2021, 759, 143530. [Google Scholar] [CrossRef] [PubMed]
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-based Joint Drought Index using SPI and EDDI and its application to climate change. Sci. Total Environ 2020, 744, 140701. [Google Scholar] [CrossRef]
- Achour, K.; Meddi, M.; Zeroual, A.; Bouabdelli, S.; Maccioni, P.; Moramarco, T. Spatio-temporal analysis and forecasting of drought in the plains of northwestern Algeria using the standardized precipitation index. J. Earth Syst. Sci. 2020, 129, 42. [Google Scholar] [CrossRef]
- Guttman, N.B. Comparing the palmer drought index and the standardized precipitation index 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- Mpelasoka, F.; Hennessy, K.; Jones, R.; Bates, B. Comparison of suitable drought indices for climate change impacts assessment over Australia towards resource management. Int. J. Climatol. 2008, 28, 1283–1292. [Google Scholar] [CrossRef]
- Yevjevich, V.M. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. In Hydrology Papers; Colorado State University: Denver, CO, USA, 1967. [Google Scholar]
- Malik, A.; Kumar, A.; Salih, S.Q.; Yaseen, Z.M. Hydrological Drought Investigation Using Streamflow Drought Index. In Intelligent Data Analytics for Decision-Support Systems in Hazard Mitigation: Theory and Practice of Hazard Mitigation; Springer: Berlin/Heidelberg, Germany, 2021; pp. 63–88. [Google Scholar]
- Aiyelokun, O.; Ogunsanwo, G.; Ojelabi, A.; Agbede, O. Gaussian Naïve Bayes Classification Algorithm for Drought and Flood Risk Reduction. In Intelligent Data Analytics for Decision-Support Systems in Hazard Mitigation: Theory and Practice of Hazard Mitigation; Springer: Berlin/Heidelberg, Germany, 2021; pp. 49–62. [Google Scholar]
- Chen, S.; Li, Q.; Zhong, W.; Wang, R.; Chen, D.; Pan, S. Improved monitoring and assessment of meteorological drought based on multi-source fused precipitation data. Int. J. Environ. Res. Public Health 2022, 19, 1542. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, W.; Zhou, T.; Wu, W.; Liu, T.; Sun, C. Plant phenomics & precision agriculture simulation of winter wheat growth by the assimilation of unmanned aerial vehicle imagery into the WOFOST model. PLoS ONE 2021, 16, e0246874. [Google Scholar]
- Araujo, J.; Born, D.G. Calculating percentage agreement correctly but writing its formula incorrectly. Behav. Anal. 1985, 8, 207. [Google Scholar] [CrossRef]
- SPI Generator. Available online: https://drought.unl.edu/monitoring/SPI/SPIProgram.aspx (accessed on 10 July 2024).
- Bayissa, Y.; Tadesse, T.; Demisse, G. Building a High-Resolution Vegetation Outlook Model to Monitor Agricultural Drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2019, 11, 371. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente Serrano, S.M. SPEI Calculator; Digital.CSIC: Madrid, Spain, 2009. [Google Scholar] [CrossRef]
- Pazhanivelan, S.; Geethalakshmi, V.; Samykannu, V.; Kumaraperumal, R.; Kancheti, M.; Kaliaperumal, R.; Raju, M.; Yadav, M.K. Evaluation of SPI and Rainfall Departure Based on Multi-Satellite Precipitation Products for Meteorological Drought Monitoring in Tamil Nadu. Water 2023, 15, 1435. [Google Scholar] [CrossRef]
- Gulacsi, A.; Kovacs, F. Drought monitoring with spectral indices calculated from MODIS satellite images in Hungary. J. Environ. Geog. 2015, 8, 11–20. [Google Scholar] [CrossRef]
- Popescu, A.; Dinu, T.A.; Stoian, E.; Serban, V. Variation of the main agricultural crops yield due to drought in Romania and Dobrogea region in the period 2000–2019, Scientific Papers Series Management. Econ. Eng. Agric. Rural. Dev. 2020, 20, 397–416. [Google Scholar]
- Serban, C.; Maftei, C.; Dobrică, G. Surface Water Change Detection via Water Indices and Predictive Modeling Using Remote Sensing Imagery: A Case Study of Nuntasi-Tuzla Lake, Romania. Water 2022, 14, 556. [Google Scholar] [CrossRef]
- Ionita, M.; Tallaksen, L.M.; Kingston, D.G.; Stagge, J.H.; Laaha, G.; Van Lanen, H.A.J.; Scholz, P.; Chelcea, S.M.; Haslinger, K. The European 2015 drought from a climatological perspective. Hydrol. Earth Syst. Sci. 2017, 21, 1397–1419. [Google Scholar] [CrossRef]
- Păltineanu, C.; Mihăilescu, I.F.; Seceleanu, I. Dobrogea: Pedoclimatic Conditions, Consumption and Irrigation Water Requirements of the Main Agricultural Crops (in Romanian); Ex Ponto: Constanta, Romania, 2000. [Google Scholar]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A review of water scarcity and drought indexes in water resources planning and management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef]
- EDO Web Portal. Available online: https://edo.jrc.ec.europa.eu/edov2/php/index.php?id=1051 (accessed on 15 October 2024).






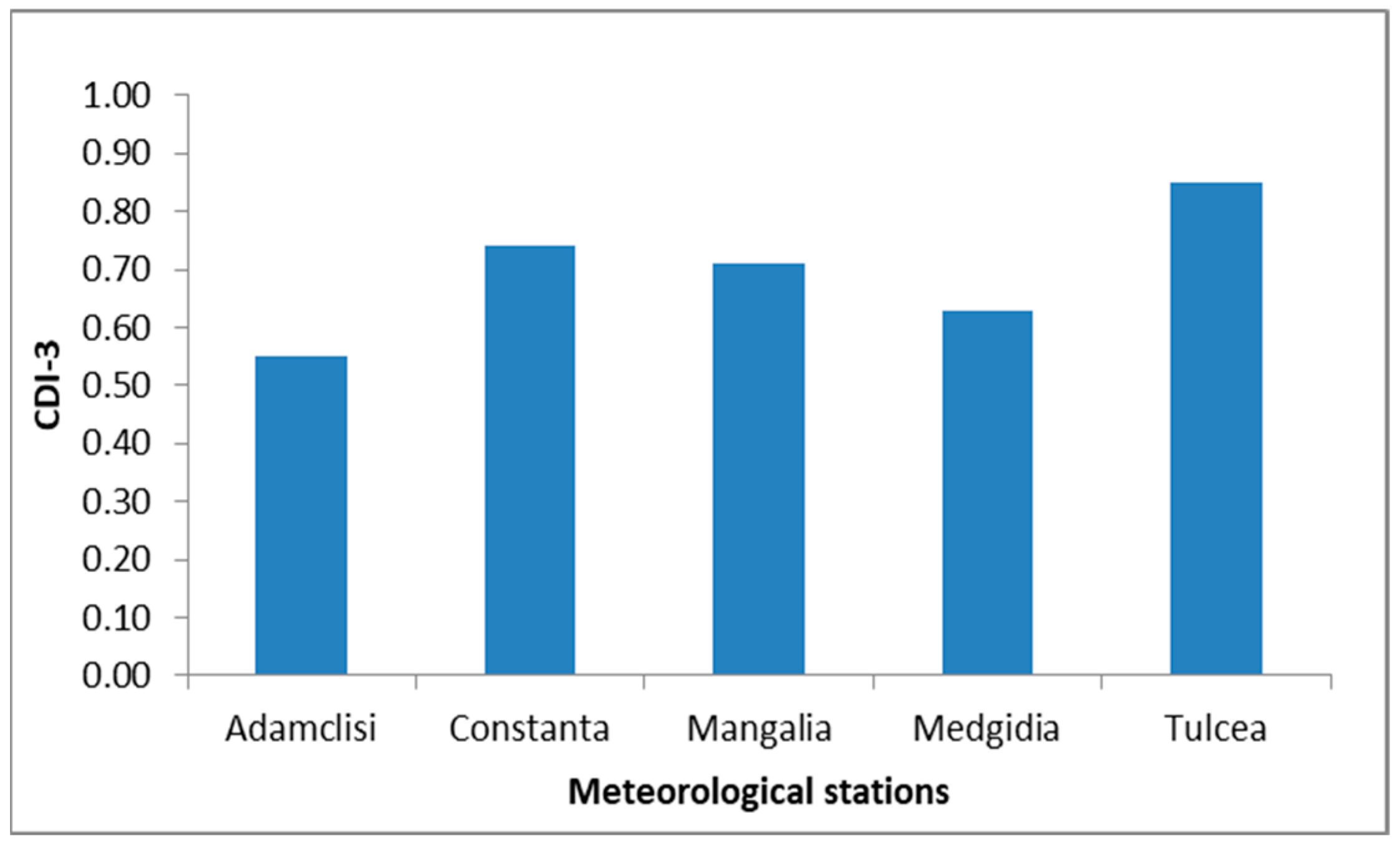

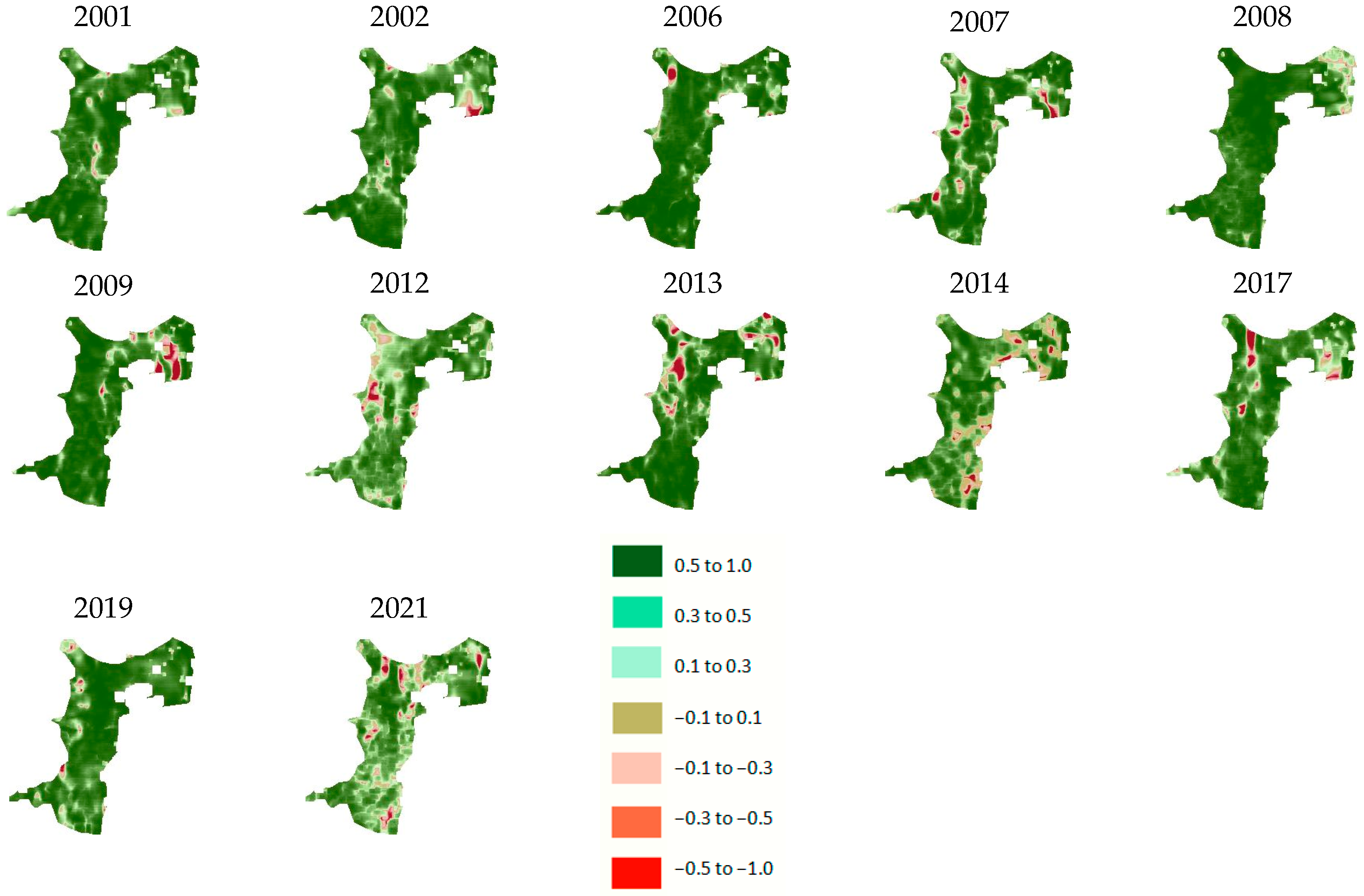
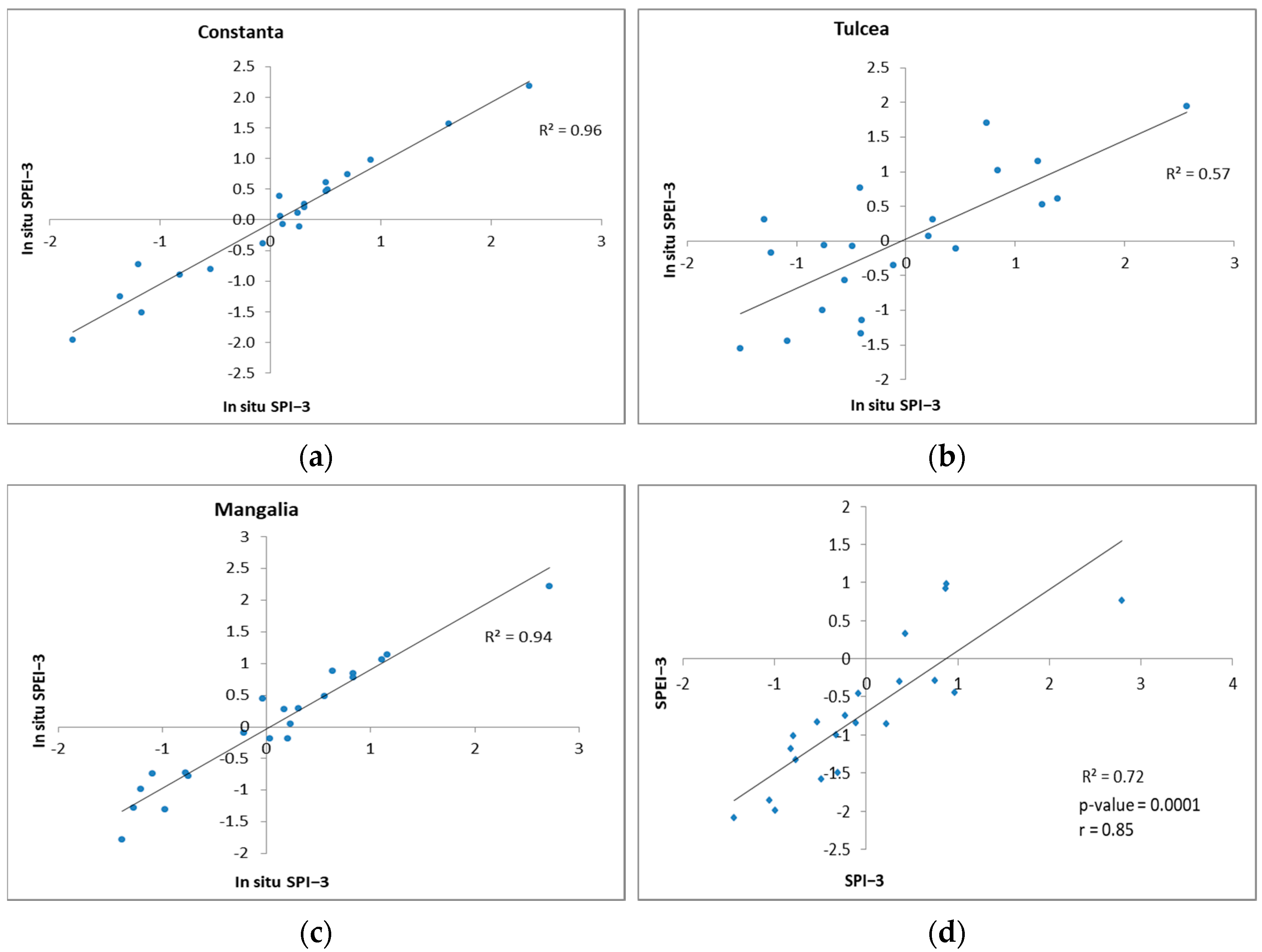
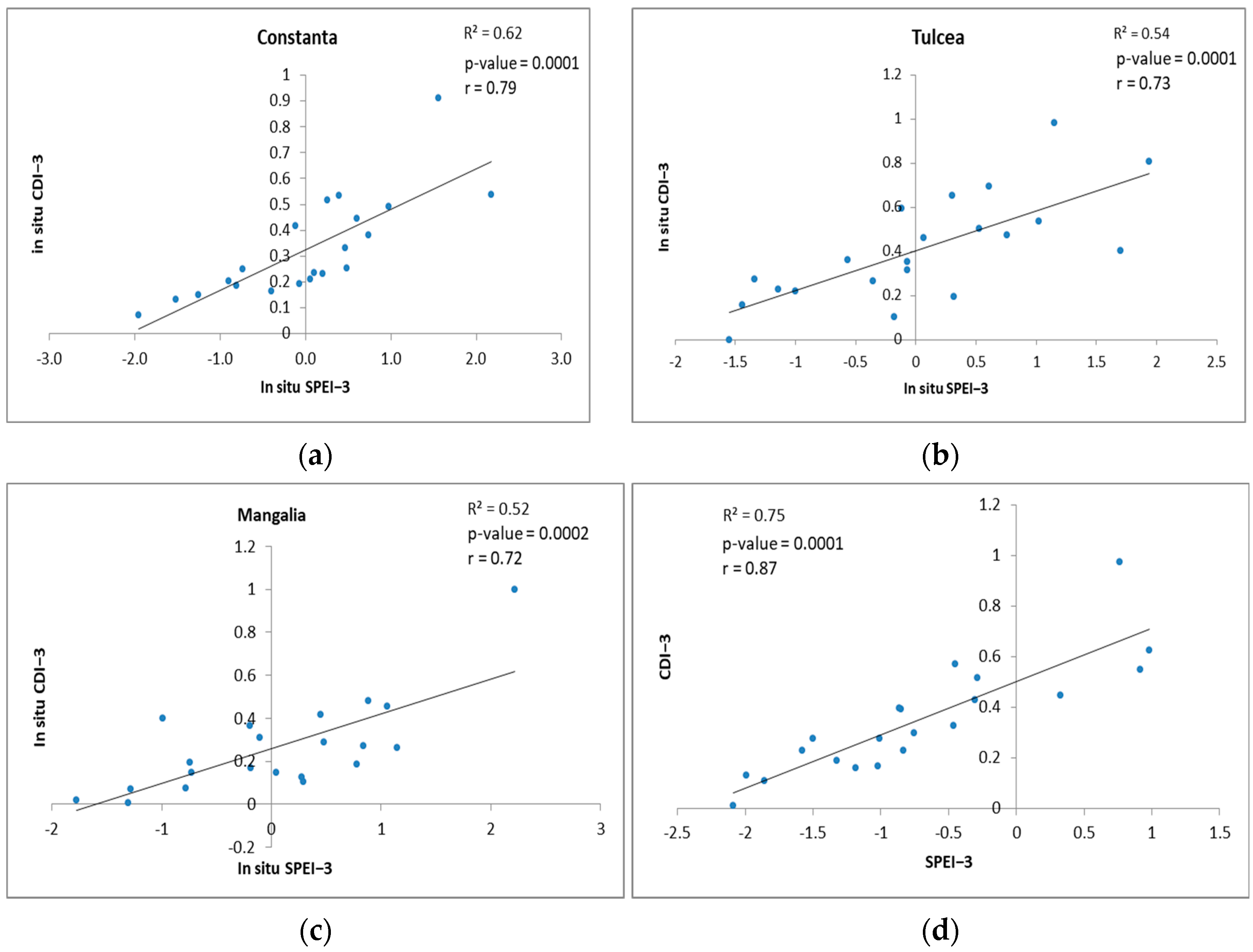
| CDI | Drought Severity Categories |
|---|---|
| >0.5 | No drought |
| 0.4–0.5 | Near Normal |
| 0.3–0.4 | Mild |
| 0.2–0.3 | Moderate |
| 0.1–0.2 | Severe |
| 0.03–0.1 | Critical |
| ≤0.03 | Extreme |
| SPI | Drought Severity Level |
|---|---|
| ≥2 | Extremely Wet |
| 1.50–1.99 | Severely Wet |
| 1.00–1.49 | Moderately Wet |
| −0.99–0.99 | Nearly Normal |
| −1.49–−1.0 | Moderate Drought |
| −1.99–−1.5 | Severe Drought |
| ≤−2 | Extreme Drought |
| Metric | Equation | Interpretation | |
|---|---|---|---|
| Pearson Correlation Coefficient (r) | (14) | r takes values from 1.0 to −1.0, meaning a positive to negative strong linear correlation; a zero or near-zero value indicates no correlation among the variables [61]. | |
| where n represents the number of samples, xi/yi are the ith value of the measured/estimated samples, and and are the average of the measured and estimated values of all samples. Strong correlations have the following values:
| |||
| Root Mean Square Error (RMSE) | (15) | The lower the value, the better the central tendencies and the smaller the errors. A value of zero is the perfect outcome [61]. | |
| Normalized Root Mean Square Error (NRMSE) | For a model, smaller values show reduced residual variance [62]. | ||
| Agreement (%) | Values close to 100% suggest strong agreement; values closer to 0% show the least agreement [63]. | ||
| Weather Station | Constanta | Tulcea | Medgidia | Mangalia | Adamclisi |
|---|---|---|---|---|---|
| Index | GPM IMERG | ||||
| r | 0.90 | 0.95 | 0.70 | 0.77 | 0.70 |
| RMSE | 7.97 | 6.20 | 10.20 | 11.73 | 10.36 |
| NRMSE | 19.7 | 14.6 | 25.0 | 27.7 | 22.20 |
| Agreement | 80.3 | 85.4 | 75.0 | 72.3 | 77.8 |
| CHIRPS | |||||
| r | 0.85 | 0.84 | 0.58 | 0.71 | 0.55 |
| RMSE | 6.16 | 6.12 | 10.45 | 8.66 | 10.73 |
| NRMSE | 15.2 | 14.4 | 25.4 | 20.4 | 23.0 |
| Agreement | 84.8 | 85.6 | 74.6 | 79.6 | 77.0 |
| Year/Drought | Mild | Moderate | Severe | Critical | Extreme |
|---|---|---|---|---|---|
| 2001 | 24.89% | 33.88% | 26.67% | 11.00% | 0.77% |
| 2002 | 0.18% | 0.08% | 0.02% | 0.02% | 0.00% |
| 2003 | 3.66% | 0.08% | 0.03% | 0.02% | 0.01% |
| 2004 | 0.11% | 0.05% | 0.03% | 0.00% | 0.00% |
| 2005 | 0.08% | 0.05% | 0.04% | 0.00% | 0.00% |
| 2006 | 22.87% | 4.85% | 0.05% | 0.03% | 0.01% |
| 2007 | 16.77% | 77.95% | 4.66% | 0.02% | 0.02% |
| 2008 | 12.58% | 19.88% | 36.10% | 3.59% | 0.01% |
| 2009 | 34.49% | 14.20% | 0.09% | 0.02% | 0.01% |
| 2010 | 30.01% | 0.21% | 0.05% | 0.03% | 0.01% |
| 2011 | 0.42% | 2.86% | 62.14% | 34.07% | 0.22% |
| 2012 | 1.28% | 20.19% | 41.04% | 34.74% | 2.38% |
| 2013 | 9.23% | 0.20% | 0.00% | 0.00% | 0.01% |
| 2014 | 60.99% | 24.33% | 0.75% | 0.01% | 0.00% |
| 2015 | 0.54% | 4.42% | 94.56% | 0.06% | 0.00% |
| 2016 | 11.03% | 25.09% | 50.05% | 13.24% | 0.01% |
| 2017 | 43.42% | 43.66% | 7.70% | 0.02% | 0.00% |
| 2018 | 14.25% | 62.00% | 11.23% | 0.05% | 0.01% |
| 2019 | 8.97% | 14.77% | 43.02% | 15.79% | 0.13% |
| 2020 | 0.30% | 0.71% | 2.68% | 21.83% | 74.22% |
| 2021 | 7.07% | 16.88% | 66.46% | 9.13% | 0.05% |
| Station | Mild Drought | Moderate Drought | Severe Drought | Critical to Extreme Drought |
|---|---|---|---|---|
| Constanta | 52% | 42% | 6% | 0 |
| Tulcea | 41% | 52% | 7% | 0 |
| Medgidia | 38% | 45% | 17% | 1% |
| Station | Total Months | No. of Drought Months | Drought (%) | Longest Drought Period | Longest Drought Duration (Months) | Severity | Intensity |
|---|---|---|---|---|---|---|---|
| Constanta | 252 | 179 | 71.03% | July 2018 to August 2019 | 14 | 1.36 | 0.10 |
| Tulcea | 252 | 178 | 70.63% | February 2019 to November 2020 | 22 | 2.81 | 0.13 |
| Medgidia | 252 | 192 | 76.19% | August 2018 to June 2020 | 22 | 3.41 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serban, C.; Maftei, C. Spatiotemporal Drought Analysis Using the Composite Drought Index (CDI) over Dobrogea, Romania. Water 2025, 17, 481. https://doi.org/10.3390/w17040481
Serban C, Maftei C. Spatiotemporal Drought Analysis Using the Composite Drought Index (CDI) over Dobrogea, Romania. Water. 2025; 17(4):481. https://doi.org/10.3390/w17040481
Chicago/Turabian StyleSerban, Cristina, and Carmen Maftei. 2025. "Spatiotemporal Drought Analysis Using the Composite Drought Index (CDI) over Dobrogea, Romania" Water 17, no. 4: 481. https://doi.org/10.3390/w17040481
APA StyleSerban, C., & Maftei, C. (2025). Spatiotemporal Drought Analysis Using the Composite Drought Index (CDI) over Dobrogea, Romania. Water, 17(4), 481. https://doi.org/10.3390/w17040481






