Enhanced Groundwater Aeration with a Geometrically Constrained Vortex
Abstract
:1. Introduction
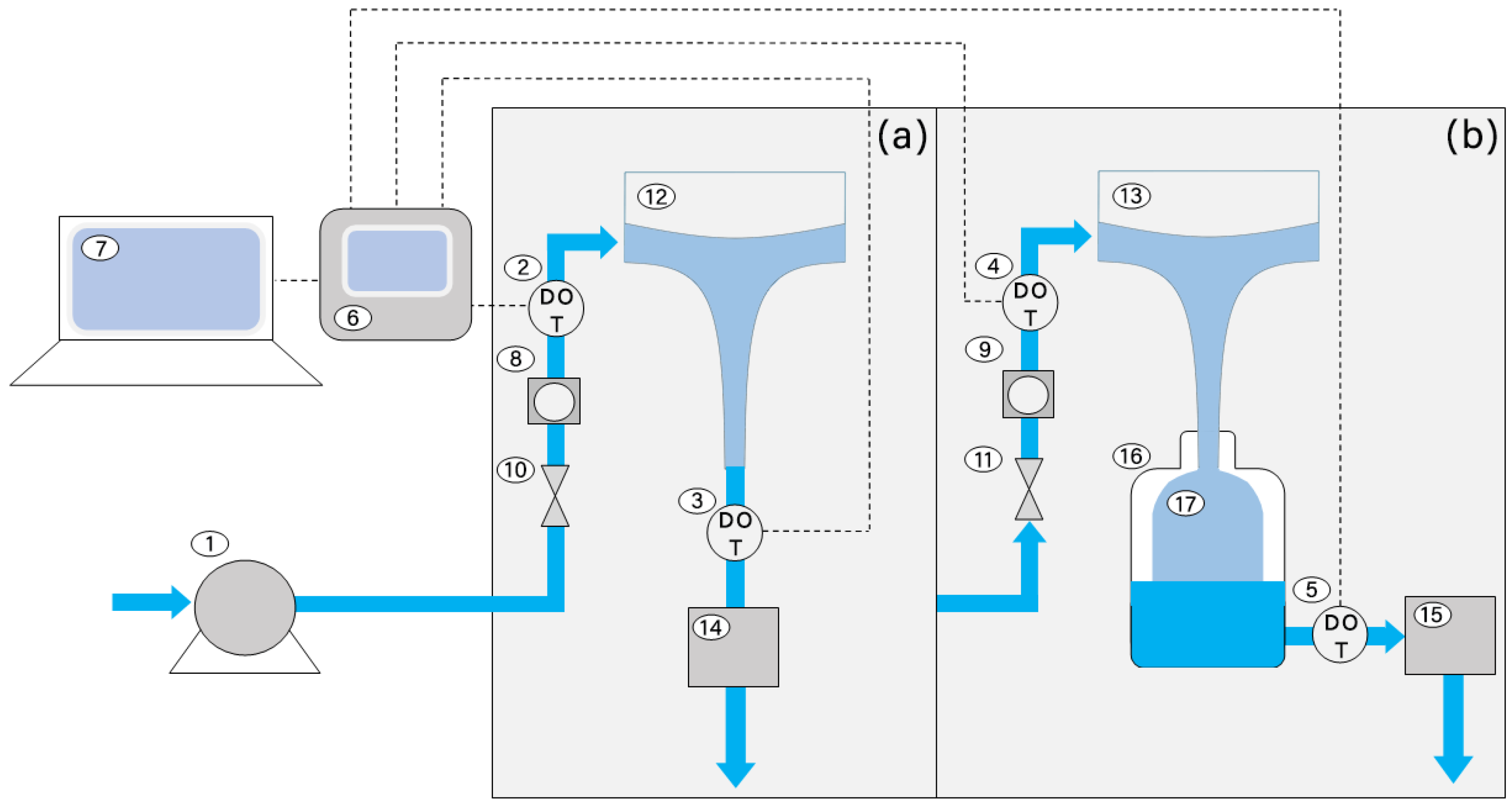
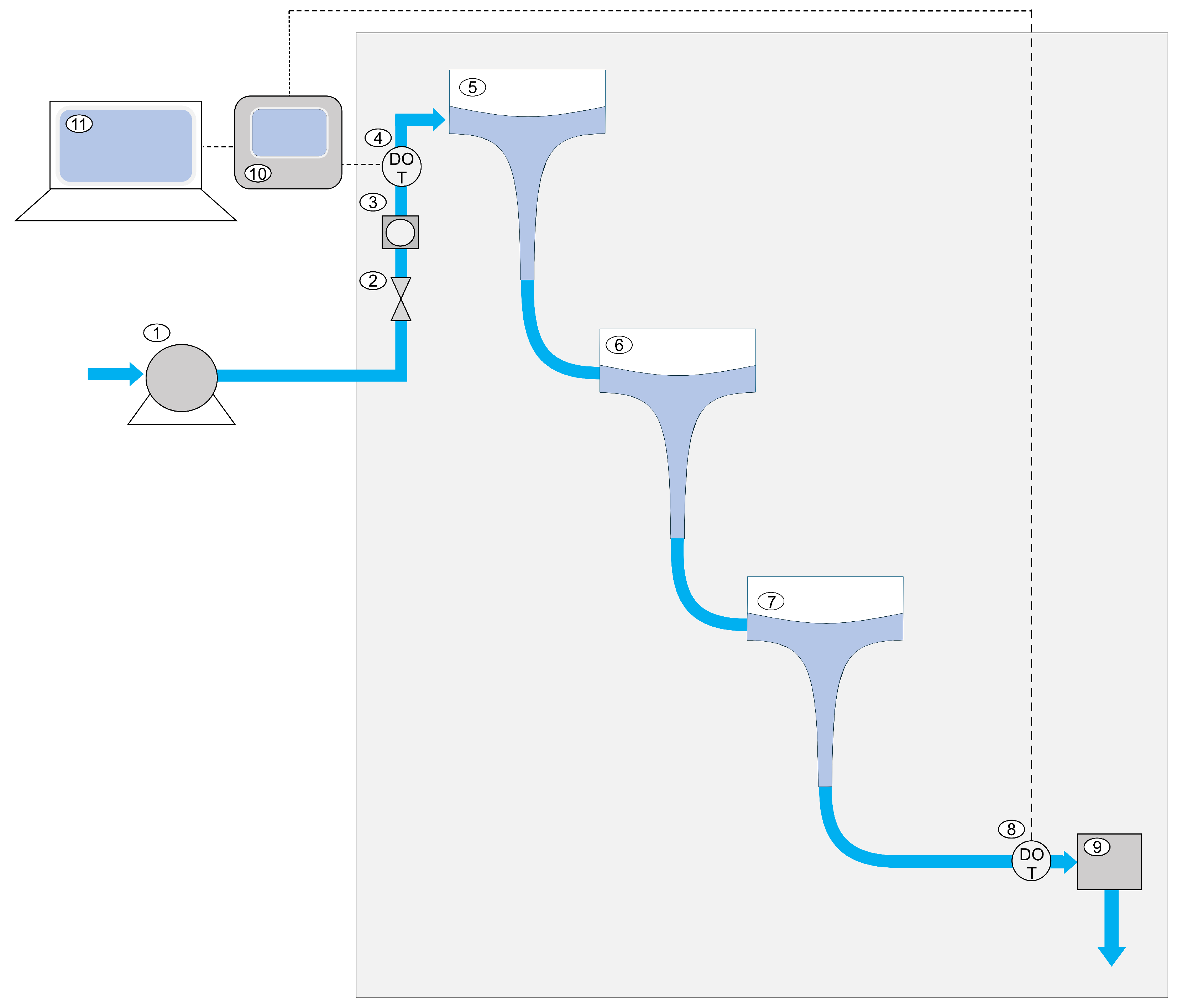
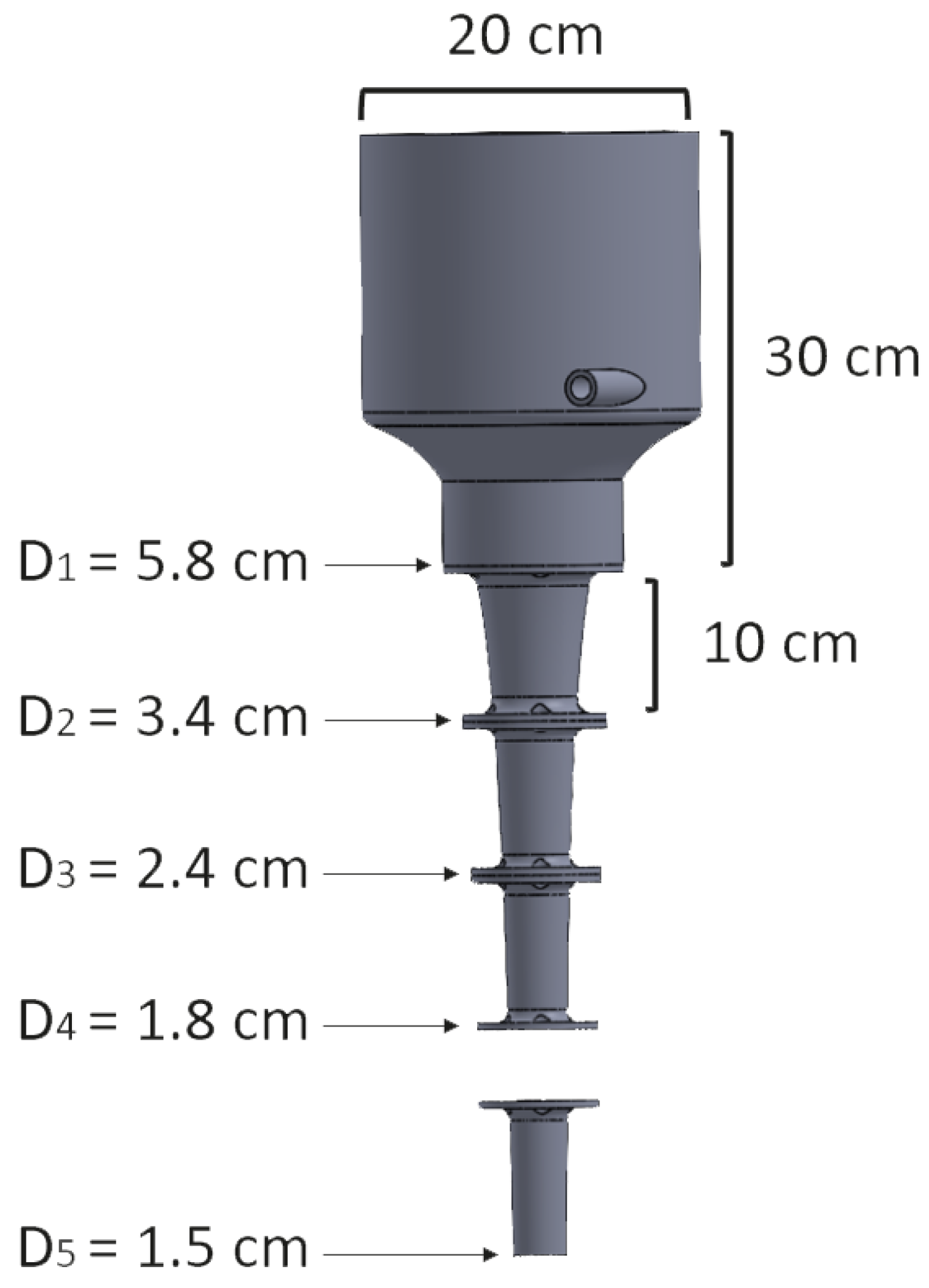
2. Materials and Methods
3. Results and Discussion
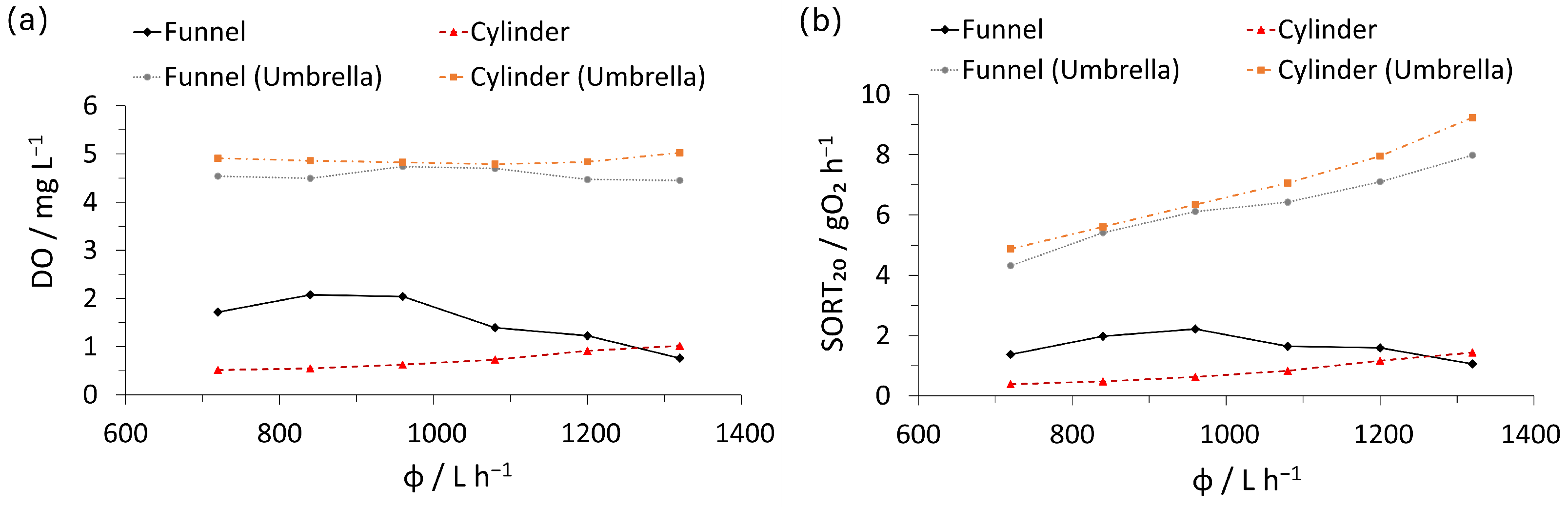
3.1. Hyperbolic Glass Funnel and Cylindrical Reactor
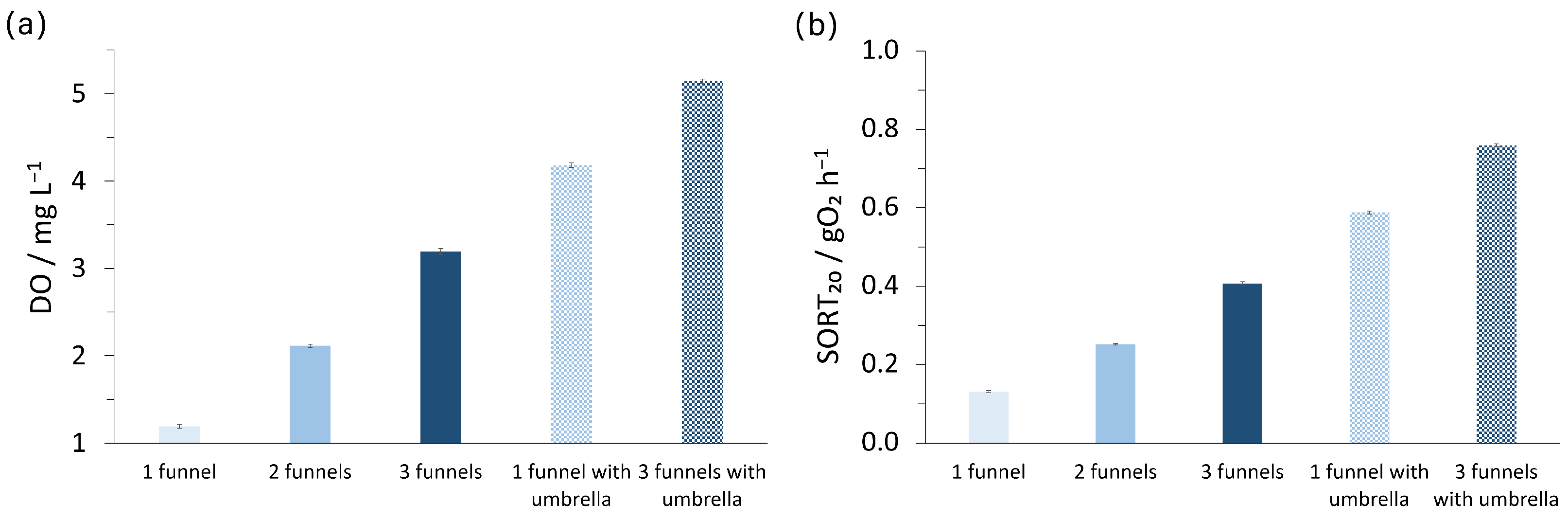
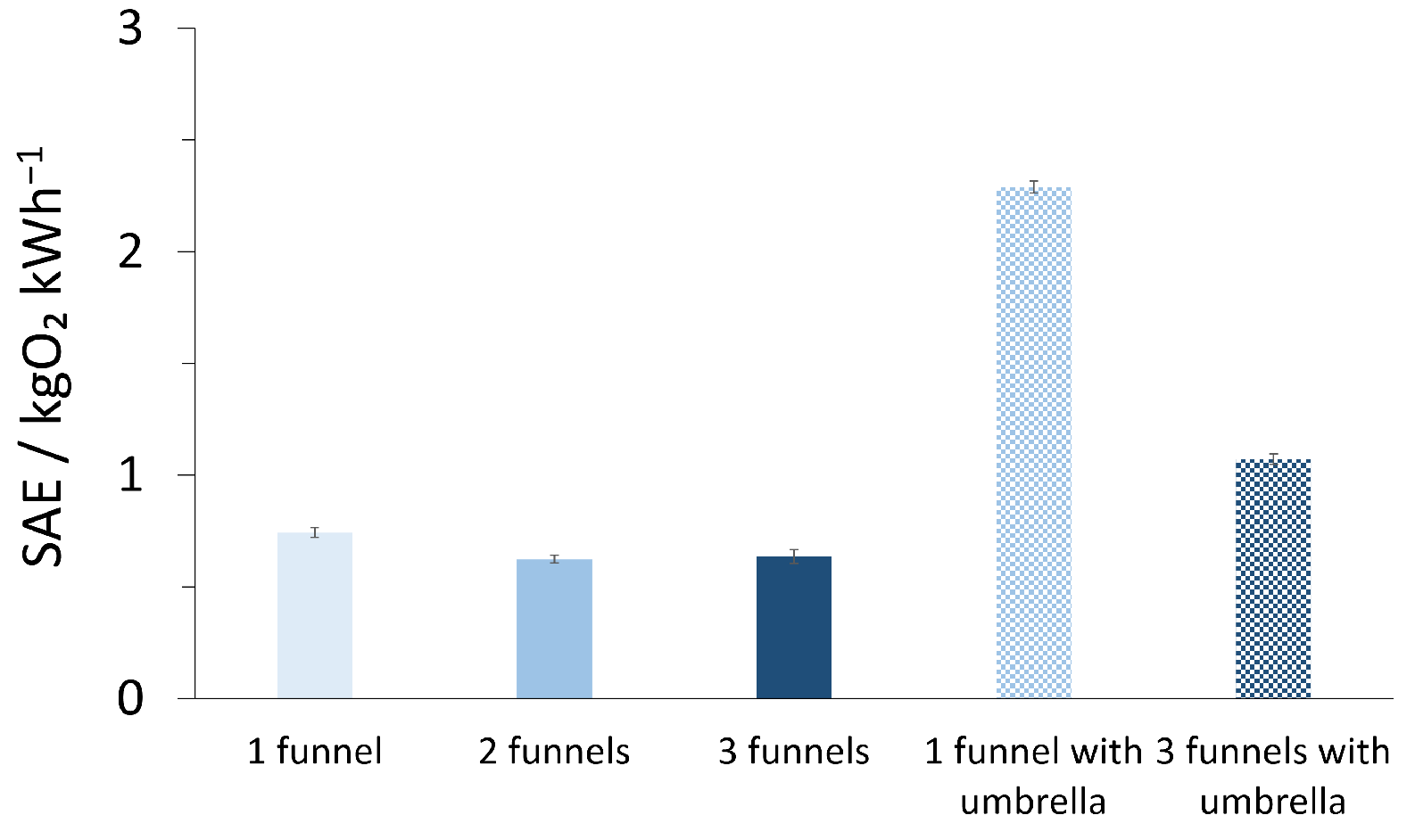
3.2. Cascade Configuration
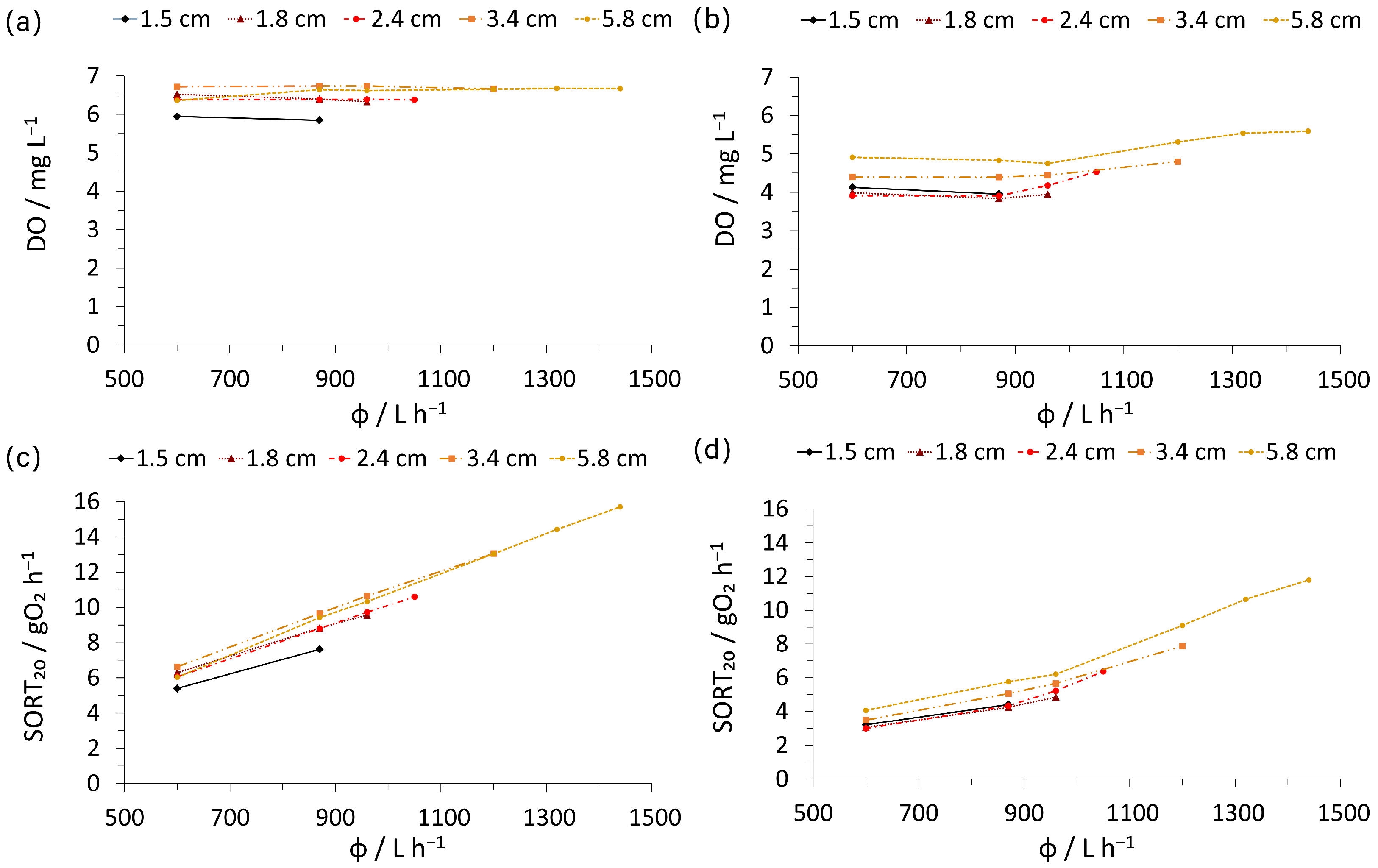
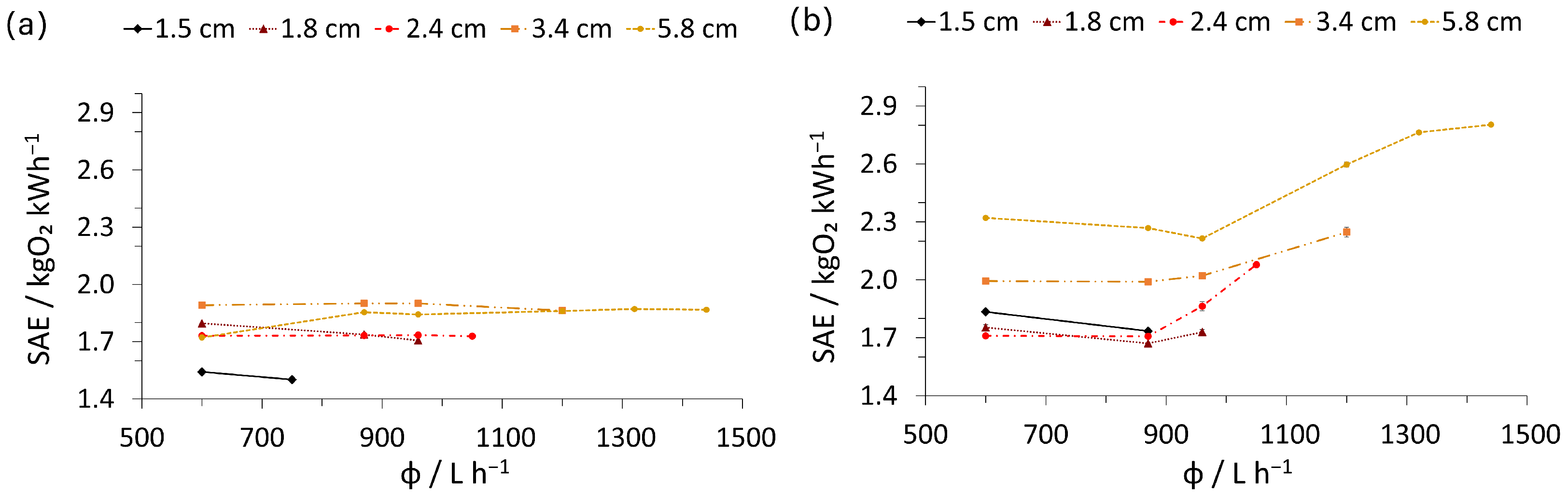
3.3. 3D-Printed Hyperbolic Funnel
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DO | Dissolved oxygen |
| SOTR20 | Standard oxygen transfer rate at 20 °C |
| SAE | Standard aeration efficiency |
| HRT | Hydraulic retention time |
| RTD | Residence time distribution |
| Volumetric liquid-phase mass transfer coefficient | |
| Volumetric liquid-phase mass transfer coefficient normalized to 20 °C | |
| FSVs | Free-surface vortices |
References
- Tsuji, K.; Müller, S.C. Spirals and Vortices in Culture, Nature, and Science; Springer Nature: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Radlberger, C. Der Hyperbolische Kegel; PKS Eigenverlag: Bad Ischl, Austria, 2014; Available online: https://www.scribd.com/doc/54990676/Radlberger-Der-Hyperbolische-Kegel-Nach-Walter-Schauberger-2002?language_settings_changed=English (accessed on 1 December 2024).
- Fitzke, F.; Mende, M.; Sindelar, C.; Werdenberg, N.; Schauberger, J.; Sàlat, A.; Grober, O. Instream River Training (IRT)—Naturnaher Flussbau nach Viktor Schauberger—Handbuch (v3.8)—eBook; Franz Fitzke, PKS Pythagoras Kepler System, Verein für Implosionsforschung: Bad Ischl, Austria, 2020; Available online: https://www.researchgate.net/publication/379669864_Instream_River_Training_IRT_-_Naturnaher_Flussbau_nach_Viktor_Schauberger_-_Handbuch_v38_-_eBook (accessed on 1 December 2024).
- Klymenko, R.; Nanninga, H.; de Kroon, E.; Agostinho, L.L.F.; Fuchs, E.C.; Woisetschläger, J.; Hoeben, W.F.L.M. Preparation of Free-Surface Hyperbolic Water Vortices. JoVE 2023, 197, e64516. [Google Scholar] [CrossRef] [PubMed]
- Agostinho, L.L.; Pecnik, R.; Woisetschläger, J.; de Kroon, E.; Şişcanu, N.; van de Griend, M.V.; Loiskandl, W.; Fuchs, E.C. Enhanced Oxygen Volumetric Mass Transfer in a Geometrically Constrained Vortex. Water 2022, 14, 771. [Google Scholar] [CrossRef]
- de Kroon, E. Iron Oxidation in Groundwater Using a Hyperbolic Water Vortex System. Master’s Thesis, Environmental Sciences and Chemical Engineering Van Hall Larenstein University of Applied Sciences, Leeuwarden, The Netherlands, 2021. [Google Scholar]
- van den Brink, C.; Frapporti, G.; Griffioen, J.; Zaadnoordijk, W.J. Statistical analysis of anthropogenic versus geochemical-controlled differences in groundwater composition in The Netherlands. J. Hydrol. 2007, 336, 470–480. [Google Scholar] [CrossRef]
- Rijksoverheid. Besluit Kwaliteit Drinkwater BES. 2010. Available online: https://wetten.overheid.nl/BWBR0028642/2010-10-10 (accessed on 1 December 2024).
- Chaturvedi, S.; Dave, P.N. Removal of iron for safe drinking water. Desalination 2012, 303, 1–11. [Google Scholar] [CrossRef]
- OpenCourseWare, T.D. Aeration and Gas Stripping. 2015. Available online: https://ocw.tudelft.nl/wp-content/uploads/Aeration-and-gas-stripping-1.pdf (accessed on 1 December 2024).
- Pöpel, H.J. Aeration and Gas Transfer; International Reference Centre for Community Water Supply: The Hague, The Netherlands, 1976; Available online: https://www.ircwash.org/sites/default/files/251-74AE.pdf (accessed on 1 December 2024).
- Rosso, D.; Stenstrom, M.K.; Larson, L.E. Aeration of large-scale municipal wastewater treatment plants: State of the art. Water Sci. Technol. 2008, 57, 973–978. [Google Scholar] [CrossRef] [PubMed]
- Drewnowski, J.; Remiszewska-Skwarek, A.; Duda, S.; Łagód, G. Aeration Process in Bioreactors as the Main Energy Consumer in a Wastewater Treatment Plant. Review of Solutions and Methods of Process Optimization. Processes 2019, 7, 311. [Google Scholar] [CrossRef]
- Marappan, J.; Anathaikamatchi, B.A.; Sakkarai, S.; Thiagarajan, R.; Muthusamy, D.; Kuppusamy, M.; Moturi, M.; Bera, A.; Ramasamy, P.; Shanmugam, S. Assessment of the new generation aeration systems efficiency and water current flow rate, its relation to the cost economics at varying salinities for Penaeus vannamei culture. Aquac. Reasearch 2020, 51, 2112–2124. [Google Scholar] [CrossRef]
- Benjamin, M.M.; Lawler, D.F. Water Quality Engineering: Physical/Chemical Treatment Processes Analysis; Wiley: Hoboken, NJ, USA, 2013; pp. 155–257. Available online: https://www.wiley.com/en-ie/Water+Quality+Engineering%3A+Physical+%2F+Chemical+Treatment+Processes-p-9781118169650 (accessed on 1 December 2024).
- Levenspiel, O. Tracer Technology; Springer: New York, NY, USA, 2012; pp. 30–33. [Google Scholar] [CrossRef]
- Mulligan, S.; Cesare, G.D.; Casserly, J.; Sherlock, R. Understanding turbulent free-surface vortex flows using a Taylor-Couette flow analogy. Sci. Rep. 2018, 8, 824. [Google Scholar] [CrossRef] [PubMed]
- Donepudi, T.; van de Griend, M.; Agostinho, L.; de Kroon, E.; Klymenko, R.; Pecnik, R.; Woisetschläger, J.; Fuchs, E. Numerical Analysis of Vortex Dynamics in Hyperbolic Funnels Using Computational Fluid Dynamics. Phys. Fluids 2024, 36, 095171. [Google Scholar] [CrossRef]
- Donepudi, T. Vortices in Hyperbolic Funnels as Aeration Systems A Numerical Study. Master’s Thesis, Faculty of Mechanical, Maritime and Materials Engineering, Delft University of Technology, Delft, The Netherlands, 2021. [Google Scholar]
- Klymenko, R.; de Kroon, E.; Agostinho, L.L.F.; Fuchs, E.C.; Woisetschläger, J.; Hoeben, W.F.L.M. Characterization of a hyperbolic vortex plasma reactor for the removal of aqueous phase micropollutants. J. Phys. D Appl. Phys. 2024, 57, 215204. [Google Scholar] [CrossRef]
- van de Griend, M. On the Theory and Applications of Hyperbolic Water Vortices. Ph.D. Thesis, University of Natural Resources and Life Sciences, Vienna, Austria, 2023. [Google Scholar]
- Cardoso, P.; Santos, A.; Rato, R.; Estrela, M. Assessment of Pump’s Performance in Water Supply Systems – Data Collected from Multiple Case Studies. J. Sustain. Dev. 2017, 6, 217. [Google Scholar] [CrossRef]
- Martin-Candilejo, A.; Santillán, D.; Garrote, L. Pump Efficiency Analysis for Proper Energy Assessment in Optimization of Water Supply Systems. Water 2020, 12, 132. [Google Scholar] [CrossRef]
- Roya, S.M.; Tanveerb, M.; Guptac, D.; Pareeka, C.M.; Mald, B.C. Prediction of standard aeration efficiency of a propeller diffused aeration system using response surface methodology and an artificial neural network. Water Supply 2021, 8, 4534. [Google Scholar] [CrossRef]
- Tanveer, M.; Roy, S.M.; Vikneswaran, M.; Renganathan, P.; Balasubramanian, S. Surface aeration systems for application in aquaculture: A review. Int. J. Fish. Aquat. Stud. 2018, 6, 342–347. [Google Scholar]
- Bahri, S.; Setiawan, R.P.A.; Hermawan, W.; Junior, M.Z. Design and Mechanism Analysis of Paddlewheel Aerator with Movable Blades. IOP Conf. Ser. Mater. Sci. Eng. 2019, 532, 012011. [Google Scholar] [CrossRef]
- Samstag, R.W.; Engineers, P.C. Overview of Wastewater Aeration. 2011. Available online: https://rsamstag.wordpress.com/wp-content/uploads/2015/02/aeration.pdf (accessed on 1 December 2024).
- Xylem. Aeration Products for Energy-Efficient Biological Treatment. 2024. Available online: https://www.xylem.com/siteassets/campaigns/oceania/sanitaire-aeration-product-range/aeration-product-range-brochure-updated2.pdf (accessed on 1 December 2024).
- Roy, S.M.; Machavaram, R.; Pareek, C.; Kim, T. Investigating the performance of a perforated pooled circular stepped cascade aeration system for intensive aquaculture. Heliyon 2024, 10, e26367. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Shitu, A.; Hang, S.; Ye, Z.; Zhao, H.; Xu, W.; Zhao, J.; Zhu, S. The effects of aerator noise on the swimming, feeding, and growth of Micropterus Salmoides. Front. Mar. Sci. 2023, 10. [Google Scholar] [CrossRef]
- Rodriguez, J.P.; Garcia, M.L.; Chen, X.; Li, W. Propeller-Induced Sediment Transport and Its Environmental Implications in Aquatic Systems. Water 2023, 16, 1647. [Google Scholar] [CrossRef]
- Roshan, R.U.; Harini, R.; Anand, T. Development of Integrated Aerator combining Paddlewheel and Propeller Aspirator Aerators for Shrimp Farming. In Next Generation Materials and Processing Technologies; Springer: Singapore, 2021; pp. 67–79. [Google Scholar] [CrossRef]
- Roy, S.; Moulick, S.; Mukherjee, C.K.; Mal, B.C. Effect of Rotational Speeds of Paddle Wheel Aerator on Aeration Cost. ResearchGate 2015, 2, 3069–3087. [Google Scholar]
- Aeration Store. DiscoPM Aeration System: User Manual. Available online: https://www.aerationstore.com/Downloads/discopm_manual.pdf (accessed on 1 December 2024).






| /L·h−1 | Funnel | Cylinder | ||||
|---|---|---|---|---|---|---|
| V/L | Du/cm | Sv/cm2 | V/L | Du/cm | Sv/cm2 | |
| 720 | 0.4 | 1.8 | 199 | 30.7 | 14 | 92 |
| 840 | 0.5 | 2.3 | 197 | 32.3 | 14.5 | 93 |
| 960 | 0.8 | 2.5 | 193 | 34 | 15 | 94 |
| 1080 | 1.2 | 3.8 | 190 | 34.7 | 14.2 | 95 |
| 1200 | 1.6 | 5.5 | 182 | 35 | 15.5 | 96 |
| 1320 | 5.1 | 6 | 179 | 37.6 | 16 | 99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klymenko, R.; Cerutti, L.; Colombo, M.B.A.; Fuchs, E.C.; Woisetschläger, J.; Hoeben, W.F.L.M.; Agostinho, L.L.F. Enhanced Groundwater Aeration with a Geometrically Constrained Vortex. Water 2025, 17, 506. https://doi.org/10.3390/w17040506
Klymenko R, Cerutti L, Colombo MBA, Fuchs EC, Woisetschläger J, Hoeben WFLM, Agostinho LLF. Enhanced Groundwater Aeration with a Geometrically Constrained Vortex. Water. 2025; 17(4):506. https://doi.org/10.3390/w17040506
Chicago/Turabian StyleKlymenko, Roman, Leticia Cerutti, Marcos B. A. Colombo, Elmar C. Fuchs, Jakob Woisetschläger, Wilfred F. L. M. Hoeben, and Luewton L. F. Agostinho. 2025. "Enhanced Groundwater Aeration with a Geometrically Constrained Vortex" Water 17, no. 4: 506. https://doi.org/10.3390/w17040506
APA StyleKlymenko, R., Cerutti, L., Colombo, M. B. A., Fuchs, E. C., Woisetschläger, J., Hoeben, W. F. L. M., & Agostinho, L. L. F. (2025). Enhanced Groundwater Aeration with a Geometrically Constrained Vortex. Water, 17(4), 506. https://doi.org/10.3390/w17040506









