Discharge Capacity of the Flood Discharge Shaft in a Tailings Reservoir: An Experimental and Numerical Study

Abstract

In China, tailings reservoirs often experience failure events due to inadequate discharge capacity or flood discharge system failures. To ensure the safe and reliable operation of the flood discharge system in a tailings reservoir, this study investigated the discharge capacity of a tailings reservoir in Henan Province, China, through hydraulic model tests and numerical simulations conducted using FLOW-3D. The results indicated that when the water head was below 0.8 m, the flow was in a non-pressurized regime with low discharge capacity. As the water head increased to 0.8–1.2 m, air began to be entrained into the flow, leading to an alternating regime between open-channel flow and full-pipe flow. Once the water head exceeded 1.2 m, the flow expelled air and transitioned into a pressurized full-pipe regime. At a water head of 1.6 m, the flow was in a pressurized full-pipe regime. The experimental flow rate, flow velocity, and flow regime of flood discharge shaft No. 1 closely matched the simulation results. Additionally, the discharge capacity of the shaft increased as the height of the discharge window was raised. The discharge capacity and flow velocity of the discharge windows on the eighth layer were 30.1% and 29.2% higher, respectively, than those on the first layer, which indicated that the system’s drainage capacity increased as the shaft length increased. However, increasing the height of the discharge window increased the likelihood of an alternating regime between open-channel flow and full-pipe flow. During the operation of the tailings reservoir drainage system, it is essential to ensure that the upper-layer discharge windows are functioning while minimizing the occurrence of unfavorable flow regimes. The discharge water head should be controlled to remain below 0.8 m. These operations not only ensure that the discharge capacity meets the requirements but also enable the drainage tunnel to operate safely and effectively over the long term. The findings of this study can provide a scientific basis for the design and safe operation of tailings reservoir drainage systems.

1. Introduction

Tailings reservoirs are hazardous structures with high potential energy, and dam failures can cause devastating damage to lives, property, and the ecological environment downstream [1]. Analysis conducted by Clark University in the United States revealed that tailings dam failures ranked 18th among 93 types of incidents worldwide [2]. Excessive floods or insufficient drainage capacity are primary causes of overtopping dam failures [3,4]. For instance, on 31 January 1978, a tailings dam near Harare, Zimbabwe, suddenly developed a 55 m-wide breach in its west wall, releasing approximately 30,000 tons of tailing, which led to the death of one child and injuries to another. The cause of this accident was heavy rainfall in the region prior to the collapse, which led to abnormal water accumulation at the top of the vertical discharge pipe. According to local investigation results, if the drainage pipe had been well designed then this issue would have been avoided [5]. Therefore, a systematic study of the discharge capacity of tailings reservoir discharge systems is essential to ensure their safe operation.

In recent years, many scholars have conducted extensive research on tailings reservoir discharge systems. Vortex shafts have been utilized in engineering for many years, and numerous projects employ this design for discharge. Over years of validation, it has been established that vortex shafts can effectively dissipate flow energy and prevent cavitation and erosion damage, though they are characterized by low discharge capacity and low inlet elevations [6]. In 1990, H.W. Hagger conducted an in-depth study on the shaft inlet design of vortex shafts and proposed a novel inlet shape where the inner wall of the intake channel extends into the vortex chamber as a guiding wall [7]. However, its complex structure led to uneven stress distribution on the guiding wall, making practical application difficult. To address this issue, Liu and Yang proposed a new type of vortex step spillway. They elucidated the hydraulic characteristics of this spillway through model tests and CFD simulations, demonstrating its effective energy dissipation capabilities [8,9]. Other researchers have also conducted extensive studies on shaft spillways. Farman et al. studied the relationship between the shaft diameter and the wall pressure and discovered that the differences in flow behaviors within larger-diameter shafts were due to the increased lateral dimensions. They demonstrated that the wall pressure decreased as the diameter increased [10,11,12]. Tastan et al. found that the inlet shape of shafts affected factors such as the air-entrained vortex and submergence depth. Compared to other inlet shapes, a trumpet-shaped inlet could avoid vortex effects and enhance discharge capacity. The circular piano key (CPK) shape offers superior discharge capacity compared to simple shaft spillways [13,14,15,16,17,18]. The Marguerite-shaped inlet shaft spillway demonstrates greater discharge capacity compared to ordinary shafts, trumpet-shaped, and CPK spillways, while also exhibiting a lower vortex intensity [19,20,21,22,23]. With rapid advancements in computer technology, computational fluid dynamics (CFD) has been widely applied. Numerous studies have demonstrated that CFD technology is applicable to liquid turbulent flows and provides reliable simulations for gas–liquid flows with high gas volume fractions, thus offering insights for the structural optimization of two-phase flow systems [24,25,26,27]. Therefore, Aydin et al. utilized CFD to simulate the hydraulic characteristics of complex siphon spillways and found that air entrainment effectively reduces siphon negative pressure and cavitation without significantly diminishing discharge capacity [28,29]. In summary, these researchers have explored various forms of shaft spillways and they indicate that the vortex-type shaft spillway has an effective energy dissipation capabilities, and that the Margaret-shaped intake has a superior discharge performance compared to conventional shaft spillways. However, these types of vertical shafts are not suitable for tailings dams with gradually increasing dam heights, which leads to the fact that most tailings dam accidents are caused by insufficient flood discharge capacity or failure of the flood discharge system.

This study focused on a proposed tailings reservoir in Henan Province, China, and utilized the gravitational similarity principle to conduct laboratory hydraulic model tests on the flood discharge system. FLOW-3D software v11.2 was employed to simulate the discharge capacity under both normal and flood conditions. Finally, data on flow regimes and velocities in the flood discharge shafts and tunnels were analyzed to evaluate the discharge capacity of the system. The results of the study provide a rational, safe, and economical technical foundation for the future design of tailings reservoirs.

2. Physical Model Test

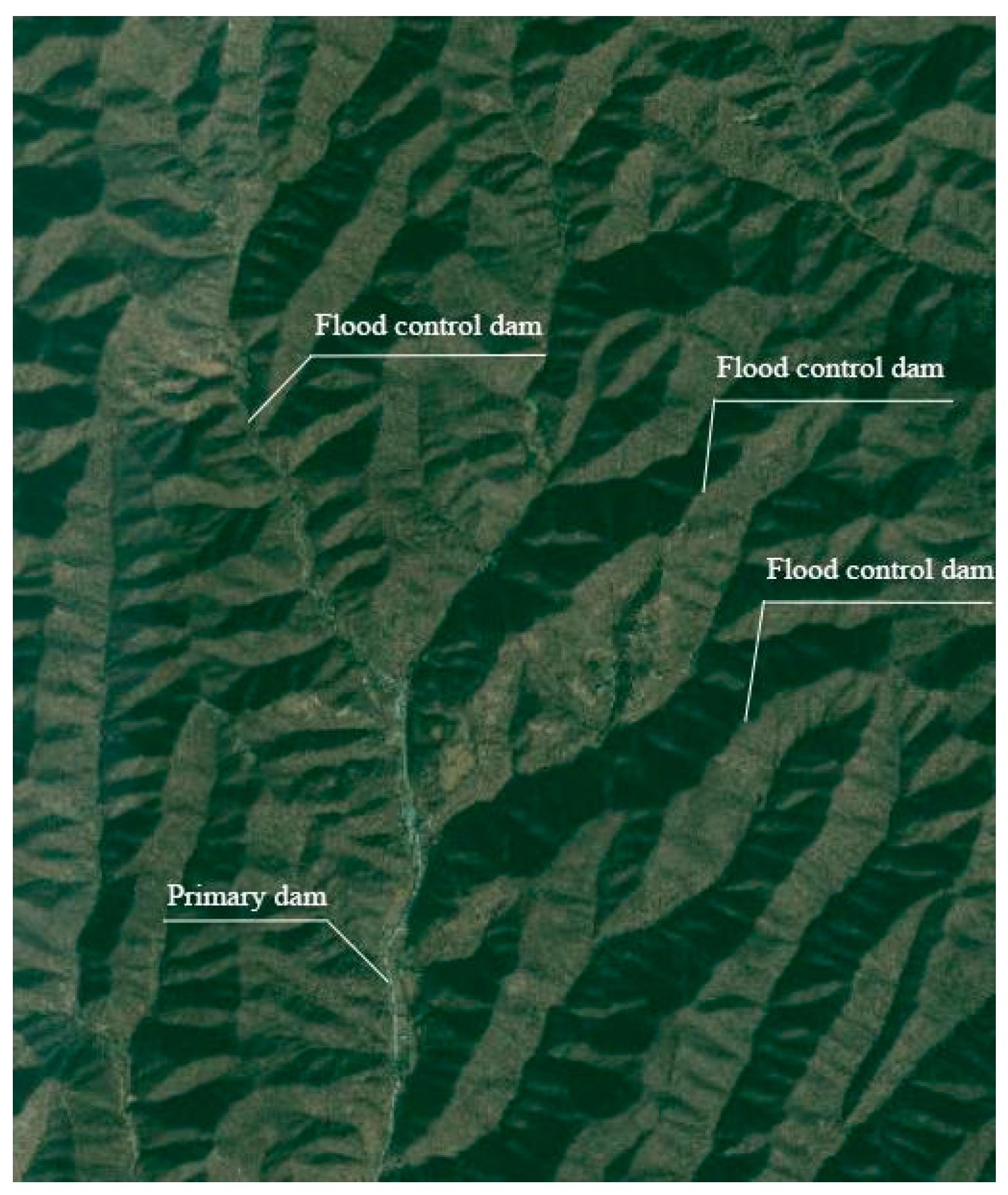
2.1. Test Prototype

A tailings reservoir in Henan Province, China, employs wet disposal and adopts an upstream method for tailings stacking. An initial dam was constructed at the gorge, with a height of 39 m and a top elevation of 626 m. The tailings reservoir adopts a construction scheme of a one-time design with two phases for implementation. The first-phase reservoir has a stacking elevation of 696 m, a total storage capacity of 3,938,900 m³, and an effective storage capacity of 3,387,400 m³, categorizing it as a Class II reservoir. The final stacking elevation of the second-phase reservoir is 738 m, with a total storage capacity of 9,985,000 m³ and an effective storage capacity of 8,587,000 m³, which also categorizes it as a Class II reservoir. The first-phase reservoir has a catchment area of 3.976 km², with two independently operating flood discharge systems installed within the reservoir. The first flood discharge system, which connects four discharge shafts (shaft No. 0: Φ3.0 m, H = 15 m; shafts No. 1–3: Φ4.0 m, H = 24–27 m), is located in the western branch gully. The second flood discharge system, which connects three discharge shafts (shafts 4–6: Φ4.0 m, H = 24–27 m), is located in the eastern branch gully. The second-phase flood discharge system involves the construction of an external discharge system upstream and the extension of the internal discharge system within the reservoir’s tunnel. The external flood diversion system for the second-phase reservoir consists of six flood regulating dams and external diversion tunnels. The external diversion system of the western branch gully is integrated with the internal discharge tunnel of the second-phase reservoir, which subsequently connects to the external flood diversion system of the first-phase reservoir. The external flood diversion system of the eastern branch gully consists of four discharge tunnels, with a total length of approximately 1830 m. According to the site photos, it can be seen that the tailings pond is of the valley type, the advantage of which is that the dam is shorter and less work and that the management and maintenance of the tailings dam will be easier in the later stage. When the tailings reservoir is used to a later stage, the pile height of the tailings reservoir increases and the storage volume inside the reservoir becomes larger. The greater longitudinal depth of the reservoir provides more room for clarification of the distance of flooding in the reservoir and the length of the dry beach. The disadvantage is that with a large catchment area, the flood discharge facilities and costs will increase. The topographic map of the tailing pond site is shown in Figure 1, and the arrangement of the flood discharge system is shown in Figure 2.

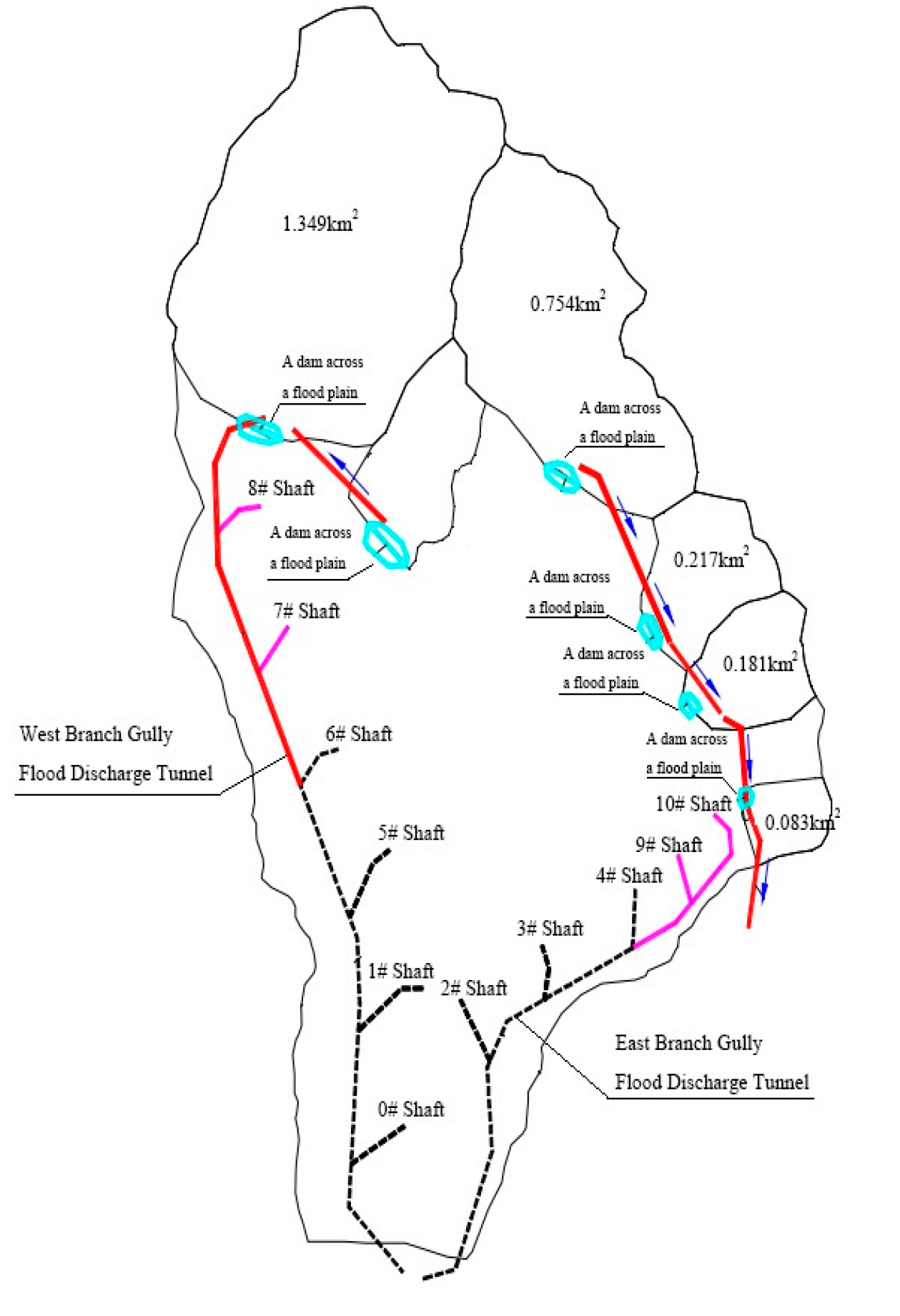
2.2. Flood Management Algorithm

The purpose of the flood control algorithm is to identify the required flood control storage capacity and flood flow rate based on the established drainage system, combining the flood process line and the curve of discharge from the drainage structures in relation to the storage capacity of the tailings pond. The discharge hydrograph is calculated through water balance analysis, thereby determining the discharge rate and flood storage capacity.

The water balance equation for any time period ∆t in the tailings pond is shown below:

$${\displaystyle \frac{1}{2}}\left({\mathrm{Q}}_{\mathrm{S}}+{\mathrm{Q}}_{\mathrm{z}}\right)\Delta \mathrm{t}-{\displaystyle \frac{1}{2}}\left({\mathrm{q}}_{\mathrm{S}}+{\mathrm{q}}_{\mathrm{Z}}\right)\Delta \mathrm{t}={\mathrm{V}}_{\mathrm{Z}}-{\mathrm{V}}_{\mathrm{S}}$$

(1)

Let $\overline{\mathrm{Q}}={\displaystyle \frac{1}{2}}\left({\mathrm{Q}}_{\mathrm{S}}+{\mathrm{Q}}_{\mathrm{Z}}\right)$, substitute it into the above formula, and after rearranging, we obtain:

$${\mathrm{V}}_{\mathrm{Z}}+{\displaystyle \frac{1}{2}}{\mathrm{q}}_{\mathrm{z}}\Delta \mathrm{t}=\overline{\mathrm{Q}}\Delta \mathrm{t}+\left({\mathrm{V}}_{\mathrm{S}}-{\displaystyle \frac{1}{2}}{\mathrm{q}}_{\mathrm{S}}\Delta \mathrm{t}\right)$$

(2)

The tailings particles with a diameter of less than 0.074 mm account for 67%. The slope of the deposition beach is determined at 1%, based on the experience of tailings dams in the same region. The flood prevention height is 3 m. Independent well-cave flood discharge systems are installed in the eastern and western tributary gullies within the dam. For this calculation, the flood regulation is performed based on the drainage well (D = 4.0 m) and tunnel (1.8 m × 1.8 m) of the eastern tributary gully system. The standard floodwater collects in the dam and is then discharged through the inclined slot—drainage well—flood discharge tunnel. The calculation results are shown in

Table 1. Flood control capacity of the reservoir.

P	Elevation of the Beach Crest (m)	Flood Protection Height (m)	Flood Protection Storage Capacity (m3/s)	Length of Tailings Pond (m)
0.5%	626	3.0	41.75 × 104	1150
0.2%	647	3.0	80.77 × 104	1257
0.2%	674	3.0	175.82 × 104	1688
0.1%	687	3.0	225.45 × 104	1756
0.1%	696	3.0	270.82 × 104	1865
0.1%	738	3.0	513.33 × 104	2160

and

Table 2. Results of the in-reservoir flood control algorithm.

P	Elevation of the Beach Crest (m)	Normal Water Level (m)	Flood Storage Capacity (m3)	Maximum Underflow (m3/s)	Highest Flood Level (m)	Safe and Ultra-High (m)	Length of Dry Beach (m)
0.5%	626	623	105,797	11.99	623.90	2.10	210
0.2%	647	644	206,631	11.40	644.87	2.13	213
0.2%	674	671	331,816	7.59	671.64	2.36	236
0.1%	687	684	366,154	7.32	684.54	2.46	246
0.1%	696	693	386,462	5.95	693.46	2.54	254
0.1%	738	735	480,249	3.11	735.30	2.70	270

.

2.3. Test Setup

The local normal model with a geometric scale of λ_L = 20 was adopted in this study [30].

Table 3. Scale relationships of physical parameters.

Physical Parameter	Flow Velocity	Flow Rate	Roughness	Time	Pressure
Scale relationship	${\mathsf{\lambda }}_{\mathrm{v}}={\mathsf{\lambda }}_{\mathrm{L}}^{0.5}$	${\mathsf{\lambda }}_{\mathrm{Q}}={\mathsf{\lambda }}_{\mathrm{L}}^{2.5}$	${\mathsf{\lambda }}_{\mathrm{n}}={\mathsf{\lambda }}_{\mathrm{L}}^{1/6}$	${\mathsf{\lambda }}_{\mathrm{t}}={\mathsf{\lambda }}_{\mathrm{L}}^{0.5}$	${\mathsf{\lambda }}_{\mathrm{p}}={\mathsf{\lambda }}_{\mathrm{L}}$
Scale factor of physical parameters	4.47	1788.85	1.65	4.47	20

lists the relationships between various physical parameters. Based on the laboratory testing conditions and the layout of the flood discharge shafts, hydraulic model tests were conducted based on the flood discharge shaft No. 1 and its downstream branch tunnels. The model consists of the five following components: a water tank, a reservoir, a flood discharge shaft with sleeves, an energy dissipation well, and a flood discharge tunnel. The water tank has a total capacity of 10 tons and employs a pump to inject water into the reservoir for simulating water levels during flood drainage. The reservoir is designed for uniform circumferential inflow and is shaped as a square, with each side length measuring five times the diameter of the flood discharge shaft. The model has a side length of 2 m, and the circumferential inflow in a reservoir area of 80 m² was simulated. The model of the flood discharge shaft has a radius of 10 cm and a height of 1.4 m. Each layer consists of discharge windows that are 15 cm high, and there are eight layers in total. Each window is equipped with a sleeve that can be used for sealing, and the sleeves can be interconnected to seal the windows of seven layers. The energy dissipation well has a height of 31 cm and a radius of 19.5 cm. The discharge tunnel has a diameter of 90 mm and a total length of 20 m, with a simulated slope of i = 0.01. The discharge pipe is designed for free discharge into the air at its outlet. To facilitate the observation of flow regimes, the entire model is made of acrylic. The roughness of acrylic is generally around 0.01, and when scaled to the prototype, it was calculated to be 0.0165, which essentially meets the requirements. The overall model is displayed in Figure 3 and Figure 4.

3. Numerical Simulation

3.1. Experimental Setup and Grid Division

The FLOW-3D software was utilized to simulate the operation of the flood discharge system at a beach top elevation of 626 m. The discharge capacity of shaft No. 1 was analyzed under both normal and flood conditions. The modeling function provided by FLOW-3D software is relatively straightforward and it lacks the precision needed for complex drainage systems. Therefore, a high-precision 3D model of the flood discharge system was constructed using Rhino software 7.0 at a 1:1 scale to enhance the simulation’s realism.

Figure 5 and Figure 6 illustrate the model’s construction and grid division. The model is divided into three parts. The mesh size for the flood discharge shaft and energy dissipation well is 0.1 m × 0.1 m × 0.1 m, while the mesh size for the flood discharge tunnel is 0.2 m × 0.2 m × 0.2 m. The total number of elements in the model is 442.6 × 10⁴.

3.2. Governing Equation

3.2.1. Turbulence Model

The turbulence models available in FLOW-3D include the standard k-ε model, RNG k-ε model, and realizable k-ε model. Compared to the standard k-ε model, the RNG k-ε model offers higher simulation accuracy. It enables precise calculations of high-resolution fluid movements and offers greater accuracy for complex fluid motion calculations [31]. Therefore, the RNG k-ε turbulence model was adopted in this study, and its governing equations are expressed as follows:

$$\text{Continuity equation:} {\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial \rho u_i}{\partial x_i}}=0$$

(3)

$$\text{Momentum equation:} \frac{\partial \rho u_i}{\partial t}+\frac{\partial }{\partial x_j}\left(\rho u_i{u}_j\right)=-\frac{\partial \rho }{\partial x_i}+\frac{\partial }{\partial x_j}\left[\left(\mu +{\mu }_t\right)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]$$

(4)

The k and ε equations are as follows:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho U_{i}k\right)}{\partial x_i}+\rho \epsilon =\frac{\partial }{\partial x_j}\left[\left(\frac{\mu +{\mu }_i}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k$$

(5)

$$\frac{\partial \rho \epsilon }{\partial t}+\frac{\partial \left(\rho U_i\epsilon \right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\frac{\mu +{\mu }_i}{{\sigma }_z}\right)\frac{\partial \epsilon }{\partial x_j}\right]+G_k\frac{\epsilon }{k}{C}_{1\epsilon }-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}$$

(6)

The equation for turbulent viscosity coefficient is expressed as follows:

$${\mathsf{\mu }}_{\mathrm{t}}=\mathsf{\rho }{\mathrm{C}}_{\mathsf{\mu }}{\displaystyle \frac{{\mathrm{k}}^2}{\mathsf{\epsilon }}}$$

(7)

where k represents turbulent kinetic energy; ε is the dissipation rate of turbulent kinetic energy; μ_t is the turbulent viscosity coefficient; ρ is the average density by volume fraction; μ is the molecular viscosity coefficient; t is the time variable; μ_i is the velocity component; and x_i is the coordinate component.

3.2.2. Free Surface Tracking

The VOF method is a technique used in CFD software (FLOW-3D v11.2) to handle free surfaces, and it has been widely used due to its high computational accuracy and relatively low computational demand [32]. This method idealizes the free surface by defining a volume fraction function F (the ratio of the fluid volume within a cell to the cell volume) to determine the free surface’s location through the solution of F’s governing equation. The value of F can have three possible cases: F = 1 indicates that the cell is filled with liquid, F = 0 indicates no liquid in the cell, and 0 < F < 1 suggests that the cell may intersect with the free surface. The function F varies with time and space, and its governing equation is expressed as:

$$\frac{\partial \mathrm{F}}{\partial \mathrm{t}}+\left[\frac{\partial \left(\mathrm{F}\mathrm{u}\right)}{\partial \mathrm{x}}+\frac{\partial \left(\mathrm{F}\mathrm{v}\right)}{\partial \mathrm{y}}+\frac{\partial \left(\mathrm{F}\mathrm{w}\right)}{\partial \mathrm{z}}\right]={\mathrm{F}}_{\mathrm{D}\mathrm{I}\mathrm{F}}+{\mathrm{F}}_{\mathrm{S}\mathrm{O}\mathrm{R}}$$

(8)

where t is the time variable; F_DIF represents the diffusion of fluid fraction; and F_SOR denotes the liquid volume source.

3.3. Computational Method and Boundary Conditions

The RNG k-ε model is an optimized version of the standard k-ε model. It improves the accuracy of the ε equation by accounting for turbulent vortices. The RNG k-ε theory provides an analytical formula for the turbulent Prandtl number, while the standard k-ε model relies on user-supplied constants. The standard k-ε model is designed for high Reynolds number flows, whereas the RNG k-ε theory offers an analytical formula that accounts for the viscosity of low Reynolds number flows. The efficacy of these formulas relies on proper treatment of near-wall regions, which gives the RNG k-ε model greater reliability and accuracy across a broader range of flows compared to the standard k-ε model. This study employed the RNG k-ε three-dimensional turbulence model for numerical simulations. The finite difference method was utilized to discretize the governing equations into a system of algebraic equations for the solution FLOW-3D employs for free surface treatment, which is the optimized TruVOF method. This method only computes the cells containing liquid surfaces, which significantly reduces the time required for model convergence, enhances the accuracy of free surface representation, and provides greater precision and efficiency for hydrodynamic problem-solving.

Under the operating condition with a beach top elevation of 626 m, the boundary conditions were set as follows. The upstream shaft inlet was defined as a fixed water head boundary, with water levels set at a normal level of 623 m and a flood level of 623.9 m, while the water was allowed to flow downward under the influence of gravity. The downstream branch tunnel outlet was set as a free outflow boundary. The walls of the remaining shaft sections, energy dissipation well sections, and tunnel sections were designated as solid wall boundaries, while the connecting section was defined as a symmetry boundary that allows water to pass through [33].

4. Analysis of Experimental and Simulation Results

4.1. Results and Analysis

4.1.1. Model Test Results

Table 4. Discharge flow rates and flow regimes of the discharge windows at different water levels in each layer of the flood discharge system.

Number of Drainage Window Layers	H = 0.4 m		H = 0.8 m		H = 1.2 m		H = 1.6 m		H = 2.4 m
	Flow Rate /(m3/s)	Flow Regime	Flow Rate /(m3/s)	Flow Regime	Flow Rate /(m3/s)	Flow Regime	Flow Rate /(m3/s)	Flow Regime	Flow Rate /(m3/s)	Flow Regime
1	3.17	Free flow	9.79	Partially pressurized flow	15.62	Partially pressurized flow	17.93	Pressurized flow	18.66	Pressurized flow
2	3.62	Free flow	9.83	Partially pressurized flow	15.36	Partially pressurized flow	18.25	Pressurized flow	19.35	Pressurized flow
3	3.14	Free flow	10.12	Partially pressurized flow	15.87	Partially pressurized flow	18.73	Pressurized flow	20.04	Pressurized flow
4	3.24	Free flow	11.23	Partially pressurized flow	16.23	Partially pressurized flow	19.38	Pressurized flow	20.72	Pressurized flow
5	3.32	Free flow	10.76	Partially pressurized flow	16.12	Partially pressurized flow	19.84	Pressurized flow	21.52	Pressurized flow
6	3.49	Free flow	11.13	Partially pressurized flow	16.46	Partially pressurized flow	20.98	Pressurized flow	22.21	Pressurized flow
7	3.54	Free flow	11.46	Partially pressurized flow	17.18	Partially pressurized flow	20.82	Pressurized flow	23.24	Pressurized flow
8	3.48	Free flow	12.21	Partially pressurized flow	18.41	Partially pressurized flow	21.98	Pressurized flow	24.27	Pressurized flow

summarizes the test results of the discharge flow rates and flow regimes of the discharge windows at different water levels in each layer of the flood discharge system. Figure 7, Figure 8 and Figure 9 depict the associated flow regimes, while Figure 10 and Figure 11 present the flow rate head and flow velocity head curves for discharge windows 1 to 8.

4.1.2. Flow Regime of the Flood Discharge System

The results in Table 2 indicated that the discharge conditions of the discharge windows on each layer are generally similar, and the flow regimes can be categorized into the following three types: free flow, partially pressurized flow, and pressurized flow.

(1)

Free flow: As Figure 7 depicts, when water began to enter the upstream tank, the water level rose gradually. When the discharge head was below 0.8 m, the flow regime at the inlet of the shaft was characterized by weir flow formed by the bottom sill ring beam of the discharge window. The water flowed into the eight discharge windows and gradually descended along the wall. After the water dropped into the energy dissipation well, it rolled and collided with each other to dissipate energy, during which a small amount of gas was mixed in the energy dissipation well. When the water level at the bottom of the energy dissipation well rose to the bottom of the horizontal pipe, the water flowed gently out along the horizontal pipe, at which point the flow inside the horizontal pipe was in an unpressurized regime.

(2)

Partially pressurized flow: As Figure 8 presents, when the drainage head ranged from 0.8 m to 1.2 m, as the water head continued to rise, the eight water streams gradually converged into a single flow, and the water tongue became increasingly thicker. Eventually, a large volume of water flowed into the shaft, where the water tongues interfered with each other, causing the flow to carry a certain amount of air into the energy dissipation well. After energy dissipation through aeration, the gas escaped to the water surface and flowed into the discharge tunnel, resulting in the water flow being mixed with numerous bubbles, rolling violently, and incorporating a large amount of gas. At this point, a vortex began to form at the inlet of the energy dissipation well, while the inlet section of the horizontal pipe exhibited an alternating regime between open-channel flow and full-pipe flows, and the latter section of the pipe demonstrated an unpressurized flow regime.

(3)

Pressurized flow: As Figure 9 illustrates, when the discharge head exceeded 1.2 m, the flow at the inlet gradually intensified downward and progressively filled the flood discharge system. When the head reached 1.6 m, the discharge situation stabilized, and the shaft gradually expelled air, resulting in a calm water surface. Full-pipe pressurized flow regimes developed in both the energy dissipation well and the horizontal pipe, at which point the discharge capacity experienced a turning point. The discharge flow approached a certain value, and as the water head increased, the discharge flow rate increased only slightly or remained essentially constant.

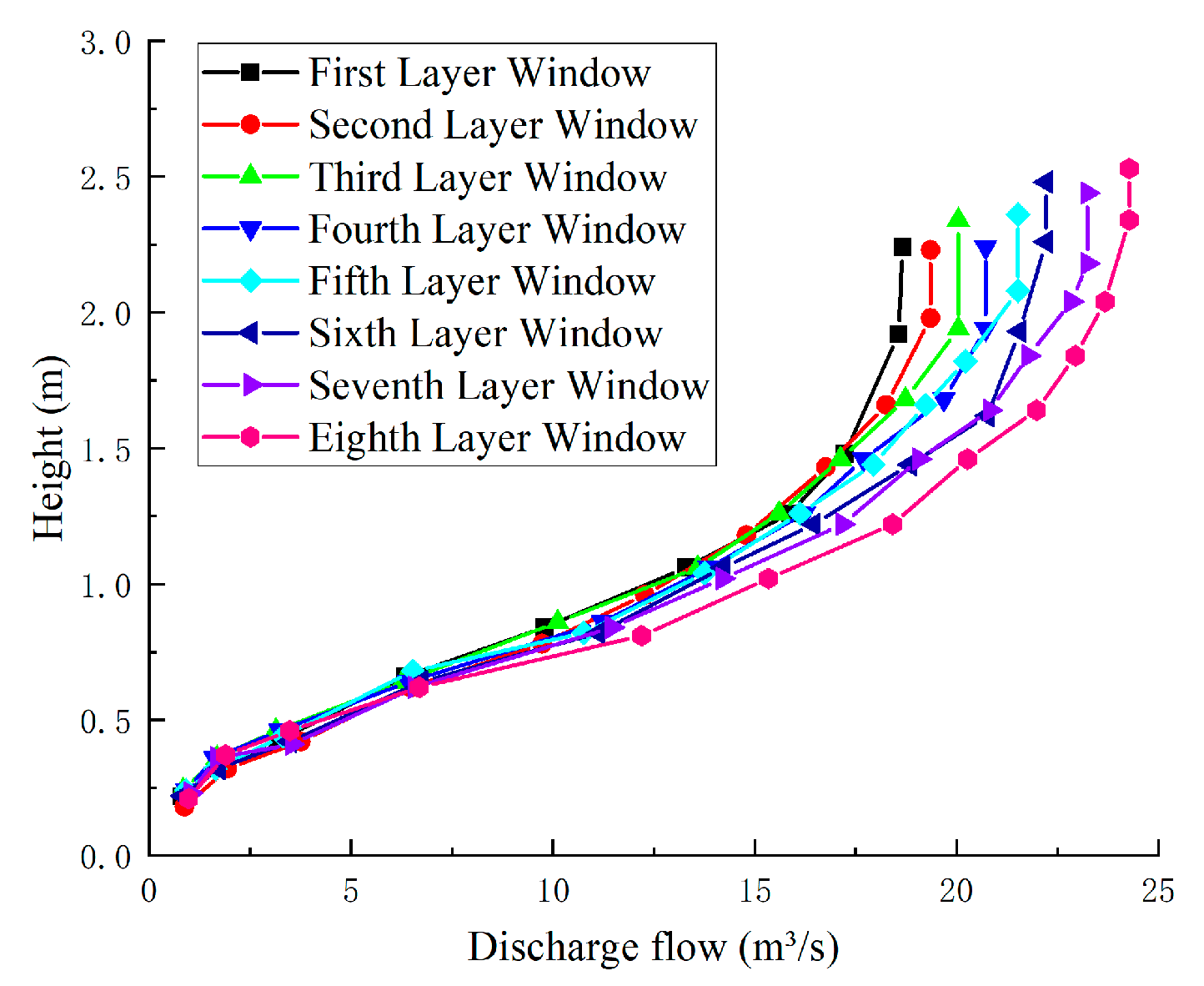
4.1.3. Flow Rate of the Flood Discharge System

Figure 10 and Figure 11 depict the flow rate head and flow velocity head curves for discharge windows 1 to 8 of the drainage shaft No. 1.

As Figure 10 and Figure 11 and Table 4 reveal, when full-pipe flow (pressurized flow) was reached, the flow regime in the flood discharge system stabilized, and the discharge flow rate also became steady. The stable maximum discharge flow was between 18.66 m³/s and 24.27 m³/s, and the maximum average flow velocity ranged from 7.296 m/s to 9.427 m/s. It is evident that as the discharge windows were elevated, the flow velocity gradually increased, and the maximum discharge flow rate also increased accordingly. Once the full-pipe flow stabilized, the discharge flow rate and flow velocity of the discharge windows on the eighth layer were 30.1% and 29.2% higher, respectively, than those on the first layer. This was attributed to the fact that as the height of the shaft increased, the gravitational potential energy of the water flow rose; however, its effectiveness in the energy dissipation well was not sufficient, resulting in an increase in the flow velocity. Consequently, the discharge flow rate also increased as the height of the shaft increased.

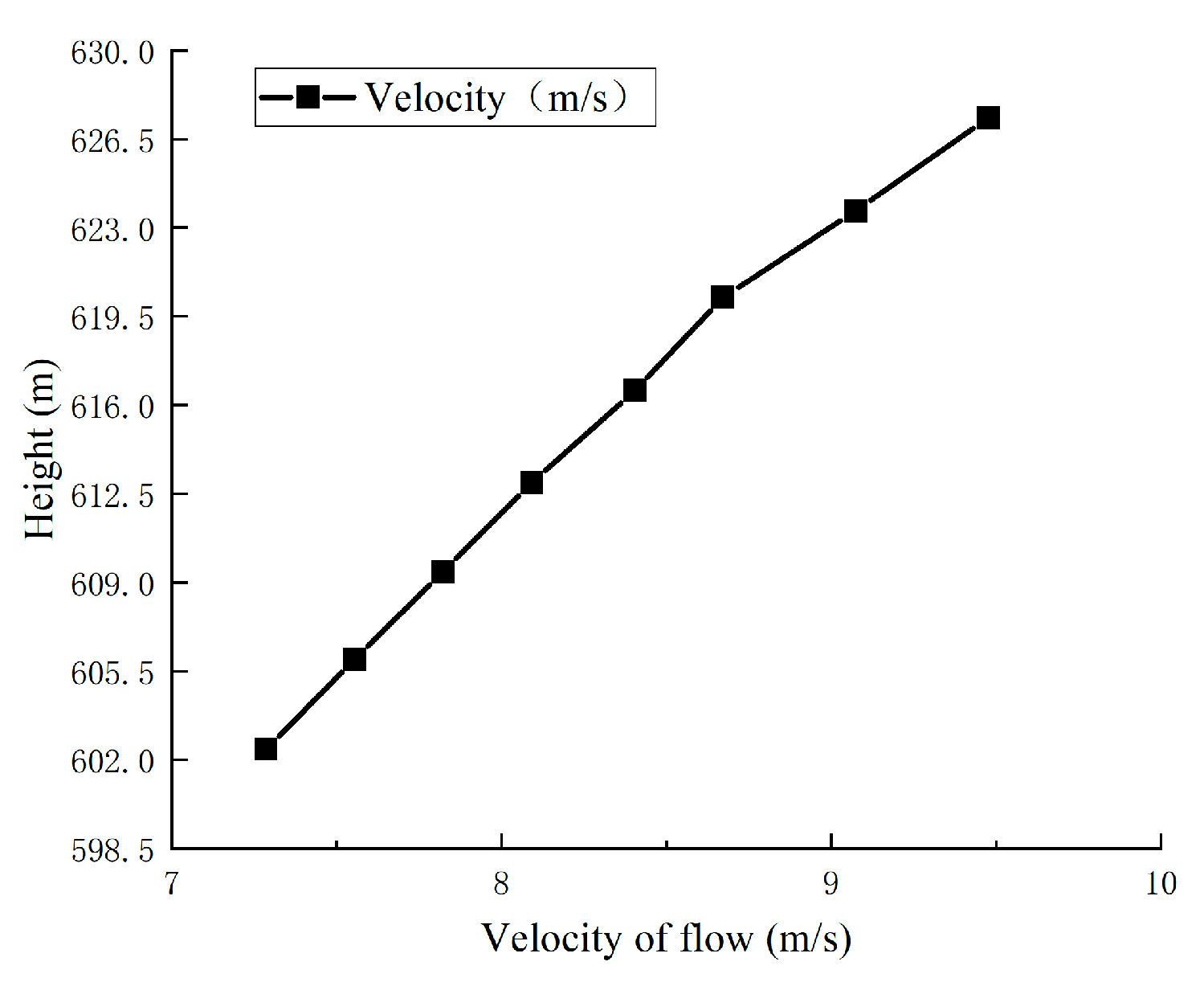
4.1.4. Analysis of Flood Tunnel Pressure

The experiment arranged five measuring points at distances of 2 m, 6 m, 10 m, 14 m, and 18 m downstream of the drainage pipe. During the discharge process, the water head was gradually increased by increments of 0.2 m (equivalent to 1 cm in the model). For each set of experiments, after the water head stabilized, the pressures at measuring points 1# to 5# were measured. Figure 12 shows the measurement results.

As Figure 12 shows, when the discharge head is low, the flow in the horizontal pipe manifests as open-channel flow, with the time-averaged pressure at measurement points showing a small positive value. However, as the head increases and discharge capacity enhances, the flow velocity within the horizontal pipe intensifies. The flow regime transitions from an alternating open-pressurized flow to a fully pressurized pipe flow. During this transition, negative pressure emerges in the time-averaged pressure at measurement points, though its magnitude gradually diminishes as the flow stabilizes. Experimental results demonstrate that the time-averaged pressure conditions within the horizontal pipe do not adversely affect the flood discharge tunnel.

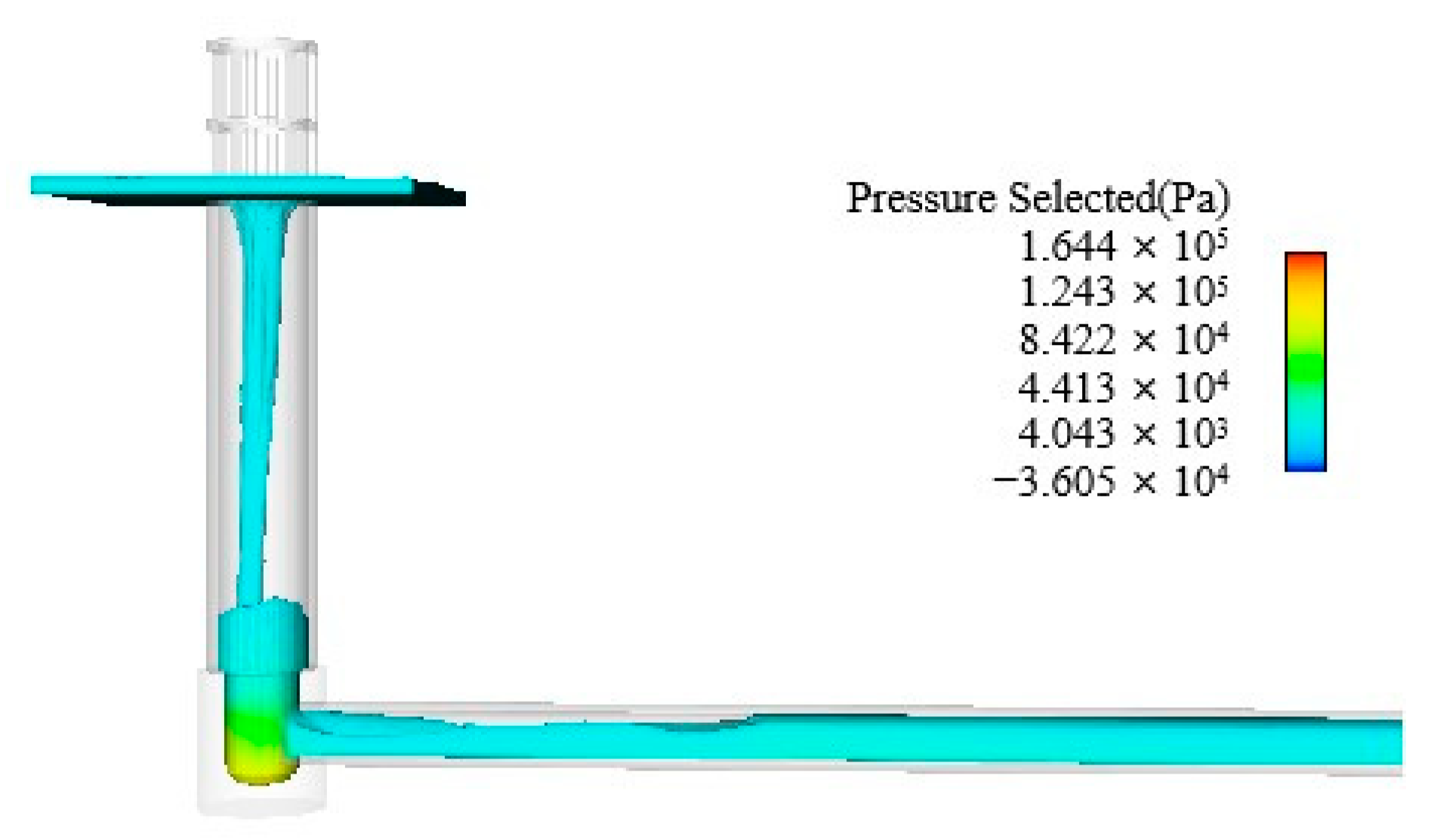
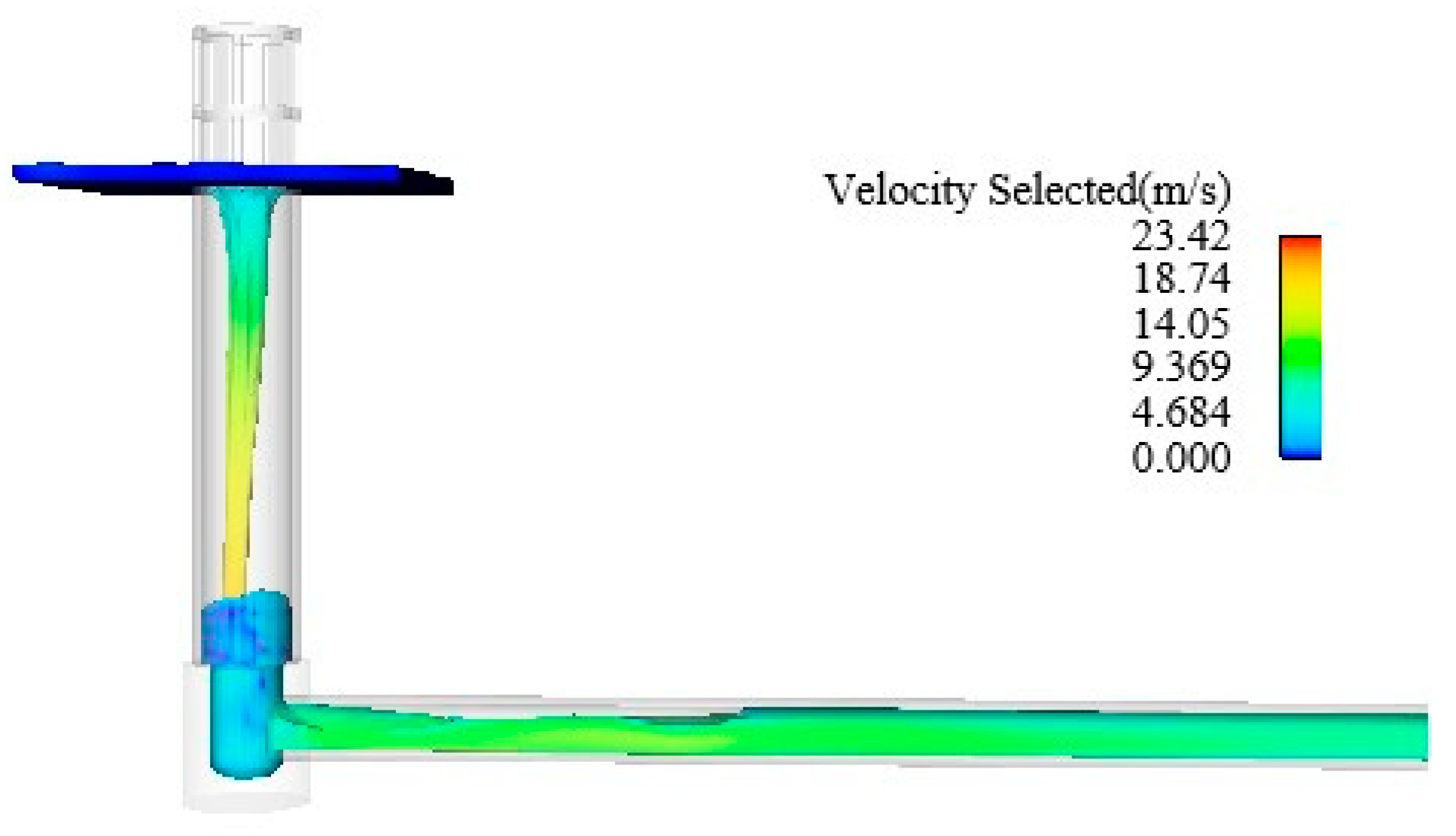
4.2. Numerical Simulation Results

4.2.1. Normal Condition

As Figure 13 and Figure 14 show, once the discharge stabilized, the flow in the discharge system transitioned from free flow to full-pipe flow under normal condition. After a period of discharge it may revert to free flow, demonstrating an alternating regime between open-channel flow and full-pipe flow, which aligned well with the model test results. Figure 13 confirms that under normal conditions the maximum pressure in the discharge system was distributed at the bottom of the energy dissipation well, reaching approximately 94.9 kPa, which did not pose a risk of damage to the structure. Due to the high flow velocity and inadequate ventilation within the shaft, negative pressure occurred at the junction of the shaft and energy dissipation well. Its maximum value was 8.34 kPa, which was less than the acceptable limit of 60 kPa, eliminating the risk of cavitation. Figure 14 depicts that the flow velocity in the shaft reached a maximum of 17.6 m/s, but after sufficient energy dissipation in the energy dissipation well, the velocity decreased. The flow velocity in the discharge tunnel was relatively uniform, with an average flow velocity of approximately 8.77 m/s. In comparison to the experimental result of 8.92 m/s, the error was only 1.71%, demonstrating good agreement.

4.2.2. Flood Condition

Figure 15 and Figure 16 indicate that after the flow stabilized, the flow in the discharge tunnel transitioned from an open channel flow to a full pipe flow under flood condition and remained in a full pipe flow regime for an extended period, which was consistent with the flow regimes observed in the high head discharge tests. Due to higher water levels and larger discharge volumes, the height of the water cushion at the junction of the shaft and energy dissipation well was also relatively high during the discharge process. At this point, the discharge capability was primarily determined by the discharge tunnel. Figure 15 demonstrates that the maximum pressure under flood conditions was distributed at the bottom of the energy dissipation well, with a maximum value of approximately 124.3 kPa, which would not cause any damage to the structure. Due to the high flow velocity and inadequate ventilation within the shaft, negative pressure occurred at the junction of the shaft and energy dissipation well. Its maximum value was 36.05 kPa, which was less than the acceptable limit of 60 kPa, eliminating the risk of cavitation. Figure 16 depicted that the maximum flow velocity in the shaft reached 18.74 m/s. After undergoing sufficient energy dissipation in the energy dissipation well, the average flow velocity in the tunnel was 9.37 m/s. Compared to the experimental result of 9.07 m/s, the error was only 3.31%, demonstrating good agreement.

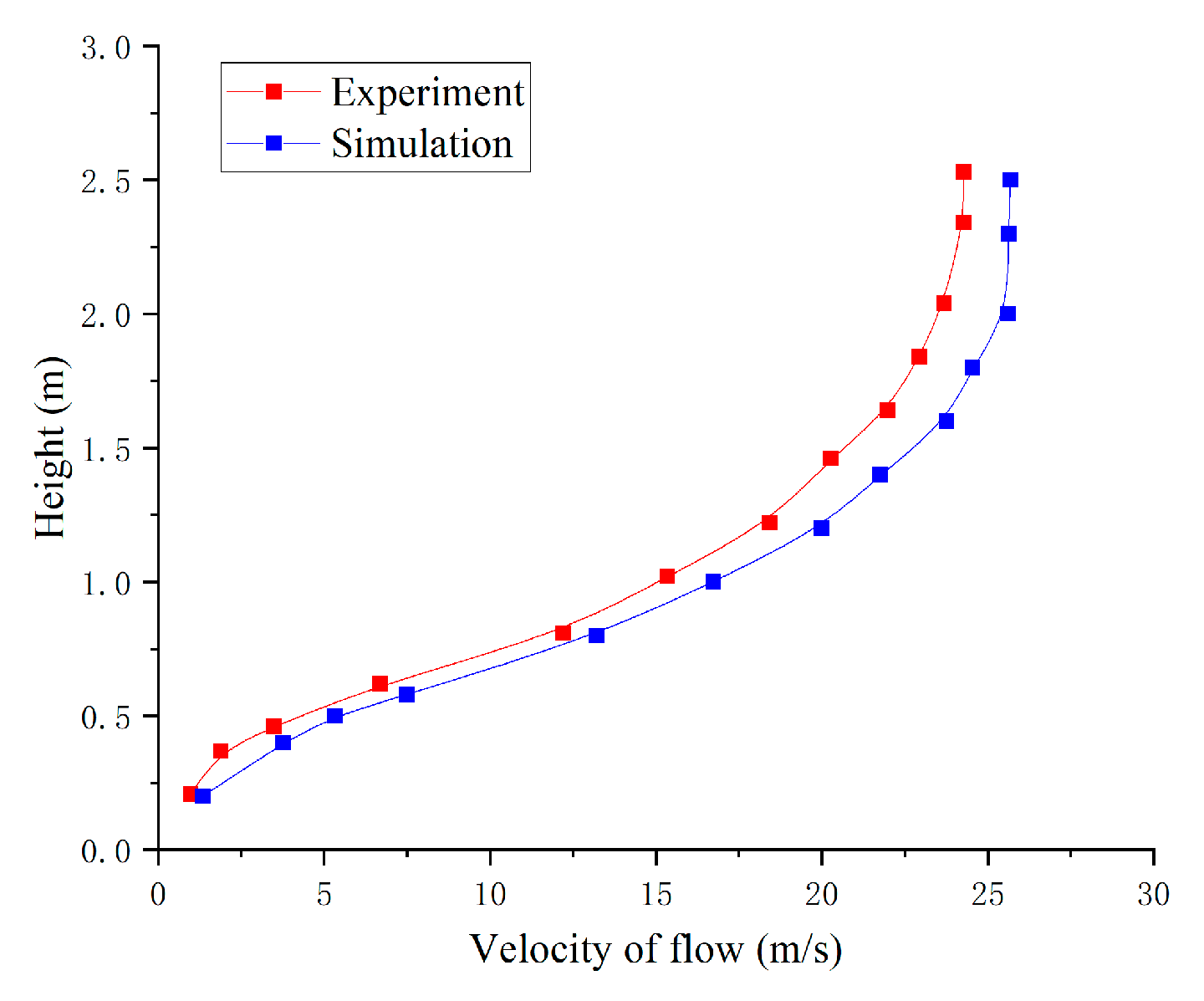
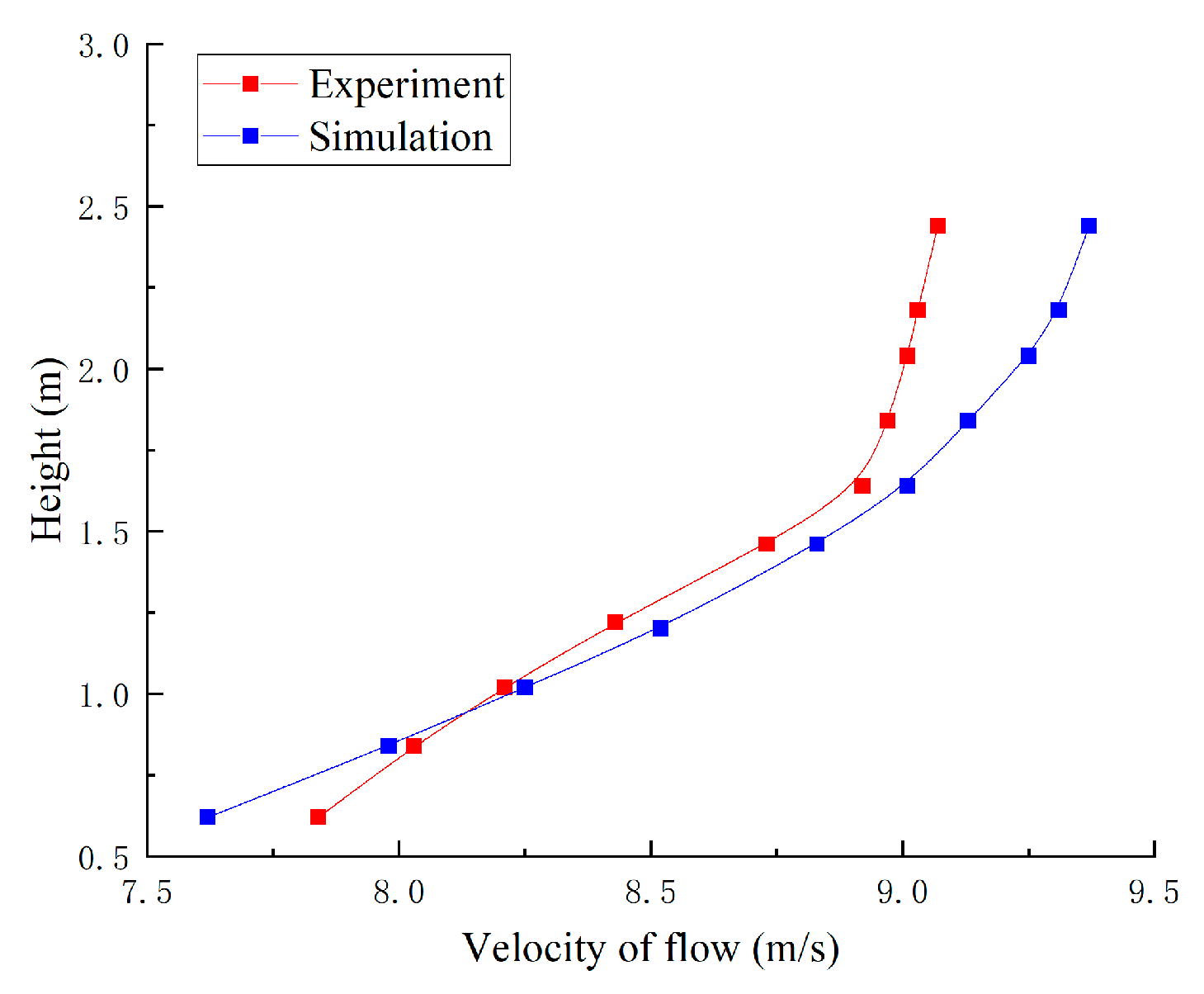
4.2.3. Comparison and Analysis of Test and Simulation Results

Figure 17 and Figure 18 show the results of the model tests and simulations. As Figure 17 shows, the results of the tests and simulations are roughly similar at low water heads. However, as the water level gradually rises, the simulated discharge flow is larger than the experimental value. This is because the model of the connection between the model’s energy dissipater well and the flood discharge tunnel does not take into account the actual wall thickness, and its size is larger. As a result, the water flow in the model test acts more fully in the energy dissipater well, with a relatively lower velocity. Therefore, the experimental discharge flow is smaller than the simulated one. Figure 18 further illustrates the cause of the discharge situation with the velocity results, which have smaller errors and a higher degree of consistency. When the flood discharge system is discharging at low water heads, the velocity shows an upward trend. As the flow state gradually transitions to full pipe flow, the velocity gradually reaches its maximum value and stabilizes.

5. Conclusions

Based on the design of a tailings reservoir in Henan Province, China, a hydraulic model test was conducted to simulate the operation of the discharge system. Additionally, numerical simulations were performed to examine the discharge conditions of the entire tailings reservoir under both normal and flood water levels, as well as the hydraulic characteristics of the discharge system. The following conclusions are drawn:

The flow regimes at the discharge windows of the drainage shaft across different layers were generally similar. When the discharge head was below 0.8 m, the flow was in an unpressurized regime. When the discharge head ranged from 0.8 m to 1.2 m, the inlet section of the horizontal pipe exhibited an alternating regime between open-channel flow and full-pipe flow, while the latter section showed unpressurized flow. When the discharge head exceeded 1.2 m, the flow gradually transitioned from partially pressurized to fully pressurized. Once the discharge head reached 1.6 m, full-pipe pressurized flow occurred in both the energy dissipation well and the horizontal pipe. Based on the analysis of the flow regimes, it is recommended to reinforce the design of the energy dissipation well and the inlet section of the discharge tunnel. During operation, it is advised to control the discharge head to be below 0.8 m to prevent adverse flow regimes that may occur at high water heads from damaging the connecting sections.

As the elevation of the discharge windows increased, the discharge capacity of the flood drainage system also gradually increased. After stabilization, the maximum discharge flow rates at the windows on different layers ranged from 18.66 m³/s to 24.27 m³/s, while the corresponding average flow velocities varied between 7.296 m/s and 9.427 m/s. The discharge flow rate and flow velocity of the discharge windows on the eighth layer were 30.1% and 29.2% higher, respectively, than those on the first layer. When the high-level discharge windows operated under high water heads, they were more likely to entrain large amounts of gas, leading to alternating open-channel and full-pipe flow phenomena at the inlet section of the horizontal pipe. This could lead to cavitation or air entrainment effects in the pipe. It is essential to thoroughly evaluate the design dimensions of the energy dissipation well and drainage shaft to minimize or prevent adverse flow regimes.

Numerical simulation results indicated that the flood discharge system was prone to generating negative pressure on the walls of the energy dissipation well under normal conditions, with a negative pressure value of 8.34 kPa. Under flood conditions, the system experienced a wider range of negative pressure, reaching 36.05 kPa, which was significantly higher than that under normal conditions. Therefore, it can be concluded that the flood discharge system would not experience cavitation under either normal or flood conditions, thus ensuring its safe operation.