Simulation of Control Process of Fluid Boundary Layer on Deposition of Travertine Particles in Huanglong Landscape Water Based on Computational Fluid Dynamics Software (CFD)
Abstract
:1. Introduction
2. Research Methods
2.1. Analysis Method
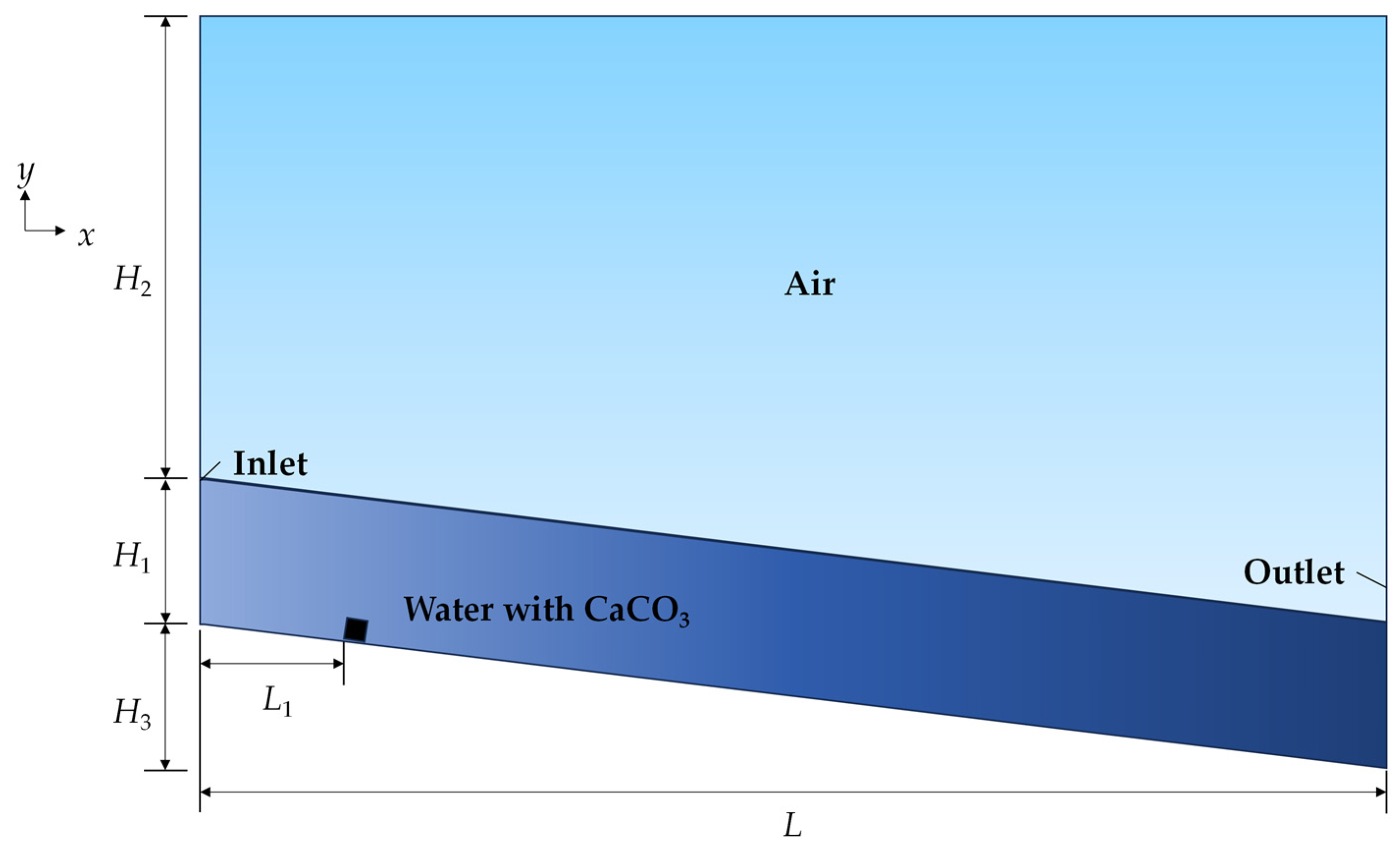
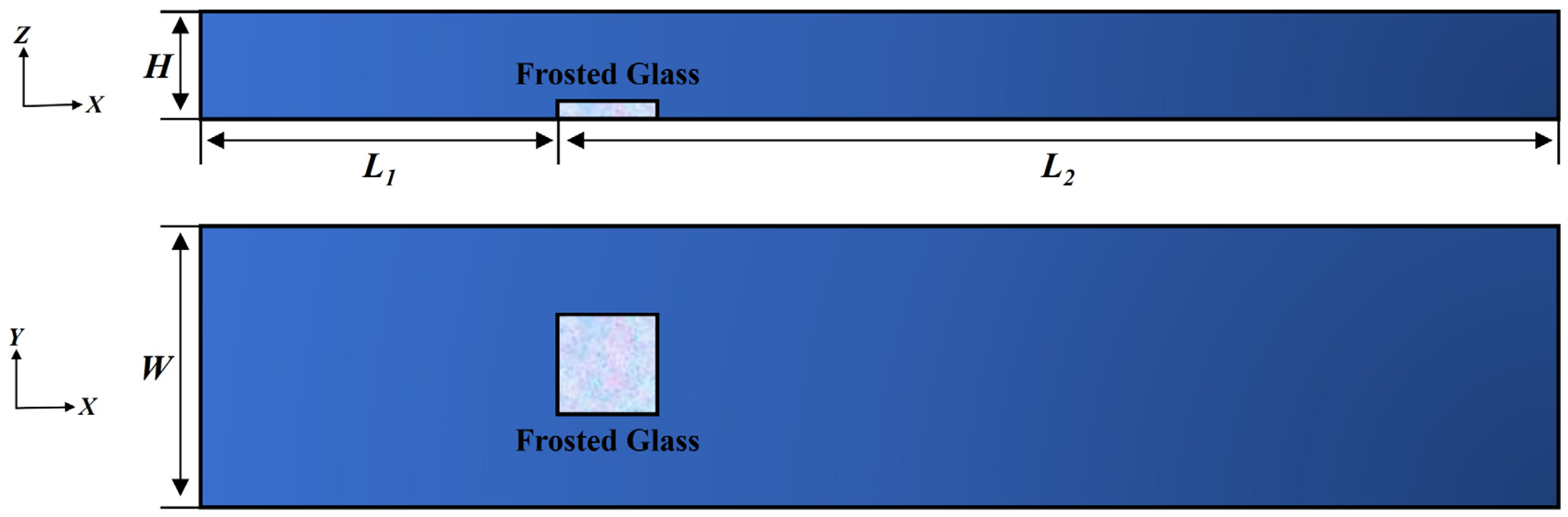
2.2. Model Construction
2.3. Density Variations in CFD Simulations
2.4. Boundary Layer Analysis
3. Results and Discussion
3.1. Horizontal Flow Field Travertine Deposition Process
3.2. Inclined Plane Flow Field Travertine Deposition Process
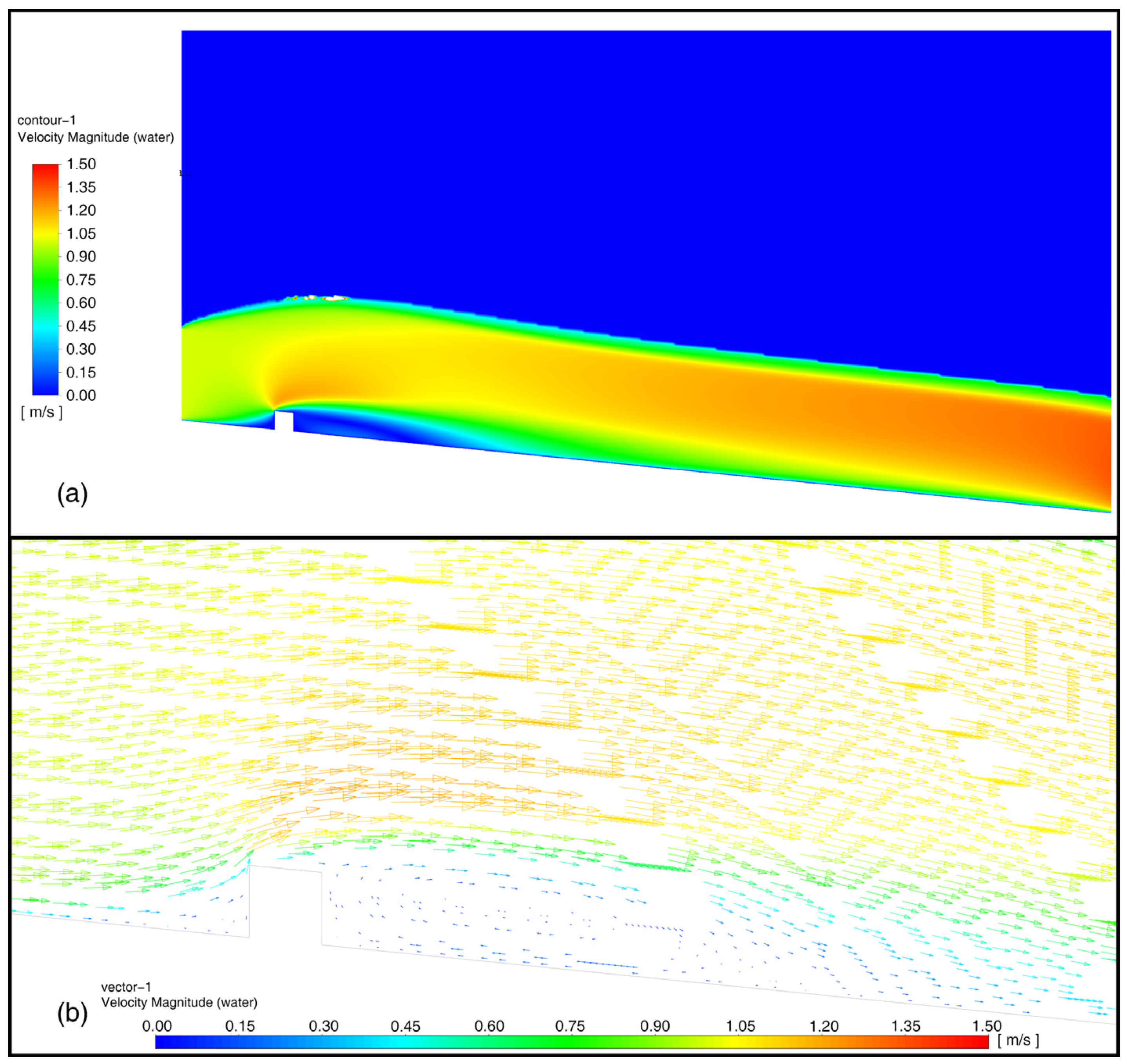
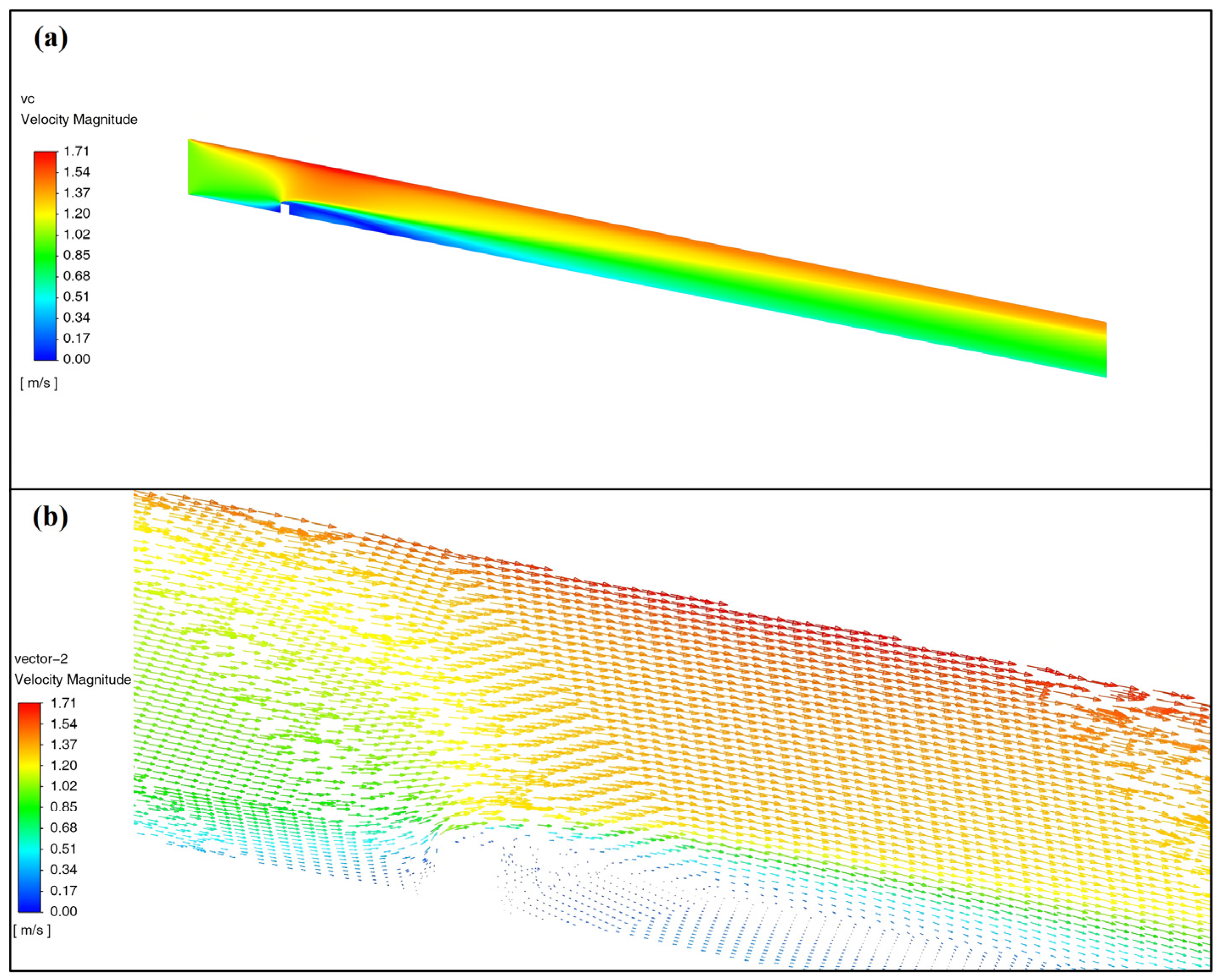
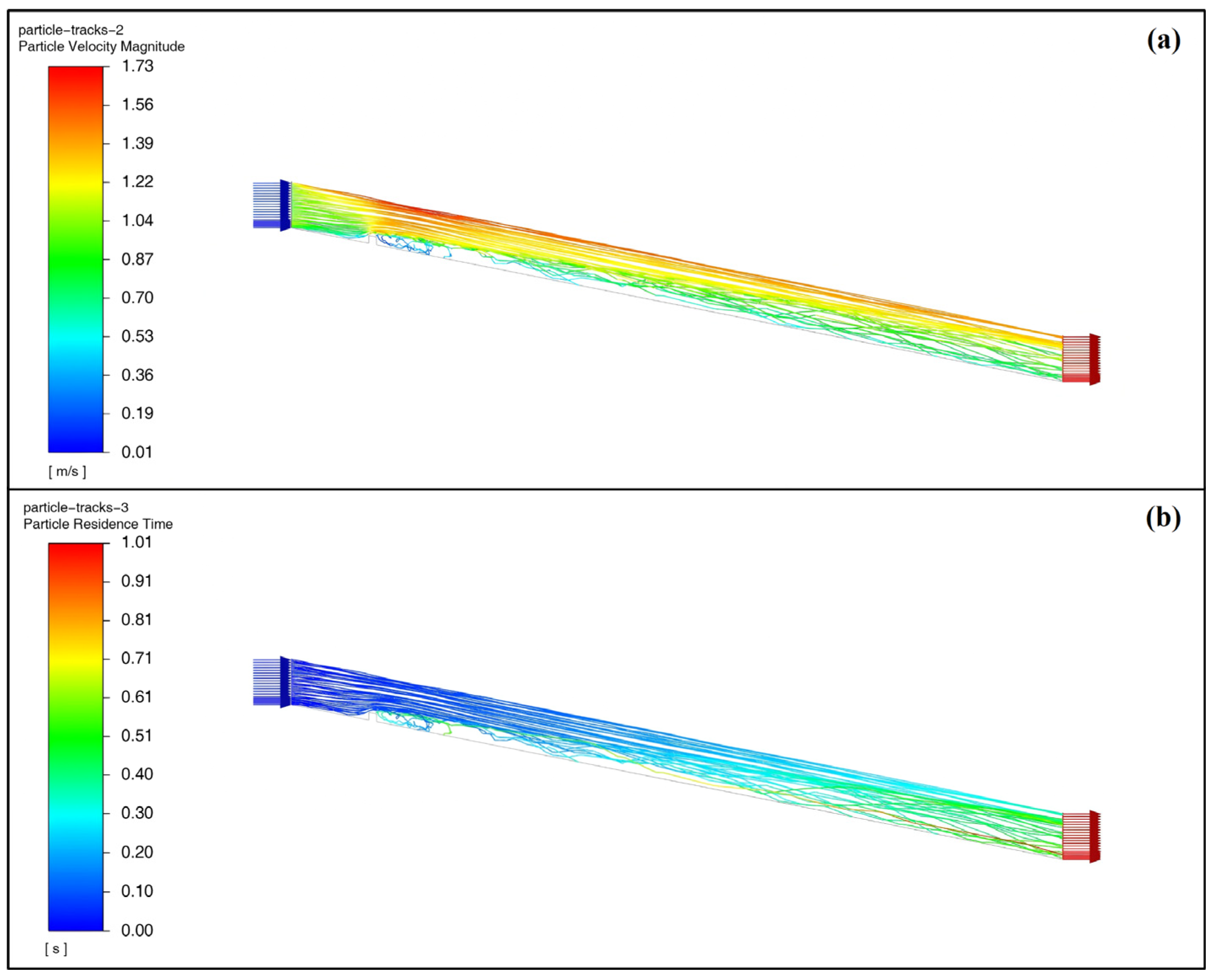
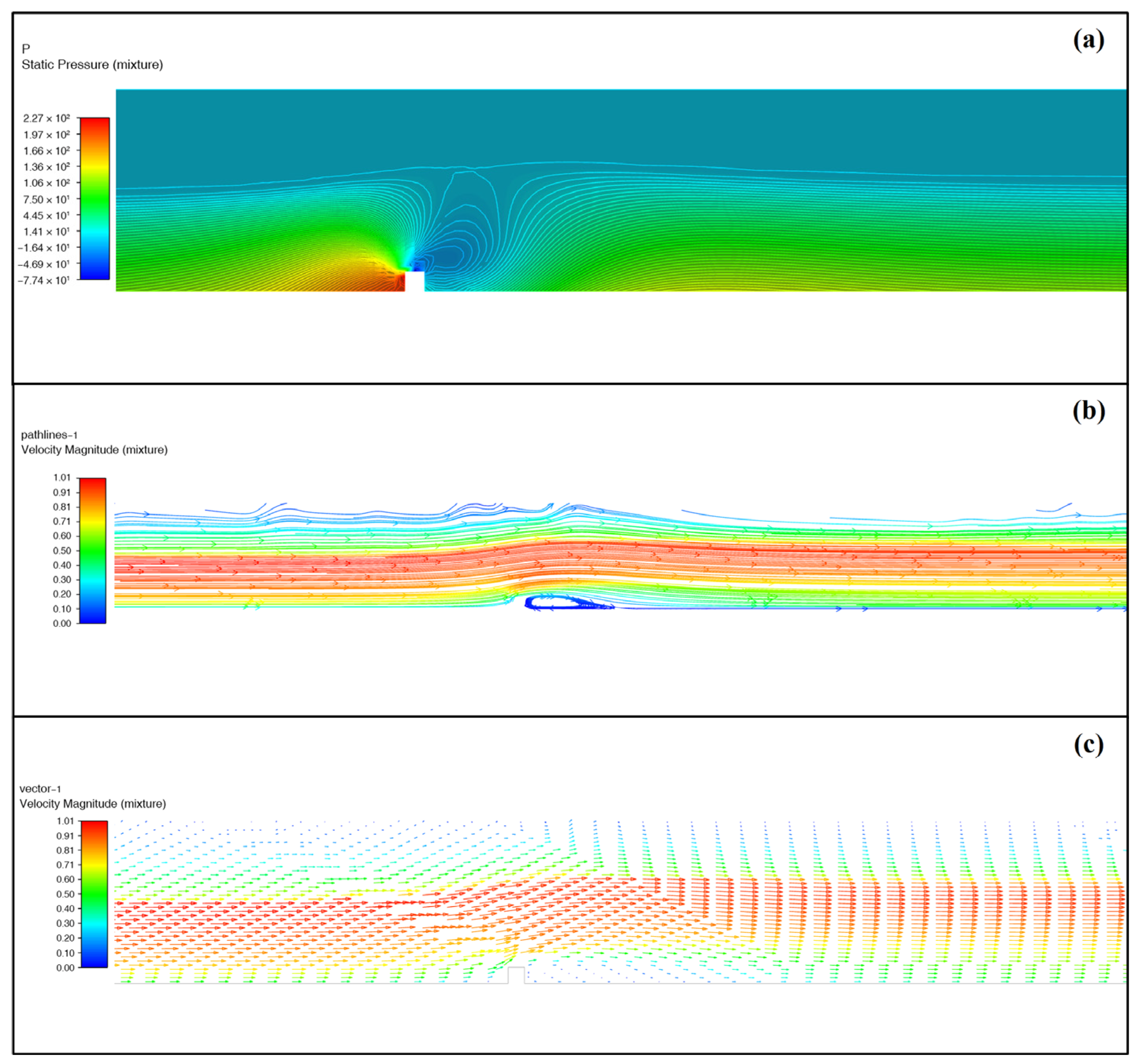
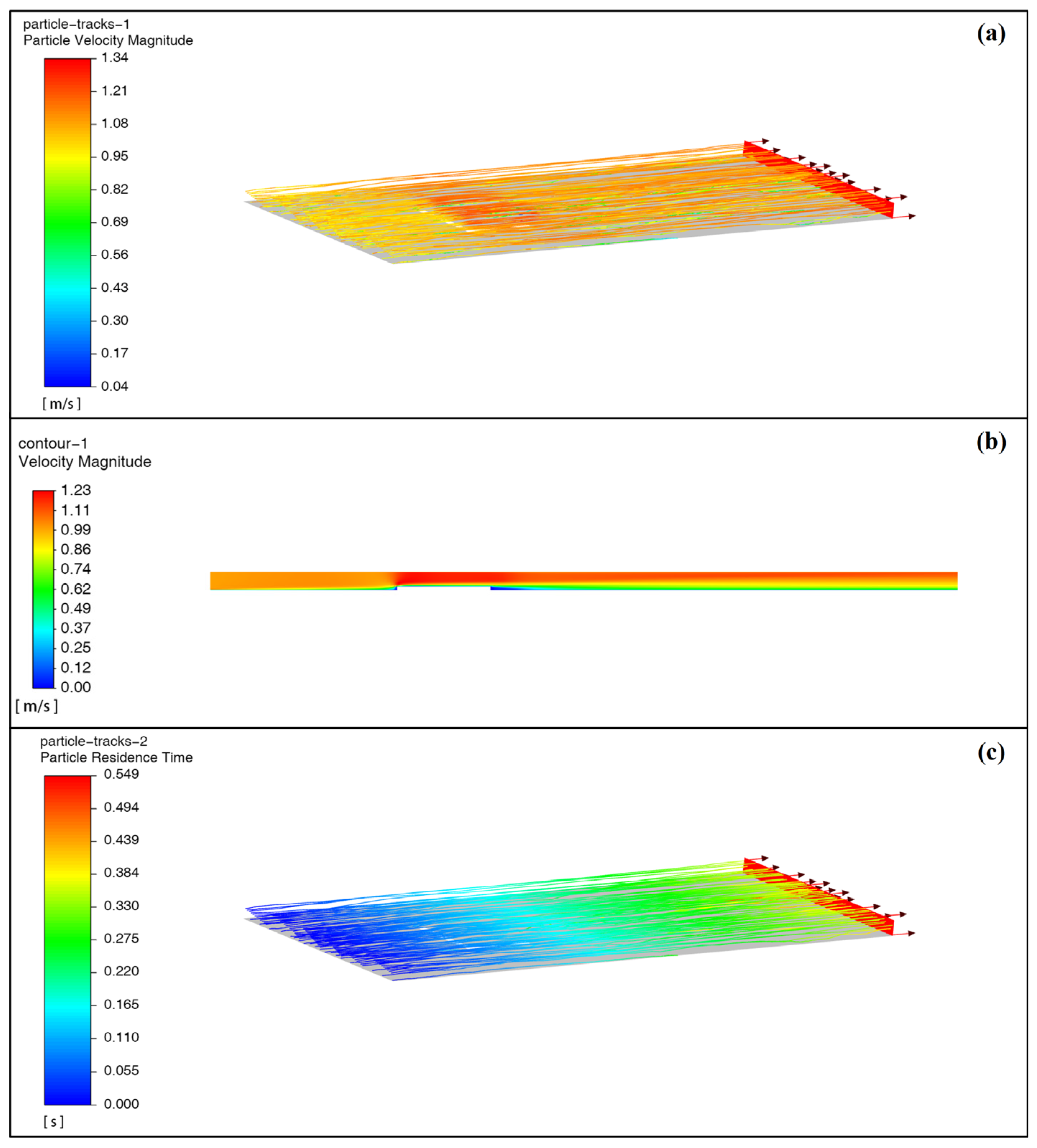
3.3. Boundary Layer Effect of Inclined Plane Flow Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pentecost, A. Travertine; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Khoury, H.N.; Clark, I.D. Mineralogy and origin of surficial uranium deposits hosted in travertine and calcrete from central Jordan. Appl. Geochem. 2014, 43, 49–65. [Google Scholar] [CrossRef]
- Wang, K.; Hu, S.; Li, W.; Liu, W.; Huang, Q.; Ma, K.; Shi, S. Depositional System of the Carboniferous Huanglong Formation, Eastern Sichuan Basin: Constraints from Sedimentology and Geochemistry. Acta Geol. Sin.-Engl. Ed. 2016, 90, 1795–1808. [Google Scholar] [CrossRef]
- Pentecost, A.; Viles, H. A review and reassessment of travertine classification. Géographie Phys. Quat. 1994, 48, 305–314. [Google Scholar] [CrossRef]
- Shi, Z.; Shi, Z.; Yin, G.; Liang, J. Travertine deposits, deep thermal metamorphism and tectonic activity in the Longmenshan tectonic region, southwestern China. Tectonophysics 2014, 633, 156–163. [Google Scholar] [CrossRef]
- Viles, H.; Pentecost, A. Tufa and travertine. In Geochemical Sediments and Landscapes; Wiley: Hoboken, NJ, USA, 2007; pp. 173–199. [Google Scholar]
- Luo, L.; Capezzuoli, E.; Vaselli, O.; Wen, H.; Lazzaroni, M.; Lu, Z.; Meloni, F.; Kele, S. Factors governing travertine deposition in fluvial systems: The Bagni San Filippo (central Italy) case study. Sediment. Geol. 2021, 426, 106023. [Google Scholar] [CrossRef]
- Croci, A.; Della Porta, G.; Capezzuoli, E. Depositional architecture of a mixed travertine-terrigenous system in a fault-controlled continental extensional basin (Messinian, Southern Tuscany, Central Italy). Sediment. Geol. 2016, 332, 13–39. [Google Scholar] [CrossRef]
- De Waele, J.; Gutiérrez, F. Karst Hydrogeology, Geomorphology and Caves; John Wiley & Sons.: Hoboken, NJ, USA, 2022. [Google Scholar]
- Zhang, T.; Dai, Q.; An, D.; Mors, R.A.; Li, Q.; Astini, R.A.; He, J.; Cui, J.; Jiang, R.; Dong, F.; et al. Effective mechanisms in the formation of pool-rimstone dams in continental carbonate systems: The case study of Huanglong, China. Sediment. Geol. 2023, 455, 106486. [Google Scholar] [CrossRef]
- Boussagol, P.; Vennin, E.; Monna, F.; Millet, L.; Bonnotte, A.; Motreuil, S.; Bundeleva, I.; Rius, D.; Visscher, P.T. Carbonate mud production in lakes is driven by degradation of microbial substances. Commun. Earth Environ. 2024, 5, 533. [Google Scholar] [CrossRef]
- Özkul, M.; Gökgöz, A.; Kele, S.; Baykara, M.O.; Shen, C.C.; Chang, Y.W.; Kaya, A.; Hançer, M.; Aratman, C.; Akin, T.; et al. Sedimentological and geochemical characteristics of a fluvial travertine: A case from the eastern Mediterranean region. Sedimentology 2014, 61, 291–318. [Google Scholar] [CrossRef]
- Ranade, V.V. Computational Flow Modeling for Chemical Reactor Engineering; Elsevier: Amsterdam, The Netherlands, 2001; Volume 5. [Google Scholar]
- Dianyu, E. Validation of CFD–DEM model for iron ore reduction at particle level and parametric study. Particuology 2020, 51, 163–172. [Google Scholar]
- Wu, W. Sediment Transport Dynamics; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Toker, E. Quaternary fluvial tufas of Sarıkavak area, southwestern Turkey: Facies and depositional systems. Quat. Int. 2017, 437, 37–50. [Google Scholar] [CrossRef]
- Iqbal, N.; Rauh, C. Coupling of discrete element model (DEM) with computational fluid mechanics (CFD): A validation study. Appl. Math. Comput. 2016, 277, 154–163. [Google Scholar] [CrossRef]
- Mahmoodi, B.; Hosseini, S.H.; Ahmadi, G. CFD–DEM simulation of a pseudo-two-dimensional spouted bed comprising coarse particles. Particuology 2019, 43, 171–180. [Google Scholar] [CrossRef]
- Marchelli, F.; Moliner, C.; Bosio, B.; Arato, E. A CFD-DEM sensitivity analysis: The case of a pseudo-2D spouted bed. Powder Technol. 2019, 353, 409–425. [Google Scholar] [CrossRef]
- Emam, S.A. Generalized Lagrange’s equations for systems with general constraints and distributed parameters. Multibody Syst. Dyn. 2020, 49, 95–117. [Google Scholar] [CrossRef]
- Paraskevopoulos, E.; Potosakis, N.; Natsiavas, S. An augmented Lagrangian formulation for the equations of motion of multibody systems subject to equality constraints. Procedia Eng. 2017, 199, 747–752. [Google Scholar] [CrossRef]
- Lin, S.; Cao, J.; Zhang, J.; Sun, T. Stability and convergence analysis for a new phase field crystal model with a nonlocal Lagrange multiplier. Math. Methods Appl. Sci. 2021, 44, 4972–4984. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, S. Novel linear decoupled and unconditionally energy stable numerical methods for the modified phase field crystal model. Appl. Numer. Math. 2021, 163, 1–14. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, Y.; Huang, Y. Stability and error estimates of GPAV-based unconditionally energy-stable scheme for phase field crystal equation. Comput. Math. Appl. 2023, 151, 461–472. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X. Efficient modified stabilized invariant energy quadratization approaches for phase-field crystal equation. Numer. Algorithms 2020, 85, 107–132. [Google Scholar] [CrossRef]
- Liang, Y.; Jia, H. Linear and unconditionally energy stable schemes for the modified phase field crystal equation. Comput. Math. Appl. 2024, 153, 197–212. [Google Scholar] [CrossRef]
- Seis, C. A Quantitative Theory for the Continuity Equation: Annales de l’Institut Henri Poincaré C, Analyse non linéaire; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Brué, E.; Nguyen, Q.H. Sharp regularity estimates for solutions of the continuity equation drifted by Sobolev vector fields. Anal. PDE 2021, 14, 2539–2559. [Google Scholar] [CrossRef]
- Roth, G.A.; Aydogan, F. Derivation of new mass, momentum, and energy conservation equations for two-phase flows. Prog. Nucl. Energy 2015, 80, 90–101. [Google Scholar] [CrossRef]
- Jain, S.S.; Moin, P. A kinetic energy–and entropy-preserving scheme for compressible two-phase flows. J. Comput. Phys. 2022, 464, 111307. [Google Scholar] [CrossRef]
- Fuhrman, D.R.; Li, Y. Instability of the realizable k–ε turbulence model beneath surface waves. Phys. Fluids 2020, 32, 115108. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef]
- Liu, Z.; Li, G. Numerical simulation of centrifugal pump impeller erosion caused by particles in lead–bismuth alloy. Int. J. Mod. Phys. B 2023, 37, 2350225. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, C.; Liu, X. Energy transfer and interaction between liquid metal with water. Energy 2024, 288, 129865. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Reid, J.P.; Bertram, A.K.; Topping, D.O.; Laskin, A.; Martin, S.T.; Petters, M.D.; Pope, F.D.; Rovelli, G. The viscosity of atmospherically relevant organic particles. Nat. Commun. 2018, 9, 956. [Google Scholar] [CrossRef]






| Experimental Instrument | Model Number | Manufacturer |
|---|---|---|
| Radar speedometer | Decatur SVR-3D | Global Water Resources, Inc. Phoenix, AZ, USA |
| Particle imaging velocity measurement system | 2D PIV | TSI Corporation, Shoreview, MN, USA |
| Model Selected | Time | Solving Multiphase Problem | Limitations of the Model |
|---|---|---|---|
| Eulerian model | Transient | Horizontal flow field travertine deposition process | The trajectory of CaCO3 particles is not being considered |
| Eulerian model | Transient | Inclined plane flow field travertine deposition process | The trajectory of CaCO3 particles is not being considered |
| DPM | Steady | Boundary layer effect of inclined plane flow field | The influence of air on water flow is not being considered. |
| VOF | Transient | A 1 m long channel | The influence of particles on water flow is not being considered. |
| DPM | Steady | The particle sedimentation measurement | The influence of air on water flow is not being considered. |
| Calculation Results | Calcium Carbonate Particles | |
|---|---|---|
| Initial concentration | 0.01% | 0.001% |
| Flow/kg·s−1 | 1.42 × 10−6 | 7.05 × 10−6 |
| Number of particles released at the inlet | 2424 | 2424 |
| Number of deposited particles | 9 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Gao, W.; Zuo, Y.; Sun, D.; Zhang, W.; Zhang, Z.; Liu, S.; Dong, J.; Wang, S.; Xu, H.; et al. Simulation of Control Process of Fluid Boundary Layer on Deposition of Travertine Particles in Huanglong Landscape Water Based on Computational Fluid Dynamics Software (CFD). Water 2025, 17, 638. https://doi.org/10.3390/w17050638
Liu X, Gao W, Zuo Y, Sun D, Zhang W, Zhang Z, Liu S, Dong J, Wang S, Xu H, et al. Simulation of Control Process of Fluid Boundary Layer on Deposition of Travertine Particles in Huanglong Landscape Water Based on Computational Fluid Dynamics Software (CFD). Water. 2025; 17(5):638. https://doi.org/10.3390/w17050638
Chicago/Turabian StyleLiu, Xinze, Wenhao Gao, Yang Zuo, Dong Sun, Weizhen Zhang, Zhipeng Zhang, Shupu Liu, Jianxing Dong, Shikuan Wang, Hao Xu, and et al. 2025. "Simulation of Control Process of Fluid Boundary Layer on Deposition of Travertine Particles in Huanglong Landscape Water Based on Computational Fluid Dynamics Software (CFD)" Water 17, no. 5: 638. https://doi.org/10.3390/w17050638
APA StyleLiu, X., Gao, W., Zuo, Y., Sun, D., Zhang, W., Zhang, Z., Liu, S., Dong, J., Wang, S., Xu, H., Chen, H., & Xu, M. (2025). Simulation of Control Process of Fluid Boundary Layer on Deposition of Travertine Particles in Huanglong Landscape Water Based on Computational Fluid Dynamics Software (CFD). Water, 17(5), 638. https://doi.org/10.3390/w17050638







