Prediction of Root-Zone Soil Moisture and Evapotranspiration in Cropland Using HYDRUS-1D Model with Different Soil Hydrodynamic Parameter Schemes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. HYDRUS-1D Model
2.3. Soil Hydraulic and Vegetation Parameters
3. Results
3.1. Determination of Soil and Vegetation Parameters
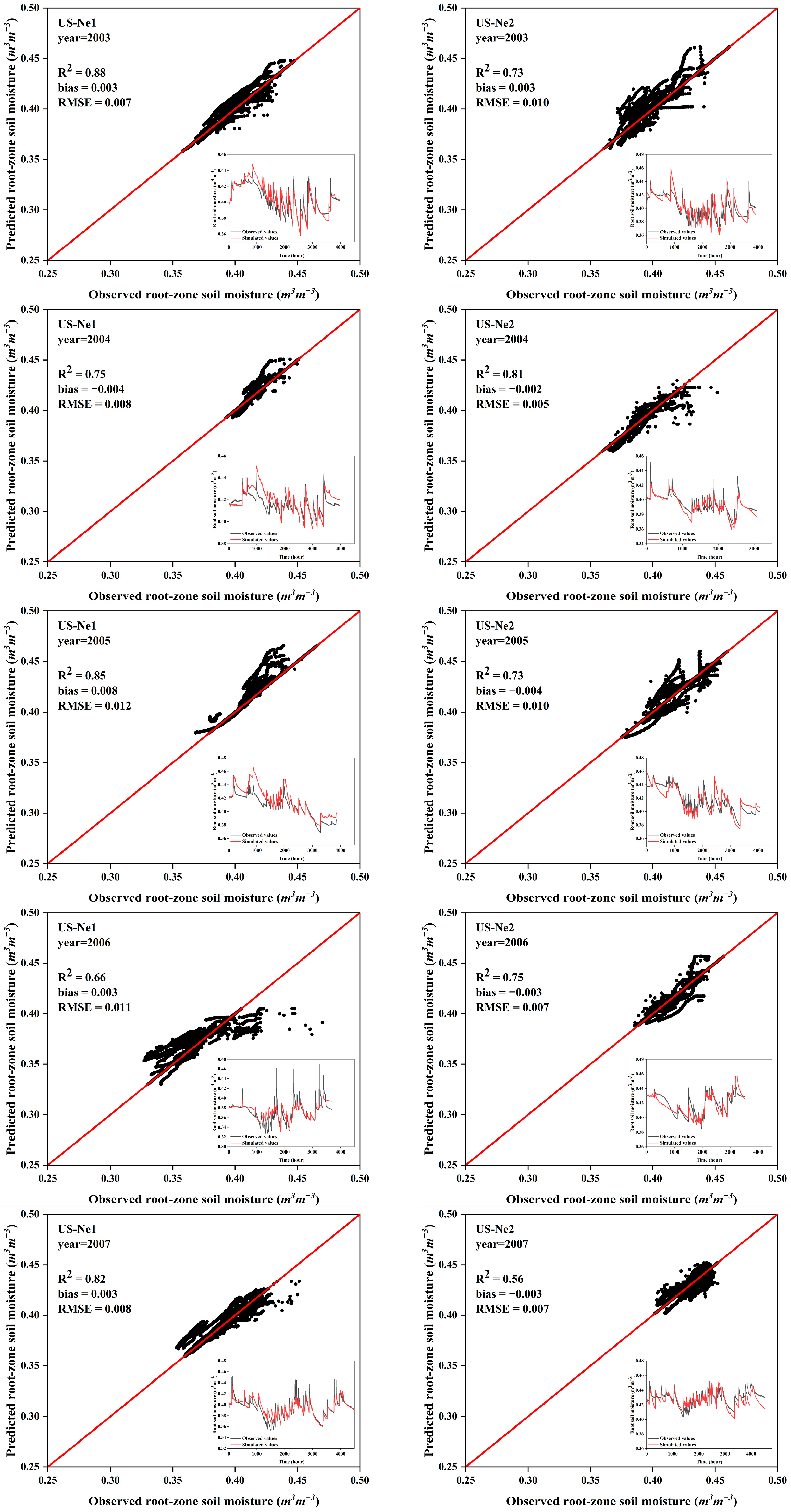
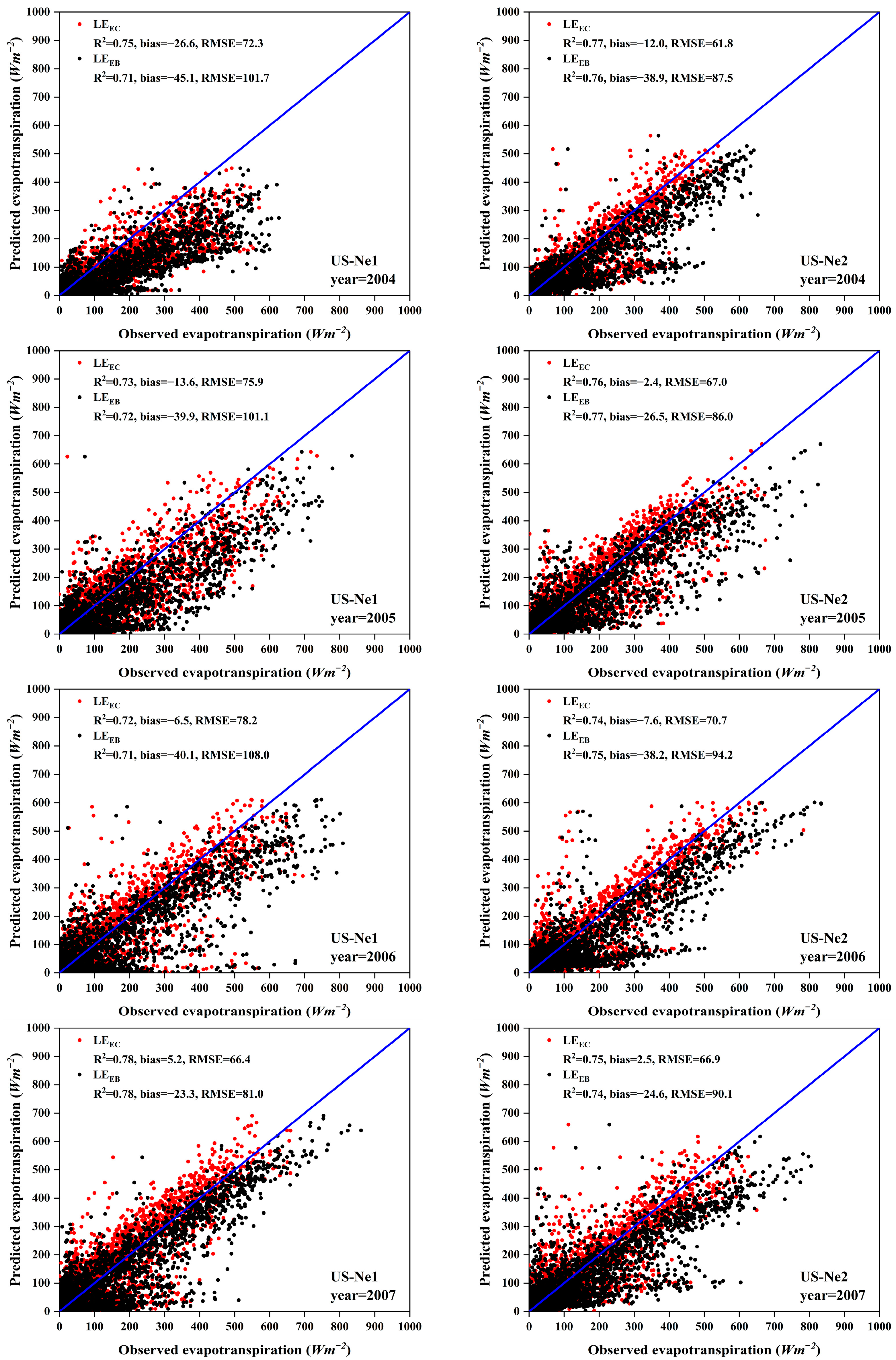
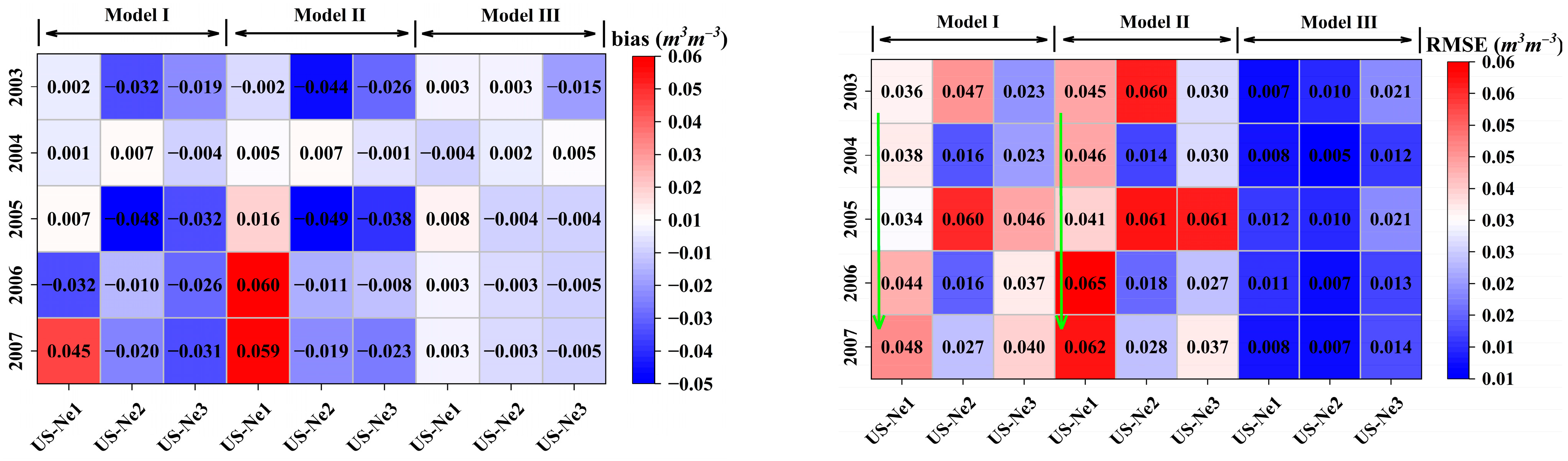
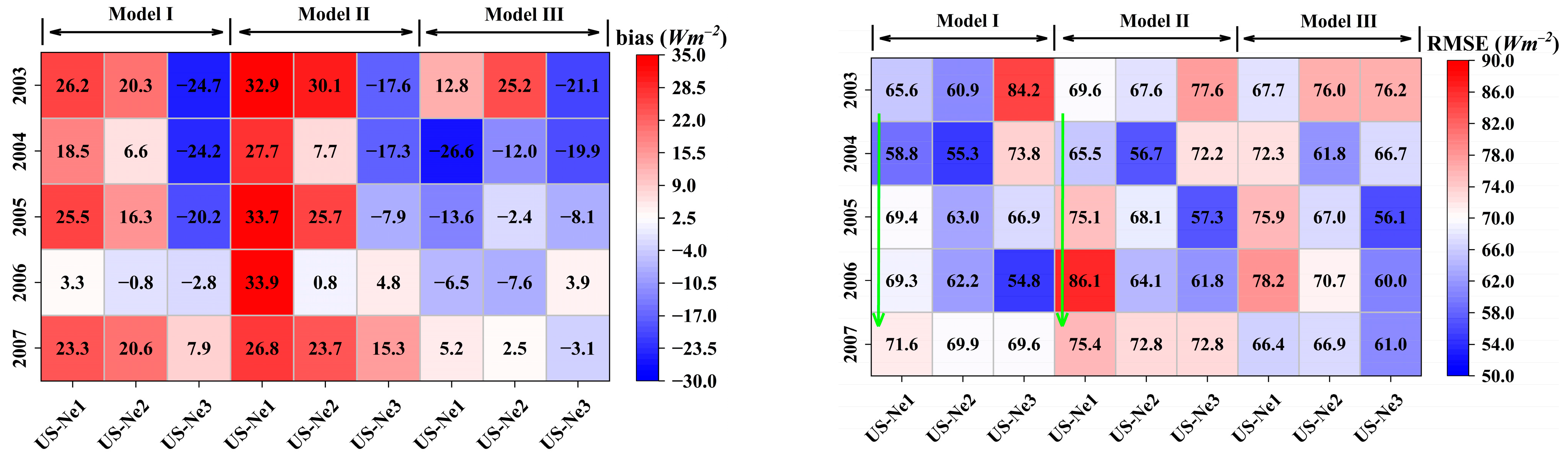
3.2. RZSM and ET Prediction in Irrigated Cropland
3.3. RZSM and ET Prediction in Rainfed Cropland
4. Discussion
4.1. The SHP Schemes Based on Soil Information
4.2. RZSM and ET Prediction with Different SHP Schemes
4.3. RZSM and ET Prediction Under Different Crop and Moisture Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Porter, J.R. Rising temperatures are likely to reduce crop yields. Nature 2005, 436, 174. [Google Scholar] [CrossRef] [PubMed]
- Fritz, S.; See, L.; Mccallum, I.; You, L.; Bun, A.; Moltchanova, E.; Duerauer, M.; Albrecht, F.; Schill, C.; Perger, C.; et al. Mapping global cropland and field size. Glob. Change Biol. 2015, 21, 1980–1992. [Google Scholar] [CrossRef] [PubMed]
- Potapov, P.; Turubanova, S.; Hansen, M.C.; Tyukavina, A.; Zalles, V.; Khan, A.; Song, X.P.; Pickens, A.; Shen, Q.; Cortez, J. Global maps of cropland extent and change show accelerated cropland expansion in the twenty-first century. Nat. Food 2022, 3, 19–28. [Google Scholar] [CrossRef]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Schlenker, W.; Roberts, M.J. Nonlinear temperature effects indicate severe damages to us crop yields under climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef]
- Iizumi, T.; Furuya, J.; Shen, Z.; Kim, W.; Okada, M.; Fujimori, S.; Hasegawa, T.; Nishimori, M. Responses of crop yield growth to global temperature and socioeconomic changes. Sci. Rep. 2017, 7, 7800. [Google Scholar] [CrossRef]
- Wang, E.; Martre, P.; Zhao, Z.; Ewert, F.; Maiorano, A.; Rötter, R.P.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W. The uncertainty of crop yield projections is reduced by improved temperature response functions. Nat. Plants 2017, 3, 1–13. [Google Scholar]
- Bodner, G.; Nakhforoosh, A.; Kaul, H. Management of crop water under drought: A review. Agron. Sustain. DEV Community 2015, 35, 401–442. [Google Scholar]
- Dietz, K.J.; Zörb, C.; Geilfus, C.M. Drought and crop yield. Plant Biol. 2021, 23, 881–893. [Google Scholar] [CrossRef]
- Li, Y.; Ye, W.; Wang, M.; Yan, X. Climate change and drought: A risk assessment of crop-yield impacts. Clim. Res. 2009, 39, 31–46. [Google Scholar] [CrossRef]
- Boyer, J.S.; Byrne, P.; Cassman, K.G.; Cooper, M.; Delmer, D.; Greene, T.; Gruis, F.; Habben, J.; Hausmann, N.; Kenny, N.; et al. The U.S. drought of 2012 in perspective: A call to action. Glob. Food Secur. 2013, 2, 139–143. [Google Scholar] [CrossRef]
- Hameed, M.; Ahmadalipour, A.; Moradkhani, H. Drought and food security in the middle east: An analytical framework. Agric. For. Meteorol. 2020, 281, 107816. [Google Scholar] [CrossRef]
- Orimoloye, I.R. Agricultural drought and its potential impacts: Enabling decision-support for food security in vulnerable regions. Front. Sustain. Food Syst. 2022, 6, 838824. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Chang, J.; Leng, G.; Xing, L. The response of agricultural drought to meteorological drought and the influencing factors: A case study in the Wei River basin, China. Agric. Water Manag. 2015, 159, 45–54. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Pan, Y.; Li, S.; Liu, Y.; Ma, Y. Agricultural drought monitoring: Progress, challenges, and prospects. J. Geogr. Sci. 2016, 26, 750–767. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, A. Uncertainties in historical changes and future projections of drought. Part ii: Model-simulated historical and future drought changes. Clim. Change 2017, 144, 535–548. [Google Scholar]
- Wang, F.; Lai, H.; Li, Y.; Feng, K.; Zhang, Z.; Tian, Q.; Zhu, X.; Yang, H. Dynamic variation of meteorological drought and its relationships with agricultural drought across China. Agric. Water Manag. 2022, 261, 107301. [Google Scholar] [CrossRef]
- Howell, T.A. Enhancing water use efficiency in irrigated agriculture. Agron. J. 2001, 93, 281–289. [Google Scholar] [CrossRef]
- Tao, F.; Yokozawa, M.; Hayashi, Y.; Lin, E. Changes in agricultural water demands and soil moisture in china over the last half-century and their effects on agricultural production. Agric. For. Meteorol. 2003, 118, 251–261. [Google Scholar] [CrossRef]
- Liao, L.; Zhang, L.; Bengtsson, L. Soil moisture variation and water consumption of spring wheat and their effects on crop yield under drip irrigation. Irrig. Drain. Syst. 2008, 22, 253–270. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of soil moisture deficit index (SMDI) and evapotranspiration deficit index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Afshar, M.H.; Bulut, B.; Duzenli, E.; Amjad, M.; Yilmaz, M.T. Global spatiotemporal consistency between meteorological and soil moisture drought indices. Agric. For. Meteorol. 2022, 316, 108848. [Google Scholar] [CrossRef]
- Touil, S.; Richa, A.; Fizir, M.; García, J.E.A.; Gómez, A.F.S. A review on smart irrigation management strategies and their effect on water savings and crop yield. Irrig. Drain. 2022, 71, 1396–1416. [Google Scholar] [CrossRef]
- Jalilvand, E.; Abolafia Rosenzweig, R.; Tajrishy, M.; Kumar, S.V.; Mohammadi, M.R.; Das, N.N. Is it possible to quantify irrigation water-use by assimilating a high-resolution satellite soil moisture product? Water Resour. Res. 2023, 59, e2022WR033342. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, H.; Gao, X.; Li, X.; Huang, J. An improved approach of winter wheat yield estimation by jointly assimilating remotely sensed leaf area index and soil moisture into the WOFOST model. Remote Sens. 2023, 15, 1825. [Google Scholar] [CrossRef]
- Casa, R.; Rossi, M.; Sappa, G.; Trotta, A. Assessing crop water demand by remote sensing and GIS for the Pontina Plain, Central Italy. Water Resour. Manag. 2009, 23, 1685–1712. [Google Scholar] [CrossRef]
- Ahmad, U.; Alvino, A.; Marino, S. A review of crop water stress assessment using remote sensing. Remote Sens. 2021, 13, 4155. [Google Scholar] [CrossRef]
- Li, Z.L.; Leng, P.; Zhou, C.; Chen, K.S.; Zhou, F.C.; Shang, G.F. Soil moisture retrieval from remote sensing measurements: Current knowledge and directions for the future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Jiménez, C.; Prigent, C.; Mueller, B.; Seneviratne, S.I.; McCabe, M.F.; Wood, E.F.; Rossow, W.B.; Balsamo, G.; Betts, A.K.; Dirmeyer, P.A.; et al. Global intercomparison of 12 land surface heat flux estimates. J. Geophys. Res. Atmos. 2011, 116, D02102. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.C.; Zhang, X.; Moradkhani, H.; Zhang, C.; Hu, C. In-situ and triple-collocation based evaluations of eight global root zone soil moisture products. Remote Sens. Environ. 2021, 254, 112248. [Google Scholar] [CrossRef]
- Yang, F.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.X.; Nemani, R.R. Prediction of continental-scale evapotranspiration by combining MODIS and Ameriflux data through support vector machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Guswa, A.J.; Celia, M.A.; Rodriguez-Iturbe, I. Models of soil moisture dynamics in ecohydrology: A comparative study. Water Resour. Res. 2002, 38, 1–5. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Sejna, M. The hydrus-1d software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media. Univ. Calif.-Riverside Res. Rep. 2005, 3, 1–240. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO crop model to simulate yield response to water: I. Concepts and underlying principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Aejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Han, M.; Zhao, C.; Šimůnek, J.; Feng, G. Evaluating the impact of groundwater on cotton growth and root zone water balance using hydrus-1d coupled with a crop growth model. Agric. Water Manag. 2015, 160, 64–75. [Google Scholar] [CrossRef]
- Li, Y.; Šimůnek, J.; Jing, L.; Zhang, Z.; Ni, L. Evaluation of water movement and water losses in a direct-seeded-rice field experiment using hydrus-1d. Agric. Water Manag. 2014, 142, 38–46. [Google Scholar] [CrossRef]
- Sahaar, S.A.; Niemann, J.D. Impact of regional characteristics on the estimation of root-zone soil moisture from the evaporative index or evaporative fraction. Agric. Water Manag. 2020, 238, 106225. [Google Scholar] [CrossRef]
- Sahaar, S.A.; Niemann, J.D.; Elhaddad, A. Using regional characteristics to improve uncalibrated estimation of root-zone soil moisture from optical/thermal remote-sensing. Remote Sens. Environ. 2022, 273, 112982. [Google Scholar] [CrossRef]
- Shelia, V.; Šimůnek, J.; Boote, K.; Hoogenbooom, G. Coupling DSSAT and hydrus-1d for simulations of soil water dynamics in the soil-plant-atmosphere system. J. Hydrol. Hydromech. 2018, 66, 232–245. [Google Scholar] [CrossRef]
- Yu, J.; Wu, Y.; Xu, L.; Peng, J.; Chen, G.; Shen, X.; Lan, R.; Zhao, C.; Zhangzhong, L. Evaluating the hydrus-1d model optimized by remote sensing data for soil moisture simulations in the maize root zone. Remote Sens. 2022, 14, 6079. [Google Scholar] [CrossRef]
- Feng, H.; Wu, Z.; Dong, J.; Zhou, J.; Brocca, L.; He, H. Transpiration–Soil evaporation partitioning determines inter-model differences in soil moisture and evapotranspiration coupling. Remote Sens. Environ. 2023, 298, 113841. [Google Scholar] [CrossRef]
- Mahmood, R.; Hubbard, K.G. Assessing bias in evapotranspiration and soil moisture estimates due to the use of modeled solar radiation and dew point temperature data. Agric. For. Meteorol. 2005, 130, 71–84. [Google Scholar] [CrossRef]
- Suyker, A.E.; Verma, S.B.; Burba, G.G.; Arkebauer, T.J. Gross primary production and ecosystem respiration of irrigated maize and irrigated soybean during a growing season. Agric. For. Meteorol. 2005, 131, 180–190. [Google Scholar] [CrossRef]
- Suyker, A.E.; Verma, S.B.; Burba, G.G.; Arkebauer, T.J.; Walters, D.T.; Hubbard, K.G. Growing season carbon dioxide exchange in irrigated and rainfed maize. Agric. For. Meteorol. 2004, 124, 1–13. [Google Scholar] [CrossRef]
- Xing, Z.; Fan, L.; Zhao, L.; De Lannoy, G.; Frappart, F.; Peng, J.; Li, X.; Zeng, J.; Al-Yaari, A.; Yang, K.; et al. A first assessment of satellite and reanalysis estimates of surface and root-zone soil moisture over the permafrost region of Qinghai-Tibet Plateau. Remote Sens. Environ. 2021, 265, 112666. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In Symposia of the Society for Experimental Biology; Cambridge University Press (CUP) Cambridge: Cambridge, UK, 1965; Volume 19, pp. 205–234. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-guidelines for computing crop water requirements-FAO irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Improved prediction of unsaturated hydraulic conductivity with the Mualem-van Genuchten model. Soil Sci. Soc. Am. J. 2000, 64, 843–851. [Google Scholar] [CrossRef]
- Kaufmann, K.W. Fitting and using growth curves. Oecologia 1981, 49, 293–299. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Frelich, L.E. Flowering phenology and height growth pattern are associated with maximum plant height, relative growth rate and stem tissue mass density in herbaceous grassland species. J. Ecol. 2011, 99, 991–1000. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-time-series global land surface satellite leaf area index product derived from MODIS and AVHRR surface reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- De Boor, C. A practical guide to splines. Appl. Math. Sci. 1978, 27, 325. [Google Scholar]
- Ordóñez, R.A.; Castellano, M.J.; Hatfield, J.L.; Helmers, M.J.; Licht, M.A.; Liebman, M.; Dietzel, R.; Martinez-Feria, R.; Iqbal, J.; Puntel, L.A.; et al. Maize and soybean root front velocity and maximum depth in Iowa, USA. Field Crops Res. 2018, 215, 122–131. [Google Scholar] [CrossRef]
- Andersen, J.; Dybkjaer, G.; Jensen, K.H.; Refsgaard, J.C.; Rasmussen, K. Use of remotely sensed precipitation and leaf area index in a distributed hydrological model. J. Hydrol. 2022, 264, 34–50. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Feng, G.; Zhu, C.; Wu, Q.; Wang, C.; Zhang, Z.; Mwiya, R.M.; Zhang, L. Evaluating the impacts of saline water irrigation on soil water-salt and summer maize yield in subsurface drainage condition using coupled HYDRUS and EPIC model. Agric. Water Manag. 2021, 258, 107175. [Google Scholar] [CrossRef]
- Dong, J.; Dirmeyer, P.A.; Lei, F.; Anderson, M.C.; Holmes, T.R.H.; Hain, C.; Crow, W.T. Soil evaporation stress determines soil moisture–evapotranspiration coupling strength in land surface modeling. Geophys. Res. Lett. 2020, 47, e2020GL090391. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]

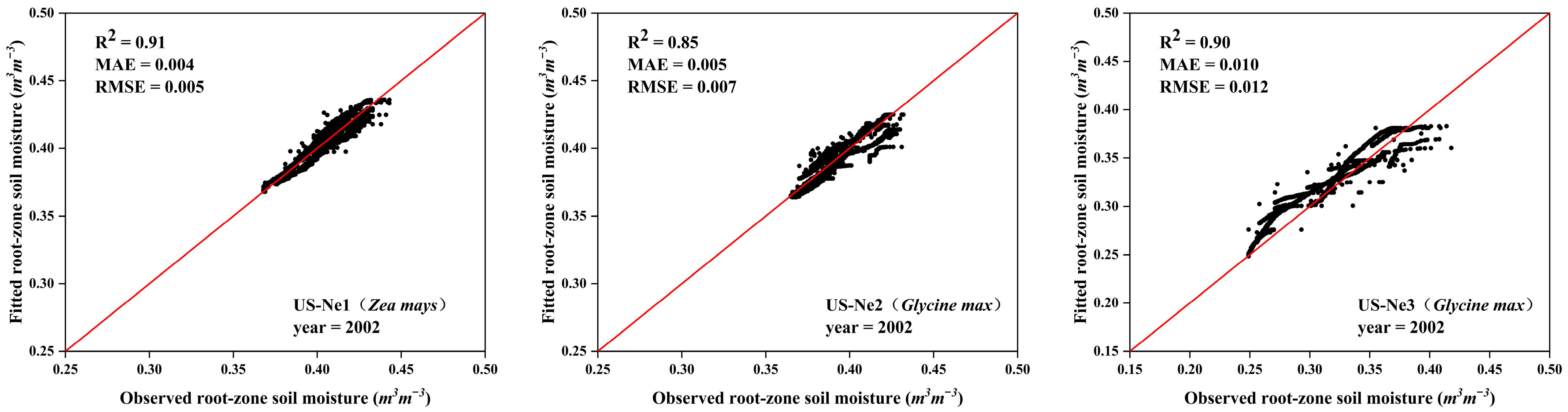
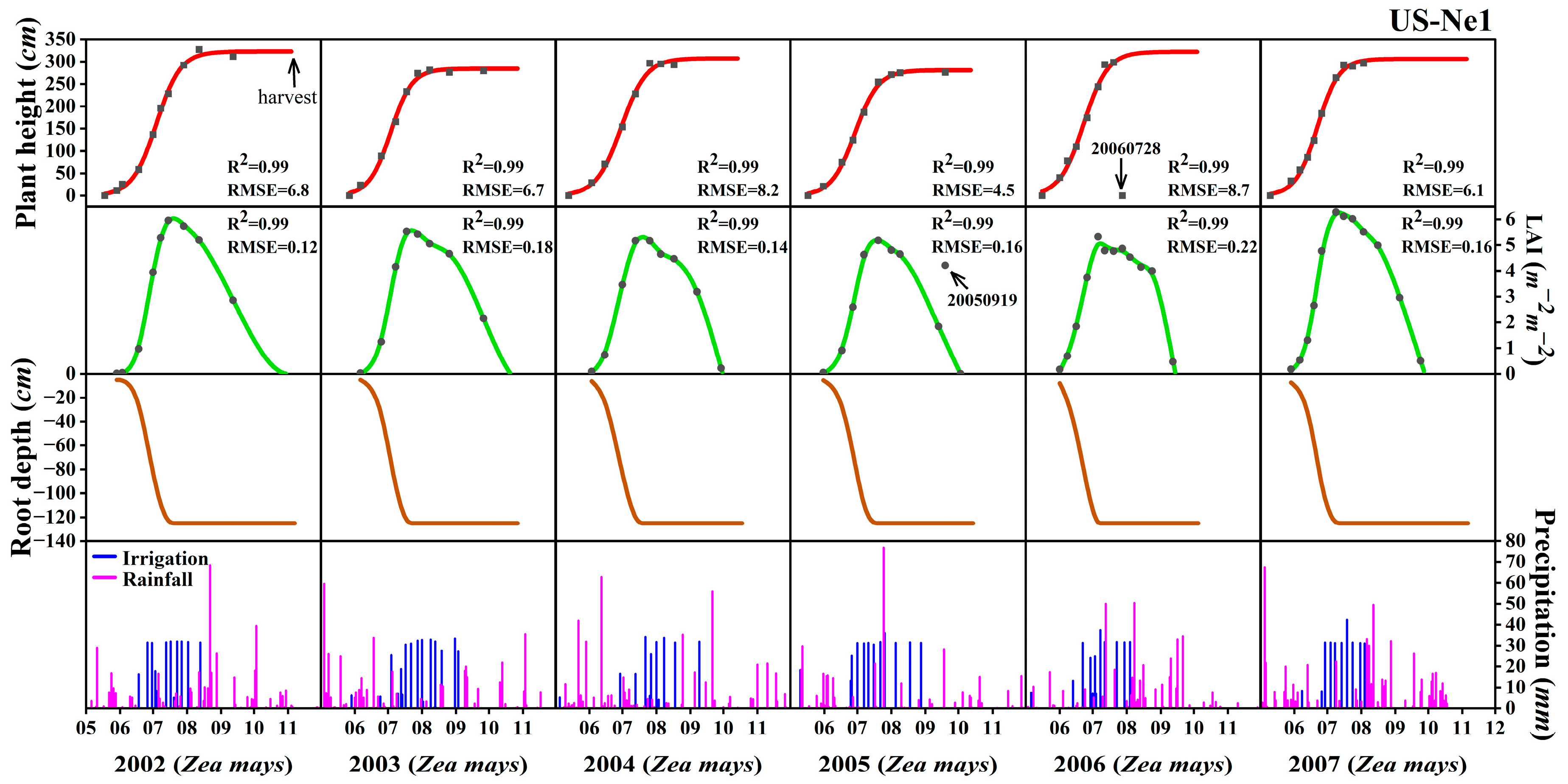








| Site | Latitude | Longitude | Clay | Sand | Planting |
|---|---|---|---|---|---|
| US-Ne1 | 41.1651 | −96.4766 | 37 | 11 | Zea mays |
| US-Ne2 | 41.1649 | −96.4701 | 33 | 12 | Zea mays, Glycine max |
| US-Ne3 | 41.1797 | −96.4397 | 35 | 8 | Zea mays, Glycine max |
| Site | θr | θs | α (1/cm) | n | Ks (cm/Hours) | l |
|---|---|---|---|---|---|---|
| US-Ne1 | 0.2 | 0.47 | 0.0007 | 1.36 | 0.16 | 2.36 |
| US-Ne2 | 0.19 | 0.47 | 0.002 | 1.15 | 0.29 | 1.15 |
| US-Ne3 | 0.14 | 0.49 | 0.0013 | 1.51 | 2.1 | 6.98 |
| ID | θr | θs | α (1/cm) | n | Ks (cm/Day) |
|---|---|---|---|---|---|
| Silty clay loams | 0.09 | 0.43 | 0.010 | 1.23 | 1.68 |
| US-Ne1 | 0.09 | 0.48 | 0.0099 | 1.46 | 12.76 |
| US-Ne2 | 0.09 | 0.47 | 0.0084 | 1.50 | 12.20 |
| US-Ne3 | 0.09 | 0.48 | 0.0091 | 1.48 | 11.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Q.-Y.; Leng, P.; Li, Z.-L.; Labed, J. Prediction of Root-Zone Soil Moisture and Evapotranspiration in Cropland Using HYDRUS-1D Model with Different Soil Hydrodynamic Parameter Schemes. Water 2025, 17, 730. https://doi.org/10.3390/w17050730
Liao Q-Y, Leng P, Li Z-L, Labed J. Prediction of Root-Zone Soil Moisture and Evapotranspiration in Cropland Using HYDRUS-1D Model with Different Soil Hydrodynamic Parameter Schemes. Water. 2025; 17(5):730. https://doi.org/10.3390/w17050730
Chicago/Turabian StyleLiao, Qian-Yu, Pei Leng, Zhao-Liang Li, and Jelila Labed. 2025. "Prediction of Root-Zone Soil Moisture and Evapotranspiration in Cropland Using HYDRUS-1D Model with Different Soil Hydrodynamic Parameter Schemes" Water 17, no. 5: 730. https://doi.org/10.3390/w17050730
APA StyleLiao, Q.-Y., Leng, P., Li, Z.-L., & Labed, J. (2025). Prediction of Root-Zone Soil Moisture and Evapotranspiration in Cropland Using HYDRUS-1D Model with Different Soil Hydrodynamic Parameter Schemes. Water, 17(5), 730. https://doi.org/10.3390/w17050730






