A Comparative Study on Leakage Magnitude Occurred in Reservoir While Passing a Tunnel Beneath Reservoir
Abstract
1. Introduction
2. Methods
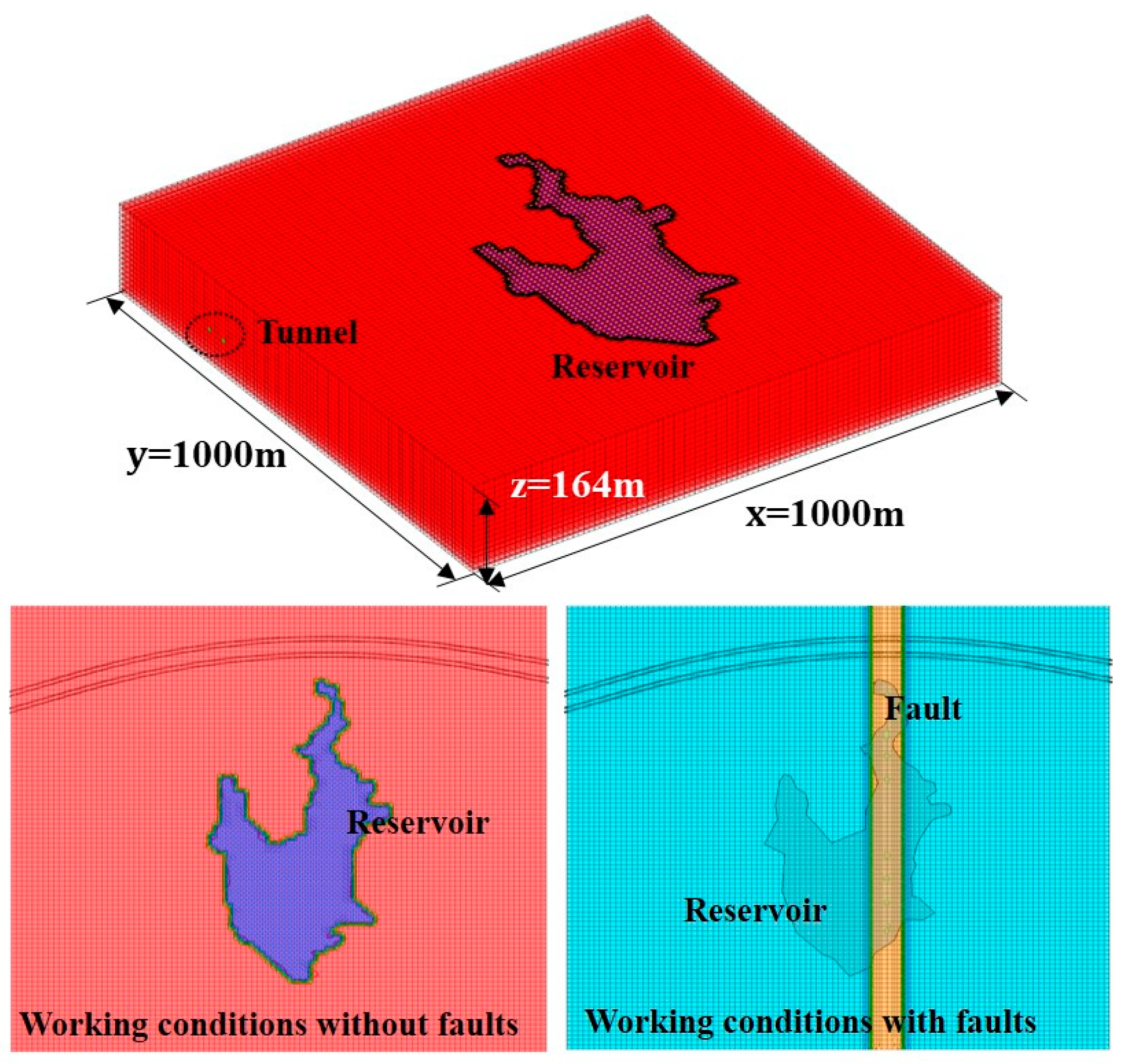
2.1. Project Overview
2.2. Mathematical Formulation
2.3. Modeling Process
2.4. Initial and Boundary Conditions
2.5. Model Verification
2.6. Parametric Study
3. Results and Analysis
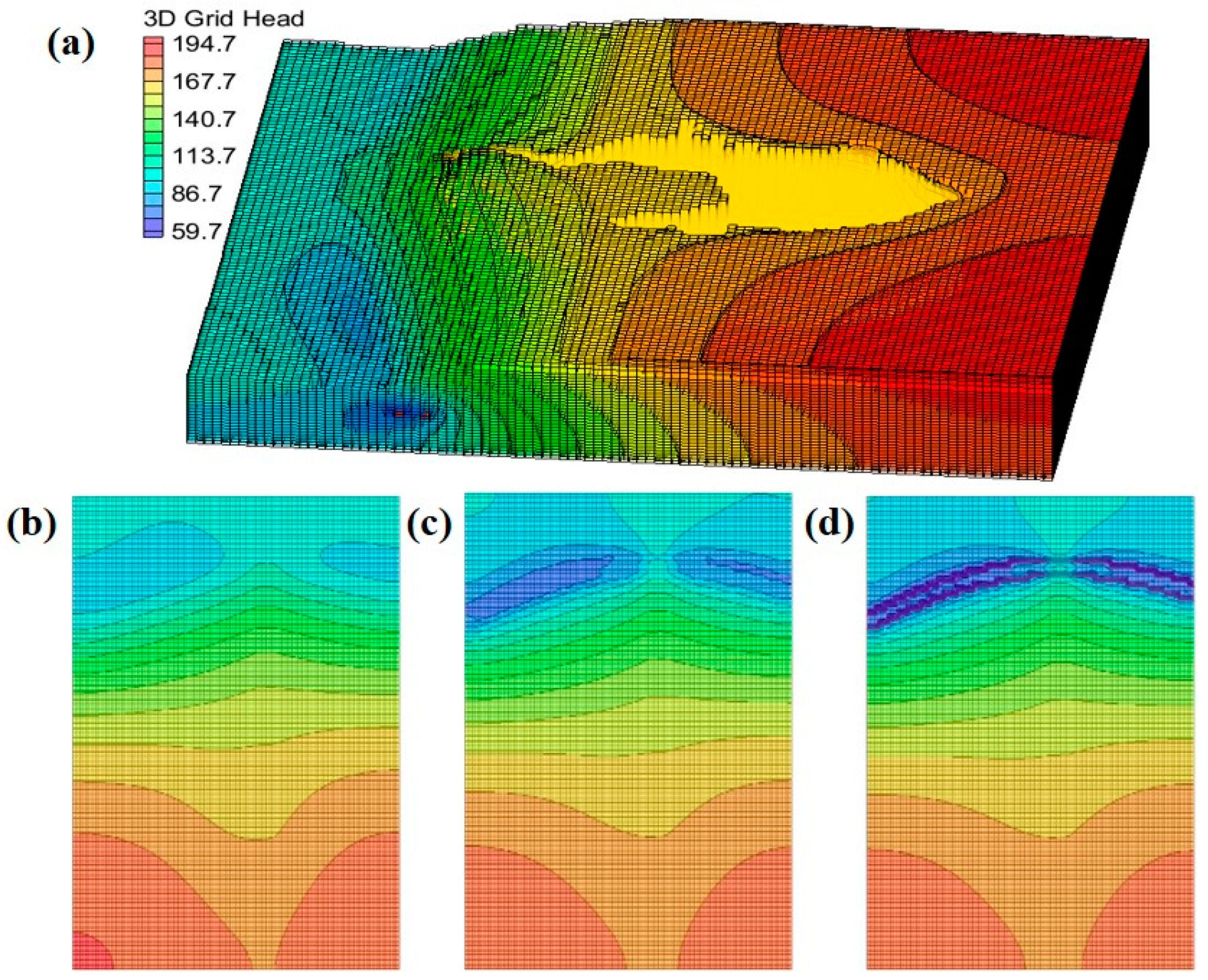
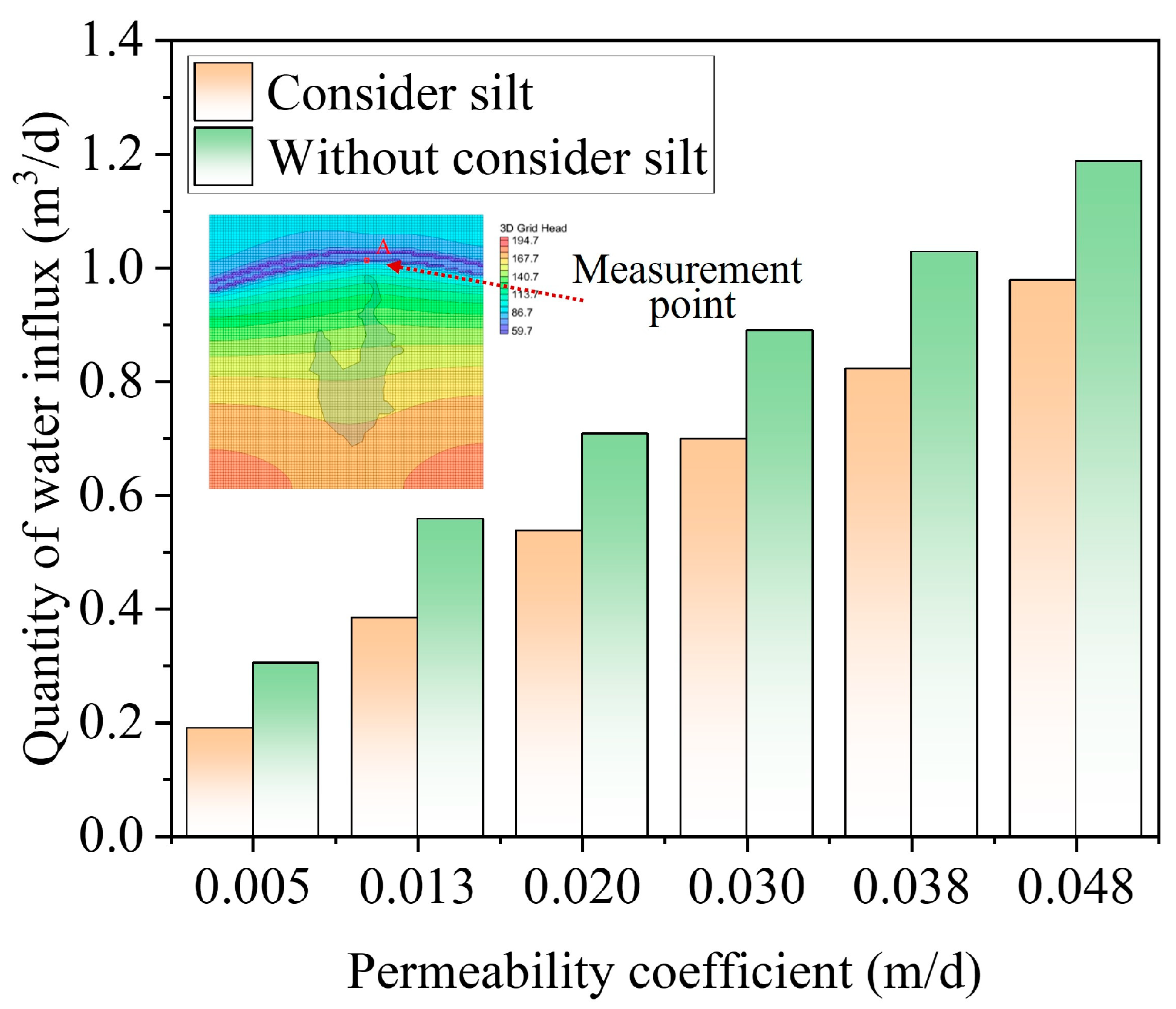
3.1. Effect of Permeability Coefficient of the Surrounding Rock
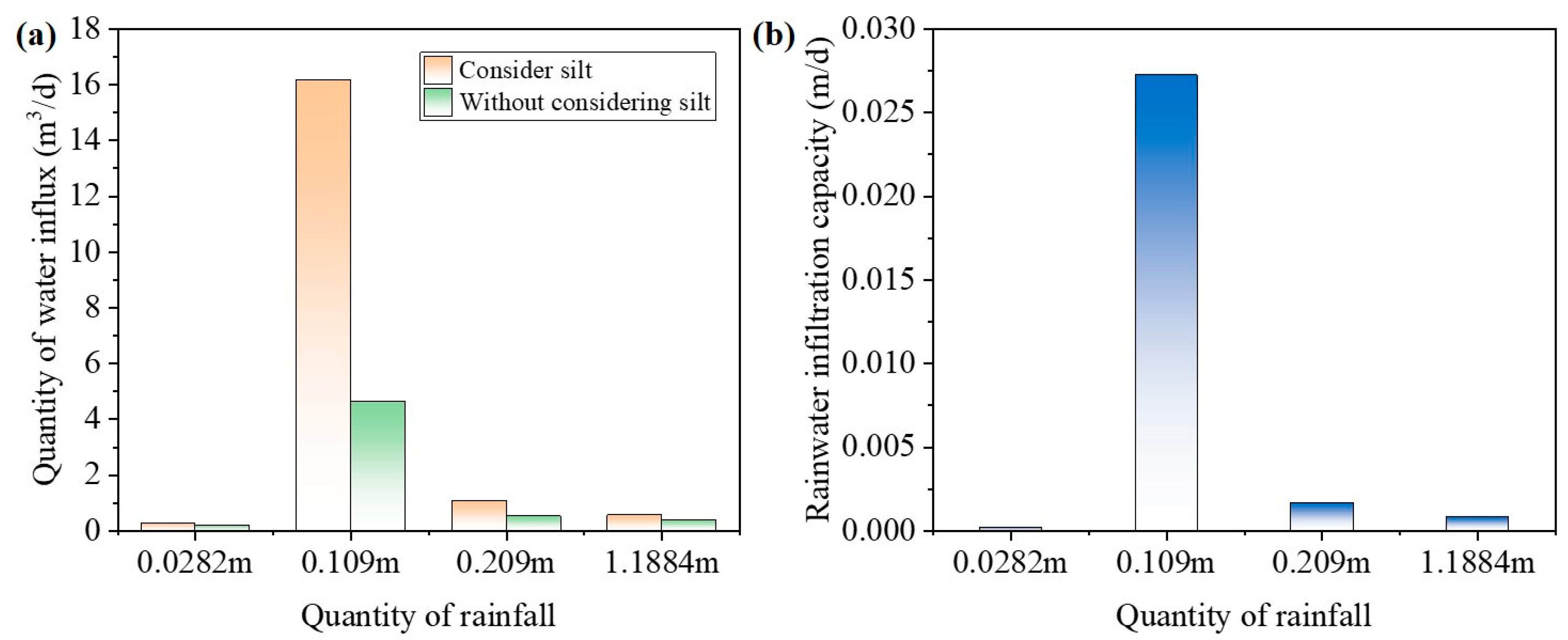
3.2. Effect of Quantity of Rainfall Recharge
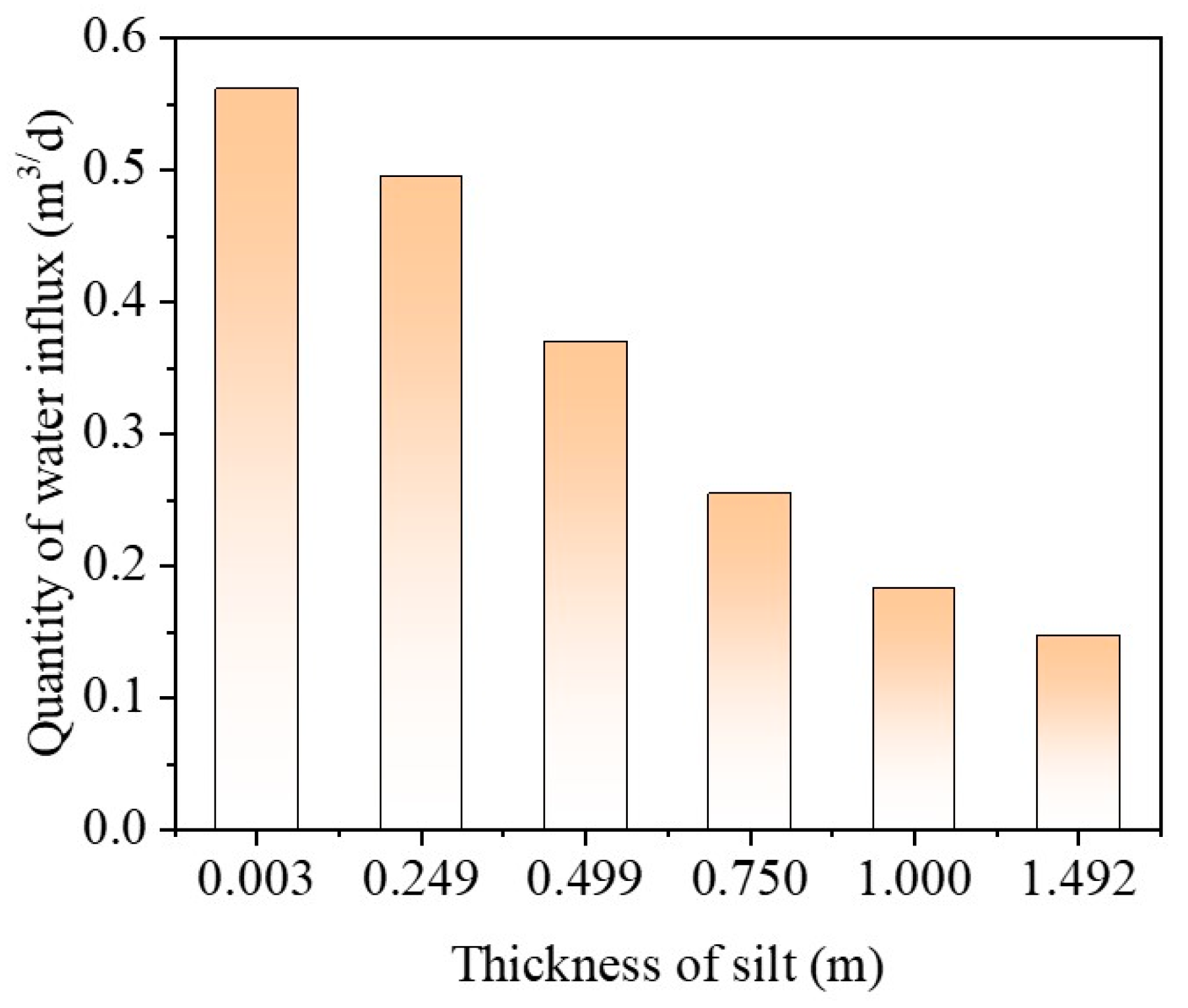
3.3. Effect of Thickness of Silt on the Bottom of the Lake
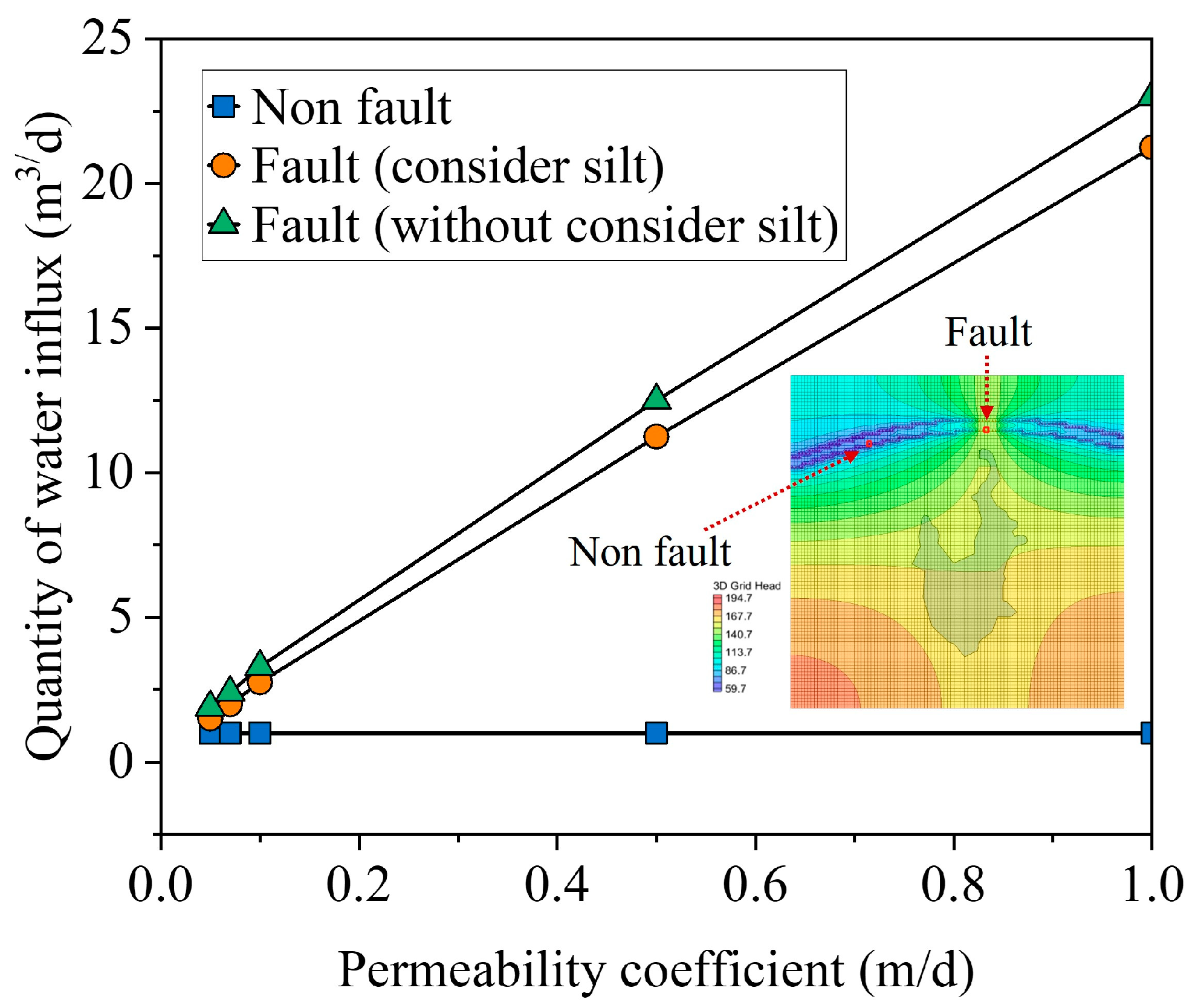
3.4. Effect of Permeability Coefficient of the Fault
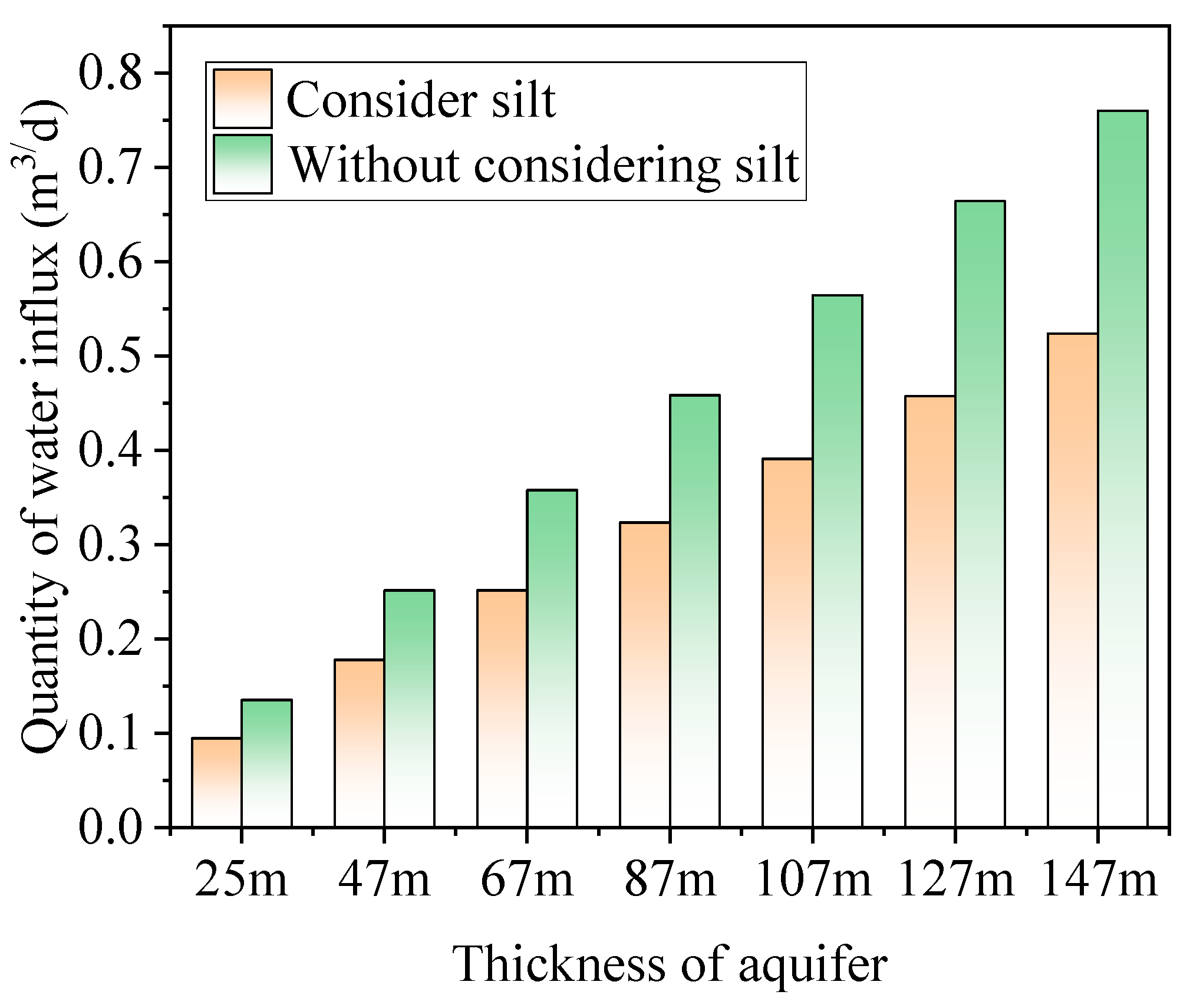
3.5. Effect of Thickness of Aquifer
4. Discussion
4.1. Without Fault
4.2. With Fault
5. Conclusions
- (1)
- All results primarily depend on the characteristics of the fault defined for the study. The presence of faults creates an effective hydraulic pathway between the tunnel and the reservoir, thereby enhancing the hydraulic connection between them. The groundwater head resulting from the tunnel surge is distributed along the center of the tunnel axis in the form of a ditch, with the head gradually decreasing in a band along the reservoir’s edge towards the tunnel axis. The existence of faults alters the seepage field of the water, leading to a higher head at the fault locations compared to non-faulted areas.
- (2)
- An increase in the permeability coefficient of the fault leads to a corresponding increase in the water inflow into the tunnel at the fault. When the water inflow from the tunnel causes a decrease in the reservoir’s water level, the water level of the reservoir decreases as the permeability coefficient of the stratum increases. The silt at the bottom of the reservoir effectively mitigates the water level drop caused by the water influx from the tunnel, significantly weakening the hydraulic connection between the reservoir and the tunnel.
- (3)
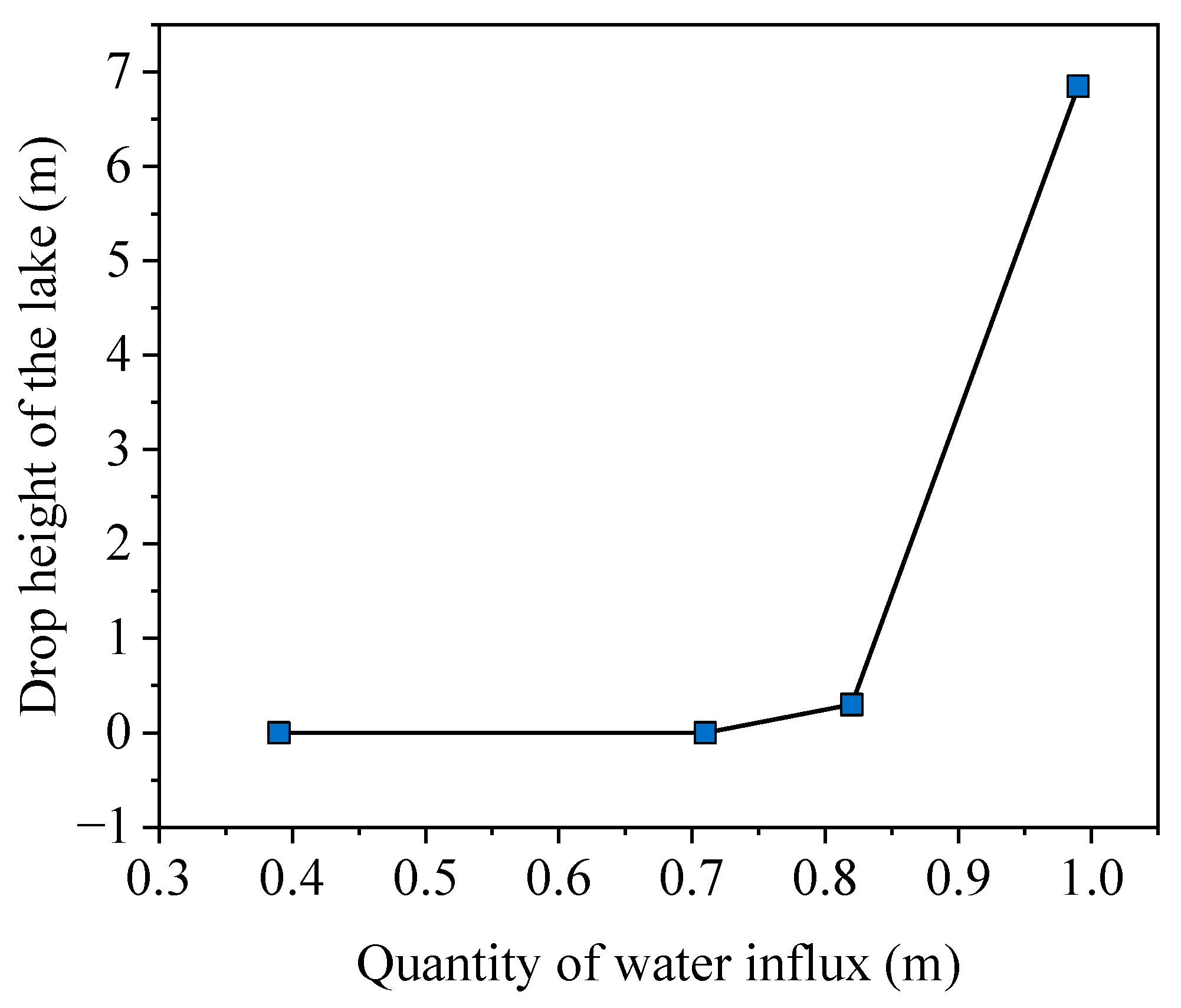
- Considering the silt layer at the bottom of the reservoir, when the daily water influx per unit length of the tunnel is less than 0.4 m3/d, there is no noticeable effect on the reservoir’s water level. When the daily water influx exceeds 0.7 m3/d, the water level decreases rapidly as the influx increases. When the daily water influx approaches 1 m3/d, the reservoir water level decreases by approximately 7 m.
- (4)
- The presence of a silt layer at the bottom of the reservoir reduces the impact of tunnel water influx on the reservoir. Even if the fault extends through the bottom of the reservoir and forms a hydraulic connection with the tunnel, when the permeability coefficients of both the stratum and the fault are relatively low, the hydraulic connection between the tunnel and the reservoir remains minimal.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Li, P. A Statistical analysis of China’s traffic tunnel development data. Engineering 2018, 4, 3–5. [Google Scholar] [CrossRef]
- Jiang, S. Quality and technical countermeasures in highway tunnel engineering. Mod. Tunn. Technol. 2017, 54, 1–12. [Google Scholar]
- Wang, X.; Zhao, Y. Comment on construction of railway tunnels in China by statistical data. Mod. Tunn. Technol. 2006, 43, 7–17. [Google Scholar]
- Shi, Z.; Xu, J.; Xie, X.; Zeng, H.; Xu, W.; Niu, G.; Xiao, Z. Disaster mechanism analysis for segments floating of large-diameter shield tunnel construction in the water-rich strata: A case study. Eng. Fail. Anal. 2024, 157, 107953. [Google Scholar] [CrossRef]
- Song, Z.; Jing, P.; Nie, L.; Mei, Z.; Jia, S.; Li, Z. Comprehensive identification and assessment of clastic rock and water-bearing breccia for water and mud inrush in tunnel: A case study. Tunn. Undergr. Space Technol. 2025, 155, 106156. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, C.; Liu, Y.; Zhou, R. An ontology-based multi-hazard coupling accidents simulation and deduction system for underground utility tunnel—A case study of earthquake-induced disaster chain. Reliab. Eng. Syst. Saf. 2025, 253, 110559. [Google Scholar]
- Yu, Z.; Zhang, G.; Li, C.; Cao, Z. Numerical investigation on work performance of the anti-freezing drainage system of tunnel utilizing TPCT. Appl. Therm. Eng. 2024, 253, 123849. [Google Scholar] [CrossRef]
- Zhao, C.; Mahmoudi, E.; Luo, M.; Jiang, M.; Lin, P. Unfavorable geology recognition in front of shallow tunnel face using machine learning. Comput. Geotech. 2023, 157, 105313. [Google Scholar]
- Qin, Y.; Shang, C.; Li, X.; Lai, J.; Shi, X.; Liu, T. Failure mechanism and countermeasures of rainfall-induced collapsed shallow loess tunnels under bad terrain: A case study. Eng. Fail. Anal. 2023, 152, 107477. [Google Scholar] [CrossRef]
- Zhang, D.; Fang, Q.; Lou, H. Grouting techniques for the unfavorable geological conditions of Xiang’an subsea tunnel in China. J. Rock Mech. Geotech. Eng. 2014, 6, 438–446. [Google Scholar]
- Fu, H.; Hu, K.; Wu, Y.; Yu, Y.; Liu, W. Seepage field and drainage system in the connection part of underwater tunnel based on conformal mapping method. Tunn. Undergr. Space Technol. 2024, 154, 106146. [Google Scholar]
- Wang, C.; Zhang, D.; Tan, D.; Ye, J.; Wang, X.; Ren, F.; Li, Q. Investigation on seepage evolution property of surrounding rock under the tunneling and water surge. Tunn. Undergr. Space Technol. 2024, 153, 105970. [Google Scholar] [CrossRef]
- Terzaghi, K.T. Theoretical Soil Mechanics; Wiley: Hoboken, NJ, USA, 1943. [Google Scholar]
- Biot Maurice, A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar]
- Witherspoon, P.A.; Tsang, Y.W.; Long, J.C.; Noorishad, J. New approaches to problems of fluid flow in fractured-rock masses. In Proceedings of the 22nd U.S. Symposium on Rock Mechanics (USRMS), Cambridge, MA, USA, 29 June–2 July 1981. [Google Scholar]
- Zhuo, J. Interfacial Element Method for Mechanical Problems in Discontinuous Media; Science Press: Beijing, China, 2000. [Google Scholar]
- Huyakorn, P.S.; Lester, B.H.; Faust, C.R. Finite element techniques for modeling groundwater flow in fractured aquifers. Water Resour. Res. 1983, 19, 1019–1035. [Google Scholar]
- Huang, M.; Ling, C.; Deng, F.; Li, H.; Fu, Z. Simulation of the self-potential response during the water inrush of tunnel beneath surface water: A case study of Shijingshan tunnel in Zhuhai. Prog. Geophys. 2024, 39, 1275–1284. [Google Scholar]
- Chen, D. Analysis and integrated mitigation of water and mud inrushing hazard in Anshi Tunnel excavation. Soil Eng. Found. 2021, 35, 323–328. [Google Scholar]
- Yang, B. Treatment Techniques for Karst Disaster of Maluqing Tunnel on Yichang-Wanzhou Railway. Chin. J. Undergr. Space Eng. 2011, 7, 581–586. [Google Scholar]
- Li, Z.; Xiao, J.; Wan, J.; Cheng, J.; Feng, H.; Zhan, H.; Yuan, S.; Huang, K. A dynamic modeling approach to predict water inflow during tunnel excavation in relatively uniform rock masses. Tunn. Undergr. Space Technol. 2024, 146, 105668. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Ghafourian, H.; Mohammed, A.H.; Rezaei, N.; Ibrahim, H.H.; Rashidi, S. Predicting tunnel water inflow using a machine learning-based solution to improve tunnel construction safety. Transp. Geotech. 2023, 40, 100978. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Noori KM, G.; Khishe, M.; Ibrahim, H.H.; Ali HF, H.; Abdulhamid, S.N. Presenting the best prediction model of water inflow into drill and blast tunnels among several machine learning techniques. Autom. Constr. 2021, 127, 103719. [Google Scholar]
- Liu, H.B.; Zhou, J.Q.; Li, C.; Tan, J.; Hou, D. Semi-empirical models for predicting stable water inflow and influence radius of a tunnel considering non-Darcian effect. J. Hydrol. 2023, 621, 129574. [Google Scholar]
- Shi, S.; Guo, W.; Li, S.; Xie, X.; Li, X.; Zhao, R.; Xue Lu, J. Prediction of tunnel water inflow based on stochastic deterministic three-dimensional fracture network. Tunn. Undergr. Space Technol. 2023, 135, 104997. [Google Scholar]
- Dall’Alba, V.; Neven, A.; de Rooij, R.; Filipponi, M.; Renard, P. Probabilistic estimation of tunnel inflow from a karstic conduit network. Eng. Geol. 2023, 312, 106950. [Google Scholar]
- Li, L.; Chen, H.; Li, J.; Sun, D.A. A semi-analytical solution to steady-state groundwater inflow into a circular tunnel considering anisotropic permeability. Tunn. Undergr. Space Technol. 2021, 116, 104115. [Google Scholar]


| Parameter | Unit | Value |
|---|---|---|
| Waterhead height of the water table | m | 164 |
| Maximum waterhead height of the reservoir | m | 164 |
| Average annual rainfall | mm | 1188.4 |
| Surface rainfall infiltration factor | 1 | 0.25 |
| Rainfall recharge | mm/d | 0.814 |
| Permeability coefficient of weathered granite | m/d | 0.048 |
| Initial storage level | m | 151–164 |
| Permeability coefficient of the silt layer | mm/d | 0.25 |
| Thickness of silt layer | m | About 0.5 |
| Parameter | Unit | Value |
|---|---|---|
| Theoretical value | m3/d | 0.72 |
| Not considering silt | m3/d | 0.88 |
| Considering silt | m3/d | 0.69 |
| Factors | Unit | Value |
|---|---|---|
| Permeability coefficient of surrounding rock | m/d | 0.005, 0.013, 0.02, 0.03, 0.038, 0.048 |
| Quantity of rainfall recharge | mm | 0.0282, 0.109, 0.209, 1.1884 |
| Thickness of silt on the bottom of the lake | m | 0.003, 0.249, 0.499, 0.75, 1, 1.492 |
| Permeability coefficient of the fault | m/d | 0.05, 0.07, 0.1, 0.5, 1 |
| Thickness of aquifer | m | 25, 47, 67, 87, 107, 127, 147 |
| Rainfall Period | Quantity of Rainfall Recharge (m) | Rainwater Infiltration Capacity (m/d) | Daily Water Inflow (m3/d) | |
|---|---|---|---|---|
| Consider Silt | Without Considering Silt | |||
| Dry season (Dec.) | 0.0282 | 0.000227 | 0.286 | 0.198 |
| Maximum value | 0.109 | 0.02725 | 16.166 | 4.652 |
| Wet season (Aug.) | 0.209 | 0.001685 | 1.078 | 0.53 |
| Annual average | 1.1884 | 0.000814 | 0.564 | 0.392 |
| Permeability Coefficients of Unfaulted Strata (m/d) | Permeability Coefficients of Faulted Strata (m/d) | Drop Height of the Lake (m) |
|---|---|---|
| 0.013 | 0.048 | 0 |
| 0.06 | 0 | |
| 0.1 | 0 | |
| 0.03 | 0.048 | 2.86 |
| 0.06 | 4.08 | |
| 0.1 | 7.44 |
| Faulted permeability coefficient (m/d) | 0.048 | 0.06 | 0.1 |
| Drop height of the lake (m) | 0 | 0 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Zhao, L.; Ya, Z.; Yu, Z.; Zhang, G. A Comparative Study on Leakage Magnitude Occurred in Reservoir While Passing a Tunnel Beneath Reservoir. Water 2025, 17, 1068. https://doi.org/10.3390/w17071068
Chen T, Zhao L, Ya Z, Yu Z, Zhang G. A Comparative Study on Leakage Magnitude Occurred in Reservoir While Passing a Tunnel Beneath Reservoir. Water. 2025; 17(7):1068. https://doi.org/10.3390/w17071068
Chicago/Turabian StyleChen, Tao, Liyuan Zhao, Zhou Ya, Zihao Yu, and Guozhu Zhang. 2025. "A Comparative Study on Leakage Magnitude Occurred in Reservoir While Passing a Tunnel Beneath Reservoir" Water 17, no. 7: 1068. https://doi.org/10.3390/w17071068
APA StyleChen, T., Zhao, L., Ya, Z., Yu, Z., & Zhang, G. (2025). A Comparative Study on Leakage Magnitude Occurred in Reservoir While Passing a Tunnel Beneath Reservoir. Water, 17(7), 1068. https://doi.org/10.3390/w17071068






