Flood Risk Management-Level Analysis of Subway Station Spaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
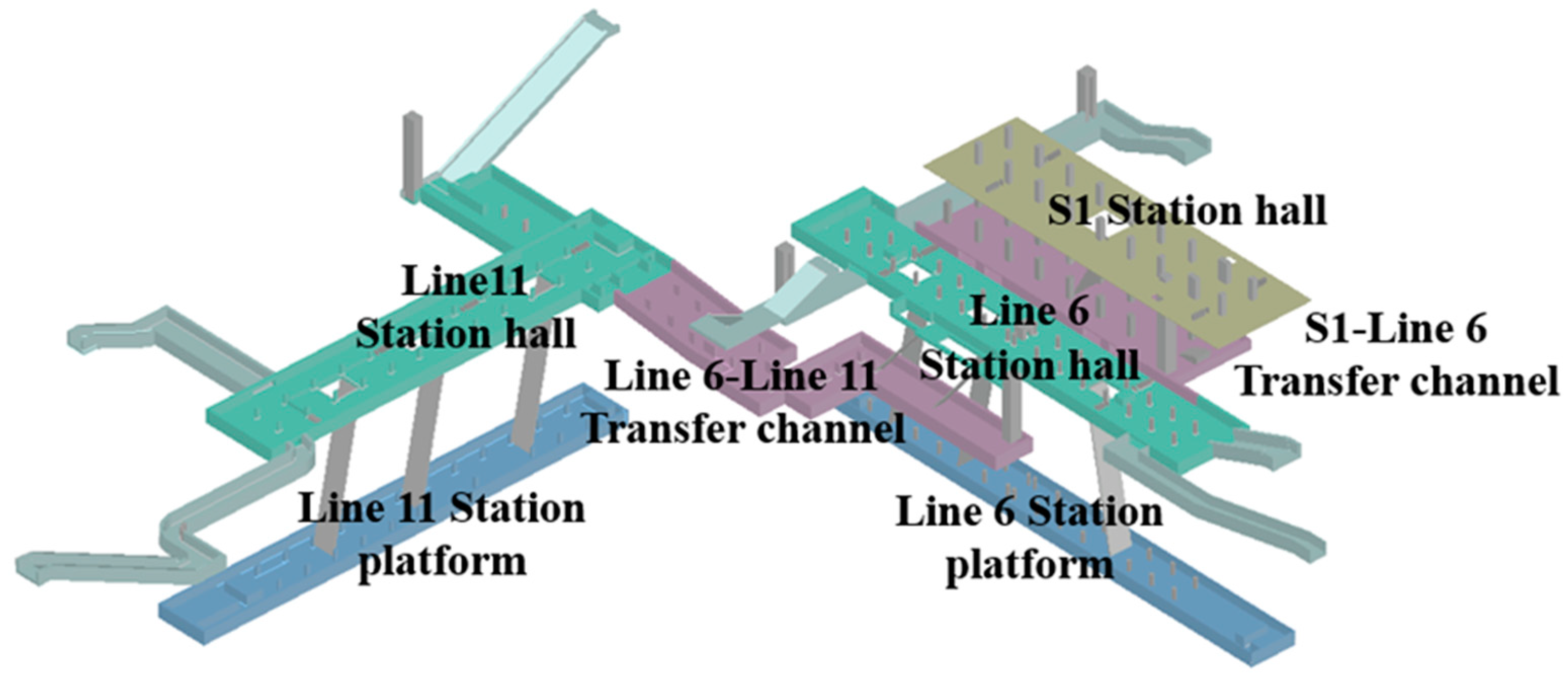
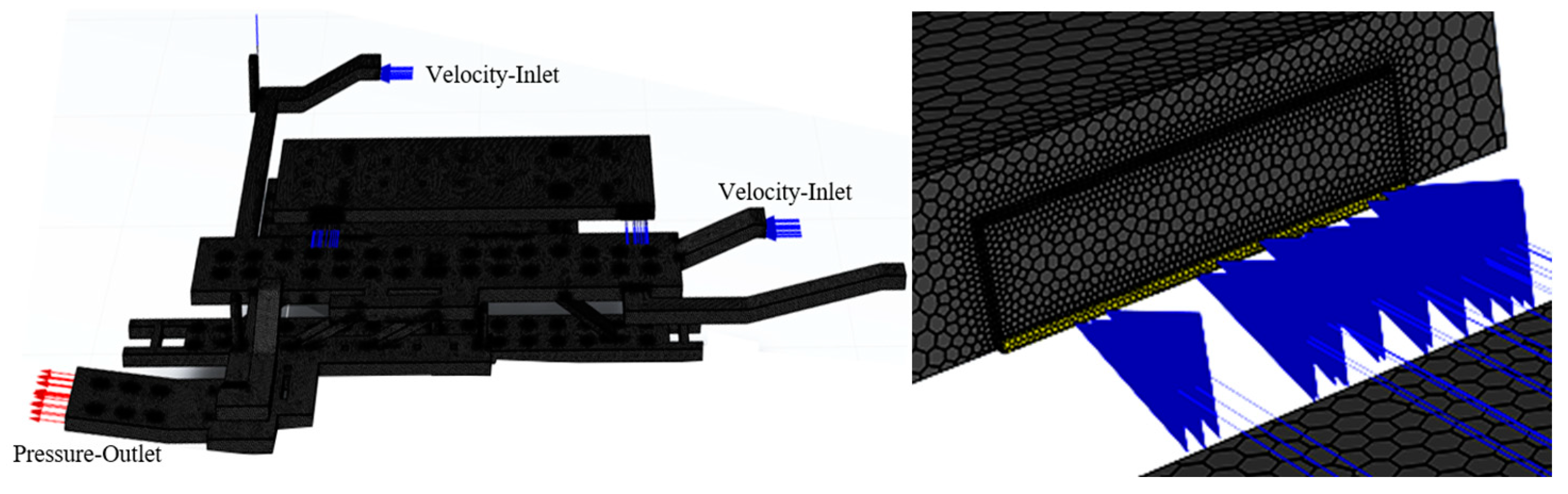
2.2. Geometric Subway Construction
2.3. Establishment of Risk Management Indicator System
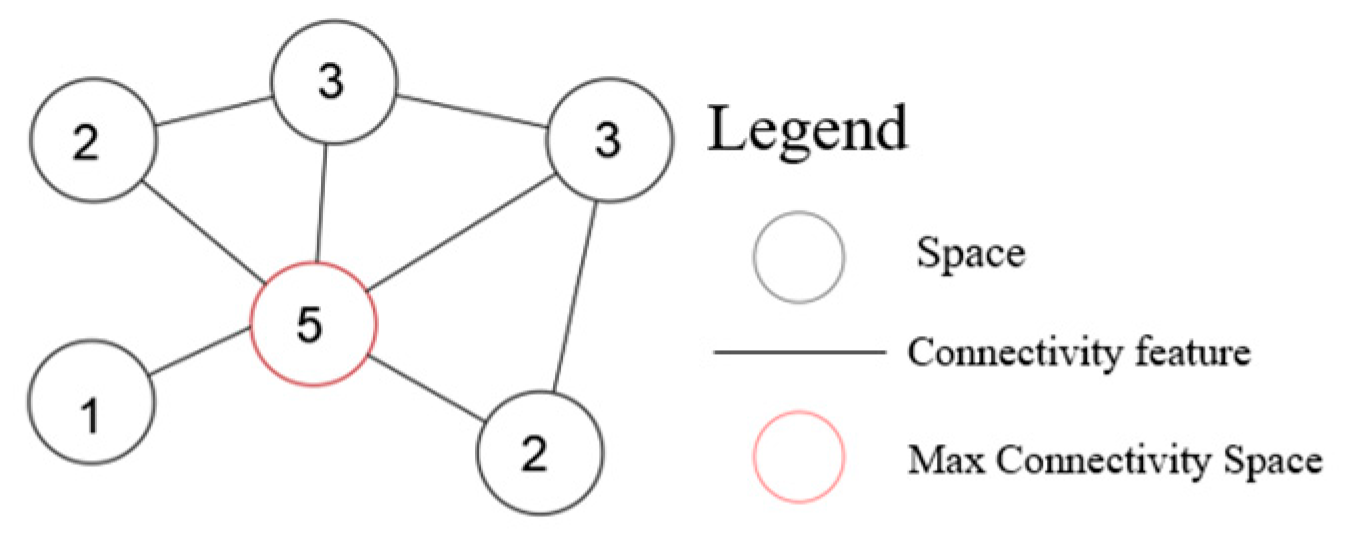
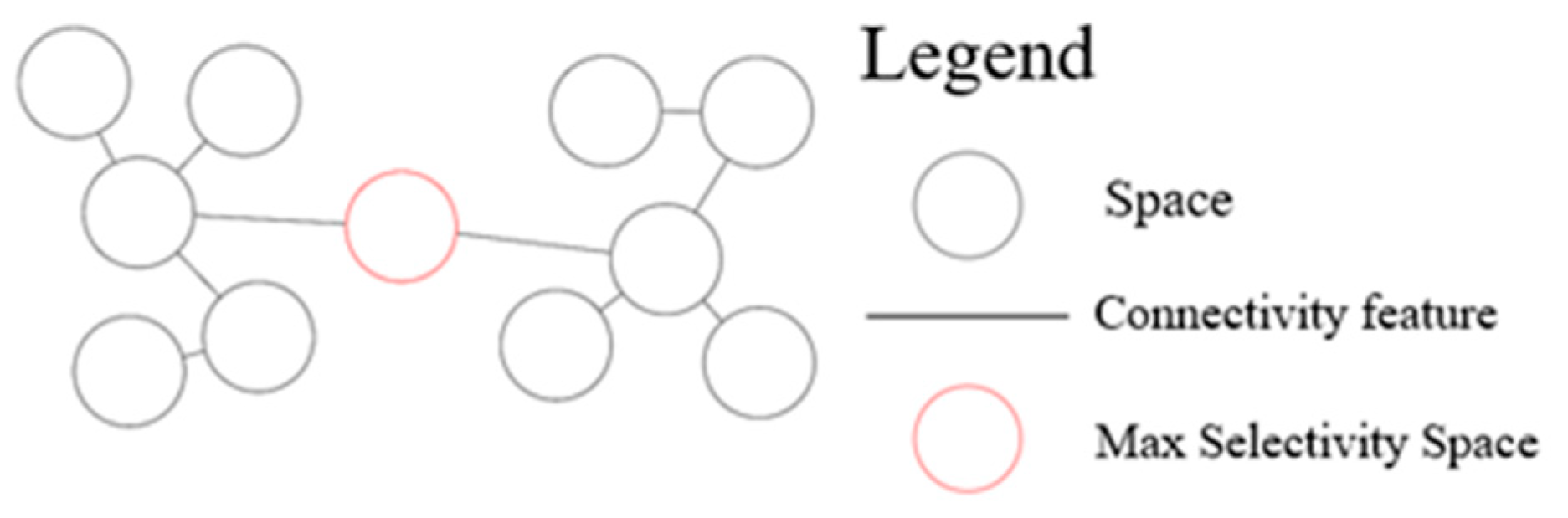
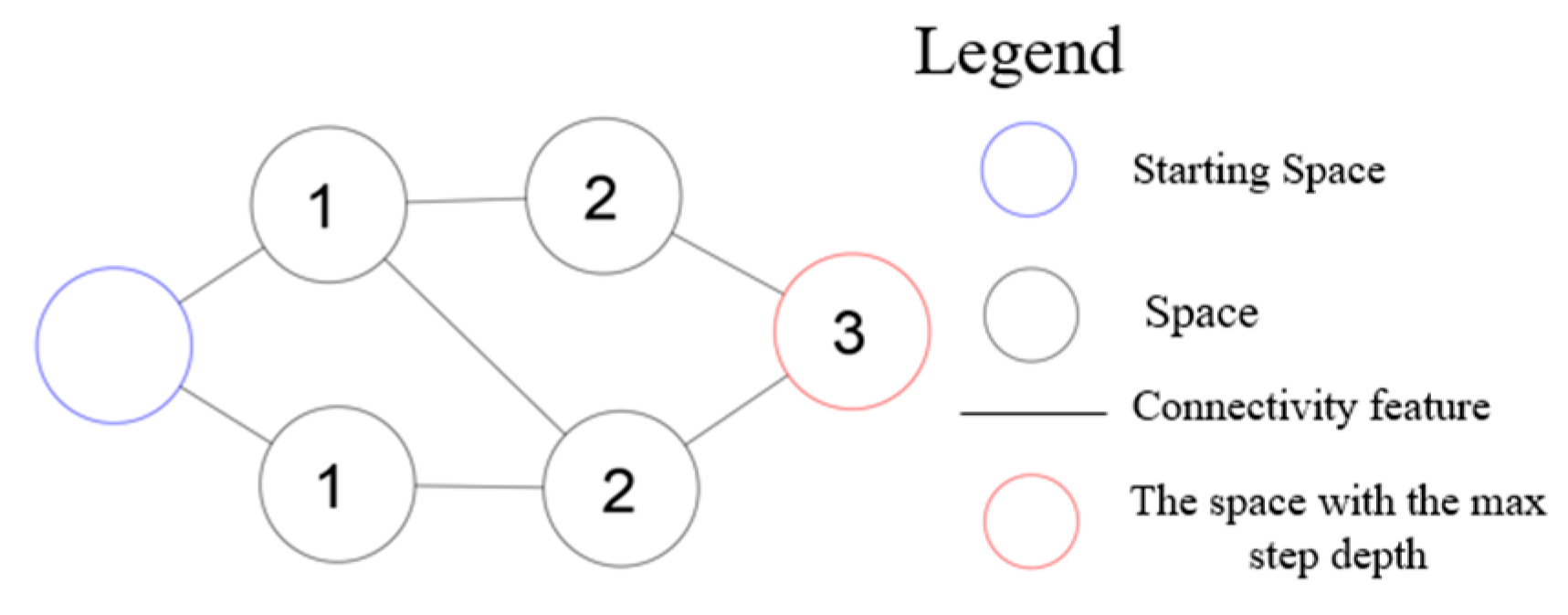
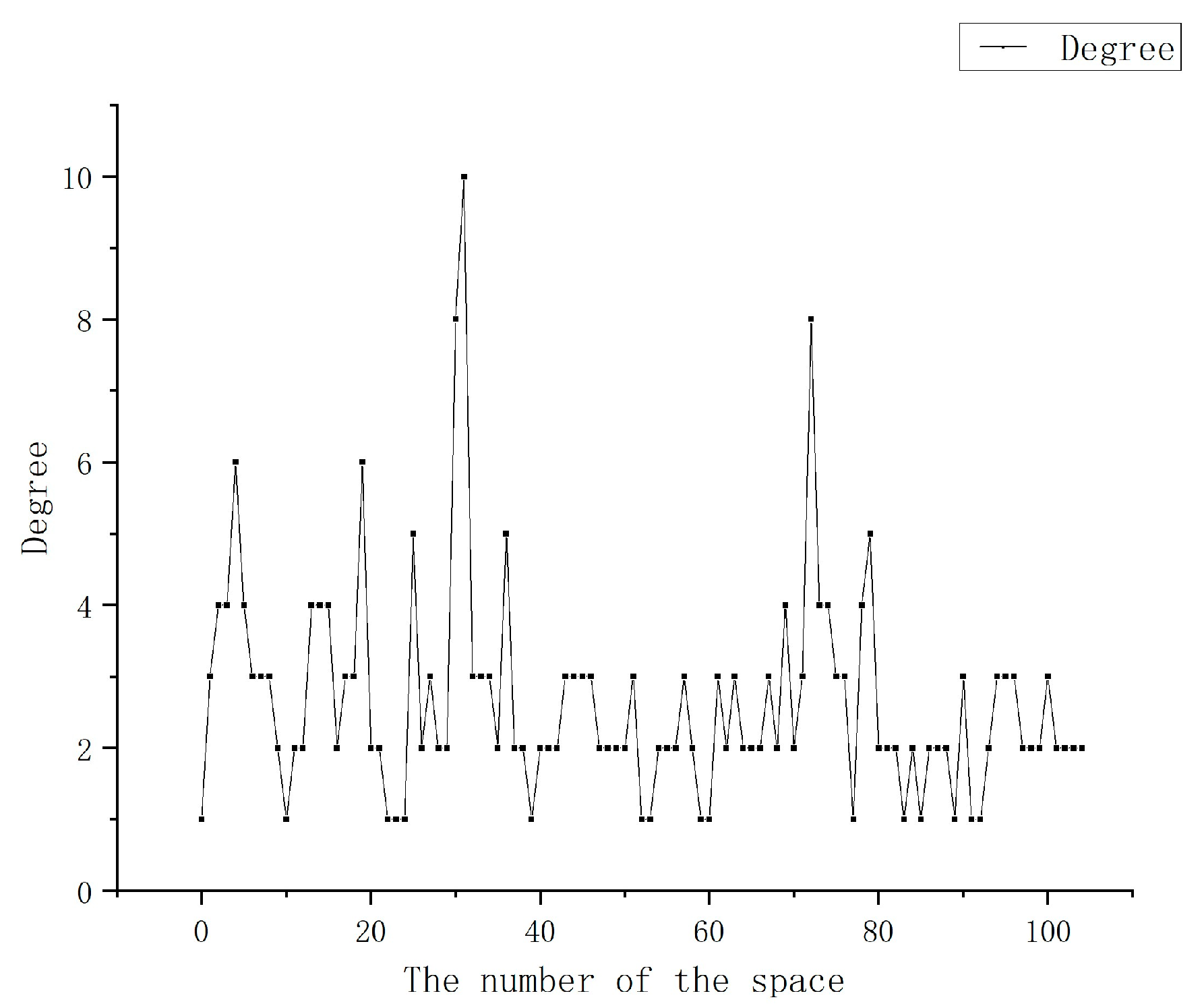
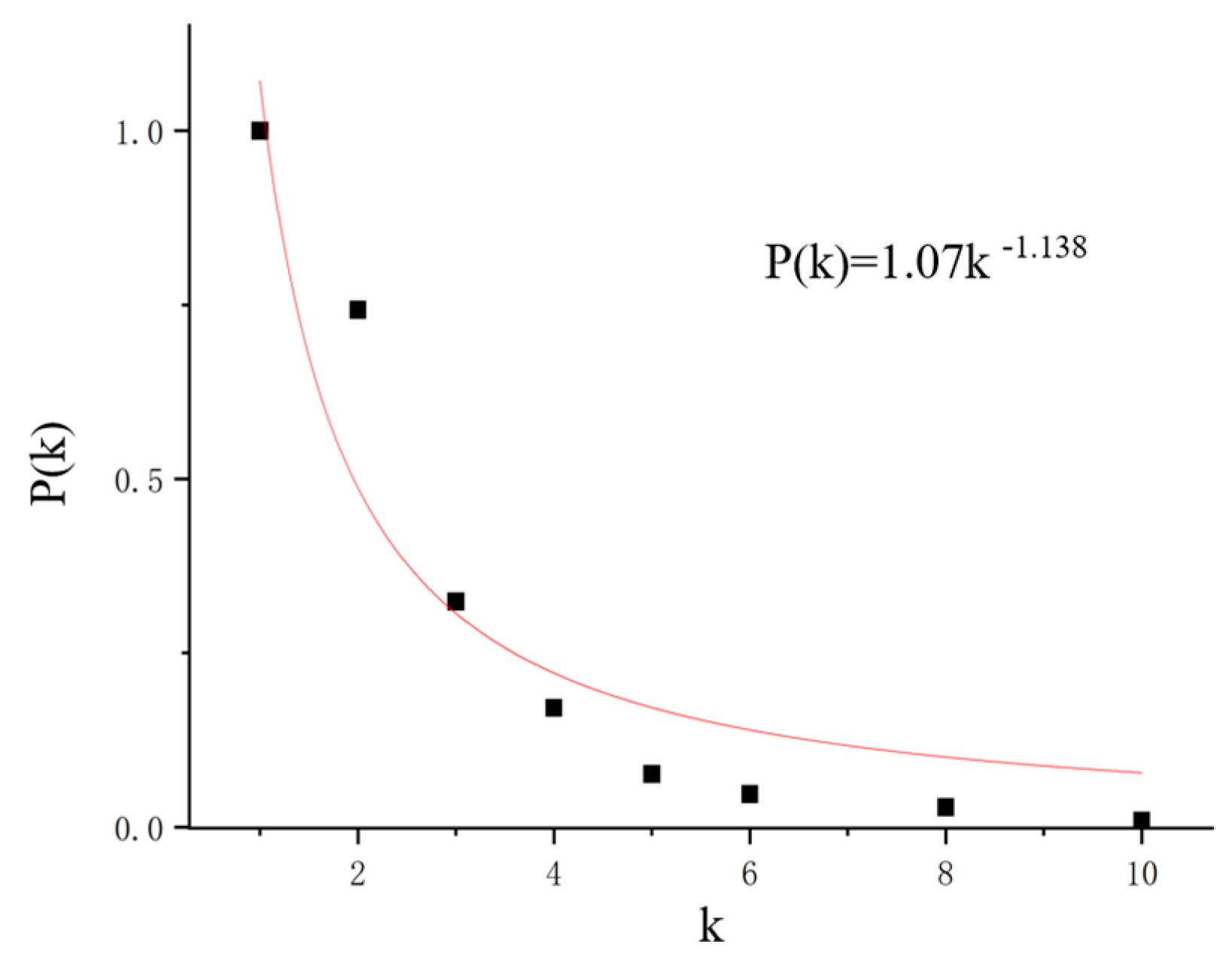
2.3.1. Subway Spatial Network Importance Indicators
2.3.2. Subway Spatial Functional Importance Indicators
2.3.3. Flood Accumulation Risk Indicators for Subway Stations
2.4. Weight Determination
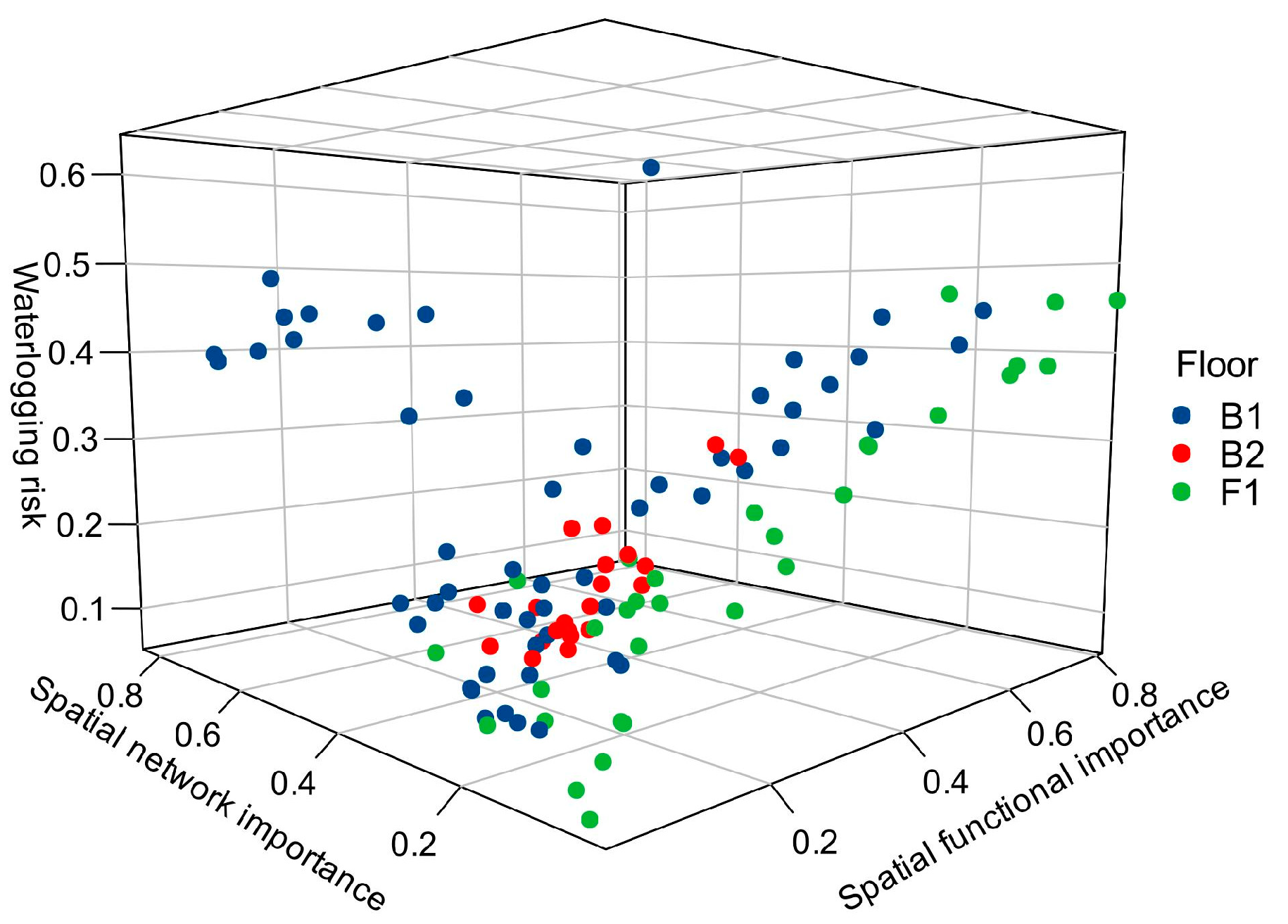
3. Results and Discussion
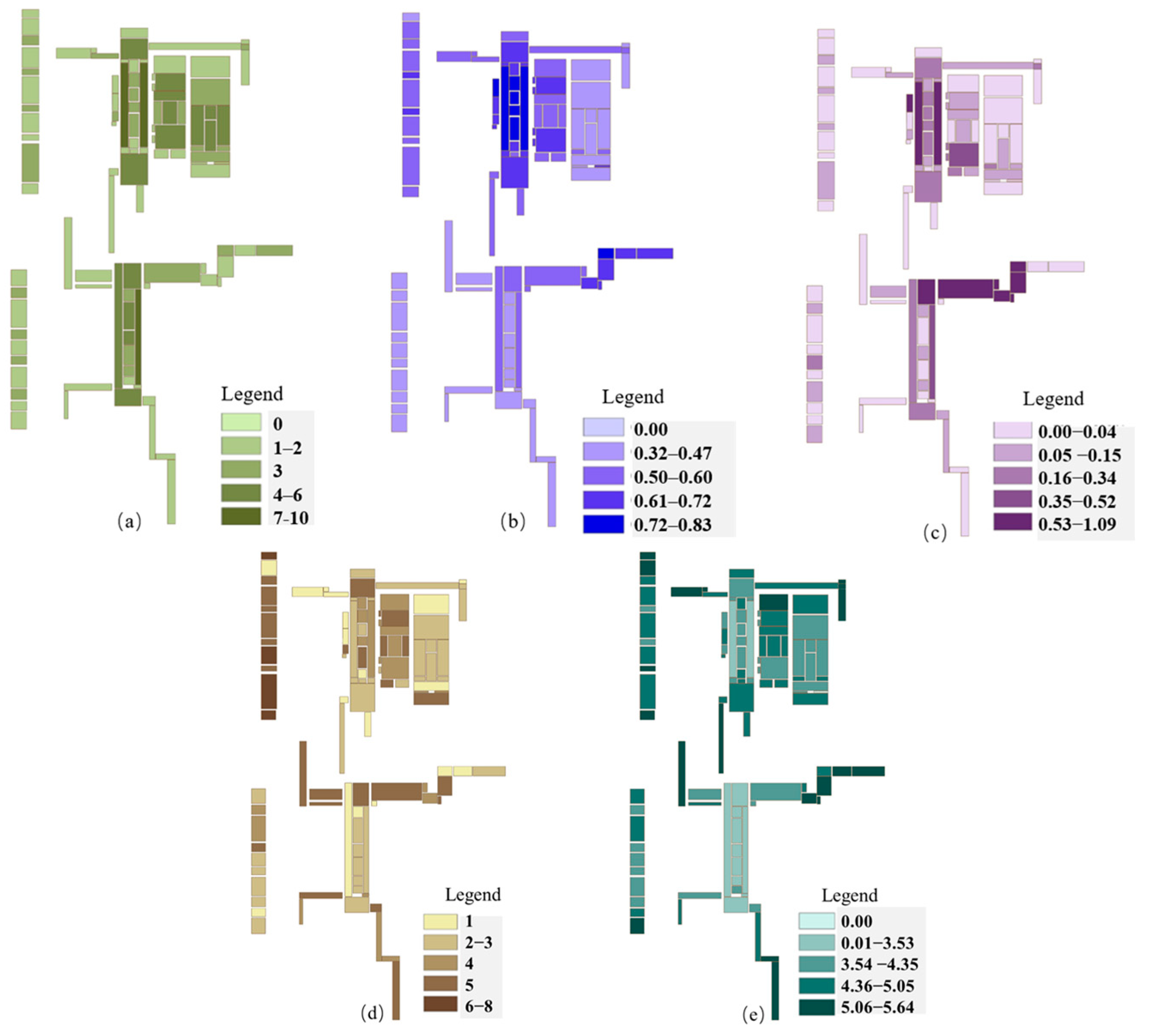
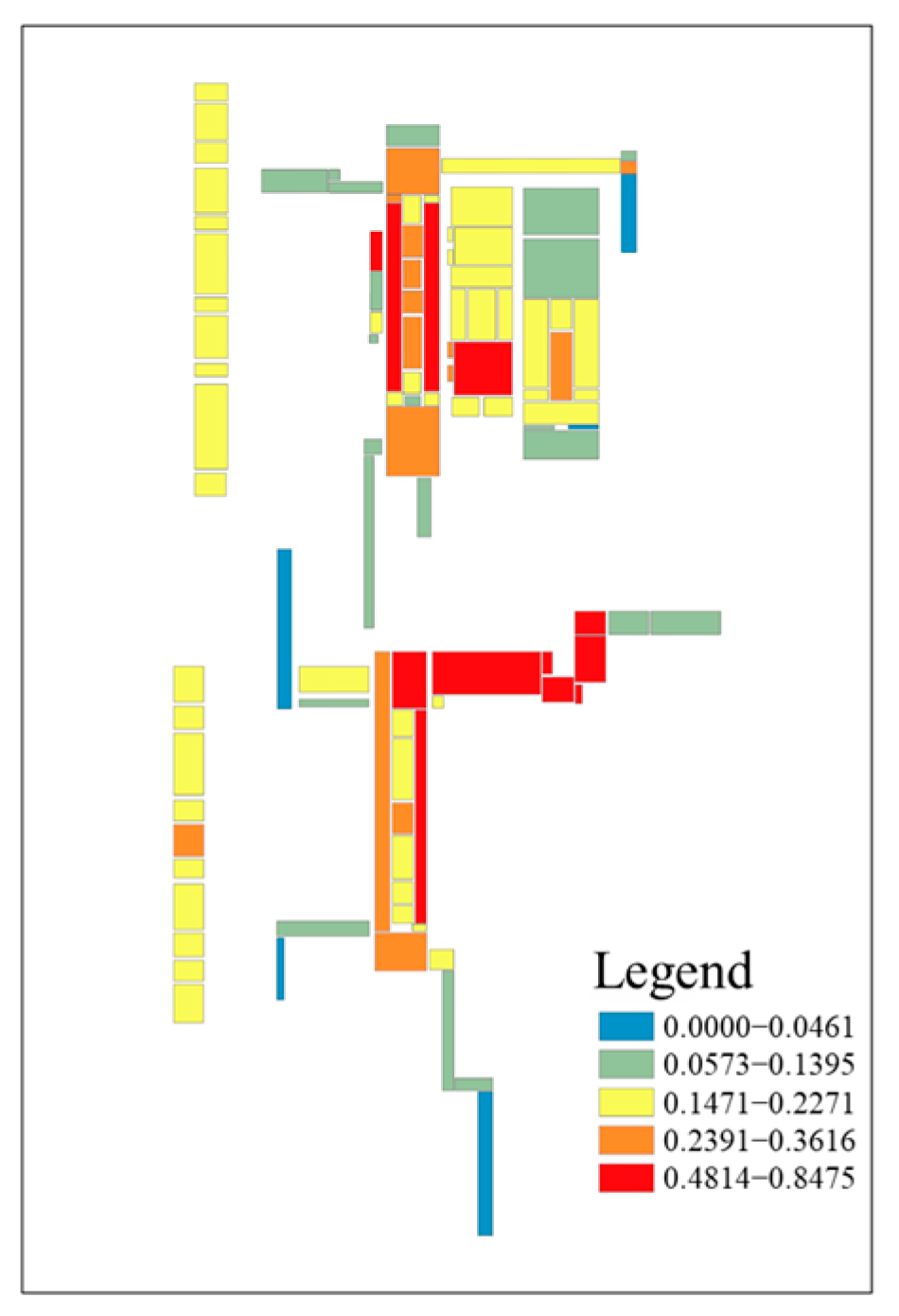
3.1. Subway Spatial Network Importance Results
3.2. Subway Spatial Functional Importance Results
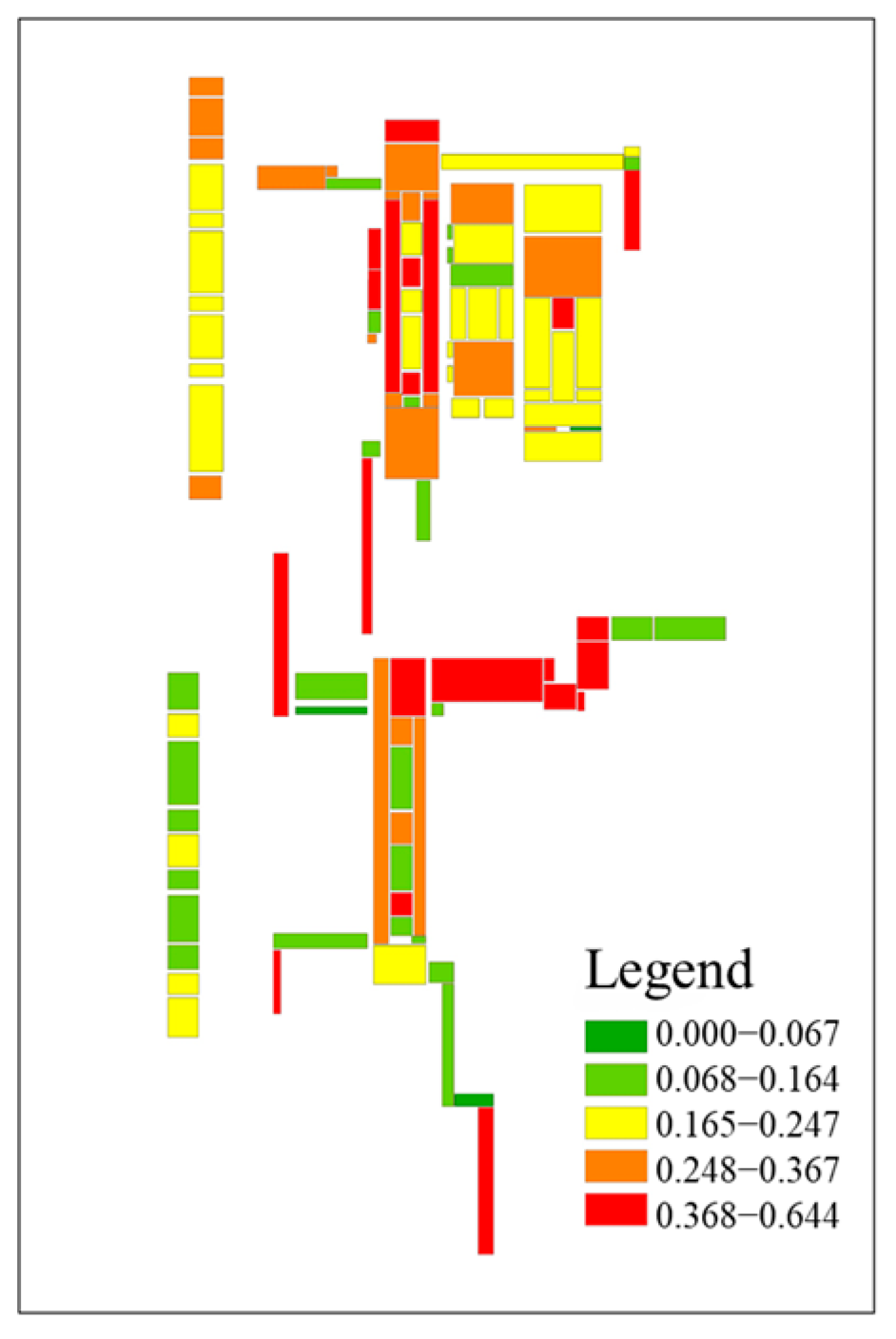
3.3. Flood Accumulation Risk Results for Subway Stations
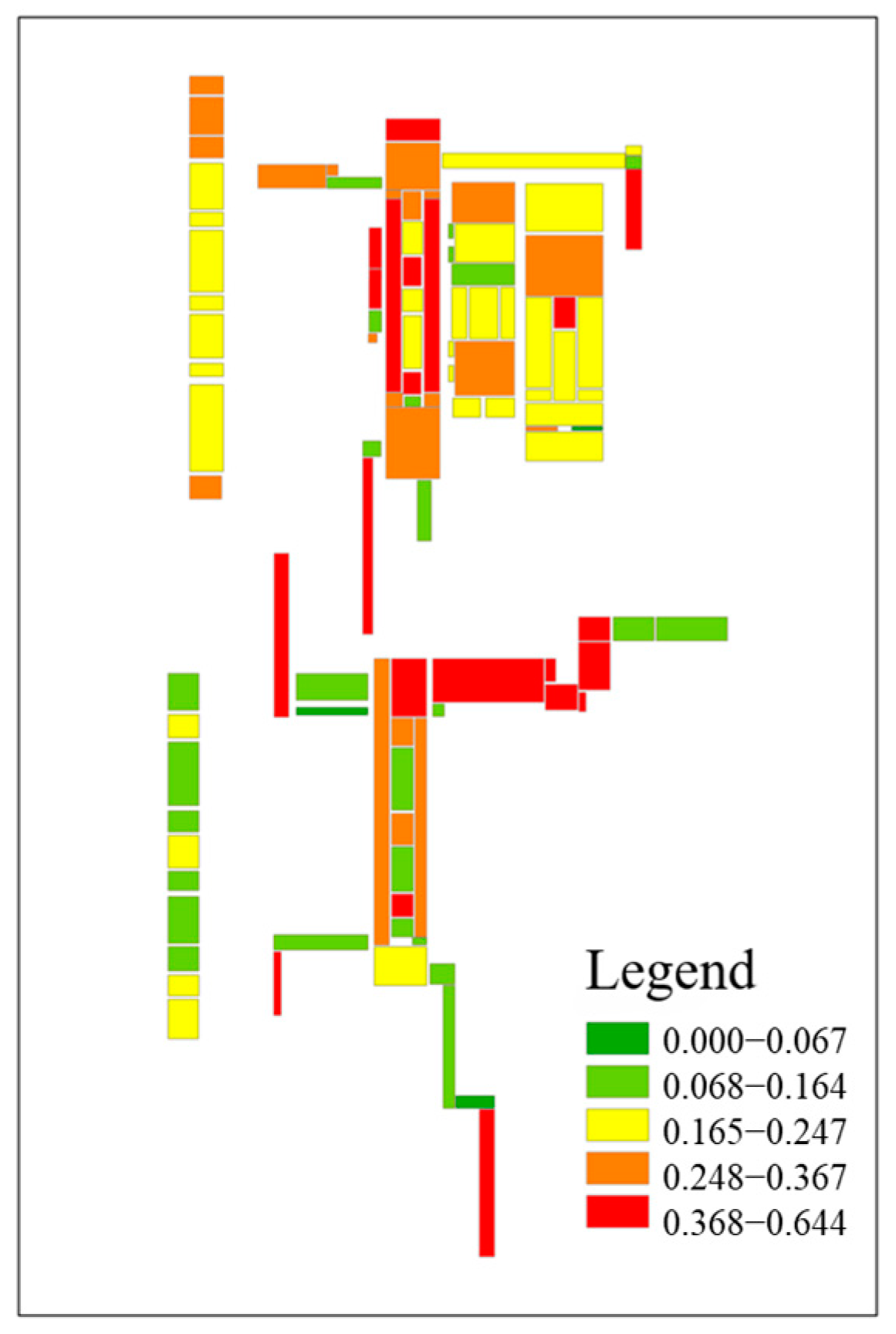
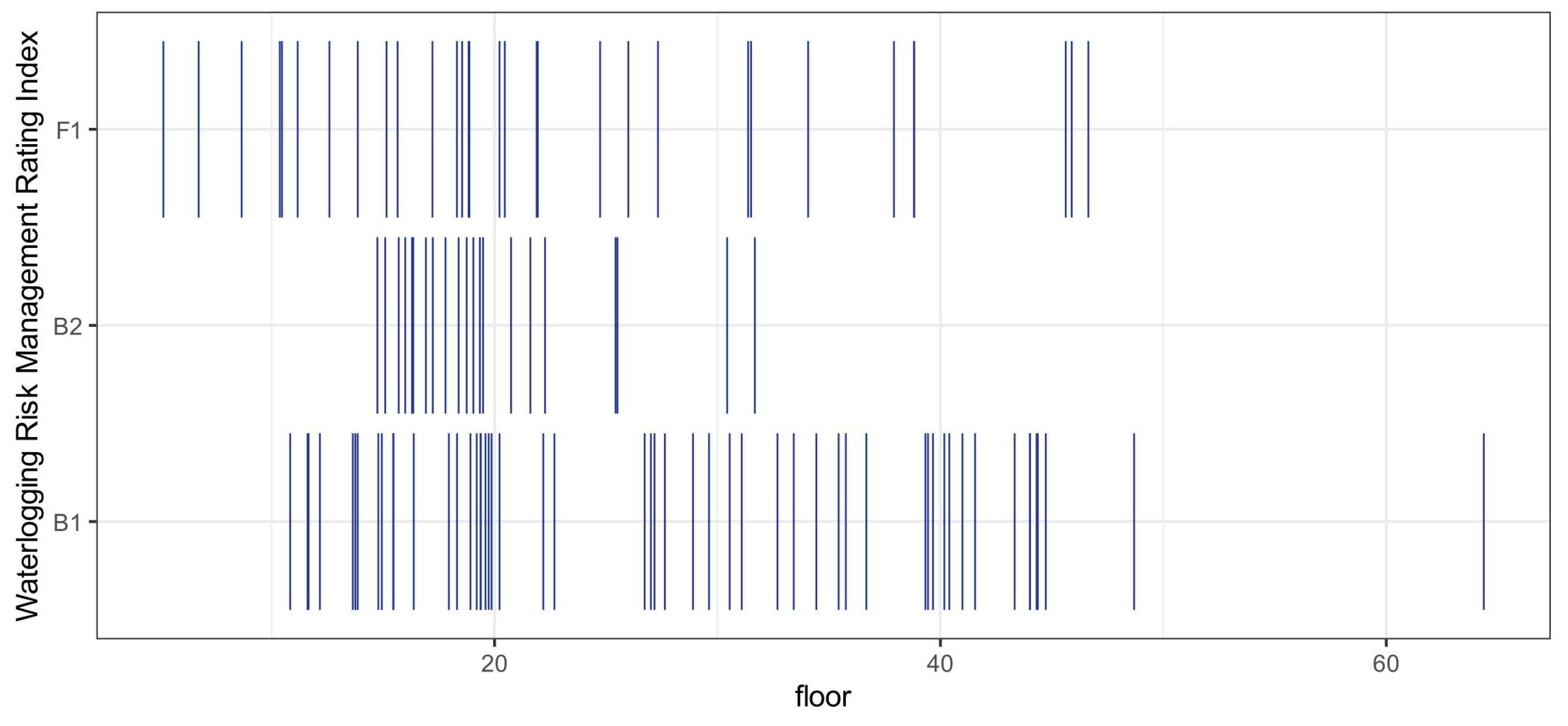
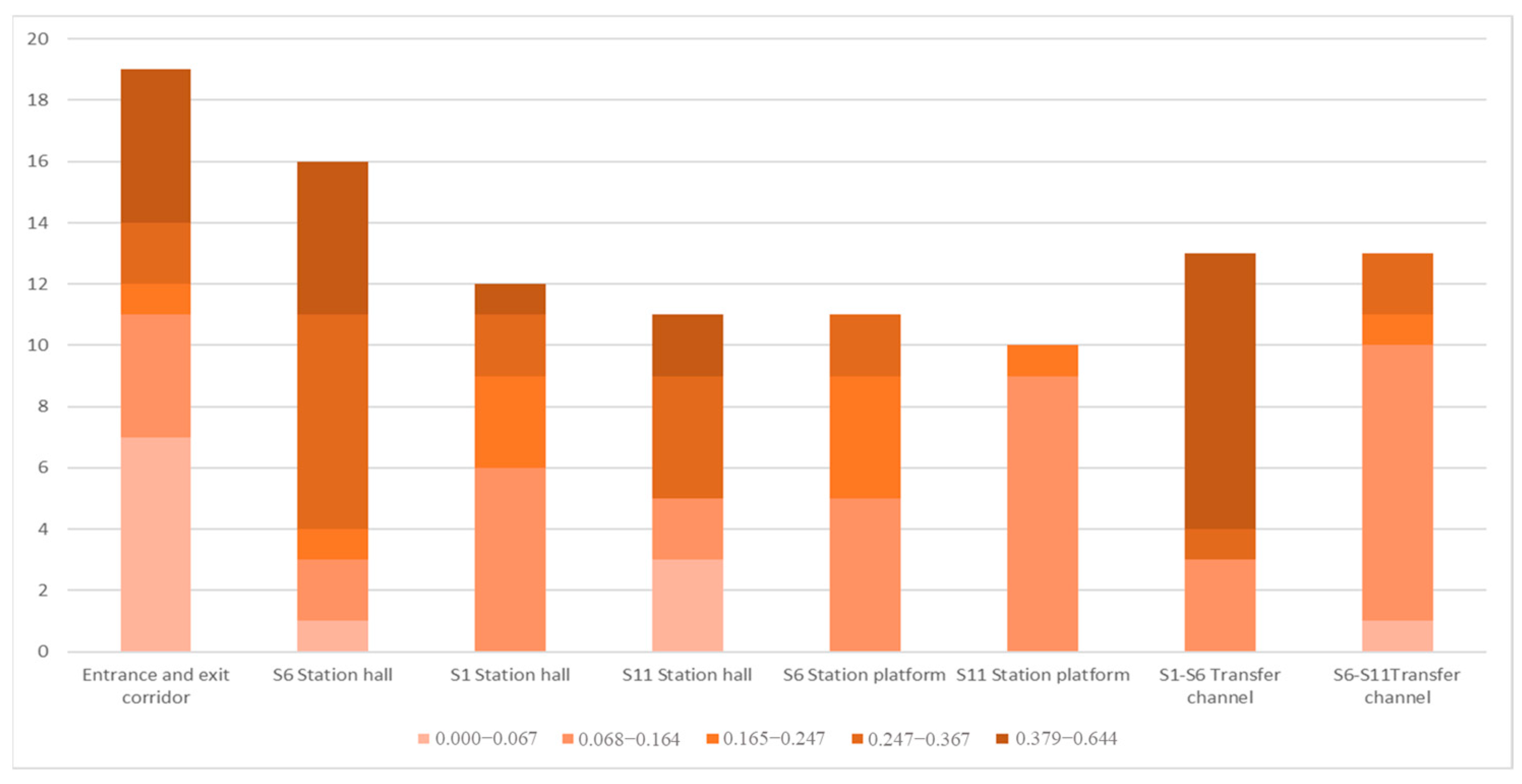
3.4. Flood Management Level Results for Subway Spaces
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef]
- Gonzva, M.; Barroca, B.; Gautier, P.-É.; Diab, Y. Modeling disruptions causing domino effects in urban guided transport systems faced by flood hazards. Nat. Hazards 2016, 86, 183–201. [Google Scholar] [CrossRef]
- Li, M.; Kwan, M.-P.; Yin, J.; Yu, D.; Wang, J. The potential effect of a 100-year pluvial flood event on metro accessibility and ridership: A case study of central Shanghai, China. Appl. Geogr. 2018, 100, 21–29. [Google Scholar] [CrossRef]
- Ruettger, K.; Lenz, W. (P2-40) Patient Allocation to Hospitals During Mass-Casualty Incidents. Prehosp. Disaster Med. 2011, 26, s148–s149. [Google Scholar] [CrossRef]
- Jiao, L.; Zhu, Y.; Huo, X.; Wu, Y.; Zhang, Y. Resilience assessment of metro stations against rainstorm disaster based on cloud model: A case study in Chongqing, China. Nat. Hazards 2023, 116, 2311–2337. [Google Scholar] [CrossRef]
- Junfeng, C.; Le, W.; Yiqi, Z.; Fucai, H.; Maohua, Z. Lessons and improvements: Subway waterlogging catastrophe in Zhengzhou, China. Tunn. Undergr. Space Technol. 2024, 144, 105541. [Google Scholar] [CrossRef]
- Xu, F.; Fang, D.; Chen, B.; Wang, H. Resilience assessment of subway system to waterlogging disaster. Sustain. Cities Soc. 2024, 113, 105710. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Shi, P.; Zhang, G.; Liu, J. Flood Risk Assessment of Metro System Using Improved Trapezoidal Fuzzy AHP: A Case Study of Guangzhou. Remote Sens. 2021, 13, 5154. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Z.; Yuan, Y.; Shao, X. Fragility analysis of a subway station structure by incremental dynamic analysis. Adv. Struct. Eng. 2016, 20, 1111–1124. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, W.; Li, H.; Chen, J. Evaluation of Flooding Disaster Risks for Subway Stations Based on the PSR Cloud Model. Sustainability 2023, 15, 15552. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Yang, J.; Yin, Z.-Y. Inundation analysis of metro systems with the storm water management model incorporated into a geographical information system: A case study in Shanghai. Hydrol. Earth Syst. Sci. 2019, 23, 4293–4307. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunn. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Ju, W.; Wu, J.; Cao, H.; Kang, Q.; Syed Salman Ali, S.; Xing, Z. Flood risk assessment of subway stations based on projection pursuit model optimized by whale algorithm: A case study of Changzhou, China. Int. J. Disaster Risk Reduct. 2023, 98, 104068. [Google Scholar] [CrossRef]
- Yu, H.; Liang, C.; Li, P.; Niu, K.; Du, F.; Shao, J.; Liu, Y.; Tang, Y. Evaluation of Waterlogging Risk in an Urban Subway Station. Adv. Civ. Eng. 2019, 2019, 5393171. [Google Scholar] [CrossRef]
- Li, L.; Yu, M.; Ma, H.; Meng, L.; Cui, Z. Development and Application of Flood Control and Waterlogging Prevention Intelligent Monitoring System Based on Subway “One Map”. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, X-3/W1-2022, 93–98. [Google Scholar] [CrossRef]
- Dong, W.; Huang, H.; Zhong, M.; Wang, H.; Hua, F. Monitoring and early warning mechanism of flood invasion into subway tunnels based on the experimental study of flooding patterns. J. Intell. Constr. 2024, 2, 1–16. [Google Scholar] [CrossRef]
- Hansen, W.G. How Accessibility Shapes Land Use. J. Am. Inst. Plan. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Wang, M.; Wang, H.; Gong, Y. Research on the Method of Determining Rainfall Thresholds for Waterlogging Risk in Subway Stations. Water 2024, 16, 1596. [Google Scholar] [CrossRef]
- Ishigaki, T.; Toda, K.; Baba, Y.; Inoue, K.; Nakagawa, H. Experimental Study on Evacuation from Underground Space by Using Real Size Models. Proceedings of Hydraulic Engineering. Proc. Hydraul. Eng. 2006, 50, 583–588. [Google Scholar] [CrossRef]
- Quagliarini, E.; Romano, G.; Bernardini, G. Investigating pedestrian behavioral patterns under different floodwater conditions: A video analysis on real flood evacuations. Saf. Sci. 2023, 161, 106083. [Google Scholar] [CrossRef]
- Kim, J.Y.; Kim, Y.O. Analysis of Pedestrian Behaviors in Subway Station Using Agent-Based Model: Case of Gangnam Station, Seoul, Korea. Buildings 2023, 13, 537. [Google Scholar] [CrossRef]
- Lu, Y.; Deng, Y.; Sun, S. Design for safety in metro station evacuation: A study of fire emergency evacuation behavior and simulation. Eng. Constr. Archit. Manag. 2023, 31, 3479–3507. [Google Scholar] [CrossRef]
- Hu, M. A high-fidelity three-dimensional simulation method for evaluating passenger flow organization and facility layout at metro stations. Simulation 2017, 93, 841–851. [Google Scholar] [CrossRef]
- Lin, Z.; Hu, S.; Zhou, T.; Zhong, Y.; Zhu, Y.; Shi, L.; Lin, H. Numerical Simulation of Flood Intrusion Process under Malfunction of Flood Retaining Facilities in Complex Subway Stations. Buildings 2022, 12, 853. [Google Scholar] [CrossRef]







| Entrance/ Exit Name | Water Accumulation Depth (m) | Stair Height (m) | Water Accumulation Depth (Effective Inflow Depth) (m) | Subway Entrance/Exit Width (m) |
|---|---|---|---|---|
| A | 0.60 | 0.37 | 0.23 | 7 |
| B | 0.62 | 0.37 | 0.25 | 7 |
| C | 0.59 | 0.37 | 0.22 | 6.3 |
| D | 0.71 | 0.5 | 0.21 | 7 |
| C1 | 0.69 | 0.43 | 0.16 | 1.1 |
| Index | Weight (%) |
|---|---|
| Connectivity | 11.453 |
| Integration | 5.159 |
| Step Depth | 7.347 |
| Selectivity | 27.719 |
| Depth (R5) | 5.333 |
| Index | Weight (%) |
|---|---|
| Spatial Area | 30.5 |
| Proportion of Facility Projected Area | 69.5 |
| Index | Weight (%) |
|---|---|
| Spatial Network Importance | 50.0 |
| Spatial Functional Importance | 37.9 |
| Flood Risk | 12.1 |
| Space ID | Integration | Selectivity | Floor | Area |
|---|---|---|---|---|
| 30 | 0.836 | 1.090 | B1 | Line 6 Station Hall |
| 40 | 0.797 | 0.894 | B1 | Line 6-Line 11 Transfer Channel |
| 31 | 0.783 | B1 | Line 6 Station Hall | |
| 27 | 0.799 | B1 | Line 6 Station Hall | |
| 32 | 0.799 | B1 | Line 6 Station Hall | |
| 61 | 0.938 | B1 | Line 6-Line 11 Transfer Channel | |
| 64 | 0.901 | B1 | Line 6-Line 11 Transfer Channel | |
| 66 | 0.888 | B1 | Line 6-Line 11 Transfer Channel |
| Flood Risk Management Index | Level | Proportion (%) |
|---|---|---|
| 0.000–0.067 | 5 | 11.43 |
| 0.068–0.164 | 4 | 38.10 |
| 0.165–0.247 | 3 | 10.47 |
| 0.248–0.367 | 2 | 19.05 |
| 0.368–0.644 | 1 | 20.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xu, X.; Hou, S.; Dang, X.; Li, Z.; Gong, Y. Flood Risk Management-Level Analysis of Subway Station Spaces. Water 2025, 17, 1084. https://doi.org/10.3390/w17071084
Li Y, Xu X, Hou S, Dang X, Li Z, Gong Y. Flood Risk Management-Level Analysis of Subway Station Spaces. Water. 2025; 17(7):1084. https://doi.org/10.3390/w17071084
Chicago/Turabian StyleLi, Yan, Xinxin Xu, Shaoxuan Hou, Xin Dang, Zhuolun Li, and Yongwei Gong. 2025. "Flood Risk Management-Level Analysis of Subway Station Spaces" Water 17, no. 7: 1084. https://doi.org/10.3390/w17071084
APA StyleLi, Y., Xu, X., Hou, S., Dang, X., Li, Z., & Gong, Y. (2025). Flood Risk Management-Level Analysis of Subway Station Spaces. Water, 17(7), 1084. https://doi.org/10.3390/w17071084







