High-Temporal-Resolution Modeling of Land Surface Temperature and Groundwater Level Impacts on Shallow Aquifer Thermal Regimes
Abstract
1. Introduction
2. Material and Methods
2.1. Classical One-Dimensional Heat Transfer Equation
2.2. Estimation of Seasonally Varying Thermal Diffusivity
2.3. Differences in the Direction of Heat Transfer Leads to Differential Rises and Declines in GWT
2.4. Seasonally Adaptive Thermal Diffusivity Numerical Model (SATDNM)
2.5. Data Source
3. Results
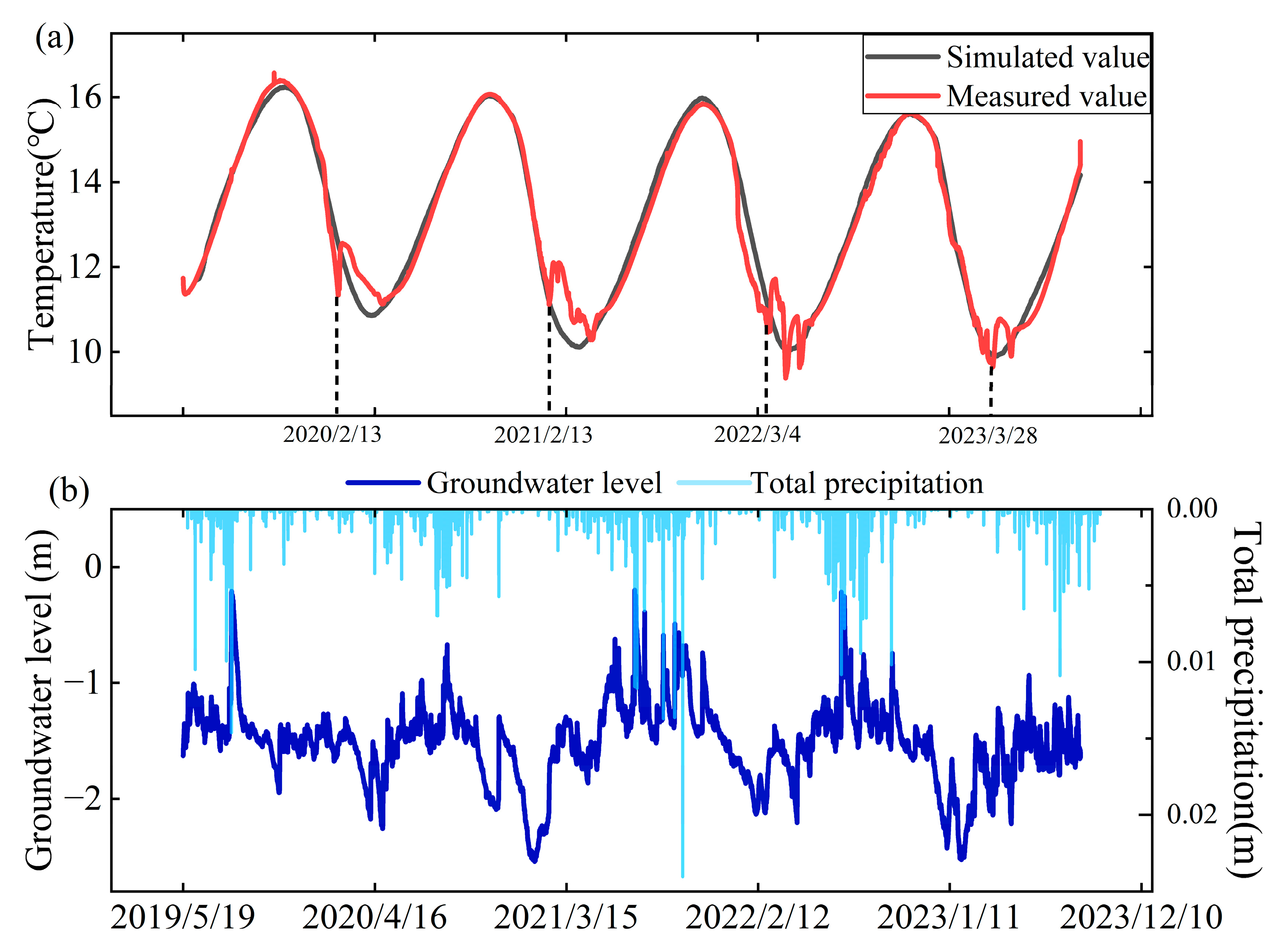
3.1. Model Evaluation
3.1.1. Comparison of SATDNM with Classical Analytical Models
3.1.2. Modeling and Testing of Vertical Variation
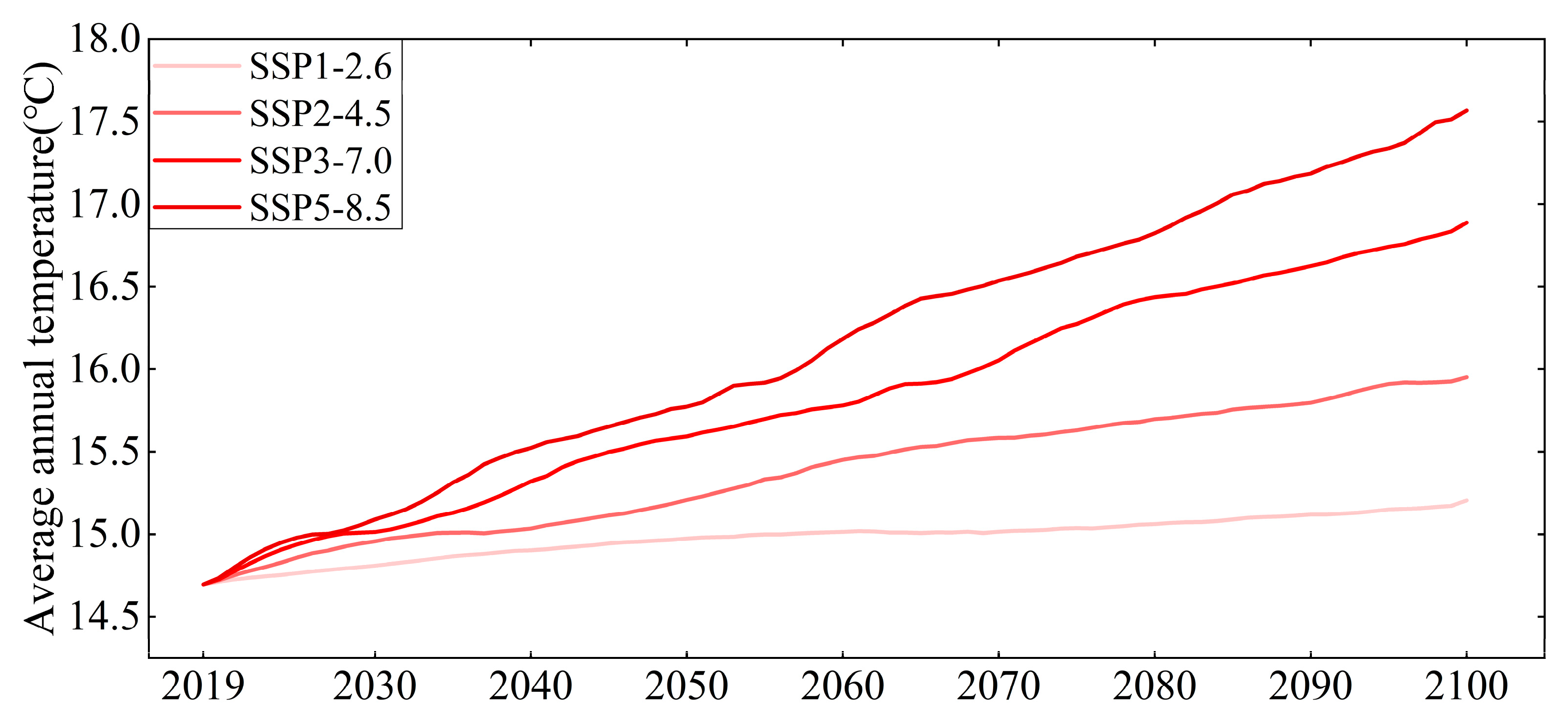
3.2. Impact of Surface Temperature on Coastal Shallow Groundwater Temperature Under Climate Change
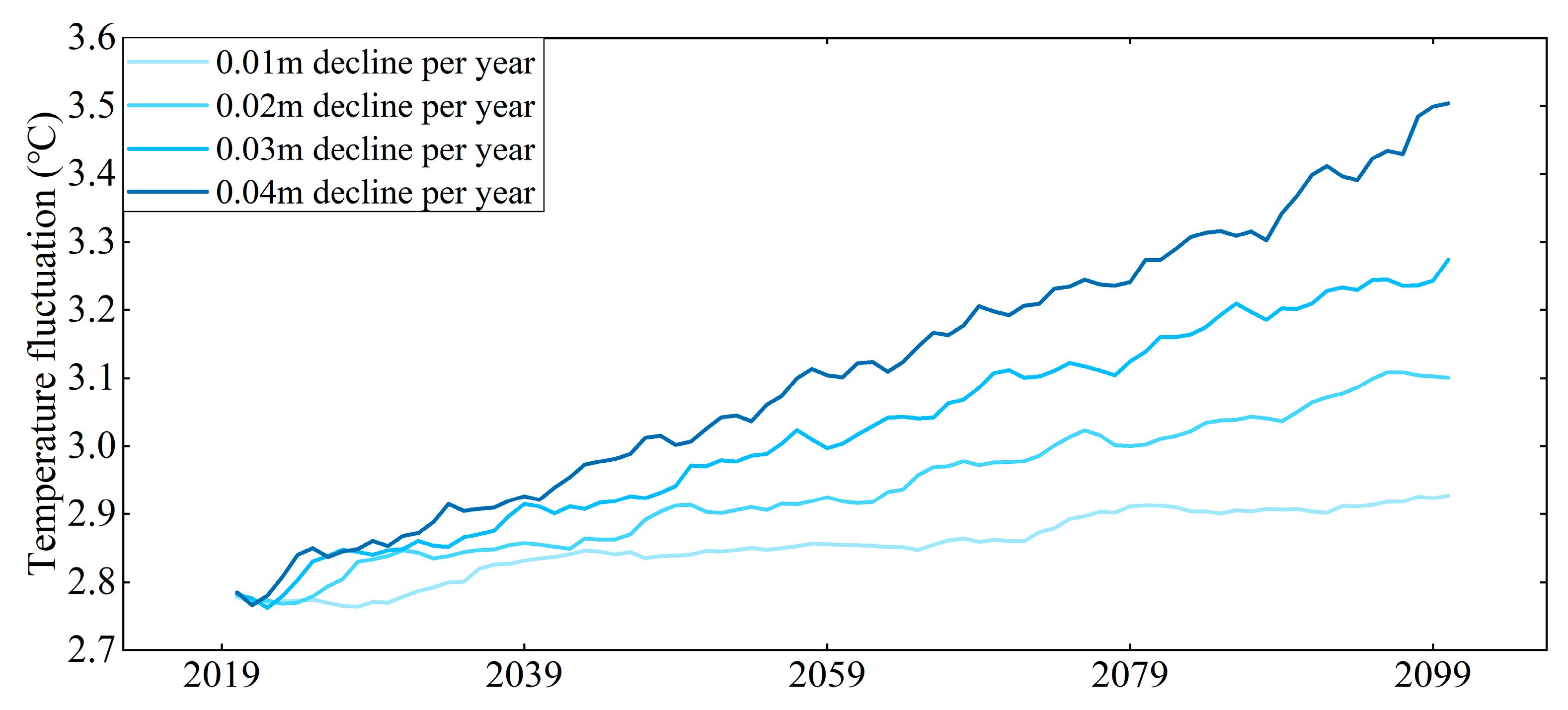
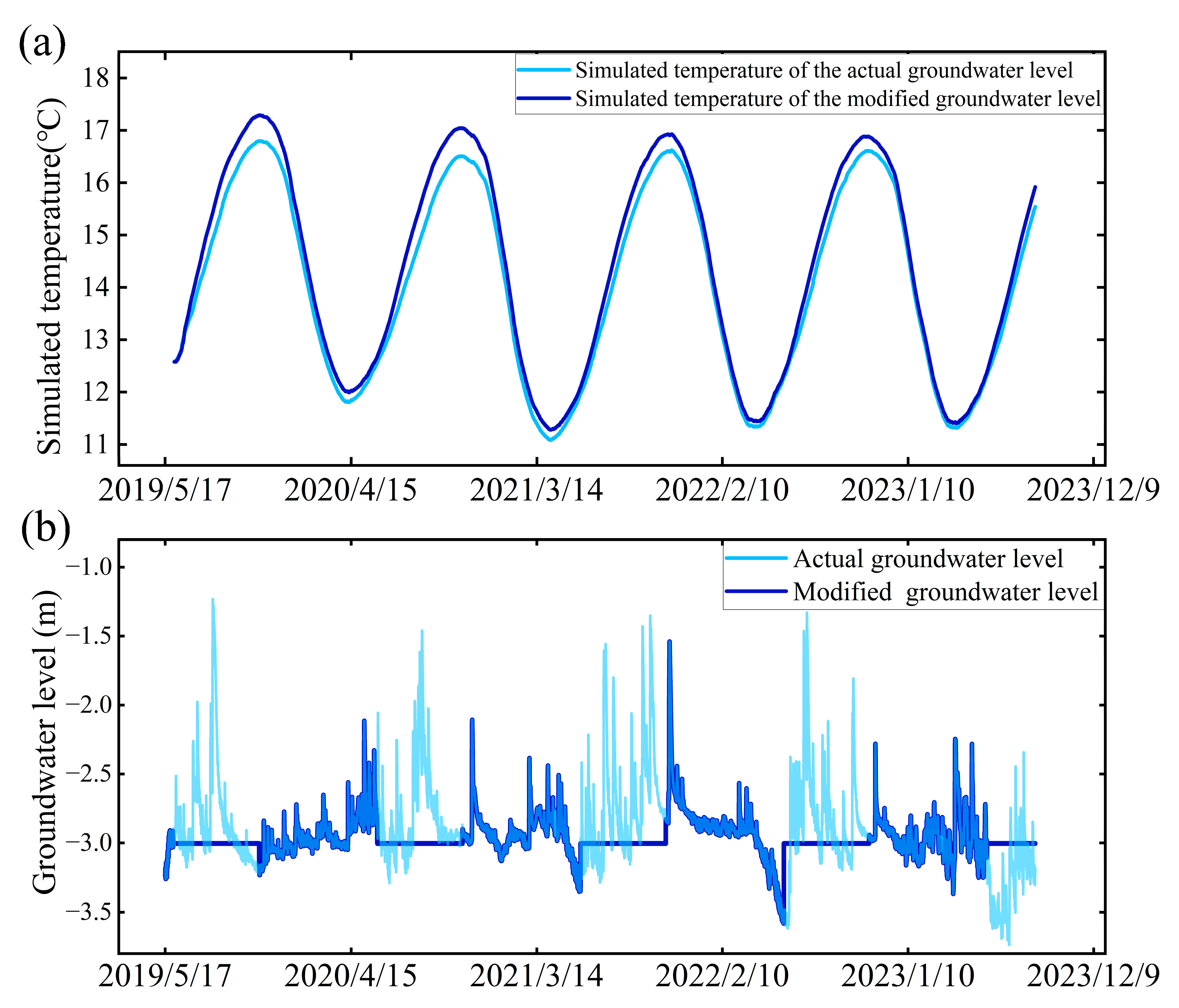
3.3. Impact of Groundwater Levels on Coastal Shallow Groundwater Temperature Under Climate Change
4. Discussion
4.1. Differences in Shallow Groundwater Temperature Responses to Short-Term Natural Extreme Rainfall and Anthropogenic Agricultural Activities
4.2. Potential Impacts of Future Groundwater Temperature Changes Under Climate Change
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amanambu, A.C.; Obarein, O.A.; Mossa, J.; Li, L.H.; Ayeni, S.S.; Balogun, O.; Oyebamiji, A.; Ochege, F.U. Groundwater system and climate change: Present status and future considerations. J. Hydrol. 2020, 589, 125163. [Google Scholar] [CrossRef]
- Kuang, X.X.; Liu, J.G.; Scanlon, B.R.; Jiao, J.J.; Jasechko, S.; Lancia, M.; Biskaborn, B.K.; Wada, Y.; Li, H.L.; Zeng, Z.Z.; et al. The changing nature of groundwater in the global water cycle. Science 2024, 383, eadf0630. [Google Scholar] [CrossRef] [PubMed]
- Kurylyk, B.L.; MacQuarrie, K.T.B.; Caissie, D.; McKenzie, J.M. Shallow groundwater thermal sensitivity to climate change and land cover disturbances: Derivation of analytical expressions and implications for stream temperature modeling. Hydrol. Earth Syst. Sci. 2015, 19, 2469–2489. [Google Scholar] [CrossRef]
- Benz, S.A.; Irvine, D.J.; Rau, G.C.; Bayer, P.; Menberg, K.; Blum, P.; Jamieson, R.C.; Griebler, C.; Kurylyk, B.L. Global groundwater warming due to climate change. Nat. Geosci. 2024, 17, 545–551. [Google Scholar] [CrossRef]
- Riedel, T. Temperature-associated changes in groundwater quality. J. Hydrol. 2019, 572, 206–212. [Google Scholar] [CrossRef]
- Saito, T.; Hamamoto, S.; Ueki, T.; Ohkubo, S.; Moldrup, P.; Kawamoto, K.; Komatsu, T. Temperature change affected groundwater quality in a confined marine aquifer during long-term heating and cooling. Water Res. 2016, 94, 120–127. [Google Scholar] [CrossRef]
- Price, P.B.; Sowers, T. Temperature dependence of metabolic rates for microbial growth, maintenance, and survival. Proc. Natl. Acad. Sci. USA 2004, 101, 4631–4636. [Google Scholar] [CrossRef]
- Jorgensen, C.J.; Jacobsen, O.S.; Elberling, B.; Aamand, J. Microbial Oxidation of Pyrite Coupled to Nitrate Reduction in Anoxic Groundwater Sediment. Environ. Sci. Technol. 2009, 43, 4851–4857. [Google Scholar] [CrossRef]
- Addy, K.; Gold, A.J.; Christianson, L.E.; David, M.B.; Schipper, L.A.; Ratigan, N.A. Denitrifying Bioreactors for Nitrate Removal: A Meta-Analysis. J. Environ. Qual. 2016, 45, 873–881. [Google Scholar] [CrossRef]
- Cogswell, C.; Heiss, J.W. Climate and Seasonal Temperature Controls on Biogeochemical Transformations in Unconfined Coastal Aquifers. J. Geophys. Res.-Biogeosciences 2021, 126, e2021JG006605. [Google Scholar] [CrossRef]
- Menberg, K.; Blum, P.; Kurylyk, B.L.; Bayer, P. Observed groundwater temperature response to recent climate change. Hydrol. Earth Syst. Sci. 2014, 18, 4453–4466. [Google Scholar] [CrossRef]
- Saito, H.; Simunek, J.; Mohanty, B.P. Numerical analysis of coupled water, vapor, and heat transport in the vadose zone. Vadose Zone J. 2006, 5, 784–800. [Google Scholar] [CrossRef]
- Mandavi, S.M.; Neyshabouri, M.R.; Fujimaki, H. Water vapour transport in a soil column in the presence of an osmotic gradient. Geoderma 2018, 315, 199–207. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Neidhardt, H.; Shao, W. Impact of climate change-induced warming on groundwater temperatures and quality. Appl. Water Sci. 2023, 13, 235. [Google Scholar] [CrossRef]
- Bense, V.F.; Kurylyk, B.L.; Bruin, J.G.H.; Visser, P. Repeated Subsurface Thermal Profiling to Reveal Temporal Variability in Deep Groundwater Flow Conditions. Water Resour. Res. 2020, 56, e2019WR026913. [Google Scholar] [CrossRef]
- Arias-Penas, D.; Castro-García, M.P.; Rey-Ronco, M.A.; Alonso-Sánchez, T. Determining the thermal diffusivity of the ground based on subsoil temperatures. Preliminary results of an experimental geothermal borehole study Q-THERMIE-UNIOVI. Geothermics 2015, 54, 35–42. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Chen, S.Y.; Zhou, B. Estimating temporal patterns of vertical groundwater flux using multidepth temperature time series: A numerical method. J. Hydrol. 2024, 639, 131623. [Google Scholar] [CrossRef]
- García-Pereira, F.; González-Rouco, J.F.; Schmid, T.; Melo-Aguilar, C.; Vegas-Cañas, C.; Steinert, N.J.; Roldan-Gómez, P.J.; Cuesta-Valero, F.J.; García-García, A.; Beltrami, H.; et al. Thermodynamic and hydrological drivers of the soil and bedrock thermal regimes in central Spain. Soil 2024, 10, 1–21. [Google Scholar] [CrossRef]
- Rau, G.C.; Halloran, L.J.S.; Cuthbert, M.O.; Andersen, M.S.; Acworth, R.I.; Tellam, J.H. Characterising the dynamics of surface water-groundwater interactions in intermittent and ephemeral streams using streambed thermal signatures. Adv. Water Resour. 2017, 107, 354–369. [Google Scholar] [CrossRef]
- Malik, M.S.; Shukla, J.P.; Mishra, S. Effect of Groundwater Level on Soil Moisture, Soil Temperature and Surface Temperature. J. Indian. Soc. Remote 2021, 49, 2143–2161. [Google Scholar] [CrossRef]
- Campbell, G.S.; Jungbauer, J.D.; Bidlake, W.R.; Hungerford, R.D. Predicting the Effect of Temperature on Soil Thermal-Conductivity. Soil. Sci. 1994, 158, 307–313. [Google Scholar] [CrossRef]
- Boukelia, A.; Eslami, H.; Rosin-Paumier, S.; Masrouri, F. Effect of temperature and initial state on variation of thermal parameters of fine compacted soils. Eur. J. Environ. Civ. Eng. 2019, 23, 1125–1138. [Google Scholar] [CrossRef]
- Van Wijk, W.R.; De Vries, D.A. Periodic Temperature Variations in a Homogeneous Soil; North-Holland: Amsterdam, The Netherland, 1963; pp. 103–143. [Google Scholar]
- Carslaw, H.; Jaeger, J. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: New York, NY, USA, 1959; p. 510. [Google Scholar]
- Hatch, C.E.; Fisher, A.T.; Revenaugh, J.S.; Constantz, J.; Ruehl, C. Quantifying surface water-groundwater interactions using time series analysis of streambed thermal records: Method development. Water Resour. Res. 2006, 42, e2005w10410. [Google Scholar] [CrossRef]
- Keery, J.; Binley, A.; Crook, N.; Smith, J.W.N. Temporal and spatial variability of groundwater-surface water fluxes: Development and application of an analytical method using temperature time series. J. Hydrol. 2007, 336, 1–16. [Google Scholar] [CrossRef]
- McCallum, A.M.; Andersen, M.S.; Rau, G.C.; Acworth, R.I. A 1-D analytical method for estimating surface water-groundwater interactions and effective thermal diffusivity using temperature time series. Water Resour. Res. 2012, 48, e2012w11532. [Google Scholar] [CrossRef]
- Luce, C.H.; Tonina, D.; Gariglio, F.; Applebee, R. Solutions for the diurnally forced advection-diffusion equation to estimate bulk fluid velocity and diffusivity in streambeds from temperature time series. Water Resour. Res. 2013, 49, 488–506. [Google Scholar] [CrossRef]
- Vandersteen, G.; Schneidewind, U.; Anibas, C.; Schmidt, C.; Seuntjens, P.; Batelaan, O. Determining groundwater-surface water exchange from temperature-time series: Combining a local polynomial method with a maximum likelihood estimator. Water Resour. Res. 2015, 51, 922–939. [Google Scholar] [CrossRef]
- Kampen, R.; Schneidewind, U.; Anibas, C.; Bertagnoli, A.; Tonina, D.; Vandersteen, G.; Luce, C.; Krause, S.; Berkel, M. LPMLE-A Frequency Domain Method to Estimate Vertical Streambed Fluxes and Sediment Thermal Properties in Semi-Infinite and Bounded Domains. Water Resour. Res. 2022, 58, e2021WR030886. [Google Scholar] [CrossRef]
- Shi, W.G.; Wang, Q.R.; Klepikova, M.; Irvine, D.J.; Rashed, A.; Liao, Z.L. BDFLUX: A new bounded domain model for quantifying vertical fluxes in streambeds using heat as a tracer. J. Hydrol. 2024, 633, 130981. [Google Scholar] [CrossRef]
- Dong, Y.; McCartney, J.S.; Lu, N. Critical Review of Thermal Conductivity Models for Unsaturated Soils. Geotech. Geol. Eng. 2015, 33, 207–221. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Daigle, H. Thermal conductivity in porous media: Percolation-based effective-medium approximation. Water Resour. Res. 2016, 52, 295–314. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Z.Y. Review of soil thermal conductivity and predictive models. Int. J. Therm. Sci. 2017, 117, 172–183. [Google Scholar] [CrossRef]
- Lu, S.; Ren, T.S.; Gong, Y.S.; Horton, R. An improved model for predicting soil thermal conductivity from water content at room temperature. Soil. Sci. Soc. Am. J. 2007, 71, 8–14. [Google Scholar] [CrossRef]
- He, H.L.; Zhao, Y.; Dyck, M.F.; Si, B.C.; Jin, H.J.; Lv, J.L.; Wang, J.X. A modified normalized model for predicting effective soil thermal conductivity. Acta Geotech. 2017, 12, 1281–1300. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; Gori, F.; Wagner, B.; Buchan, G.D. Modelling approaches to predicting thermal conductivity of soils at high temperatures. Int. J. Energ. Res. 2000, 24, 403–423. [Google Scholar] [CrossRef]
- Rau, G.C.; Andersen, M.S.; Acworth, R.I. Experimental investigation of the thermal dispersivity term and its significance in the heat transport equation for flow in sediments. Water Resour. Res. 2012, 48, e2011wr011038. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Reeder, R.C. Soil thermal conductivity: Effects of density, moisture, salt concentration, and organic matter. Soil. Sci. Soc. Am. J. 2000, 64, 1285–1290. [Google Scholar] [CrossRef]
- Bittelli, M.; Ventura, F.; Campbell, G.S.; Snyder, R.L.; Gallegati, F.; Pisa, P.R. Coupling of heat, water vapor, and liquid water fluxes to compute evaporation in bare soils. J. Hydrol. 2008, 362, 191–205. [Google Scholar] [CrossRef]
- Du, C.Y.; Yu, J.J.; Wang, P.; Zhang, Y.C. Analysing the mechanisms of soil water and vapour transport in the desert vadose zone of the extremely arid region of northern China. J. Hydrol. 2018, 558, 592–606. [Google Scholar] [CrossRef]
- Rondanelli, R.; Molina, A.; Falvey, M. The Atacama Surface Solar Maximum. Bull. Am. Meteorol. Soc. 2015, 96, 405–418. [Google Scholar] [CrossRef]
- Jing, W.Q.; Wang, J.F. A Dynamics of Surface Temperature Forced by Solar Radiation. Geophys. Res. Lett. 2023, 50, e2022GL101222. [Google Scholar] [CrossRef]
- Fan, X.W.; Duan, Q.Y.; Shen, C.W.; Wu, Y.; Xing, C. Global surface air temperatures in CMIP6: Historical performance and future changes. Environ. Res. Lett. 2020, 15, 104056. [Google Scholar] [CrossRef]
- Jasechko, S.; Seybold, H.; Perrone, D.; Fan, Y.; Shamsudduha, M.; Taylor, R.G.; Fallatah, O.; Kirchner, J.W. Rapid groundwater decline and some cases of recovery in aquifers globally. Nature 2024, 625, 715–721. [Google Scholar] [CrossRef]
- Sharma, C.; Basagaoglu, H.; Yoosefdoost, I.; Wootten, A.; Chakraborty-Reddy, D.; Bertetti, F.P.; Mirchi, A.; Chakraborty, D. Efficacy of mitigation strategies for aquifer sustainability under climate change. Nat. Sustain. 2025, 8, 44–53. [Google Scholar] [CrossRef]
- Gordu, F.; Nachabe, M.H. Inferences of Groundwater Response to Projected Hydroclimatic Changes in North Florida. J. Hydrol. Eng. 2023, 28, 04023001. [Google Scholar] [CrossRef]
- Bera, B.; Shit, P.K.; Sengupta, N.; Saha, S.; Bhattacharjee, S. Steady declining trend of groundwater table and severe water crisis in unconfined hard rock aquifers in extended part of Chota Nagpur Plateau, India. Appl. Water Sci. 2022, 12, 31. [Google Scholar] [CrossRef]
- Le Brocque, A.F.; Kath, J.; Reardon-Smith, K. Chronic groundwater decline: A multi-decadal analysis of groundwater trends under extreme climate cycles. J. Hydrol. 2018, 561, 976–986. [Google Scholar] [CrossRef]
- Panahi, G.; Eskafi, M.H.; Faridhosseini, A.; Khodashenas, S.R.; Rohani, A. Prediction of groundwater level fluctuations under climate change based on machine learning algorithms in the Mashhad Aquifer, Iran. J. Water Clim. Change 2023, 14, 1039–1059. [Google Scholar] [CrossRef]
- Dong, Y.; Jiang, C.S.; Suri, M.R.; Pee, D.; Meng, L.K.; Goldstein, R.E.R. Groundwater level changes with a focus on agricultural areas in the Mid-Atlantic region of the United States, 2002–2016. Environ. Res. 2019, 171, 193–203. [Google Scholar] [CrossRef]
- Silva, R.C.G.; Reinecke, R.; Copty, N.K.; Barry, D.A.; Heggy, E.; Labat, D.; Roggero, P.P.; Borchardt, D.; Rode, M.; Gómez-Hernández, J.J.; et al. Multi-decadal groundwater observations reveal surprisingly stable levels in southwestern Europe. Commun. Earth Environ. 2024, 5, 387. [Google Scholar] [CrossRef]
- Song, S.H.; Zemansky, G. Groundwater level fluctuation in the Waimea Plains, New Zealand: Changes in a coastal aquifer within the last 30 years. Environ. Earth Sci. 2013, 70, 2167–2178. [Google Scholar] [CrossRef]
- O’Driscoll, M.; Humphrey, C.J.r.; Iverson, G.; Bowden, J.; Harrison, J. Rising groundwater levels in Dare County, North Carolina: Implications for onsite wastewater management for coastal communities. J. Water Clim. Change 2024, 15, 3666–3688. [Google Scholar] [CrossRef]
- Fan, X.M.; Min, T.; Dai, X.J. The Spatio-Temporal Dynamic Patterns of Shallow Groundwater Level and Salinity: The Yellow River Delta, China. Water 2023, 15, 1426. [Google Scholar] [CrossRef]
- Panda, D.K.; Mishra, A.; Kumar, A. Quantification of trends in groundwater levels of Gujarat in western India. Hydrol. Sci. J. 2012, 57, 1325–1336. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.C.; Jing, J.H.; Sun, J.C. Response of groundwater to climate change under extreme climate conditions in North China Plain. J. Earth Sci. 2014, 25, 612–618. [Google Scholar] [CrossRef]
- Chen, K.W.; Guo, Z.L.; Yin, M.S.; Liang, X.Y.; Chang, Z.B.; Yang, S.; Wei, X.O.; Zhai, X.C.; Zheng, C.M. Using Rainfall-Induced Groundwater Temperature Response to Estimate Lateral Flow Velocity. Water Resour. Res. 2024, 60, e2023WR036715. [Google Scholar] [CrossRef]
- Luo, M.M.; Wan, L.; Liao, C.L.; Jakada, H.; Zhou, H. Geographic and transport controls of temperature response in karst springs. J. Hydrol. 2023, 623, 129850. [Google Scholar] [CrossRef]
- Benz, S.A.; Bayer, P.; Goettsche, F.M.; Olesen, F.S.; Blum, P. Linking Surface Urban Heat Islands with Groundwater Temperatures. Environ. Sci. Technol. 2016, 50, 70–78. [Google Scholar] [CrossRef]
- Attard, G.; Rossier, Y.; Winiarski, T.; Eisenlohr, L. Deterministic modeling of the impact of underground structures on urban groundwater temperature. Sci. Total Environ. 2016, 572, 986–994. [Google Scholar] [CrossRef]
- Benz, S.A.; Bayer, P.; Blum, P. Identifying anthropogenic anomalies in air, surface and groundwater temperatures in Germany. Sci. Total Environ. 2017, 584, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Kohler, T.A.; Lenton, T.M.; Svenning, J.C.; Scheffer, M. Future of the human climate niche. Proc. Natl. Acad. Sci. USA 2020, 117, 11350–11355. [Google Scholar] [CrossRef] [PubMed]
- Bhattarai, N.; Lobell, D.B.; Balwinder-Singh; Fishman, R.; Kustas, W.P.; Pokhrel, Y.; Jain, M. Warming temperatures exacerbate groundwater depletion rates in India. Sci. Adv. 2023, 9, eadi1401. [Google Scholar] [CrossRef]
- Rosa, L.; Sangiorgio, M. Global water gaps under future warming levels. Nat. Commun. 2025, 16, 1192. [Google Scholar] [CrossRef]
- Di Cicco, M.; Di Lorenzo, T.; Fiasca, B.; Galmarini, E.; Vaccarelli, I.; Cerasoli, F.; Di Camillo, A.T.; Galassi, D.M.P. Some like it hot: Thermal preference of the groundwater amphipod Niphargus longicaudatus (Costa, 1851) and climate change implications. J. Therm. Biol. 2023, 116, 103654. [Google Scholar] [CrossRef]
- Benjamin, J.R.; Heltzel, J.M.; Dunham, J.B.; Heck, M.; Banish, N. Thermal Regimes, Nonnative Trout, and Their Influences on Native Bull Trout in the Upper Klamath River Basin, Oregon. Trans. Am. Fish. Soc. 2016, 145, 1318–1330. [Google Scholar] [CrossRef]
- Griebler, C.; Brielmann, H.; Haberer, C.M.; Kaschuba, S.; Kellermann, C.; Stumpp, C.; Hegler, F.; Kuntz, D.; Walker-Hertkorn, S.; Lueders, T. Potential impacts of geothermal energy use and storage of heat on groundwater quality, biodiversity, and ecosystem processes. Environ. Earth Sci. 2016, 75, 1391. [Google Scholar] [CrossRef]
- Castaño-Sánchez, A.; Hose, G.C.; Reboleira, A.S.P.S. Salinity and temperature increase impact groundwater crustaceans. Sci. Rep. 2020, 10, 12328. [Google Scholar] [CrossRef]
- Cheng, K.H.; Jiao, J.J.; Lee, J.H.W.; Luo, X. Synergistic controls of water column stability and groundwater phosphate on coastal algal blooms. Water Res. 2024, 255, 121467. [Google Scholar] [CrossRef]
- Tong, Y.; Lei, K.; Wang, L.; Li, Y.; Lan, W.; Cheng, Y.; Deng, Z.A.; Zhai, J.; Huang, Z. Spatial-temporal characteristics and the importance of environmental factors in relation to algal blooms in coastal seas. Sci. Total Environ. 2024, 957, 177686. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; MacQuarrie, K.T.B.; Voss, C.I. Climate change impacts on the temperature and magnitude of groundwater discharge from shallow, unconfined aquifers. Water Resour. Res. 2014, 50, 3253–3274. [Google Scholar] [CrossRef]
- Nygren, M.; Giese, M.; Kløve, B.; Haaf, E.; Rossi, P.M.; Barthel, R. Changes in seasonality of groundwater level fluctuations in a temperate-cold climate transition zone. J. Hydrol. X 2020, 8, 100062. [Google Scholar] [CrossRef]
- Sun, Q.H.; Zhang, X.B.; Zwiers, F.; Westra, S.; Alexander, L. A Global, Continental, and Regional Analysis of Changes in Extreme Precipitation. J. Clim. 2021, 34, 243–258. [Google Scholar] [CrossRef]
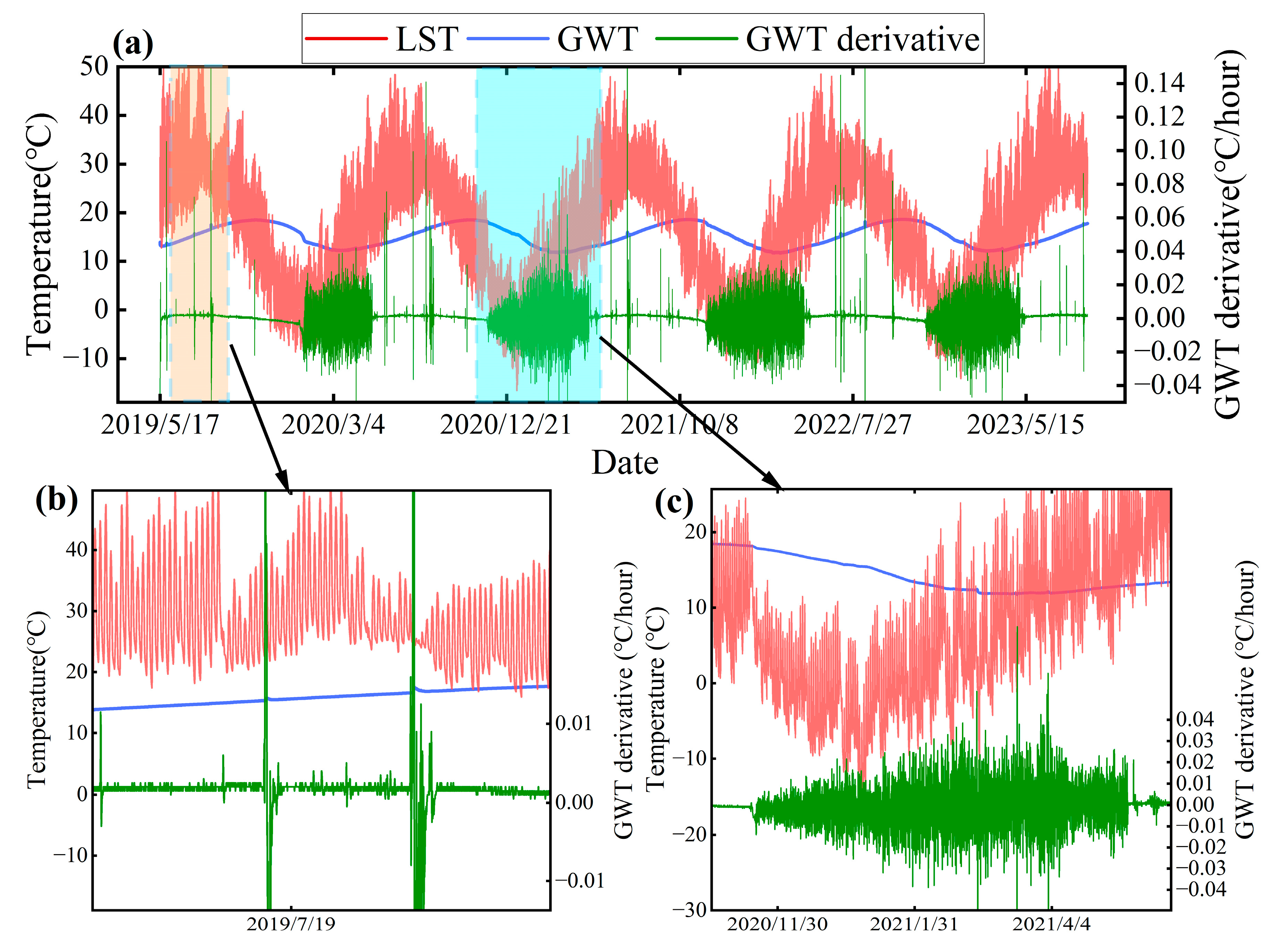
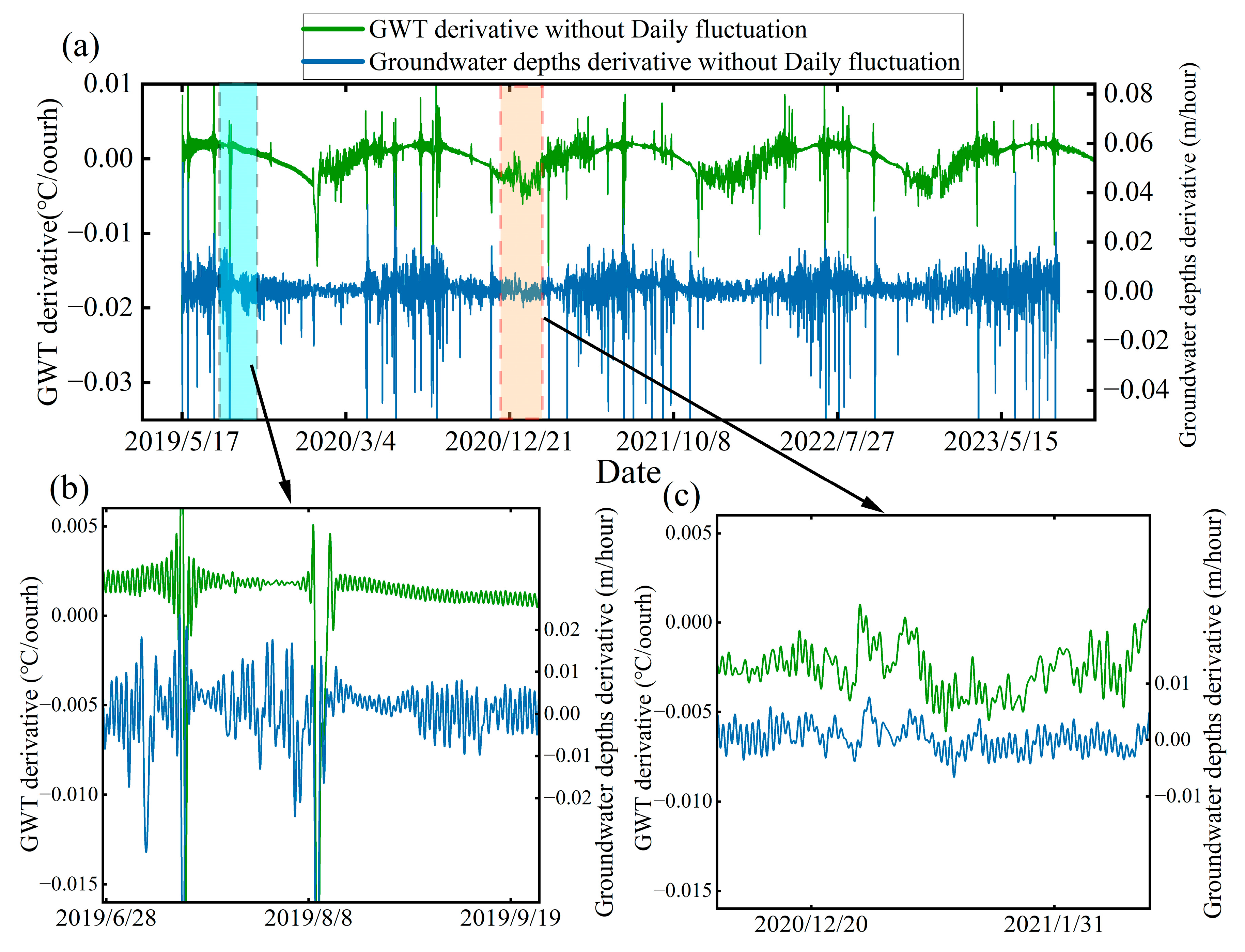
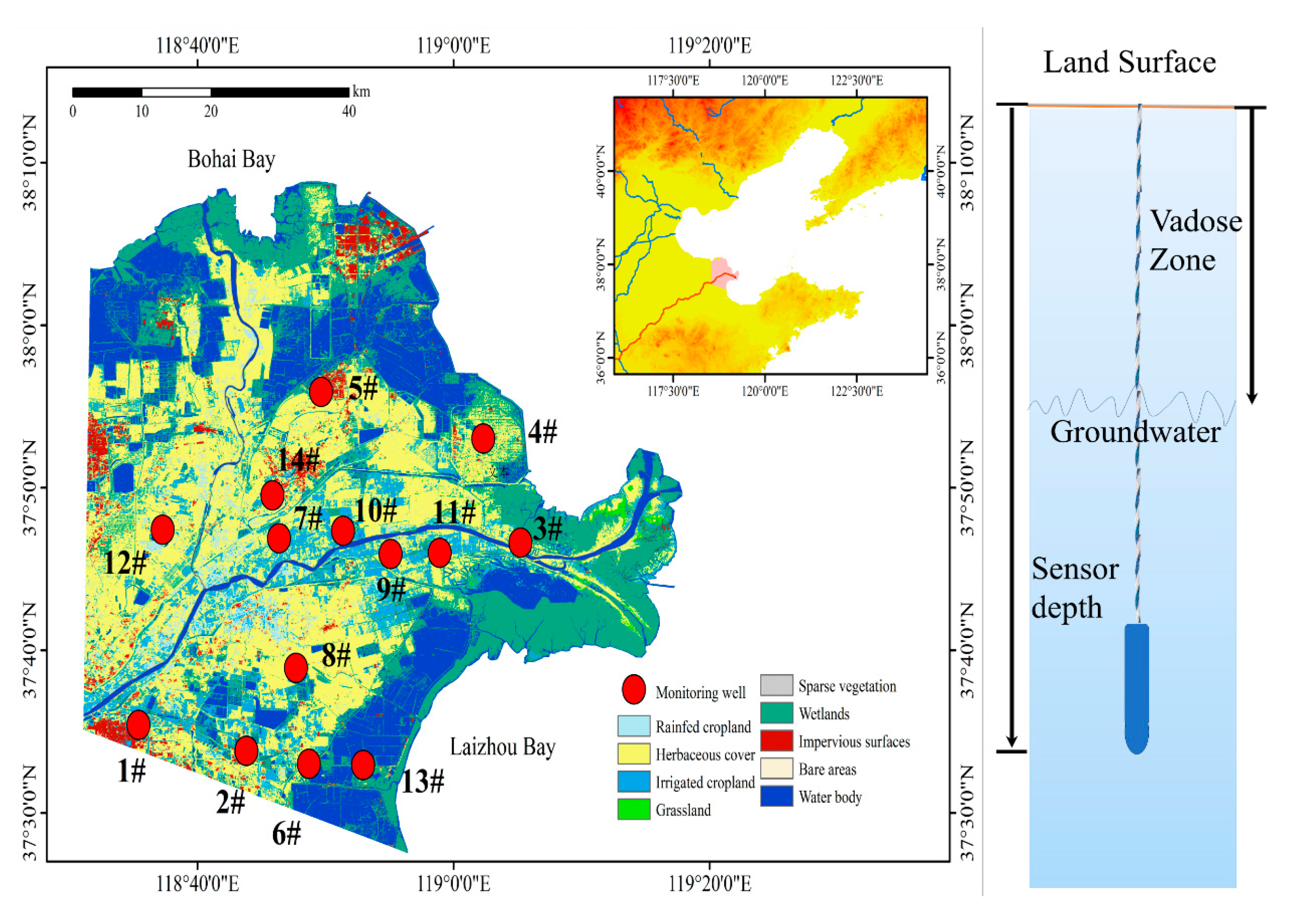
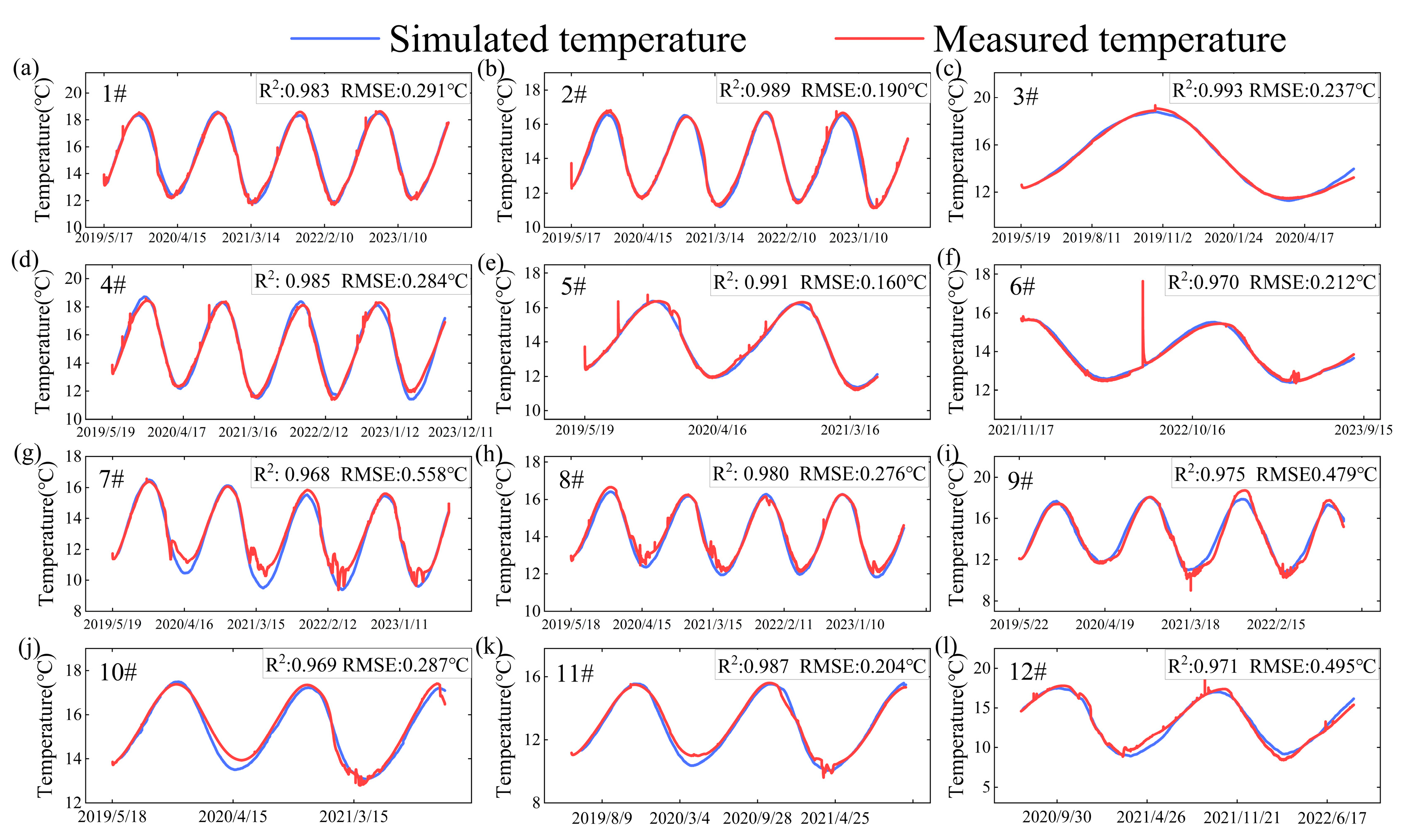





| Parameters | Values | Unit |
|---|---|---|
| Porosity, | 0.5–0.55 | |
| Volumetric heat capacity of solid, | (1.5–2.5) × 106 | J⋅m−3⋅K−1 |
| Volumetric heat capacity of water, | 4.18 × 106 | J⋅m−3⋅K−1 |
| Unsaturated aquifer thermal conductivity (warming), | 1–2.6 | W·m−1·K−1 |
| Saturated aquifer thermal conductivity (warming), | 1.43–3 | W·m−1·K−1 |
| Unsaturated aquifer thermal conductivity (cooling), | 0.2–1.9 | W·m−1·K−1 |
| Saturated aquifer thermal conductivity (cooling), | 0.35–2.4 | W·m−1·K−1 |
| GWL variation coefficient (warming) | 0–150 | |
| GWL variation coefficient (cooling) | 0–400 | |
| Temperature gradient coefficient, | 0.025–0.05 | |
| Fourier number, | 0.2–0.32 |
| Parameters | Values | Unit |
|---|---|---|
| Porosity, p | 0.5 | |
| Volumetric heat capacity of solid, | 1.59× 106 | J⋅m−3⋅K−1 |
| Volumetric heat capacity of water, | 4.18 × 106 | J⋅m−3⋅K−1 |
| Unsaturated aquifer thermal conductivity (warming), | 2.4 | W·m−1·K−1 |
| Saturated aquifer thermal conductivity (warming), | 2.7 | W·m−1·K−1 |
| Unsaturated aquifer thermal conductivity (cooling), | 1.05 | W·m−1·K−1 |
| Saturated aquifer thermal conductivity (cooling), | 1.3 | W·m−1·K−1 |
| GWL variation coefficient (wetting), | 150 | |
| GWL variation coefficient (drying), | 220 | |
| Temperature gradient coefficient, | 0.05 | |
| Fourier number, | 0.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Wang, D.; Luo, F.; Tian, X.; Bi, X.; Zhou, Z.; Hu, W. High-Temporal-Resolution Modeling of Land Surface Temperature and Groundwater Level Impacts on Shallow Aquifer Thermal Regimes. Water 2025, 17, 1107. https://doi.org/10.3390/w17071107
Wei Y, Wang D, Luo F, Tian X, Bi X, Zhou Z, Hu W. High-Temporal-Resolution Modeling of Land Surface Temperature and Groundwater Level Impacts on Shallow Aquifer Thermal Regimes. Water. 2025; 17(7):1107. https://doi.org/10.3390/w17071107
Chicago/Turabian StyleWei, Yulong, De Wang, Fubin Luo, Xinpeng Tian, Xiaoli Bi, Zixiang Zhou, and Wenjing Hu. 2025. "High-Temporal-Resolution Modeling of Land Surface Temperature and Groundwater Level Impacts on Shallow Aquifer Thermal Regimes" Water 17, no. 7: 1107. https://doi.org/10.3390/w17071107
APA StyleWei, Y., Wang, D., Luo, F., Tian, X., Bi, X., Zhou, Z., & Hu, W. (2025). High-Temporal-Resolution Modeling of Land Surface Temperature and Groundwater Level Impacts on Shallow Aquifer Thermal Regimes. Water, 17(7), 1107. https://doi.org/10.3390/w17071107





