A Data-Driven Decision Support System for Wave Power Plant Location Selection
Abstract
1. Introduction
2. Literature Review and Methodology
2.1. Application of Fuzzy Decision Support Systems in Renewable Energy Plant Location Selection
2.2. Methodology

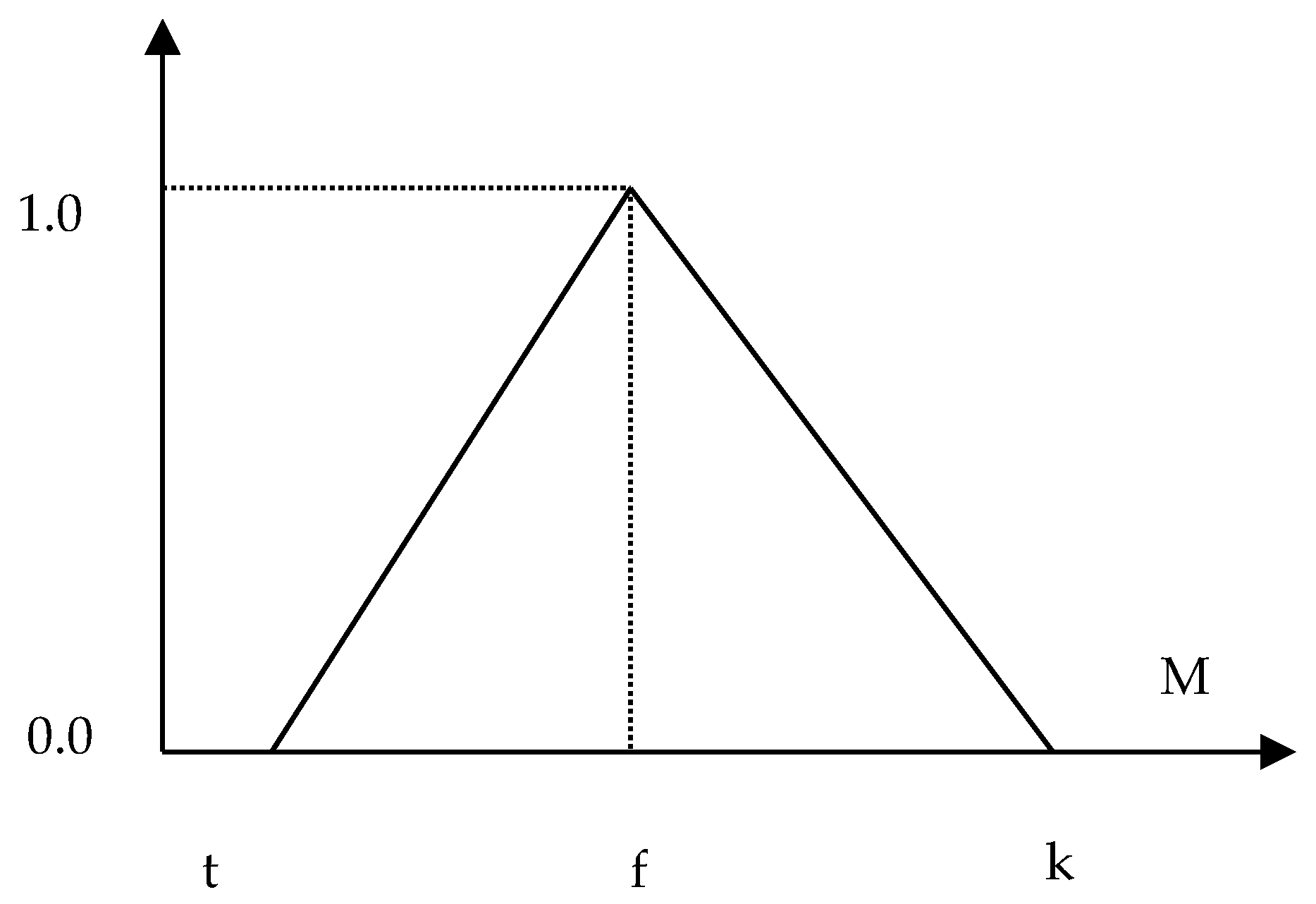
2.2.1. Fuzzy Sets
2.2.2. Fuzzy AHP Model
2.2.3. The Processes of the TODIM Model
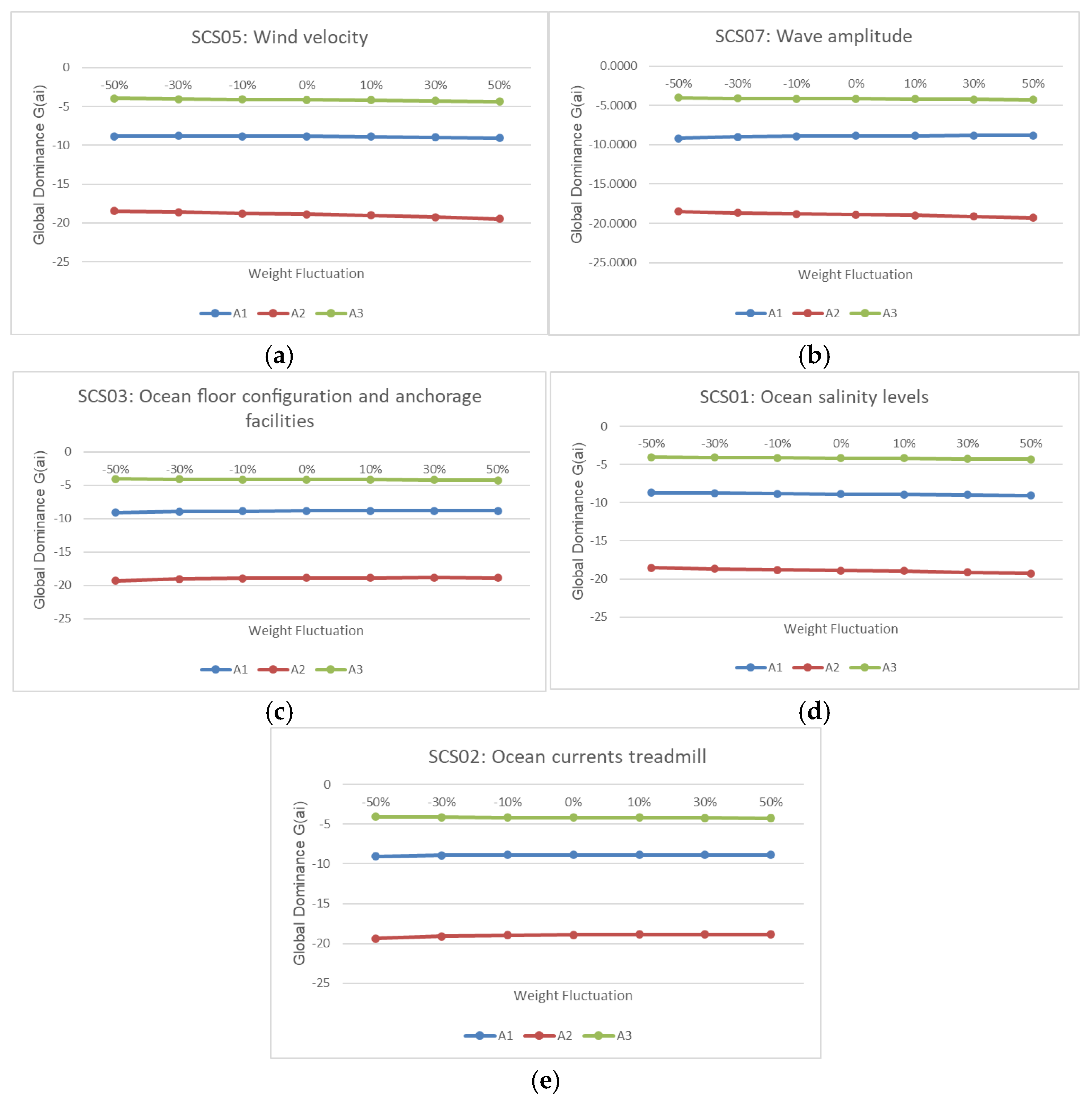
3. Results and Discussion
4. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ky, V. Promising Wave Energy in Vietnam. Vietnam National Energy Efficiency Program. 2010. Available online: http://vneec.gov.vn/tin-tuc/activities/t7972/promising-wave-energy-in-vietnam.html (accessed on 8 November 2024).
- Du, V. Tài Nguyên Năng Lượng Tái Tạo Biển Việt Nam Và Giải Pháp Phát Triển. Năng Lượng Việt Nam. 2020. Available online: https://nangluongvietnam.vn/tai-nguyen-nang-luong-tai-tao-bien-viet-nam-va-giai-phap-phat-trien-25772.html (accessed on 8 November 2024).
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Siksnelyte-Butkiene, I.; Zavadskas, E.K.; Streimikiene, D. Multi-Criteria Decision-Making (MCDM) for the Assessment of Renewable Energy Technologies in a Household: A Review. Energies 2020, 13, 1164. [Google Scholar] [CrossRef]
- Ghasempour, R.; Nazari, M.A.; Ebrahimi, M.; Ahmadi, M.H.; Hadiyanto, H. Multi-Criteria Decision Making (MCDM) Approach for Selecting Solar Plants Site and Technology: A Review. Int. J. Renew. Energy Dev. 2019, 8, 15–25. [Google Scholar] [CrossRef]
- Abu-Taha, R. Multi-criteria applications in renewable energy analysis: A literature review. In Proceedings of the PICMET’11: Technology Management in the Energy Smart World (PICMET), Portland, OR, USA, 31 July–4 August 2011; pp. 1–8. [Google Scholar]
- Benmoussa, N.; Elyamami, A.; Mansouri, K.; Qbadou, M.; Illoussamen, E. A Multi-Criteria Decision Making Approach for Enhancing University Accreditation Process. Eng. Technol. Appl. Sci. Res. 2019, 9, 3726–3733. [Google Scholar] [CrossRef]
- Deepa, N.; Duraj Raj Vincent, P.M.; Senthil Kumar, N.; Srinivasan, K.; Chang, C.-Y.; Bashir, A.K. An Efficient Ensemble VTOPES Multi-Criteria Decision-Making Model for Sustainable Sugarcane Farms. Sustainability 2019, 11, 4288. [Google Scholar] [CrossRef]
- Rehman, A.U.; Abidi, M.H.; Umer, U.; Usmani, Y.S. Multi-Criteria Decision-Making Approach for Selecting Wind Energy Power Plant Locations. Sustainability 2019, 11, 6112. [Google Scholar] [CrossRef]
- Chachuli, F.S.M.; Ludin, N.A.; Mat, S.; Sopian, K. Renewable energy performance evaluation studies using the data envelopment analysis (DEA): A systematic review. J. Renew. Sustain. Energy 2020, 12, 062701. [Google Scholar] [CrossRef]
- Elkadeem, M.R.; Elaziz, M.A.; Ullah, Z.; Wang, S.; Sharshir, S.W. Optimal Planning of Renewable Energy-Integrated Distribution System Considering Uncertainties. IEEE Access 2019, 7, 164887–164907. [Google Scholar] [CrossRef]
- Narendra, B.H.; Widiatmaka, W.; Kusmana, C.; Karlinasari, L.; Machfud, M. Multi-dimensional rapid appraisal technique for evaluating the sustainability of energy plantation forests in East Lombok District, Indonesia. Biodivers. J. Biol. Divers. 2019, 20, 1027–1033. [Google Scholar] [CrossRef]
- Erdin, C.; Akbaş, H.E. A Comparative Analysis of Fuzzy TOPSIS and Geographic Information Systems (GIS) for the Location Selection of Shopping Malls: A Case Study from Turkey. Sustainability 2019, 11, 3837. [Google Scholar] [CrossRef]
- Ioannou, K.; Tsantopoulos, G.; Arabatzis, G.; Andreopoulou, Z.; Zafeiriou, E. A Spatial Decision Support System Framework for the Evaluation of Biomass Energy Production Locations: Case Study in the Regional Unit of Drama, Greece. Sustainability 2018, 10, 531. [Google Scholar] [CrossRef]
- Çoban, V. Solar energy plant project selection with AHP decision-making method based on hesitant fuzzy linguistic evaluation. Complex Intell. Syst. 2020, 6, 507–529. [Google Scholar] [CrossRef]
- Guerrero-Liquet, G.C.; Sánchez-Lozano, J.M.; García-Cascales, M.S.; Lamata, M.T.; Verdegay, J.L. Decision-Making for Risk Management in Sustainable Renewable Energy Facilities: A Case Study in the Dominican Republic. Sustainability 2016, 8, 455. [Google Scholar] [CrossRef]
- Wątróbski, J.; Ziemba, P.; Wolski, W. MCDA-based Decision Support System for Sustainable Management—RES Case Study. In Proceedings of the 2016 Federated Conference on Computer Science and Information Systems, Gdansk, Poland, 11–14 September 2016; pp. 1235–1239. [Google Scholar]
- Budak, G.; Chen, X.; Celik, S.; Ozturk, B. A systematic approach for assessment of renewable energy using analytic hierarchy process. Energy Sustain. Soc. 2019, 9, 37. [Google Scholar] [CrossRef]
- Subagyo; Yanuar, J.P.M.; Bambang, P.N.; Saleh, A.; Akhmad, F.W. The Suitable Location for a Hybrid Renewable Energy Wind-Solar Power Plant: A Review by Bibliometric. IOP Conf. Series: Earth Environ. Sci. 2023, 1266, 012090. [Google Scholar] [CrossRef]
- Şengül, Ü.; Eren, M.; Shiraz, S.E.; Gezder, V.; Şengül, A.B. Fuzzy TOPSIS method for ranking renewable energy supply systems in Turkey. Renew. Energy 2015, 75, 617–625. [Google Scholar] [CrossRef]
- Wang, C.; Nguyen, H.; Nhieu, N.; Hsu, H. A prospect theory extension of data envelopment analysis model for wave-wind energy site selection in New Zealand. Manag. Decis. Econ. 2023, 45, 539–553. [Google Scholar] [CrossRef]
- Wakeyama, T.; Ehara, S. Renewable Energy Potential Evaluation and Analysis for Use by using GIS—A Case Study of Northern-Tohoku Area and Tokyo Metropolis, Japan. Int. J. Environ. Sci. Dev. 2010, 1, 446–453. [Google Scholar] [CrossRef]
- Besser, A.; Kazak, J.K.; Świąder, M.; Szewrański, S. A Customized Decision Support System for Renewable Energy Application by Housing Association. Sustainability 2019, 11, 4377. [Google Scholar] [CrossRef]
- Ottenburger, S.S.; Möhrle, S.; Müller, T.O.; Raskob, W. A Novel MCDA-Based Methodology Dealing with Dynamics and Ambiguities Resulting from Citizen Participation in the Context of the Energy Transition. Algorithms 2022, 15, 47. [Google Scholar] [CrossRef]
- Wilkens, I.; Schmuck, P. Transdisciplinary Evaluation of Energy Scenarios for a German Village Using Multi-Criteria Decision Analysis. Sustainability 2012, 4, 604–629. [Google Scholar] [CrossRef]
- Zsembinszki, G.; Fernández, A.G.; Cabeza, L.F. Selection of the Appropriate Phase Change Material for Two Innovative Compact Energy Storage Systems in Residential Buildings. Appl. Sci. 2020, 10, 2116. [Google Scholar] [CrossRef]
- Tietze, I.; Lazar, L.; Hottenroth, H.; Lewerenz, S. LAEND: A Model for Multi-Objective Investment Optimisation of Residential Quarters Considering Costs and Environmental Impacts. Energies 2020, 13, 614. [Google Scholar] [CrossRef]
- Horschig, T.; Thrän, D. Are decisions well supported for the energy transition? A review on modeling approaches for renewable energy policy evaluation. Energy, Sustain. Soc. 2017, 7, 5. [Google Scholar] [CrossRef]
- Li, Q.; Lin, T.; Yu, Q.; Du, H.; Li, J.; Fu, X. Review of Deep Reinforcement Learning and Its Application in Modern Renewable Power System Control. Energies 2023, 16, 4143. [Google Scholar] [CrossRef]
- Zhang, S.-F.; Liu, S.-Y.; Zhai, R.-H. An extended GRA method for MCDM with interval-valued triangular fuzzy assessments and unknown weights. Comput. Ind. Eng. 2011, 61, 1336–1341. [Google Scholar] [CrossRef]
- Chang, D.-Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Ruzgys, A.; Volvačiovas, R.; Ignatavičius, Č.; Turskis, Z. Integrated Evaluation of External Wall Insulation in Residential Buildings Using Swara-Todim MCDM Method. J. Civ. Eng. Manag. 2014, 20, 103–110. [Google Scholar] [CrossRef]
- Thịnh, N.N.; Nguyên, Đ.V.; Lê Thị Phụng, N.T.B. Nghiên cứu xác định năng lượng sóng biển khu vực Nam Trung Bộ. Tạp Chí Khí Tượng Thuỷ Văn 2021, 722, 59–67. [Google Scholar]
- Trung, P. Dòng Năng Lượng Sóng Hướng Bờ Và Dọc Bờ Biển Nam Trung Bộ. Tạp Chí Khoa Học Và Công Nghệ Thủy Lợi 2019, 52, 1–8. [Google Scholar]
- Marinescu, M.; Olivares, A.; Staffetti, E.; Sun, J. Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression for Wind Velocity Field Estimation from Aircraft-Derived Data. Mathematics 2023, 11, 1018. [Google Scholar] [CrossRef]
- Amir, H.F.A.; Chee, F.P. Full Scale Measurement of Wind Intensity Using in situ Method. J. Clean Energy Technol. 2014, 2, 295–298. [Google Scholar] [CrossRef]
- Ghosh, S.; Chakraborty, T.; Saha, S.; Majumder, M.; Pal, M. Development of the location suitability index for wave energy production by ANN and MCDM techniques. Renew. Sustain. Energy Rev. 2016, 59, 1017–1028. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nhieu, N.-L.; Nguyen, H.-P.; Wang, J.-W. Simulation-Based Optimization Integrated Multiple Criteria Decision-Making Framework for Wave Energy Site Selection: A Case Study of Australia. IEEE Access 2021, 9, 167458–167476. [Google Scholar] [CrossRef]
- Vasileiou, M.; Loukogeorgaki, E.; Vagiona, D.G. GIS-based multi-criteria decision analysis for site selection of hybrid offshore wind and wave energy systems in Greece. Renew. Sustain. Energy Rev. 2017, 73, 745–757. [Google Scholar] [CrossRef]
- Jiang, B.; Xu, Z.; Yang, S.; Chen, Y.; Ren, Q. Profile Autonomous Underwater Vehicle System for Offshore Surveys. Sensors 2023, 23, 3722. [Google Scholar] [CrossRef]
- Poort, J.; Lucazeau, F.; Le Gal, V.; Cin, M.D.; Leroux, E.; Bouzid, A.; Rabineau, M.; Palomino, D.; Battani, A.; Akhmanov, G.G.; et al. Heat flow in the Western Mediterranean: Thermal anomalies on the margins, the seafloor and the transfer zones. Mar. Geol. 2020, 419, 106064. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Etemad-Shahidi, A.; Stewart, R.A. Site Selection of Combined Offshore Wind and Wave Energy Farms: A Systematic Review. Energies 2023, 16, 2074. [Google Scholar] [CrossRef]
- Nambiar, A.; Draycott, S.; Payne, G.S.; Sellar, B.; Kiprakis, A. Influence of tidal turbine control on performance and loads. Appl. Ocean Res. 2021, 114, 102806. [Google Scholar] [CrossRef]
- Ghosh, S. Wave energy potential site selection based on MCDM and neural network analysis. In Application of Geographical Information Systems and Soft Computation Techniques in Water and Water Based Renewable Energy Problems; Springer: Singapore, 2018; pp. 107–120. [Google Scholar]
- Chakraborty, T. A MCDM-NBO approach for selection of installation location for wave energy power plants. In Application of Geographical Information Systems and Soft Computation Techniques in Water and Water Based Renewable Energy Problems; Springer: Singapore, 2018; pp. 121–140. [Google Scholar]
- Shao, M.; Zhang, S.; Sun, J.; Han, Z.; Shao, Z.; Yi, C. GIS-MCDM-Based Approach to Site Selection of Wave Power Plants for Islands in China. Energies 2022, 15, 4118. [Google Scholar] [CrossRef]
- Chen, Z.-Y.; Chu, Y.-H.; Su, C.-L. Intercomparisons of Tropospheric Wind Velocities Measured by Multi-Frequency Wind Profilers and Rawinsonde. Atmosphere 2021, 12, 1284. [Google Scholar] [CrossRef]
- Zhong, J.; Liu, J.; Liang, G. Mean Wind Velocity Distribution at Near-ground Level Obtained Through Field Measurements. In Proceedings of the 16th ROOMVENT Conference (ROOMVENT 2022), E3S Web of Conferences, Xi’an, China, 16–19 September 2022; Volume 356, p. 04003. [Google Scholar]
- Medvedev, A.V.; Ratovsky, K.G.; Tolstikov, M.V.; Vasilyev, R.V.; Artamonov, M.F. Method for Determining Neutral Wind Velocity Vectors Using Measurements of Internal Gravity Wave Group and Phase Velocities. Atmosphere 2019, 10, 546. [Google Scholar] [CrossRef]
- Kale, S.A.; Godse, R.V.; Haribhau, G.P. Performance Evaluation of Small Wind Turbine Diffusers with Different Diameters. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 1077–1080. [Google Scholar] [CrossRef]
- Castro-Santos, L.; Filgueira-Vizoso, A. The decarbonisation of Galicia using renewable marine energy. Renew. Energy Power Qual. J. 2023, 19, 115–120. [Google Scholar] [CrossRef]
- Zirek, E.; Sunar, F. Change Detection of Seafloor Topography by Modeling Multitemporal Multibeam Echosounder Measurements. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-7, 221–227. [Google Scholar] [CrossRef]
- Jeong, M.-H.; Jeon, S.-B.; Lee, T.-Y.; Youm, M.K.; Lee, D.-H. Vessel Trajectory Reconstruction Based on Functional Data Analysis Using Automatic Identification System Data. Appl. Sci. 2020, 10, 881. [Google Scholar] [CrossRef]
- Tu, E.; Zhang, G.; Rachmawati, L.; Rajabally, E.; Huang, G.-B. Exploiting AIS Data for Intelligent Maritime Navigation: A Comprehensive Survey from Data to Methodology. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1559–1582. [Google Scholar] [CrossRef]
- Wu, L.; Xu, Y.; Wang, Q.; Wang, F.; Xu, Z. Mapping Global Shipping Density from AIS Data. J. Navig. 2016, 70, 67–81. [Google Scholar] [CrossRef]
- Medvedev, A.; Ratovsky, K.; Tolstikov, M.; Alsatkin, S.; Shcherbakov, A. A statistical study of internal gravity wave characteristics using the combined Irkutsk Incoherent Scatter Radar and Digisonde data. J. Atmos. Solar-Terr. Phys. 2015, 132, 13–21. [Google Scholar] [CrossRef]
- Greig, N.C.; Hines, E.M.; Cope, S.; Liu, X. Using Satellite AIS to Analyze Vessel Speeds Off the Coast of Washington State, U.S., as a Risk Analysis for Cetacean-Vessel Collisions. Front. Mar. Sci. 2020, 7, 109. [Google Scholar] [CrossRef]
- Goerlandt, F.; Montewka, J. Maritime transportation risk analysis: Review and analysis in light of some foundational issues. Reliab. Eng. Syst. Saf. 2015, 138, 115–134. [Google Scholar] [CrossRef]
- Tercan, E.; Tapkın, S.; Latinopoulos, D.; Dereli, M.A.; Tsiropoulos, A.; Ak, M.F. A GIS-based multi-criteria model for offshore wind energy power plants site selection in both sides of the Aegean Sea. Environ. Monit. Assess. 2020, 192, 652. [Google Scholar] [CrossRef] [PubMed]
- Oh, H.-T.; Chung, Y.; Jeon, G.; Shim, J. Review of the marine environmental impact assessment reports regarding offshore wind farm. Fish. Aquat. Sci. 2021, 24, 341–350. [Google Scholar] [CrossRef]
- Spyridonidou, S.; Vagiona, D.G. Systematic Review of Site-Selection Processes in Onshore and Offshore Wind Energy Research. Energies 2020, 13, 5906. [Google Scholar] [CrossRef]
- Juhola, S.; Laurila, A.; Groundstroem, F.; Klein, J. Climate risks to the renewable energy sector: Assessment and adaptation within energy companies. Bus. Strat. Environ. 2023, 33, 1906–1919. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.; Hu, Y.; Ke, Y.; Li, L. An extended TODIM-PROMETHEE method for waste-to-energy plant site selection based on sustainability perspective. Energy 2018, 156, 1–16. [Google Scholar] [CrossRef]

| Location | Information | Description |
|---|---|---|
| Location 1 (A1) | Near Quang Ngai, central Vietnam, along the South China Sea. | Strong wave activity influenced by the northeast monsoon; proximity to Quang Ngai city supports logistical and operational. Mean Wave Height Estimate: 1.5–2.5 m during the monsoon season; 0.5–1.5 m during calmer periods. |
| Location 2 (A2) | Close to Quy Nhon, a coastal city in Binh Dinh province | Consistent wave activity; relatively deep waters close to shore; accessible via major roads and port infrastructure. Mean Wave Height Estimate: 1.2–2.0 m during the monsoon season; 0.5–1.2 m during the rest of the year. |
| Location 3 (A3) | South of Quy Nhon, near the coastline of Phu Yen province | Rugged coastline with strong, consistent wave patterns; remote location reduces competing coastal development pressures. Mean Wave Height Estimate: 1.8–3.0 m during the monsoon season; 1.0–2.0 m in calmer conditions. |
| No | Main Criteria | Sub-Criteria | Interpretation | Source |
|---|---|---|---|---|
| 1 | Efficiency Potential | Ocean salinity levels (SCS01) | Salinity affects the density and electrical conductivity of seawater, which can influence the performance and durability of materials in wave energy converters (WECs). | [35,36,37,38] |
| Ocean currents treadmill (SCS02) | Refers to the continuous movement of ocean currents. These currents can impact the efficiency of wave energy systems and need to be accounted for in the site selection. | [35,36,39] | ||
| Ocean floor configuration and anchorage Facilities (SCS03) | The layout of the ocean floor affects the installation and stability of WECs. Anchorage facilities ensure the secure positioning of devices. | [40,41,42] | ||
| 2 | Technological | Significant wave height (SCS04) | The average height of the highest one-third of waves over a set period, which helps evaluate the energy generation potential and structural resilience required for WECs. | [21,37,38,43,44,45,46] |
| Wind velocity (SCS05) | The speed of the wind, which directly influences wave height, frequency, and energy potential. | [37,45,46,47,48,49,50] | ||
| Wind duration (SCS06) | The length of time the wind blows over the water surface. Longer durations result in higher waves and more wave energy. | [48,49] | ||
| Wave amplitude (SCS07) | The vertical distance between a wave‘s crest and its resting state. Larger amplitudes indicate higher energy potential. | [21,43,45,51,52] | ||
| 3 | Transport and Environment | Coastal erosion (SCS08) | The degradation of coastlines can influence site stability and accessibility for the maintenance and operation of wave energy projects. | [53,54] |
| Shipping density (SCS09) | High shipping activity in a region can lead to safety and logistical challenges for deploying WECs | [55] | ||
| Geological disaster (SCS10) | Specific climate conditions (temperature, storms, and seasonal variability) affect the design, durability, and operational lifespan of WECs. | [44,56,57] | ||
| 4 | Economic and Social | Protection law (SCS11) | Legal frameworks and regulations for protecting marine ecosystems and ensuring compliance with environmental and operational standards. | [58,59,60] |
| Labor resource (SCS12) | Availability of skilled and unskilled labor for the installation, operation, and maintenance of wave energy projects. | [61] | ||
| Safety condition (SCS13) | Includes measures to ensure the safety of workers, equipment, and nearby marine activities during the installation and operation of WECs. | [61,62] | ||
| Tourism potential (SCS14) | Refers to the extent to which the project impacts local tourism, including both positive and negative effects. | [37,38,47] |
| No | Criteria | Fuzzy Geometric Mean of Each Row | Fuzzy Weights | BNP | Normalization | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | SCS01 | 0.8004 | 1.1244 | 1.5413 | 0.0403 | 0.0760 | 0.1408 | 0.0857 | 0.0764 |
| 2 | SCS02 | 0.7485 | 1.0359 | 1.4188 | 0.0377 | 0.0701 | 0.1296 | 0.0791 | 0.0705 |
| 3 | SCS03 | 0.8375 | 1.1621 | 1.5889 | 0.0422 | 0.0786 | 0.1451 | 0.0886 | 0.0790 |
| 4 | SCS04 | 0.7493 | 1.0302 | 1.4073 | 0.0377 | 0.0697 | 0.1285 | 0.0786 | 0.0701 |
| 5 | SCS05 | 1.8478 | 2.4160 | 3.0743 | 0.0930 | 0.1634 | 0.2808 | 0.1791 | 0.1596 |
| 6 | SCS06 | 0.6413 | 0.8641 | 1.1715 | 0.0323 | 0.0584 | 0.1070 | 0.0659 | 0.0588 |
| 7 | SCS07 | 0.9403 | 1.2731 | 1.6788 | 0.0473 | 0.0861 | 0.1533 | 0.0956 | 0.0852 |
| 8 | SCS08 | 0.7708 | 1.0392 | 1.3776 | 0.0388 | 0.0703 | 0.1258 | 0.0783 | 0.0698 |
| 9 | SCS09 | 0.7136 | 0.9508 | 1.2634 | 0.0359 | 0.0643 | 0.1154 | 0.0719 | 0.0641 |
| 10 | SCS10 | 0.6229 | 0.8337 | 1.1397 | 0.0314 | 0.0564 | 0.1041 | 0.0639 | 0.0570 |
| 11 | SCS11 | 0.5736 | 0.7690 | 1.0628 | 0.0289 | 0.0520 | 0.0971 | 0.0593 | 0.0529 |
| 12 | SCS12 | 0.6923 | 0.9348 | 1.2653 | 0.0349 | 0.0632 | 0.1156 | 0.0712 | 0.0635 |
| 13 | SCS13 | 0.5348 | 0.7172 | 0.9898 | 0.0269 | 0.0485 | 0.0904 | 0.0553 | 0.0493 |
| 14 | SCS14 | 0.4763 | 0.6353 | 0.8824 | 0.0240 | 0.0430 | 0.0806 | 0.0492 | 0.0438 |
| Location 1 (A1) | Location 2 (A2) | Location 3 (A3) | |
|---|---|---|---|
| SCS01 | 0.3333 | 0.3333 | 0.3333 |
| SCS02 | 0.3333 | 0.2857 | 0.3810 |
| SCS03 | 0.3182 | 0.2727 | 0.4091 |
| SCS04 | 0.3500 | 0.3500 | 0.3000 |
| SCS05 | 0.2857 | 0.2857 | 0.4286 |
| SCS06 | 0.3500 | 0.4000 | 0.2500 |
| SCS07 | 0.3077 | 0.3462 | 0.3462 |
| SCS08 | 0.3333 | 0.3333 | 0.3333 |
| SCS09 | 0.3600 | 0.2800 | 0.3600 |
| SCS10 | 0.3043 | 0.3043 | 0.3913 |
| SCS11 | 0.3333 | 0.2857 | 0.3810 |
| SCS12 | 0.3182 | 0.2727 | 0.4091 |
| SCS13 | 0.3913 | 0.2609 | 0.3478 |
| SCS14 | 0.3478 | 0.2609 | 0.3913 |
| Location 1 (A1) | Location 2 (A2) | Location 3 (A3) | |
|---|---|---|---|
| Location 1 (A1) | 0.0000 | −1.1590 | −7.7067 |
| Location 2 (A2) | −7.4166 | 0.0000 | −11.4822 |
| Location 3 (A3) | −2.4973 | −1.6585 | 0.0000 |
| Alternatives | Global Dominance G(ai) | Relative Overall Value V(ai) | Ranking |
|---|---|---|---|
| Location 1 (A1) | −8.8657 | 0.6805 | 2 |
| Location 2 (A2) | −18.8988 | 0.0000 | 3 |
| Location 3 (A3) | −4.1558 | 1.0000 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kongklad, G.; Thanh, N.V.; Pattanaporkratana, A.; Chattham, N.; Jeenanunta, C. A Data-Driven Decision Support System for Wave Power Plant Location Selection. Water 2025, 17, 948. https://doi.org/10.3390/w17070948
Kongklad G, Thanh NV, Pattanaporkratana A, Chattham N, Jeenanunta C. A Data-Driven Decision Support System for Wave Power Plant Location Selection. Water. 2025; 17(7):948. https://doi.org/10.3390/w17070948
Chicago/Turabian StyleKongklad, Gunganist, Nguyen Van Thanh, Apichart Pattanaporkratana, Nattaporn Chattham, and Chawalit Jeenanunta. 2025. "A Data-Driven Decision Support System for Wave Power Plant Location Selection" Water 17, no. 7: 948. https://doi.org/10.3390/w17070948
APA StyleKongklad, G., Thanh, N. V., Pattanaporkratana, A., Chattham, N., & Jeenanunta, C. (2025). A Data-Driven Decision Support System for Wave Power Plant Location Selection. Water, 17(7), 948. https://doi.org/10.3390/w17070948










