A Two-Stage, Self-Pressure-Controlled Smart Manhole System with Motor-Driven and Lifting Mechanisms for Enhanced Flood Disaster Preparedness
Abstract
:1. Introduction
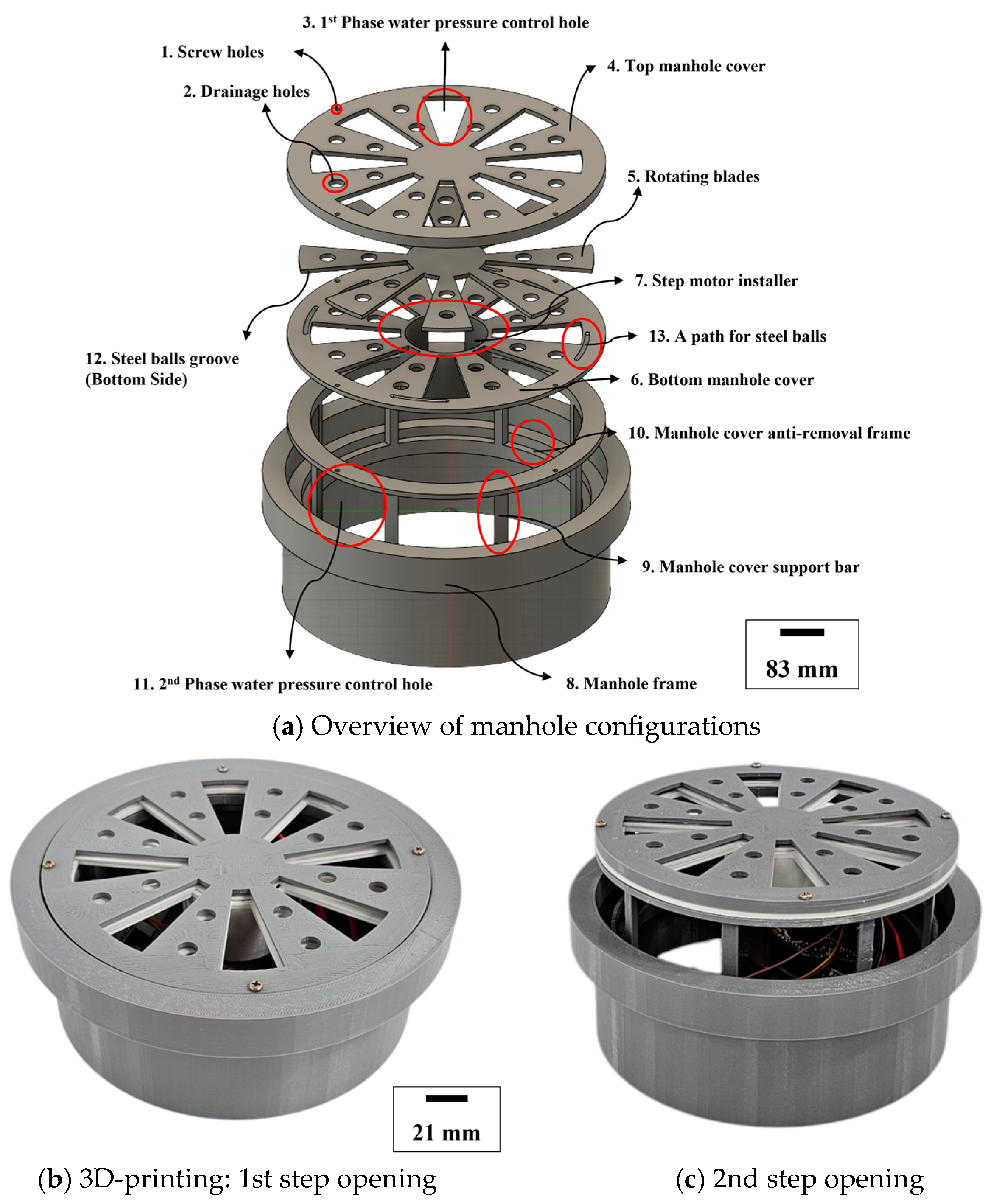
- Motor-Driven Rotating Blade: In the first stage, a rotating blade assembly enlarges the drainage pathway, mitigating initial pressure buildup.
- Controlled Vertical Lift: Under extremely high backflow pressure, the manhole cover lifts by a defined amount, dispersing any residual surge while minimizing obstruction to traffic or pedestrians.
2. Smart Manhole Solution and Analysis
2.1. Three-Dimensional Printing Fabrication and Control Algorithm
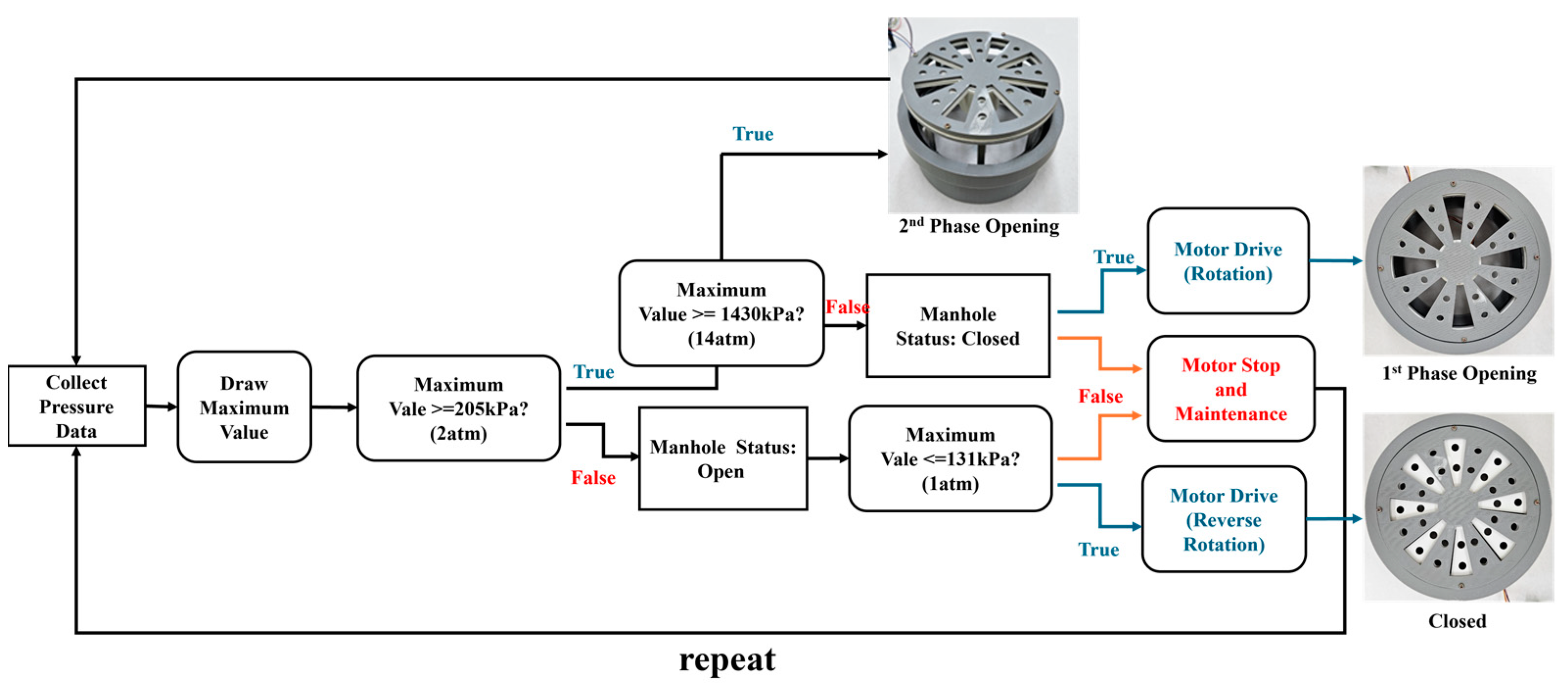
- First Threshold Check (2 atm/205 kPa)
- ○
- If the maximum measured pressure is at least 205 kPa, the system sets the manhole to “open” status (i.e., first-phase control). While the manhole is open, if the measured pressure later drops to or below 131 kPa (safe level), the stepper motor rotates in reverse, returning the manhole to “closed”. Conversely, if the manhole is open and the pressure remains above 131 kPa, the motor stops and a maintenance state is triggered.
- Second Threshold Check (14 atm/1430 kPa)
- ○
- If the sensor—located approximately two meters below the manhole cover—detects a maximum pressure below 205 kPa (i.e., not meeting the threshold for first-phase, motor-driven control), the system then checks whether the pressure exceeds 1430 kPa (14 atm). Upon reaching or surpassing this level, the manhole cover naturally rises in response to the hydraulic force, triggering the second-phase control. In this elevated position, the cover remains “closed” from above to withstand extremely high internal pressures. Depending on subsequent flow conditions, the motor may either initiate or shut off. This dual-step approach ensures a rapid response to abrupt surges—providing an early opportunity for the motorized system to relieve pressure—while still maintaining a fail-safe mechanism if the first-phase control proves insufficient.
2.2. Theoretical Basis
2.3. Computational Fluid Dynamics
3. Results
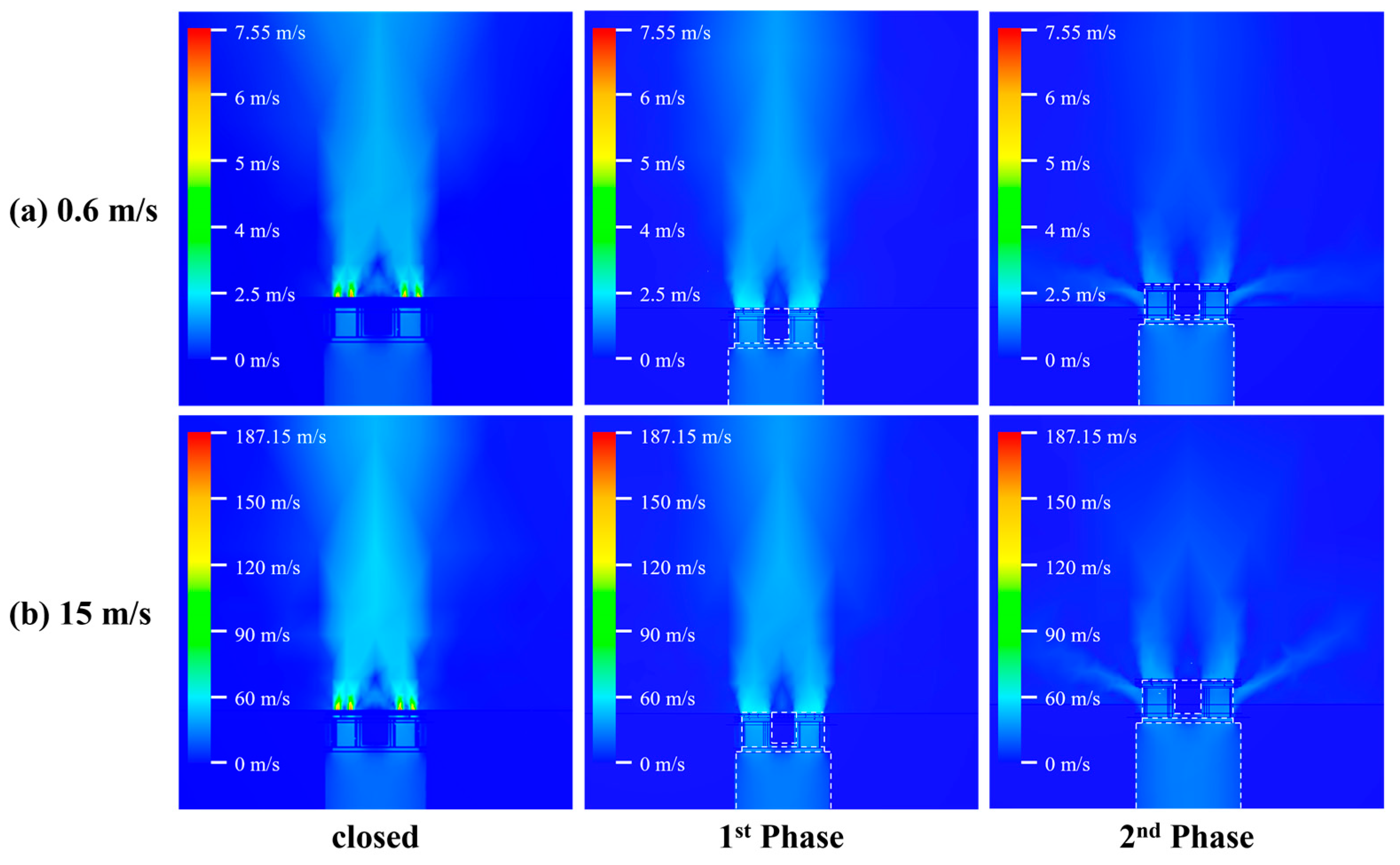
3.1. Simulation Results
3.2. Analysis of Calculated Hydraulic Pressure Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| FIRM | Flood Inundation and Recession Model |
| GIS | Geographic Information System |
| k–ε | k-epsilon (turbulence model) |
| kPa | Kilopascal |
| mm/h | Millimeters per hour |
| m/s | Meters per second |
| PIV | Particle Image Velocimetry |
| PISO | Pressure-Implicit with Splitting of Operators |
| SWMM | Storm Water Management Model |
| VOF | Volume of Fluid |
Nomenclatures
| A | Cross-sectional area, m2 |
| E | Total energy (in fluid flow/thermodynamics), J/kg |
| g | Gravitational acceleration, m/s2 |
| h | Hydraulic head (water column height), m |
| I | Moment of inertia |
| k | Turbulent kinetic energy (in k–ε model), m2/s2 |
| p | Pressure (general/dynamic, depending on context), Pa or kPa |
| Pr | Prandtl number, - |
| Q | Flow rate, m3/s |
| t | Time, s |
| Ui | Velocity vector components, m/s |
| v | Flow velocity, m/s |
| α | Angular acceleration, rad/s2 |
| δij | Kronecker delta |
| ε | Turbulent dissipation rate (in k–ε model), m2/s3 |
| μ | Dynamic viscosity, Pa·s |
| μt | Turbulent viscosity, Pa·s |
| ρ | Density of fluid, kg/m3 |
| τ | Torque, J/rad |
| θ | Angle, rad |
| ω | Angular velocity, rad/s |
References
- Kim, T.-H. The Risk of Manhole Cover Displacement Due to Heavy Rainfall? National Disaster and Safety Research Institute of Republic of Korea. 2014. Available online: https://www.mois.go.kr/frt/bbs/type010/commonSelectBoardArticle.do?bbsId=BBSMSTR_000000000008&nttId=42694 (accessed on 23 July 2014).
- The Hankyoreh. Torrential Downpour Turns Seoul’s Manholes into Death Traps. 2023. Available online: https://english.hani.co.kr/arti/english_edition/e_national/1054420.html (accessed on 11 August 2022).
- Wang, J.; Vasconcelos, J. Manhole Cover Displacement Caused by the Release of Entrapped Air Pockets; Auburn University: Auburn, AL, USA, 2018. [Google Scholar] [CrossRef]
- Heo, P. Manhole to Prevent Stormwater Backflow. KR102145783B1, Filed 4 July 2018, and Issued 12 August 2020. Available online: https://patents.google.com/patent/KR102145783B1/ko?inventor=%ED%97%88%ED%8F%89%EC%A7%84 (accessed on 26 March 2025).
- Kim, S. Flow Control Device for Stormwater Manholes. KR101301697B1, Filed 18 October 2011, and Issued 27 August 2013. Available online: https://patents.google.com/patent/KR101301697B1/ko?oq=KR101301697B1 (accessed on 15 November 2024).
- Kim, J. Stormwater Manhole with Infiltration-Type Flood Control Function. KR101962037B1, Filed 7 April 2017, and Issued 26 March 2019. Available online: https://patents.google.com/patent/KR101962037B1/ko?oq=KR101962037B1 (accessed on 26 March 2025).
- Choi, G. Backflow Prevention Device for Manhole Connected to Sewer Pipe. KR102008815B1, Filed 4 July 2019, and Issued 2 August 2019. Available online: https://patents.google.com/patent/KR102008815B1/ko?oq=KR102008815B1 (accessed on 15 November 2024).
- Lee, S. Double Manhole Cover with Hydraulic Pressure Adjustment Function. KR100987500B1, Filed 18 October 2011, and Issued 27 August 2013. Available online: https://patents.google.com/patent/KR100987500B1/ko?oq=KR100987500B1 (accessed on 26 March 2025).
- Nam, D. Manhole Cover for Preventing Displacement with Hydraulic Pressure Adjustment Function. KR101448569B1, Filed 18 February 2014, and Issued 1 October 2014. Available online: https://patents.google.com/patent/KR101448569B1/ko?q=(%EC%88%98%EC%95%95%EC%A1%B0%EC%A0%88%EA%B8%B0%EB%8A%A5%EC%9D%84%EA%B0%96%EB%8A%94%EC%9D%B4%ED%83%88%EB%B0%A9%EC%A7%80%EC%9A%A9%EB%A7%A8%ED%99%80%EB%9A%9C%EA%BB%91)&oq=%EC%88%98%EC%95%95%EC%A1%B0%EC%A0%88+%EA%B8%B0%EB%8A%A5%EC%9D%84+%EA%B0%96%EB%8A%94+%EC%9D%B4%ED%83%88%EB%B0%A9%EC%A7%80%EC%9A%A9+%EB%A7%A8%ED%99%80%EB%9A%9C%EA%BB%91 (accessed on 26 March 2025).
- Jeon, B.; Choi, K. Manhole Cover with Backflow Prevention Function. KR102619464B1, Filed 21 October 2022, and Issued 26 December 2023. Available online: https://patents.google.com/patent/KR102619464B1/ko?oq=KR102619464B1 (accessed on 26 March 2025).
- Lee, S.; Lee, Y. Design and Implementation of a Manhole Management System Using Wireless Communication. J. Digit. Ind. Inf. Stud. 2017, 13, 53–61. [Google Scholar]
- Lee, H. Design and Fabrication of a Manhole Floating Device Using 3D Printing and Structural Analysis. J. Korea Acad.-Ind. Coop. Soc. 2018, 19, 648–654. [Google Scholar]
- Gebregziabher, M.; Demissie, Y. Modeling Urban Flood Inundation and Recession Impacted by Manholes. Water 2020, 12, 1160. [Google Scholar] [CrossRef]
- Sifa, Y.B.; Baseka, V.G.; Masanja, M. Computational Fluid Dynamics of Manhole Overflow Due to Storm-water Inflow. J. Mekanika Indonesia 2020, 18, 33–48. [Google Scholar] [CrossRef]
- Mathurin, D.; Fuamba, M.; Mahdi, T.-F. Manhole Storage Capacity Influence on Transient Flow Modeling during Storm Sewer Flooding Event. J. Water Manag. Model. 2009, 17, 257–279. [Google Scholar] [CrossRef]
- Nabende, A.; Semwogerere, T.; Awichi, R.O. Mathematical Modelling of Sewage Overflow Through Pipe-Manhole Drainage Sewer Systems Using CFD: A Case of Mbale City, Eastern Uganda. East Afr. J. Eng. 2020, 2, 33–45. [Google Scholar] [CrossRef]
- Martins, R.; Rubinato, M.; Kesserwani, G.; Leandro, J.; Djordjević, S.; Shucksmith, J. On the Characteristics of Velocity Fields in the Vicinity of Manhole Inlet Grates During Flood Events. Water Resour. Res. 2018, 54, 6408–6422. [Google Scholar] [CrossRef]
- Beg, M.N.A.; Carvalho, R.F.; Lopes, P.; Leandro, J.; Melo, N. Numerical Investigation of the Flow Field inside a Manhole-Pipe Drainage System. In Proceedings of the Hydraulic Structures and Water System Management. 6th IAHR International Symposium on Hydraulic Structures, Portland, OR, USA, 27–30 June 2016; Crookston, B., Tullis, B., Eds.; USU Library: Logan, UT, USA, 2016; pp. 61–71, ISBN 978-1-884575-75-4. [Google Scholar] [CrossRef]
- Arao, S.; Mihara, T.; Kusuda, T. An Optimal Design Method of Storm Sewer Network Considered with Manhole Energy Loss. Doboku Gakkai Ronbunshu 1999, 1999, 109–120. [Google Scholar] [CrossRef] [PubMed]
- Munson, B.R. Fundamentals of Fluid Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kim, D.Y.; Lee, B.; Kim, M.; Moon, J.H. Thermal assessment of lithium-ion battery pack system with heat pipe assisted passive cooling using Simulink. Therm. Sci. Eng. Prog. 2023, 46, 102230. [Google Scholar] [CrossRef]

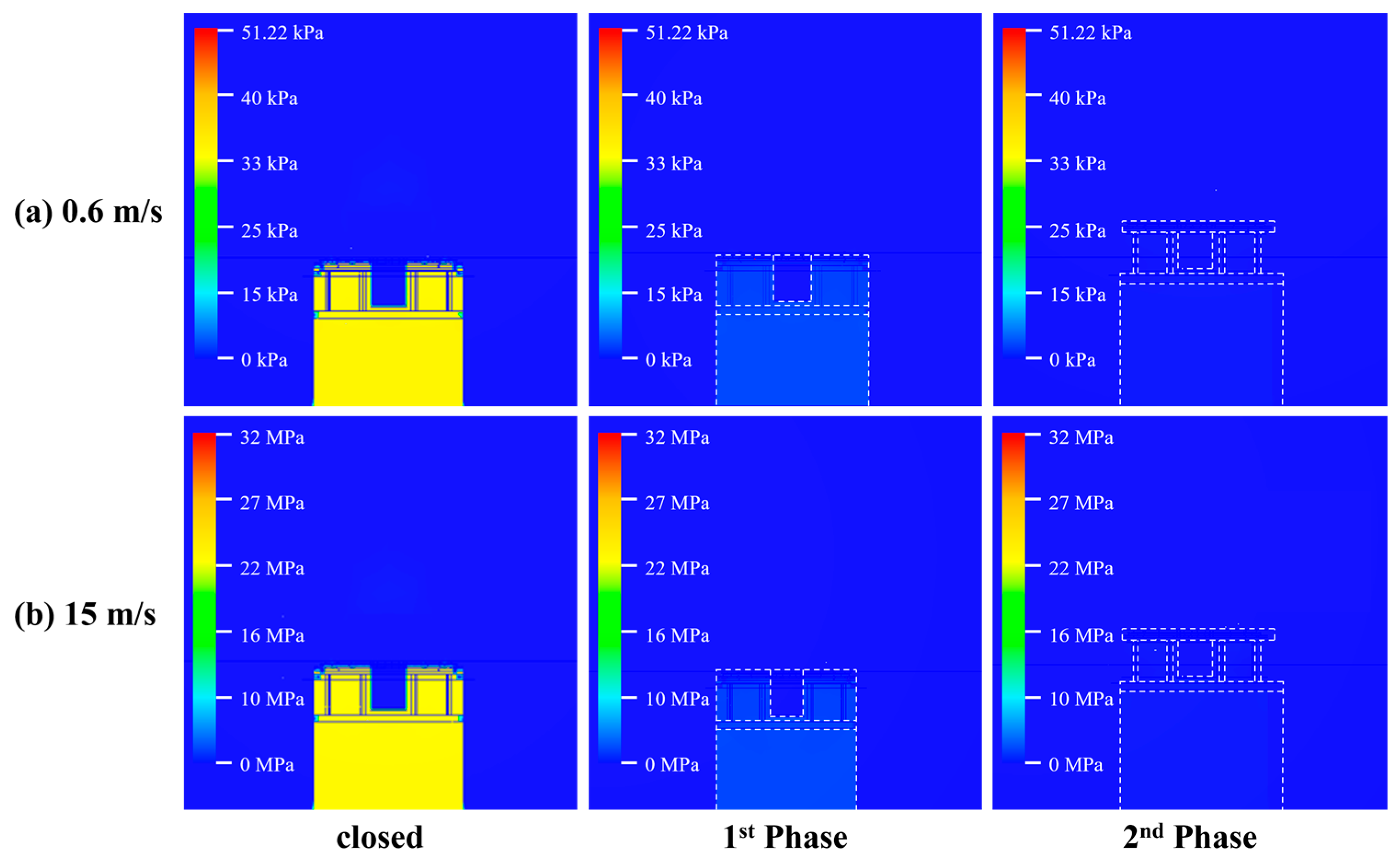
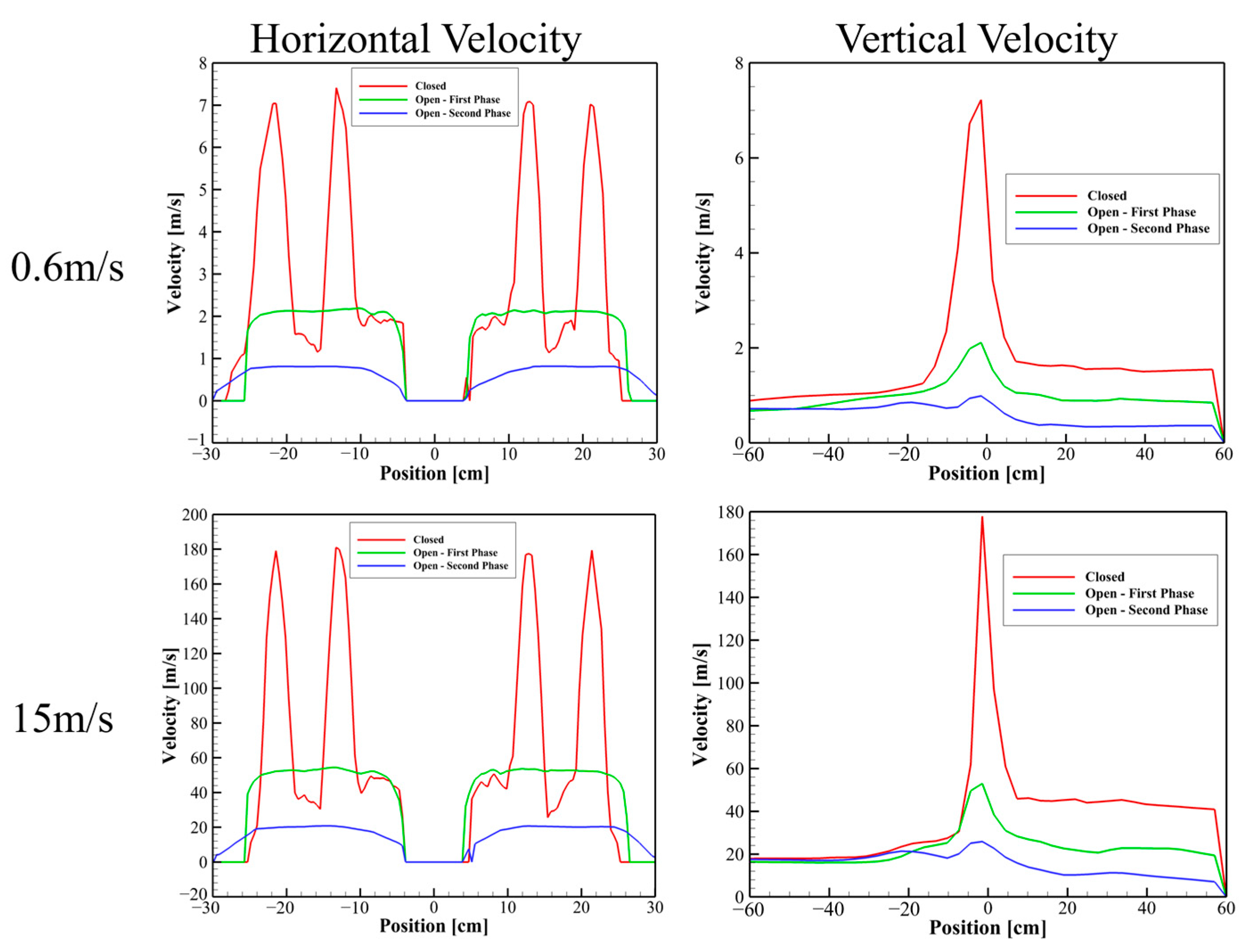
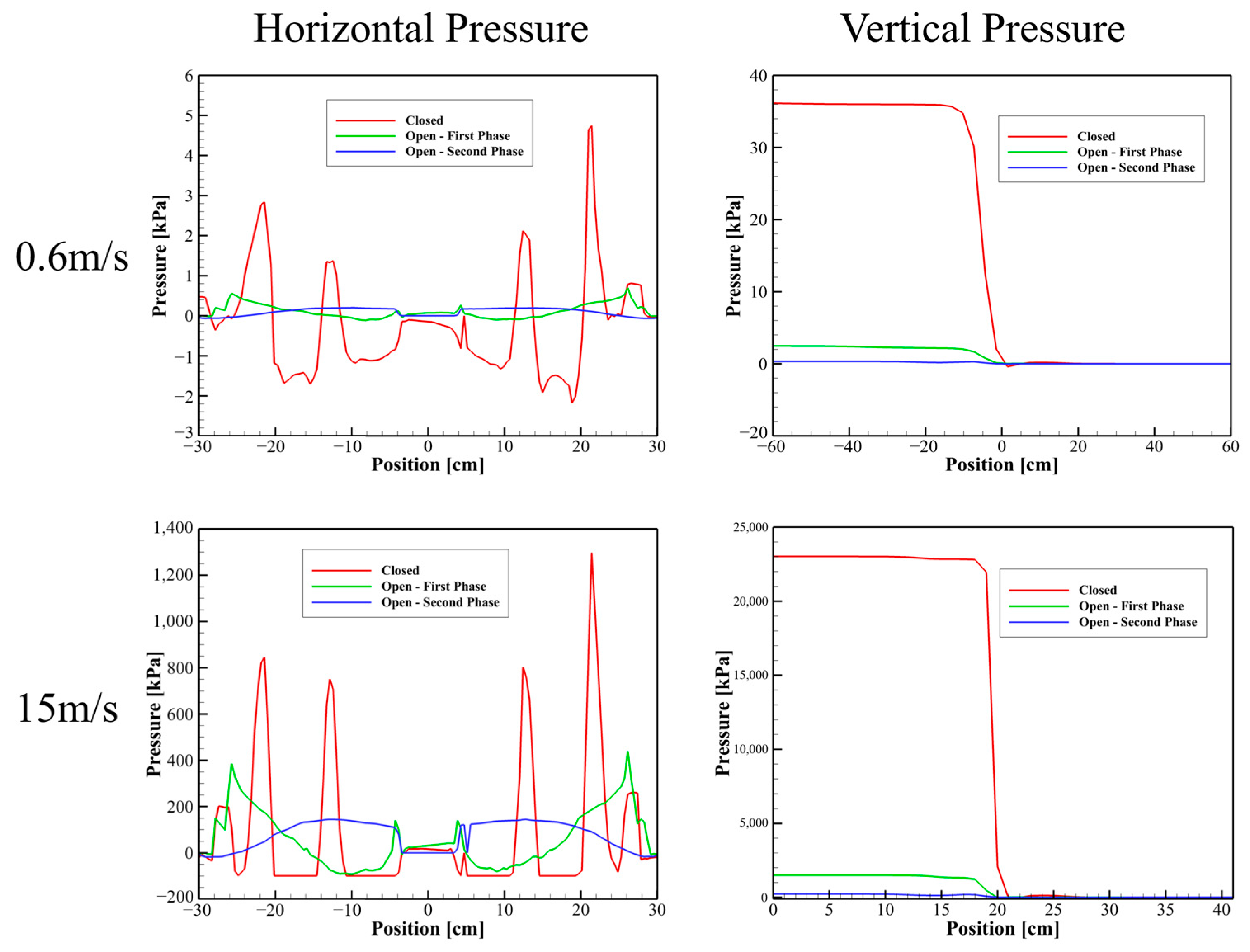
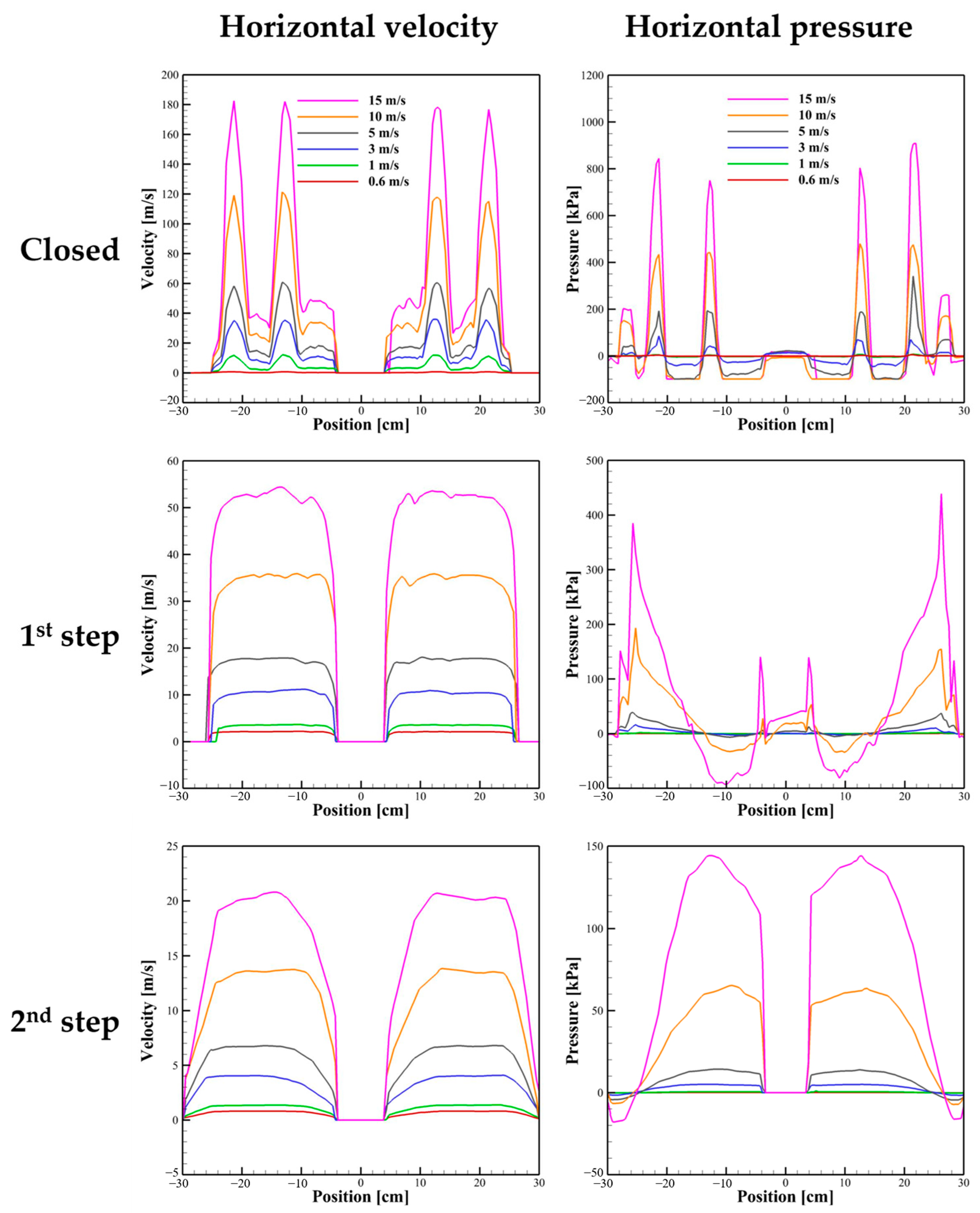
| Closed [kPa] | 1st Step [kPa] | 2nd Step [kPa] | |
|---|---|---|---|
| 0.6 m/s | 36.14 | 2.48 | 0.34 |
| 1 m/s | 101.07 | 7.01 | 0.97 |
| 3 m/s | 916.35 | 60.35 | 8.74 |
| 5 m/s | 2537.62 | 168.92 | 24.31 |
| 10 m/s | 10,138.40 | 678.20 | 104.29 |
| 15 m/s | 23,027.40 | 1511.71 | 237.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Lee, S.; Moon, J.-H. A Two-Stage, Self-Pressure-Controlled Smart Manhole System with Motor-Driven and Lifting Mechanisms for Enhanced Flood Disaster Preparedness. Water 2025, 17, 978. https://doi.org/10.3390/w17070978
Kim J, Lee S, Moon J-H. A Two-Stage, Self-Pressure-Controlled Smart Manhole System with Motor-Driven and Lifting Mechanisms for Enhanced Flood Disaster Preparedness. Water. 2025; 17(7):978. https://doi.org/10.3390/w17070978
Chicago/Turabian StyleKim, Jikyum, Sumin Lee, and Joo-Hyun Moon. 2025. "A Two-Stage, Self-Pressure-Controlled Smart Manhole System with Motor-Driven and Lifting Mechanisms for Enhanced Flood Disaster Preparedness" Water 17, no. 7: 978. https://doi.org/10.3390/w17070978
APA StyleKim, J., Lee, S., & Moon, J.-H. (2025). A Two-Stage, Self-Pressure-Controlled Smart Manhole System with Motor-Driven and Lifting Mechanisms for Enhanced Flood Disaster Preparedness. Water, 17(7), 978. https://doi.org/10.3390/w17070978








