Selection of a Turbulence Model for Wave Evolution on a New Ecological Hollow Cube
Abstract
:1. Introduction
2. Numerical Model
2.1. Governing Equations
2.2. Turbulence Models
2.2.1. Standard k-ε Model
2.2.2. Stabilized k-ω SST Model
2.2.3. Buoyancy-Modified k-ω SST Model
2.2.4. LES Model
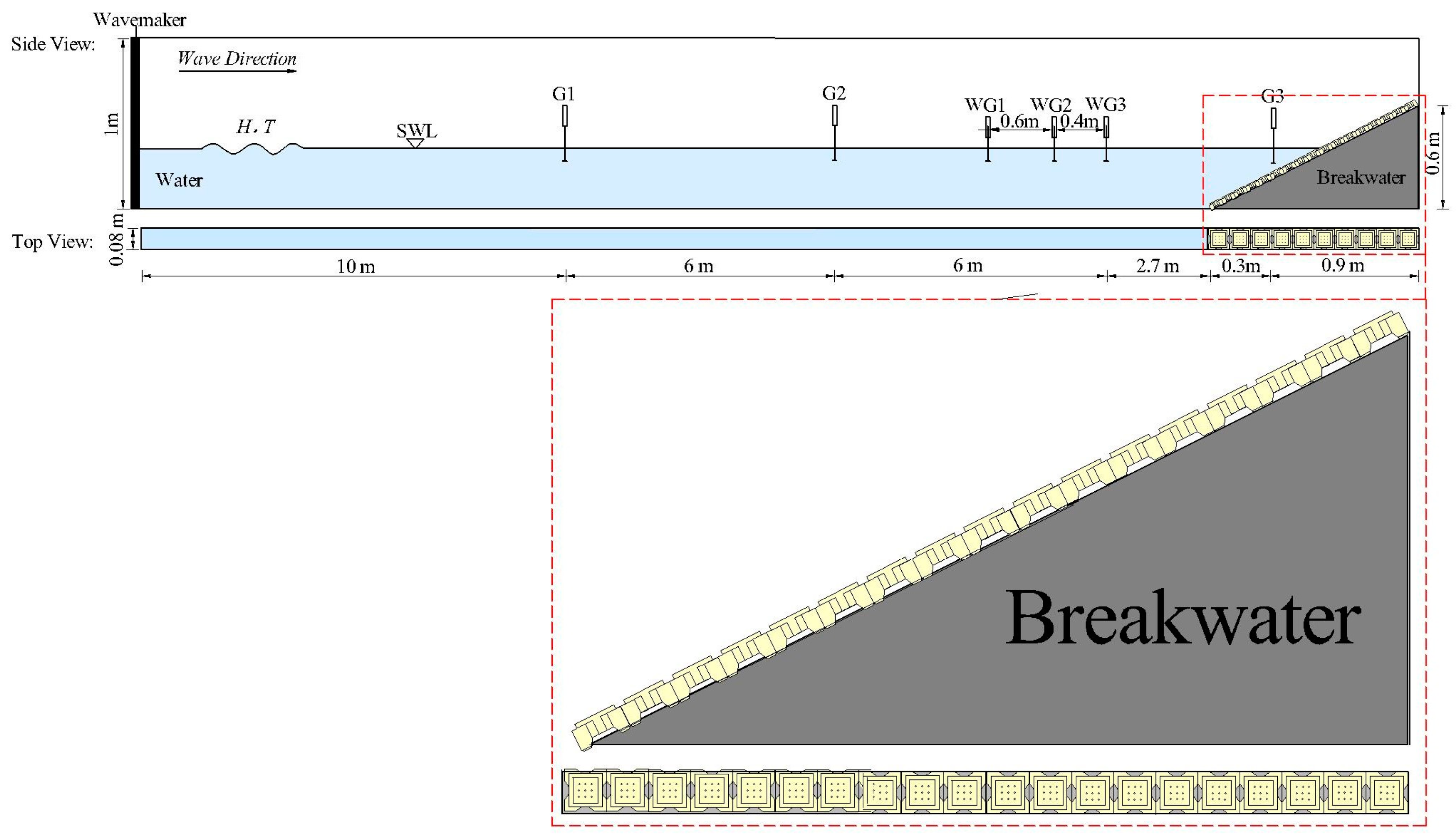
3. Geometric Model, Mesh, and Post Processing
3.1. The New Ecological Hollow Cube
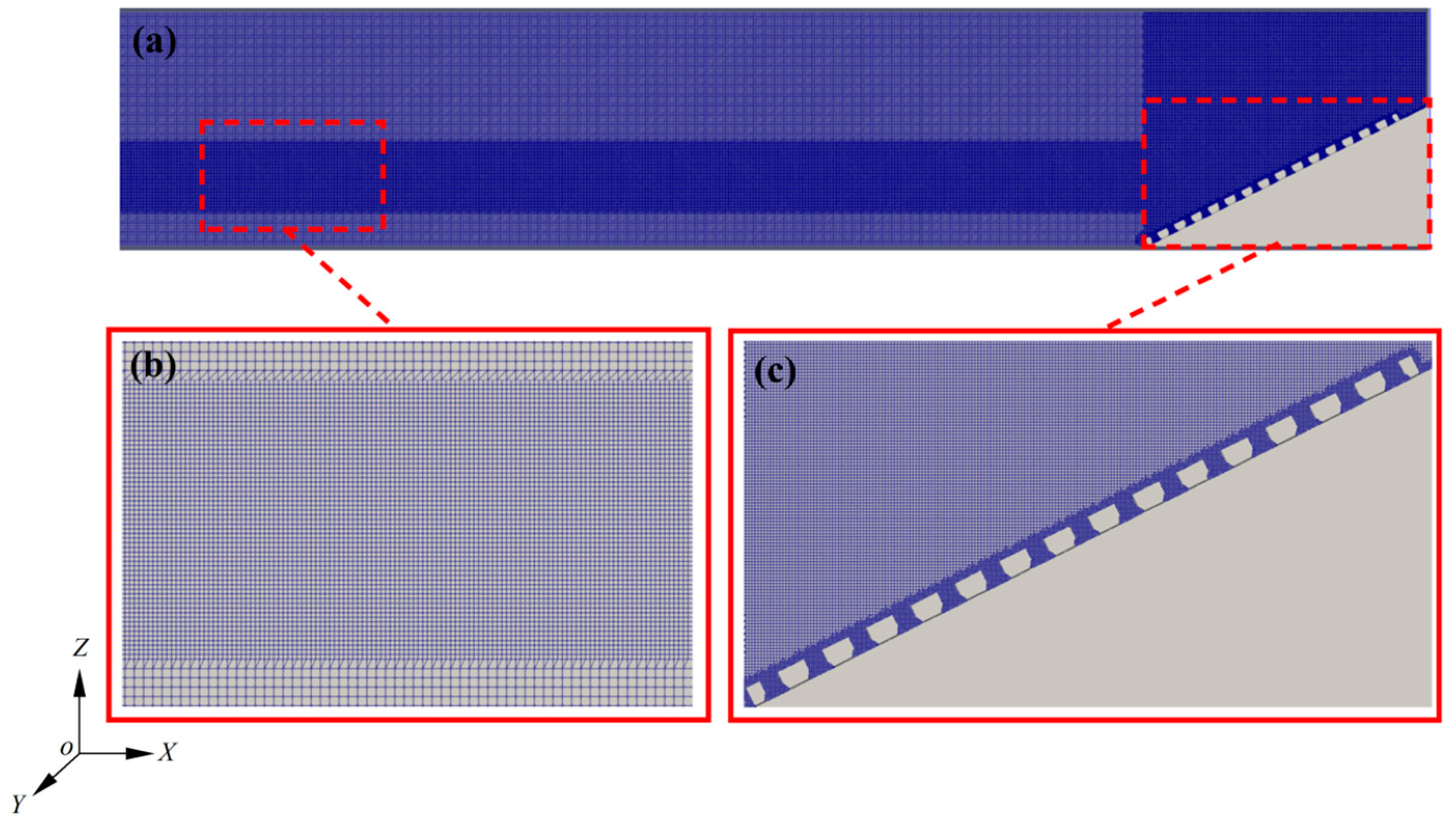
3.2. Mesh
3.3. Boundary Conditions
3.4. Post Processing of the Wave Run-Up and Reflection Coefficient
4. The Results and Discussion
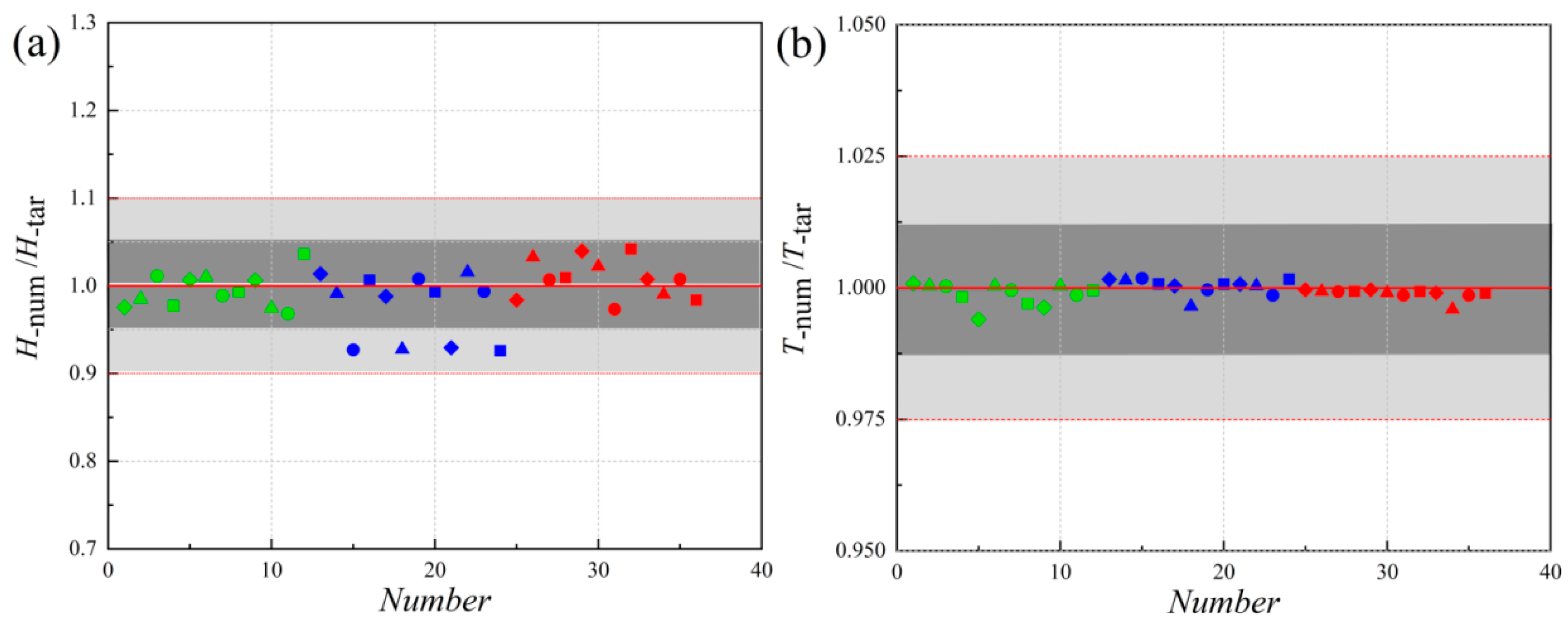
4.1. Wave Height and Period
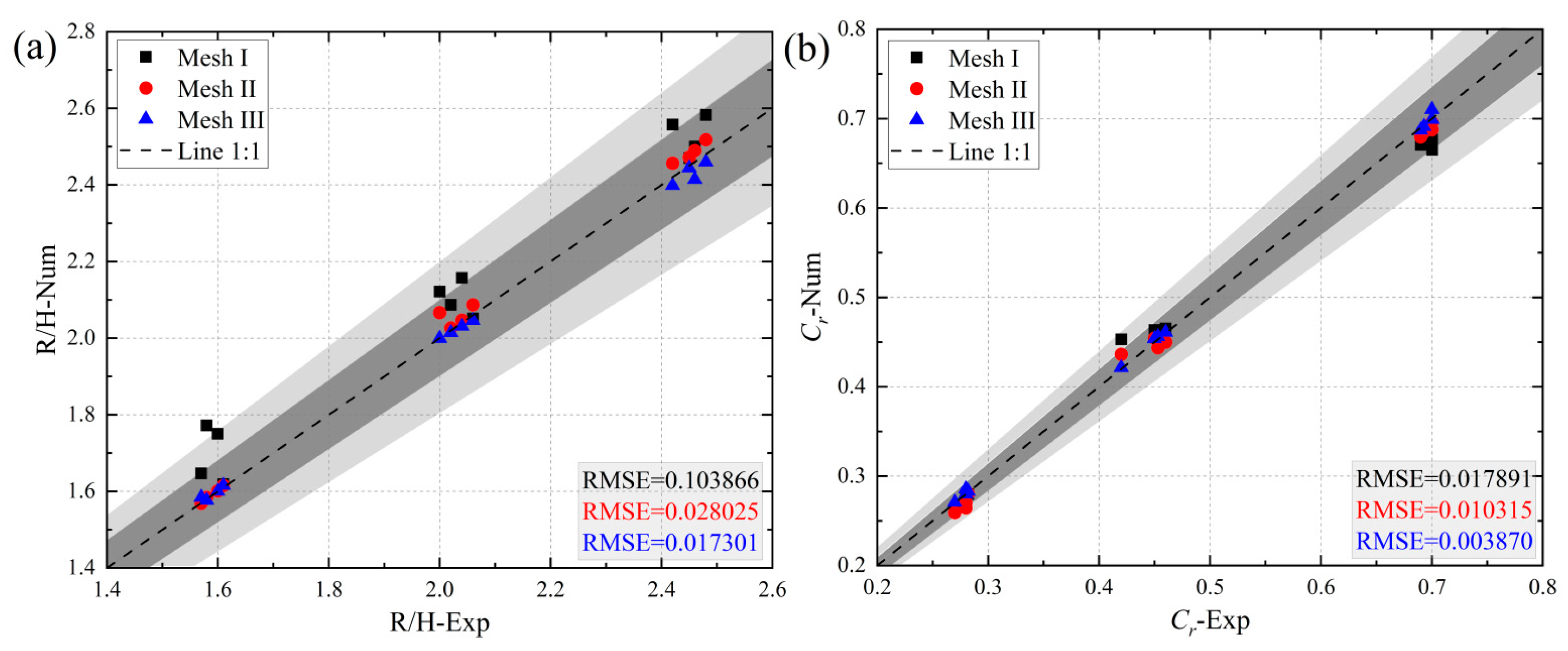
4.2. Validation of Numerical Model
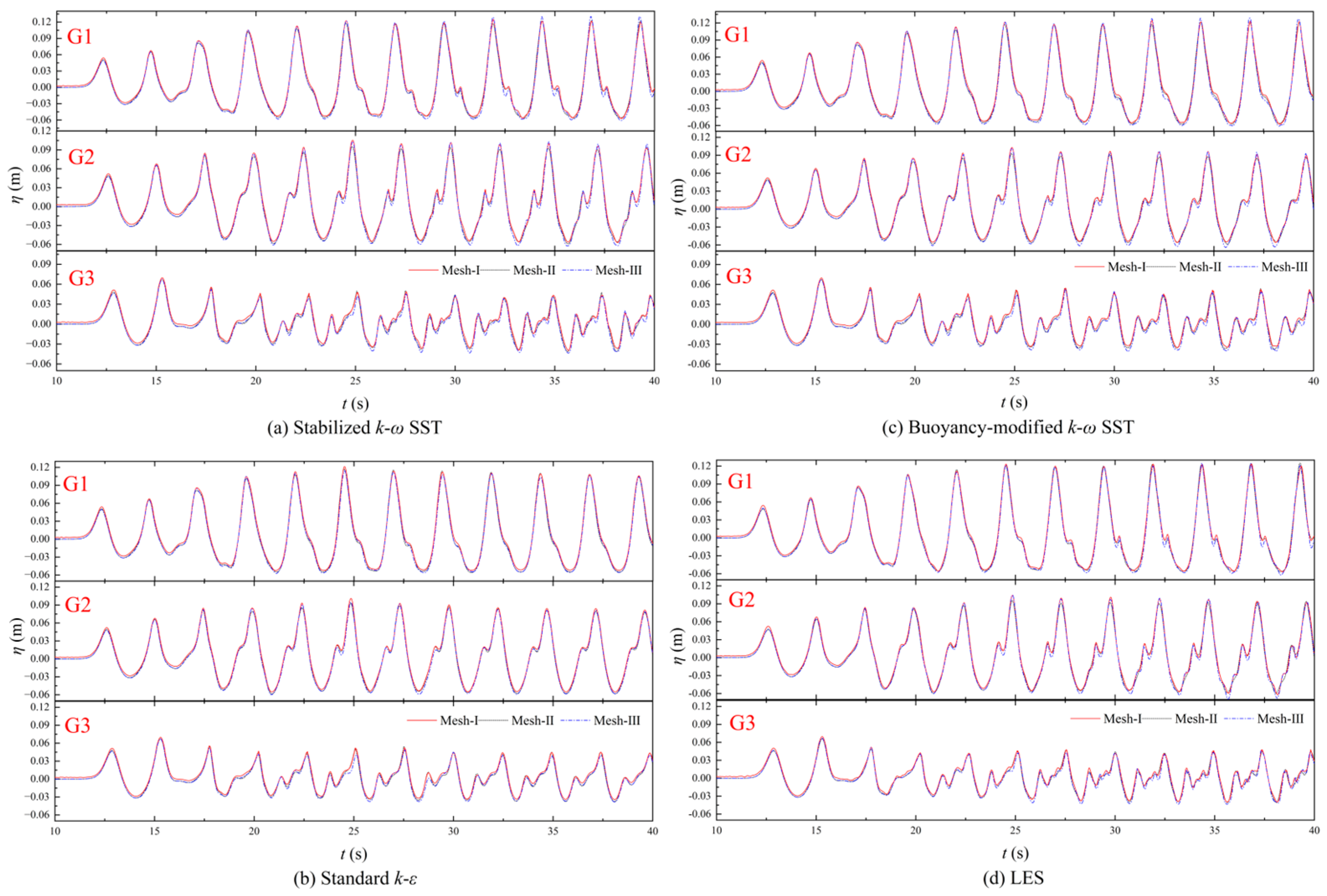
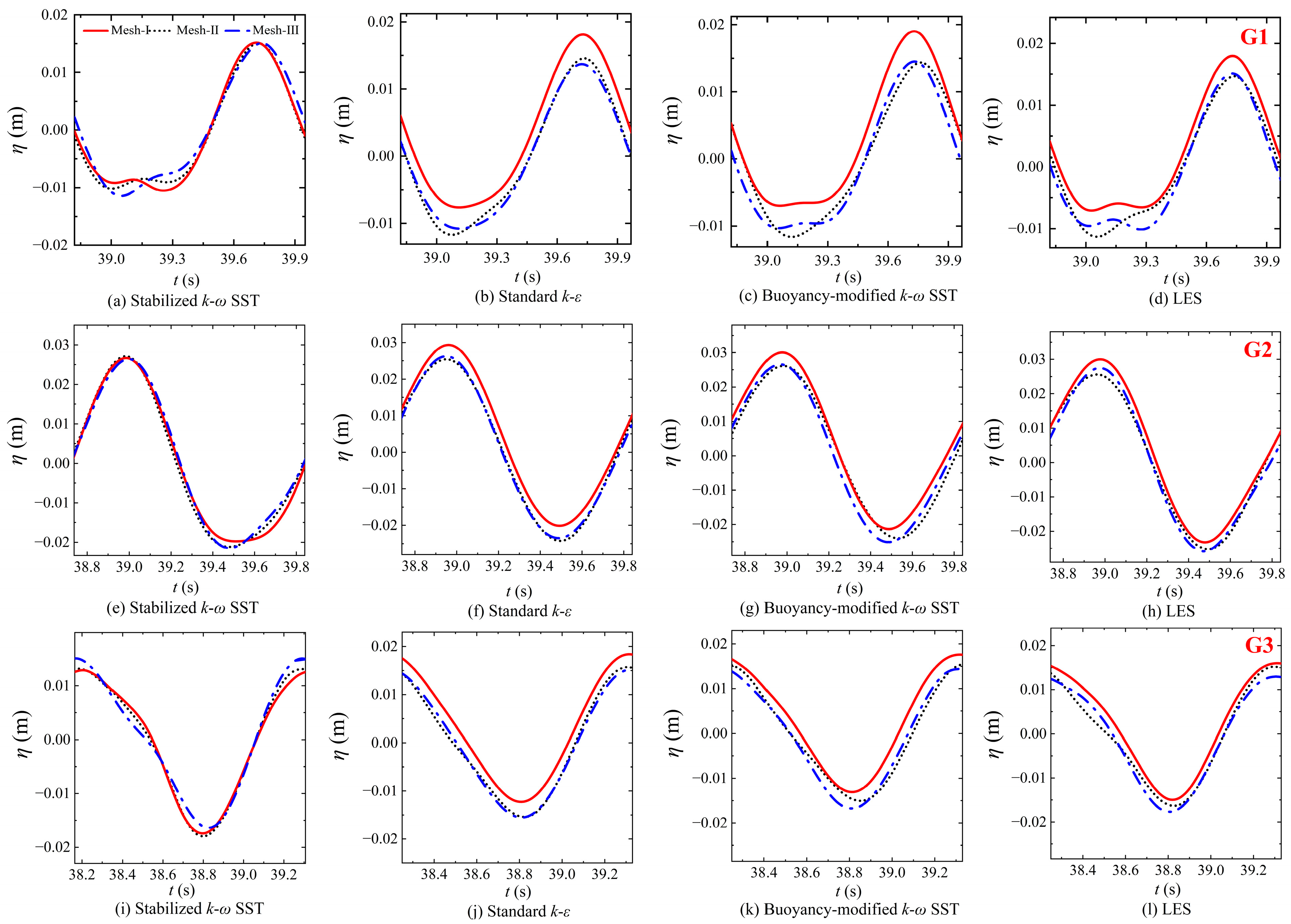
4.3. Wave Profile Evolution
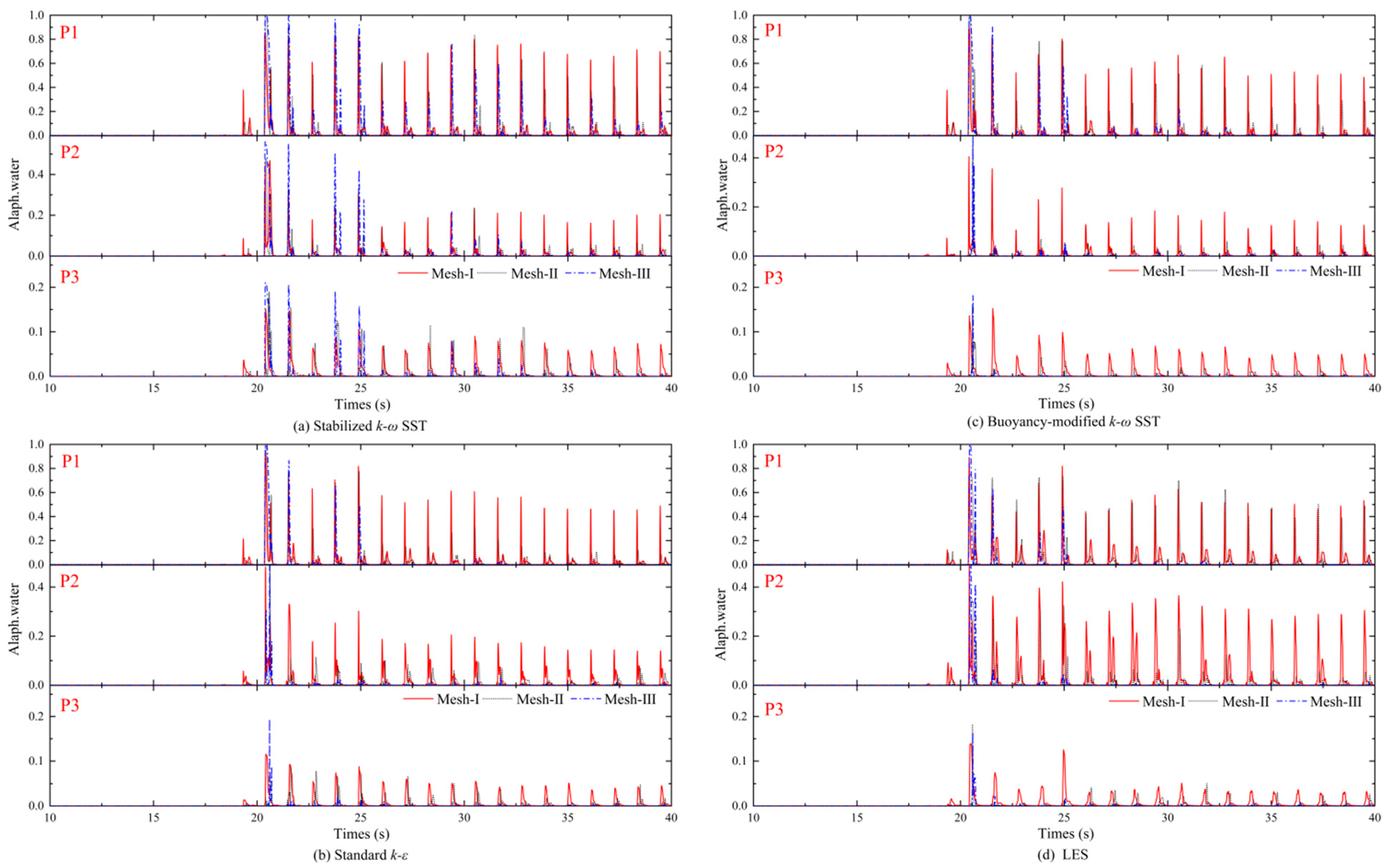
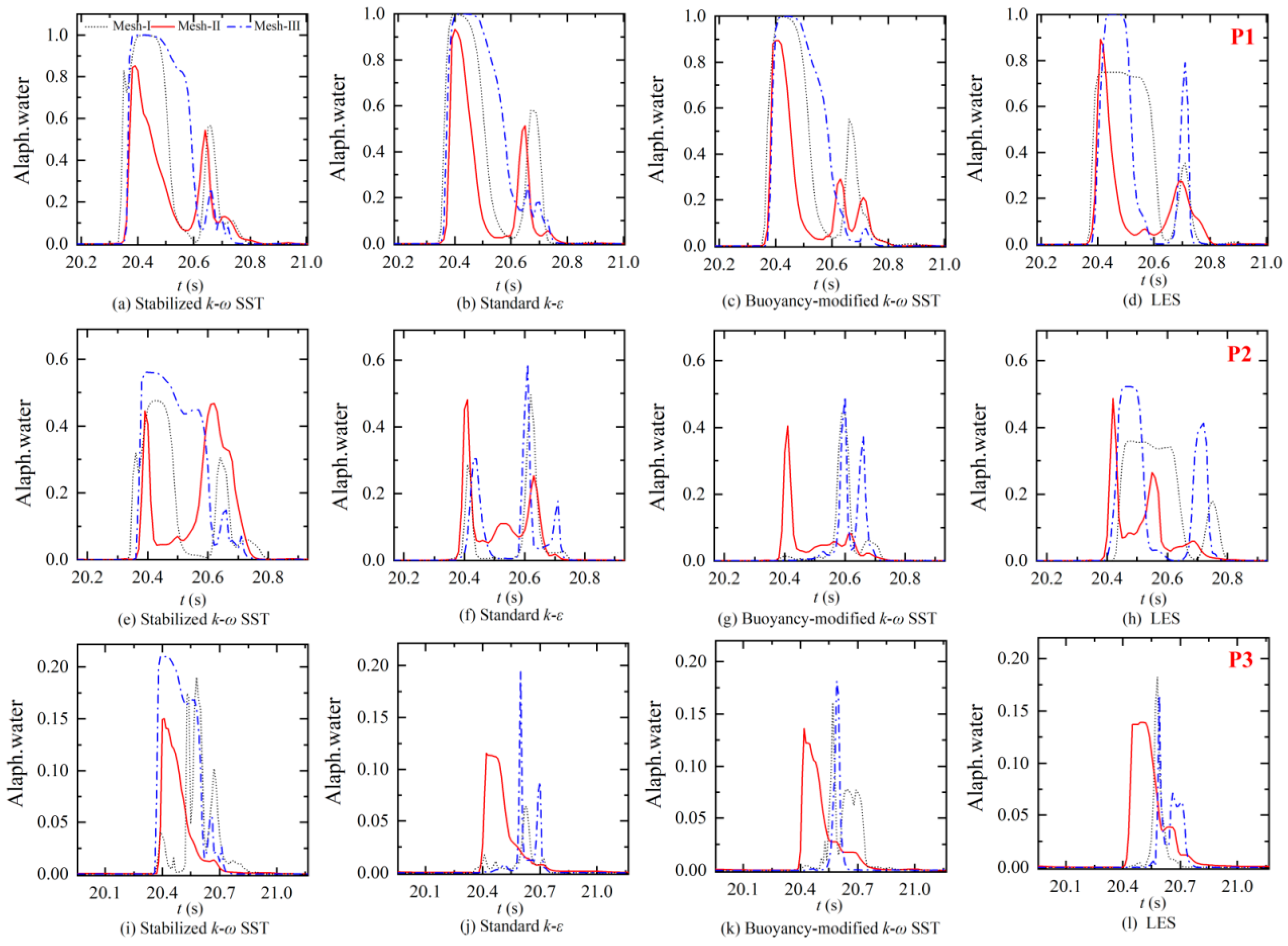
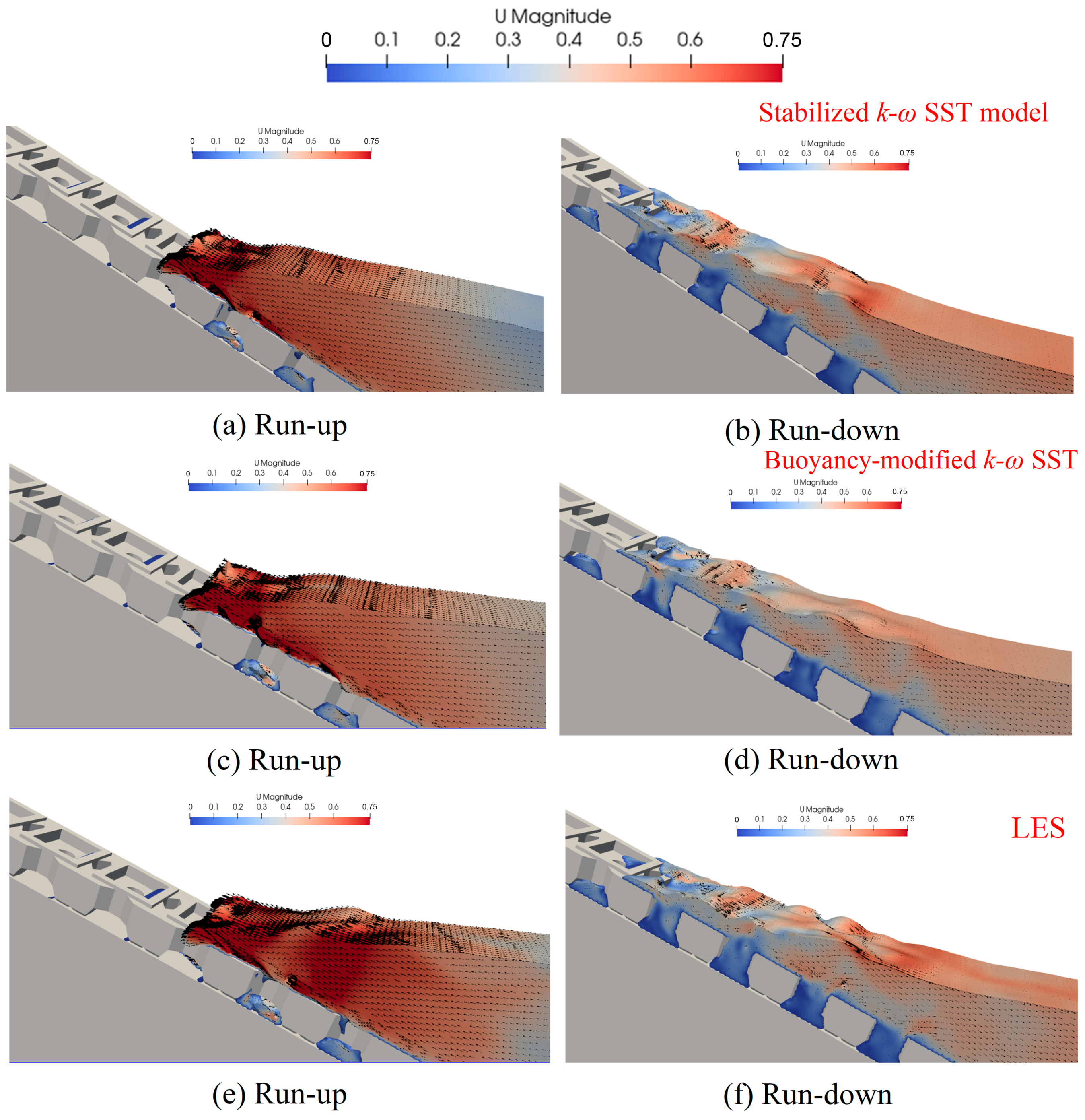
4.4. Wave Run-Up
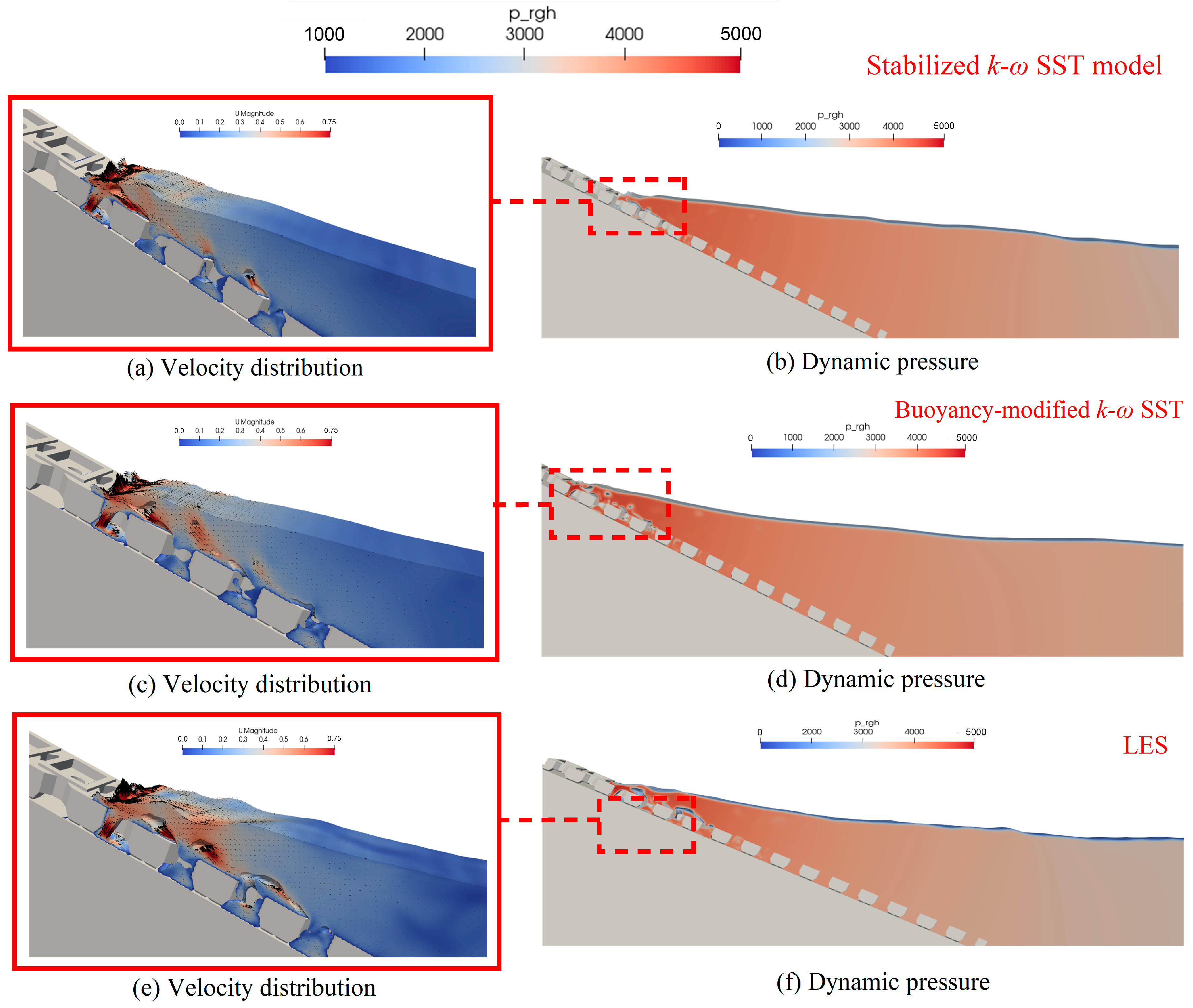
4.5. Wave Velocity Distribution and Dynamic Pressure Fields
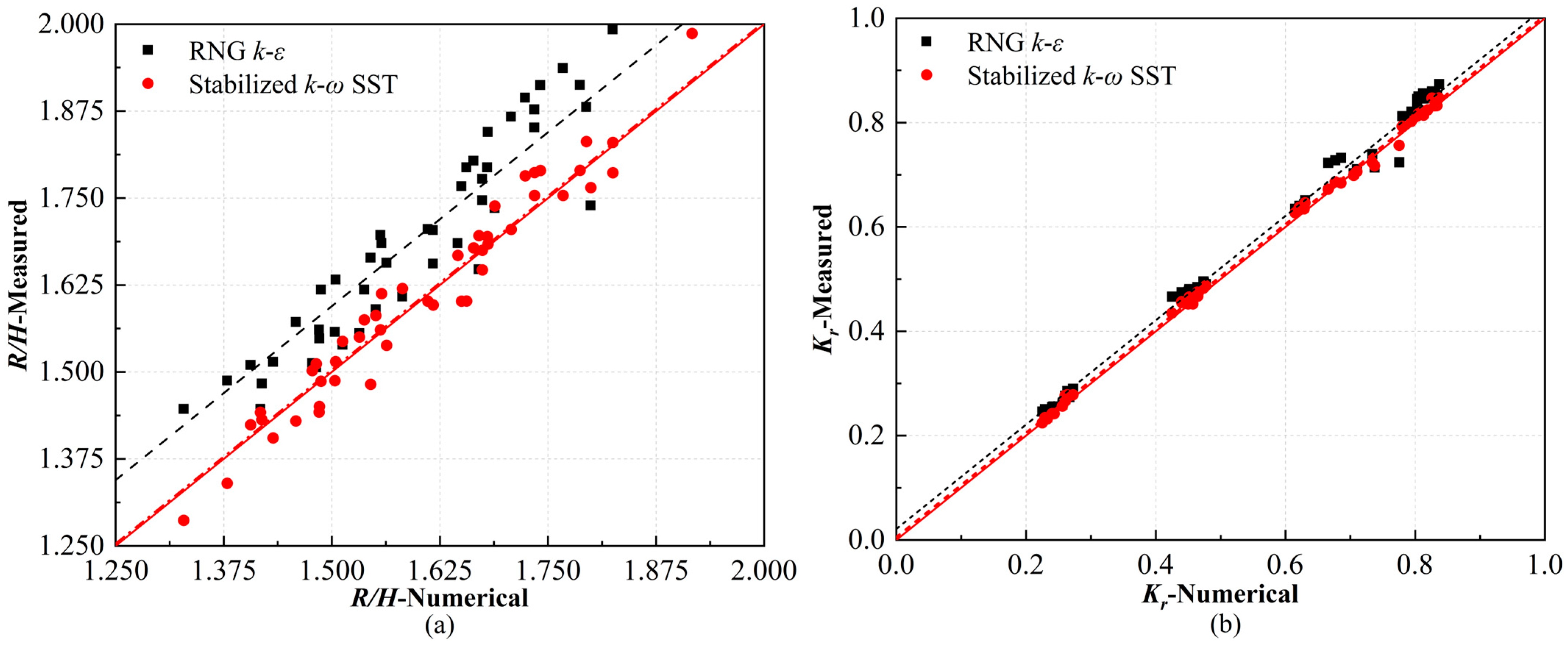
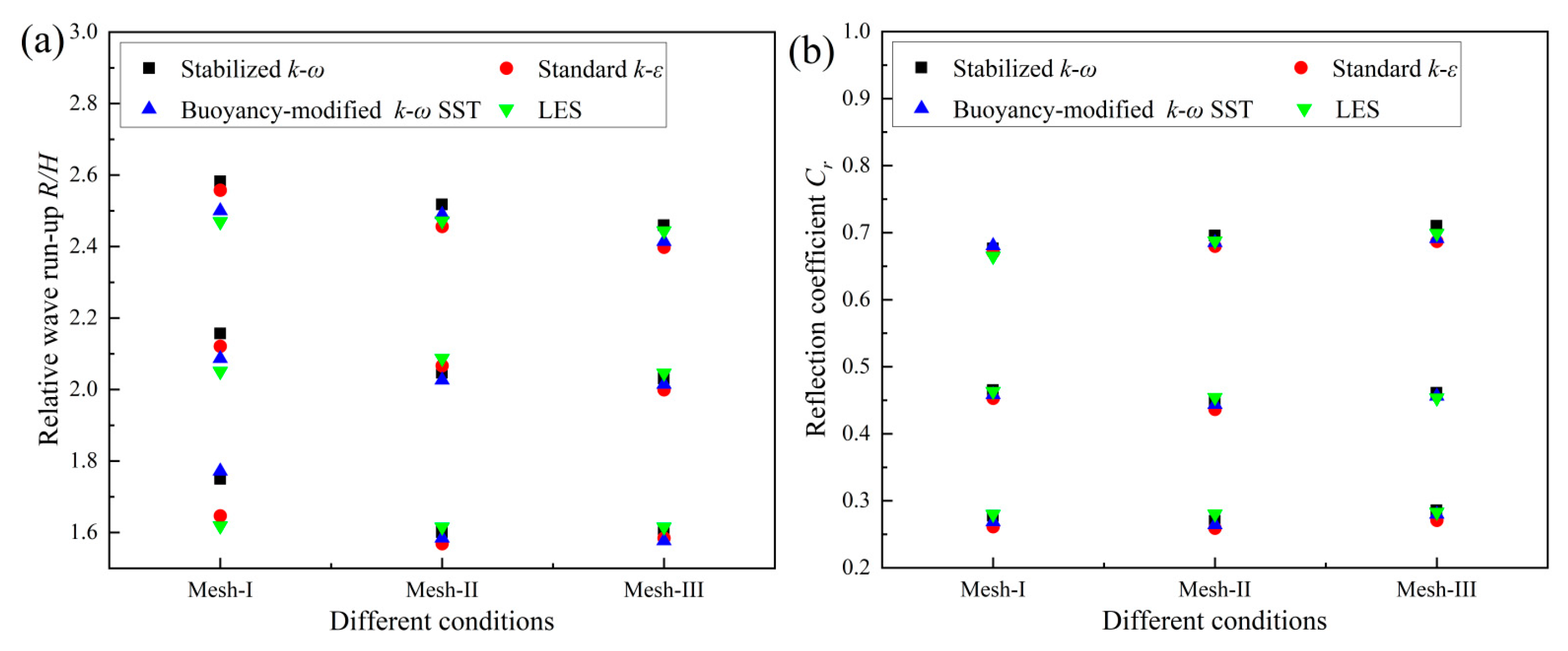
4.6. Sensitivity Analysis of the Wave Run-Up and Reflection Coefficient
5. Conclusions
- (1)
- The stabilized k-ω model demonstrates superior performance in capturing wave evolution on the new ecological hollow cube. The wave profiles simulated with the standard k-ε, buoyancy-modified k-ω SST, and LES models show a slight decrease in wave height on three different grid systems (the RMSE values were 1.35112 × 10−5, 2.12065× 10−5, 2.00269 × 10−5). In contrast, the wave profiles obtained with the stabilized k-ω SST model maintain good consistency (the RMSE value is 0.17832 × 10−5), with almost no wave height drop observed, suggesting better stability and grid independence under this condition.
- (2)
- The parameter “alpha water” is more sensitive to the grids, and the models are less consistent among different grids, but all of them can capture the maximum value of alpha water better, among which the stable k-ω SST model can capture more alpha water values and shows a prediction advantage (the RMSE value of stable k-ω SST under Mesh I and Mesh II is 0.000362).
- (3)
- The pressure fields predicted by all four turbulence models are generally similar, with higher pressures observed near the new ecological hollow cube. The stabilized k-ω and buoyancy-modified k-ω SST models predict slightly higher overall pressures compared to the standard k-ε and LES models. Regarding velocity distributions, the stabilized k-ω and standard k-ε models show very similar patterns. The LES model, however, exhibits excessive turbulent kinetic energy generation. The stabilized k-ω, standard k-ε, and buoyancy-modified k-ω SST models are better suited for mitigating this issue of excessive turbulence kinetic energy production, resulting in smoother free-surface representations.
- (4)
- The numerical results for the new ecological hollow cube exhibit some grid dependence. The analysis of discretization errors across the four turbulence models reveals a high degree of consistency across the three wave conditions. The highest error values are consistently observed under the Wave-I condition (the average GCI21 values for wave run-up and reflection were 6.3725 and 7.2575, respectively), while the lowest error values are found under the Wave-III conditions (the average GCI21 values for wave run-up and reflection were 2.63 and 1.315, respectively).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cr | Reflection coefficient [-] |
| RMSE | Root mean square error [-] |
| R | Wave run-up height related to regular waves [m] |
| Ru,2% | Wave run-up height exceeded by 2% of incident waves [m] |
| Ru,2%/H | Relative run-up [-] |
| T | Wave period |
| Tm−1,0 | Spectral wave period [s] |
| L | Wavelength in deep water based on T (=gT2/2π) [m] |
| Lm−1,0 | Spectral wavelength in deep water (=gTm−1,02/2π) [m] |
| g | Acceleration due to gravity [m/s2] |
| H | Wave height for regular waves [m] |
| Hm0 | Incident spectral significant wave height at the toe of the structure [m] |
| h | Water depth at toe of the structure [m] |
| ξ | Breaker parameter (regular waves) (=tan α/(H/L)0.5) [-] |
| α | Angle between structure slope and horizontal [◦] |
| ERE | Extrapolated relative error |
| GCI | Grid convergence index |
References
- Bruce, T.; Van Der Meer, J.; Franco, L.; Pearson, J.M. Overtopping performance of different armour units for rubble mound breakwaters. Coast. Eng. 2009, 56, 166–179. [Google Scholar] [CrossRef]
- Zhao, H.; Ding, F.; Ye, J.; Jiang, H.; Chen, W.; Gu, W.; Yu, G.; Li, Q. Physical Experimental Study on the Wave Reflection and Run-Up of a New Ecological Hollow Cube. J. Mar. Sci. Eng. 2024, 12, 664. [Google Scholar] [CrossRef]
- Campos, Á.; Molina-Sanchez, R.; Castillo, C. Damage in rubble mound breakwaters. Part II: Review of the definition, parameterization, and measurement of damage. J. Mar. Sci. Eng. 2020, 8, 306. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 439. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 96–116. [Google Scholar]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.; Speziale, C. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A Fluid Dyn. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD (Third Edition) (Hardcover); DCW Industries: La Canada, CA USA, 2006. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Brown, S.A.; Greaves, D.M.; Magar, V.; Conley, D.C. Evaluation of turbulence closure models under spilling and plunging breakers in the surf zone. Coast. Eng. 2016, 114, 177–193. [Google Scholar] [CrossRef]
- Mayer, S.; Madsen, P.A. Simulation of breaking waves in the surf zone using a Navier-Stokes solver. Coast. Eng. 2001, 2000, 928–941. [Google Scholar]
- Devolder, B.; Troch, P.; Rauwoens, P. Performance of a buoyancy-modified k-ω and k-ω SST turbulence model for simulating wave breaking under regular waves using OpenFOAM®. Coast. Eng. 2018, 138, 49–65. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Application of a buoyancy-modified k-ω SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM®. Coast. Eng. 2017, 125, 81–94. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R.; Roenby, J. Performance of interFoam on the simulation of progressive waves. Coast. Eng. J. 2019, 61, 380–400. [Google Scholar] [CrossRef]
- Bradford, S.F. Numerical simulation of surf zone dynamics. J. Waterw. Port Coast. Ocean. Eng. 2000, 126, 1–13. [Google Scholar] [CrossRef]
- Ting, F.C.; Kirby, J.T. Observation of undertow and turbulence in a laboratory surf zone. Coast. Eng. 1994, 24, 51–80. [Google Scholar] [CrossRef]
- Galera-Calero, L.; Blanco, J.M.; Izquierdo, U.; Esteban, G.A. Performance assessment of three turbulence models validated through an experimental wave flume under different scenarios of wave generation. J. Mar. Sci. Eng. 2020, 8, 881. [Google Scholar] [CrossRef]
- Qu, S.; Liu, S.; Ong, M.C. An evaluation of different RANS turbulence models for simulating breaking waves past a vertical cylinder. Ocean. Eng. 2021, 234, 109195. [Google Scholar] [CrossRef]
- Zhou, H.; Ye, J. Numerical study on the hydrodynamic performance of a revetment breakwater in the South China Sea: A case study. Ocean. Eng. 2022, 256, 111497. [Google Scholar] [CrossRef]
- Vieira, F.; Taveira-Pinto, F.; Rosa-Santos, P. Damage evolution in single-layer cube armoured breakwaters with a regular placement pattern. Coast. Eng. 2021, 169, 103943. [Google Scholar] [CrossRef]
- Shen, Z.; Huang, D.; Wang, G.; Jin, F. Numerical study of wave interaction with armour layers using the resolved CFD-DEM coupling method. Coast. Eng. 2024, 187, 104421. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Three-dimensional interaction of waves and porous coastal structures using OpenFOAM®. Part I: Formulation and validation. Coast. Eng. 2014, 83, 243–258. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, Z.; Liu, Y. Numerical study of solitary wave interaction with a vegetated platform. Ocean. Eng. 2019, 192, 106561. [Google Scholar] [CrossRef]
- Wang, Y.; Li, D.; Ye, J.; Zhao, H.; Mao, M.; Bai, F.; Hu, J.; Zhang, H. Numerical Analysis of Wave Interaction with a New Ecological Quadrangular Hollow Block. Water 2025, 17, 96. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Horiuti, K. A Statistically-Derived Subgrid-Scale Kinetic Energy Model for the Large-Eddy Simulation of Turbulent Flows. J. Phys. Soc. Jpn. 1985, 54, 2834–2839. [Google Scholar] [CrossRef]
- Ye, J.; Shan, J.; Zhou, H.; Yan, N. Numerical modelling of the wave interaction with revetment breakwater built on reclaimed coral reef islands in the South China Sea—Experimental verification. Ocean. Eng. 2021, 235, 109325. [Google Scholar] [CrossRef]
- Mansard, E.P.D.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least Squares Method. Coast. Eng. Proc. 1980, 1, 8. [Google Scholar] [CrossRef]
- EurOtop. Manual on Wave Overtopping of Sea Defences and Related Structures, an Overtopping Manual Largely Based on European Research, But for Worldwide Application; Van der Meer, J.W., Allsop, N.W.H., Bruce, T., De Rouck, J., Kortenhaus, A., Pullen, T., Schüttrumpf, H., Troch, P., Zanuttigh, B., Eds.; 2018; Available online: https://www.overtopping-manual.com (accessed on 10 March 2025).
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]
- Zanuttigh, B.; Van Der Meer, J. Wave reflection from coastal structures in design conditions. Coast. Eng. 2008, 55, 771–779. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. Coastal Engineering Manual; U.S. Army Corps of Engineers: Washington, DC, USA, 2002; Volume 2.
- Schoonees, T.; Kerpen, N.B.; Schlurmann, T. Full-scale experimental study on wave reflection and run-up at stepped revetments. Coast. Eng. 2022, 172, 104045. [Google Scholar] [CrossRef]



| Coefficient | |||||
|---|---|---|---|---|---|
| Value | 0.09 | 1 | 1.30 | 1.44 | 1.92 |
| Grid Information | Cell Number (Million) | Minimum Size in the x, y, and z Direction (m) |
|---|---|---|
| Mesh-I | 891,844 | 0.005 × 0.005 × 0.005 |
| Mesh-II | 2,922,119 | 0.0025 × 0.0025 × 0.0025 |
| Mesh-III | 8,909,544 | 0.00125 × 0.00125 × 0.00125 |
| Test No. | Water Depth (m) | Period (s) | Wave Height (m) |
|---|---|---|---|
| Wave-I | 0.3 | 2.46 | 0.08 |
| Wave-II | 1.79 | 0.06 | |
| Wave-III | 1.12 | 0.04 |
| Label | Coordinates (x, z, y) (cm) |
|---|---|
| P1 | (x = 0.74525, z = 0.004, y = 0.40512) |
| P2 | (x = 0.7515, z = 0.004, y = 0.40825) |
| P3 | (x = 0.7565, z = 0.004, y = 0.41075) |
| Type | Partition Scheme | Values | Wave-I | Wave-II | Wave-III |
|---|---|---|---|---|---|
| Standard k-ε | Mesh I | R/H | 1.75000 | 1.60125 | 1.57000 |
| Cr | 0.27773 | 0.26991 | 0.28575 | ||
| Mesh II | R/H | 2.15667 | 2.04667 | 2.03125 | |
| Cr | 0.46507 | 0.44991 | 0.461 | ||
| Mesh III | R/H | 2.58219 | 2.51781 | 2.45969 | |
| Cr | 0.67653 | 0.69569 | 0.71023 | ||
| R/H | −7.02350 | −6.11255 | −4.45310 | ||
| Cr | −1.17734 | −0.22264 | −0.12940 | ||
| R/H | 1.25% | 1.26% | 1.35% | ||
| Cr | 1.24% | 2.21% | 3.20% | ||
| R/H | 6.27% | 6.02% | 4.80% | ||
| Cr | 6.55% | 2.28% | 1.82% | ||
| Stabilized k-ω SST | Mesh I | R/H | 1.64688 | 1.56875 | 1.58438 |
| Cr | 0.26136 | 0.25905 | 0.27081 | ||
| Mesh II | R/H | 2.12125 | 2.06667 | 1.95933 | |
| Cr | 0.45292 | 0.43634 | 0.431241 | ||
| Mesh III | R/H | 2.5575 | 2.45625 | 2.39813 | |
| Cr | 0.67056 | 0.6798 | 0.68706 | ||
| R/H | −3.78187 | −0.22172 | −0.61746 | ||
| Cr | −1.14567 | −0.21597 | 0.05407 | ||
| R/H | 1.44% | 8.08% | 3.57% | ||
| Cr | 1.23% | 2.20% | 4.16% | ||
| R/H | 4.12% | 1.43% | 1.74% | ||
| Cr | 6.73% | 2.29% | 1.01% | ||
| Buoyancy-modified k-ω SST | Mesh I | R/H | 1.58438 | 1.57688 | 1.77188 |
| Cr | 0.26432 | 0.28003 | 0.26852 | ||
| Mesh II | R/H | 2.02667 | 2.01458 | 2.08667 | |
| Cr | 0.44362 | 0.45617 | 0.4583 | ||
| Mesh III | R/H | 2.48969 | 2.41406 | 2.49975 | |
| Cr | 0.68529 | 0.69106 | 0.68056 | ||
| R/H | −0.84036 | −0.25113 | −0.24806 | ||
| Cr | −7.85221 | −2.99801 | 0.76371 | ||
| R/H | 1.32% | 2.05% | 2.13% | ||
| Cr | 1.20% | 1.53% | 1.32% | ||
| R/H | 5.16% | 2.44% | 2.36% | ||
| Cr | 7.45% | 3.63% | 0.71% | ||
| LES | Mesh I | R/H | 1.61875 | 1.61563 | 1.61563 |
| Cr | 0.27988 | 0.28047 | 0.28308 | ||
| Mesh II | R/H | 2.05125 | 2.08708 | 2.04583 | |
| Cr | 0.46338 | 0.45438 | 0.45369 | ||
| Mesh III | R/H | 2.46969 | 2.47188 | 2.44406 | |
| Cr | 0.665 | 0.6878 | 0.6991 | ||
| R/H | −11.25289 | −3.74310 | −0.47801 | ||
| Cr | −1.57841 | −0.22776 | −0.10606 | ||
| R/H | 1.14% | 1.43% | 4.38% | ||
| Cr | 1.18% | 2.23% | 3.67% | ||
| R/H | 9.94% | 4.15% | 1.62% | ||
| Cr | 8.30% | 2.27% | 1.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Ye, J.; Wang, K.; Zhou, Y.; Zeng, Z.; Li, Q.; Zhao, X. Selection of a Turbulence Model for Wave Evolution on a New Ecological Hollow Cube. Water 2025, 17, 1149. https://doi.org/10.3390/w17081149
Zhao H, Ye J, Wang K, Zhou Y, Zeng Z, Li Q, Zhao X. Selection of a Turbulence Model for Wave Evolution on a New Ecological Hollow Cube. Water. 2025; 17(8):1149. https://doi.org/10.3390/w17081149
Chicago/Turabian StyleZhao, Haitao, Junwei Ye, Kaifang Wang, Yian Zhou, Zhen Zeng, Qiang Li, and Xizeng Zhao. 2025. "Selection of a Turbulence Model for Wave Evolution on a New Ecological Hollow Cube" Water 17, no. 8: 1149. https://doi.org/10.3390/w17081149
APA StyleZhao, H., Ye, J., Wang, K., Zhou, Y., Zeng, Z., Li, Q., & Zhao, X. (2025). Selection of a Turbulence Model for Wave Evolution on a New Ecological Hollow Cube. Water, 17(8), 1149. https://doi.org/10.3390/w17081149






