Field Calibration of a Time-Domain Reflectometry Sensor for Water Content Measurement in Soils with Low Content of Coarse Fragments †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Sensor
2.2. Field Sites
2.3. Calibration Protocol
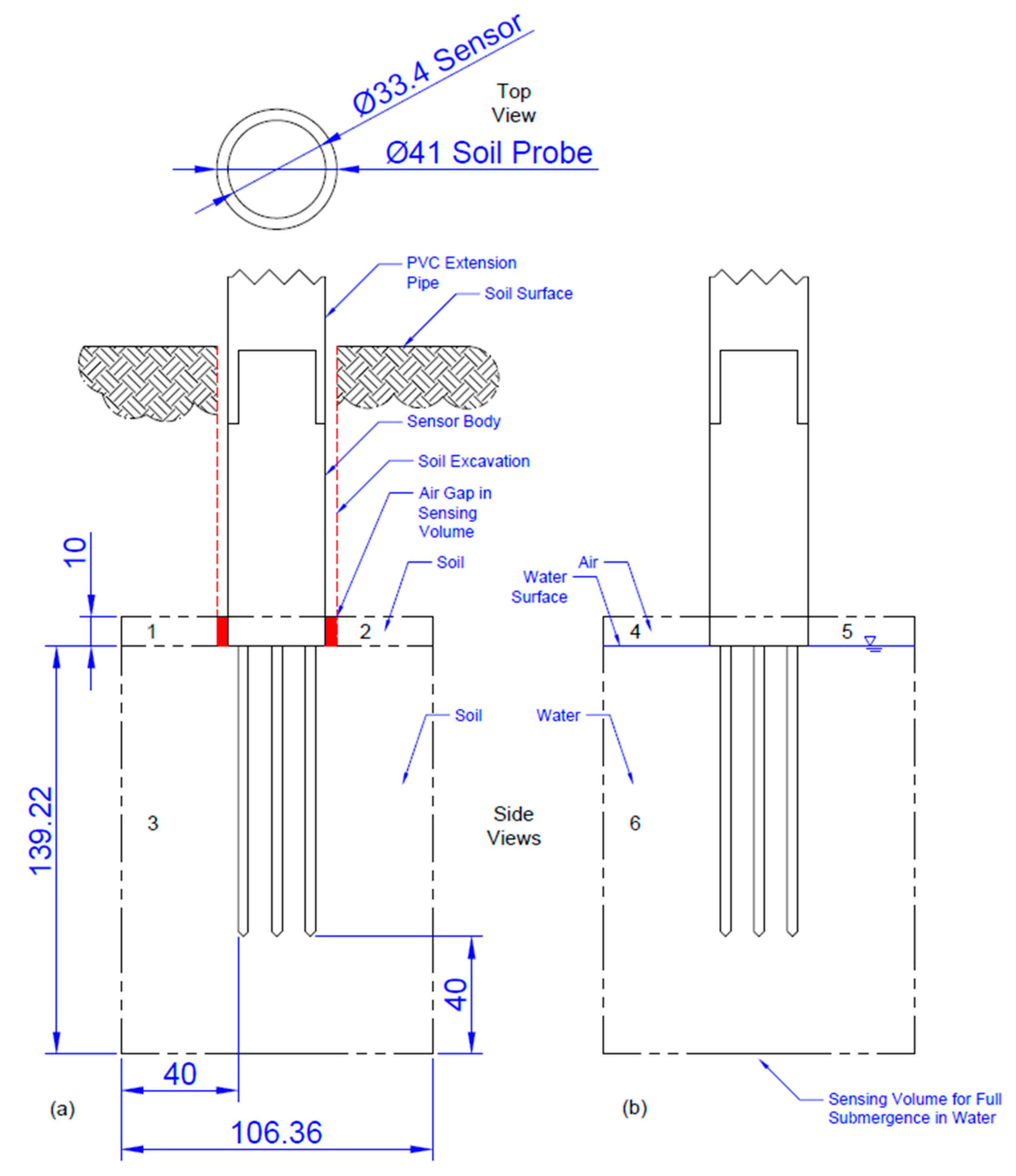
2.3.1. Materials for Soil Sampling
2.3.2. Collection of Soil Samples
2.3.3. Calibration
2.3.4. Validation
2.4. Statistical Analyses
3. Results and Discussion
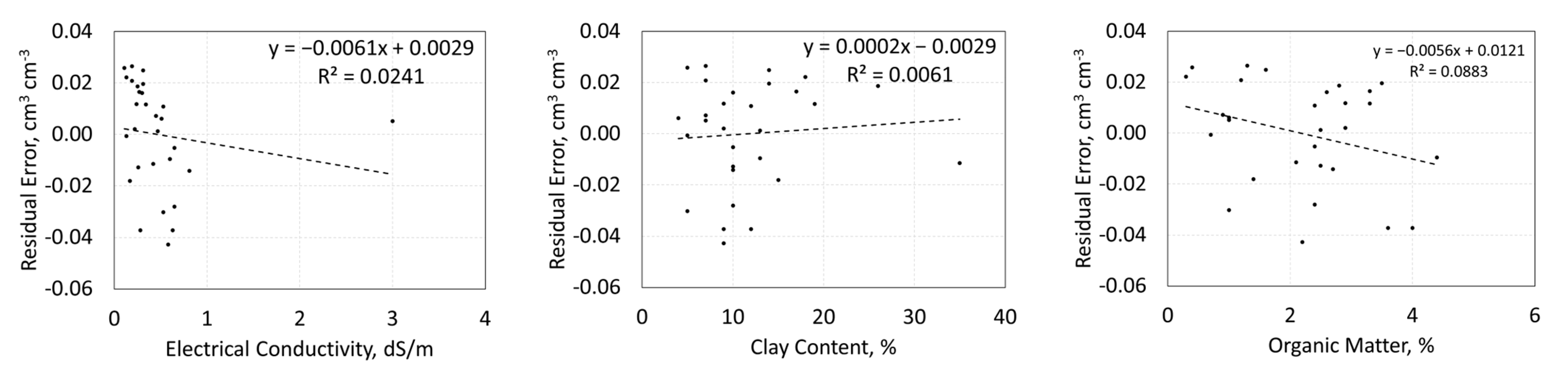
3.1. Residual Error Dependency on Soil Properties
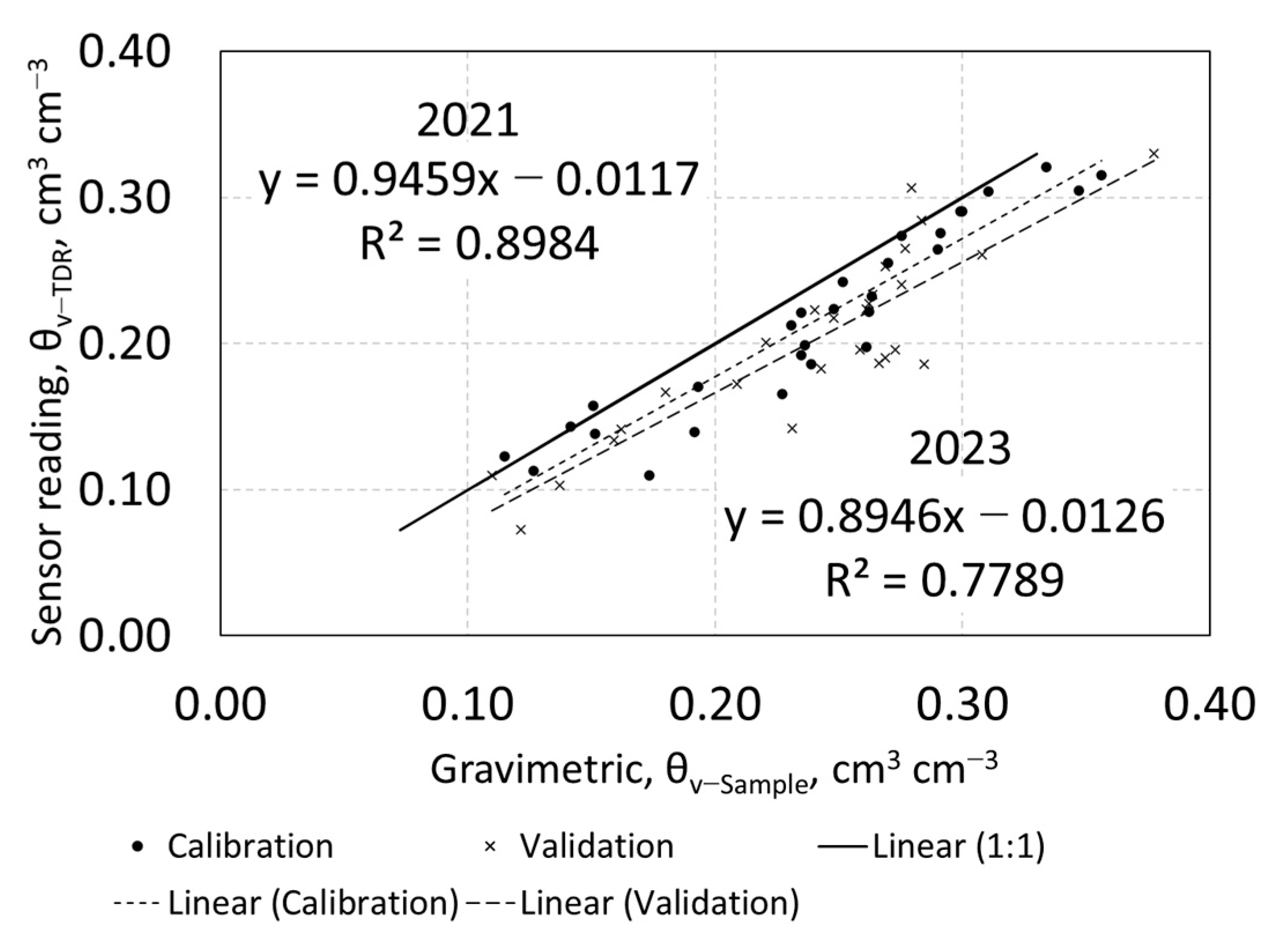
3.2. Calibration Statistics
3.3. Validation of Calibration
4. Management Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. The Future of Food and Agriculture—Trends and Challenges. Rome 2017. Available online: https://www.fao.org/3/a-i6583e.pdf (accessed on 3 July 2024).
- Cooley, H.; Christian-Smith, J.; Gleick, P.H. Sustaining California Agriculture in an Uncertain Future; Pacific Institute: Oakland, CA, USA, 2009; Volume 81, Available online: https://pacinst.org/wp-content/uploads/2014/04/sustaining-california-agriculture-pacinst-full-report.pdf (accessed on 2 April 2025).
- Varble, J.L.; Chávez, J.L. Performance evaluation and calibration of soil water content and potential sensors for agricultural soils in eastern Colorado. Agric. Water Manag. 2011, 101, 93–106. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Hignett, C.; Evett, S. Chapter 1: Direct and surrogate measures of soil water content. In Field Estimation of Soil Water Content: A Practical Guide to Methods, Instrumentation and Sensor Technology; Cepuder, P., Evett, S.R., Heng, L.K., Hignett, C., Laurent, J.P., Ruelle, P., Eds.; Training Course Series No. 30; International Atomic Energy Agency: Vienna, Austria, 2008; pp. 1–22. Available online: https://www-pub.iaea.org/mtcd/publications/pdf/tcs-30_web.pdf (accessed on 26 February 2020).
- Evett, S.R.; Cepuder, P. Chapter 5: Capacitance sensors for use in access tubes. In Field Estimation of Soil Water Content: A Practical Guide to Methods, Instrumentation, and Sensor Technology; Evett, S.R., Heng, L.K., Moutonnet, P., Nguyenm, M.L., Eds.; IAEA-Training Course Series No. 30. International Atomic Energy Agency: Vienna, Austria, 2008; pp. 73–90. Available online: https://www-pub.iaea.org/mtcd/publications/pdf/tcs-30_web.pdf (accessed on 26 February 2020).
- Feng, G.; Sui, R. Evaluation and calibration of soil moisture sensors in undisturbed soils. Am. Soc. Agric. Biol. Eng. 2020, 63, 265–274. [Google Scholar] [CrossRef]
- Datta, S.; Taghvaeian, S.; Ochsner, T.E.; Moriasi, D.; Gowda, P.; Steiner, J.L. Performance assessment of five different soil moisture sensors under irrigated field conditions in Oklahoma. Sensors 2018, 18, 3786. [Google Scholar] [CrossRef]
- Evett, S.R.; Tolk, J.A.; Howell, T.A. Time domain reflectometry laboratory calibration in travel time, bulk electrical conductivity, and effective frequency. Vadose Zone J. 2005, 4, 1020–1029. [Google Scholar] [CrossRef]
- Quinones, H.; Ruelle, P. Operative Calibration Methodology of a TDR Sensor for Soil Moisture Monitoring under Irrigated Crops. Subsurf. Sens. Technol. Appl. 2001, 2, 31–45. [Google Scholar] [CrossRef]
- Birendra, K.C.; Chau, H.W.; Mohssen, M.; Cameron, K.; Safa, M.; Mclndoe, I.; Rutter, H.; Dark, A.; Lee, M.; Pandey, V.P.; et al. Assessment of spatial and temporal variability in soil moisture using multi-length TDR probes to calibrate Aquafex sensors. Irrig. Sci. 2021, 39, 703–713. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, P.; Yang, X.; Zhen, Q.; Zhang, X. Comparison of the accuracy of two soil moisture sensors and calibration models for different soil types on the loess plateau. Soil Use Manag. 2020, 37, 584–594. [Google Scholar] [CrossRef]
- Kim, K.; Sim, J.; Kim, T.H. Evaluation of the effects of soil properties and electrical conductivity on the water content reflectometer calibration for landfill cover soils. Soil Water Res. 2017, 12, 10–17. [Google Scholar] [CrossRef]
- Sharma, K.; Irmak, S.; Kukal, M.S.; Vuran, M.C.; Jhala, A.; Qiao, X. Evaluation of soil moisture sensing technologies in silt loam and loamy sand soils: Assessment of performance, temperature sensitivity, and site—And sensor—Specific calibration functions. Trans. ASABE 2021, 64, 1123–1139. [Google Scholar] [CrossRef]
- Xiao, K.; Bai, W.; Wang, S. Multifactor analysis of calibration and service quality of the soil moisture sensor applied in subgrade engineering. Adv. Mater. Sci. Eng. 2021, 7548996. [Google Scholar] [CrossRef]
- Zhu, Y.; Irmak, S.; Jhala, A.J.; Vuran, M.C.; Diotto, A. Time-domain and frequency-domain reflectometry type soil moisture sensor performance and soil temperature effects in fine- and coarse-textured soils. Appl. Eng. Agric. 2019, 32, 117–134. [Google Scholar] [CrossRef]
- Singh, J.; Heeren, D.M.; Rudnick, D.R.; Woldt, W.E.; Bai, G.; Ge, Y.; Luck, J.D. Soil structure and texture effects on the precision of soil water content measurements with a capacitance based electromagnetic sensor. Trans. ASABE 2020, 63, 141–152. [Google Scholar] [CrossRef]
- Acclima. Data Sheet: True TDR-310H Soil Water-Temperature-BEC Sensor; Acclima, Inc.: Meridian, ID, USA, 2019; Available online: https://acclima.com/wp-content/uploads/Acclima-TDR310H-Data-Sheet.pdf (accessed on 25 February 2021).
- Soil Survey Staff, Natural Resources Conservation Service, United States Department of Agriculture. Web Soil Survey. Available online: https://websoilsurvey.nrcs.usda.gov/app/ (accessed on 27 March 2021).
- Becker, S.M.; Franz, T.E.; Abimbola, O.; Steele, D.D.; Flores, J.P.; Jia, X.; Scherer, T.F.; Rudnick, D.R.; Neale, C.M.U. Feasibility assessment on use of proximal geophysical sensors to support precision management. Vadose Zone J. 2022, e20228. [Google Scholar] [CrossRef]
- Neale, C.M.U.; (University of Nebraska-Lincoln, Lincoln, NE, USA). Personal communication, 2020.
- Franz, T.; (University of Nebraska-Lincoln, Lincoln, NE, USA). Personal communication, 2021.
- Gardner, W.H. Water content. In Methods of Soil Analysis, Part 1: Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; Agronomy No. 9; ASA and SSSA: Madison, WI, USA, 1986; pp. 635–662. [Google Scholar]
- Anderson, J.; (Acclima Inc., Meridian, ID, USA). Personal communication, 2022.
- Acclima. Data Sheet: True TDR-310H Soil Water-Temperature-BEC Sensor; Acclima, Inc.: Meridian, ID, USA, 2023; Available online: https://acclima.com/digital-tdr-soil-moisture-sensors/ (accessed on 2 April 2025).
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Avdeef, A. Do you know your r2? ADMET DMPK 2021, 9, 69–74. [Google Scholar] [CrossRef]
- Abebe, T.H. The Derivation and Choice of Appropriate Test Statistic (Z, t, F and Chi-Square Test) in Research Methodology. Math. Lett. 2019, 5, 33. [Google Scholar] [CrossRef]
- Johnson, R.A. Miller and Freund’s Probability and Statistics for Engineers, 6th ed.; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 2000. [Google Scholar]
- Evett, S.; (USDA-ARS, Bushland, TX, USA). Personal communication, 2022.
- Cosh, M.H.; Ochsner, T.E.; McKee, L.; Dong, J.; Basara, J.B.; Evett, S.R.; Hatch, C.E.; Small, E.E.; Steele-Dunne, S.C.; Zreda, M.; et al. The soil moisture active passive arena, Oklahoma, in situ sensor testbed (SMAP-MOISST): Testbed design and evaluation of in situ sensors. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Adeyemi, O.; Norton, T.; Grove, I.; Peets, S. Performance Evaluation of Three Newly Developed Soil Moisture Sensors. In Proceedings of the CIGR-AgEng Conference, Aarhus, Denmark, 26–29 June 2016; Available online: https://conferences.au.dk/uploads/tx_powermail/olutobi_cigr_paper.pdf (accessed on 2 April 2025).
- Singh, J.; Lo, T.; Rudnick, D.R.; Dorr, T.J.; Burr, C.A.; Werle, R.; Muñoz-Arriola, F. Performance assessment of factory and field calibrations for electromagnetic sensors in a loam soil. Agric. Water Manag. 2018, 196, 87–98. [Google Scholar] [CrossRef]
- Chávez, J.L.; Evett, S. Using soil water sensors to improve irrigation management. In Proceedings of the 24th Annual Central Plains Irrigation Conference, Colby, KS, USA, 21–22 February 2012; Available online: https://web.archive.org/web/20170603022742/https://www.ksre.k-state.edu/irrigate/oow/p12/Chavez12.pdf (accessed on 2 April 2025).
- Ferrarezi, R.S.; Nogueira, T.A.R.; Zepeda, S.G.C. Performance of soil moisture sensors in Florida Sandy Soils. Water 2020, 12, 358. [Google Scholar] [CrossRef]
- Rowlandson, T.L.; Berg, A.A.; Bullock, P.R.; Ojo, E.R.; McNairn, H.; Wiseman, G.; Cosh, M.H. Evaluation of several calibration procedures for a portable soil moisture sensor. J. Hydrol. 2013, 498, 335–344. [Google Scholar] [CrossRef]
- Sharma, K.; Irmak, S.; Kukal, M.S. Propagation of soil moisture sensing uncertainty into estimation of total soil water, evapotranspiration and irrigation decision-making. Agric. Water Manag. 2021, 243, 106454. [Google Scholar] [CrossRef]
- Maisha, R.M.; Steele, D.D. Field Calibration of a Time Domain Reflectometry Sensor with an Extension Pipe for Soil Water Content Measurement. In Proceedings of the ASABE Annual International Meeting, Houston, TX, USA, 20 July 2022; ASABE Paper No. 2201013; ASABE: St. Joseph, MI, USA, 2022. [Google Scholar] [CrossRef]






| Reference | Lab/Field | Soil Type | Setting or Purpose | Sensor Type | Site(s) | Statistics a | Soil Water Content Release Curve b | Brief Summary |
|---|---|---|---|---|---|---|---|---|
| [11] | Field | Sandy loam | Irrigation | TDR, Aquaflex | 1 | R2 | No | TDR sensor was calibrated using the gravimetric method, and the obtained R2 was 0.98 |
| [8] | Factory calibration | Sandy loam, silty clay loam | Irrigation | TDR315, CS655, GSI, SM100, CropX | 2 | RMSE, RSR, MBE, index of agreement (k), Pearson correlation coefficient (r) | No | TDR sensor overestimated in fine sandy loam and silty clay loam soil with RMSE values of 0.028 and 0.064 m3 m−3, respectively |
| [9] | Lab | Silty clay, clay, clay loam | Irrigation | TDR-100 | Slope, intercept, R2, RMSE | No | Sensor underestimated in each of the soil types when the soil was air dried (RMSE 0.0196, 0.0085, and 0.0097 m3 m−3, respectively) and overestimated when silty clay and clay soil was saturated (RMSE 0.00364, 0.00353, and 0.00189 m3 m−3, respectively) | |
| [7] | Field and Lab | Six soil types | Irrigation | TDR315, CS655, GSI | 2 | R2, RMSE | No | TDR315 overestimated θv for clay soil, with an RMSE range from 0.03 to 0.17 cm3 cm−3 |
| [12] | Lab | Sandy, sandy–feldspathic sandstone mixture (3:1), loessial, dark loessial, and Lou soil | Hydrological application | TDR315L, Diviner 2000 | 6 | R2, RMSE | No | An average R2 of 0.9820 and RMSE of 0.026 m3 m−3 was obtained by the TDR315L sensor |
| [13] | Lab | 28 soil types | Irrigation | TDR | 14 | R2 | No | Clay and fine particles affected the sensor EC readings with the lowest R2 of 0.3861 |
| [14] | Field | Silt loam, loamy sand | Irrigation | TDR315L, CS616, CS655, 5TE, 10HS, EC-5, SM150, JD field connect, TEROS 21(MPS-6) | 2 | RMSE, MBE, R2, SE, CI | Yes | Acclima TDR351L sensor performed better in the loamy sand soil, with an RMSE of 0.02 m3 m−3 |
| [10] | Field and Lab | Eolian sand, clay | Irrigation | TDR | 1 | t-test | No | Sensor responded well with continuous drip irrigation |
| [15] | Lab | Saline soil | Strength and stability of soil structure | TDR | 1 | R2, absolute error | No | TDR overestimated moisture content, with an R2 of 0.8464 |
| [16] | Lab | Silt loam and loamy sand | Irrigation | TDR300 (High clay mode), TDR300 (Standard mode), 5TE, 10HS, SM150, CS616, CS620 | 2 | RMSE | No | TDR300 high clay mode sensor performed best in the silt loam soil, with an RMSE of 0.020 m3 m−3 |
| (This study) | Field | Sand, loamy sand, clay loam, sandy clay loam, and sandy loam | Irrigation | TDR-310H | 3 | RMSE, MBE, slope, intercept, R2, t-test, CI | No | TDR-310H underestimated θv, with an RMSE of 0.032 cm3 cm−3, an MBE of −0.025 cm3 cm−3, and an R2 of 0.8984 |
| Year | Site 1 | Site 2 | Site 3 |
|---|---|---|---|
| 2021 | Corn (Zea mays L.) | Corn | Pinto bean (Phaseolus vulgaris L.) |
| 2022 | Corn | Corn | Corn |
| 2023 | Pinto bean | Corn | Corn |
| Site # | Statistic | Electrical Conductivity (EC), dS m−1 | Field Capacity, cm3 cm−3 | Permanent Wilting Point, cm3 cm−3 | Bulk Density, g cm−3 | Organic Matter, % | % Sand | % Silt | % Clay |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Average | 0.244 | 0.22 | 0.13 | 1.45 | 1.94 | 66.2 | 17 | 16.8 |
| Maximum | 0.42 | 0.34 | 0.22 | 1.59 | 3.5 | 94 | 26 | 35 | |
| Minimum | 0.11 | 0.07 | 0.05 | 1.36 | 0.3 | 44 | 1 | 5 | |
| 2 | Average | 0.58 | 0.23 | 0.13 | 1.46 | 2.152 | 72.8 | 18.3 | 9.2 |
| Maximum | 0.81 | 0.33 | 0.18 | 1.58 | 4.4 | 84 | 24 | 13 | |
| Minimum | 0.45 | 0.17 | 0.11 | 1.28 | 0.22 | 64 | 9 | 4 | |
| 3 | Average | 0.59 | 0.20 | 0.11 | 1.53 | 1.852 | 74.2 | 17.8 | 8 |
| Maximum | 3 1 | 0.27 | 0.16 | 1.78 | 3.6 | 84 | 25 | 12 | |
| Minimum | 0.09 | 0.13 | 0.06 | 1.29 | 0.26 | 63 | 9 | 3 |
| Parameters | Intercept | Slope |
| Ho = null hypothesis | a = 0 | b = 1 |
| Ha = alternative hypothesis | a ≠ 0 | b ≠ 1 |
| Statistics | Bias Error cm3 cm−3 | Absolute Error cm3 cm−3 |
|---|---|---|
| Mean | −0.025 | 0.026 |
| Maximum | 0.008 | 0.064 |
| Minimum | −0.064 | 0.001 |
| Standard Deviation | 0.021 | 0.020 |
| Coefficient of Variation % | −84 | 75 |
| Item | Year 2021 | 2021 95% Confidence Interval | Year 2023 | |
|---|---|---|---|---|
| Minimum | Maximum | |||
| Slope | 0.950 | 0.82 | 1.08 | 0.871 |
| Intercept, cm3 cm−3 | 0.0357 | 0.0072 | 0.0642 | 0.0639 |
| No. of samples | 29 | NA | NA | 27 |
| Sample maximum θv | 0.36 | NA | NA | 0.38 |
| Sample minimum θv | 0.11 | NA | NA | 0.11 |
| Sensor maximum θv | 0.32 | NA | NA | 0.33 |
| Sensor minimum θv | 0.11 | NA | NA | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maisha, R.; Steele, D.D.; Daigh, A.L.M.; Heeren, D.M.; Franz, T. Field Calibration of a Time-Domain Reflectometry Sensor for Water Content Measurement in Soils with Low Content of Coarse Fragments. Water 2025, 17, 1203. https://doi.org/10.3390/w17081203
Maisha R, Steele DD, Daigh ALM, Heeren DM, Franz T. Field Calibration of a Time-Domain Reflectometry Sensor for Water Content Measurement in Soils with Low Content of Coarse Fragments. Water. 2025; 17(8):1203. https://doi.org/10.3390/w17081203
Chicago/Turabian StyleMaisha, Rehnuma, Dean D. Steele, Aaron Lee M. Daigh, Derek M. Heeren, and Trenton Franz. 2025. "Field Calibration of a Time-Domain Reflectometry Sensor for Water Content Measurement in Soils with Low Content of Coarse Fragments" Water 17, no. 8: 1203. https://doi.org/10.3390/w17081203
APA StyleMaisha, R., Steele, D. D., Daigh, A. L. M., Heeren, D. M., & Franz, T. (2025). Field Calibration of a Time-Domain Reflectometry Sensor for Water Content Measurement in Soils with Low Content of Coarse Fragments. Water, 17(8), 1203. https://doi.org/10.3390/w17081203






