Evaluating Hydrologic Response of an Agricultural Watershed for Watershed Analysis
Abstract
:1. Introduction

2. Materials and Methods
2.1. SWAT Model Description
2.2. Maquoketa River Watershed and SWAT Input Data
2.3. Influence Coefficient Method
2.4. Simulation Approach
3. Results and Discussion
3.1. Sensitivity Analysis
| Model parameter | Variable name | Range | Model initial estimates |
|---|---|---|---|
| Curve Number (for AGRL) | CN | 69–85 | 77 |
| Soil evaporation compensation factor | ESCO | 0.75–0.95 | 0.95 |
| Plant uptake compensation factor | EPCO | 0.01–1 | 1.0 |
| Soil available water capacity (mm) | SOL_AWC | ±0.04 | - |
| Baseflow alpha factor | ALPHA_BF | 0.05–0.8 | 0.048 |
| Groundwater revap coefficient | GW_REVAP | 0.02–0.2 | 0.02 |
| Groundwater delay time (day) | GW_DELAY | 0–100 | 31 |
| Deep aquifer percolation fraction | RECHRG_DP | 0–1 | 0.05 |

| Parameter | Initial value | Parameter | Response variable (Surface Runoff) | Response variable (Baseflow) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | ΔP | MeanPm | F1 | F2 | ΔF | MeanFm | F1 | F2 | ΔF | MeanFm | ||||||
| CN | 77 | 85 | 69 | 16 | 77 | 310 | 173 | 137 | 241 | 8.57 | 2.73 | 21 | 181 | −160 | 101 | −10.0 | −7.63 |
| ESCO | 0.95 | 0.5 | 1 | 0.5 | 0.75 | 214 | 249 | −34 | 231 | −68.9 | −0.22 | 69 | 110 | −41 | 90 | −82.2 | −0.69 |
| EPCO | 1 | 0.01 | 1 | 0.99 | 0.505 | 264 | 249 | 15 | 256 | 15.09 | 0.03 | 124 | 110 | 14 | 117 | 14.1 | 0.06 |
| SOL_AWC | 0.04 | −0.04 | 0.08 | 0.04 | 232 | 259 | −27 | 246 | −336 | −0.05 | 95 | 135 | −40 | 115 | −503 | −0.17 | |
| ALPHA_BF | 0.048 | 0.048 | 0.8 | 0.75 | 0.424 | 249 | 249 | 0 | 249 | 0 | 0 | 110 | 114 | −4 | 112 | −4.7 | −0.02 |
| GW_REVAP | 0.02 | 0.02 | 0.2 | 0.18 | 0.11 | 249 | 249 | 0 | 249 | 0 | 0 | 110 | 95 | 15 | 102 | 85.6 | 0.09 |
| GW_DELAY | 31 | 0 | 100 | 100 | 50 | 249 | 249 | 0 | 249 | 0 | 0 | 108 | 106 | 1 | 108 | 0.0 | 0.01 |
| RECHARG_DP | 0.05 | 0 | 1 | 1 | 0.5 | 249 | 249 | 0 | 249 | 0 | 0 | 113 | 91 | 22 | 102 | 22.3 | 0.11 |
3.2. Calibration and Validation
| Parameter | Value |
|---|---|
| CN (for AGRL only) | 72 |
| ESCO | 0.85 |
| SOL_AWC | −0.04 |
| GW_REVAP | 0.15 |
| GW_DELAY | 50 |
| RECHRG_DP | 0.5 |
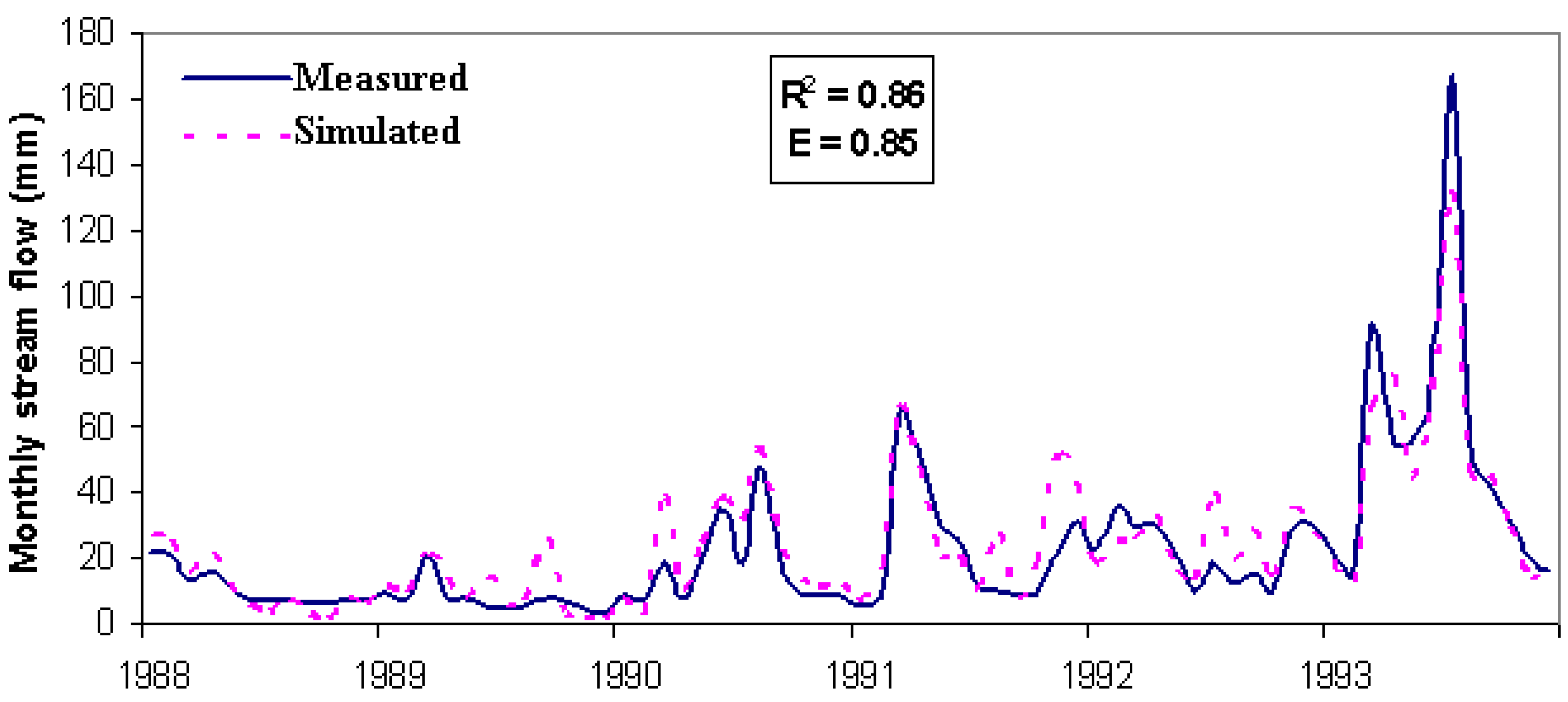

4. Conclusions
References
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Johansen, N.B.; Imhoff, J.C.; Kittle, J.L.; Donigian, A.S. Hydrologic Simulation Program—FORTRAN (HSPF): User’s Manual for Release 8; EPA-600/3-84-066; U.S.; Environmental Protection Agency: Athens, GA, USA, 1984. [Google Scholar]
- U.S. Army Corps of Engineers Hydrologic Engineering Center (USACE-HEC). In HEC-HMS Hydrologic Modeling System User’S Manual; USACE-HEC: Davis, CA, USA, 2000.
- CREAMS: A Field-Scale Model for Chemicals, Runoff, and Erosion from Agricultural Management Systems; Conservation Research Report No. 26; Knisel, W.G. (Ed.) USA-SEA: Washington, DC, USA, 1980.
- Williams, J.R.; Jones, C.A.; Dyke, P.T. A modeling approach to determining the relationship between erosion and soil productivity. Trans. ASAE 1984, 27, 129–144. [Google Scholar] [CrossRef]
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. AGNPS: A non-point source pollution model for evaluating agricultural watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Saleh, A.; Arnold, J.G.; Gassman, P.W.; Hauck, L.M.; Rosenthal, W.D.; Williams, J.R.; McFarland, A.M.S. Application of SWAT for the Upper North Bosque River watershed. Trans. ASAE 2000, 43, 1077–1087. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical development, applications, and future directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Simulating hydrologic budgets for three Illinois watersheds. J. Hydrol. 1996, 176, 57–77. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the Upper Mississippi River Basin. J. Hydrol. 1999, 227, 21–40. [Google Scholar] [CrossRef]
- FitzHugh, T.W.; Mackay, D.S. Impacts of input parameter spatial aggregation on an agricultural nonpoint source pollution model. J. Hydrol. 2000, 236, 35–53. [Google Scholar] [CrossRef]
- Jha, M.K.; Gassman, P.W.; Secchi, S.; Gu, R.; Arnold, J.G. Effect of watershed subdivision on SWAT flow, sediment, and nutrient predictions. J. Am. Water Resour. Assoc. 2004, 40, 811–825. [Google Scholar] [CrossRef]
- Jha, M.K.; Pan, Z.; Takle, E.S.; Gu, R. Impacts of climate change on streamflow in the Upper Mississippi River Basin: A regional climate model perspective. J. Geophys. Res. 2004, 109, D09105. [Google Scholar]
- Stone, M.C.; Hotchkiss, R.H.; Hubbard, C.M.; Fontaine, T.A.; Mearns, L.O.; Arnold, J.G. Impacts of climate change on Missouri River basin water yield. J. Am. Water Resour. Assoc. 2001, 37, 1119–1130. [Google Scholar] [CrossRef]
- Whittemore, R.C. The BASINS Model. Water Environ. Technol. 1998, 10, 57–61. [Google Scholar]
- SWAT Literature Database for Peer-reviewed Articles. Available online: https://www.card.iastate.edu/swat_articles (accessed on 20 January 2011).
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.-G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Allen, P.M.; Walker, C. Continental scale simulation of the hydrologic balance. J. Am. Water Resour. Assoc. 1999, 35, 1037–1052. [Google Scholar] [CrossRef]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of daily and monthly stream discharge from small watershed using the SWAT Model. Trans. ASAE 2000, 43, 1431–1439. [Google Scholar] [CrossRef]
- Sexton, A.M.; Shismohammadi, A.; Sedghi, A.M.; Montas, H.J. Impact of parameter uncertainty on critical SWAT output simulations. Trans. ASABE 2011, 54, 461–471. [Google Scholar] [CrossRef]
- Shen, Z.; Hong, Q.; Yu, H.; Niu, J. Parameter uncertainty analysis of non-point source pollution from different land use types. Sci. Total Environ. 2010, 408, 1971–1978. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.R.; Srinivasan, R.; Bosch, D. Calibration and uncertainty analysis of the SWAT model using Genetic Algorithms and Bayesian Model Averaging. J. Hydrol. 2009, 374, 307–317. [Google Scholar] [CrossRef]
- Tolson, B.A.; Shoemaker, C.A. Efficient prediction uncertainty approximation in the calibration of environmental simulation models. Water Resour. Res. 2008, 44, 1–19. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation, Version 2000; Blackland Research Center, Texas Agricultural Experiment Station: Temple, TX, USA, 2000. [Google Scholar]
- Upper Mississippi River Basin Loading Database (Nutrients and Sediments). Available online: http://www.umesc.usgs.gov/data_library/sediment_nutrients/sediment_nutrient_page.html (accessed on 20 January 2011).
- U.S. Environmental Protection Agency (USEPA). BASINS 3.0: Better Assessment Science Integrating Point and Nonpoint Sources; U.S. Environmental Protection Agency, Office of Water, Office of Science and Technology: Washington, DC, USA, 2001. [Google Scholar]
- Di Luzio, M.; Srinivasan, R.; Arnold, J.G.; Neitsch, S.L. Soil and Water Assessment Tool: ArcView GIS Interface Manual: Version 2000, GSWRL Report 02-03, BRC Report 02-07; Texas Water Resources Institute TR-193: College Station, TX, USA; 346.
- U.S. Department of Agriculture (USDA). State Soil Geographic (STATSGO) Data Base: Data Use Information; Miscellaneous Publication Number 1492; U.S. Department of Agriculture: Fort Worth, TX, USA, 1994. [Google Scholar]
- Iowa Environmental Mesonet—A weather database for the state of Iowa. Available online: http://www.mesonet.agron.iastate.edu (accessed on 20 January 2011).
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: New York, NY, USA, 1992. [Google Scholar]
- Gu, R.; Li, Y. River temperature sensitivity to hydraulic and meteorological parameters. J. Environ. Manage. 2002, 66, 43–56. [Google Scholar] [CrossRef] [PubMed]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jha, M.K. Evaluating Hydrologic Response of an Agricultural Watershed for Watershed Analysis. Water 2011, 3, 604-617. https://doi.org/10.3390/w3020604
Jha MK. Evaluating Hydrologic Response of an Agricultural Watershed for Watershed Analysis. Water. 2011; 3(2):604-617. https://doi.org/10.3390/w3020604
Chicago/Turabian StyleJha, Manoj Kumar. 2011. "Evaluating Hydrologic Response of an Agricultural Watershed for Watershed Analysis" Water 3, no. 2: 604-617. https://doi.org/10.3390/w3020604
APA StyleJha, M. K. (2011). Evaluating Hydrologic Response of an Agricultural Watershed for Watershed Analysis. Water, 3(2), 604-617. https://doi.org/10.3390/w3020604





