1. Introduction
The Water Framework Directive (WFD) aims to achieve the ambitious goal of attaining good qualitative and quantitative status of all European water bodies, rivers, lakes, groundwater bodies and coastal waters by 2015, in agreement with defined timelines and different programs [
1]. Also, WFD committed European Union member states to submit their river basin management plans to the European Commission in March 2010 [
2]. Among the actions in response to these demands, the WFD encourages Member States to direct their efforts towards wastewater reuse [
3]. Wastewater reuse is becoming particularly important in those zones where the water resource is quantitatively and qualitatively scarce [
4,
5]. On the other hand, the WFD also provides the bases to achieve a sustainable use of water for the long term, taking into account environmental, economic and social considerations [
6].
Selecting a sustainable treatment for wastewater reuse facilities presents a serious challenge for project managers as well as for other stakeholders and actors involved in the decision-making process [
7]. There are several factors that determine which is the most appropriate treatment technology. These factors depend on the special needs and characteristics of each site, so they may be different from place to place. So, due to contextual differences that exist among countries, an appropriate technology for one specific site might not be suitable for another. The complexity of the problem stems from the existence of a number of factors that influence the selection of appropriate technology [
8,
9]. Therefore, for each case, there are several combinations of wastewater reclamation and reuse treatments. Moreover, the appropriate disinfection technology, or reuse level should be studied specifically for each treatment plant. Furthermore, the decision makers have an additional difficulty because they must simultaneously consider treatment cost, water quality goals and sustainability criteria. Therefore, tangible and intangible criteria need to be analyzed together. This research work has focused on implementing sustainability criteria in decision making for selecting wastewater disinfection technology.
Each regeneration technology has certain characteristics and the choice of appropriate technology for each reuse project should be made depending on many factors, including the quality and volume of water to regenerate, the quality that must be reached for use, the capital costs, the operation and maintenance costs, land requirements, the reliability, and environmental and social criteria among others. Therefore, the suitable technique is that which provides higher performance at a lower cost, but not only, must also take into account what is sustainable in terms of meeting local needs. So, the problem is to select the optimal available technology to implement in a particular site, and to meet a specific wastewater treatment objective. The regeneration treatments can be classified into pretreatments and disinfecting treatments. The pretreatments are a prior step to disinfection and aim to prepare the water for proper disinfecting, removing solids and organic matter, mainly. Disinfection treatments reduce levels of pathogens, and may also mean adding a residual level of disinfectant to reclaimed water. However, one should avoid the generation of disinfectant. Some of the main existing technologies of wastewater regeneration are listed in
Table 1. On the other hand, the development of new technologies and the improvement of some of the existing technologies, making them economically competitive, have created major difficulties in selecting an optimal technology for a specific case.
Table 1.
Main technologies of regeneration.
Table 1.
Main technologies of regeneration.
| Regeneration process | Type | Technology |
|---|
| Pretreatment | Physical | Sand filter, ultrafiltration |
| Physical and Chemical | Coagulation and flocculation and sedimentation/filtration |
| Physical and Biological | Infiltration-percolation, constructed wetlands |
| Disinfection | Physical | Ultraviolet radiation, reverse osmosis |
| Chemical | Chlorination, ozonation |
| Biological | Natural Systems (maturation ponds, constructed wetlands,…) |
The proposed methodology, which integrates the analytic hierarchy process (AHP) with a Delphi technique, provides project managers with a tool to evaluate multi-criteria and multi-alternative problems which involve non-commeasurable decision criteria [
10,
11]. Other multi-criteria decision analysis techniques (MCDA) have been applied in the field of wastewater infrastructures. Some of them are aimed to solve the problem of location of a wastewater treatment plant using methodologies based on the analytic hierarchy process under fuzziness [
12,
13], or by use of fuzzy technique for order of preference by similarity to an ideal solution [
14]. Methodologies such as Promethee V can also be found to assist the decision maker in selecting alternatives for rehabilitating water networks [
15]. Methodologies which integrate analytical hierarchy process and grey relation analysis have been proposed in the optimal selection of full scale tannery effluent treatment plants [
16], or the application of AHP with life cycle assessment, life cycle costing, and field data in selection of wastewater treatment alternatives [
17]. Hybrid stochastic-interval analytic hierarchy process and Monte Carlo simulation have been applied in determining the ultimate use of the treated water [
18].
The expert system proposed to select the optimal disinfection treatment is a hybrid method combining the AHP with the Delphi method and the VIKOR technique. The AHP procedure is capable of dealing with traditional economical criteria together with system sustainability, reliability, risks to human health and to the environment, social aspects, and other criteria non-commensurable. The Delphi technique is performed to facilitate an efficient panel of experts’ dynamic process. Finally, the VIKOR technique finds a compromise solution that is closest to the ideal in the decision making process addressing conflicting and non-commensurable criteria. The disinfection techniques are evaluated according to all established criteria. The compromise solution provides maximum utility of the majority, and minimum use of the opponent. This paper presents a hybrid multiple criteria model for selecting the best sustainable disinfection technique for wastewater reuse projects.
2. Design of the Decision Hierarchy Structure
Selecting a suitable technological technique for wastewater treated disinfection is always associated with different multiobjective and hierarchy features [
19]. The first phase of the Delphi-AHP process has been exploration of the disinfection treatments and criteria under discussion between experts. At the beginning of the project, there are many incidences where no information is available, which is why in these early stages expert judgment is especially useful [
20]. The experts were selected among wastewater treatment engineers and project managers with diverse experience in the design, construction, control and operation of wastewater treatment plants. Initially, 15 experts from consulting firms, construction companies, control and operation of wastewater treatment plants, government and universities were consulted. Eventually, three of them were discarded due to the inconsistency of their responses. The process of questionnaire development and data collection lasted three months, while processing them and getting results took just one month. The costs associated with the proposed methodology stem only from the work done by the project engineers. The same expert panel was used for all the questionnaires.
In this case, an anonymous questionnaire where each expert contributes with additional criteria or techniques that they feel are pertinent to the goal has been used. The following step was to feed back the collated information and ask them to reconsider their proposals to move toward a consensus. Those criteria and techniques that the expert panel considers as low importance are removed [
21].
The hierarchy structure of the model is schematically shown in
Figure 1. The first level explains the overall objective of the decision problem, that is, the selection of a disinfection technology for treated wastewater reuse, the second level shows the subordinate criteria based on which optimal disinfection treatment is selected and the third level is the disinfection technologies which are to be prioritized. This hierarchy system can be tailored according to particular conditions.
Figure 1.
Hierarchy for selecting a sustainable disinfection technique for wastewater reuse projects.
Figure 1.
Hierarchy for selecting a sustainable disinfection technique for wastewater reuse projects.
The criteria considered mainly consist of technical performance, economic profit and sustainability criteria. Decision makers usually take a number of indices into account for the evaluation of these concepts. In this case, the criteria evaluated were as follows:
Reliability of the system (RS). The selected technology must be reliable, that is, the system must have adequate performance, under specific conditions and for a period of time [
22]. This criterion considers the following aspects of reliability: the variability of treatment effectiveness under normal and emergency operation, the probability of mechanical failures, the impacts of failures upon effluent quality, the way the process responds to changes in affluent, and the minimum requirements for water quality inlet to optimal performance of technology.
Operational simplicity (OS). The choice should take into account the special needs of system operations and maintenance. If the operation of the system requires skilled workers, it can be rejected by decision makers, in particular if located in remote areas. Operational and maintenance simplicity should be a prime affair, since simplicity could determine the long-term operating success of the system.
Efficiency in reducing pathogenic microorganisms (EP). Wastewater treated must be disinfected to the extent that the final water quality will comply with the regulatory standard or requirements for a specific reuse. This criterion evaluates not only the ability to eliminate pathogens, but also the ability to remove other undesirable contaminants. The efficiency of a process can be evaluated on past experience, and from full-scale plants or pilot-plant studies [
23].
Capital cost (CC) is another major aspect to take into account in the economic criteria, which greatly influences the selection of a particular technology [
16]. This criterion includes, on one hand, costs for construction works and the procurement and installation of electro-mechanical equipment necessary to implement the full system. On the other, it includes the procurement cost of the space necessary to accommodate the facilities.
Operation & Maintenance cost (OM) can be as important, or even more, than the construction costs over the life-time of the system [
24]. The criterion includes all costs associated with the different processes of operation and maintenance of each technological alternative, such as maintenance and repair cost, personnel cost, energy cost and chemical products cost among others.
Additional treatments (AT). Some disinfection technologies need, previously or subsequently, additional treatments, or even subsequent treatments of waste generated. Dechlorination [
25], the destruction of residual ozone, rejection of water treatment in membrane systems, among others processes, may be necessary and should be considered as a cost.
Environmental impacts (EI) take into consideration the point of view of the local population affected by the facilities, focusing on the inconvenience the facility may cause: the production of unwanted noises in the surrounding area, the aesthetic or visual impact caused by the presence of the facilities on the landscape, bad smells which can be produced by the different treatment technologies, and other unwanted emissions like gases or vapors that should be minimized.
Use of natural resources (NR) shows the consumption of natural resources, mainly energy, which is determined by the different treatment technologies [
26].
Safety Risk (SR). Evaluation of both human and environmental risks, that is, to assess the safety for workers in different processes, and the security in case of bad operations or accidents.
Nowadays, the technologies mainly used in the disinfection of treated wastewater are:
Chlorination (CLH). Chlorination is the addition of chlorine to water as chlorine gas, sodium or calcium hypochlorite, or chlorine dioxide. The required quantity depends on the water and on the disinfection requirements. Chlorine is a disinfectant with strong disinfection capability and low cost, so it is widely applied around the world [
27].
Ozonization (OZO). Ozone is one of the most powerful disinfectants, due to its high oxidizing capacity, suitable for the treatment of water. Ozone emerged as a popular alternative to chlorine. Compared to chlorine, ozonization is a highly effective agent that readily oxidizes organic matter, various microbes, pesticides and chemical residuals, at low concentrations and short contact times [
28]. Its greatest advantage is that not produce unwanted by-products, since ozone becomes oxygen. Disinfection by ozone has increased popularity in recent years.
Ultraviolet radiation (UVR) technology is one of the most applied in wastewater treatment plants, as tertiary treatment for disinfection of effluent. This is because of its ability to inactivate a wide range of pathogens without the formation of harmful byproducts [
29]. In ultraviolet disinfection, water is exposed to short wave ultraviolet light. This is an effective germicide and does not affect the water quality. This is a technology that applies both to drinking water treatment and disinfection of treated wastewater.
Membrane filtration (MFI) can be used instead of the decanter to separate solids from the liquid. In waste water treatments, membrane filtration can be defined as a separation process that uses semi permeable membrane to divide the treated wastewater into two portions: a permeate with the material passing through the membranes, and a retentate consisting of residues that do not pass through the filter. The main types of membrane filtration are: microfiltration, ultrafiltration, nanofiltration, and reverse osmosis [
30,
31].
Natural systems (NSY). Photochemical reactions induced by natural light have been known for some time. Maturation ponds, and more recently, constructed wetlands, are shown as natural systems to take into consideration disinfection of treated wastewater for reuse in many special cases [
32]. These systems have proven to be efficient at removing not only the conventional water quality parameters but also to have great potential for the elimination of emerging organic contaminants [
33,
34]. Waste stabilization ponds are a method of wastewater treatment, which has been applied where land availability is not a problem. Among the types of ponds that are usually designed, as tertiary treatment, a maturation pond is a pond, normally 0.9–1.5 m deep, primarily responsible for pathogen removal by various mechanisms, including UV disinfection and daily high pH levels.
3. Pairwise Comparison of Elements of the Hierarchical Structure and Consistency Analysis for the Criteria
The AHP methodology employs a pairwise comparison technique which reduces the complexity of the problem, since only two elements are compared at the same time. This pairwise comparison technique is developed in three steps: elaborating a comparison matrix at each level of the hierarchy, calculating the priorities for each element of the hierarchy, and analyzing consistency [
35].
To determine the relative weights of criteria, experts were asked by a second questionnaire to make pairwise comparisons using a 1–9 preference scale (see
Table 2). This scale has been widely validated for its effectiveness through theoretical comparisons with a large number of other scales [
36]. This second questionnaire was filled in by each expert indicating his preference for each criterion. The results of the survey are included in
Table 3. Then, pairwise comparison matrix for the criteria is constructed using the average value obtained as geometric mean of each expert values (
aij). These average values yield a reciprocal
n-by-
n matrix
A = [
aij ], where
aii = 1 (on the diagonal) and
aji = 1/
aij. The principal eigenvector of
A is the desired priority vector ω. To find this priority vector, the linear system
Aω = λ ω must be solved [
37], and hence det[
A − λ·
I] = 0 must be calculated.
Table 2.
Preference scale for pairwise comparison.
Table 2.
Preference scale for pairwise comparison.
| Intensity of importance | Definition | Explanation |
|---|
| 9 | Extremely preferred | A criterion or technique is extremely preferred to another |
| 7 | Very strongly preferred | A criterion or technique is very strongly preferred to another |
| 5 | Moderately preferred | A criterion or technique is moderately preferred to another |
| 3 | Slightly preferred | A criterion or technique is slightly preferred to another |
| 1 | Equally preferred | A criterion or technique is equally preferred to another |
| 1/3 | Slightly non-preferred | A criterion or technique is slightly non-preferred to another |
| 1/5 | Moderately non-preferred | A criterion or technique is moderately non-preferred to another |
| 1/7 | Strongly non-preferred | A criterion or technique is very strongly non-preferred to another |
| 1/9 | Extremely non-preferred | A criterion or technique is extremely non-preferred to another |
Table 3.
Evaluation results of each expert of the main criteria with respect to the overall goal.
Table 3.
Evaluation results of each expert of the main criteria with respect to the overall goal.
| Pairwise Criteria | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | E10 | E11 | E12 | Geometric Mean |
|---|
| RS | vs | OS | 7 | 9 | 3 | 7 | 7 | 3 | 7 | 9 | 3 | 3 | 7 | 1/3 | 4.2702 |
| RS | vs | EP | 9 | 3 | 3 | 9 | 9 | 5 | 9 | 3 | 5 | 7 | 7 | 3 | 5.4258 |
| RS | vs | CC | 3 | 1 | 1/5 | 3 | 3 | 1/3 | 3 | 1 | 1/5 | 3 | 3 | 1/7 | 1.0277 |
| RS | vs | OM | 3 | 5 | 1/7 | 3 | 3 | 1/5 | 1 | 7 | 1/3 | 1/3 | 3 | 1/5 | 1.0502 |
| RS | vs | AT | 5 | 9 | 1/5 | 5 | 5 | 1/3 | 3 | 9 | 3 | 3 | 5 | 1/3 | 2.3634 |
| RS | vs | EI | 5 | 5 | 3 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 7 | 1 | 4.3094 |
| RS | vs | NR | 9 | 5 | 5 | 9 | 9 | 7 | 7 | 5 | 7 | 5 | 5 | 3 | 6.0372 |
| RS | vs | SR | 7 | 7 | 3 | 5 | 7 | 5 | 7 | 7 | 7 | 5 | 7 | 5 | 5.8307 |
| OS | vs | EP | 3 | 1/7 | 1 | 3 | 3 | 3 | 3 | 1/7 | 3 | 3 | 3 | 5 | 1.7198 |
| OS | vs | CC | 1/5 | 1/9 | 1/5 | 1/5 | 1/5 | 1/3 | 1/5 | 1/9 | 1/5 | 1/5 | 1/7 | 1/5 | 0.1840 |
| OS | vs | OM | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 | 1/7 | 1/3 | 1/7 | 1/7 | 1/5 | 1/3 | 0.2002 |
| OS | vs | AT | 1/3 | 1 | 1/5 | 1/3 | 1/3 | 1/3 | 1/5 | 1 | 1 | 1/5 | 1/5 | 1 | 0.4055 |
| OS | vs | EI | 1/3 | 1/5 | 3 | 1/3 | 1/3 | 3 | 1/3 | 1/5 | 5 | 1/3 | 1/3 | 3 | 0.6645 |
| OS | vs | NR | 3 | 1/5 | 5 | 3 | 3 | 5 | 1 | 1/5 | 3 | 1 | 1/5 | 5 | 1.4422 |
| OS | vs | SR | 1 | 1/3 | 3 | 1/3 | 1 | 3 | 1 | 1/3 | 5 | 1 | 1/3 | 7 | 1.1198 |
| EP | vs | CC | 1/7 | 1/3 | 1/5 | 1/7 | 1/7 | 1/5 | 1/7 | 1/3 | 1/7 | 1/7 | 1/7 | 1/9 | 0.1704 |
| EP | vs | OM | 1/7 | 3 | 1/5 | 1/7 | 1/7 | 1/7 | 1/9 | 5 | 1/5 | 1/9 | 1/7 | 1/7 | 0.2511 |
| EP | vs | AT | 1/5 | 7 | 1/3 | 1/5 | 1/5 | 1/3 | 1/7 | 7 | 1/3 | 1/7 | 1/5 | 1/5 | 0.3886 |
| EP | vs | EI | 1/5 | 3 | 3 | 1/5 | 1/5 | 3 | 1/5 | 3 | 3 | 1/5 | 1/3 | 1/3 | 0.6730 |
| EP | vs | NR | 1 | 3 | 3 | 3 | 1 | 5 | 1/3 | 3 | 5 | 1/3 | 1/5 | 1 | 1.3733 |
| EP | vs | SR | 1/3 | 5 | 3 | 1/5 | 1/3 | 3 | 1/3 | 5 | 3 | 1 | 1/3 | 3 | 1.1435 |
| CC | vs | OM | 1 | 5 | 1 | 1 | 1 | 1/3 | 1/3 | 7 | 3 | 1/3 | 1/3 | 3 | 1.1198 |
| CC | vs | AT | 3 | 9 | 3 | 3 | 3 | 3 | 1 | 9 | 5 | 1 | 3 | 5 | 3.2666 |
| CC | vs | EI | 3 | 5 | 5 | 3 | 3 | 5 | 3 | 5 | 5 | 3 | 7 | 7 | 4.2745 |
| CC | vs | NR | 7 | 5 | 7 | 7 | 7 | 7 | 5 | 5 | 9 | 5 | 3 | 9 | 6.0802 |
| CC | vs | SR | 5 | 7 | 5 | 5 | 5 | 5 | 5 | 7 | 9 | 5 | 5 | 9 | 5.8327 |
| OM | vs | AT | 3 | 5 | 3 | 3 | 1 | 5 | 3 | 3 | 5 | 3 | 3 | 3 | 3.1105 |
| OM | vs | EI | 3 | 1 | 5 | 3 | 3 | 7 | 5 | 1/3 | 7 | 5 | 5 | 5 | 3.2479 |
| OM | vs | NR | 7 | 1 | 5 | 5 | 5 | 9 | 7 | 1/3 | 9 | 9 | 3 | 7 | 4.2129 |
| OM | vs | SR | 5 | 3 | 5 | 5 | 3 | 7 | 7 | 3 | 9 | 7 | 5 | 9 | 5.2794 |
| AT | vs | EI | 1 | 1/5 | 3 | 3 | 1 | 3 | 3 | 1/5 | 5 | 3 | 3 | 3 | 1.6599 |
| AT | vs | NR | 5 | 1/5 | 3 | 5 | 5 | 5 | 5 | 1/5 | 5 | 5 | 3 | 5 | 2.6854 |
| AT | vs | SR | 3 | 1/3 | 3 | 1/3 | 3 | 3 | 5 | 1/3 | 5 | 3 | 3 | 7 | 2.0240 |
| EI | vs | NR | 5 | 1 | 1 | 5 | 5 | 3 | 3 | 1 | 3 | 3 | 1/3 | 3 | 2.1567 |
| EI | vs | SR | 3 | 3 | 1 | 1/3 | 3 | 1 | 3 | 3 | 3 | 1/3 | 3 | 5 | 1.8074 |
| NR | vs | SR | 1/3 | 3 | 1 | 1/5 | 1/3 | 1/3 | 1 | 3 | 1 | 1/5 | 5 | 3 | 0.8745 |
| CR | 0.034 | 0.064 | 0.082 | 0.090 | 0.036 | 0.078 | 0.027 | 0.099 | 0.098 | 0.079 | 0.093 | 0.054 | 0.0081 |
The involvement of experts may be affected by bias, misinterpretation and self-perception in general that could lead to inconsistencies in decision-making [
38]. The Saaty’s AHP methodology allows the evaluation of the consistency of the pairwise comparison matrix by obtaining an index called consistency ratio (CR). A maximum for CR is established depending on the order of the matrix, which should not be exceeded in order to guarantee the procedure. This consistency ratio is determined by the ratio between the consistency index (CI) and the random consistency index (RCI):
The determination of the consistency index is obtained by the following relation:
where λ
max is the maximum eigenvalue of the pairwise comparison matrix and n is the order of matrix. The RCI value is fixed and depends of the order of the matrix, as shown in
Table 4. To check if CR is adequate, Saaty suggests that if that ratio is upper to 0.10, for order of matrix (
n) upper than four, the expert opinions may be too inconsistent to be trustworthy, and therefore those subjective judgments should be revised [
35]. This verification was obtained not only for the mean values, but also for the judgment of each expert independently (see
Table 3). As can be seen, the consistency values are within the tolerance limits. Pairwise comparison matrix, priority vector and consistency ratio are shown in
Table 5, and relative weights of criteria in
Table 6.
Table 4.
Random consistency index (RCI).
Table 4.
Random consistency index (RCI).
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| RCI | 0 | 0 | 0.52 | 0.89 | 1.11 | 1.25 | 1.35 | 1.40 | 1.45 | 1.49 |
Table 5.
Pairwise comparison matrix, priority vector and consistency ratio for the criteria.
Table 5.
Pairwise comparison matrix, priority vector and consistency ratio for the criteria.
| RS | OS | EP | CC | OM | AT | EI | NR | SR | Priority vector |
|---|
| RS | 1.0000 | 4.2702 | 5.4258 | 1.0277 | 1.0502 | 2.3634 | 4.3094 | 6.0372 | 5.8307 | 0.2271 |
| OS | 0.2342 | 1.0000 | 1.7198 | 0.1840 | 0.2002 | 0.4055 | 0.6645 | 1.4422 | 1.1198 | 0.0481 |
| EP | 0.1843 | 0.5815 | 1.0000 | 0.1704 | 0.2511 | 0.3886 | 0.6730 | 1.3733 | 1.1435 | 0.0419 |
| CC | 0.9730 | 5.4351 | 5.8683 | 1.0000 | 1.1198 | 3.2666 | 4.2745 | 6.0802 | 5.8327 | 0.2437 |
| OM | 0.9730 | 4.9949 | 3.9818 | 0.8930 | 1.0000 | 3.1105 | 3.2479 | 4.2129 | 5.2794 | 0.2083 |
| AT | 0.4231 | 2.4662 | 2.5735 | 0.3061 | 0.3215 | 1.0000 | 1.6599 | 2.6854 | 2.0240 | 0.0919 |
| EI | 0.2321 | 1.5050 | 1.4858 | 0.2339 | 0.3079 | 0.6025 | 1.0000 | 2.1567 | 1.8074 | 0.0635 |
| NR | 0.1656 | 0.6934 | 0.7282 | 0.1645 | 0.2374 | 0.3724 | 0.4637 | 1.0000 | 0.8745 | 0.0359 |
| SR | 0.1715 | 0.8930 | 0.8745 | 0.1714 | 0.1894 | 0.4941 | 0.5533 | 1.1435 | 1.0000 | 0.0397 |
| λmax = | 9.0942 | CI = | 0.0118 | CR = | 0.0081 | <0.10 | | | | |
Table 6.
Relative weights of criteria.
Table 6.
Relative weights of criteria.
| Acronym | Criteria | Weight |
|---|
| RS | Reliability of the system | 0.2268 |
| OS | Operational simplicity | 0.0478 |
| EP | Efficiency in reducing pathogens | 0.0415 |
| CC | Capital cost | 0.2442 |
| OM | O&M cost | 0.2092 |
| AT | Additional treatments | 0.0919 |
| EI | Environmental impacts | 0.0632 |
| NR | Use of natural resources | 0.0357 |
| SR | Safety Risk | 0.0396 |
4. Evaluation of Disinfection Technologies According to Each Criterion
Finally, a third questionnaire was sent to the panel of experts to evaluate the alternatives for each criterion. In this last questionnaire, the experts indicate their preference by pairwise comparison, of the best disinfection of treated wastewater alternative, basing only on each of the criteria individually. For this evaluation, the same 1–9 preference scale shown in
Table 2 was used. To better illustrate the model, as an example, the result of this third questionnaire for evaluating disinfection technologies with respect to a particular criterion—the reliability of the system—is shown in
Table 7. As in the evaluation criteria, the geometric mean of the results of each pairwise comparison was used.
The next step was to construct the pairwise comparison matrices for the disinfection technologies. Then, priority vectors were obtained by applying eigenvector method for each pairwise comparison matrix. Moreover, also consistency analysis was performed for each case.
Table 8 shows results of all techniques assessments for the first criterion. To obtain overall priorities, a matrix of priority vectors for disinfection technologies was constructed as shown in
Table 9. Finally, the overall priority result was obtained by matrix multiplication between the matrix of priority vectors for disinfection technologies and the priority vector of the criteria as shown also in
Table 9.
Table 7.
Evaluation results of each expert of technologies based on the criterion reliability of the system.
Table 7.
Evaluation results of each expert of technologies based on the criterion reliability of the system.
| Pairwise Techniques | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | E10 | E11 | E12 | Geometric Mean |
|---|
| CHL | vs | OZO | 1/3 | 1 | 1/3 | 1/3 | 1/3 | 1 | 1/3 | 1/3 | 1 | 1/3 | 1 | 1/3 | 0.4807 |
| CHL | vs | UVR | 1/7 | 1/5 | 1/7 | 3 | 1/7 | 1/5 | 1/7 | 1/7 | 1/5 | 3 | 1/9 | 1/7 | 0.2528 |
| CHL | vs | MFI | 1/5 | 1/7 | 1/5 | 7 | 1/5 | 1/7 | 1/5 | 1/5 | 1/7 | 7 | 1/5 | 1/5 | 0.3325 |
| CHL | vs | NSY | 3 | 1 | 3 | 1/5 | 3 | 1 | 3 | 3 | 1 | 1/5 | 1/7 | 3 | 1.1263 |
| OZO | vs | UVR | 1/5 | 1/5 | 1/5 | 3 | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 | 3 | 1/9 | 1/5 | 0.2991 |
| OZO | vs | MFI | 1/3 | 1/7 | 1/3 | 9 | 1/3 | 1/7 | 1/3 | 1/3 | 1/7 | 7 | 1/5 | 1/3 | 0.4384 |
| OZO | vs | NSY | 5 | 1 | 5 | 1/3 | 5 | 1 | 5 | 5 | 1 | 1/3 | 1/7 | 5 | 1.5832 |
| UVR | vs | MFI | 3 | 1/3 | 3 | 7 | 3 | 1/3 | 3 | 3 | 1/3 | 5 | 5 | 3 | 2.0240 |
| UVR | vs | NSY | 9 | 3 | 9 | 1/5 | 9 | 3 | 9 | 9 | 3 | 1/5 | 3 | 9 | 3.3088 |
| MFI | vs | NSY | 7 | 7 | 7 | 1/7 | 7 | 7 | 7 | 7 | 7 | 1/7 | 1/3 | 7 | 2.8393 |
Table 8.
Priority vector and consistency analysis of the pairwise comparison matrix for the disinfection technologies with respect to reliability of the system.
Table 8.
Priority vector and consistency analysis of the pairwise comparison matrix for the disinfection technologies with respect to reliability of the system.
| CHL | OZO | UVR | MFI | NSY | Priority vector |
|---|
| CHL | 1.0000 | 0.4807 | 0.2528 | 0.3325 | 1.1263 | 0.0911 |
| OZO | 2.0801 | 1.0000 | 0.2991 | 0.4384 | 1.5832 | 0.1426 |
| UVR | 3.9563 | 3.3437 | 1.0000 | 2.0240 | 3.3088 | 0.4087 |
| MFI | 3.0072 | 2.2811 | 0.4941 | 1.0000 | 2.8393 | 0.2619 |
| NSY | 0.8879 | 0.6316 | 0.3022 | 0.3522 | 1.0000 | 0.0956 |
| λmax = | 9.0942 | CI = | 0.0118 | CR = | 0.0081 | < 0.10 |
Table 9.
Matrix of priority vectors and global priorities for each of the disinfection technologies.
Table 9.
Matrix of priority vectors and global priorities for each of the disinfection technologies.
| RS | OS | EP | CC | OM | AT | EI | NR | SR | Global Priorities |
|---|
| CHL | 0.0900 | 0.2415 | 0.0869 | 0.4309 | 0.1688 | 0.0692 | 0.0569 | 0.0986 | 0.0481 | 0.1915 |
| OZO | 0.1415 | 0.1429 | 0.1263 | 0.1576 | 0.1634 | 0.1018 | 0.1233 | 0.1590 | 0.1556 | 0.1458 |
| UVR | 0.4115 | 0.1128 | 0.4496 | 0.2999 | 0.1195 | 0.1858 | 0.4382 | 0.2153 | 0.3968 | 0.2838 |
| MFI | 0.2621 | 0.0591 | 0.3005 | 0.0432 | 0.0388 | 0.2885 | 0.0693 | 0.0386 | 0.0613 | 0.1281 |
| NSY | 0.0949 | 0.4437 | 0.0367 | 0.0684 | 0.5095 | 0.3547 | 0.3123 | 0.4885 | 0.3382 | 0.2507 |
5. Compromise Solution and Stability Analysis Applying VIKOR
The VIKOR method was developed to optimize multicriteria complex systems [
39,
40]. The aim of this methodology is to determine a compromise solution and establish the stability of the adopted decision. [
41,
42]. The method ranks the disinfection technologies
Di according to the value of three scalar quantities (
Si,
Ri, and
Qi) to be calculated for each option [
43]. The input data are the elements
dij of the decision matrix.
The explanation of this methodology involves the following steps:
Step 1. For each criterion, the best dj* and worst dj− performances among all the disinfection techniques are determined; dj* = max (dij, j = 1, …, J), dj− = min (dij, j = 1, …, J), if the i-th function is benefit type; dj* = min (dij, j = 1, …, J), dj− = max (dij, j = 1, …, J), if the i-th function is cost type.
Step 2. Calculate the values
Sj and
Rj,
j = 1, 2, ...,
J, by the relations:
where
pj is the priority of each criterion.
Step 3. Compute the values
Qj,
j = 1, 2, …,
J, by the relation:
The meaning of
S*,
S−,
R*, and
R− is:
The parameter υ shows the weights of most of the criteria strategy or the largest group’s utility value. This parameter is fixed by the decision maker in the [0,1] interval giving a different weight of importance to each addend into the Qi expression. Practically, if one assumes υ > 0.5, more importance is given to the first term and hence to the global performance of the disinfection technology in respect to the whole of the criteria. Using a υ value smaller than 0.5 gives more weight to the second term that is related to the magnitude of the worst performances exhibited by the disinfection technologies in respect to each single criterion. In our case, as the two aspects are considered equally relevant, υ = 0.5 was used.
Step 4. Rank the disinfection technologies by the values S, R and Q, from the minimum value, resulting in three ranking lists.
Step 5. The best disinfection technique classified by the value of
Q is the compromise solution, provided that the following conditions are met [
44]:
Acceptable advantage: when QD(2) − QD(1) ≥ ΔQ; where QD(2) is the disinfection technology with second position in the ranking list by Q; ΔQ = 1/(J − 1), where J is the number of disinfection technologies evaluated.
Acceptable stability: The compromise solution is stable if also it is the best ranked by S or by R, or by both, as well. This compromise solution is stable within the decision-making process, which could be: voting by majority rule (when υ > 0.5 is needed), or by consensus υ ≈ 0.5, or with veto (υ < 0.5).
When any of these conditions is not met, a set of compromise solutions is proposed:
Disinfection technologies D(1) and D(2) if only the second condition is not satisfied;
Disinfection technologies D(1), D(2), …, D(k) if the first condition is not satisfied; D(k) is obtained by the relation QD(k) − QD(1) ≈ ΔQ (the positions of these techniques are in closeness).
The best disinfection technology is determined by the compromise ranking method. This compromise solution provides a maximum group utility of the majority, with measure S, which represents concordance, and a minimum of disapproval of the opponent, with measure R which represents disagreement. The methodology defines the weight stability intervals for the compromise solution with the starting input data given by the experts.
This case study is based on the decision matrix in
Table 9. Then, the best
dj* and worst
dj− values and the weights of criteria
pj, are evaluated to obtain the
Si and
Ri values in
Table 10. In the same table, the
S*,
S−,
R*, and
R− values are also reported, and finally, the
Qi value is determined for each option, assuming the value 0.5 for υ. The ranking of the techniques by
R,
S and
Q in descending order is shown in
Table 11.
Table 10.
Si, Ri, and Qi values (υ = 0.5) for each disinfection technology.
Table 10.
Si, Ri, and Qi values (υ = 0.5) for each disinfection technology.
| Disinfection | CHL | OZO | UVR | MFI | NSY |
|---|
| Si | 0.6655 | 0.7735 | 0.3730 | 0.7779 | 0.5208 |
| Ri | 0.2268 | 0.1905 | 0.1734 | 0.2442 | 0.2284 |
| Qi | 0.7386 | 0.6157 | 0.0000 | 1.0000 | 0.5706 |
| | S* = 0.3730 | R* = 0.1734 | S− = 0.7779 | R− = 0.2442 | |
Table 11.
The ranking of projects in descending order by S, R and Q.
Table 11.
The ranking of projects in descending order by S, R and Q.
| Position | 1 | 2 | 3 | 4 | 5 |
|---|
| By S | UVR | NSY | CHL | OZO | MFI |
| By R | UVR | OZO | CHL | NSY | MFI |
| By Q | UVR | NSY | OZO | CHL | MFI |
As shown in
Table 11, the disinfection technique UVR, ultraviolet radiation, is the best ranked by
Q. Also, the conditions one and two are satisfied:
6. Conclusions
This paper presents an expert system using a hybrid method combining the AHP with the Delphi method and the VIKOR technique to select a sustainable disinfection technology for wastewater reuse projects. Technical, economic, and environmental criteria were considered to investigate the performance of the disinfection technologies. The results show that the main criteria for selecting the best technique for expert judgment are: capital cost (24.42%), reliability of the system (22.68%) and operation and maintenance costs (20.92%). It is interesting to note that economic criteria is greatly emphasized by the panel of experts, and greatly influences the selection of the disinfection technology. This fact may be because most of the experts were selected in the area of Valencia (Spain), because the study was conducted there. Although the study aims to be a general example for the application of the procedure above, it is influenced by the experience of engineers in this scenario; that is, scarce water resources, and diverse experience in the treatment of wastewater and reuse technologies, especially for the location of irrigation, and which is heavily influenced by costs. So, probably, this is the scenario that experts have often faced.
The weights of each criterion for the selection of disinfection technology are illustrated in
Figure 2.
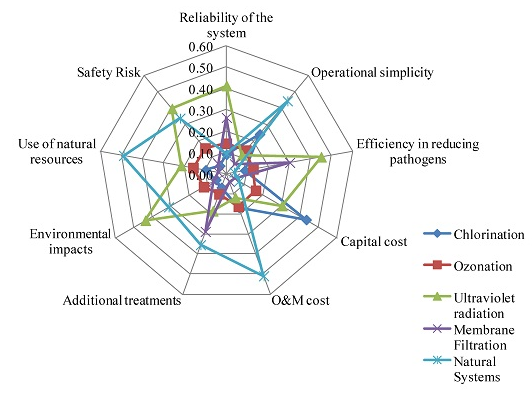
Figure 3 shows the weights of each technique for each criterion. The technologies of ultraviolet radiation and the natural systems are the better ranked. It should be noted that
Figure 3 does not consider the prioritization of criteria. However, the results from the selection of the best alternative confirm this fact, as is shown in
Figure 4: there are global priorities for each of the techniques, where the ultraviolet radiation technology is the most preferred by the experts (28.38%), followed by natural systems alternative (25.07%). Moreover, this result coincides with the fact that, nowadays, ultraviolet radiation technology is being widely implemented in the disinfection of wastewater treated for reuse. Finally, the application of the VIKOR technique verifies that this is the best choice, so it can be concluded that choosing ultraviolet radiation technology seems to give the best overall account of technical, economic, and environmental concerns.
This methodology can be tailored to the needs of each particular case, and the importance given to each criterion may be changed by the panel of experts. In conclusion, the Delphi-AHP-VIKOR expert system proposed in this paper has been shown to be a reliable method in selecting a sustainable disinfection technique for wastewater reuse projects, and the results obtained can be used to support project managers’ decisions in selecting the most suitable disinfection technology.
Figure 2.
The priorities of each criterion for the selection of disinfection techniques.
Figure 2.
The priorities of each criterion for the selection of disinfection techniques.
Figure 3.
The weights of each disinfection technology for each criterion.
Figure 3.
The weights of each disinfection technology for each criterion.
Figure 4.
Global priorities for each of the disinfection technologies.
Figure 4.
Global priorities for each of the disinfection technologies.