An Innovative Approach for Drainage Network Sizing

Abstract

In this paper, a procedure for the optimal design of rural drainage networks is presented and demonstrated. The suggested approach, exploring the potentialities offered by heuristic methods for the solution of complex optimization problems, is based on the use of a Genetic Algorithm (GA), coupled with a steady and uniform flow hydraulic module. In particular, this work has focused: on one hand, on the problems of a technical nature posed by the correct sizing of a drainage network; on the other hand, on the possibility to use a simple but nevertheless efficient GA to reach the minimal cost solution very quickly. The suitability of the approach is tested with reference to small and large scale drainage networks, already considered in the literature.

1. Introduction

The problem of the optimal design of rural drainage channels can be approached from two distinct points of view, namely the optimal design of a single channel and the optimal design of an entire channel network. Historically, due to the lack of computers and adequate numerical techniques, the optimization of the single channel’s shape and design has been considered first, and useful analytic solutions can be found in classic hydraulic engineering texts [1]. Despite the precocious availability of these results, researchers have also considered this theme recently. Guo and Hughes [2] presented an analytical procedure for the determination of the best configuration for a trapezoidal cross section of a single channel, able to minimize both frictional resistance and construction cost, taking into account the freeboard and bank slope. Mironenko et al. [3] studied the design of channels with parabolic cross-section. Loganathan [4] presented optimal conditions for a parabolic channel cross section accounting for freeboard and limitations on the velocity and channel sizes. Froehlich [5] used the Langrange’s multiplier method to determine optimal channel cross sections, incorporating in his formulation of the optimization problem, as additional constraints, both limited flow top width and depth. Monadjemi [6] used Langrange’s multipliers method to find the best hydraulic cross section area for different channel shapes. In particular, he solved the problem of optimizing the lining costs, and found that the minimization of the wetted perimeter and the minimization of the cross section area are mathematically equivalent. Swamee et al. [7,8] proposed an approach for optimal open channel design where seepage losses were also considered. Das [9] proposed an optimization model for the design of trapezoidal channels, which considers the flooding probability; the same author [10] proposed an optimization strategy to design open channels with composite lining along the perimeter. Jain et al. [11] considered spatial variations of the velocity across a proposed composite channel cross section, and approximated the solution to this problem using a Genetic Algorithm (GA). Chahar [12] faced the design of parabolic cross section channels using a nonlinear unconstrained optimization method. More recently, Reddy and Adarsh [13] used a Genetic Algorithm (GA) as Particle Swarm Optimization (PSO) to optimally design a composite trapezoidal irrigation channel.

Of course, in practical applications it is important to consider the optimal design of an entire drainage network consisting of multiple channels. With reference to this topic, few studies about the optimization of free surface rural drainage networks are available, while interest of researchers has been focused mainly on the optimal design of drainage networks. Despite their specific characteristics, there is an obvious conceptual link between these two problems. For this reason, and due to the scarcity of contributions on the topic of rural drainage network optimization, the literature available in the field of urban drainage networks will be also considered here. While numerous works focus on the optimal layout of urban drainage networks [14,15,16,17,18,19,20,21,22,23], the majority of research results concerns the optimal channel sizing of a network whose layout is already known. In other cases, the optimization procedures were oriented to solve more general problems. For instance, Lee et al. [24] proposed a methodology for efficient rehabilitation of sewer systems; Chill and Mays [25] and Zhang et al. [26] proposed different procedures to determine the optimal locations to place various types of developments in a watershed to reduce the negative impacts of urbanization on watershed stormwater systems, and then changes in flow rates and volume from natural to developed conditions; Oxley and Mays [27] proposed an optimization model, based upon the simulated annealing method, to optimize the size and location of detention basin systems including the outlet structures subject to design constraints. An interesting review of the optimal design procedures available for sewer networks has been made by Guo et al. [28].

Generally speaking, the techniques proposed for the optimal sizing of drainage networks differ by:

-

the choice of the decision variables (longitudinal slopes, ground elevations, crown elevations, etc.);

-

the constraints used during the optimization procedure;

-

one or more Objective Functions (OF) considered within the optimization procedure;

-

the optimization algorithm used;

-

the hydraulic model used to evaluate the performances of the drainage network;

-

the model used to evaluate the discharges through the network.

Classical nonlinear optimization methods, based on gradient techniques, are not satisfactory when applied to the optimal drainage network design problem, because they have a tendency to get stuck in local optima while searching for global solutions in a non-convex discrete search space. As a result of developments in Artificial Intelligence and Operation Research, different alternative optimization techniques, such as the Evolutionary Computation approaches, have emerged during the last 30 years. With reference to the ability to achieve fast results, Wang et al. [29] made a comparison between GA [30,31,32,33,34], Particle Swarm Optimization [35] and Ant Colony Algorithm [36,37,38], showing that the Ant Colony methods require minor computational burden. Afshar et al. [39] used Cellular Automata approaches, obtaining results comparable to other methods but with higher computational efficiency. Conversely, GA allows obtaining the most accurate solution [32]: this class of algorithms is very robust in handling complex problems that display large variability and intermittency in input parameters and a large degree of nonlinearity in functional relationships [40,41].

In this paper, we propose a GA procedure aiming at the optimal design of rural drainage networks, which enables the network channels to convey the required discharges with minimum construction and maintenance costs, achieving the best compromise between the numerous technical conflicting requirements. In order to develop the main structure of the optimization procedure, the network hydraulic performance is evaluated by means of a very simple hydraulic model, based on a uniform and steady state stage discharge formula, and the a priori knowledge of discharges flowing through each link of the network. However, these assumptions can be easily relaxed, considering realistic hydraulic simulators, coupled with hydrological models able to evaluate the surface runoff to the channel network [42,43].

Besides the main objective of providing a general methodology for the optimal sizing of rural drainage network channels, additional objectives are considered in this paper, namely:

-

exploring the influence, on the optimal design of the network, of the value assigned to the invert elevation of the network ending node;

-

the analysis of the influence of the technical constraint which imposes, at each junction node of the network, that the size of the channel downstream is not smaller than that of the channels upstream;

-

exploring the influence of the mutation probability, which is a GA parameter to be tuned in order to achieve good solutions [44,45,46].

In the following sections, the problem of the optimal rural drainage network design is formulated, the assumptions made are described, and the optimization model is briefly recalled. Then, two case studies are presented and analyzed. Finally, a discussion of the results obtained is carried out, and general conclusions are drawn.

2. Methods

2.1. Problem Formulation

In practical cases, the problem of the rural drainage network design can have many competing solutions, and a criterion should be defined in order to choose a solution that is optimal. In the present case, we define the optimal network that minimizes the construction cost, and the OF is defined accordingly. The optimization process needs much input data, such as the layout of the system, the ground elevation at the network nodes, the location of the network outlet, the unit costs for construction, the shape of the cross sections, the range of variability of the decision variables, and the flow discharges through the network channels. Feasible solutions should satisfy a set of constraints, in order to take into account physical limitations, technical standards and good engineering practices.

With reference to Figure 1, the constraints that can be considered are summarized as follows:

c1:

if h is the water depth corresponding to the design discharge Q, the design filling degree is defined as δ = h/(H_exc − c), where H_exc is the excavation depth and c is the ground subsidence. Overflow of the channels should be avoided: this constraint is represented by the condition δ ≤ δ_max, where δ = 1 − f_b/(H_exc − c), and f_b is a convenient freeboard. The design discharge is defined as $Q=Q_{T_2}$, where T₂ = 10 ÷ 20 years is the design return period.

c2:

a maximum excavation depth H_exc,max has to be considered in order to limit the excavation costs and to avoid excessive drainage of sub-surface flow, with subsequent need for irrigation.

c3:

in order to reduce the construction costs, the erosion of non-lined channels bottom and banks should be controlled, taking into account the effects of moderate return period flows Q_f. A criterion based on the definition of a threshold velocity V_er can be used to evaluate the start of erosion: if V_f is the velocity corresponding to the frequent flow discharge Q_f, the constraint is expressed as V_f ≤ V_er. For the evaluation of V_er, the approach proposed by USDA [47] can be used, while $Q_f=Q_{T_1}$ is the flow corresponding to a moderate return period T₁ ≤ T₂.

c4:

sediment deposition should be avoided during flow conditions that have a frequency higher than 3 ÷ 6 times per year. If V_vf is the velocity corresponding to the very frequent flow discharge Q_vf, the constraint is expressed as V_vf ≥ V_dep. The limit velocity V_dep is a function of the diameter of the particles carried by flow, while $Q_{vf}\cong \left(\frac{1}{15}÷\frac{1}{10}\right)Q_{T_2}$.

c5:

a sufficient freeboard f_cr, equal to the thickness of the crop-roots layer, has to be considered in order to protect crop even during flow conditions that have a frequency higher than 3 ÷ 6 times per year. If h_vf is the water depth corresponding to Q_vf, and δ_vf = h_vf/(H_exc − c) is the filling degree corresponding to Q_vf, this constraint is expressed as δ_vf ≤ δ_cr, where δ_cr = 1 − f_cr/(H_exc − c).

c6:

at each node of the network, the dimensions of the channel downstream should not be smaller than those of the channels upstream [48,49]).

With reference to a network made up of N_r reaches and N_n nodes, let Ω_r be the set of the N_r reaches, Ω_n the set of the N_n nodes, and Ω_up(j) the set of the reaches whose downstream end coincides with the upstream end of the generic reach j ϵ Ω_r. For first order channels, the set Ω_up(j) is empty. The problem of the optimal rural network design is formulated as the minimization of the following OF:

$$OF={\displaystyle \sum _{j\in {\mathrm{\Omega }}_r}{C}_j\left(CS\left(j\right),Z_{exc}\left(j,up\left(j\right)\right),Z_{exc}\left(j,up\left(j\right)\right)\right)}$$

(1)

where C_j is the construction cost of the channel j, $CS\left(j\right)=\left[\begin{array}{cccc}{C}_1\left(j\right)& C_2\left(j\right)& \mathrm{...}& C{S}_{N_{sp}}\left(j\right)\end{array}\right]$ is the vector of the channel’s geometric characteristics, up(j) and dw(j) are the upstream and downstream end nodes of the channel j, Z_exc(j,n) is the bottom elevation at the end n of the channel j. In particular, the cost OF of the network is the sum of C_exc and C_lin, where C_exc refers to the cost of excavation, waste transport and landfill, while C_lin refers to the lining cost. In order to evaluate C_exc, the scheme of the trench considered in the calculations is shown in Figure 1.

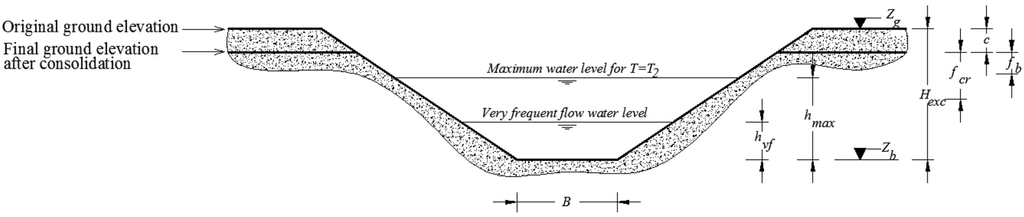
Figure 1. Rural drainage networks: definition sketch of the symbols used.

Figure 1. Rural drainage networks: definition sketch of the symbols used.

The OF is subject to the following constraints:

c₁:

$$\mathrm{\delta }(j,n)\le {\mathrm{\delta }}_{\text{max}}(j,n)\forall j\in {\mathrm{\Omega }}_r,n=up\left(j\right),dw\left(j\right)$$

(2)

c₂:

$$H_{exc}(j,n)\le H_{exc,\text{max}}(j,n)\forall j\in {\mathrm{\Omega }}_r,n=up\left(j\right),dw\left(j\right)$$

(3)

c₃:

$$V_f(j,n)\le V_{er}(j,n)\forall j\in {\mathrm{\Omega }}_r,n=up\left(j\right),dw\left(j\right)$$

(4)

c₄:

$$V_{vf}(j,n)\ge V_{dep}(j,n)\forall j\in {\mathrm{\Omega }}_r,n=up\left(j\right),dw\left(j\right)$$

(5)

c₅:

$${\mathrm{\delta }}_{vf}(j,n)\le {\mathrm{\delta }}_{cr}(j,n)\forall j\in {\mathrm{\Omega }}_r,n=up\left(j\right),dw\left(j\right)$$

(6)

c₆:

$$C{S}_i(j)\ge C{S}_i(k)i=1,2,\mathrm{...},N_{sp},\forall j\in {\mathrm{\Omega }}_r,\forall k\in {\mathrm{\Omega }}_{up}\left(j\right)$$

(7)

Though more general approaches and numerical models may be applied [50,51,52,53,54,55,56,57,58,59], in this work, for the sake of simplicity, in order to show the potential of the approach proposed for the optimal sizing of the drainage network, the actual hydraulic behavior of the whole network is neglected, and the performance of each channel is evaluated only by means of an appropriate state stage-discharge formula corresponding to uniform and steady state conditions. In particular, the Manning’s equation $V=n_M^{-1}{R}^{2/3}{i}^{1/2}$ is adopted, where n_M is the Manning coefficient, R is the hydraulic radius, i = sin [tan⁻¹ (s)], and s is the channel’s longitudinal slope.

2.2. The Genetic Algorithm

The Genetic Algorithm implemented by the authors has been described in Palumbo et al. [60]. For this reason, it will be only briefly depicted in this section. GAs are a class of heuristic techniques, inspired by the biological concepts of natural evolution and selection of individuals, which are used to sample the search space, in order to approximate the optimal solution. The candidate solutions of the optimization problem, called individuals, differ by their appearance (phenotype), i.e., by the value of the decision variables. The phenotype is coded as a genotype string, which is in turn formed by sub-strings, each representing the binary Gray coding of the decision variables. The individual characteristics determine the individual’s Fitness Function (FF) value, which depends both on the OF value related to the phenotype and on the degree of satisfaction of constraints.

At the beginning, an initial population of N individuals is randomly generated. The individuals are ranked in increasing order, according to their fitness, and a selection probability, which decreases with the ranking order, is assigned to each individual. Finally, the individuals are picked, according to their selection probability, and accumulated in a “mating pool”, in order to form couples of parents of the subsequent generation individuals. In this work, “exponential ranking” is used to select the individuals to be inserted in the mating pool for the subsequent steps of the GA processes. After “selection”, other operators can be introduced, namely “crossover”, “mutation”, and “elitism”. When the decision variables satisfy the problem constraints, the FF value coincides with the OF. Conversely, the FF value is calculated by adding penalization terms to the OF value when one or more constraints are not satisfied. This mechanism biases the selection in favor of those individuals that satisfy the constraints.

In this work, trapezoidal cross sections with fixed bank slope are adopted, and then the vector CS(j) degenerates to the bottom width B(j) of the channel j. The trench bottom elevation continuity is considered at the nodes of the rural drainage network:

$$H_{exc}\left(j,up\left(j\right)\right)=H_{exc}\left(k,dw\left(k\right)\right)\forall j\in {\mathrm{\Omega }}_r,\forall k\in {\mathrm{\Omega }}_{up}\left(j\right)$$

(8)

Under these hypotheses, the phenotype of a candidate network is completely characterized by a vector containing the height of the trench $H_{exc}^{nen}$ at the downstream end of the network and, for each reach, the slope s of the channel together with the bottom width B.

The actual form of the FF adopted is the following:

$$\begin{array}{r}FF=OF+p_{fb}{\displaystyle \sum _{j\in {\mathrm{\Omega }}_r}\text{max}\left\{0,\underset{n=up\left(j\right),dw\left(j\right)}{\text{max}}\left\{\delta \left(j,n\right)-{\delta }_{\text{max}}\left(j,n\right)\right\}\right\}}+\\ p_{exc}{\displaystyle \sum _{j\in {\mathrm{\Omega }}_r}\text{max}\left\{0,\underset{n=up\left(j\right),dw\left(j\right)}{\text{max}}\left\{H_{exc}\left(j,n\right)-H_{exc,\text{max}}\left(j,n\right)\right\}\right\}}+p_{er}{\displaystyle \sum _{j\in {\mathrm{\Omega }}_r}\text{max}\left\{0,\underset{n=up\left(j\right),dw\left(j\right)}{\text{max}}\left\{V_f\left(j,n\right)-V_{er}\left(j,n\right)\right\}\right\}}+\\ p_{dep}{\displaystyle \sum _{j\in {\mathrm{\Omega }}_r}\text{max}\left\{0,\underset{n=up\left(j\right),dw\left(j\right)}{\text{max}}\left\{V_{dep}\left(j,n\right)-V_{vf}\left(j,n\right)\right\}\right\}}+p_{cr}{\displaystyle \sum _{j\in {\mathrm{\Omega }}_r}\text{max}\left\{0,\underset{n=up\left(j\right),dw\left(j\right)}{\text{max}}\left\{{\delta }_{vf}\left(j,n\right)-{\delta }_{cr}\left(j,n\right)\right\}\right\}}+\\ p_{sz}{\displaystyle \sum _{j\in {\mathrm{\Omega }}_r}\text{max}\left\{0,\underset{k\in {\mathrm{\Omega }}_{dw}\left(up\left(j\right)\right)}{\text{max}}\left\{B\left(l\right)-B\left(k\right)\right\}\right\}}\end{array}$$

(9)

In Equation (9), the symbols p_fb, p_exc, p_er, p_dep, p_cr and p_sz represent the unit penalties corresponding to the constraints of Equations (2)–(7), respectively.

The following GA parameters have been used during the numerical experiments: N = 300 individuals during each generation; I = 5000 generations; crossover probability c_p = 1; N_e = 5 individuals preserved by the elitism operator; the values of the unit penalization coefficients p_fb, p_exc, p_ser, p_dep, p_cr, p_sz may vary from an application to another, and usually fall in the interval (10⁶, 10¹⁵) when the relevant constraint is activated, while the value zero is used if the constraint is discarded. The mutation probability m_p is variable in the range (0.01 ÷ 6.0) %.

3. Results and Discussion

The optimization procedure discussed in this work is applied to two case studies. The first application is taken from the existing literature about the drainage networks’ optimal design, and is used to test the GA adopted for the optimization. The second application is used to demonstrate the feasibility of the approach for real world applications.

3.1. Genetic Algorithm Verification: World Bank Network (1991)

In the literature, there is a general lack of case studies referring to the optimization of rural drainage networks, while many case studies are available for urban drainage networks. For this reason, the model implemented is easily adapted to solve the problem of the optimal urban drainage network, and then is applied to an urban drainage network with circular pipes taken from the literature [33,61,62].

The network layout is shown in Figure 2. The characteristics of this test case (network geometry, pipe diameters allowed, pipes costs, excavation costs) are summarized by Afshar and Zamani [62], and they are not repeated here. The following constraints are assumed: the maximum filling degree of the pipes is δ_max = 0.82; the maximum excavation depth considered is H_exc,max = 4.5 m; the maximum allowed flow velocity is V_max = 2.5 m/s; the minimum allowed flow velocity is V_min = 0.5 m/s; the minimum soil cover depth is H_cov,min = 1.5 m. A set of 2⁹ = 512 longitudinal slopes is considered in the range (0.01 ÷ 0.08) m/m, with a step equal to 1.36986 × 10⁻⁴ m/m. Finally, the diameters considered in the calculations are 2⁴ = 16.

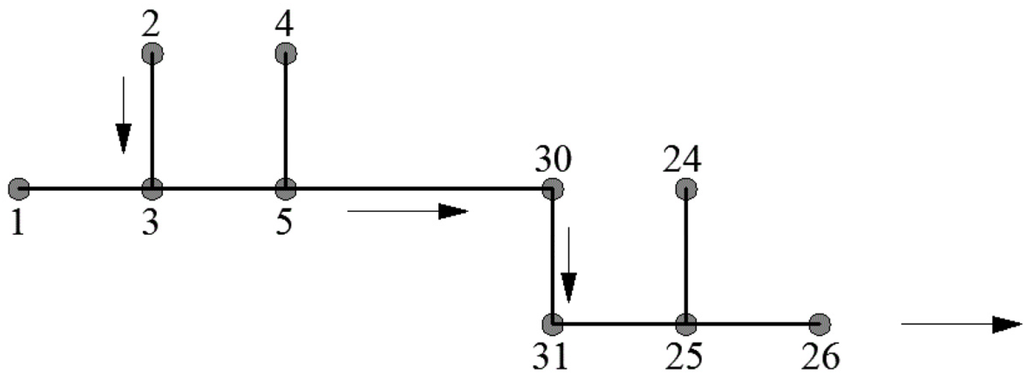
Figure 2. World Bank (1991) [61] case study. Layout.

Figure 2. World Bank (1991) [61] case study. Layout.

The mutation probability m_p must be intended here as the number N_bm of bits involved in the mutation process, divided by the total number N_bt of bits which constitute the genotype of the generic individual. Different analyses are performed in order to evaluate how the optimization process is influenced by the values assigned to the network ending node excavation $H_{exc}^{nen}$ and to the mutation probability m_p. Aiming at this, two sets of runs are considered:

-

Case WB-1: $H_{exc}^{nen}$ is not a decision variable, and its value is taken equal to 2.00 m;

-

Case WB-2: $H_{exc}^{nen}$ is left free to vary in the range (0.45 ÷ 2.00) m with step 0.05 m.

For each set of runs, the algorithm is restarted using different initial populations, in order to assess the robustness of the optimization model outcome, and considering variable values of the mutation probability m_p.

The results obtained for the case WB-1 are summarized in Table 1.

Table 1. World Bank (1991) [61] case study. Optimal results for the case WB-1.

Nbm	Pop 1	Pop 2	Pop 3	Pop 4	Pop 5	Min	Max	Max	RMS
1	199,381.54	208,480.70	221,530.28	199,337.83	199,288.43	199,288.43	221,530.28	205,603.76	4866.32
2	199,088.63	199,108.37	199,125.11	199,097.66	199,097.79	199,088.63	199,125.11	199,103.51	8.68
3	199,095.89	199,108.37	199,166.08	199,118.22	199,105.76	199,095.89	199,166.08	199,118.87	17.45
4	199,109.00	199,105.76	199,108.50	199,097.52	199,111.85	199,097.52	199,111.85	199,106.53	8.30
5	199,098.83	199,124.74	199,128.56	199,245.57	199,169.35	199,098.83	199,245.57	199,153.41	36.96
6	199,158.12	199,213.63	199,235.26	199,242.11	199,154.04	199,154.04	199,242.11	199,200.63	52.83
7	199,324.87	199,383.58	199,599.30	199,287.05	199,247.62	199,247.62	199,599.30	199,368.48	136.85

Table 1. World Bank (1991) [61] case study. Optimal results for the case WB-1.

Nbm	Pop 1	Pop 2	Pop 3	Pop 4	Pop 5	Min	Max	Max	RMS
1	199,381.54	208,480.70	221,530.28	199,337.83	199,288.43	199,288.43	221,530.28	205,603.76	4866.32
2	199,088.63	199,108.37	199,125.11	199,097.66	199,097.79	199,088.63	199,125.11	199,103.51	8.68
3	199,095.89	199,108.37	199,166.08	199,118.22	199,105.76	199,095.89	199,166.08	199,118.87	17.45
4	199,109.00	199,105.76	199,108.50	199,097.52	199,111.85	199,097.52	199,111.85	199,106.53	8.30
5	199,098.83	199,124.74	199,128.56	199,245.57	199,169.35	199,098.83	199,245.57	199,153.41	36.96
6	199,158.12	199,213.63	199,235.26	199,242.11	199,154.04	199,154.04	199,242.11	199,200.63	52.83
7	199,324.87	199,383.58	199,599.30	199,287.05	199,247.62	199,247.62	199,599.30	199,368.48	136.85

In particular, the information reported in the generic row are as follows: the number N_bm of bits involved in the mutation process, the optimal cost obtained for different initial populations (Pop1, Pop2, …) with fixed N_bm, the minimum cost obtained (Min), the maximum cost (Max), the average cost (Ave), and the Root Mean Square error (RMS) of the costs. Note that the solutions are not penalized: the constraints are satisfied, and OF coincides with FF. The best solution is OF = 199,088.63, and it is obtained for N_bm = 2, corresponding to m_p = 0.017. It is interesting to observe that the average optimal cost Ave attains its minimum value for N_bm = 2 as well, while the maximum cost Max and the root mean square error RMS of the costs are close to their minimum for N_bm = 2. This ensures that, for the present application, the most important numerical parameter is m_p: a good choice of m_p leads to reliable solutions.

The results obtained for the case WB-2 are summarized in Table 2. Again, no optimal solution is penalized: the best value for the objective function is OF = 199,088.63 and it is found for N_bm ranging between 2 and 4, corresponding to m_p ϵ (0.013 ÷ 0.027). The functions Ave, Max and RMS attain their minimum values in the same range.

Table 2. World Bank (1991) [61] case study. Optimal results for the case WB-2.

Nbm	Pop 1	Pop 2	Pop 3	Pop 4	Pop 5	Min	Max	Ave	RMS
1	202,802.76	199,320.22	199,289.02	199,312.14	199,299.74	199,299.74	202,802.76	200,004.78	747.88
2	199,088.63	199,098.47	199,183.11	199,088.63	199,098.47	199,088.63	199,183.11	199,111.46	19.10
3	199,105.76	199,088.63	199,088.63	199,128.11	199,135.48	199,088.63	199,128.11	199,109.32	12.72
4	199,095.89	199,088.63	199,129.97	199,111.93	199,118.18	199,088.63	199,129.97	199,108.92	11.27
5	199,136.47	199,240.47	199,139.26	199,202.66	199,089.27	199,089.27	199,240.47	199,161.62	40.45
6	199,199.19	199,206.59	199,133.30	199,123.84	199,220.07	199,199.19	199,220.07	199,176.60	43.20
7	199,180.98	199,145.15	199,170.09	199,114.00	199,227.68	199,145.15	199,227.68	199,167.58	39.16
8	199,198.38	199,201.65	199,264.49	199,203.22	199,822.13	199,198.38	199,822.13	199,337.97	155.81
9	199,260.81	199,304.59	199,396.04	199,297.51	199,267.17	199,260.81	199,396.04	199,305.23	99.26
10	199,258.31	199,326.11	199,963.77	199,972.76	199,318.42	199,258.31	199,963.77	199,567.88	259.66

Table 2. World Bank (1991) [61] case study. Optimal results for the case WB-2.

Nbm	Pop 1	Pop 2	Pop 3	Pop 4	Pop 5	Min	Max	Ave	RMS
1	202,802.76	199,320.22	199,289.02	199,312.14	199,299.74	199,299.74	202,802.76	200,004.78	747.88
2	199,088.63	199,098.47	199,183.11	199,088.63	199,098.47	199,088.63	199,183.11	199,111.46	19.10
3	199,105.76	199,088.63	199,088.63	199,128.11	199,135.48	199,088.63	199,128.11	199,109.32	12.72
4	199,095.89	199,088.63	199,129.97	199,111.93	199,118.18	199,088.63	199,129.97	199,108.92	11.27
5	199,136.47	199,240.47	199,139.26	199,202.66	199,089.27	199,089.27	199,240.47	199,161.62	40.45
6	199,199.19	199,206.59	199,133.30	199,123.84	199,220.07	199,199.19	199,220.07	199,176.60	43.20
7	199,180.98	199,145.15	199,170.09	199,114.00	199,227.68	199,145.15	199,227.68	199,167.58	39.16
8	199,198.38	199,201.65	199,264.49	199,203.22	199,822.13	199,198.38	199,822.13	199,337.97	155.81
9	199,260.81	199,304.59	199,396.04	199,297.51	199,267.17	199,260.81	199,396.04	199,305.23	99.26
10	199,258.31	199,326.11	199,963.77	199,972.76	199,318.42	199,258.31	199,963.77	199,567.88	259.66

In Table 3, the results obtained for this set of runs are compared with those obtained by other authors.

Table 3. World Bank (1991) case study. Optimal results obtained by various researchers.

Model	Cost ($)
SEWER (World Bank 1991) [62]	199,480
Afshar and Zamani (2002) [63]	199,320
Afshar et al. (GA-TRANS2, 2006) [36]	199,244
Proposed Model	199,088.63

Table 3. World Bank (1991) case study. Optimal results obtained by various researchers.

Model	Cost ($)
SEWER (World Bank 1991) [62]	199,480
Afshar and Zamani (2002) [63]	199,320
Afshar et al. (GA-TRANS2, 2006) [36]	199,244
Proposed Model	199,088.63

By inspection of the results listed in the Table 1, Table 2 and Table 3, it is possible to state that:

-

the best result obtained for this test case is better than those found by previous authors (Table 3);

-

for this test case, there is no difference between the best results obtained considering $H_{exc}^{nen}$ fixed and equal to 2.00 m, or left free to vary in the range (0.45 ÷ 2.00) m;

-

the best solutions for OF are obtained for N_bm ranging in the interval (2 ÷ 4), which corresponds to m_p ranging approximately in the interval (0.013 ÷ 0.027). This result is in agreement with the values of m_p often suggested in the GA literature, with reference to hydraulic engineering applications [28,63];

-

the functions Ave, Max and RMS attain their minimum values in the same range of m_p where OF is minimized. This fact ensures the reliability of the optimal solution found.

The characteristics of the optimal network obtained with the proposed approach are listed in Table 4. It is interesting to observe that, in the case under examination, the constraint c₆ (no decreasing size of the channel in the downstream direction) is automatically satisfied and then superfluous.

Table 4. World Bank (1991) [61] case study. Optimal decision variables and hydraulic characteristics.

Branch	Crown Elevation (m)		Diameter (mm)	Slope (m/m)	Velocity (m/s)	Filling Degree (m/m)
	Upstream	Downstream
1–3	1394.5963	1387.0884	150	0.072	2.063	0.456
2–3	1393.8938	1387.0884	250	0.028	2.057	0.624
3–5	1385.4855	1380.2767	300	0.027	2.307	0.684
4–5	1376.6060	1374.4658	150	0.076	2.499	0.739
5–30	1387.0884	1380.2767	300	0.030	2.453	0.674
30–31	1380.2767	1378.3178	450	0.018	2.496	0.711
31–25	1378.3178	1377.4986	450	0.018	2.496	0.711
24–25	1377.4986	1374.4658	450	0.017	2.437	0.727
25–26	1374.4658	1371.0000	500	0.016	2.494	0.681

Table 4. World Bank (1991) [61] case study. Optimal decision variables and hydraulic characteristics.

Branch	Crown Elevation (m)		Diameter (mm)	Slope (m/m)	Velocity (m/s)	Filling Degree (m/m)
	Upstream	Downstream
1–3	1394.5963	1387.0884	150	0.072	2.063	0.456
2–3	1393.8938	1387.0884	250	0.028	2.057	0.624
3–5	1385.4855	1380.2767	300	0.027	2.307	0.684
4–5	1376.6060	1374.4658	150	0.076	2.499	0.739
5–30	1387.0884	1380.2767	300	0.030	2.453	0.674
30–31	1380.2767	1378.3178	450	0.018	2.496	0.711
31–25	1378.3178	1377.4986	450	0.018	2.496	0.711
24–25	1377.4986	1374.4658	450	0.017	2.437	0.727
25–26	1374.4658	1371.0000	500	0.016	2.494	0.681

3.2. Case Study: Biggiero and Pianese Network (1996)

The model is applied to a case study available in the literature [64,65], which is used to demonstrate the feasibility of the approach for real world applications. The test considered is a rural drainage network consisting of 37 reaches, whose total length is 8310 m, and 38 nodes (Figure 3). The characteristics of the network are reported in Table 5. For the sake of simplicity, though without loss of generality, the value of the frequent discharge Q_f has been taken equal to the value of the very frequent discharge Q_vf.

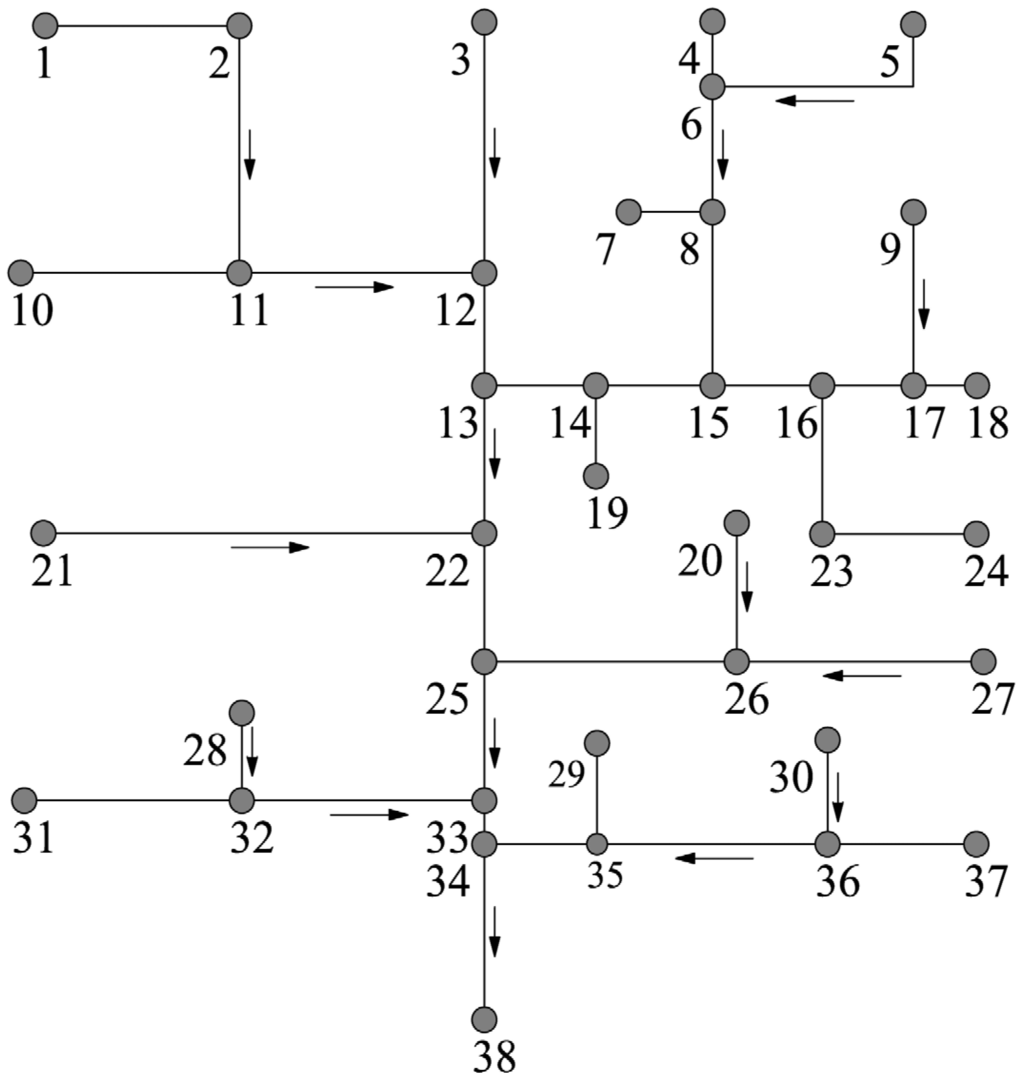
Figure 3. Biggiero and Pianese (1996) [64] case study. Layout.

Figure 3. Biggiero and Pianese (1996) [64] case study. Layout.

Table 5. Biggiero and Pianese (1996) [64] case study. Geometric and hydraulic characteristics of the problem.

Branch	Ground Elevation (m)		Horizontal Length (m)	Q (m3/s)	Qf ≡ Qvf (m3/s)
	Upstream	Downstream
1–2	13.604	13.204	200	0.10373	0.010373
2–11	13.204	12.204	400	0.19977	0.019977
10–11	12.654	12.204	250	0.14310	0.014310
11–12	12.204	11.694	300	0.44535	0.044535
3–12	12.454	11.694	400	0.15754	0.015754
4–6	12.819	12.534	150	0.095607	0.0095607
5–6	13.129	12.534	350	0.15382	0.015382
6–8	12.534	12.160	220	0.30989	0.030989
7–8	12.320	12.160	100	0.051418	0.0051418
8–15	12.160	11.840	200	0.41000	0.041000
18–17	12.285	12.173	70	0.049872	0.0049872
9–17	12.515	12.173	190	0.096821	0.0096821
17–16	12.173	12.008	110	0.16984	0.016984
24–23	12.408	12.138	180	0.079993	0.0079993
23–16	12.138	12.008	260	0.12276	0.012276
16–15	12.008	11.840	120	0.32731	0.032731
15–14	11.840	11.645	150	0.76748	0.076748
19–14	11.705	11.645	150	0.059884	0.0059884
14–13	11.645	11.405	200	0.85356	0.085356
12–13	11.694	11.405	170	0.64189	0.064189
13–22	11.405	10.925	300	1.5406	0.15406
21–22	11.860	10.925	550	0.23869	0.023869
22–25	10.925	10.645	200	1.8285	0.18285
20–26	11.441	11.041	250	0.095221	0.0095221
27–26	11.521	11.041	320	0.14660	0.014660
26–25	11.041	10.645	330	0.32110	0.032110
25–33	10.645	10.370	250	2.1774	0.21774
31–32	11.245	10.820	250	0.12171	0.012171
28–32	11.067	10.820	130	0.093266	0.0093266
32–33	10.820	10.370	300	0.32767	0.032767
37–36	11.011	10.595	320	0.14874	0.014874
30–36	10.791	10.595	140	0.062599	0.0062599
36–35	10.595	10.391	170	0.27880	0.027880
29–35	10.547	10.391	120	0.081949	0.0081949
35–34	10.391	10.270	110	0.37467	0.037467
33–34	10.370	10.270	100	2.4675	0.24675
34–38	10.270	10.000	300	2.8255	0.28255

Table 5. Biggiero and Pianese (1996) [64] case study. Geometric and hydraulic characteristics of the problem.

Branch	Ground Elevation (m)		Horizontal Length (m)	Q (m3/s)	Qf ≡ Qvf (m3/s)
	Upstream	Downstream
1–2	13.604	13.204	200	0.10373	0.010373
2–11	13.204	12.204	400	0.19977	0.019977
10–11	12.654	12.204	250	0.14310	0.014310
11–12	12.204	11.694	300	0.44535	0.044535
3–12	12.454	11.694	400	0.15754	0.015754
4–6	12.819	12.534	150	0.095607	0.0095607
5–6	13.129	12.534	350	0.15382	0.015382
6–8	12.534	12.160	220	0.30989	0.030989
7–8	12.320	12.160	100	0.051418	0.0051418
8–15	12.160	11.840	200	0.41000	0.041000
18–17	12.285	12.173	70	0.049872	0.0049872
9–17	12.515	12.173	190	0.096821	0.0096821
17–16	12.173	12.008	110	0.16984	0.016984
24–23	12.408	12.138	180	0.079993	0.0079993
23–16	12.138	12.008	260	0.12276	0.012276
16–15	12.008	11.840	120	0.32731	0.032731
15–14	11.840	11.645	150	0.76748	0.076748
19–14	11.705	11.645	150	0.059884	0.0059884
14–13	11.645	11.405	200	0.85356	0.085356
12–13	11.694	11.405	170	0.64189	0.064189
13–22	11.405	10.925	300	1.5406	0.15406
21–22	11.860	10.925	550	0.23869	0.023869
22–25	10.925	10.645	200	1.8285	0.18285
20–26	11.441	11.041	250	0.095221	0.0095221
27–26	11.521	11.041	320	0.14660	0.014660
26–25	11.041	10.645	330	0.32110	0.032110
25–33	10.645	10.370	250	2.1774	0.21774
31–32	11.245	10.820	250	0.12171	0.012171
28–32	11.067	10.820	130	0.093266	0.0093266
32–33	10.820	10.370	300	0.32767	0.032767
37–36	11.011	10.595	320	0.14874	0.014874
30–36	10.791	10.595	140	0.062599	0.0062599
36–35	10.595	10.391	170	0.27880	0.027880
29–35	10.547	10.391	120	0.081949	0.0081949
35–34	10.391	10.270	110	0.37467	0.037467
33–34	10.370	10.270	100	2.4675	0.24675
34–38	10.270	10.000	300	2.8255	0.28255

The cross section shape is assumed trapezoidal, with bottom width B, while the angle between the banks and the horizontal plane is α = 45°. The values allowed for B range from 0.30 to 4.00 m, and are reported in Table 6.

Table 6. Biggiero and Pianese (1996) [64] case study. Bottom width B and network ending node excavation. $H_{exc}^{nen}$: the values.

ID	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
B (m)	0.30	0.50	0.80	1.00	1.50	2.00	2.50	3.00	3.50	4.00	-	-	-	-	-	-
$H_{exc}^{nen}$ (m)	0.40	0.45	0.50	0.55	0.60	0.65	0.70	0.80	0.90	1.00	1.10	1.20	1.30	1.40	1.45	1.50

Table 6. Biggiero and Pianese (1996) [64] case study. Bottom width B and network ending node excavation. $H_{exc}^{nen}$: the values.

ID	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
B (m)	0.30	0.50	0.80	1.00	1.50	2.00	2.50	3.00	3.50	4.00	-	-	-	-	-	-
$H_{exc}^{nen}$ (m)	0.40	0.45	0.50	0.55	0.60	0.65	0.70	0.80	0.90	1.00	1.10	1.20	1.30	1.40	1.45	1.50

In order to evaluate the network construction cost, the waste transport and landfill are neglected, while only excavation costs are considered. In particular, the unit excavation costs are equal to 9.97 €/m³ for H_exc ≤ 2.00 m, and are equal to 10.29 €/m³ for H_exc > 2.00 m.

The parameters used for the evaluation of Equations (2), (4) and (5), corresponding to constraints c₁, c₃ and c₅, are chosen as follows: f_b = 0 m (and then δ_max = 1), c = 0 m, f_cr = 0.30 m. Without loss of generality, the constraints c₂ and c₄ about the maximum excavation and the deposition velocity, respectively, have been discarded. The limit velocity V_er is evaluated considering silt gravels, characterized by Plastic Index value PI = 16 and porosity p = 0.35, while the sediment concentration in the water flowing through the channels is assumed to be equal to 0.7%. Under these assumptions, the approach proposed in USDA [47] allows evaluation of the erosion velocity V_er as a function of the water depth h_vf corresponding to the very frequent discharge Q_vf, using the formula $V_{er}=2.44\cdot h_{vf}^{0.19}$.

Four different series of tests are performed:

-

Case BP-1A: $H_{exc}^{nen}$ is not a decision variable, and its value is taken equal to 1.50 m, while the constraint c₆ is effective;

-

Case BP-1B: $H_{exc}^{nen}$ is not a decision variable, and its value is taken equal to 1.50 m, while the constraint c₆ is discarded;

-

Case BP-2A: $H_{exc}^{nen}$ is considered as a decision variable, and it is left free to vary in the range (0.40 ÷ 1.50), while the constraint c₆ is effective;

-

Case BP-2B: $H_{exc}^{nen}$ is considered as a decision variable, and it is left free to vary in the range (0.40 ÷ 1.50), while the constraint c₆ is discarded.

In each reach, a set of 2⁹ = 512 longitudinal slopes is considered, variable in the range (0.0001 ÷ 0.0064) m/m with step equal to 0.00001233 m/m, while the 2⁴ values allowed for the decision variable $H_{exc}^{nen}$ are reported in Table 6. In order to evaluate the FF in Equation (9), the unit penalization coefficients are chosen as follows: p_fb = p_er = p_cr = 10⁹, and p_exc = p_dep = 0. The value used for the unit penalty coefficient p_sz is 10⁹ for the cases BP-1A and BP-2A, while it is zero for the cases BP-1B and BP-2B. For each case, the algorithm is restarted from different initial populations (Pop1, Pop2, …), and considering variable mutation probability values m_p.

The results obtained for the cases BP-1A and BP-1B are reported in Table 7. With reference to the case BP-1A, the best solution is OF = 98,972.09€, and it is obtained for N_bm = 5, corresponding to m_p = 0.0075. For the same case, the average optimal cost Ave attains its minimum value for N_bm = 9, corresponding to m_p = 0.0150, together with the maximum cost Max and the root mean square RMS of the costs. With reference to the case BP-1B, the best solution is OF = 85,539.03€, and it is obtained for N_bm = 5, corresponding to m_p = 0.0075: due to the absence of the constraint about the channel width, a degree of freedom is added, and the best result obtained for the case BP-1B is not greater than the best result for BP-1A. The optimal values for Ave, Max and RMS are obtained for m_p ranging in the interval (0.0075 ÷ 0.0225).

The results for the cases BP-2A and BP-2B are reported in Table 8.

Table 7. Biggiero and Pianese (1996) [64] case study. Optimal results for the cases BP-1A and BP-1B.

Case	mp	Nbm	Pop1	Pop2	Pop3	Pop4	Pop5	Min	Max	Ave	RMS
BP-1A	0.001	1	150,114.97	173,070	141,479.11	145,121.82	135,643.23	135,643.23	173,070	149,085.82	28,989.15
	0.0075	5	122,515.75	100,911.57	109,885.81	108,321.04	98,972.09	98,972.09	122,515.75	108,121.25	10,754.46
	0.015	9	121,415.61	108,932.41	101,410.7	99,967.7	102,357.2	99,967.7	121,415.61	106,816.72	10,145.37
	0.0225	14	131,916.7	147,795.94	191,307.27	141,376.08	143,637.42	131,916.7	191,307.27	151,206.68	30,785.86
	0.03	19	153,819.02	145,978.72	170,365.79	209,552.47	134,984.9	134,984.9	209,552.47	162,940.18	36,507.51
	0.0375	24	209,401.27	152,818.34	221,438.39	216,116.22	157,821.18	152,818.34	221,438.39	191,519.08	49,230.73
BP-1B	0.001	1	104,690.99	96,109.18	132,357.17	110,152.17	122,785.97	96,109.18	132,357.17	113,219.1	12,986.66
	0.0075	5	135,483.19	100,798.7	91,897.17	85,539.03	93,541.7	85,539.03	135,483.19	101,451.96	10,159.75
	0.015	9	87,205.04	106,330.03	101,287.47	103,712.54	135,992.85	87,205.04	135,992.85	106,905.58	11,343.42
	0.0225	14	106,298.84	90,893.8	109,810.09	99,335.51	96,656.07	90,893.8	109,810.09	100,598.86	6710.11
	0.03	19	109,417.35	100,446.6	108,456.51	103,556.18	99,369.49	99,369.49	109,417.35	104,249.23	7837.56
	0.0375	24	126,757.81	104,155.58	101,745.82	102,967.66	104,154.92	101,745.82	126,757.81	107,956.36	10,195.95

Table 7. Biggiero and Pianese (1996) [64] case study. Optimal results for the cases BP-1A and BP-1B.

Case	mp	Nbm	Pop1	Pop2	Pop3	Pop4	Pop5	Min	Max	Ave	RMS
BP-1A	0.001	1	150,114.97	173,070	141,479.11	145,121.82	135,643.23	135,643.23	173,070	149,085.82	28,989.15
	0.0075	5	122,515.75	100,911.57	109,885.81	108,321.04	98,972.09	98,972.09	122,515.75	108,121.25	10,754.46
	0.015	9	121,415.61	108,932.41	101,410.7	99,967.7	102,357.2	99,967.7	121,415.61	106,816.72	10,145.37
	0.0225	14	131,916.7	147,795.94	191,307.27	141,376.08	143,637.42	131,916.7	191,307.27	151,206.68	30,785.86
	0.03	19	153,819.02	145,978.72	170,365.79	209,552.47	134,984.9	134,984.9	209,552.47	162,940.18	36,507.51
	0.0375	24	209,401.27	152,818.34	221,438.39	216,116.22	157,821.18	152,818.34	221,438.39	191,519.08	49,230.73
BP-1B	0.001	1	104,690.99	96,109.18	132,357.17	110,152.17	122,785.97	96,109.18	132,357.17	113,219.1	12,986.66
	0.0075	5	135,483.19	100,798.7	91,897.17	85,539.03	93,541.7	85,539.03	135,483.19	101,451.96	10,159.75
	0.015	9	87,205.04	106,330.03	101,287.47	103,712.54	135,992.85	87,205.04	135,992.85	106,905.58	11,343.42
	0.0225	14	106,298.84	90,893.8	109,810.09	99,335.51	96,656.07	90,893.8	109,810.09	100,598.86	6710.11
	0.03	19	109,417.35	100,446.6	108,456.51	103,556.18	99,369.49	99,369.49	109,417.35	104,249.23	7837.56
	0.0375	24	126,757.81	104,155.58	101,745.82	102,967.66	104,154.92	101,745.82	126,757.81	107,956.36	10,195.95

Table 8. Biggiero and Pianese (1996) [64] case study. Optimal results for the cases BP-2A and BP-2B.

Case	mp	Nbm	Pop1	Pop2	Pop3	Pop4	Pop5	Min	Max	Ave	RMS
BP-2A	0.001	1	114,994.54	129,701.43	123,222.31	121,269.94	110,152.71	110,152.71	129,701.43	119,868.19	11,874.28
	0.0075	5	99,147.22	111,655.69	98,806.23	104,279.08	94,343.22	94,343.22	111,655.69	101,646.29	4255.66
	0.015	9	104,551.42	99,804.07	108,322.84	106,931.04	104,584.26	99,804.07	108,322.84	104,838.73	4935.65
	0.0225	14	131,596.06	142,020.01	126,446.31	137,005.42	148,466.35	126,446.31	148,466.35	137,106.83	19,500.35
	0.03	19	149,737.04	132,467.33	197,257.66	157,626.5	198,950.1	132,467.33	198,950.1	167,207.72	34,740.54
	0.0375	24	205,444.33	204,105.65	176,471.38	181,740.54	264,992.84	176,471.38	264,992.84	206,550.95	52,179.77
BP-2B	0.001	1	105,278.18	88,998.65	100,389.65	109,368.9	116,342.27	88,998.65	116,342.27	104,075.53	14,338.91
	0.0075	5	84,640.15	77,488.21	79,381.09	77,382.45	90,499.754	77,382.45	90,499.75	81,878.33	4431.97
	0.015	9	82,917.73	73,353.32	74,360.86	92,763.82	87,478.171	73,353.32	92,763.82	82,174.78	5172.12
	0.0225	14	88,965.44	86,126.22	82,616.31	101,479.54	125,238.16	82,616.31	125,238.16	96,885.14	12,610.8
	0.03	19	85,571.29	96,805.84	91,319.61	83,952.82	97,789.09	83,952.82	97,789.09	91,087.73	8322.36
	0.0375	24	99,792.81	112,730.92	94,426.29	99,286.95	111,468.22	94,426.29	112,730.92	103,541.04	13,883.82

Table 8. Biggiero and Pianese (1996) [64] case study. Optimal results for the cases BP-2A and BP-2B.

Case	mp	Nbm	Pop1	Pop2	Pop3	Pop4	Pop5	Min	Max	Ave	RMS
BP-2A	0.001	1	114,994.54	129,701.43	123,222.31	121,269.94	110,152.71	110,152.71	129,701.43	119,868.19	11,874.28
	0.0075	5	99,147.22	111,655.69	98,806.23	104,279.08	94,343.22	94,343.22	111,655.69	101,646.29	4255.66
	0.015	9	104,551.42	99,804.07	108,322.84	106,931.04	104,584.26	99,804.07	108,322.84	104,838.73	4935.65
	0.0225	14	131,596.06	142,020.01	126,446.31	137,005.42	148,466.35	126,446.31	148,466.35	137,106.83	19,500.35
	0.03	19	149,737.04	132,467.33	197,257.66	157,626.5	198,950.1	132,467.33	198,950.1	167,207.72	34,740.54
	0.0375	24	205,444.33	204,105.65	176,471.38	181,740.54	264,992.84	176,471.38	264,992.84	206,550.95	52,179.77
BP-2B	0.001	1	105,278.18	88,998.65	100,389.65	109,368.9	116,342.27	88,998.65	116,342.27	104,075.53	14,338.91
	0.0075	5	84,640.15	77,488.21	79,381.09	77,382.45	90,499.754	77,382.45	90,499.75	81,878.33	4431.97
	0.015	9	82,917.73	73,353.32	74,360.86	92,763.82	87,478.171	73,353.32	92,763.82	82,174.78	5172.12
	0.0225	14	88,965.44	86,126.22	82,616.31	101,479.54	125,238.16	82,616.31	125,238.16	96,885.14	12,610.8
	0.03	19	85,571.29	96,805.84	91,319.61	83,952.82	97,789.09	83,952.82	97,789.09	91,087.73	8322.36
	0.0375	24	99,792.81	112,730.92	94,426.29	99,286.95	111,468.22	94,426.29	112,730.92	103,541.04	13,883.82

With reference to the case BP-2A, the best solution is OF = 94,343.22€, and it is obtained for N_bm = 5, corresponding to m_p = 0.0075: due to the absence of the constraint about the excavation at the network ending node of the network, a degree of freedom is added, and the optimal solution is not greater than that obtained for the case BP-1A. For the same case, Ave and RMS attain their minimum values for N_bm = 5, corresponding to m_p = 0.075, while Max is minimized using m_p = 0.015. With reference to the case BP-2B, the best solution is OF = 73,353.32€, and it is obtained for N_bm = 9, corresponding to m_p = 0.015: as expected, the best result obtained for the case BP-2B is not greater than the best results for BP-1B and BP-2A. The optimal values for Ave, Max and RMS are obtained for m_p = 0.0075.

The optimal network characteristics are reported in Table 9 for all the cases examined. From the inspection of this Table, it is clear that the optimal decision variables are strongly sensitive to the constraints applied. For instance, with reference to the network ending reach 34–38, its bottom width B lies in the range (1.00 ÷ 1.50) m, depending on the case examined. The same is true for the first order channels. For example, the bottom width B of reach 1–2 lies in the range (0.30 ÷ 0.50) m, while the slope lies in the range (0.00145 ÷ 0.00247) m/m.

By exploring the results listed in the Tables above, it is possible to draw the following observations:

-

the optimal results depend strongly on the constraints that are applied. In particular, the optimal result of the most constrained case (BP-1A) is 35% greater than that of less constrained case (BP-2B);

-

when the constraint c₆ is not explicitly enforced (cases BP-1B and BP-2B), it may happen (Table 9) that the channel bottom width decreases downstream, despite the increase of the design discharge Q. This is true when the decrease of the channel width is sufficient to compensate, from an economical point of view, the increase of the channel longitudinal slope;

-

differently from the World Bank case study, there is a significant difference between the cases of $H_{exc}^{nen}$ fixed or variable in a range. As expected, the optimal results for the cases BP-2A and BP-2B are not greater than those related to the cases BP-1A and BP-1B;

-

the best solutions for OF, Ave, Max and RMS are obtained for m_p ranging in the interval (0.0075 ÷ 0.0225), and again this result is in agreement with the values of m_p often suggested in the GA literature.

Comparing the best solution cost obtained, in this work, for the case BP-2A, in which the technical constraint c₆ is effective, with the cost of the network considered in [64], obtained using the same unit costs and value of $H_{exc}^{nen}$ ($H_{exc}^{nen}$ = 1.4 m) (see the following Table 10 and Figure 4, in which the geometric characteristics reported in [64] and the geometric characteristics obtained for the case BP-2A have been reported), it is possible to observe that the minimum cost network obtained by the proposed optimization procedure is € 94,343.22/€ 275,339.25 = 34.3% of the cost of original network, designed just to be effective from a technical point of view, but without considering the need to reduce the intervention costs. In order to show the convergence properties of the presented approach, the behavior of the fitness function for the case BP-2A has been reported in Figure 5.

Table 9. Biggiero and Pianese (1996) [64] case study. Optimal decision variables.

Reach	Case BP-1A		Case BP-1B		Case BP-2A		Case BP-2B
	B	s	B	s	B	s	B	s
	(m)	(m/m)	(m)	(m/m)	(m)	(m/m)	(m)	(m/m)
1–2	0.5	0.00195	0.3	0.00247	0.3	0.00179	0.3	0.00145
2–11	0.8	0.00308	0.3	0.00237	0.5	0.00248	0.5	0.00267
10–11	0.3	0.00254	0.3	0.0018	0.8	0.00188	0.5	0.00227
11–12	0.8	0.00311	0.8	0.00315	1	0.00262	0.7	0.00177
3–12	0.5	0.00354	0.3	0.00303	0.3	0.00257	0.3	0.00194
4–6	0.3	0.00195	0.3	0.00382	0.8	0.00349	1.3	0.00334
5–6	0.3	0.00172	0.3	0.00247	0.3	0.00215	0.3	0.00207
6–8	0.5	0.00274	0.3	0.00279	0.8	0.00116	0.5	0.00154
7–8	0.3	0.00469	0.3	0.00629	0.8	0.00276	0.4	0.00111
8–15	0.5	0.00262	0.3	0.0013	0.8	0.00591	0.5	0.00246
18–17	0.8	0.00281	0.3	0.00328	0.3	0.00365	0.5	0.00023
9–17	0.8	0.00232	0.3	0.00215	0.3	0.00379	0.4	0.00131
17–16	0.8	0.00343	0.3	0.00455	0.3	0.00257	0.5	0.00277
24–23	0.8	0.00181	0.8	0.00157	0.8	0.00121	0.4	0.0018
23–16	0.8	0.00154	0.8	0.00223	0.8	0.00249	0.3	0.00111
16–15	0.8	0.00291	0.8	0.00174	0.8	0.00515	0.3	0.00188
15–14	1.5	0.00047	0.3	0.00303	1	0.00019	0.6	0.00228
19–14	0.8	0.00297	0.3	0.0055	0.3	0.00576	0.3	0.00278
14–13	1.5	0.00237	0.3	0.0012	1	0.00123	0.5	0.00149
12–13	0.8	0.00132	0.3	0.00319	1	0.00456	0.7	0.0039
13–22	1.5	0.00147	0.8	0.00139	1	0.00158	0.8	0.00203
21–22	0.3	0.00253	0.8	0.00292	0.3	0.00301	0.3	0.00274
22–25	1.5	0.00306	0.8	0.00211	1	0.00112	1.5	0.00091
20–26	0.3	0.00158	0.3	0.0017	0.3	0.0025	0.3	0.00145
27–26	0.5	0.00151	0.3	0.00149	0.3	0.00211	0.4	0.00127
26–25	0.5	0.00376	0.8	0.00354	0.8	0.00268	0.5	0.00264
25–33	1.5	0.00155	0.8	0.00159	1	0.00167	1.1	0.00217
31–32	0.3	0.00165	0.8	0.00226	0.5	0.00174	0.4	0.00196
28–32	0.8	0.00207	0.3	0.00276	0.3	0.00192	0.5	0.0027
32–33	0.8	0.00471	0.3	0.00421	0.8	0.00432	0.3	0.00388
37–36	0.5	0.00137	0.3	0.00141	0.3	0.00222	0.4	0.00122
30–36	0.3	0.0018	0.3	0.00223	0.3	0.00387	0.3	0.00223
36–35	0.5	0.00501	0.3	0.00472	0.3	0.00164	0.3	0.00443
29–35	0.8	0.00629	0.3	0.00623	0.8	0.00482	0.3	0.00399
35–34	0.8	0.00483	0.8	0.00462	0.8	0.00639	0.3	0.00281
33–34	1.5	0.00216	0.3	0.00252	1	0.00223	1	0.00137
34–38	1.5	0.00094	0.8	0.001	1	0.00101	1.1	0.00111
$H_{exc}^{nen}$ (m)	1.5		1.5		1.4		1.3

Table 9. Biggiero and Pianese (1996) [64] case study. Optimal decision variables.

Reach	Case BP-1A		Case BP-1B		Case BP-2A		Case BP-2B
	B	s	B	s	B	s	B	s
	(m)	(m/m)	(m)	(m/m)	(m)	(m/m)	(m)	(m/m)
1–2	0.5	0.00195	0.3	0.00247	0.3	0.00179	0.3	0.00145
2–11	0.8	0.00308	0.3	0.00237	0.5	0.00248	0.5	0.00267
10–11	0.3	0.00254	0.3	0.0018	0.8	0.00188	0.5	0.00227
11–12	0.8	0.00311	0.8	0.00315	1	0.00262	0.7	0.00177
3–12	0.5	0.00354	0.3	0.00303	0.3	0.00257	0.3	0.00194
4–6	0.3	0.00195	0.3	0.00382	0.8	0.00349	1.3	0.00334
5–6	0.3	0.00172	0.3	0.00247	0.3	0.00215	0.3	0.00207
6–8	0.5	0.00274	0.3	0.00279	0.8	0.00116	0.5	0.00154
7–8	0.3	0.00469	0.3	0.00629	0.8	0.00276	0.4	0.00111
8–15	0.5	0.00262	0.3	0.0013	0.8	0.00591	0.5	0.00246
18–17	0.8	0.00281	0.3	0.00328	0.3	0.00365	0.5	0.00023
9–17	0.8	0.00232	0.3	0.00215	0.3	0.00379	0.4	0.00131
17–16	0.8	0.00343	0.3	0.00455	0.3	0.00257	0.5	0.00277
24–23	0.8	0.00181	0.8	0.00157	0.8	0.00121	0.4	0.0018
23–16	0.8	0.00154	0.8	0.00223	0.8	0.00249	0.3	0.00111
16–15	0.8	0.00291	0.8	0.00174	0.8	0.00515	0.3	0.00188
15–14	1.5	0.00047	0.3	0.00303	1	0.00019	0.6	0.00228
19–14	0.8	0.00297	0.3	0.0055	0.3	0.00576	0.3	0.00278
14–13	1.5	0.00237	0.3	0.0012	1	0.00123	0.5	0.00149
12–13	0.8	0.00132	0.3	0.00319	1	0.00456	0.7	0.0039
13–22	1.5	0.00147	0.8	0.00139	1	0.00158	0.8	0.00203
21–22	0.3	0.00253	0.8	0.00292	0.3	0.00301	0.3	0.00274
22–25	1.5	0.00306	0.8	0.00211	1	0.00112	1.5	0.00091
20–26	0.3	0.00158	0.3	0.0017	0.3	0.0025	0.3	0.00145
27–26	0.5	0.00151	0.3	0.00149	0.3	0.00211	0.4	0.00127
26–25	0.5	0.00376	0.8	0.00354	0.8	0.00268	0.5	0.00264
25–33	1.5	0.00155	0.8	0.00159	1	0.00167	1.1	0.00217
31–32	0.3	0.00165	0.8	0.00226	0.5	0.00174	0.4	0.00196
28–32	0.8	0.00207	0.3	0.00276	0.3	0.00192	0.5	0.0027
32–33	0.8	0.00471	0.3	0.00421	0.8	0.00432	0.3	0.00388
37–36	0.5	0.00137	0.3	0.00141	0.3	0.00222	0.4	0.00122
30–36	0.3	0.0018	0.3	0.00223	0.3	0.00387	0.3	0.00223
36–35	0.5	0.00501	0.3	0.00472	0.3	0.00164	0.3	0.00443
29–35	0.8	0.00629	0.3	0.00623	0.8	0.00482	0.3	0.00399
35–34	0.8	0.00483	0.8	0.00462	0.8	0.00639	0.3	0.00281
33–34	1.5	0.00216	0.3	0.00252	1	0.00223	1	0.00137
34–38	1.5	0.00094	0.8	0.001	1	0.00101	1.1	0.00111
$H_{exc}^{nen}$ (m)	1.5		1.5		1.4		1.3

Table 10. Geometric characteristics reported in Biggiero and Pianese (1996) [64] vs. geometric characteristics obtained for the case BP-2A.

Reach	Biggiero&Pianese (1996)		Case BP-2A
	B	s	B	s
	(m)	(m/m)	(m)	(m/m)
1–2	0.5	0.00200	0.3	0.00179
2–11	0.5	0.00250	0.5	0.00248
10–11	0.5	0.00180	0.8	0.00188
11–12	0.8	0.00170	1.0	0.00262
3–12	0.8	0.00190	0.3	0.00257
4–6	0.5	0.00190	0.8	0.00349
5–6	0.8	0.00170	0.3	0.00215
6–8	0.8	0.00170	0.8	0.00116
7–8	0.5	0.00160	0.8	0.00276
8–15	1.0	0.00160	0.8	0.00591
18–17	0.5	0.00160	0.3	0.00365
9–17	0.5	0.00180	0.3	0.00379
17–16	0.5	0.00150	0.3	0.00257
24–23	0.5	0.00150	0.8	0.00121
23–16	0.8	0.00050	0.8	0.00249
16–15	0.8	0.00140	0.8	0.00515
15–14	1.5	0.00130	1.0	0.00019
19–14	0.5	0.00040	0.3	0.00576
14–13	1.5	0.00120	1.0	0.00123
12–13	1.5	0.00170	1.0	0.00456
13–22	2.0	0.00160	1.0	0.00158
21–22	1.0	0.00170	0.3	0.00301
22–25	2.0	0.00140	1.0	0.00112
20–26	0.5	0.00160	0.3	0.0025
27–26	0.8	0.00150	0.3	0.00211
26–25	1.0	0.00120	0.8	0.00268
25–33	2.0	0.00110	1.0	0.00167
31–32	0.5	0.00170	0.5	0.00174
28–32	0.5	0.00190	0.3	0.00192
32–33	1.0	0.00150	0.8	0.00432
37–36	0.8	0.00130	0.3	0.00222
30–36	0.5	0.00140	0.3	0.00387
36–35	0.8	0.00120	0.3	0.00164
29–35	0.5	0.00130	0.8	0.00482
35–34	1.0	0.00110	0.8	0.00639
33–34	2.5	0.00100	1.0	0.00223
34–38	2.5	0.00090	1.0	0.00101
$H_{exc}^{nen}$ (m)	1.4		1.4

Table 10. Geometric characteristics reported in Biggiero and Pianese (1996) [64] vs. geometric characteristics obtained for the case BP-2A.

Reach	Biggiero&Pianese (1996)		Case BP-2A
	B	s	B	s
	(m)	(m/m)	(m)	(m/m)
1–2	0.5	0.00200	0.3	0.00179
2–11	0.5	0.00250	0.5	0.00248
10–11	0.5	0.00180	0.8	0.00188
11–12	0.8	0.00170	1.0	0.00262
3–12	0.8	0.00190	0.3	0.00257
4–6	0.5	0.00190	0.8	0.00349
5–6	0.8	0.00170	0.3	0.00215
6–8	0.8	0.00170	0.8	0.00116
7–8	0.5	0.00160	0.8	0.00276
8–15	1.0	0.00160	0.8	0.00591
18–17	0.5	0.00160	0.3	0.00365
9–17	0.5	0.00180	0.3	0.00379
17–16	0.5	0.00150	0.3	0.00257
24–23	0.5	0.00150	0.8	0.00121
23–16	0.8	0.00050	0.8	0.00249
16–15	0.8	0.00140	0.8	0.00515
15–14	1.5	0.00130	1.0	0.00019
19–14	0.5	0.00040	0.3	0.00576
14–13	1.5	0.00120	1.0	0.00123
12–13	1.5	0.00170	1.0	0.00456
13–22	2.0	0.00160	1.0	0.00158
21–22	1.0	0.00170	0.3	0.00301
22–25	2.0	0.00140	1.0	0.00112
20–26	0.5	0.00160	0.3	0.0025
27–26	0.8	0.00150	0.3	0.00211
26–25	1.0	0.00120	0.8	0.00268
25–33	2.0	0.00110	1.0	0.00167
31–32	0.5	0.00170	0.5	0.00174
28–32	0.5	0.00190	0.3	0.00192
32–33	1.0	0.00150	0.8	0.00432
37–36	0.8	0.00130	0.3	0.00222
30–36	0.5	0.00140	0.3	0.00387
36–35	0.8	0.00120	0.3	0.00164
29–35	0.5	0.00130	0.8	0.00482
35–34	1.0	0.00110	0.8	0.00639
33–34	2.5	0.00100	1.0	0.00223
34–38	2.5	0.00090	1.0	0.00101
$H_{exc}^{nen}$ (m)	1.4		1.4

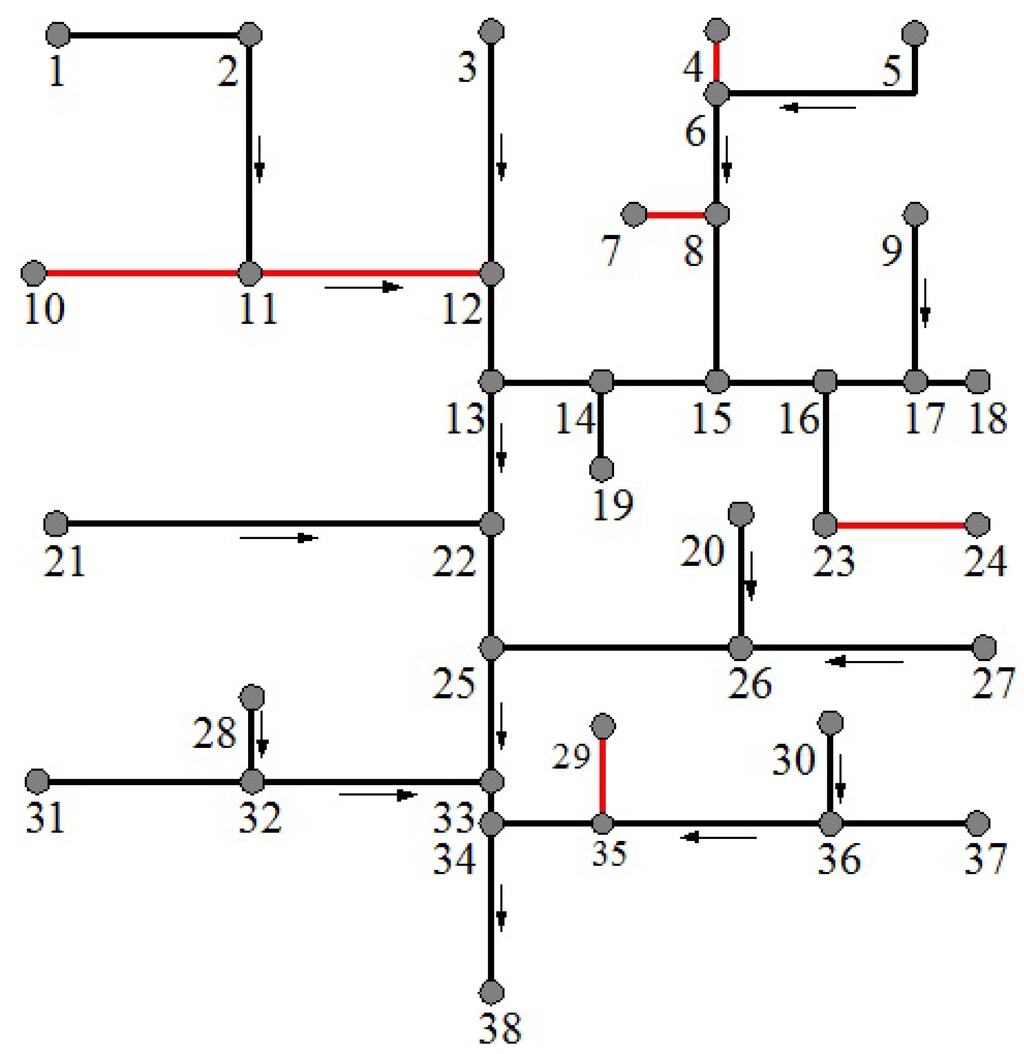
Figure 4. Biggiero and Pianese (1996) [64] vs. case BP-2A. Layout.

Figure 4. Biggiero and Pianese (1996) [64] vs. case BP-2A. Layout.

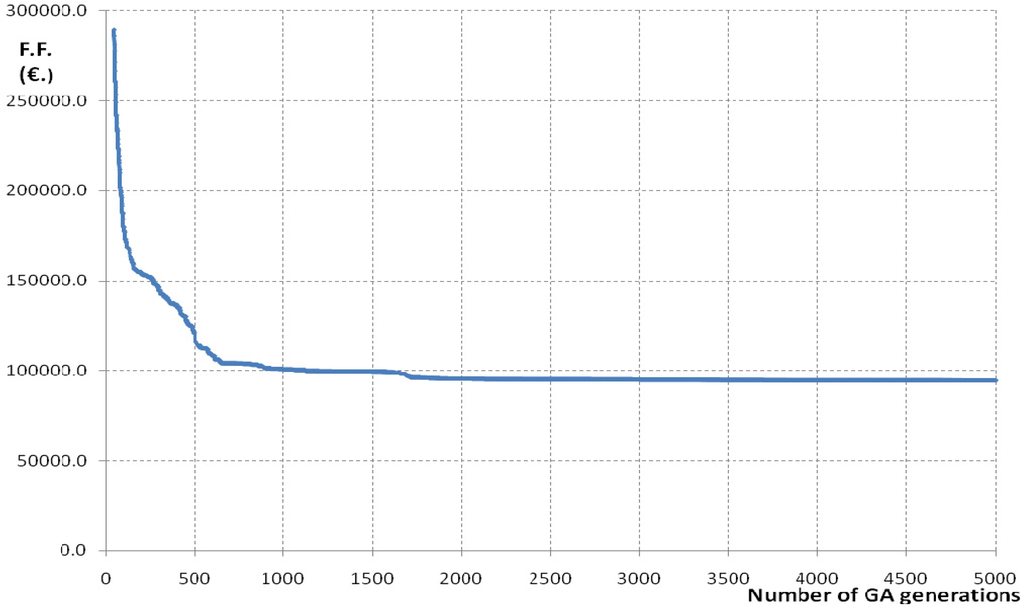
Figure 5. The behavior of fitness function for the case BP-2A.

Figure 5. The behavior of fitness function for the case BP-2A.

4. Conclusions

In this work, an automated tool for the optimal design of rural drainage networks is proposed and its application and effectiveness are demonstrated. The optimization procedure makes use of a GA for the choice of the channels’ geometric characteristics that minimize the construction cost, while a uniform flow stage–discharge formula is used to evaluate the hydraulic performance of the channels and the degree of satisfaction of constraints.

Two case studies are considered. The first application, taken from the literature about the optimal design of urban drainage networks, is used to demonstrate the ability of the GA to approximate the optimal solution of the drainage network problem. The second application refers to a realistic large rural drainage network. The results of this application show that:

-

the cost of the optimal rural drainage network can be very sensitive to the choice of the value to assign to the ending node excavation depth. In particular, the optimal solution obtained fixing the ending node elevation can be much more expansive than the optimal solution obtained with the ending node excavation left free to vary in a given interval. For this reason, fixing a priori the network outlet elevation should be avoided, when possible, technically valid solutions could be obtained by exploiting the possibility that the network outlet channel leaps into the receiving water body;

-

in many cases, the optimization procedure tries to find the optimal solution by increasing the channels slope and reducing the channel width; consequently, the channels’ width may decrease in the downstream direction, despite the fact that the design discharges increase downstream. Of course, the solutions with decreasing channels’ cross section in the downstream direction are not desirable, because they are inefficient when backwater effects are present during on-stationary conditions. For this reason, the constraint c₆ should be always enforced in practical cases;

-

the optimal values of the mutation probability mp fall in the range (0.0075, 0.0225) for the cases examined. This result is in good agreement with the values of mp often suggested in the GA literature, with reference to hydraulic engineering applications.

The approach proposed in this work is based on the preventive knowledge of the discharges flowing through each channel of the drainage network, and on the hypotheses of steady and uniform flow conditions. These limitations, though unable to help in establishing very different minimum cost solutions (Cimorelli et al. [43]), can be removed considering a hydrologic model for the evaluation of the discharges, and using a hydraulic model (De Saint Venant Equations or their parabolic approximation) in order to evaluate the hydraulic performance of the channels.