The Tradeoffs between Market Returns from Agricultural Crops and Non-Market Ecosystem Service Benefits on an Irrigated Agricultural Landscape in the Presence of Groundwater Overdraft
Abstract
:1. Introduction
2. Method
2.1. The Economic Model
2.2. The Ecosystem Service Model
2.3. Efficiency Frontier
2.4. Conservation Policies
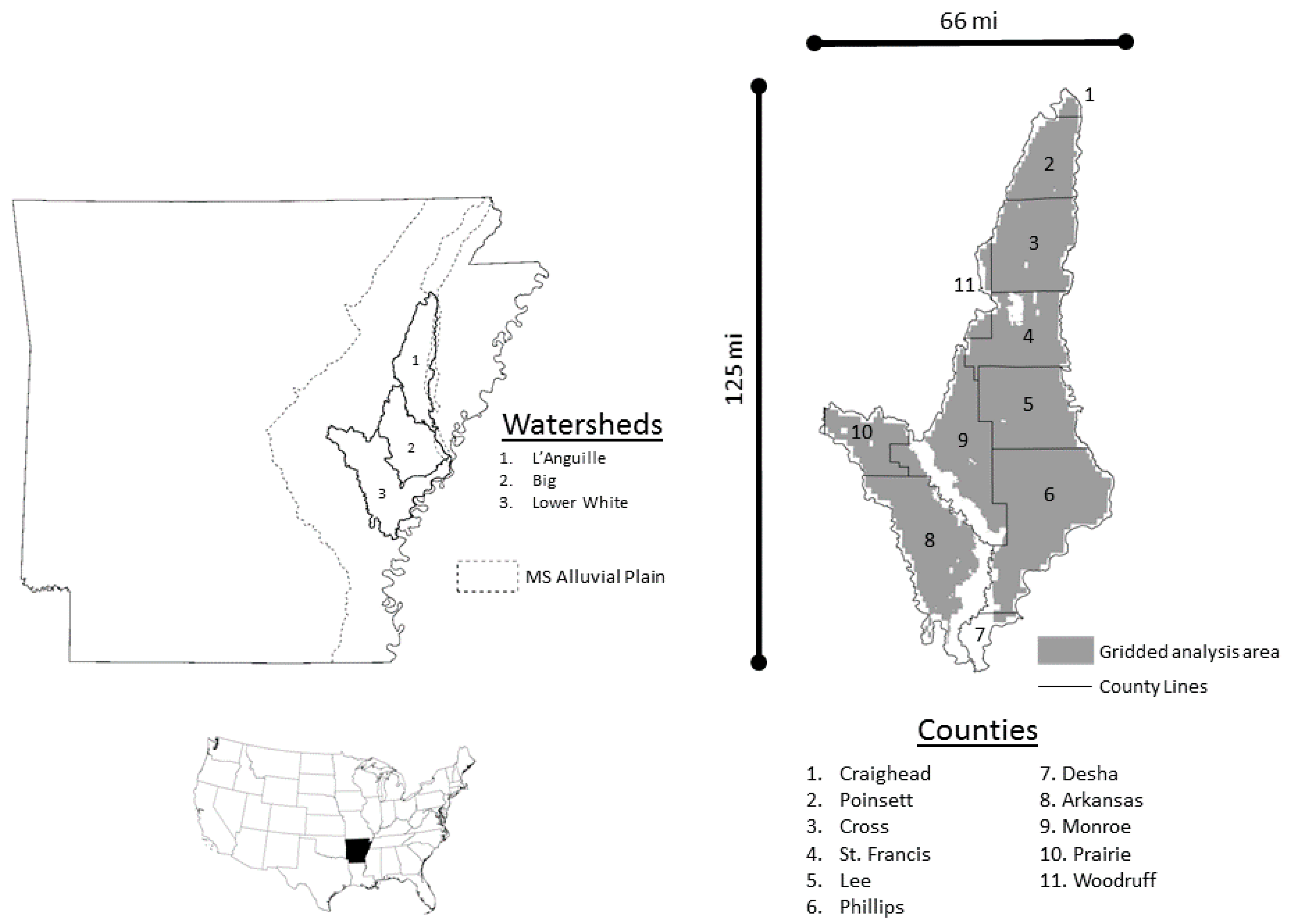
3. Data
3.1. Aquifer
3.2. Farm Production and the On-Farm Reservoir and Tail-Water Recovery System
3.3. Water Purification and Greenhouse Gases
4. Results
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blomquist, W.; Heikkila, T.; Schlager, E. Institutions and conjunctive water management among three western states. Nat. Resour. J. 2002, 41, 653–683. [Google Scholar]
- Kovacs, K.; Popp, M.; Brye, K.; West, G. On-Farm reservoir adoption in the presence of spatially explicit groundwater use and recharge. J. Agric. Resour. Econ. 2015, 40, 23–49. [Google Scholar]
- Noel, J.; Gardner, B.D.; Moore, C. Optimal regional conjunctive water management. Am. J. Agric. Econ. 1980, 62, 489–498. [Google Scholar] [CrossRef]
- Popp, J.; Wailes, E.; Young, K.; Smartt, J.; Intarapapong, W. Use of on-farm reservoirs in rice production: Results from the MARORA model. J. Agric. Appl. Econ. 2003, 35, 69–86. [Google Scholar] [CrossRef]
- Arkansas Natural Resources Commission (ANRC). Arkansas Water Plan Update 2014|Summary; Arkansas Natural Resources Commission: Little Rock, AR, USA, 2015.
- Wang, C.; Segarra, E. The economics of commonly owned groundwater when user demand is perfectly inelastic. J. Agric. Resour. Econ. 2011, 36, 95–120. [Google Scholar]
- Kovacs, K.; Wailes, E.; West, G.; Popp, J.; Bektemirov, K. Optimal spatial-dynamic management of groundwater conservation and surface water quality with on-farm reservoirs. J. Agric. Appl. Econ. 2014, 46, 1–29. [Google Scholar]
- Chan, K.M.A.; Shaw, M.R.; Cameron, D.R.; Underwood, E.C.; Daily, G.C. Conservation planning for ecosystem services. PLoS Biol. 2006, 4, e379. [Google Scholar] [CrossRef] [PubMed]
- Egoh, B.; Reyers, B.; Rouget, M.; Richardson, D.M.; Le Maitre, D.C.; van Jaarsveld, A.S. Mapping ecosystem services for planning and management. Agric. Ecosyst. Environ. 2008, 127, 135–140. [Google Scholar] [CrossRef]
- Egoh, B.; Reyers, B.; Rouget, M.; Bode, M.; Richardson, D.M. Spatial congruence between biodiversity and ecosystem services in South Africa. Biol. Conserv. 2009, 142, 553–562. [Google Scholar] [CrossRef]
- Naidoo, R.; Balmford, A.; Costanza, R.; Fisher, B.; Green, R.E.; Lehner, B.; Malcolm, T.R.; Ricketts, T.H. Global mapping of ecosystem services and conservation priorities. Proc. Natl. Acad. Sci. USA 2008, 105, 9495–9500. [Google Scholar] [CrossRef] [PubMed]
- Raudsepp-Hearne, C.; Peterson, G.; Bennett, E. Ecosystem service bundles for analyzing tradeoffs in diverse landscapes. Proc. Natl. Acad. Sci. USA 2010, 107, 5242–5247. [Google Scholar] [CrossRef] [PubMed]
- Nelson, E.; Polasky, S.; Lewis, D.; Plantinga, A.; Lonsdorf, E.; White, D.; Bael, D.; Lawler, J.J. Efficiency of incentives to jointly increase carbon sequestration and species conservation on a landscape. Proc. Natl. Acad. Sci. USA 2008, 105, 9471–9476. [Google Scholar] [CrossRef] [PubMed]
- Polasky, S.; Nelson, E.; Camm, J.; Csuti, B.; Fackler, P.; Lonsdorf, E.; Montgomery, C.; White, D.; Arthur, J.; Garber-Yonts, B.; et al. Where to put things? Spatial land management to sustain biodiversity and economic returns. Biol. Conserv. 2008, 141, 1505–1524. [Google Scholar] [CrossRef]
- White, C.; Halpern, B.; Kappel, C. Ecosystem service tradeoff analysis reveals the value of marine spatial planning for multiple ocean uses. Proc. Natl. Acad. Sci. USA 2012, 109, 4696–4701. [Google Scholar] [CrossRef] [PubMed]
- Nalley, L.; Popp, M.; Fortin, C. The impact of reducing green house gas emissions in crop agriculture: A spatial and production level analysis. Agric. Resour. Econ. Rev. 2011, 40, 63–80. [Google Scholar] [CrossRef]
- Popp, M.; Nalley, L.; Fortin, C.; Smith, A.; Brye, K. Estimating net carbon emissions and agricultural response to potential carbon offset policies. Agron. J. 2011, 103, 1132–1143. [Google Scholar] [CrossRef]
- Barker, J.; Baumgardner, G.; Turner, D.; Lee, J. Potential carbon benefits of the Conservation Reserve Program in the United States. J. Biogeogr. 1995, 22, 743–751. [Google Scholar] [CrossRef]
- Tol, R.S.J. The economic effects of climate change. J. Econ. Perspect. 2009, 23, 29–51. [Google Scholar] [CrossRef]
- Tallis, H.T.; Ricketts, T.; Guerry, A.D.; Nelson, E.; Ennaanay, D.; Wolny, S.; Olwero, N.; Vigerstol, K.; Pennington, D.; Mendoza, G.; et al. InVEST 2.1 beta User’s Guide; The Natural Capital Project: Stanford, CA, USA, 2011; Available online: http://www.naturalcapitalproject.org/InVEST.html (accessed on 28 April 2013).
- Sharpley, A.; (Crop, Soil, and Environmental Sciences, University of Arkansas). Personal communication, 11 July 2013.
- General Algebraic Modeling System (GAMS). GAMS Release 24.7.3; General Algebraic Modeling System Development Corporation: Washington, DC, USA, 2016. [Google Scholar]
- Division of Agriculture—University of Arkansas. 2012 Crop and Enterprise Budgets; AG-1272; University of Arkansas: Little Rock, AR, USA, 2012; Available online: http://www.uaex.edu/depts/ag_economics/budgets/2012/Budgets 2012.pdf (accessed on 25 July 2013).
- Johnson, D.M.; Mueller, R. The 2009 Cropland Data Layer. Photogramm. Eng. Remote Sens. 2010, 76, 1201–1205. [Google Scholar]
- U.S. Department of Agriculture (USDA)—National Agricultural Statistics Service (NASS) Arkansas Field Office. Soybean Irrigated and Non-Irrigated. Available online: http://www.nass.usda.gov/Statistics_by_State/Arkansas/Publications/County_Estimates/ (accessed on 10 November 2012).
- U.S. Department of the Treasury. Interest Rate Statistics. Available online: http://www.treasury.gov/resource-center/data-chart-center/interest-rates/Pages/default.aspx (accessed on 13 December 2012).
- Arkansas Natural Resources Commission (ANRC). Arkansas Groundwater Protection and Management Report for 2011; Arkansas Natural Resources Commission: Little Rock, AR, USA, 2012.
- Reed, T.B. Recalibration of a Groundwater Flow Model of the Mississippi River Valley Alluvial Aquifer of Northeastern Arkansas, 1918–1998, with Simulations of Water Levels Caused by Projected Groundwater Withdrawals through 2049; U.S. Geological Survey Water Resources Investigations Report 03-4109; U.S. Geological Survey: Little Rock, AR, USA, 2003.
- Flanders, A.; Baker, R.; Barber, T.; Faske, T.; Ginn, H.; Grimes, C.; Hardke, J.; Lawson, K.; Lorenz, G.; Mazzanti, R.; et al. 2014 Crop Production Budgets for Farm Planning; University of Arkansas Cooperative Extension Service, Division of Agriculture: Little Rock, AR, USA, 2014; Available online: http://www.uaex.edu/farm-ranch/economics-marketing/farm-planning/budgets/crop-budgets.aspx (accessed on 15 January 2015).
- Great Pacific Trading Company (GPTC). Charts and Quotes. Available online: http://www.gptc.com/quotes.html (accessed on 20 November 2012).
- U.S. Department of Agriculture (USDA)—Farm Service Agency (FSA). Conservation Reserve Program Statistics. Available online: http://www.fsa.usda.gov/programs-and-services/conservation-programs/reports-and-statistics/conservation-reserve-program-statistics/index (accessed on 14 June 2015).
- Young, K.B.; Wailes, E.J.; Popp, J.H.; Smartt, J. Value of water conservation improvements on Arkansas rice farms. J. Asfmra 2004, 67, 119–126. [Google Scholar]
- Smartt, J.H.; Wailes, E.J.; Young, K.B.; Popp, J.S. MARORA (Modified Arkansas Off-Stream Reservoir Analysis) Program Description and User’s Guide; University of Arkansas: Fayetteville, AR, USA, 2002; unpublished manuscript; Available online: http://agribus.uark.edu/2893.php (accessed on 28 April 2013).
- Arkansas Land Information Board. Five Meter Resolution Digital Elevation Model. SDE Raster Digital Data; 2006. Available online: http://www.geostor.arkansas.gov/G6/Home.html?id=629c0f9562c2f9cd95ffd8ef564a5d7f (accessed on 12 May 2013). [Google Scholar]
- Hite, D.; Hudson, D.; Intarapapong, W. Willingness to pay for water quality improvements: The case of precision application technology. J. Agric. Resour. Econ. 2002, 27, 433–449. [Google Scholar]
- Cole, A. Arkansas Population Projections: 2003–2025; Center for Business and Economic Research, University of Arkansas: Fayetteville, AR, USA, 2003; Available online: http://cber.uark.edu/439.asp (accessed on 18 July 2013).
- Kossoy, A.; Peszko, G.; Oppermann, K.; Prytz, N.; Klein, N.; Blok, K.; Lam, L.; Wong, L.; Borkent, B. State and Trends of Carbon Pricing 2015 (September); World Bank: Washington, DC, USA, 2005. [Google Scholar]
- U.S. Department of Agriculture (USDA). Natural Resources Conservation Service (NRCS), Arkansas. 2014 EQIP Conservation Practices and Payment Rates. Available online: http://www.nrcs.usda.gov/wps/portal/nrcs/detail/ar/home/?cid=STELPRDB1240703 (accessed on 13 August 2014).
- European Commission Emission Trading Scheme. Auctions by the Transitional Common Auction Platform. January 2015. Available online: http://ec.europa.eu/clima/policies/ets/cap/auctioning/docs/cap_report_201503_en.pdf (accessed on 19 July 2015).
- Ward, F.A.; Pulido-Velazquez, M. Water Conservation in irrigation can increase water use. Proc. Natl. Acad. Sci. USA 2008, 105, 18215–18220. [Google Scholar] [CrossRef] [PubMed]




| Without Reservoirs | With Reservoirs | ||||||
|---|---|---|---|---|---|---|---|
| Efficiency Frontiers | Present Value of Economic Returns | Present Value of Optimized Ecosystem Service(s) | Present Value of Ecosystem Services | Efficiency Frontiers | Present Value of Economic Returns | Present Value of Optimized Ecosystem Service(s) | Present Value of Ecosystem Services |
| All ecosystem service values | |||||||
| A | 1,649 | 1,532 | 1,532 | F | 1,649 | 1,532 | 1,532 |
| B | 2,768 | 1,000 | 1,000 | G | 3,021 | 1,000 | 1,000 |
| C | 3,021 | 819 | 819 | H | 3,322 | 819 | 819 |
| D | 3,322 | 567 | 567 | I | 3,656 | 567 | 567 |
| E | 4,559 | −2,345 | −2,345 | J | 4,757 | −2,206 | −2,206 |
| Groundwater supply values only | |||||||
| K | 1,649 | 60 | 1,532 | P | 1,650 | 60 | 1,529 |
| L | 2,539 | 50 | 885 | Q | 4,169 | 50 | −620 |
| M | 3,463 | 20 | 331 | R | 4,449 | 20 | −796 |
| N | 4,118 | −10 | −450 | S | 4,638 | −10 | −1,178 |
| O | 4,559 | −68 | −2,345 | T | 4,757 | −56 | −2,206 |
| Water purification values only | |||||||
| U | 1,649 | 32 | 1,532 | Z | 1,649 | 32 | 1,531 |
| V | 3,957 | 25 | −1,526 | AA | 4,102 | 25 | −1,348 |
| W | 4,102 | 23 | −1,699 | BB | 4,260 | 23 | −1,524 |
| X | 4,260 | 19 | −1,895 | CC | 4,429 | 19 | −1,720 |
| Y | 4,559 | −1 | −2,345 | DD | 4,757 | −2 | −2,206 |
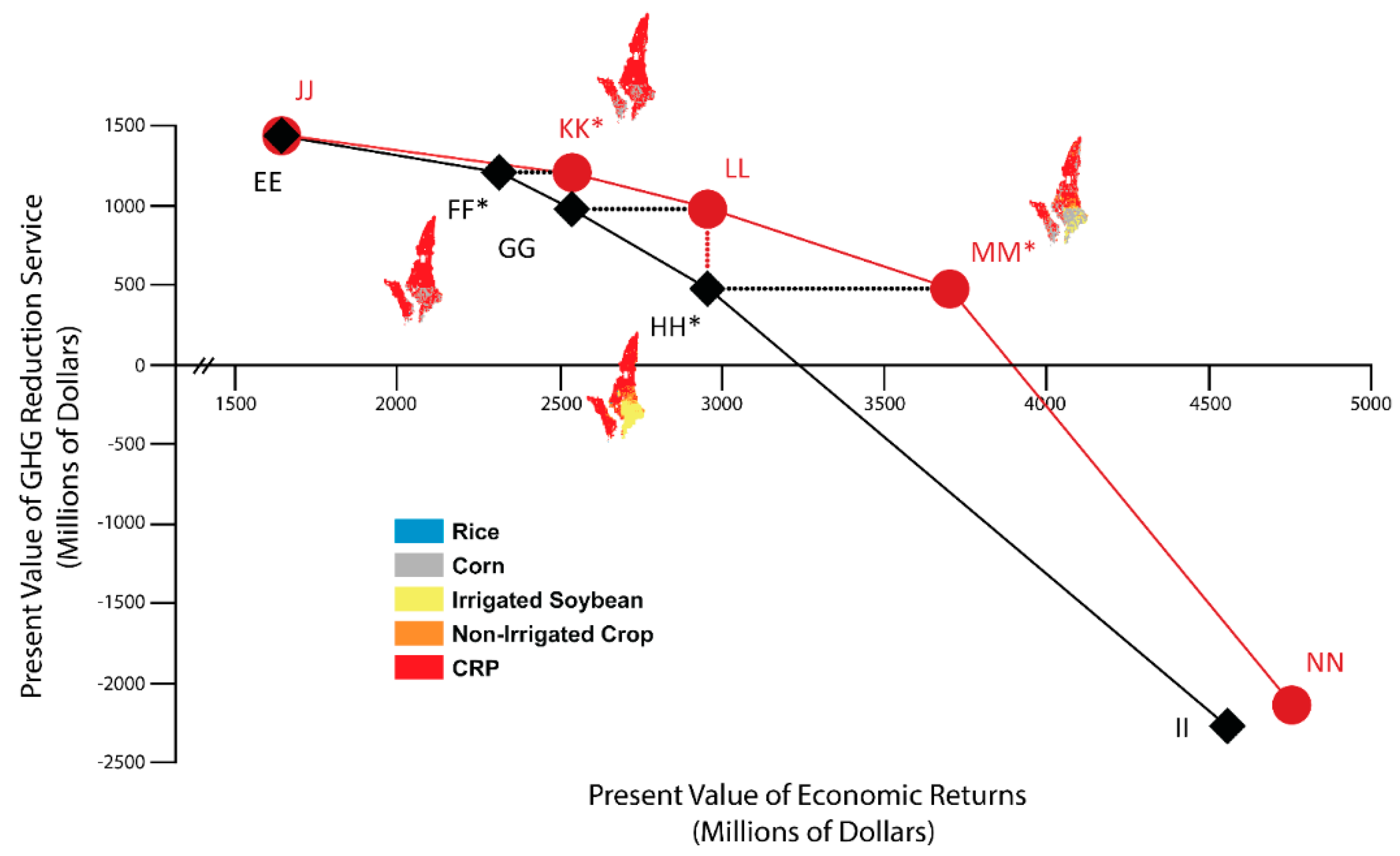
| Greenhouse gas reduction values only | |||||||
| EE | 1,649 | 1,439 | 1,532 | JJ | 1,649 | 1,439 | 1,532 |
| FF | 2,319 | 1,200 | 1,269 | KK | 2,456 | 1,200 | 1,276 |
| GG | 2,456 | 9,69 | 1,033 | LL | 2,961 | 969 | 1,033 |
| HH | 2,961 | 478 | 516 | MM | 3,708 | 478 | 5,18 |
| II | 4,559 | −2,276 | −2,345 | NN | 4,757 | −2,147 | −2,206 |
| Ecosystem Service or Land Cover Value | Without Reservoirs | With Reservoirs | ||||
|---|---|---|---|---|---|---|
| A | C | E | F | H | J | |
| Greenhouse gases | 1,439 | 771 | −2,276 | 1,439 | 760 | −2,147 |
| Groundwater supply | 60 | 27 | −68 | 60 | 41 | −56 |
| Water purification | 32 | 21 | −1 | 32 | 19 | −2 |
| Total ecosystem services | 1,532 | 819 | −2,345 | 1,532 | 819 | −2,206 |
| Rice | 0 | 0 | 769 | 0 | 0 | 932 |
| Irrigated soybeans | 0 | 121 | 674 | 0 | 21 | 698 |
| Non-irrigated crop | 0 | 543 | 625 | 0 | 477 | 587 |
| Corn | 0 | 1,300 | 1,940 | 0 | 1,953 | 2,081 |
| Cotton | 0 | 54 | 430 | 0 | 21 | 439 |
| CRP | 1,649 | 1,003 | 121 | 1,649 | 851 | 20 |
| Total economic return | 1,649 | 3,021 | 4,559 | 1,649 | 3,322 | 4,757 |
| Total of economic return and ecosystem service value (Value to society) | 3,181 | 3,840 | 2,214 | 3,181 | 4,141 | 2,551 |
| Ecosystem Service or Land Cover Value | Without Reservoirs | With Reservoirs | ||||
|---|---|---|---|---|---|---|
| L | M | N | Q | R | S | |
| Greenhouse gases | 813 | 300 | −442 | −672 | −816 | −1,167 |
| Groundwater supply | 50 | 20 | −10 | 50 | 20 | −10 |
| Water purification | 22 | 11 | 2 | 2 | 0 | 0 |
| Total ecosystem services | 885 | 331 | −450 | −620 | −796 | −1,178 |
| Rice | 0 | 0 | 125 | 702 | 757 | 816 |
| Irrigated soybeans | 0 | 0 | 315 | 290 | 377 | 634 |
| Non-irrigated crop | 945 | 942 | 937 | 817 | 823 | 646 |
| Corn | 521 | 1,703 | 1,959 | 1,952 | 2,056 | 2,079 |
| Cotton | 16 | 132 | 423 | 386 | 412 | 437 |
| CRP | 1,058 | 685 | 360 | 23 | 24 | 25 |
| Total economic return | 2,539 | 3,462 | 4,118 | 4,169 | 4,449 | 4,638 |
| Total of economic return and ecosystem service value (Value to society) | 3,424 | 3,793 | 3,668 | 3,549 | 3,653 | 3,460 |
| Ecosystem Service or Land Cover Value | Without Reservoirs | With Reservoirs | ||||
|---|---|---|---|---|---|---|
| V | W | X | AA | BB | CC | |
| Greenhouse gases | −1,506 | −1,671 | −1,858 | −1,340 | −1,509 | −1,697 |
| Groundwater supply | −45 | −51 | −57 | −32 | −37 | −43 |
| Water purification | 25 | 23 | 19 | 25 | 23 | 19 |
| Total ecosystem services | −1,526 | −1,699 | −1,895 | −1,348 | −1,524 | −1,720 |
| Rice | 739 | 746 | 758 | 887 | 904 | 924 |
| Irrigated soybeans | 547 | 587 | 625 | 556 | 601 | 635 |
| Non-irrigated crop | 347 | 377 | 440 | 319 | 362 | 419 |
| Corn | 1,574 | 1,685 | 1,778 | 1,675 | 1,788 | 1,898 |
| Cotton | 233 | 265 | 311 | 228 | 260 | 307 |
| CRP | 518 | 443 | 348 | 438 | 346 | 246 |
| Total economic return | 3,957 | 4,102 | 4,260 | 4,102 | 4,260 | 4,429 |
| Total of economic return and ecosystem service value (Value to society) | 2,431 | 2,403 | 2,365 | 2,754 | 2,736 | 2,709 |
| Ecosystem Service or Land Cover Value | Without Reservoirs | With Reservoirs | ||||
|---|---|---|---|---|---|---|
| FF | GG | HH | KK | LL | MM | |
| Greenhouse gases | 1,200 | 969 | 478 | 1,200 | 969 | 478 |
| Groundwater supply | 41 | 41 | 25 | 49 | 42 | 28 |
| Water purification | 28 | 23 | 13 | 28 | 22 | 11 |
| Total ecosystem services | 1,269 | 1,033 | 516 | 1,276 | 1,033 | 518 |
| Rice | 0 | 1 | 28 | 0 | 0 | 0 |
| Irrigated soybeans | 2 | 650 | 856 | 0 | 4 | 266 |
| Non-irrigated crop | 63 | 570 | 907 | 0 | 80 | 604 |
| Corn | 853 | 0 | 0 | 1,087 | 1,756 | 2,076 |
| Cotton | 15 | 73 | 374 | 15 | 16 | 134 |
| CRP | 1,386 | 1,162 | 796 | 1,354 | 1,104 | 628 |
| Total economic return | 2,319 | 2,456 | 2,961 | 2,456 | 2,961 | 3,708 |
| Total of economic return and ecosystem service value (Value to society) | 3,588 | 3,489 | 3,477 | 3,732 | 3,994 | 4,226 |
| Ecosystem Service or Land Cover Value | Baseline (Point J) | Conservation Policies | |||
|---|---|---|---|---|---|
| Cost-Share Reservoir Construction Costs a | Tax on Ground-Water b | Total Maximum Daily Load c | Carbon Credits d | ||
| Greenhouse gases | −2,147 | −1,815 | −1,715 | −1,948 | −1,203 |
| Groundwater supply | −56 | −40 | −39 | −49 | −20 |
| Water purification | −2 | −2 | −2 | 7 | −1 |
| Total ecosystem services | −2,206 | −1,857 | −1,755 | −1,991 | −1,224 |
| Rice | 932 | 962 | 902 | 963 | 754 |
| Irrigated soybeans | 698 | 716 | 687 | 670 | 690 |
| Non-irrigated crop | 587 | 523 | 597 | 482 | 644 |
| Corn | 2,081 | 2,083 | 2,086 | 2,056 | 2,087 |
| Cotton | 439 | 437 | 442 | 373 | 445 |
| CRP | 20 | 12 | 25 | 111 | 50 |
| Total economic return before government transfer | 4,757 | 4,734 | 4,738 | 4,654 | 4,669 |
| Government transfer | 0 | 98 | −125 | 0 | 2,521 |
| Total of economic return before government transfer and ecosystem service value (Value to society) | 2,551 | 2,877 | 2,983 | 2,663 | 3,445 |
| Economic cost per dollar of ecosystem service value gained (dollars) e | - | 0.07 | 0.04 | 0.48 | 0.09 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovacs, K.F.; Xu, Y.; West, G.H.; Popp, M. The Tradeoffs between Market Returns from Agricultural Crops and Non-Market Ecosystem Service Benefits on an Irrigated Agricultural Landscape in the Presence of Groundwater Overdraft. Water 2016, 8, 501. https://doi.org/10.3390/w8110501
Kovacs KF, Xu Y, West GH, Popp M. The Tradeoffs between Market Returns from Agricultural Crops and Non-Market Ecosystem Service Benefits on an Irrigated Agricultural Landscape in the Presence of Groundwater Overdraft. Water. 2016; 8(11):501. https://doi.org/10.3390/w8110501
Chicago/Turabian StyleKovacs, Kent F., Ying Xu, Grant H. West, and Michael Popp. 2016. "The Tradeoffs between Market Returns from Agricultural Crops and Non-Market Ecosystem Service Benefits on an Irrigated Agricultural Landscape in the Presence of Groundwater Overdraft" Water 8, no. 11: 501. https://doi.org/10.3390/w8110501
APA StyleKovacs, K. F., Xu, Y., West, G. H., & Popp, M. (2016). The Tradeoffs between Market Returns from Agricultural Crops and Non-Market Ecosystem Service Benefits on an Irrigated Agricultural Landscape in the Presence of Groundwater Overdraft. Water, 8(11), 501. https://doi.org/10.3390/w8110501






