Computing Economies of Scope Using Robust Partial Frontier Nonparametric Methods
Abstract
:1. Introduction
2. Computing Economies of Scope
2.1. Nonparametric Methods
2.2. Proposed Methodology
2.3. Conditional and Unconditional Efficiency Scores
3. Case Study
3.1. Economies of Scope and the Portuguese Water Sector
3.2. Simulated Case Study
3.3. Results
3.3.1. Proposed Methodology
3.3.2. Conditional and Unconditional Efficiency Scores
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| CRS | Constant Returns to Scale |
| DEA | Data Envelopment Analysis |
| FDH | Free Disposal Hull |
| VRS | Variable Returns to Scale |
| Ws | Water services |
| Ww | Wastewater services |
References
- Bel, G.; Warner, M. Does privatization of solid waste and water services reduce costs? A review of empirical studies. Resources. Conserv. Recycl. 2008, 52, 1337–1348. [Google Scholar] [CrossRef]
- Baumol, W.; Panzar, J.; Willig, R. Contestable Markets and the Theory of Industry Structure; Harcourt Brace Jovanovich: New York, NY, USA, 1988. [Google Scholar]
- Panzar, J.; Willig, R. The economy of scope. Am. Econ. Rev. 1981, 71, 268–272. [Google Scholar]
- Fraquelli, G.; Piacenza, M.; Vannoni, D. Scope and scale economies in multi-utilities: Evidence from gas, water and electricity combinations. Appl. Econ. 2004, 36, 2045–2057. [Google Scholar] [CrossRef]
- Abbott, M.; Cohen, B. Productivity and efficiency in the water industry. Util. Policy 2009, 17, 233–244. [Google Scholar] [CrossRef]
- Farsi, M.; Filippini, M. An analysis of cost efficiency in Swiss multi-utilities. Energy Econ. 2009, 31, 306–315. [Google Scholar] [CrossRef]
- Färe, R. Addition and efficiency. Q. J. Econ. 1986, 51, 861–865. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lovell, K. Productions Frontiers; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Grosskopf, S.; Yaisawarng, S. Economies of scope in the provision of local public services. Natl. Tax J. 1990, 43, 61–74. [Google Scholar]
- Ferrier, G.; Grosskopf, S.; Hayes, K.; Yaisawarng, S. Economies of diversification in the banking industry. J. Monet. Econ. 1993, 31, 229–249. [Google Scholar] [CrossRef]
- Prior, D.; Solà, M. Technical efficiency and economies of diversification in health care. Health Care Manag. Sci. 2000, 3, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Cummins, J.D.; Weiss, M.; Zi, H. Economies of Scope in Financial Services: A DEA Bootstrapping Analysis of the US Insurance Industry; Working Paper; Wharton Financial Institutions Center: Philadelphia, PA, USA, 2003. [Google Scholar]
- Growitsch, C.; Wetzel, H. Testing for Economies of Scope in European Railways: An Efficiency Analysis; Working Paper no. 72; University of Lüneburg: Lüneburg, Germany, 2007. [Google Scholar]
- Arocena, P. Cost and quality gains from diversification and vertical integration in the electricity industry: A DEA Approach. Energy Econ. 2008, 30, 39–58. [Google Scholar] [CrossRef]
- De Witte, K.; Marques, R. Big and beautiful? On non-parametrically measuring scale economies in non-convex technologies. J. Product. Anal. 2011, 35, 213–226. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P. Sensitivity analysis of efficiency scores: How to bootstrap in nonparametric frontier models? Manag. Sci. 1998, 44, 49–61. [Google Scholar] [CrossRef]
- Dyson, R.G.; Shale, E.A. Data envelopment analysis, operational research and uncertainty. J. Oper. Res. Soc. 2010, 61, 25–34. [Google Scholar] [CrossRef]
- Fuentes, R.; Torregrosa, T.; Ballenilla, E. Conditional Order-m Efficiency of Wastewater Treatment Plants: The Role of Environmental Factors. Water 2015, 7, 5503–5524. [Google Scholar] [CrossRef]
- Daraio, C.; Simar, L. Advanced Robust and Nonparametric Methods in Efficiency Analysis. Methodology and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Deprins, D.; Simar, L.; Tulkens, H. Measuring labor efficiency in post offices. In The Performance of Public Enterprises: Concepts and Measurements (pp. 243–268); Marchand, M., Pestieau, P., Tulkens, H., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Daraio, C.; Simar, L. Introducing environmental variables in nonparametric frontier models: A probabilistic approach. J. Product. Anal. 2005, 24, 93–121. [Google Scholar] [CrossRef]
- Carvalho, P.; Marques, R. The influence of the operational environment on the efficiency of water utilities. J. Environ. Manag. 2011, 92, 2698–2707. [Google Scholar] [CrossRef] [PubMed]
- Fried, H.; Lovell, K.; Schmidt, S. The Measurement of Productive Efficiency and Productivity Growth; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Cazals, C.; Florens, J.; Simar, L. Nonparametric frontier estimation: A robust approach. J. Econom. 2002, 106, 1–25. [Google Scholar] [CrossRef]
- Aragon, Y.; Daouia, A.; Thomas-Agnan, C. Nonparametric frontier estimation: A conditional quantile-based approach. Econom. Theory 2005, 21, 358–389. [Google Scholar] [CrossRef]
- Daouia, A.; Simar, L. Nonparametric efficiency analysis: A multivariate conditional quantile approach. J. Econom. 2007, 140, 375–400. [Google Scholar] [CrossRef]
- Morita, H. Analysis of economies of scope by data envelopment analysis: Comparison of efficient frontiers. Int. Trans. Oper. Res. 2003, 10, 393–402. [Google Scholar] [CrossRef]
- Carvalho, P.; Marques, R. Computing economies of vertical integration, economies of scope and economies of scale using partial frontier nonparametric methods. Eur. J. Oper. Res. 2014, 234, 292–307. [Google Scholar] [CrossRef]
- Chavas, J.P.; Kim, K. Economies of diversification: A generalization and decomposition of economies of scope. Int. J. Prod. Econ. 2010, 126, 229–235. [Google Scholar] [CrossRef]
- Zhu, J. Quantitative Models for Performance Evaluation and Benchmarking; Kluwer Academic Publishers: Norwell, MA, USA, 2003. [Google Scholar]
- Chen, Y. Measuring super-efficiency in DEA in the presence of infeasibility. Eur. J. Oper. Res. 2005, 161, 545–551. [Google Scholar] [CrossRef]
- Aitchison, J.; Aitken, C. Multivariate binary discrimination by Kernel Method. Biometrika 1976, 63, 413–420. [Google Scholar] [CrossRef]
- Marques, R. Regulation of Water and Wastewater Services: An International Comparison; IWA Publishing: London, UK, 2010. [Google Scholar]
- Berg, S.; Marques, R. Quantitative studies of water and sanitation utilities: A benchmarking literature survey. Water Policy 2011, 13, 591–606. [Google Scholar] [CrossRef]
- Ferro, G.; Lentini, E.; Mercadier, A. Economías de Escala en Agua y Saneamiento: Examen de la Literatura; Working Papers hal-00460661; HAL: Villeurbanne, France, 2010. [Google Scholar]
- Cruz, N.F.; Carvalho, P.; Marques, R. Disentangling the cost efficiency of jointly provided water and wastewater services. Util. Policy 2013, 24, 70–77. [Google Scholar] [CrossRef]
- Beasley, J.E. Determining teaching and research efficiencies. J. Oper. Res. Soc. 1995, 46, 441–452. [Google Scholar] [CrossRef]
- Chen, Y.; Du, J.; Sherman, H.D.; Zhu, J. DEA model with shared resources and efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 339–349. [Google Scholar] [CrossRef]
- Marques, R.; De Witte, K. Is big better? On scale and economies of scope in the Portuguese water sector. Econ. Model. 2011, 28, 1009–1016. [Google Scholar] [CrossRef]
- Fraquelli, G.; Moiso, V. Cost Efficiency and Economies of Scale in the Italian Water Industry; Working Paper; Hermes Press: Pavia, Italy, 2005. [Google Scholar]
- Lynk, E.L. Privatisation, joint production and the comparative efficiencies of private and public ownership: The UK water industry case. Fisc. Stud. 1993, 14, 98–116. [Google Scholar] [CrossRef]
- Hunt, L.; Lynk, E. Privatization and efficiency in the UK water industry: An empirical analysis. Oxf. Bull. Econ. Stat. 1995, 57, 371–388. [Google Scholar] [CrossRef]
- Martins, R.; Fortunato, A.; Coelho, F. Cost Structure of the Portuguese Water Industry: A Cubic Cost Function Application; Working Paper, No. 9; University of Coimbra: Coimbra, Portugal, 2006. [Google Scholar]
- Worthington, A.C. Productivity, Efficiency and Technological Progress in Australia’s Urban Water Utilities; Waterlines Report; National Water Commission: Canberra, Australia, 2011. [Google Scholar]



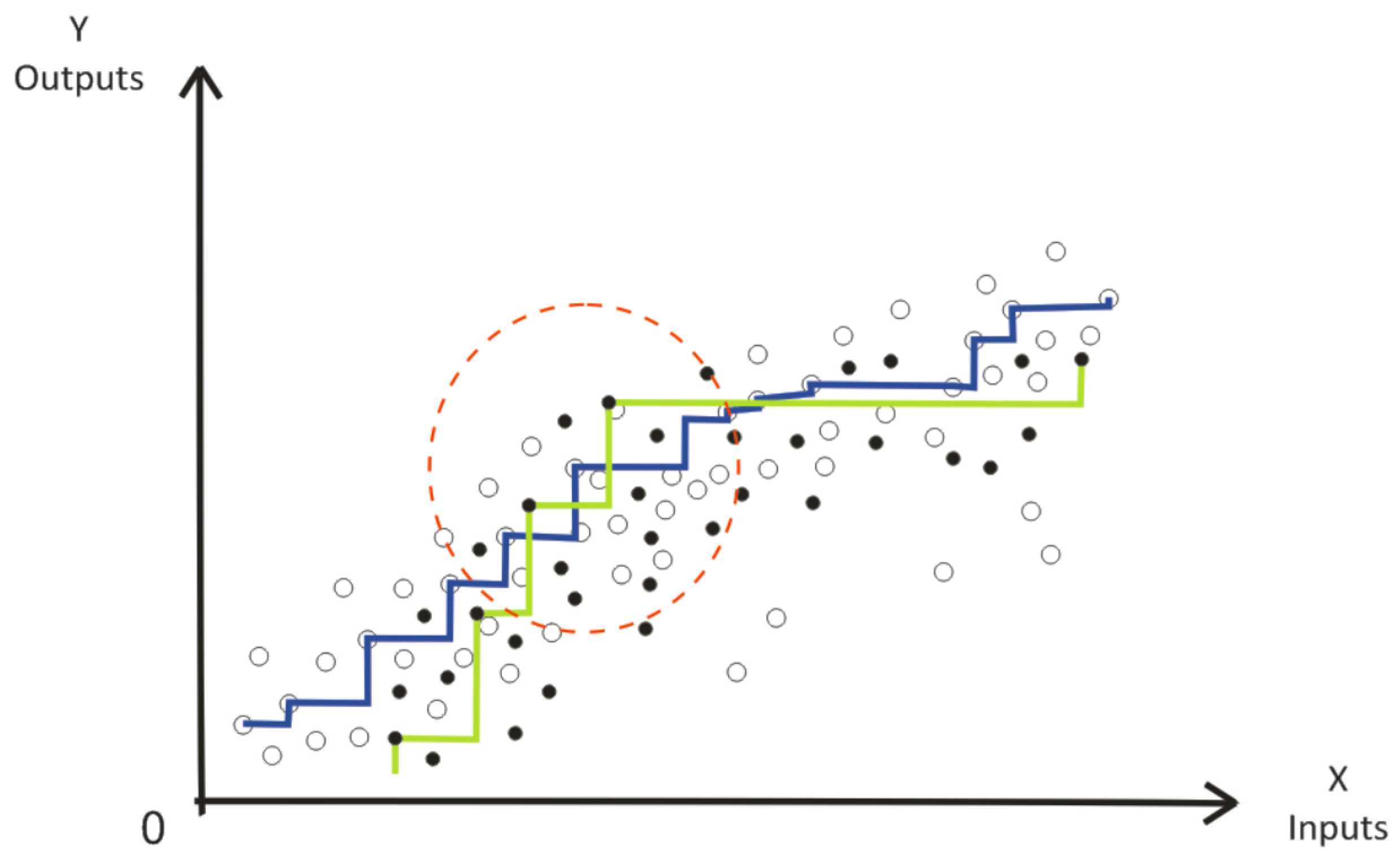
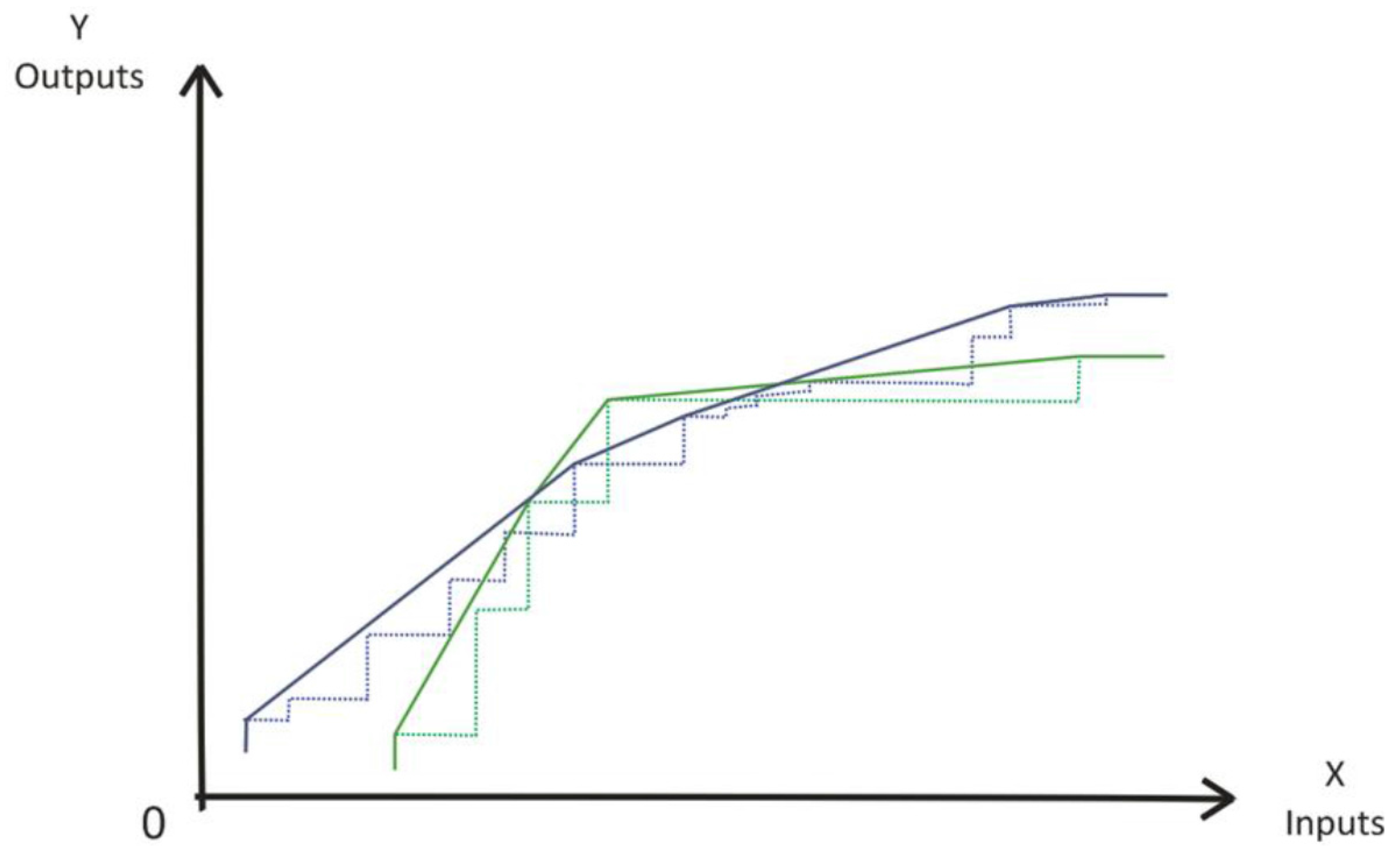








| STATISTICS | INPUTS | OUTPUTS | |||||
|---|---|---|---|---|---|---|---|
| Labor cost (water) | Other costs (water) | Capital cost (water) | Delivered water volume (retail and wholesale) | Water customers | 1/3 volume of collected wastewater + 2/3 volume of treated wastewater | Wastewater customers | |
| (103 €) | (103 €) | (103 €) | (103 m3) | (no.) | (103 m3) | (no.) | |
| Average | 4605 | 6505 | 5074 | 24,543 | 54,673 | 0 | 0 |
| St. Deviation | 10,884 | 12,568 | 12,812 | 65,423 | 98,259 | 0 | 0 |
| Minimum | 167 | 299 | 144 | 916 | 6730 | 0 | 0 |
| Maximum | 43,856 | 47,436 | 45,388 | 223,116 | 346,699 | 0 | 0 |
| Median | 884 | 1833 | 673 | 2490 | 22,464 | 0 | 0 |
| Observations (no.) | 68 | ||||||
| STATISTICS | INPUTS | OUTPUTS | |||||
|---|---|---|---|---|---|---|---|
| Labor cost (water) + Labor cost (wastewater) | Other costs (water) + Other costs (wastewater) | Capital cost (water) + Capital cost (wastewater) | Delivered water volume (retail and wholesale) | Water customers | 1/3 volume of collected wastewater + 2/3 volume of treated wastewater | Wastewater customers | |
| (103 €) | (103 €) | (103 €) | (103 m3) | (no.) | (103 m3) | (no.) | |
| Average | 3261 | 6125 | 2783 | 6246 | 48,359 | 2192 | 36,154 |
| St. Deviation | 3517 | 7021 | 2405 | 5979 | 45,290 | 2185 | 39,790 |
| Minimum | 26 | 395 | 73 | 293 | 4553 | 70 | 1223 |
| Maximum | 18,150 | 30,321 | 10,907 | 23,852 | 185,784 | 11,879 | 185,561 |
| Median | 1930 | 3621 | 1947 | 3869 | 30,400 | 1366 | 18,672 |
| Observations (no.) | 253 | ||||||
| STATISTICS | INPUTS | OUTPUTS | |||||
|---|---|---|---|---|---|---|---|
| Labor cost (wastewater) | Other costs (wastewater) | Capital cost (wastewater) | Delivered water volume (retail and wholesale) | Water customers | 1/3 volume of collected wastewater + 2/3 volume of treated wastewater | Wastewater customers | |
| (103 €) | (103 €) | (103 €) | (103 m3) | (no.) | (103 m3) | (no.) | |
| Average | 954 | 1742 | 800 | 0 | 0 | 2296 | 36,183 |
| St. Deviation | 1182 | 2354 | 907 | 0 | 0 | 2220 | 38,793 |
| Minimum | 1 | 0 | 0 | 0 | 0 | 13 | 1223 |
| Maximum | 5815 | 12,125 | 4,840 | 0 | 0 | 11,879 | 185,561 |
| Median | 490 | 968 | 466 | 0 | 0 | 1368 | 21,354 |
| Observations (no.) | 103 | ||||||
| Utilities | Statistics | Inputs | Outputs | ||
|---|---|---|---|---|---|
| X1 | X2 | YA | YB | ||
| A | Average | 1.176 | 0.986 | 1.834 | ----- |
| Median | 1.304 | 1.058 | 1.562 | ----- | |
| St. Deviation | 0.575 | 0.505 | 1.129 | ----- | |
| Minimum | 0.137 | 0.107 | 0.244 | ----- | |
| Maximum | 1.977 | 1.922 | 4.610 | ----- | |
| Observations (no.) | 50 | ||||
| B | Average | 1.047 | 0.990 | ----- | 1.739 |
| Median | 1.140 | 1.070 | ----- | 1.564 | |
| St. Deviation | 0.565 | 0.567 | ----- | 1.109 | |
| Minimum | 0.196 | 0.142 | ----- | 0.127 | |
| Maximum | 1.968 | 1.994 | ----- | 4.276 | |
| Observations (no.) | 40 | ||||
| A+B | Average | 2.223 | 1.976 | 1.834 | 1.739 |
| Median | 2.205 | 1.959 | 1.562 | 1.564 | |
| St. Deviation | 0.797 | 0.751 | 1.118 | 1.095 | |
| Minimum | 0.333 | 0.249 | 0.244 | 0.127 | |
| Maximum | 3.945 | 3.916 | 4.610 | 4.276 | |
| Observations (no.) | 2000 (=40 × 50) | ||||
| AB | Average | 2.699 | 2.908 | 1.383 | 1.517 |
| Median | 2.927 | 3.036 | 1.388 | 1.512 | |
| St. Deviation | 1.447 | 1.456 | 0.284 | 0.376 | |
| Minimum | 0.273 | 0.329 | 0.665 | 0.640 | |
| Maximum | 4.998 | 4.976 | 1.842 | 2.129 | |
| Observations (no.) | 100 | ||||
| Order-α frontier of the joint production (WsWw utilities) | Statistics relative for the period 2002–2008 | Efficiencies of WsWw utilities relative to their own frontier (θ) | Efficiencies of WsWw utilities relative to the frontier of Ws+Ww utilities (θ j) | Ratio = θj/θ | Economies of Scope | Diseconomies of Scope | ||
|---|---|---|---|---|---|---|---|---|
| Ratios > 1 | WsWw utilities with ratios > 1 (no.) | Ratios < 1 | WsWw utilities with ratios < 1 (no.) | |||||
| α = 0.990 | Average | 0.876 | 0.972 | 1.110 | 1.272 | 23 51% | 0.913 | 22 49% |
| Median | 0.851 | 0.833 | 1.003 | 1.165 | 0.931 | |||
| St. Deviation | 0.296 | 0.486 | 0.373 | 0.385 | 0.068 | |||
| Maximum | 2.420 | 2.997 | 3.235 | 2.238 | 0.984 | |||
| Minimum | 0.502 | 0.493 | 0.714 | 1.024 | 0.727 | |||
| α = 0.995 | Average | 0.830 | 0.972 | 1.172 | 1.293 | 29 64% | 0.920 | 16 36% |
| Median | 0.821 | 0.833 | 1.059 | 1.185 | 0.965 | |||
| St. Deviation | 0.287 | 0.486 | 0.425 | 0.382 | 0.080 | |||
| Maximum | 2.420 | 2.997 | 4.127 | 2.532 | 0.993 | |||
| Minimum | 0.491 | 0.493 | 0.714 | 1.008 | 0.727 | |||
| α = 0.999 | Average | 0.772 | 0.972 | 1.226 | 1.321 | 34 76% | 0.949 | 11 24% |
| Median | 0.786 | 0.833 | 1.090 | 1.196 | 0.974 | |||
| St. Deviation | 0.152 | 0.486 | 0.502 | 0.445 | 0.048 | |||
| Maximum | 1.000 | 2.997 | 5.591 | 3.101 | 0.993 | |||
| Minimum | 0.475 | 0.493 | 0.814 | 1.004 | 0.865 | |||
| Order-Frontier of the Joint Production AB | Utilities AB Located above the Frontier of the Joint Production | Average of Ratios | % Utilities AB with Ratios (Economies of Scope) | % Utilities AB with Ratios (Diseconomies of Scope) | |
|---|---|---|---|---|---|
| CRS | α = 0.987 | 24% | 0.727 | 8% | 92% |
| α = 0.989 | 9% | 0.881 | 20% | 80% | |
| α = 0.99 | 1% | 1.092 | 55% | 45% | |
| α = 0.999 | 0% | 1.196 | 67% | 33% | |
| VRS | α = 0.987 | 24% | 0.669 | 8% | 92% |
| α = 0.989 | 9% | 0.815 | 27% | 73% | |
| α = 0.99 | 1% | 0.843 | 26% | 74% | |
| α = 0.999 | 0% | 0.853 | 26% | 74% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, P.; Cunha Marques, R. Computing Economies of Scope Using Robust Partial Frontier Nonparametric Methods. Water 2016, 8, 82. https://doi.org/10.3390/w8030082
Carvalho P, Cunha Marques R. Computing Economies of Scope Using Robust Partial Frontier Nonparametric Methods. Water. 2016; 8(3):82. https://doi.org/10.3390/w8030082
Chicago/Turabian StyleCarvalho, Pedro, and Rui Cunha Marques. 2016. "Computing Economies of Scope Using Robust Partial Frontier Nonparametric Methods" Water 8, no. 3: 82. https://doi.org/10.3390/w8030082
APA StyleCarvalho, P., & Cunha Marques, R. (2016). Computing Economies of Scope Using Robust Partial Frontier Nonparametric Methods. Water, 8(3), 82. https://doi.org/10.3390/w8030082







