Abstract
Although close relationships between the water quality of streams and the types of land use within their watersheds have been well-documented in previous studies, many aspects of these relationships remain unclear. We examined the relationships between urban land use and water quality using data collected from 527 sample points in five major rivers in Korea—the Han, Geum, Nakdong, Younsan, and Seomjin Rivers. Water quality data were derived from samples collected and analyzed under the guidelines of the Korean National Aquatic Ecological Monitoring Program, and land use was quantified using products provided by the Korean Ministry of the Environment, which were used to create a Geographic Information System. Linear models (LMs) and generalized additive models were developed to describe the relationships between urban land use and stream water quality, including biological oxygen demand (BOD), total nitrogen (TN), and total phosphorous (TP). A comparison between LMs and non-linear models (in terms of R2 and Akaike’s information criterion values) indicated that the general additive models had a better fit and suggested a non-linear relationship between urban land use and water quality. Non-linear models for BOD, TN, and TP showed that each parameter had a similar relationship with urban land use, which had two breakpoints. The non-linear models suggested that the relationships between urban land use and water quality could be categorized into three regions, based on the proportion of urban land use. In moderate urban land use conditions, negative impacts of urban land use on water quality were observed, which confirmed the findings of previous studies. However, the relationships were different in very low urbanization or very high urbanization conditions. Our results could be used to develop strategies for more efficient stream restoration and management, which would enhance water quality based on the degree of urbanization in watersheds. In particular, land use management for enhancing stream water quality might be more effective when urban land use is in the range of 1.1%–31.5% of a watershed. If urban land use exceeds 31.5% in a watershed, a more comprehensive approach would be required because water quality would not respond as rapidly as expected.
1. Introduction
Land use can have direct impacts on hydrologic systems within a watershed [1,2,3,4]. The negative impacts of urban land use in watersheds on adjacent reservoirs, streams, and rivers have been well-documented and are a key concern for restoration and management. In general, previous studies have reported that watersheds with high percentages of developed areas (e.g., urban areas and agricultural areas) tend to have higher concentrations of water pollutants and nutrients [1,2,3,4,5,6,7,8,9,10]. Different types of urban land use, including commercial, residential, and industrial development, have significant impacts on water quality. The proportion of land use type in a watershed has been shown to be closely associated with many water quality parameters in various aquatic systems [2,4]. The usefulness of water quality indices as indicators of water pollution has been verified for assessing spatial changes and for classifying water quality. In many countries, chemical parameters, such as dissolved oxygen (DO), pH, biochemical oxygen demand (BOD), chemical oxygen demand (COD), total nitrogen (TN), and total phosphorous (TP), have served as the main criteria for determining the condition of rivers and for managing aquatic ecosystem resources. Environmental Policy Law (EPL) in Korea has also used various chemical criteria (e.g., pH, BOD, COD, TOC, SS, DO, TP, etc.) to manage the water quality of rivers and streams.
In previous studies, the most commonly used techniques to determine the relationships between land uses in watersheds and water quality indicators were correlation or regression analyses. These approaches assume linear relationships between land uses in watersheds and water quality indicators, suggesting that the degree of water quality variance is the same regardless of the degree of land use intensity in watersheds. Recently, some studies have reported that the relationships between urban land uses and the chemical, biological, and physical characteristics of streams might not be linear [6,9,11,12,13,14,15]. It has been reported that the average threshold of imperviousness at which water quality degradation first occurs is 10% [11,16]. Similarly, Coles et al. [12] reported that significant changes in aquatic health were observed between low and moderate levels (0 to 35) of urbanization intensity (0–100 scale, low to high urbanization intensity) in New England coastal streams. In addition, they found a “threshold effect” in which the water quality indicators no longer changed as the intensity of urbanization increased. More recently, Crim [13] confirmed the presence of a threshold and suggested that it might be much lower than 10% for an impervious surface. In his study, the concentrations of water quality indicators increased considerably as the impervious surface in a watershed increased from 0 to 4% in west-central Georgia, USA. Together with previous studies, his results imply that even a small increase in the impervious surface in a watershed might have significant impacts on the chemical characteristics of water and the biota of streams. This nonlinearity may be derived from the random nature of the hydrodynamic conditions of river systems, meteorological processes, and a shortage of available monitoring data [15,17,18]. It is also noteworthy that there was only one breakpoint (i.e., threshold) in the relationships between land uses and water quality indicators, regardless of the different thresholds reported in previous studies. The presence of a threshold and non-linear relationships between land use and water quality increases the uncertainty and the degree of complexity in water quality management and land use planning for decision makers and policy makers when attempting to enhance water quality and minimize the adverse impacts of various land uses [19].
Despite the possible presence of a non-linear relationship between water quality and land uses, linear correlation and regression analyses have been broadly used to investigate such relationships in various fields of study, including water chemistry, ecology, and hydrology. It is very clear that linear correlation and regression are useful techniques when quantifying the magnitude, direction, and significance of the relationships between land use variables (i.e., impervious areas, developed areas, agricultural areas, etc.) and water quality in a number of previous studies [1,2,3,4,20]. Despite the various benefits, conventional linear-type approaches may not accurately represent the true nature of the relationships between land uses and water quality [6,9,21]. In addition, this may lead to a misunderstanding by stream managers, land use planners, and decision makers about the impact of different land uses on water quality, particularly during the stages of development with small and large extents of urbanization.
To avoid nonlinearity issues when dealing with the relationships between land uses and water quality, several approaches have been proposed, including stochastic, fuzzy, and interval mathematical programs [19,22,23,24,25,26]. One popular method is to transform the data when making non-linear models linear in the analyses of the relationships between urban land use and river water quality [22], and when determining interval parameters in non-linear optimization models of stream water quality management [15]. However, it is very clear that the presence and shape of the non-linearity in the relationships should be examined prior to applying these methods.
Our first goal was to test for the presence of non-linear relationships between urban land use and water quality indicators in streams in Korea. To test for the presence of non-linearity, this study compared the ability of linear and non-linear models to explain the variance in water quality indicators when responding to the degree of urbanization in watersheds. We hypothesized that a non-linear model would explain the variance in water quality parameters in response to the degree of urbanization better than would a linear model (LM), if the relationships between urban land use and water quality indicators were non-linear. Otherwise, a LM would outperform a non-linear model.
Second, this study also investigated the number of breakpoints in the relationships when non-linear relationships were present. Previous studies have reported that there is either one breakpoint (i.e., threshold) or no breakpoint (i.e., linear regression or correlation) in the relationship. However, if the relationships between land uses in watersheds and water quality indicators are sufficiently complex, more than one breakpoint can exist in the relationships. Thus, the number of breakpoints can represent the complexity of the relationships. If there is only one breakpoint (i.e., threshold), we need to consider only two intervals, including areas with a small and large extent of urbanization in stream management processes. We believe that the presence of non-linearity and the number of breakpoints can provide useful insights into land use planning and stream management. Land managers, planners, stream managers, and policy makers can apply different strategies for different levels of urbanization to enhance the water quality and to minimize the adverse impacts of urban land uses on streams.
We adopted generalized additive models (GAMs) for investigation in this study. GAMs have been shown to be very flexible, providing an excellent fit for non-linear relationships and for datasets with significant noise among the predictor variables [22]. This model is a generalization of multiple regressions, in which the additive nature of the model is maintained, but the simple lines of the linear regression are replaced by nonparametric functional curves with multiple parameters. Compared with an LM, GAMs are data-driven rather than model-driven, and GAMs allow determination of the shape of the response curves from the data instead of fitting an a priori parametric model, which is limited in its available shape of response [27]. GAMs have been widely used in various fields, such as species distribution [28,29,30,31,32,33], plant ecology [34,35,36], and water quality dynamics [21,37,38]. For example, Murase et al. [29] applied GAMs to fishery-survey data to reveal the influences of environmental factors, including surface water temperature, salinity, chlorophyll, near-seabed water temperature, salinity, and depth, on the distribution patterns of Japanese anchovy, sand lance, and krill. The results of their study showed a non-linear response of fishes to environmental factors. Richard et al. [21] applied GAMs to explore the functional relationships between four water quality indicators (TN, TP, ammonia, nitrate) and environmental factors, such as catchment inflow, wind speed, and tidal current in the Broadwater Estuary in the Gold Coast region of Australia, using short-term monitoring data. Based on a GAM assessment, they reported that nutrient concentrations within a subtropical estuary were non-linear for various environmental factors and were most dependent on catchment inflow.
2. Materials and Methods
2.1. Study Streams and Sampling Sites
South Korea is located between 127°30′ E and 37°00′ N and occupies an area of about 100,032 km2, covering almost the entire southern half of the Korean Peninsula (Figure 1). Approximately two-thirds of the annual precipitation (1388.7 mm) is concentrated in the summer (June through September). Thus, seasonal precipitation and water flow levels fluctuate widely, and stream flow generally diminishes during drought periods, which are characteristic of winter and early spring. The annual average temperature for 2006–2010 was 12.8 °C, with monthly averages ranging from a low of −12.8 °C in January to a high of 29.32 °C in August.
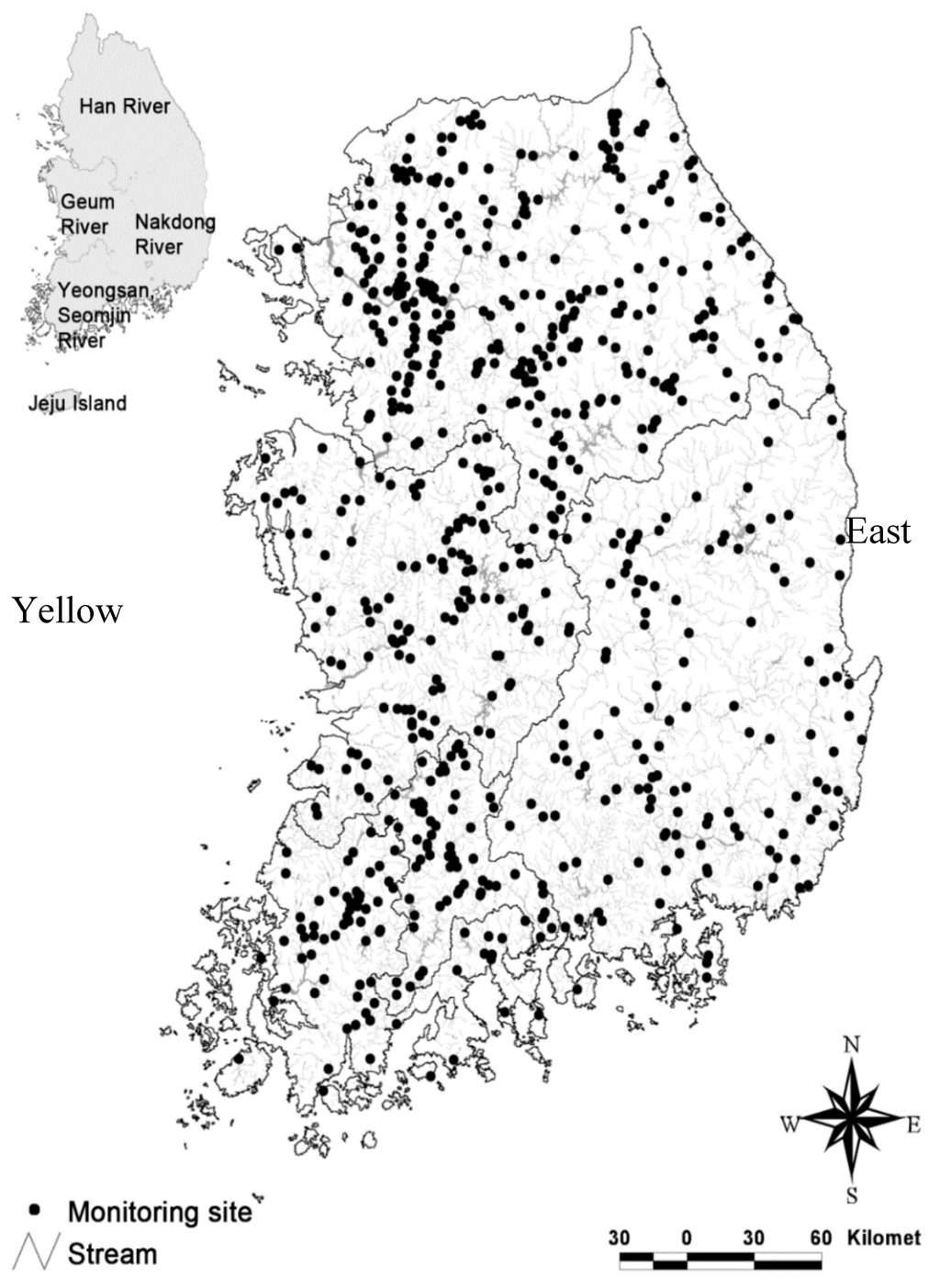
Figure 1.
The five major river systems and the locations of National Aquatic Ecological Monitoring Program (NAEMP) monitoring sites. Most streams on the east side can be characterized by a short length, low water temperature, and fast flow rate.
Five major rivers (i.e., the Han, Geum, Nakdong, Youngsan, and Seomjin Rivers) and their independent tributaries and small streams are distributed throughout the country. The Youngsan and Seomjin Rivers are usually treated as one river system (Youngsan–Seomjin River) because their watersheds are located close to one another. Among the five major rivers, the Han River has the largest basin, occupying approximately a quarter of the country. The east side of the country is mountainous, with watersheds that are less disturbed and are covered by dense pine, oak, and mixed forest. In the eastern mountainous areas, most streams are small, flow down steep slopes, and run directly into the East Sea. Most river systems and streams in the western and southwestern areas flow toward the Yellow Sea. Seasonal fluctuations in water levels in the small streams in the eastern areas are particularly extreme because of the steep slopes and low groundwater levels. The headstreams of the five major rivers are located in similar areas in the central part of the eastern mountains.
2.2. Water Quality Variables
As part of the National Aquatic Ecological Monitoring Program (NAEMP), South Korea’s Ministry of the Environment (MOE) has monitored numerous aspects of streams and rivers using biochemical, physical, and biological indicators at 720 long-term monitoring sites in tributaries and the main stem of five rivers across the country. The assessment criteria and sampling protocol used by the NAEMP were developed in a preliminary study from 2003 to 2006, and a geographic information system (GIS) database for the locations of all sampling sites was also constructed in the study. The first nationwide monitoring under this protocol started in 2007 at 720 preselected sampling sites. According to the NAEMP protocol, all field survey teams consisted of staff from five universities who had to complete the field survey and water sampling within a month, twice a year. Water samples used for the determination of BOD, TN, TP, and other water quality variables were collected in prewashed 2ℓ bottles. All water samples collected from the five river systems by staff from the five universities were transported in a cooler and analyzed in a commercial laboratory (Chungmyung Environmental Co. Ltd., Seoul, Korea). Laboratory measurements were conducted to determine BOD, TN, and TP following Standard methods [39]. BOD was determined by the difference of dissolved oxygen concentration after a five-day incubation. TP was measured in the unfiltered water by ascorbic acid method after persulfate oxidation. TN was determined by UV spectrophotometric method after potassium sulfate digestion.
Five major river systems that included 527 of the 720 NAEMP sampling sites in 2007 were investigated in this study. We excluded data sampled from sites in islands and estuary areas. We found that some sites only had data during the spring or no data during the fall due to the streams drying up. We excluded these data from our dataset for analysis. We also excluded data sampled from small independent streams running directly into the sea rather than into one of the five major river systems. These streams were mostly located in the eastern mountainous areas and were characterized by a very short length, high flow rate, and low water temperature.
In this study, we focused on the common water quality indicators, including BOD, TN, and TP, monitored in 2007 under the NAEMP. The reason for the use of a sampling dataset collected in 2007 was to match it with the year of the Land Use/Land Cover (LULC) GIS map released by the Ministry of Environment (MOE), Korea. The MOE releases the LULC digital map irregularly, and they released the 2007 LULC digital map in 2009.
BOD is a measure of the amount of dissolved oxygen required by aerobic biological organisms in a body of water to break down organic material, where higher values indicate poorer water conditions and higher pollution levels. TN is a measure of the mixture of organic, ammoniac, nitrite, and nitric nitrogen, which contribute to the eutrophication of a water body. Nitrogen oxidizes into NO3 when discharged into streams or lakes and consumes dissolved oxygen, acting like organic matter. The rapid and high rate of consummation of dissolved oxygen degrades aquatic habitats. Representing the total quantity of phosphorus compounds, TP is also used as an index of eutrophication in streams and lakes. Phosphorus, together with nitrogen, is known as a nutritive salt that can cause eutrophication and red tides. Phosphorus acts as a limiting factor in algae growth in water systems. Consequently, the internal concentration of TP in a water body is a crucial element in controlling algae growth [40]. TP is discharged as organic phosphorus and PO4–P, with organic phosphorus being a component of agricultural fertilizer that can be toxic in water bodies.
2.3. Measuring the Proportion of Urban Land Use
To calculate the proportions of each type of land use at each sampling site, we used the digital land use and land cover (LULC) map from the Korean MOE. The LULC map is a representation of the land surface based on satellite imagery and data from photographic analyses, and it has been widely used for environmental management. According to the MOE classification, land use types were divided into seven major categories and 23 subcategories. The seven main LULC categories were the following: (1) urban areas; (2) agricultural areas; (3) paddy areas; (4) forested areas; (5) grassland; (6) wetland; and (7) bare soils. In this study, urban land use includes residential areas, commercial areas, roads, and industrial areas.
Water contamination in a stream is highly dependent on storm water runoff in the surrounding drainage areas. It is likely that land uses in drainage areas that are in close proximity to the streams are more likely to have stronger influences on the chemical and biological conditions of streams than are those farther away. Thus, we focused on the land uses in sub-drainage areas adjacent to the sampling site. Another reason for using these sub-drainage areas was the policy issue of riparian land management. The MOE has prioritized the management of riparian areas as an urgent policy area and managing the entire watershed of a stream is a long-term policy in their stream and watershed management strategies. At the same time, some streams have more than one sampling site. Thus, using a watershed could be problematic, because water quality indicators could vary while land uses are the same within the watershed.
To capture the proportion of each type of land use, we used sub-drainage areas from the sampling site rather than the entire watershed area of the stream because small drainage areas can reveal the effects of land use on adjacent streams more clearly. We delineated the drainage areas from the locations of sampling sites using a GIS and digital elevation model (50 m resolution), and these small drainage boundaries were overlaid on the LULC map (Figure 2). The NAEMP monitoring protocol allows field surveyors of each monitoring area to select the best sampling point within a 50 m radius of the sampling site. Figure 2 shows representative locations from all sampling areas (i.e., water quality, biological indicators, and riparian habitats), rather than the exact location of each sampling site. Despite the protocol recommendation that all areas use the same sampling site, there is the possibility that each sampling area can have a different sampling location within a 100m radius from a sampling site. In delineating the sub-drainage area for each sampling site, we tried to draw the boundary slightly upward from the sampling site. Thus, the location of the sampling site within the sub-drainage boundary used in this study is slightly upstream (approximately <200-m) from the outlet point of each sub-drainage boundary.
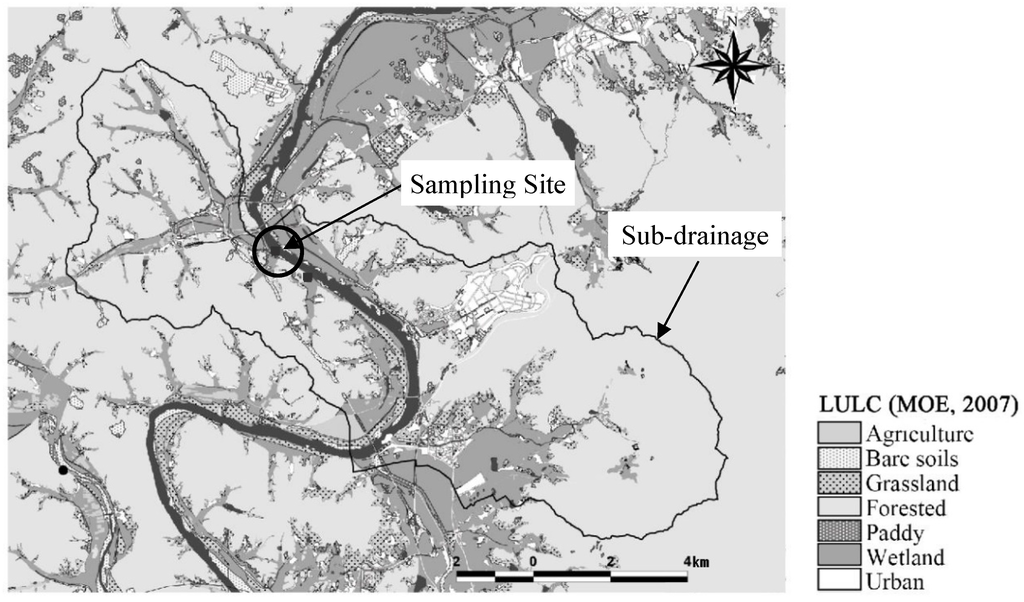
Figure 2.
An example of a sub-drainage area used to measure the proportion of urban land use in an area adjacent to a monitoring site. Sub-drainage areas were delineated using a geographical information system (GIS) with a digital elevation map.
2.4. Data Distributions and Transformation
Water quality data are often bounded at zero and highly skewed, containing infrequent points at high values. This skewedness in the data is not surprising given that many water quality indices are strongly related to stream flow, which is typically modeled as a lognormal or other highly skewed distribution. Thus, data for groundwater quality are typically log-transformed prior to statistical analysis [41]. A preliminary analysis indicated that the proportion of urban land use and all water quality indicators in the study areas were considerably skewed, and thus all data used in the study were log-transformed before the analysis.
2.5. Linear Models (LMs) and Generalized Additive Models (GAMs)
In this study, the LM and GAM were analyzed using the statistical software R (R Core Development Team). To compare models, we used the coefficient of determination (R2) and Akaike’s information criterion (AICc). The AICc was derived from information theory, which differs from statistical hypothesis testing. The AICc method can be used to determine the relative likelihood that two (or more) models can explain the data. This method can show whether one model fits the data significantly better than another, allowing the user to reject unlikely models. The larger the AICc value for a model, the less probable it is.
3. Results
3.1. Descriptive Statistics
The mean area of small zones was 130.08, and the mean proportion of urban land use was 8.74%, with a maximum of 75.42% within the sub-drainage areas. Urbanization values were relatively normally distributed around the mean value, but the proportion of urban land use was high in some particular sites. The mean values for BOD, TN, and TP were 2.09 mg/L, 2.52 mg/L, and 0.13 mg/L, respectively, in the study areas (Table 1). According to the criteria of the Korean MOE, these values were categorized as level II (moderately good), VI (extremely poor), and III (normal) for BOD, TN, and TP, respectively. These results show that water quality was good based on BOD, but poor based on TN and TP levels. The descriptive statistics and box plots for the water quality indicators suggest that the physiochemical properties of the five rivers varied greatly from site to site.

Table 1.
Descriptive statistics for water quality indices and the proportions of urban land use. A large variation in the variables was observed in the study areas.
3.2. Relationships between Urban Land Use and Water Quality Indices
A correlation analysis was conducted to examine the relationships among water quality variables and the proportion of urban land use (Table 2). The results indicated that the proportion of urban land use values were significantly correlated with all water quality variables, including BOD (r = 0.419), TN (r = 0.445), and TP (r = 0.438). The results also suggested a strong correlation among water quality indicators. For example, BOD was correlated with TN (r = 0.592) and TP (r = 0.459). TN was also strongly correlated with TP (r = 0.613). These results indicated that higher proportions of urban land use were associated with higher concentrations of BOD, TN, and TP in streams. Overall, the correlation analysis revealed close relationships between urban land use types with extensive human activities and poor water quality.

Table 2.
Pearson-correlations between the proportion of urban land use and water quality indicators. All variables used in the study displayed strong correlations with each other.
3.3.The Linear and Non-Linear Models
3.3.1. Linear Models (LMs)
The proportion of urban areas within a sub-drainage area was regressed against BOD, TN, and TP (Table 3). In the LMs, the variables for urban land use significantly explained the variance in all water quality indices(Table 3). Based on the linear models, the relationship with the percentage of urban land use explained 18% of the variation in BOD and 20% of the variation in both TN and TP (p < 0.01). In these models, urban land use negatively affected all water quality indices, including BOD (b = 0.33, β = 0.42), TN (b = 0.29, β = 0.45), and TP (b = 0.45, β = 0.44).To compare the goodness-of-fit between LMs and GAMs, the AICc values of linear models were calculated for BOD (288.32), TN (69.88), and TP (561.72).

Table 3.
Outputs from linear models of the relationships between the proportion of urban land use and water quality indicators. All water quality variables were strongly influenced by the proportion of urban land use.
3.3.2. Generalized Additive Models (GAMs)
Statistical link function selection for assessing non-linear models was conducted according to the lower AICc and deviance values (goodness of fit) in Table 4. For BOD, there was no difference in the deviances of the identity function (50.31) and log function (50.31), but the identity function had a lower AICc value (273.69). For TN, the values of the AICc of the identity function (43.85) and inverse function (43.95) were almost identical, but the identity function had a lower deviance value (32.64). Similarly, the deviance values of the identity function and log function were the same (82.81), but the identity function had a lower AICc value (537.82). The comparison of AICc and deviance values among link functions indicated that the use of identity functions was appropriate to fit the models.

Table 4.
AICc and deviance values for BOD, TN, and TP used to select the statistical function for assessing GAMs. The identity function had the lowest AICc and deviance values.
From Table 5, it can be seen that urban land use had a negative impact on water quality. The mean effects of urban land use on BOD, TN, and TP in the GAMs were 6.02, 5.94, and 6.76, respectively. All models including BOD (F = 19.02, p < 0.01), TP (F = 23.87, p < 0.01), and TP (F = 20.73, p < 0.01) were statistically significant, and the model explained 21.3%, 25.1%, and 24.5% of the variance of the BOD, TN, and TP in streams, respectively. The AICc values of the GAM models for BOD, TN, and TP were 273.86, 44.02, and 537.99, respectively.

Table 5.
The results of the generalized additive models (GAMs) for the relationships between the proportion of urban land use and water quality indicators. The non-linear model for TN had the highest R2 value.
3.3.3. Comparison between LMs and GAMs
In the two types of regression models (linear and non-linear models), the urban land use had a negative impact on water quality in terms of the BOD, TN, and TP in streams. The LM and GAM explained 18% and 21.3% of the variance in the BOD level in streams, respectively. Compared with the R2 of the LM (20%), the higher R2 of the GAM (25%) indicated that the non-linear model had a higher explanatory power than that of the LM for the variance in TN. Similarly, the higher R2 of the GAM (R2 = 0.24) better explained the variance in the TP concentration in streams than did the LM (R2 = 0.2). Thus, it was clear that, compared with the LM, the non-linear model (i.e., GAM) better explained the variances in the BOD, TN, and TP in streams according to the proportion of urban land use in sub-drainage areas. The greatest improvement in explanatory power was observed between the LM and non-linear model (i.e., GAM) for the variance in the TN concentration in streams.
All AICc values of the assessed GAMs (Table 4) appeared to be lower than those of the LMs (Table 2). Specifically, the non-linear model of BOD (AICc = 273.86) had lower AICc values than those of the LM (288.32). A considerable decrease in AICc values was also observed between linear and non-linear models for TN and TP. Specifically, the AICc value of the non-linear model (44.02) for TN was lower than that of the LM (69.88). Similarly, the AICc value of the non-linear model for TP (537.99) was significantly lower than that of the LM (561.72).
In all cases, the non-linear models (i.e., GAMs) had higher coefficients of determination (R2) and lower AICc values than those of the LMs. These results were indicative of the presence of non-linear relationships between the proportion of urban land use and water quality indicators in the study areas.
4. Discussion
The GAMs better explained the relationships between the proportion of urban land use and water quality and suggested that these relationships were non-linear. Interestingly, the shapes of all the relationships between urban land use and water quality variables in the assessed GAMs were similar. In addition, the shapes of the relationships in GAMs suggested that there was more than one breakpoint that divided the relationships of urban land use and water quality variables into several regions. However, we divided the scatter plots of GAMs for BOD, TN, and TP into three regions using two breakpoints (0 and 1.5 of the log transformed percentage urban land use) to characterize the intervals, despite the possibility of another breakpoint around 0.7 of the log-transformed percentage of urban land use (Figure 3).
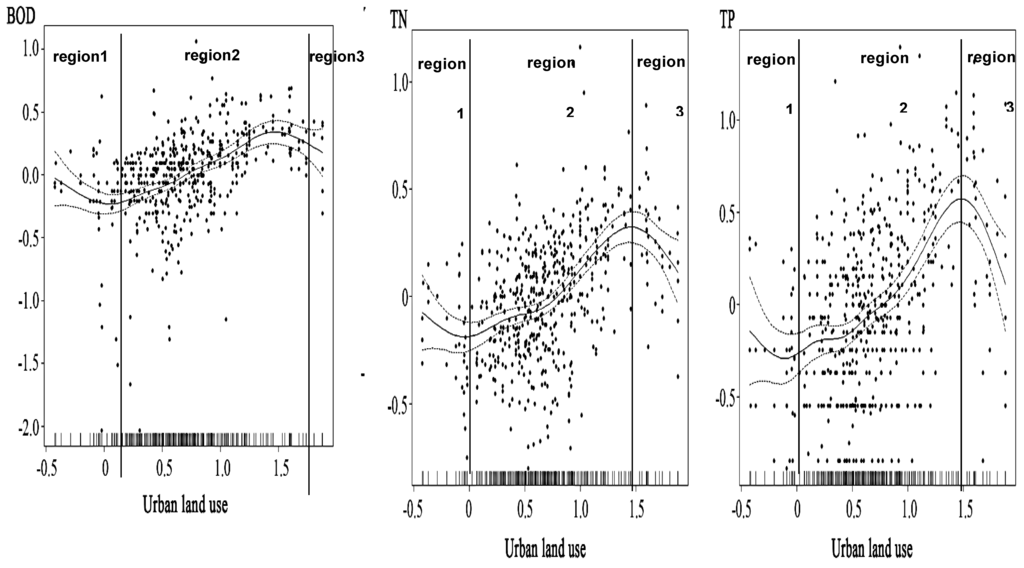
Figure 3.
Regionalized zones in the non-linear relationships between urban land use and biological oxygen demand (BOD), total nitrogen (TN), and total phosphorous (TP) in streams. All variables were log-transformed.
In Region 1 (0% ≤ urban land use ≤1%), each water quality variable almost invariably responded non-linearly to a gradient of the proportion of urban land use, or even indicated a positive impact of urban land use on water quality variables. However, only a few cases fell into Region 1, and the range (±95% confidence intervals) of the cases was relatively large. The relationships in Region 1 were quite different from our expectation, and the findings of many previous studies that have reported a negative influence of urban land use on water quality indicators (e.g., [1,2,3,4,15,20]). Such a relationship was not observed in Region 1. Areas where the proportion of urban land use in the watershed was less than 1% might be undeveloped natural areas, which are very rare in Korea. The sampling sites falling into the Region 1 category were in headstreams located in mountainous areas. The influence of urban land use on stream water quality in Region 1 cases was likely to be modest at best, and stream water quality would therefore be more affected by other environmental and anthropogenic variables, such as agricultural land use [42], geology [43], soil type [44], plant litter [45], and waste water released from scattered rural houses.
In Region 2 (1.1% ≤ urban land use ≤31.5%), the relationships between urban land use and water quality displayed similar patterns to those reported in many previous studies. An increase in the amount of urban land use in the watershed had a significant negative impact on the BOD, TN, and TP in streams. Most cases in this study fell into Region 2, and the range (±95% confidence intervals) of the cases was relatively small. The BOD, TN, and TP rapidly increased as urban land use increased. However, the slopes of the relationships were slightly different. Specifically, the slope of the relationship between urban land use and BOD was relatively gentle, while the slope of the relationships between urban land use and the concentration of TP was steep. In Figure 3, Region 2 of the BOD and TN model are divided into sub-regions at approximately 0.5 of the log-transformed urban land use (approximately 3.2% of the actual percentage urban land use). Slopes were relatively gentle until the percentage urban land use reached 3.2%, beyond which they became steeper.
In Region 3 (31.6% ≤ urban land use), the relationships between urban land use and water quality variables dramatically changed direction at the 1.5 breakpoint in the log-transformed percentage of urban land use. Like Region 1, water quality variations at very high levels of urbanization in Region 3 were somewhat different from those reported in previous studies, which used mostly LMs. In the GAMs, the variations in BOD, TN, and TP were independent of the variation in urban land use, or even decreased as the proportion of urban land use increased. Compared with Region 1, few cases fell in this region, and the range (±95% confidence intervals) of the cases was relatively large. In Region 3, reducing urbanized areas might not be effective for enhancing stream water quality. There should be additional considerations, such as the placement of riparian vegetation buffers.
The most important parameter in determining the abstraction of urban land use is frequently the area of the impervious surface connected directly to the drainage system. This is because impervious surfaces connected to the drainage system allow for a runoff volume that closely approximates the amount of incident precipitation [6]. In contrast, precipitation that falls on pervious surfaces or on areas not directly connected to the drainage system will infiltrate the ground surface and will not contribute to the immediate runoff. Previous studies have shown that the effects of impervious surface areas on stream water quality differ depending on the watershed, based on random effect solutions and random coefficient model simulations [46].
As discussed earlier, previous studies indicated that a 10% cover of impervious areas in a watershed is the average threshold at which water quality degradation first occurs [11,16]. Coles et al. [12] reported that significant changes in aquatic health could occur at low and moderate levels (0 to 35%) of urban land cover. Crim [13] suggested the threshold might be much lower than 10% cover of impervious surfaces. In his study, the concentrations of water quality indicators increased considerably as the amount of impervious surface in a watershed increased from 0 to 4% in west-central Georgia, USA. Similarly, Nagy et al. [6] reported that an alteration in stream conditions can occur at low levels of development. It is difficult to compare our results directly with previous studies due to the different measurements (e.g., proportion of impervious areas, degree of urbanization, and proportion of urban land use) and different spatial scales (e.g., entire watershed, buffer zones, sub-drainage areas in riparian areas) used in the analyses. Our results suggest that water quality degradation could occur at extremely low levels of urban development (around 1% urban land cover), particularly in sub-drainage areas near streams or riparian zones.
It was slightly surprising to observe the pattern of the relationships between urban land use and water quality indicators, which were downward slopes in Regions 1 and 3. In this study, we were unable to identify the cause of the patterns displayed in Regions 1 and 3. One possible explanation could be the type of land cover across the entire watershed, for example, a high proportion of urban land in riparian areas and a high proportion of forested area throughout the entire watershed. Other variables could be the presence of sewage treatment facilities, drainage systems, pollution control systems for non-point source pollutants established by local authorities, and a high vegetation density in riparian areas. Thus further studies considering these factors are needed to explain the patterns in Regions 1 and 3. The results of this study also suggested that different strategies should be used corresponding to different degrees of urbanization for enhancing stream water quality. Decreasing urban land use in a watershed could be an effective way to improve the water quality in moderately urbanized areas. However, decreasing urban land use in a watershed might not be effective in highly urbanized areas, because water quality might not be improved as much as expected.
5. Conclusions
In general, streams in urbanized areas are likely to have higher levels of oxygen demand, nutrients, suspended solids, ammonium, hydrocarbons, and metals. The negative impacts of urban land use on adjacent reservoirs, streams, and rivers have been well-documented and are a key concern for stream restoration, stream management, land planners, and land managers [2,5,6,7,8,9,10,47,48,49]. To establish effective water quality management policies, it is essential to understand the true nature of the relationship between water quality and urban land use.
In this study, we assessed LMs and non-linear models (GAMs) for the associations of BOD, TN, and TP with urban land use in the sub-drainage areas of five major river systems in Korea. Regardless of the type of model used, a higher proportion of urban land use had a significant impact on the degradation of stream water quality. Comparisons between LMs and non-linear models, based on R2 and AICc values, indicated that the non-linear models (GAMs) could describe the relationships between urban land use and water quality more accurately. The GAMs demonstrated non-linear relationships between urban land use and water quality indicators (i.e., BOD, TN, and TP) in streams and also revealed several breakpoints in the relationships. Based on two breakpoints, the relationships could be categorized into three regions. Only Region 2 showed similar relationships between land use and water quality to those reported in many previous studies using linear models. Regions with extremely low or extremely high levels of urban land use had a somewhat different relationship with the findings of previous studies. Stream restoration, stream management, and watershed land use policies should differ among these different regions. Water quality might not be improved as much as expected by reducing the extent of the urban area in areas with extremely low or high levels of urban land use. In particular, a comprehensive approach, including the installation of sewage treatment facilities or establishing riparian vegetation for filtering non-point source pollutants should be used.
In this study, we were not able to identify the cause of the unexpected pattern seen among the relationships between urban land use and water quality in areas with extremely low or high levels of urban land use. Further studies are needed, with a consideration of sewage treatment facilities, drainage systems, and the land cover across the entire watershed. It is also noteworthy that previous studies indicated that 3%–4% of impervious area cover in a watershed could cause degradation of water quality in streams. Interestingly enough, our GAMs suggested that this value might be even lower than 3%–4%. To understand the threshold value of urban areas, GAMs may need to be assessed at other spatial scales.
The results of this study are useful for stream restoration and management, because they highlight the negative impacts of urban land use and the non-linear relationships between urban land use and water quality. Water quality variance might differ with the degree of urbanization. Thus, improved water quality could be attainable by crafting management plans according to a region’s specific urbanization characteristics.
Acknowledgments
This study was conducted under the project, “National Aquatic Ecosystem Health Survey and Assessment” in Korea, and was supported by the Ministry of the Environment and the National Institute of Environmental Research, Korea.
Author Contributions
All of the authors contributed extensively to the work. Sun-Ah Hwang and Sang-Woo Lee designed the research, performed the data analysis, and wrote the manuscript. Soon-Jin Hwang and Se-Rin Park contributed to the data interpretation, discussion, and editing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bolstad, P.V.; Swank, W.T. Cumulative impacts of land use on water quality in a southern Appalachian watershed. J. Am. Water Resour. Assoc. 1997, 33, 519–533. [Google Scholar] [CrossRef]
- Lenat, D.R.; Crawford, J.K. Effects of land use on water quality and aquatic biota of three North Carolina Piedmont streams. Hydrobiologia 1994, 294, 185–199. [Google Scholar] [CrossRef]
- Paul, M.J.; Meyer, J.L. Streams in the urban landscape. Annu. Rev. Ecol. Evol. Syst. 2001, 32, 333–365. [Google Scholar] [CrossRef]
- Tong, S.T.Y.; Chen, W. Modeling the relationship between land use and surface water quality. J. Environ. Manag. 2002, 66, 377–393. [Google Scholar] [CrossRef]
- Meierdiercks, K.L.; Smith, J.A.; Baeck, M.L.; Miller, A.J. Analyses of urban drainage network structure and its impact on hydrologic response. J. Am. Water Resour. Assoc. 2010, 46, 932–943. [Google Scholar] [CrossRef]
- Nagy, R.C.; Lockaby, B.G.; Kalin, L.; Anderson, C. Effects of urbanization on stream hydrology and water quality: The Florida Gulf Coast. Hydrol. Process. 2012, 26, 2019–2030. [Google Scholar] [CrossRef]
- Roberts, A.D.; Prince, S.D. Effects of urban and non-urban land cover on nitrogen and phosphorus runoff to Chesapeake Bay. Ecol. Indic. 2010, 10, 459–474. [Google Scholar] [CrossRef]
- Sun, R.H.; Chen, L.D.; Chen, W.L.; Ji, Y.H. Effect of land-use patterns on total nitrogen concentration in the upstream regions of the Haihe river basin, China. Environ. Manag. 2013, 51, 45–58. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Thompson, J.; Kolka, R.; Franz, K.; Stewart, T. Using the Storm Water Management Model to predict urban headwater stream hydrological response to climate and land cover change. Hydrol. Earth Syst. Sci. 2013, 17, 4743–4758. [Google Scholar] [CrossRef]
- Wu, J.; Stewart, T.; Thompson, J.; Kolka, R.; Franz, K. Watershed features and stream water quality: Gaining insight through path analysis in a Midwest urban landscape, U.S.A. Landsc. Urban Plan. 2015, 143, 219–229. [Google Scholar] [CrossRef]
- Bledsoe, B.P.; Watson, C.C. Effects of urbanization on channel instability. J. Am. Water Resour. Assoc. 2001, 37, 255–270. [Google Scholar] [CrossRef]
- Coles, J.F.; Cuffney, T.F.; McMahon, G.; Beaulieu, K.M. The Effects of Urbanization on the Biological, Physical, and Chemical Characteristics of Coastal New England Streams; U.S. Geological Survey Professional Paper 1695; USGS: Reston, VA, USA, 2004. [Google Scholar]
- Crim, J.F. Water Quality Changes across an Urban-Rural Land Use Gradient in Streams of the West Georgia Piedmont. Master’s Thesis, Auburn University, Auburn, AL, USA, 17 December 2007. [Google Scholar]
- Walsh, C.J.; Fletcher, T.D.; Ladson, A.R. Stream restoration in urban catchments through redesigning storm water systems: Looking to the catchment to save the stream. J. North Am. Benthol. Soc. 2005, 24, 690–705. [Google Scholar] [CrossRef]
- Qin, X.; Huang, G.; Chen, B.; Zhang, B. An interval-parameter Waste-Load-Allocation model for river water quality management under uncertainty. Environ. Manag. 2009, 43, 999–1012. [Google Scholar] [CrossRef] [PubMed]
- Arnold, C.L.; Gibbons, C.J. Impervious surface coverage. J. Am. Plan. Assoc. 1996, 62, 243–258. [Google Scholar] [CrossRef]
- Revelli, R.; Ridolfi, L. Stochastic dynamics of BOD in a stream with random inputs. Adv. Water Resour. 2004, 27, 943–952. [Google Scholar] [CrossRef]
- Karmakar, S.; Mujumdar, P.P. Grey fuzzy optimization model for water quality management of a river system. Adv. Water Resour. 2006, 29, 1088–1105. [Google Scholar] [CrossRef]
- Loucks, D.P. Managing America’s rivers: Who’s doing it? Int. J. River Basin Manag. 2003, 1, 21–31. [Google Scholar] [CrossRef]
- Ahearn, D.S.; Sheibley, R.W.; Dahlgren, R.A.; Anderson, M.; Johnson, J.; Tate, K.W. Land use and land cover influence on water quality in the last free-flowing river draining the western Sierra Nevada, California. J. Hydrol. 2005, 313, 234–247. [Google Scholar] [CrossRef]
- Richards, R.; Chaloupka, M.; Strauss, D.; Tomlinson, R. Using Generalized Additive Modelling to understand the drivers of long-term nutrient dynamics in the Broadwater Estuary (a subtropical estuary), Gold Coast, Australia. J. Coast. Res. 2014, 30, 1321–1329. [Google Scholar] [CrossRef]
- Hill, T.; Lewicki, P. STATISTICS Methods and Applications; StatSoft: Washington, DC, USA, 2007. [Google Scholar]
- Huang, G.H. A hybrid inexact-stochastic water management model. Eur. J. Oper. Res. 1998, 107, 137–158. [Google Scholar] [CrossRef]
- Huang, G.H.; Loucks, D.P. An inexact two-stage stochastic programming model for water resources management under uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 95–118. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Nie, S.L. Mixed interval-fuzzy two-stage integer programming and its application to flood-diversion planning. Eng. Optim. 2007, 39, 163–183. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Nie, S.L.; Liu, L. Inexact multistage stochastic integer programming for water resources management under uncertainty. J. Environ. Manag. 2008, 88, 93–107. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, A. GIS modeling of submerged macrophyte distribution using Generalized Additive Models. Plant Ecol. 1998, 139, 113–124. [Google Scholar] [CrossRef]
- Guisan, A.; Edwards, T.C.; Hastie, T. Generalized linear and generalized additive models in studies of species distributions: Setting the scene. Ecol. Model. 2002, 157, 89–100. [Google Scholar] [CrossRef]
- Murase, H.; Nagashima, H.; Yonezaki, S.; Matsukura, R.; Kitakado, T. Application of a generalized additive model (GAM) to reveal relationships between environmental factors and distributions of pelagic fish and krill: A case study in Sendai Bay, Japan. ICES J. Mar. Sci. 2009, 66, 1417–1424. [Google Scholar] [CrossRef]
- Swartzman, G. Analysis of the summer distribution of fish schools in the Pacific Eastern Boundary Current. ICES J. Mar. Sci. 1997, 54, 105–116. [Google Scholar] [CrossRef]
- Swartzman, G.; Brodeur, R.; Napp, J.; Hunt, G.; Demer, D.; Hewitt, R. Spatial proximity of age-0 walleye Pollock (Theragra Chalcogramma) to zooplankton near the Pribilof Islands, Bering Sea, Alaska. ICES J. Mar. Sci. 1999, 56, 545–560. [Google Scholar] [CrossRef]
- Taylor, J.C.; Rand, P.S. Spatial overlap and distribution of anchovies (Anchoa spp.) and copepods in a shallow stratified estuary. Aquat. Living Resour. 2003, 16, 191–196. [Google Scholar] [CrossRef]
- Winter, A.; Coyle, K.O.; Swartzman, G. Variations in age-0 pollock distribution among eastern Bering Sea nursery areas: A comparative study through acoustic indices. Deep. Sea Res. II 2007, 54, 2869–2884. [Google Scholar] [CrossRef]
- Yee, T.W.; Mitchell, N.D. Generalized additive models in plant ecology. J. Veg. Sci. 1991, 2, 587–602. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapman & Hall: New York, NY, USA, 1990. [Google Scholar]
- Chambers, J.M.; Hastie, T.J. Statistical Models in S; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- Richard, E.; Hughes, L.; Gee, D.; Tomlinson, R. Using Generalized Additive Models for water quality assessment: A case study example from Australia. In Proceedings of the 12th International Coastal Symposium (ICS2013), Plymouth, UK, 8–12 April 2013.
- Morton, R.; Henderson, B. Estimation of nonlinear trends in water quality: An improved approach using generalized additive models. Water Resour. Res. 2009, 44, w07420. [Google Scholar] [CrossRef]
- APHA. Standard Methods for the Examination of Water and Wastewater, 21st ed.; American Public Health Association: Washington, DC, USA, 2001. [Google Scholar]
- Horne, A.J.; Goldman, C.R. Limnology; McGraw-Hill, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Gaugush, R.F. Statistical Methods for Reservoir Water Quality Investigations; Instruction Report E-86-2; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1986. [Google Scholar]
- Lassaletta, L.; Garcı´a-Go´mez, H.; Gimeno, B.S.; Rovira, J.B. Headwater streams: Neglected ecosystems in the EU Water Framework Directive. Implications for nitrogen pollution control. Environ. Sci. Policy 2010, 13, 423–433. [Google Scholar] [CrossRef]
- Liu, Z.J.; Weller, D.E.; Correll, D.L.; Jordan, T.E. Effects of land cover and geology on stream chemistry in watersheds of Chesapeake Bay. J. Am. Water Resour. Assoc. 2000, 36, 1349–1365. [Google Scholar] [CrossRef]
- Mayer, P.M.; Reynolds, S.K.; McCutchen, M.D.; Canfield, T.J. Meta-analysis of nitrogen removal in riparian buffers. J. Environ. Qual. 2007, 36, 1172–1180. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; McDowell, W.H.; Zou, X.; Ruan, H.; Wang, J.; Ma, Z. Qualitative differences in headwater stream dissolved organic matter and riparian water-extractable soil organic matter under four different vegetation types along an altitudinal gradient in the Wuyi Mountains of China. Appl. Geochem. 2015, 52, 67–75. [Google Scholar] [CrossRef]
- Schueler, T.R. The importance of imperviousness. Watershed Prot. Tech. 1994, 1, 100–111. [Google Scholar]
- United States Geological Survey (USGS). The Quality of Our Nation’s Waters–Nutrients and Pesticides; USGS Circular 1225; USGS: Reston, VA, USA, 1999. [Google Scholar]
- Porcella, D.B.; Sorensen, D.L. Characteristics of Non-Point Source Urban Runoff and Its Effects on Stream Ecosystems; EPA-600/3-80-032; EPA: Washington, DC, USA, 1980. [Google Scholar]
- Latimer, J.S.; Quinn, J.G. Aliphatic petroleum and biogenic hydrocarbons entering Narragansett Bay from tributaries under dry weather conditions. Estuaries 1998, 21, 91–107. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).