Variations in the Runoff-Sediment Relationship of the Weihe River Basin Based on the Copula Function
Abstract
:1. Introduction
2. Study Area and Dataset
2.1. Study Area
2.2. Dataset
3. Methodology
3.1. The Double Mass Curve Method
3.2. The Archimedean Copula Function
3.3. The Combinations of High-Low Runoff and Sediment
4. Results and Discussion
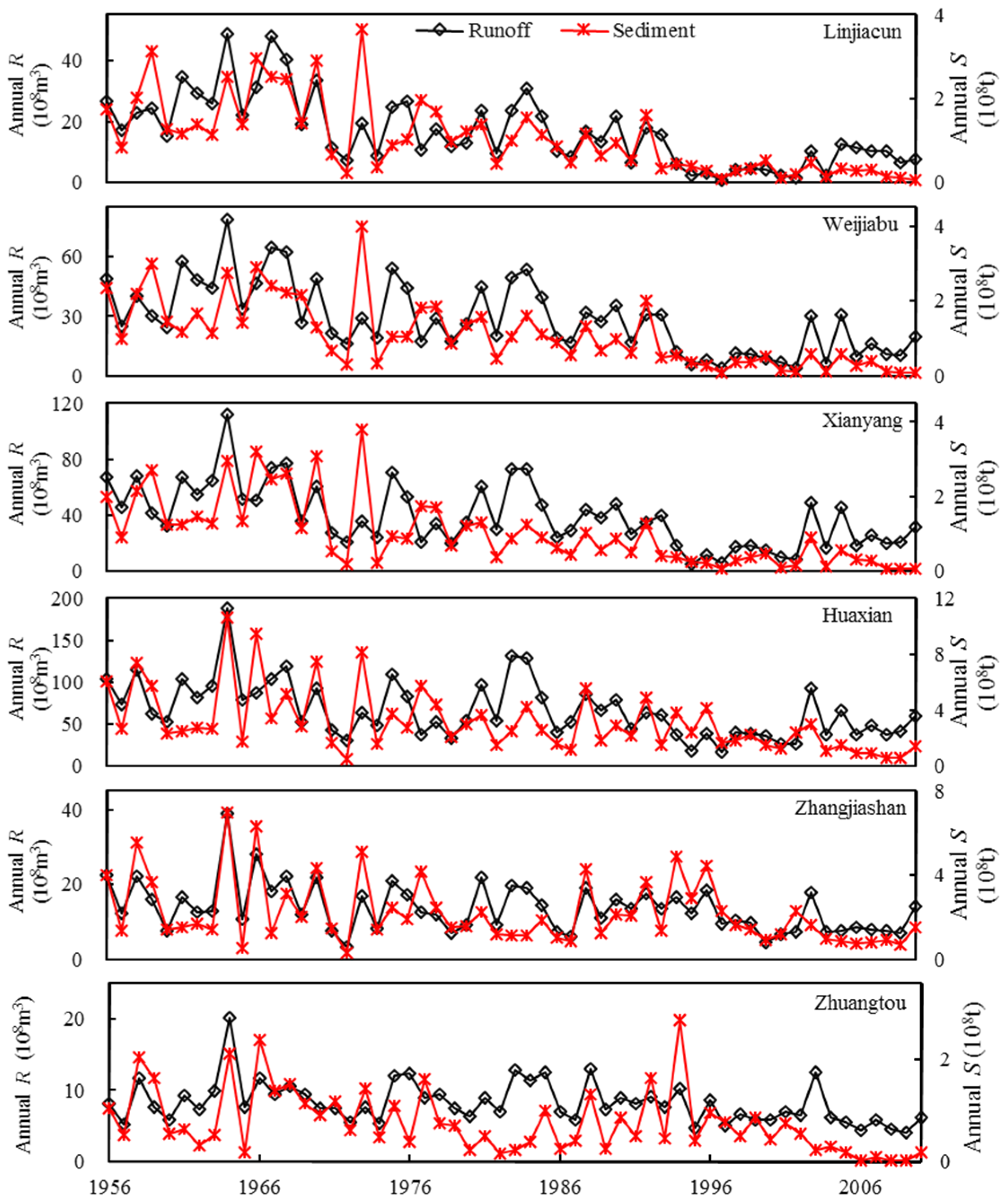
4.1. Variations in Annual Runoff and Sediment
4.2. Detection of RSR Change Points
4.3. Copula Function of Runoff-Sediment before and after the Change Points of RSR
4.4. The Synchronous-Asynchronous Joint Probability of High-Low Runoff and Sediment
- The symmetry of the Clayton, Frank and Gumbel-Hougaard copulas generates asynchronous joint probabilities of the RH-SL combination equal to that of the RL-SH combination, which are similar to that of RH-SN, RN-SH, RN-SL and RL-SN combinations.
- The synchronous joint probabilities of the RN-SN combination, varying from 27.46% to 35.61%, are the highest within the nine different combinations in the P1 and P2 scenarios. The sum of synchronous joint probabilities in P2 is larger than that in P1 at the Weijiabu, Xianyang and Zhuangtou stations, while it is opposite at the Huaxian station.
- The asynchronous joint probabilities of the RH-SL and RL-SH combinations, which vary from 0.12% to 2.79%, are the lowest within the nine different possible combinations in P1 and P2. The joint probabilities of the RH-SL and RL-SH combinations are small, underlying a close relationship between runoff and sediment yield. The small joint probabilities of the RL-SH combination can provide an advantage in jointly operating runoff and sediment yield. The sums of the asynchronous joint probabilities are smaller compared with those of the synchronous joint probabilities obtained for P1 and P2, with the exception of P2 at the Huaxian station. The asynchronous joint probabilities of six different combinations (i.e., RH-SL, RH-SN, RN-SH, RN-SL, RL-SH and RL-SN) in P2 are lower compared with those in P1 at the mainstream WRB Weijiabu and Xianyang stations with the exception of the RN-SL and RL-SN combinations at the Xianyang station. The asynchronous joint probabilities at the Huaxian station for six different combinations are higher in P2 relative to P1.
- The difference between the sum of synchronous or asynchronous joint probabilities in P1 and P2 is largest at the Weijiabu station, following the Xianyang station, while the change is small at the Huaxian and Zhuangtou stations located downstream of the Weihe River.
5. Conclusions
- (1)
- The annual runoff and sediment yield display decreasing trends throughout the WRB. Human activity mainly defined by soil and water conservation measures, water projects and industrial and domestic water use is the main culprit of the decreasing runoff and sediment yield.
- (2)
- The RSR inflection points principally occurred around 1983 at the Weijiabu, Xianyang, Huaxian and Zhuangtou stations, which failed to pass the significane test at the Linjiacun and Zhangjiashan stations. The inflection points are largely the result of the irregular effects of human activity on runoff and sediment yield.
- (3)
- The synchronous joint probability values of the combined normal runoff and normal sediment yield, which vary from 27.46% to 35.61%, are the highest of the nine different combinations. The high correlation between annual runoff and sediment yield produces particularly low asynchronous joint probabilities (i.e., 0.12% to 2.79%) for the combination of high (or low) runoff and low (or high) sediment yield. The sum of synchronous joint probabilities in P2 is larger than that in P1 at the Weijiabu, Xianyang and Zhuangtou stations, while it is opposite at the Huaxian stations.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Arnell, N.W. Climate change and global water resources. Glob. Environ. Chang. 1999, 9, 31–49. [Google Scholar] [CrossRef]
- Walling, D.E. Human impact on land–ocean sediment transfer by the world’s rivers. Geomorphology 2006, 79, 192–216. [Google Scholar] [CrossRef]
- Wang, F.; Hessel, R.; Mu, X.M.; Maroulis, J.; Zhao, G.J.; Geissen, V.; Ritsema, C. Distinguishing the impacts of human activities and climate variability on runoff and sediment load change based on paired periods with similar weather conditions: A case in the Yan River, China. J. Hydrol. 2015, 527, 884–893. [Google Scholar] [CrossRef]
- Gao, P.; Geissen, V.; Ritsema, C.J.; Mu, X.M.; Wang, F. Impact of climate change and anthropogenic activities on stream flow and sediment discharge in the Wei River basin, China. Hydrol. Earth Syst. Sci. 2013, 17, 961–972. [Google Scholar] [CrossRef]
- Ye, Z.X.; Chen, Y.N.; Zhang, X. Dynamics of runoff, river sediments and climate change in the upper reaches of the Tarim River, China. Quat. Int. 2014, 36, 13–19. [Google Scholar] [CrossRef]
- Dunjó, G.; Pardini, G.; Gispert, M. The role of land use–land cover on runoff generation and sediment yield at a microplot scale, in a small Mediterranean catchment. J. Arid Environ. 2004, 57, 239–256. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, G.Y.; Su, B.D.; Disse, M.; Jiang, T.; Xu, C.Y. Periodicity of sediment load and runoff in the Yangtze River basin and possible impacts of climatic changes and human activities. Hydrol. Sci. J. 2008, 53, 457–465. [Google Scholar] [CrossRef]
- Mayor, A.G.; Bautista, S.; Bellot, J. Scale-dependent variation in runoff and sediment yield in a semiarid Mediterranean catchment. J. Hydrol. 2011, 397, 128–135. [Google Scholar] [CrossRef]
- Gebremicael, T.G.; Mohamed, Y.A.; Betrie, G.D.; Zaag, P.; Teferi, E. Trend analysis of runoff and sediment fluxes in the Upper Blue Nile basin: A combined analysis of statistical tests, physically-based models and landuse maps. J. Hydrol. 2013, 482, 57–68. [Google Scholar] [CrossRef]
- Nadal-Romero, E.; González-Hidalgo, J.C.; Cortesi, N.; Desir, G.; Gómezd, J.A.; Lasantae, T.; Lucíaf, A.; Marínc, C.; Martínez-Murillog, J.F.; Pachecoh, E.; et al. Relationship of runoff, erosion and sediment yield to weather types in the Iberian Peninsula. Geomorphology 2015, 228, 372–381. [Google Scholar] [CrossRef]
- Tian, P.; Zhai, J.Q.; Zhao, G.J.; Mu, X.M. Dynamics of runoff and suspend sediment transport in a highly erodible catchment on the Chinese Loess Plateau. Land Degrad. Dev. 2015, 27, 839–850. [Google Scholar] [CrossRef]
- Zhang, J.P.; Ding, Z.H.; You, J.J. The joint probability distribution of runoff and sediment and its change characteristics with multi-time scales. J. Hydrol. Hydromech. 2014, 3, 218–225. [Google Scholar] [CrossRef]
- Zhang, J.P.; Ding, Z.H.; Guo, B.T. Study on evolution trends and encounter risk of runoff and sediment in Jinghe river. J. Hydrol. Eng. 2015, 34, 11–16. (In Chinese) [Google Scholar]
- Zhou, N.Q.; Zhao, L.; Shen, X.P. Copula-based probability evaluation of rich-poor runoff and sediment encounter in Dongting Lake Basin. Sci. Geogr. Sin. 2014, 34, 242–248. [Google Scholar]
- Guo, A.J.; Chang, J.X.; Liu, D.F.; Wang, Y.M.; Huang, Q.; Li, Y.Y. Variations in the precipitation–runoff relationship of the Weihe River Basin. Hydrol. Res. 2016. [Google Scholar] [CrossRef]
- Sraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: a case study of the Litija station on the Sava River. Hydrol. Process. 2014, 29, 225–238. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.W.; Xu, X.Y.; Lei, H.M. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric copula in multivariate flood frequency analysis. Adv. Water Resour. 2006, 29, 1115–1167. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Trivariate Flood Frequency Analysis Using the Gumbel–Hougaard Copula. J. Hydrol. Eng. 2007, 12, 431–439. [Google Scholar] [CrossRef]
- Yan, B.W.; Chen, L. Coincidence probability of precipitation for the middle route of South-to-North water transfer project in China. J. Hydrol. 2013, 499, 19–26. [Google Scholar] [CrossRef]
- Mazouz, R.; Assani, A.A.; Quessy, J.F.; Légaré, G. Comparison of the interannual variability of spring heavy floods characteristics of tributaries of the St. Lawrence River in Quebec (Canada). Adv. Water Resour. 2012, 35, 110–120. [Google Scholar] [CrossRef]
- Chang, J.X.; Wang, Y.M.; Istanbulluoglu, E.; Bai, T.; Huang, Q.; Yang, D.W.; Huang, S.Z. Impact of climate change and human activities on runoff in the Weihe River Basin, China. Quat. Int. 2015, 380, 169–179. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wu, B.S.; Wang, G.Q. Fluvial processes and morphological response in the Yellow and Weihe Rivers to closure and operation of Sanmenxia Dam. Geomorphology 2007, 91, 65–79. [Google Scholar] [CrossRef]
- Zheng, S.; Wu, B.; Thorne, C.; Tan, G. Case Study of Variation of Sedimentation in the Yellow and Wei Rivers. J. Hydraul. Eng. 2015, 141, 05014009. [Google Scholar] [CrossRef]
- Merriam, C.F. A comprehensive study of the rainfall on the Susquehanna Valley. Trans. Am. Geophys. Union 1937, 18, 471–476. [Google Scholar] [CrossRef]
- Searcy, J.K.; Hardisoni, C.H.; Langbein, W.B. Double Mass Curves, Geological Survey Water Supply Paper 1541-B; US Geological Survey: Washington, DC, USA, 1960.
- Nelsen, R.B. An Introduction to Copulas (Lecture Notes in Statistics 139); Springer: New York, NY, USA, 1999. [Google Scholar]
- Jiang, C.; Zhang, W.; Wang, B.; Han, X. Structural reliability analysis using a copula-function-based evidence theory model. Comput. Struct. 2014, 143, 19–31. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Yan, J.; Holmes, M. Fast large-sample goodness-of-fit tests for copulas. Stat. Sin. 2011, 21, 841–871. [Google Scholar] [CrossRef]
- Masina, M.; Lamberti, A.; Archetti, R. Coastal flooding: A copula based approach for estimating the joint probability of water levels and waves. Coast. Eng. 2015, 97, 37–52. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Han, C.B.; Jia, Z.F.; Liu, Y.; Li, P.C. Analysis on characteristics of runoff and sediment of Zhangjiashan hydrological station and case study for Jing he River. Trans. CSAE 2012, 28, 48–55. [Google Scholar]
- Ma, Y.; Qin, B.S.; Wang, H.; Zhao, J.X. Variations of water and sediment of the Weihe River and impact factors analysis. Soil Water Conserv. China 2002, 8, 18–20. (In Chinese) [Google Scholar]
- Ran, D.C. Water and sediment variation and ecological protection measures in the middle reach of the Yellow River. Resour. Sci. 2006, 28, 93–100. (In Chinese) [Google Scholar]
- Weiss, L.L.; Wilson, W.T. Evaluation of significance of slope changes in double-mass curves. Trans. Am. Geopphys. Union 1953, 34, 893–896. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regressionand time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Machado, M.J.; Botero, B.A.; López, J.; Francés, F.; Díez-Herrero, A.; Benito, G. Flood frequency analysis of historical flood data under stationary and non-stationary modelling. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 525–568. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: Berlin, Germany, 2002. [Google Scholar]
- Xiong, L.H.; Jiang, C.; Xu, C.Y.; Yu, K.X.; Guo, S.L. A framework of change-point detection for multivariate hydrological series. Water Resour. Res. 2015, 51, 8198–8217. [Google Scholar] [CrossRef]
- Dias, A. Copula Inference for Finance and Insurance. Ph.D. Thesis, Eidgenössische Technische Hochschule Zürich, Zürich, Switzerland, 2004. [Google Scholar]
- Dung, N.V.; Merz, B.; Bárdossy, A.; Apel, H. Handling uncertainty in bivariate quantile estimation—An application to flood hazard analysis in the Mekong Delta. J. Hydrol. 2015, 527, 704–717. [Google Scholar] [CrossRef]
- Serinaldi, F. An uncertain journey around the tails of multivariate hydrological distributions. Water Resour. Res. 2013, 49, 6527–6547. [Google Scholar] [CrossRef]
- Serinaldi, F. Assessing the applicability of fractional order statistics for computing confidence intervals for extreme quantiles. J. Hydrol. 2009, 376, 528–541. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.; Singh, V.P. Uncertainty evaluation of copula analysis of hydrological droughts in the East River basin, China. Glob. Planet. Chang. 2015, 129, 1–9. [Google Scholar] [CrossRef]
- Serinaldi, F. Can we tell more than we can know? The limits of bivariate drought analysis in the United States. Stoch. Environ. Res. Risk Assess. 2015, 60, 1–14. [Google Scholar]
- Hyndman, R.J.; Bashtannyk, D.M.; Grunwald, G.K. Estimating and visualizing conditional densities. J. Comput. Graph. Stat. 1996, 5, 315–336. [Google Scholar]
- Hdrcde: Highest Density Regions and Conditional Density Estimation. Available online: http://www.robjhyndman.com/software/hdrcde (accessed on 19 May 2016).





| Archimedean Copula | Range | |
|---|---|---|
| Clayton | ||
| Frank | ||
| Gumbel-hougaard |
| Combination | SH | SN | SL |
|---|---|---|---|
| RH | |||
| RN | |||
| RL |
| Measure | Terrace | Afforestation | Grass Planting | Dam Building | Water Projects | Industrial and Domestic Water | |
|---|---|---|---|---|---|---|---|
| 1960s | |||||||
| S reduction | (104 t) | 181 | 13 | 14 | 146 | 1162 | 0 |
| R reduction | (104 m3) | 905 | 320 | 84 | 137 | 85021 | 7260 |
| 1970s | |||||||
| S reduction | (104 t) | 700 | 84 | 29 | 866 | 4312 | 0 |
| R reduction | (104 m3) | 3630 | 1118 | 213 | 848 | 222263 | 9419 |
| 1980s | |||||||
| S reduction | (104 t) | 1428 | 190 | 125 | 555 | 2835 | 0 |
| R reduction | (104 m3) | 8418 | 3870 | 823 | 528 | 227204 | 11102 |
| 1990s | |||||||
| S reduction | (104 t) | 1841 | 331 | 271 | 298 | 2582 | 0 |
| R reduction | (104 m3) | 8338 | 4063 | 1543 | 304 | 256822 | 13756 |
| Station | Linjiacun | Weijiabu | Xianyang | Huaxian | Zhangjiashan | Zhuangtou |
|---|---|---|---|---|---|---|
| Change point | 1975 | 1982 * | 1983 * | 1981 * | 1983 | 1981 * |
| Station | Period | Clayton | Gumbel-Hougaard | Frank | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | AICc | Sn | p-Value | θ | AICc | Sn | p-Value | θ | AICc | Sn | p-Value | ||
| Linjiacun | 1956–2010 | 1.88 | −171.13 | 0.101 | 0.003 | 2.23 | −180.88 | 0.053 | 0.002 | 8.26 | −195.32 | 0.022 | 0.495 |
| Weijiabu | 1956–1982 | 1.55 | −82.97 | 0.033 | 0.416 | 1.63 | −76.63 | 0.048 | 0.073 | 3.81 | −78.75 | 0.050 | 0.076 |
| 1983–2010 | 1.75 | −80.61 | 0.110 | 0.001 | 2.49 | −91.53 | 0.036 | 0.160 | 8.66 | −95.12 | 0.030 | 0.479 | |
| Xianyang | 1956–1983 | 1.05 | −87.42 | 0.031 | 0.486 | 3.32 | −65.20 | 0.033 | 0.458 | 1.44 | −87.326 | 0.034 | 0.479 |
| 1984–2010 | 1.15 | −78.15 | 0.115 | 0.001 | 2.12 | −87.97 | 0.030 | 0.410 | 6.42 | −90.20 | 0.027 | 0.471 | |
| Huaxian | 1956–1981 | 1.39 | −86.02 | 0.032 | 0.433 | 1.61 | −82.69 | 0.031 | 0.648 | 3.77 | −85.08 | 0.034 | 0.462 |
| 1982–2010 | 0.41 | −89.04 | 0.085 | 0.020 | 1.36 | −94.18 | 0.047 | 0.112 | 2.50 | −92.98 | 0.056 | 0.027 | |
| Zhangjiashan | 1956–2010 | 1.50 | −185.84 | 0.070 | 0.010 | 2.14 | −200.35 | 0.017 | 0.793 | 6.00 | −200.09 | 0.027 | 0.290 |
| Zhuangtou | 1956–1981 | 1.22 | −81.31 | 0.049 | 0.098 | 1.61 | −81.63 | 0.033 | 0.558 | 3.87 | −83.00 | 0.038 | 0.366 |
| 1981–2010 | 1.24 | −81.16 | 0.049 | 0.035 | 2.00 | −74.08 | 0.034 | 0.345 | 3.92 | −82.78 | 0.041 | 0.159 | |
| Station | Period | Synchronous Joint Probabilities (%) | Asynchronous Joint Probabilities (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RH-SH | RN-SN | RL-SL | RH-SL | RH-SN | RN-SH | RN-SL | RL-SH | RL-SN | ||
| Linjiacun | 1956–2010 | 17.41 (15.84, 19.34) | 35.12 (32.50, 38.71) | 17.41 (15.84, 19.34) | 0.15 (0.03, 0.59) | 7.44 (5.94, 9.30) | 7.44 (5.94, 9.30) | 7.44 (5.94, 9.30) | 0.15 (0.03, 0.59) | 7.44 (5.94, 9.30) |
| Weijiabu | 1956–1982 | 11.51 (8.01, 13.02) | 30.14 (26.08, 32.41) | 16.63 (10.43, 18.50) | 1.00 (0.65, 4.21) | 12.48 (11.98, 13.24) | 12.48 (11.98, 13.24) | 7.38 (6.61, 11.06) | 1.00 (0.65, 4.21) | 7.38 (6.61, 11.06) |
| 1983–2010 | 17.69 (15.22, 20.11) | 35.61 (31.57, 40.22) | 17.66 (15.22, 20.11) | 0.12 (0.05, 0.72) | 7.20 (6.31, 9.59) | 7.20 (6.31, 9.59) | 7.20 (6.31, 9.59) | 0.12 (0.05, 0.72) | 7.20 (6.31, 9.59) | |
| Xianyang | 1956–1983 | 10.14 (7.91, 12.69) | 28.32 (26.00, 31.90) | 14.54 (10.21, 18.12) | 1.81 (0.85, 5.68) | 13.04 (12.30, 13.24) | 13.04 (12.30, 13.24) | 8.65 (7.07, 12.14) | 1.81 (0.85, 5.68) | 8.65 (7.07, 12.14) |
| 1984–2010 | 15.90 (13.15, 18.78) | 32.56 (28.91, 37.64) | 15.90 (13.15, 18.78) | 0.40 (0.14, 1.60) | 8.71 (7.34, 10.88) | 8.71 (7.34, 10.88) | 8.71 (7.34, 10.88) | 0.40 (0.14, 1.60) | 8.71 (7.34, 10.88) | |
| Huaxian | 1956–1981 | 11.10 (8.25, 14.05) | 29.55 (26.29, 34.06) | 16.03 (10.96, 19.55) | 1.21 (0.31, 4.26) | 12.69 (11.08, 13.24) | 12.69 (11.08, 13.24) | 7.76 (5.57, 11.11) | 1.21 (0.31, 4.26) | 7.76 (5.57, 11.11) |
| 1982–2010 | 11.95 (6.25, 15.98) | 27.46 (25.00, 31.32) | 9.95 (6.25, 13.49) | 2.79 (0.93, 6.25) | 10.27 (8.09, 12.50) | 10.27 (8.09, 12.50) | 12.26 (10.59, 12.62) | 2.79 (0.93, 6.25) | 12.26 (10.59, 12.62) | |
| Zhangjiashan | 1956–2010 | 17.14 (13.90, 19.06) | 32.93 (29.03, 36.20) | 14.67 (11.55, 16.80) | 0.56 (0.35, 3.01) | 7.30 (6.65, 10.44) | 7.30 (6.65, 10.44) | 9.77 (9.06, 12.35) | 0.56 (0.35, 3.01) | 9.77 (9.06, 12.35) |
| Zhuangtou | 1956–1981 | 12.89 (9.52, 17.00) | 28.62 (25.91, 34.40) | 12.89 (9.52, 17.00) | 1.42 (0.46, 4.26) | 10.69 (8.93, 12.29) | 10.69 (8.93, 12.29) | 10.69 (8.93, 12.29) | 1.42 (0.46, 4.26) | 10.69 (8.93, 12.29) |
| 1982–2010 | 12.95 (9.97, 16.07) | 28.68 (26.17, 32.86) | 12.95 (9.97, 16.07) | 1.39 (0.55, 4.49) | 10.66 (9.18, 12.34) | 10.66 (9.18, 12.34) | 10.66 (9.18, 12.34) | 1.39 (0.55, 4.49) | 10.66 (9.18, 12.34) | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, A.; Chang, J.; Wang, Y.; Huang, Q. Variations in the Runoff-Sediment Relationship of the Weihe River Basin Based on the Copula Function. Water 2016, 8, 223. https://doi.org/10.3390/w8060223
Guo A, Chang J, Wang Y, Huang Q. Variations in the Runoff-Sediment Relationship of the Weihe River Basin Based on the Copula Function. Water. 2016; 8(6):223. https://doi.org/10.3390/w8060223
Chicago/Turabian StyleGuo, Aijun, Jianxia Chang, Yimin Wang, and Qiang Huang. 2016. "Variations in the Runoff-Sediment Relationship of the Weihe River Basin Based on the Copula Function" Water 8, no. 6: 223. https://doi.org/10.3390/w8060223
APA StyleGuo, A., Chang, J., Wang, Y., & Huang, Q. (2016). Variations in the Runoff-Sediment Relationship of the Weihe River Basin Based on the Copula Function. Water, 8(6), 223. https://doi.org/10.3390/w8060223





