Next Article in Journal
Evaluation of Satellite Precipitation Products with Rain Gauge Data at Different Scales: Implications for Hydrological Applications
Previous Article in Journal
Conflict Management in Participatory Approaches to Water Management: A Case Study of Lake Ontario and the St. Lawrence River Regulation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 8
Issue 7
10.3390/w8070282
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

An Assessment of the Effectiveness of Tree-Based Models for Multi-Variate Flood Damage Assessment in Australia

by
Roozbeh Hasanzadeh Nafari
1,*,
Tuan Ngo
2 and
Priyan Mendis
3
1
Centre for Disaster Management and Public Safety (CDMPS), Department of Infrastructure Engineering, The University of Melbourne, Melbourne 3010, Australia
2
Director of the Advanced Protective Technologies for Engineering Structures (APTES) Group, Department of Infrastructure Engineering, The University of Melbourne, Melbourne 3010, Australia
3
Department of Infrastructure Engineering, The University of Melbourne, Melbourne 3010, Australia
*
Author to whom correspondence should be addressed.
Water 2016, 8(7), 282; https://doi.org/10.3390/w8070282
Submission received: 7 May 2016 / Revised: 30 June 2016 / Accepted: 1 July 2016 / Published: 9 July 2016
Browse Figures
Versions Notes

Abstract

:
Flood is a frequent natural hazard that has significant financial consequences for Australia. In Australia, physical losses caused by floods are commonly estimated by stage-damage functions. These methods usually consider only the depth of the water and the type of buildings at risk. However, flood damage is a complicated process, and it is dependent on a variety of factors which are rarely taken into account. This study explores the interaction, importance, and influence of water depth, flow velocity, water contamination, precautionary measures, emergency measures, flood experience, floor area, building value, building quality, and socioeconomic status. The study uses tree-based models (regression trees and bagging decision trees) and a dataset collected from 2012 to 2013 flood events in Queensland, which includes information on structural damages, impact parameters, and resistance variables. The tree-based approaches show water depth, floor area, precautionary measures, building value, and building quality to be important damage-influencing parameters. Furthermore, the performance of the tree-based models is validated and contrasted with the outcomes of a multi-parameter loss function (FLFArs) from Australia. The tree-based models are shown to be more accurate than the stage-damage function. Consequently, considering more parameters and taking advantage of tree-based models is recommended. The outcome is important for improving established Australian flood loss models and assisting decision-makers and insurance companies dealing with flood risk assessment.

Graphical Abstract

1. Introduction

In recent decades, flood risk is growing, due to climate change and increase in vulnerability of properties at risk [1,2,3]. In Australia, floods are the most costly of all disaster types [4], contributing 29% of the total cost of the nation’s economy and the built environment [5,6]. Accordingly, flood risk management is attracting more attention [7,8,9], and results are used to inform disaster management policy and support the development of risk reduction measures [10,11]. Flood risk management has to be based upon an appropriate evaluation of flood hazard and flood vulnerability [12,13], including an assessment of damage and effectiveness of risk reduction measures [14,15,16]. Therefore, loss estimation and consequence assessment is an indispensable part of flood risk management [17,18]. However, compared to the available methods and information on flood hazard, flood damage models are still crude, and understanding of the damage process is largely unknown [11,15,19,20].
Flood losses can be grouped into four different classifications: direct tangible, direct intangible, indirect tangible, and indirect intangible damages [21]. The direct classification takes place due to physical contact with flooded objects, but the indirect category is induced by the direct damage on a wider scale of space and time [22,23,24]. Tangible losses can be quantified financially, while intangible losses cannot [7,25]. The existing methods for flood damage assessment are commonly focused on direct tangible damages of residential, industrial, agricultural, and commercial sectors. However, residential buildings are usually more affected by floods [26]. Consequently, the focus of this study is on direct, tangible damage to residential building structures after a short inundation.
Stage-damage functions are the international standard of flood loss assessment [2,27,28]. The simplicity of stage-damage functions is the main reason for their common usage. However, studies have shown that they might be subject to significant uncertainties since some influencing parameters are neglected in their damage assessment [15,26]. Flood damage is a complicated process and is dependent on a variety of parameters. These can be classified into impact parameters (e.g., flood depth, flood duration, flow velocity, water contamination, and return period) and resistance parameters (e.g., building characteristics, private precaution, early warning, emergency measures, flood experience, and socioeconomic status) [24]. These parameters may not be independent of each other, and their single or joint effects are widely unknown [15]. However, the majority of flood damage models have attempted to propose simplified approaches based on the type or use of elements at risk and the inundation depth of water [8]. Consequently, using these models might increase the uncertainty of results, particularly when they are employed in study areas other than the area of origin [6,27,29,30].
Nonetheless, there are some exceptions. Wind et al. (1999); Penning-Rowsell and Green (2000); Smith (1994); and Parker et al. (2007) studied the effects of early warning time and preparedness on the magnitude of flood damages [15,21,31,32,33], and some multi-parameter models have recently been developed for quantifying the single or joint effects of influencing parameters [26]. For instance, in the UK, a conceptual model has been drawn up to suggest the critical parameters that should be considered in flood loss assessment, albeit without discussing the weight of contributions or the importance of parameters [15,34]. In Japan, a multi-variate model has been developed by Zhai et al. (2005), although the performance of the model has not been validated or compared with other flood loss models [15,35]. In Germany, a Bayesian network for flood damage assessment has been developed by Vogel et al. (2013) [36]. Another multi-parameter model is related to 2002, 2005 and 2006 flood events in Germany and has been established and developed by Thieken et al. (2005), Kreibich et al. (2005, 2007) and Elmer et al. (2010). This multi-parameter model (FLEMO) has been developed, applied, and validated for private households and companies at both the micro- and meso-scale [7,24,28,37,38,39,40,41,42]. These studies have demonstrated that multi-parameters consideration can improve flood loss modelling in Germany [15].
The interaction or influence of different parameters can be explored with a tree-based modelling statistical analysis. This approach has frequently been used by hydrology and water resource researchers. However, it is still novel in the domain of flood-loss modelling. Merz et al. (2013) have recently analysed the FLEMO flood loss model dataset with a tree-based data mining approach. The results of this study revealed that the depth of water, area of buildings, return period of flood, contamination, duration of flooding, and precautionary measures, respectively, have the highest influences on flood loss assessment in the region of study [15,26]. Also, these analyses show that the tree-based damage model is more accurate than the FLEMO multi-parameter model. Another study with the same concept has been developed for the city of Can Tho in the Mekong Delta. In this area of study, as opposed to Germany, the flood had a shallow depth with a long duration. Consequently, inundation duration, equated with the depth of water, was the greatest influencing factor. In addition to these two parameters, the single or joint effects of 22 more predictors have been evaluated and examined [26].
To our knowledge, the tree-based approach has not been developed and validated for Australia, and we hypothesise that this method would be more accurate than the existing traditional stage-damage functions. The objective of this study is to employ tree-based data mining methods to examine the effect and importance of damage-influencing parameters using a dataset collected from 2012 to 2013 flood events in Queensland. The performance of the tree-based models is also compared with the outcomes of a newly established multi-parameter loss function (FLFArs) from Australia.

2. Study Area and Data

For this study, two areas were chosen. The first survey area is the city of Bundaberg in Queensland, Australia, located in the vicinity of the Burnett River waterway north of the state capital, Brisbane (Figure 1). The Burnett River catchment is located in South-East Queensland, with the main system incorporating the rivers of Three Moon Creek, Burnett River, Nogo Creek, Auburn River and the Boyne River, in addition to many other creeks and tributaries. The total Burnett River catchment area is approximately 33,000 square kilometres. This area is bound by the catchments of the Fitzroy and Kolan Rivers to the north; the Dawson and Condamine Rivers to the east and the Brisbane and Mary Rivers to the South. The Burnett River catchment has had a long history of flooding that has impacted both the urban centres and rural areas [43]. The Bundaberg ground elevation and the Burnett River catchment are illustrated in Figure 2 and Figure 3. In recent years, the city of Bundaberg has experienced some extreme flood events. The most recent flood responses from Bundaberg Regional Council date back to the floods in November 2010, January 2013, February 2013, and February 2015 [2]. During the flood event in January 2013, 200 businesses were inundated, and over 2000 residents and 70 hospital patients were evacuated. Furthermore, the performance of lifelines was disrupted, and infrastructures were impacted [44]. This flood event that occurred from 21 to 29 January 2013 was a result of the Tropical Cyclone Oswald, and the associated rainfall and flooding had a catastrophic effect on Queensland and it is considered to be the worst flood experienced in Bundaberg’s recorded history. The height of the floodwaters in Bundaberg city from Burnett River reached 9.53 metres at its peak, and over 2000 properties were affected [2]. The extension of the water depth is illustrated in Figure 4. Bundaberg Regional Council estimated that the public infrastructure damage from the flood event of 2013 was approximately AUD 103 million [2]. The second study area is the city of Roma, located on Bungil Creek, a tributary of the Condamine River in the Maranoa region in Queensland (Figure 5). The flood event in 2012 is considered to be the worst flood experienced in Roma’s history, having inundated 444 homes. This flood event that occurred from late January to early February 2012 was a result of heavy rainfall. The boundary of the flood is illustrated in Figure 6. The Maranoa Regional Council estimated that the public infrastructure damage from the natural disaster events of 2012 was approximately AUD 50 million [2]. The return periods of both flood events have been estimated to be approximately 100 years, based on the flood frequency analyses [43].
The empirical dataset used for this study (457 loss cases from the 2013 flood and 150 loss cases from the 2012 flood) was gathered after these two flood events from the Queensland Reconstruction Authority, a governmental responder organisation to Queensland disaster events. The official dataset—which was collected by either two or three post-disaster on-site surveys based on a standardised procedure and unified guidelines of the survey—provides data on the intensity of hazard (i.e., water depth, information on water contamination, and information on flow velocity), characteristics of buildings (i.e., material, floor space, construction type, number of building storeys, information on utilities and solar panels, and emergency measures undertaken), and the magnitude of losses. It is worth mentioning that for every building, the magnitude of damage has been explained based on the affected structural components. Accordingly, based on the average value of damaged items relative to the total value of the structure, the descriptions of damages have been exchanged into a percentage of damages [2]. Further complementary data (e.g., building age, length of residency, average replacement building value, the number of residences, and socioeconomic status) was collected from the National Exposure Information System of Australia [51]. Consequently, the final dataset provides 20 attributes on 607 inundations. Candidate predictors are either extracted directly from one attribute (e.g., water depth or building area) or transformed from several attributes (e.g., building quality or flow velocity). Data preparation and data transformation are discussed further below.
  • Water depth and water contamination: this information was collected in two post-disaster surveys. The value of water depth fluctuated between 0 cm and 700 cm above ground. However, for 96% of buildings, this attribute was equal to or less than 350 cm. Also, the existence of sewage, biological, or chemical contamination has been checked and reported by visual inspection and smell. Accordingly, water contamination was ranked based on the reported material and the existing chemical hazards, from 0 (no contamination) to 2 (chemical contamination), with 1 representing only sewage contamination.
  • Flow velocity: flow velocity was assessed according to the comments of inspectors about the amount of water penetration inside of buildings, the volume of deposited materials, and the type of sediment next to the house (mud, sand, gravel or stone). Afterwards, this information was transformed and ranked as calm (1: no deposit or only mud sediment), medium (2: sand sediment or a considerable amount of water penetration), or high (3: gravel or stone sediment or high volume of deposits) flow velocity.
  • Emergency measures: the dataset provides information about whether or not people undertook any action against water infiltration, e.g., pumping water out or cut-off of electricity supply. Subsequently, these actions were ranked from 0 (no measure was undertaken) to 3 (many measures were undertaken), with 1 representing that only water was pumped out, and 2 representing that only electricity supply was cut off. The “cut-off of electricity supply” measure had a greater weight due to the high value of electrical equipment [2].
  • Precaution measures: the indicators of precaution measures were defined and ranked based on the construction type (3: high-set open under, 2: low-set with suspended floor, or 1: high-set enclosed under or slab on ground); protection of utilities and power system against water impacts (1: no protection, 2: protected); availability of solar-panel power provider (1: not available, 2: available); and the number of building storeys (1: one-storey buildings, 2: two-storey buildings). Eventually, precaution measure indicators were calculated and weighted by multiplying the above ranks.
  • Flood experience: the areas of study have experienced a variety of flood events in recent years [2,52]. Therefore, this parameter has been assessed and averaged according to the length of residency. Overall, about 11% of households moved into the areas one year or less before the events, weighted 1. About 31% of families settled there in the last five years, weighted as 2. Residents with more than five years length of residency were weighted 3.
  • Building quality: this item is a function of age (i.e., constructed pre- or post-1981) and material (e.g., timber, brick, concrete, or metal) of buildings. Age of buildings was weighted 1 if the structure was constructed pre-1981 and 2 if it was constructed post-1981. Also, the resistance of different materials against impacts of water is judged and ranked: 1 for timber, 2 for brick, and 3 for concrete or metal, according to the Australian building guidelines for flood prone areas [53]. Finally, this candidate predictor is defined by multiplying the weight of age by the weight of the material.
  • The value and floor space of building: for every building, the value was calculated by multiplying the total area reported by the inspectors by the average replacement value per square metre extracted from the national exposure information system of Australia [51]. In this study, besides considering the area of the buildings, the contribution of the residents’ density with the extent of losses has been taken into account. Accordingly, floor space of the building was calculated per person, by dividing the total area by the number of residents.
  • Socioeconomic status: this category includes information about ownership status and monthly income (i.e., low: $1–$599, middle: $600–$1,999, or high: greater than $2,000). Also, it represents buildings whose residents need special attention (i.e., aged less than five or more than 65; needing assistance with a core activity; or do not speak English well) or low education residents (i.e., the highest educational attainment of all building residents is year 11 or below).
Following the approach of Merz et al. (2013) and Chinh et al. (2015), these predictors were classified into five main categories: (1) flood impact; (2) emergency measures; (3) precaution and flood experience; (4) building characteristics; and (5) socioeconomic status (Table 1). Table 2 shows the Pearson correlation coefficient of the final candidate predictors and the loss ratio. As expected, and as other researchers have claimed [2,15,24], water depth has the highest absolute correlation with loss ratios (Figure 7). However, many other variables—such as flow velocity, contamination, precaution measure, floor space per person, the value of the affected building, and building quality—are also significantly correlated to damage ratio.

3. Statistical Methods

Regression trees and bagging decision trees were applied to determine the prominent damage-influencing parameters, to understand their effect on the extent of structural damage, and to compare the performance of the tree-based models with an established flood loss function. The tree-based analyses were performed with the Weka machine learning software [54].

3.1. Regression Trees

Regression trees are machine learning methods for constructing prediction models from data where the target variables are continuous values [55]. Tree-based regression models are known for their simplicity and efficiency when facing up to domains with a large number of variables and data [56]. They are constructed by sub-dividing the predictor data space into smaller areas such that in each split, the dataset is partitioned into two sub-spaces. In this regard, each terminal node is labelled with a question and the binary branches are labelled with the answers. Subdivision should be performed in such a way that the predictive accuracy is maximised, and errors are minimised. In other words, the algorithm searches over all possible split values of all predictor variables to identify the split which minimises an error criterion. Overall, trees should be complicated enough to take advantage of information that increases predictive power, while simple enough to ignore random noises that do not enhance the accuracy of results [15].
If a decision tree model is fully grown, it may lose some generalisation capability, and if the training data contains any errors, it can lead to poor performance on unforeseen cases. This issue is known as overfitting and needs careful attention [57,58]. One way to avoid overfitting is tree pruning, which was employed in this study. Tree pruning is a technique in machine learning that decreases the size of decision trees by taking off sections of the tree that give little power to classify instances. Pruning reduces the complexity of the final classifier and hence improves predictive accuracy by the reduction of overfitting [59].
In this study, the target variables were relative structural loss values and trees were constructed using the entire dataset. Therefore, some repeated binary partitioning questions construct the structure of the tree, from the root node to the terminal nodes (or leaves). Terminal node values give the average loss ratio of all data values of the terminal node [15]. In other words, the prediction of loss ratio is the average of the training dataset that belongs to every leaf.
The prediction error used for Figure 8 is estimated by a 10-fold cross-validation technique based on the average absolute deviation of the estimated ratios from the observed values (MAE). In this regard, the shuffled data was first partitioned into 10 equally-sized segments (folds). A tree was computed 10 times. In each iteration, a different fold of the data was held out for model testing while the remaining nine folds were used for model training. Eventually, the error was averaged over all constructed models [6,60].

3.2. Bagging Decision Trees

The bagging predictor is a method for generating a multiple version of a predictor and using this to get an aggregated predictor. The multiple version is formed by making bootstrap replicates of the entire dataset and using each replica to grow a new regression tree. The response of a bagging decision tree is the average of all individual regression trees. Bootstrapping and ensemble models make the response strong enough to cope with variation in data and avoid the overfitting issue. Tests on real and simulated datasets using regression trees have shown that compared to an individual regression tree, bagging can substantially enhance the stability and accuracy of the model’s performance [15,61,62,63,64]. About one-third of data is not used for training the individual regression trees. This segment, called out-of-bag data, is the observation data utilised for error estimation and feature importance assessment.
The quality of a bagging tree, used for exploring the feature importance, is measured by the average error of predictions of all regression trees compared with the observation data (out-of-bag data). In this regard, the values of one variable in the out-of-bag examples is randomly permuted, and the increase in the out-of-bag error is measured: the greater the growth, the more important the feature [15,26,62].

3.3. Comparing the Performance of the Tree-Based Models with FLFArs

The tree-based models constructed in the previous stages, based the on the entire dataset, were utilised for loss ratio estimation and comparison with the stage-damage function. For a meaningful comparison, all models should be derived from the same dataset [15]. Accordingly, the performance of the tree-based model was compared with a newly established multi-parameter flood loss model (FLFArs) [2], which has been derived from the same flood event data.
The results of the damage models have been compared with the following resampling procedure. First, 100 samples are randomly pulled out from the original data set, and each model is implemented with this random sample. Errors in the estimates from the aforementioned models in contrast to the actual values are evaluated by three error measures: mean absolute error (MAE), root mean square error (RMSE), and correlation coefficient. Then, this step is repeated 200 times and the average of errors converged to a final constant value. Finally, the performance of the damage models is compared according to the converged values of the averaged errors (Figure 11).

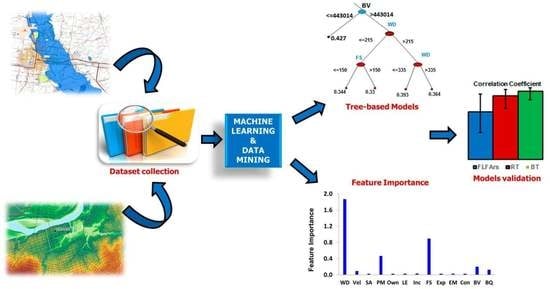
4. Results and Discussion

4.1. Importance and Interaction of the Damage Influencing Parameters

4.1.1. Regression Trees

Regression trees were created in different sizes. Figure 8 compares the various trees based on the cost error parameter. The largest tree was stopped with 19 terminal nodes (Figure 9). As stated before, trees should be complicated enough to take advantage of information that increases predictive power, while simple enough to ignore random noises that do not enhance the accuracy of results [15]. Accordingly, after using tree pruning technique for all sizes of regression trees, the tree with 19 terminal nodes and a minimum value of error (0.0652) was selected. In this tree, five predictors out of the 13 candidates were considered and correlated with loss ratios. Table 3 shows how many times these predictors were used in decision nodes and how these parameters are correlated with loss ratios. A positive correlation means that the loss ratio increases or decreases as the candidate predictor increases or decreases, and the reverse for a negative correlation.
Water depth is the most significant predictor, available in nine decision nodes and correlating positively with the loss ratio. This outcome is as expected, and accords with previous research [11,32]. After water depth, floor area (space area per person) is the most important influencing factor, correlating negatively with loss ratio. The space area might be substantial if the depth of water is greater than 64 cm. This result accords with the findings of Thieken et al. (2005) and Merz et al. (2013), who showed that the building loss ratio decreases if the total floor space of the building exceeds 139 m2 or 120 m2 [15,24]. However, in this study, the area of the building reduces the extent of losses if it exceeds 150 m2 per person (Figure 9).
Another important factor that correlates negatively with the extent of losses is the precautionary measures. In the pruned tree with 19 leaves, the precautionary measures are important only for larger water depths (>177.5 cm). This outcome is opposite to the results of the studies in Germany, where the effects of the precautionary measures were significant only for shallow water depths [15,39]. This matter can be explained according to the flood characteristics and the precaution measures considered. As stated, in this study, water depth was the most significant impact factor. On the other hand, the construction type (i.e., how much the first floor has been raised up) and the number of building storeys had the most influential effects on the weighting of the precautionary measures. Accordingly, when the flood depth is shallow, and hazard has little impact, these measurements do not significantly affect the calculated extent of losses. However, when the impact of the flood (water depth) is considerable, precautionary measures—either by substantially decreasing the water depth on the floor of the building, or by protecting the building fabrics placed at higher levels—will remarkably reduce the extent of losses.
As with precautionary measures, building quality has an inverse effect on the structural loss ratios if the water depth is greater than 177.5 cm. This accords with the above finding that water depth is the greatest influencing factor of the floods, and the resistance parameters are meaningful if the depth of water (hazard impact) is significant. The building value indicator was also presented in three decision nodes of the right part of the tree. Nonetheless, its correlation with the loss ratio is not clear. In other words, on this dataset and in large flood depths, variation in the building value does not have a defined relationship with the trend of the loss ratio. This can be interpreted as a weak local correlation between this predictor and the loss ratio, or as an inherent uncertainty in the data.
Water contamination and flow velocity were not found to correlate with the loss ratios. This result confirms the outcome of Kreibich et al. (2009) and Merz et al. (2013), who showed that the effects of the flow velocity and the water contamination are significant only if the depth of water is shallow and the level of energy head is low [15,65]. Since in this study these predictors are reported simultaneously with large flood depths, they do not have a major effect on the extent of the damage. Other defined indicators such as emergency measures, flood experience, and socioeconomic status do not have an evident meaningful relationship with the loss ratios, although these parameters (e.g., water contamination, flow velocity and socioeconomic status) might be related to the loss ratios if an unpruned tree was grown on the dataset. As stated, although unpruned trees might have better performance on the original data, overfitting phenomena could affect their performance for an independent dataset. Accordingly, the authors have not developed unpruned trees for this part of the study. Furthermore, due to the joint effects of parameters, the interaction of emergency measures should also be discussed in the context of warnings and alerts issued during the event.

4.1.2. Bagging Decision Trees

As mentioned earlier, the bagging decision tree is formed by making bootstrap replicates of the entire dataset and using each replica for growing a new regression tree. This step was completed up to 200 times until the average of the ensemble errors became stable. Afterwards, the feature importance and the ranking of the predictors were calculated based on the results achieved from random permute. The grading of the predictors is water depth, space area per person, precautionary measures, building value, building quality and flow velocity (Figure 10). Other candidates show slight feature importance. This ranking is very similar to the results obtained from the regression trees, see Table 3.

4.1.3. Performance of the Applied Damage Models

In this part of the study, the performance of the tree-based models was compared with FLFArs multi-parameter flood loss function. As mentioned before, both approaches (the tree-based models and the stage-damage function) were derived based on the same dataset.
To compare the performance of the tree-based models with FLFArs, 200 sets of 100 affected buildings were randomly drawn from the original dataset; each model was applied to every building record and the errors were calculated and averaged over all samples.
Results show that there is a distinct improvement in the tree-based models’ performance over the FLFArs model, which is due to the consideration of more candidate predictors. Also, there is a small improvement in the fulfilment of the bagging decision tree compared to the regression tree. The metrics are the higher value of the correlation coefficients, the lower value of the errors, and the lower variation of the results. This improvement is due to the reduction in the variances of the dataset and the greater accuracy of the model (Figure 11). In Figure 11, MAE represents the average absolute deviation of the estimated ratios from the observed values and is a quantity used to measure how close the estimates are to the empirical data. The RMSE also expresses the variation of the estimated ratios from the observed ratios. It signifies the standard deviation of the differences between the modelled values and observed values [41,66].

5. Conclusions

Flood damage assessment is an important component of flood risk management since inaccurate damage estimation leads to wasted effort, money, and resources for the organisations involved in risk mitigation. The majority of flood damage models have attempted to propose simplified approaches based on the type or use of elements at risk and the inundation depth of water. However, flood damage is a complicated process, dependent on a variety of factors. Accordingly, the traditional stage-damage functions are subject to significant uncertainties since some influencing factors are usually neglected. If the water depth is the only hydraulic factor considered, the models are not flexible enough to transfer and use in a new area of study. On the other hand, multi-variable models are also subject to uncertainty, particularly since additional variables are taken into account. Therefore, they also entail additional sources of uncertainty. This study used a multi-variate statistical analysis to explore the interaction and effect of many influencing parameters on the extent of flood losses. In this regard, tree-based approaches (e.g., regression trees and bagging decision trees) have been applied, and a dataset collected from 2012 to 2013 flood events in Queensland has been utilised. Previous studies have shown that tree-based models are very effective in identifying the significant damage-influencing parameters and their interactions with the extent of losses since they can extract the local relevance of every predictor. Accordingly, this study has taken advantage of this approach.
The results of the Australian dataset show that water depth is the most significant predictor, correlating positively with the loss ratio. After water depth, floor space per person is the most important influencing factor, correlating negatively with loss ratio. This predictor is substantial if the depth of water is greater than 64 cm and the area of the building exceeds 150 m2 per person. Another important factor that correlates negatively with the extent of losses is the precautionary measures. The precautionary measures are important only for large flood depths (>177.5 cm). This outcome is opposite to the results of the studies in Germany, where the effects of the precautionary measures were significant only for shallow water depths. As with precautionary measures, building quality has an inverse effect on the structural loss ratios if the water depth is greater than 177.5 cm. The building value indicator was also presented in three decision nodes of the tree. However, its correlation with the loss ratio is not specified. In this study area, water contamination and flow velocity were not correlated with the loss ratios. Also, it has been shown that socioeconomic status does not play a fundamental role in flood loss mitigation in the areas of study. As the results of the tree-based approaches show, the following damage-influencing parameters are important: water depth, floor space per person, precautionary measures, building value, and building quality. The high importance of water depth is in accordance with traditional stage-damage functions. However, to the best of our knowledge, the influences of other parameters have not been studied comprehensively for flood damage assessment in Australia.
Finally, the performance of the tree-based models was compared with the outcomes of a newly established multi-parameter flood loss function (FLFArs) from Australia. It is demonstrated that the new tree-based model, due to considering more parameters, can estimate the extent of losses more accurately. The evaluation of model performance in this paper is based on random samples which are not independent of the data used for model development. Hence, the comparison of model performance does not give information about the transferability of the models.
Accordingly, it is recommended that further development of Australian flood damage models consider more candidate predictors (especially the important parameters stated in this study), and take advantage of tree-based models. Further research will be aimed at examining a more comprehensive dataset to explore the significance of other influencing factors (e.g., return period, long duration flooding, sediment loading, and early warning) and using an independent dataset to evaluate the level of transferability of the tree-based models in time and space.

Acknowledgments

We would like to thank the Queensland Reconstruction Authority for their kind support and for providing us with invaluable resources and datasets. Also, the authors would like to acknowledge the ongoing financial contribution and support from the Bushfire and Natural Hazards CRC.

Author Contributions

Roozbeh Hasanzadeh Nafari and Tuan Ngo built the initial concept of this work. Priyan Mendis contributed ideas regarding the structure and content of the article. The analysis was implemented by Roozbeh Hasanzadeh Nafari under the supervision of Tuan Ngo. Roozbeh Hasanzadeh Nafari prepared the initial version of the article, which was further refined and edited by Tuan Ngo and Priyan Mendis.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Elmer, F.; Hoymann, J.; Düthmann, D.; Vorogushyn, S.; Kreibich, H. Drivers of flood risk change in residential areas. Nat. Hazards Earth Syst. Sci. 2012, 12, 1641–1657. [Google Scholar] [CrossRef]
  2. Hasanzadeh Nafari, R.; Ngo, T.; Lehman, W. Calibration and validation of FLFArs—A new flood loss function for Australian residential structures. Nat. Hazards Earth Syst. Sci. 2016, 16, 15–27. [Google Scholar] [CrossRef]
  3. Kundzewicz, Z.W.; Ulbrich, U.; Brücher, T.; Graczyk, D.; Krüger, A.; Leckebusch, G.C.; Menzel, L.; Pińskwar, I.; Radziejewski, M.; Szwed, M. Summer floods in Central Europe—Climate change track? Nat. Hazards 2005, 36, 165–189. [Google Scholar] [CrossRef]
  4. Box, P.; Thomalla, F.; van den Honert, R. Flood risk in Australia: Whose responsibility is it, anyway? Water 2013, 5, 1580–1597. [Google Scholar] [CrossRef]
  5. Economic Costs of Natural Disasters in Australia. Available online: https://bitre.gov.au/publications/2001/files/report_103.pdf (accessed on 4 July 2016).
  6. Hasanzadeh Nafari, R.; Ngo, T.; Lehman, W. Development and evaluation of FLFAcs—A new Flood Loss Function for Australian commercial structures. Int. J. Dis. Risk Reduct. 2016, 17, 13–23. [Google Scholar] [CrossRef]
  7. Kreibich, H.; Seifert, I.; Merz, B.; Thieken, A.H. Development of FLEMOcs—A new model for the estimation of flood losses in the commercial sector. Hydrol. Sci. J. 2010, 55, 1302–1314. [Google Scholar] [CrossRef]
  8. Schröter, K.; Kreibich, H.; Vogel, K.; Riggelsen, C.; Scherbaum, F.; Merz, B. How useful are complex flood damage models? Water Resour. Res. 2014, 50, 3378–3395. [Google Scholar] [CrossRef]
  9. Van Ootegem, L.; Verhofstadt, E.; van Herck, K.; Creten, T. Multivariate pluvial flood damage models. Environ. Impact Assess. Rev. 2015, 54, 91–100. [Google Scholar] [CrossRef]
  10. Emanuelsson, M.A.E.; Mcintyre, N.; Hunt, C.F.; Mawle, R.; Kitson, J.; Voulvoulis, N. Flood risk assessment for infrastructure networks. J. Flood Risk Manag. 2014, 7, 31–41. [Google Scholar] [CrossRef]
  11. Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review article “assessment of economic flood damage”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
  12. Chen, A.S.; Hammond, M.J.; Djordjević, S.; Butler, D.; Khan, D.M.; Veerbeek, W. From hazard to impact: Flood damage assessment tools for mega cities. Nat. Hazards 2016, 82, 857–890. [Google Scholar] [CrossRef]
  13. Olsen, A.S.; Zhou, Q.; Linde, J.J.; Arnbjerg-Nielsen, K. Comparing methods of calculating expected annual damage in urban pluvial flood risk assessments. Water 2015, 7, 255–270. [Google Scholar] [CrossRef] [Green Version]
  14. Bubeck, P.; Aerts, J.C.J.H.; de Moel, H.; Kreibich, H. Preface: Flood-risk analysis and integrated management. Nat. Hazards Earth Syst. Sci. 2016, 16, 1005–1010. [Google Scholar] [CrossRef]
  15. Merz, B.; Kreibich, H.; Lall, U. Multi-variate flood damage assessment: A tree-based data-mining approach. Nat. Hazards Earth Syst. Sci. 2013, 13, 53–64. [Google Scholar] [CrossRef]
  16. Morita, M. Flood risk impact factor for comparatively evaluating the main causes that contribute to flood risk in urban drainage areas. Water 2014, 6, 253–270. [Google Scholar] [CrossRef]
  17. De Moel, H.; Jongman, B.; Kreibich, H.; Merz, B.; Penning-Rowsell, E.; Ward, P.J. Flood risk assessments at different spatial scales. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 865–890. [Google Scholar] [CrossRef]
  18. Handmer, J.; Abrahams, J.; Betts, R.; Dawson, M. Towards a consistent approach to disaster loss assessment across Australia. Aust. J. Emerg. Manag. 2005, 20, 10–18. [Google Scholar]
  19. Gall, M.; Borden, K.A.; Cutter, S.L. When do losses count? Six fallacies of natural hazards loss data. Bull. Am. Meteorol. Soc. 2009, 90, 799–809. [Google Scholar] [CrossRef]
  20. Gerl, T.; Bochow, M.; Kreibich, H. Flood Damage Modeling on the Basis of Urban Structure Mapping Using High-Resolution Remote Sensing Data. Water 2014, 6, 2367–2393. [Google Scholar] [CrossRef]
  21. Wind, H.G.; Nierop, T.M.; de Blois, C.J.; de Kok, J.L. Analys is of flood damages from the 1993 and 1995 Meuse floods. Water Resour. Res. 1999, 35, 3459–3465. [Google Scholar] [CrossRef]
  22. Jonkman, S.; Dawson, R. Issues and Challenges in Flood Risk Management—Editorial for the Special Issue on Flood Risk Management. Water 2012, 4, 785–792. [Google Scholar] [CrossRef]
  23. Meyer, V.; Becker, N.; Markantonis, V.; Schwarze, R.; van den Bergh, J.C.J.M.; Bouwer, L.M.; Bubeck, P.; Ciavola, P.; Genovese, E.; Green, C.; et al. Review article: Assessing the costs of natural hazards-state of the art and knowledge gaps. Nat. Hazards Earth Syst. Sci. 2013, 13, 1351–1373. [Google Scholar] [CrossRef] [Green Version]
  24. Thieken, A.H.; Müller, M.; Kreibich, H.; Merz, B. Flood damage and influencing factors: New insights from the August 2002 flood in Germany. Water Resour. Res. 2005, 41, 1–16. [Google Scholar] [CrossRef]
  25. André, C.; Monfort, D.; Bouzit, M.; Vinchon, C. Contribution of insurance data to cost assessment of coastal flood damage to residential buildings: Insights gained from Johanna (2008) and Xynthia (2010) storm events. Nat. Hazards Earth Syst. Sci. 2013, 13, 2003–2012. [Google Scholar] [CrossRef]
  26. Chinh, D.; Gain, A.; Dung, N.; Haase, D.; Kreibich, H. Multi-Variate Analyses of Flood Loss in Can Tho City, Mekong Delta. Water 2015, 8, 6. [Google Scholar] [CrossRef]
  27. Cammerer, H.; Thieken, A.H.; Lammel, J. Adaptability and transferability of flood loss functions in residential areas. Nat. Hazards Earth Syst. Sci. 2013, 13, 3063–3081. [Google Scholar] [CrossRef]
  28. Thieken, A.H.; Kreibich, H.; Merz, B. Improved modelling of flood losses in private households. In Natural Systems and Global Change; Kundzewicz, Z., Hattermann, F., Eds.; Polish Academy of Sciences and Potsdam Institute of Climate Impact Research: Poznan, Poland; Potsdam, Germany, 2006; pp. 142–150. [Google Scholar]
  29. Chang, L.F.; Lin, C.H.; Su, M.D. Application of geographic weighted regression to establish flood-damage functions reflecting spatial variation. Water SA 2008, 34, 209–216. [Google Scholar]
  30. McBean, E.; Fortin, M.; Gorrie, J. A critical analysis of residential flood damage estimation curves. Can. J. Civ. Eng. 1986, 13, 86–94. [Google Scholar] [CrossRef]
  31. Parker, D.; Tapsell, S.; McCarthy, S. Enhancing the human benefits of flood warnings. Nat. Hazards 2007, 43, 397–414. [Google Scholar] [CrossRef]
  32. Penning-Rowsell, E.C.; Green, C. New Insights into the Appraisal of Flood-Alleviation Benefits: (1) Flood Damage and Flood Loss Information. Water Environ. J. 2000, 14, 347–353. [Google Scholar] [CrossRef]
  33. Smith, D. Flood damage estimation—A review of urban stage-damage curves and loss function. Water SA 1994, 20, 231–238. [Google Scholar]
  34. Nicholas, J.; Holt, G.D.; Proverbs, D.G. Towards standardising the assessment of flood damaged properties in the UK. Struct. Surv. 2001, 19, 163–172. [Google Scholar] [CrossRef]
  35. Zhai, G.; Fukuzono, T.; Ikeda, S.; Guofang, Z.; Fukuzono, T.; Ikeda, S. Modeling Flood Damage: Case of Tokai Flood 2000. J. Am. Water Resour. Assoc. 2005, 41, 77–92. [Google Scholar] [CrossRef]
  36. Vogel, K.; Riggelsen, C.; Scherbaum, F.; Schroeter, K.; Kreibich, H.; Merz, B. Challenges for Bayesian Network Learning in a Flood Damage Assessment Application. In Proceedings of the 11th International Conference on Structural Safety & Reliability, Columbia University, New York, NY, USA, 16–20 June 2013; pp. 3123–3130.
  37. Elmer, F.; Thieken, A. H.; Pech, I.; Kreibich, H. Influence of flood frequency on residential building losses. Nat. Hazards Earth Syst. Sci. 2010, 10, 2145–2159. [Google Scholar] [CrossRef]
  38. Kreibich, H.; Müller, M.; Thieken, A.H.; Merz, B. Flood precaution of companies and their ability to cope with the flood in August 2002 in Saxony, Germany. Water Resour. Res. 2007, 43, 1–15. [Google Scholar] [CrossRef]
  39. Kreibich, H.; Thieken, A.H.; Petrow, T.; Müller, M.; Merz, B. Flood loss reduction of private households due to building precautionary measures—Lessons learned from the Elbe flood in August 2002. Nat. Hazards Earth Syst. Sci. 2005, 5, 117–126. [Google Scholar] [CrossRef]
  40. Kreibich, H.; Thieken, A.H. Assessment of damage caused by high groundwater inundation. Water Resour. Res. 2008, 44, 1–14. [Google Scholar] [CrossRef]
  41. Seifert, I.; Kreibich, H.; Merz, B.; Thieken, A.H. Application and validation of FLEMOcs—A flood-loss estimation model for the commercial sector. Hydrol. Sci. J. 2010, 55, 1315–1324. [Google Scholar] [CrossRef]
  42. Thieken, A.H.; Olschewski, A.; Kreibich, H.; Kobsch, S.; Merz, B. Development and evaluation of FLEMOps—A new Flood Loss Estimation MOdel for the private sector. WIT Trans. Ecol. Environ. 2008, 118. [Google Scholar] [CrossRef]
  43. North Burnett Regional Council. Flood Mitigation Study. Available online: http://www.northburnett.qld.gov.au/res/file/flood_mitigation_study_140114.pdf (accessed on 7 March 2016).
  44. Queensland Government. Queensland 2013 Flood Recovery Plan (for the Events of January–February 2013). Available online: http://qldreconstruction.org.au/u/lib/cms2/lg-flood-recovery-plan.pdf (accessed on 15 July 2015).
  45. Queensland Government. Queensland Government Statistician’s Office, Queensland Regional Profiles, Bundaberg Statistical Area Level 2 (SA2). Available online: http://statistics.qgso.qld.gov.au/qld-regional-profiles?region-type=SA2_11&region-ids=8075 (accessed on 15 July 2015).
  46. Bundaberg Regional Council. Burnett River Floodplain-Bundaberg Ground Elevations. Available online: http://www.bundaberg.qld.gov.au/flood/mapping (accessed on 30 September 2015).
  47. Bundaberg Regional Council. Burnett River Catchment Map. Available online: http://www.bundaberg.qld.gov.au/flood/mapping (accessed on 30 September 2015).
  48. Bundaberg Regional Council. 2013 Flood Calibration Map—Paradise Dam to Bundaberg Port. Available online: http://www.bundaberg.qld.gov.au/flood/mapping (accessed on 30 September 2015).
  49. Queensland Government. Queensland Government Statistician’s Office, Queensland Regional Profiles, Maranoa Regional Council. Available online: http://statistics.oesr.qld.gov.au/qld-regional-profiles (accessed on 30 April 2015).
  50. Qld Department of Natural Resources and Mines. Interactive Floodcheck Map. Available online: http://dnrm-floodcheck.esriaustraliaonline.com.au/floodcheck/ (accessed on 30 September 2015).
  51. Dunford, M.A.; Power, L.; Cook, B. National Exposure Information System (NEXIS) Building Exposure-Statistical Area Level 1 (SA1). Available online: http://dx.doi.org/10.4225/25/5420C7F537B15 (accessed on 15 July 2015).
  52. Van den Honert, R.C.; McAneney, J. The 2011 Brisbane floods: Causes, impacts and implications. Water 2011, 3, 1149–1173. [Google Scholar] [CrossRef]
  53. Vulnerability of Buildings to Flood Damage: Guidance on Building in Flood Prone Areas. Available online: http://www.ses.nsw.gov.au/content/documents/pdf/resources/Building_Guidelines.pdf (accessed on 4 July 2016).
  54. Kalmegh, S. Analysis of WEKA Data Mining Algorithm REPTree, Simple Cart and RandomTree for Classification of Indian News. Int. J. Innov. Sci. Eng. Technol. 2015, 2, 438–446. [Google Scholar]
  55. Loh, W.Y. Classification and regression trees. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
  56. Buja, A.; Lee, Y. Data mining criteria for tree-based regression and classification. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 27–36.
  57. Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
  58. Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ. 2003, 86, 554–565. [Google Scholar] [CrossRef]
  59. Bramer, M. Avoiding overfitting of decision trees. Princ. Data Min. 2007, 119–134. [Google Scholar]
  60. Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. In Encyclopedia of Database Systems; Springer US: New York, NY, USA, 2009; pp. 532–538. [Google Scholar]
  61. Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
  62. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  63. Elghazel, H.; Aussem, A. Unsupervised feature selection with ensemble learning. Mach. Learn. 2013, 98, 157–180. [Google Scholar] [CrossRef]
  64. Machová, K.; Barčák, F.; Bednár, P. A bagging method using decision trees in the role of base classifiers. Acta Polytech. Hungarica 2006, 3, 121–132. [Google Scholar]
  65. Kreibich, H.; Piroth, K.; Seifert, I.; Maiwald, H.; Kunert, U.; Schwarz, J.; Merz, B.; Thieken, A.H. Is flow velocity a significant parameter in flood damage modelling? Nat. Hazards Earth Syst. Sci. 2009, 9, 1679–1692. [Google Scholar] [CrossRef]
  66. Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
Water 08 00282 g001 1024
Figure 1. Map of Bundaberg Regional Council [45].
Figure 1. Map of Bundaberg Regional Council [45].
Water 08 00282 g001
Water 08 00282 g002 1024
Figure 2. Bundaberg ground elevation [46].
Figure 2. Bundaberg ground elevation [46].
Water 08 00282 g002
Water 08 00282 g003 1024
Figure 3. A part of the Burnett River catchment related to the area of the study [47].
Figure 3. A part of the Burnett River catchment related to the area of the study [47].
Water 08 00282 g003
Water 08 00282 g004 1024
Figure 4. Inundation map of 2013 flood [48].
Figure 4. Inundation map of 2013 flood [48].
Water 08 00282 g004
Water 08 00282 g005 1024
Figure 5. Map of Maranoa Regional Council [49].
Figure 5. Map of Maranoa Regional Council [49].
Water 08 00282 g005
Water 08 00282 g006 1024
Figure 6. Boundary of the 2012 historic flood event [50].
Figure 6. Boundary of the 2012 historic flood event [50].
Water 08 00282 g006
Water 08 00282 g007 1024
Figure 7. Scatter plot showing the relation between loss ratio and water depth (structural loss ratio does not cover the damages of mobile contents, and it is only limited to all building fabrics including stationary interiors).
Figure 7. Scatter plot showing the relation between loss ratio and water depth (structural loss ratio does not cover the damages of mobile contents, and it is only limited to all building fabrics including stationary interiors).
Water 08 00282 g007
Water 08 00282 g008 1024
Figure 8. Comparison of various pruned regression-trees, based on the mean absolute error (MAE) calculated by a 10-fold cross-validation technique.
Figure 8. Comparison of various pruned regression-trees, based on the mean absolute error (MAE) calculated by a 10-fold cross-validation technique.
Water 08 00282 g008
Water 08 00282 g009 1024
Figure 9. Regression tree with 19 leaves for estimating the structural loss ratios (WD: water depth, FS: floor space, PM: precaution measures, BV: building value, BQ: building quality).
Figure 9. Regression tree with 19 leaves for estimating the structural loss ratios (WD: water depth, FS: floor space, PM: precaution measures, BV: building value, BQ: building quality).
Water 08 00282 g009
Water 08 00282 g010 1024
Figure 10. Out-of-bag feature importance for bagging decision trees.
Figure 10. Out-of-bag feature importance for bagging decision trees.
Water 08 00282 g010
Water 08 00282 g011 1024
Figure 11. Comparison of the flood damage estimation models (FLFArs: Australian stage-damage function, RT: regression tree, BT: bagging decision trees). Bar graphs represent the converged average values of the results, calculated over 200 sets of data samples, and the error bars show the spread of the results.
Figure 11. Comparison of the flood damage estimation models (FLFArs: Australian stage-damage function, RT: regression tree, BT: bagging decision trees). Bar graphs represent the converged average values of the results, calculated over 200 sets of data samples, and the error bars show the spread of the results.
Water 08 00282 g011
Table
Table 1. Description of the 13 candidate predictors (C: continuous, O: ordinal, N: nominal).
Table 1. Description of the 13 candidate predictors (C: continuous, O: ordinal, N: nominal).
CategoriesPredictorsTypeRange
Flood impactWDWater depthCbetween 0 cm and 700 cm above ground
Vel.Flow velocityO1 = calm to 3 = high
Con.Water ContaminationO0 = no contamination to 2 = heavy contamination
EmergencyEMEmergency MeasuresO0 = no measure undertaken to 3 = many measures undertaken
Precaution, experiencePMPrecaution MeasuresO1 = no measure undertaken to 4 = many measures undertaken
Exp.Flood experienceO1 = few flood experience to 3 = recent flood experience
Building characteristicBQBuilding qualityO1 = very bad to 6 = very good
BVBuilding valueC1756 to 3594000 AUD
FSFloor space per personC13 to 870 m2
Socioeconomic statusSASpecial attention residentN0 = No, 1 = Yes
Own.Ownership statusN0 = rent, 1 = own
Inc.Monthly incomeO1 = $1–$599, 2 = $600–$1,999, 3 = greater than $2,000
LELow education residentsN0 = No, 1 = Yes
Table
Table 2. Pearson correlation of the 13 final candidate predictors, see Table 1, and loss ratio. Significant correlations (5% significance level) are marked bold.
Table 2. Pearson correlation of the 13 final candidate predictors, see Table 1, and loss ratio. Significant correlations (5% significance level) are marked bold.
Pearson Correlation Coefficient
-WDVel.Con.EMPMExp.BQBVFSSAOwn.Inc.LE
Loss Ratio0.620.230.19−0.05−0.16−0.03−0.07−0.14−0.150.04−0.03−0.040.02
Table
Table 3. Damage-influencing variables of regression tree with 19 leaves.
Table 3. Damage-influencing variables of regression tree with 19 leaves.
Candidate PredictorsNo. of Decision NodesCorrelation with Loss Ratio
Water depth9+
Floor space3−
Precaution measures2−
Building value3N.A.
Building quality1−

Share and Cite

MDPI and ACS Style

Hasanzadeh Nafari, R.; Ngo, T.; Mendis, P. An Assessment of the Effectiveness of Tree-Based Models for Multi-Variate Flood Damage Assessment in Australia. Water 2016, 8, 282. https://doi.org/10.3390/w8070282

AMA Style

Hasanzadeh Nafari R, Ngo T, Mendis P. An Assessment of the Effectiveness of Tree-Based Models for Multi-Variate Flood Damage Assessment in Australia. Water. 2016; 8(7):282. https://doi.org/10.3390/w8070282

Chicago/Turabian Style

Hasanzadeh Nafari, Roozbeh, Tuan Ngo, and Priyan Mendis. 2016. "An Assessment of the Effectiveness of Tree-Based Models for Multi-Variate Flood Damage Assessment in Australia" Water 8, no. 7: 282. https://doi.org/10.3390/w8070282

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop