Assessing the Uncertainty of Multiple Input Datasets in the Prediction of Water Resource Components
Abstract
:1. Introduction
2. Materials and Methods
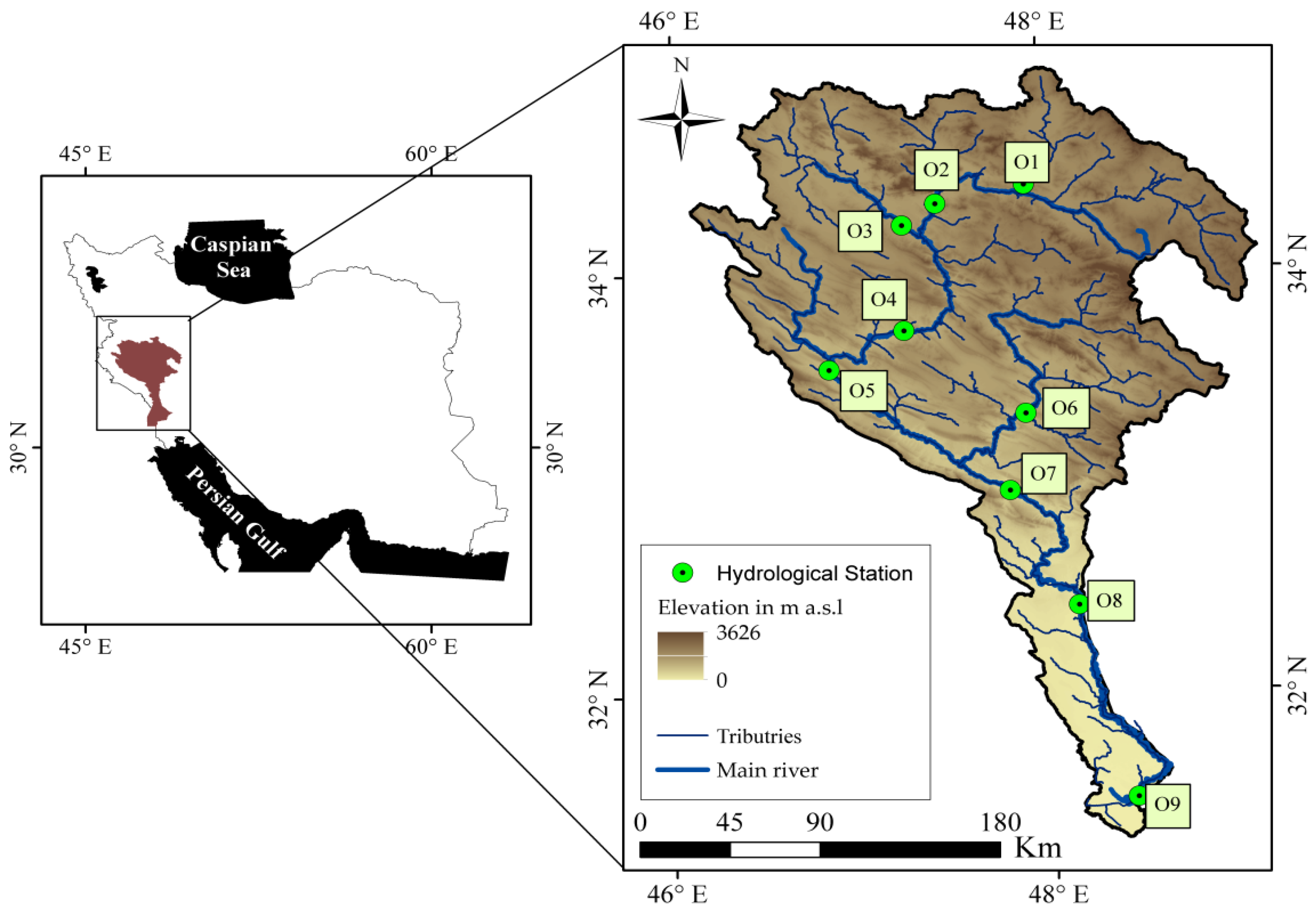
2.1. Study Area
2.2. Hydrological Simulation
2.3. Model Calibration and Parameterization
2.4. Data and Model Setup
2.5. Statistical Analysis: Multiple Comparison Test
2.6. Analytical Framework
- (1)
- Run each configuration before calibration and calculate the model efficiency criterion, bR2, [28] for the nine discharge outlets. Examining model performance based on default parameters (Table 3) is important in determining how the model should be calibrated and which parameters should be adjusted [17]. Harmel et al. [40] also defined “initial evaluation of model performance” as the first step to make the best judgment to guide model refinement. If important processes or key input information are neglected, then the model should not be calibrated, because wrong and meaningless parameters will be obtained. Furthermore, comparison of the pre- and post-calibrated parameter ranges (uncertainties) indicates the information content of the variable(s) used to calibrate the model. If we achieve a large reduction in the parameter uncertainties, then the variable(s) used to calibrate the model (as they appear in the objective function) have high information content.
- (2)
- Calibrate each configuration in the same way against the monthly observed river discharges. Then compare the efficiency criteria from after calibration with those from before.
- (3)
- Perform a multiple comparison significance test [39] on non-calibrated and calibrated configurations to identify configurations that are significantly different or similar to each other in terms of bR2 efficiency criteria and classify them into three classes (Class1 with high performance, Class2 with medium performance, Class3 with low performance). The selection of the number of classes and the classification were based on the null hypothesis and pair-wise comparison of the configurations. We started with C1L1 and made a pairwise comparison with the remaining seven models. Those that were significantly different from C1L1 were taken out of this class. Now, all other members of C1L1 except C1L1 were compared with each other pairwise. The set that was similar with C1L1, but was different from the others was also taken out of this class. We continued this until all members of a group were not significantly different in a pair-wise comparison. We repeated this process for the configurations that were not in the first class.
- (4)
- Calculate and compare the annual WY, BW, SW, and ET for each model using calibrated parameter ranges obtained in the 480 simulations at the sub-basin level. The components were then aggregated to the entire watershed level using the weighted area average method.
- (5)
- Calculate and quantify the uncertainties of the water resource components WY, BW, SW, and ET resulting from the different configurations using the coefficient of variation (%CV).
3. Results and Discussion
3.1. Model Performance and Parameters
3.2. Estimation of Water Resource Variables
3.3. Uncertainty in Water Resource Variables
4. Conclusions
- (i)
- Multiple model configurations built for a region with datasets coming from different sources produce significantly different parameter sets after calibration, albeit with similar calibration results.
- (ii)
- Subsequently, water resource components are significantly different for different configurations, resulting in large model output uncertainties.
- (iii)
- Discharge prediction seems to be less sensitive to different land uses, which is the same conclusion made by Yen et al. [11]. Additionally, the present study pointed to the impact of both land use and climate data on different components of water resources, such as SW and ET.
- (iv)
- The uncertainty is larger for SW and ET compared to WY. Decreasing uncertainty for these components relies on observed records data.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kalantari, Z.; Lyon, S.W.; Jansson, P.E.; Stolte, J.; French, H.K.; Folkeson, L.; Sassner, M. Modeller subjectivity and calibration impacts on hydrological model applications: An event-based comparison for a road-adjacent catchment in South-East Norway. Sci. Total Environ. 2015, 502, 315–329. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, R.; Tachikawa, Y.; Takara, K. Input data resolution analysis for distributed hydrological modeling. J. Hydrol. 2006, 319, 36–50. [Google Scholar] [CrossRef]
- Montanari, A.; Di Baldassarre, G. Data errors and hydrological modelling: The role of model structure to propagate observation uncertainty. Adv. Water Resour. 2013, 51, 498–504. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [Green Version]
- Martina, M.L.V.; Todini, E. Watershed hydrological modeling: Toward physically meaningful processes representation. Water Sci. Technol. Libr. 2008, 63, 229–241. [Google Scholar]
- Confesor, R.B.; Whittaker, G.W. Automatic calibration of hydrologic models with multi-objective evolutionary algorithm and Pareto optimization. J. Am. Water Resour. Assoc. 2007, 43, 981–989. [Google Scholar] [CrossRef]
- Kim, S.M.; Benham, B.L.; Brannan, K.M.; Zeckoski, R.W.; Doherty, J. Comparison of hydrologic calibration of HSPF using automatic and manual methods. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.Y.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Faramarzi, M.; Srinivasan, R.; Iravani, M.; Bladon, K.D.; Abbaspour, K.C.; Zehnder, A.J.B.; Goss, G.G. Setting up a hydrological model of Alberta: Data discrimination analyses prior to calibration. Environ. Model. Softw. 2015, 74, 48–65. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Yen, H.; Sharifi, A.; Kalin, L.; Mirhosseini, G.; Arnold, J.G. Assessment of model predictions and parameter transferability by alternative land use data on watershed modeling. J. Hydrol. 2015, 527, 458–470. [Google Scholar] [CrossRef]
- Cotter, A.S.; Chaubey, I.; Costello, T.A.; Soerens, T.S.; Nelson, M.A. Water quality model output uncertainty as affected by spatial resolution of input data. J. Am. Water Resour. Assoc. 2003, 39, 977–986. [Google Scholar] [CrossRef]
- Yen, H.; Su, Y.W.; Wolfe, J.E.; Chen, S.T.; Hsu, Y.C.; Tseng, W.H.; Brady, D.M.; Jeong, J.; Arnold, J.G. Assessment of input uncertainty by seasonally categorized latent variables using SWAT. J. Hydrol. 2015, 531, 685–695. [Google Scholar] [CrossRef]
- Biemans, H.; Hutjes, R.W.A.; Kabat, P.; Strengers, B.J.; Gerten, D.; Rost, S. Effects of precipitation uncertainty on discharge calculations for main river basins. J. Hydrometeorol. JHM 2009, 10, 1011–1025. [Google Scholar] [CrossRef]
- Zhang, P.P.; Liu, R.M.; Bao, Y.M.; Wang, J.W.; Yu, W.W.; Shen, Z.Y. Uncertainty of SWAT model at different DEM resolutions in a large mountainous watershed. Water Res. 2014, 53, 132–144. [Google Scholar] [CrossRef] [PubMed]
- Rouholahnejad, E.; Abbaspour, K.C.; Srinivasan, R.; Bacu, V.; Lehmann, A. Water resources of the Black Sea Basin at high spatial and temporal resolution. Water Resour. Res. 2014, 50, 5866–5885. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Klove, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Monteiro, J.A.F.; Strauch, M.; Srinivasan, R.; Abbaspour, K.; Gücker, B. Accuracy of grid precipitation data for Brazil: Application in river discharge modelling of the Tocantins catchment. Hydrol. Process. 2015, 30, 1419–1430. [Google Scholar] [CrossRef]
- Strauch, M.; Bernhofer, C.; Koide, S.; Volk, M.; Lorz, C.; Makeschin, F. Using precipitation data ensemble for uncertainty analysis in SWAT streamflow simulation. J. Hydrol. 2012, 414, 413–424. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Espinoza, J.C.V.; Ronchail, J.; Rotunno, O.C. Assessment of different precipitation datasets and their impacts on the water balance of the Negro River basin. J. Hydrol. 2011, 404, 304–322. [Google Scholar] [CrossRef]
- Oweis, T.; Siadat, H.; Abbasi, F. Improving On-Farm Agricultural Water Productivity in the Karkheh River Basin (KRB); CPWF Project Report-Project Number 08: CGIAR Challenge Program on Water and Food; Department for International Development: Chatham, UK, 2009.
- Ahmad, M.U.D.; Giordano, M. The Karkheh river basin: The food basket of Iran under pressure. Water Int. 2010, 35, 522–544. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. CGIAR-CSI SRTM 90 m Database. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 15 January 2008).
- Masih, I. Understanding Hydrological Variability for Improved Water Management in the Semi-Arid Karkheh Basin, Iran; CRC Press/Balkema: Leiden, The Netherlands, 2011. [Google Scholar]
- Saghafian, B.; Davtalab, R. Mapping snow characteristics based on snow observation probability. Int. J. Climatol. 2007, 27, 1277–1286. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool. Theoretical Documentation: Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2005. [Google Scholar]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-ailpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Monteiro, J.A.F.; Kamali, B.; Srinivasan, R.; Abbaspour, K.C.; Gücker, B. Modelling the effect of riparian vegetation restoration on sediment transport in a human-impacted Brazilian catchment. Ecohydrology 2016, 9, 1289–1303. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the West African sub-continent using the SWAT hydrologic model. J. Hydrol. 2008, 352, 30–49. [Google Scholar] [CrossRef]
- Ministry of Energy of Iran. An Overview of National Water Planning of Iran; Ministry of Energy of Iran: Tehran, Iran, 1998. (In Persian) [Google Scholar]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIO5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- USGS. Global Land Cover Characterization; United State Geological Survey: Washington, DC, USA, 1997.
- Iran Water and Power Resources Development Company (IWPCO). Systematic Planning of Karkheh Watershed; Land Use Studies; Iranian Ministry of Energy: Tehran, Iran, 2009. (In Persian) [Google Scholar]
- Iran Water and Power Resources Development Company (IWPCO). Systematic Studies of Karkheh River Basin; Iranian Ministry of Energy: Tehran, Iran, 2010. (In Persian) [Google Scholar]
- Vaghefi, S.A.; Mousavi, S.J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Analyses of the impact of climate change on water resources components, drought and wheat yield in semiarid regions: Karkheh river basin in Iran. Hydrol. Process. 2014, 28, 2018–2032. [Google Scholar] [CrossRef]
- Kouchi, D.H.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of calibrated parameters and water resource estimates on different objective functions and optimization algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Zar, J.H. Statistical procedures for biological-research-a citation classic commentary on biostatistical analysis. Agric. Biol. Environ. Sci. 1989, 6, 1–20. [Google Scholar]
- Harmel, R.D.; Smith, P.K.; Migliaccio, K.W.; Chaubey, I.; Douglas-Mankin, K.R.; Benham, B.; Shukla, S.; Munoz-Carpena, R.; Robson, B.J. Evaluating, interpreting, and communicating performance of hydrologic/water quality models considering intended use: A review and recommendations. Environ. Model. Softw. 2014, 57, 40–51. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Vu, M.T.; Raghavan, S.V.; Liong, S.Y. SWAT use of gridded observations for simulating runoff—A Vietnam river basin study. Hydrol. Earth Syst. Sci. 2012, 16, 2801–2811. [Google Scholar] [CrossRef] [Green Version]
- Thom, V.T.; Khoi, D.N.; Linh, D.Q. Using gridded rainfall products in simulating streamflow in a tropical catchment—A case study of the Srepok River Catchment, Vietnam. J. Hydrol. Hydromech. 2017, 65, 18–25. [Google Scholar] [CrossRef]
- Kamali, B.; Houshmand Kouchi, D.; Yang, H.; Abbaspour, K.C. Multilevel drought hazard assessment under climate change scenarios in semi-srid regions—A case study of the Karkheh River Basin in Iran. Water 2017, 9, 241. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Abbaspour, K.C. Calibration of hydrologic models: When is a model calibrated? In Proceedings of the Modsim 2005: International Congress on Modelling and Simulation: Advances and Applications for Management and Decision Making, Melbourne, Australia, 12–15 December 2005; pp. 2449–2455. [Google Scholar]
- Bardossy, A. Calibration of hydrological model parameters for ungauged catchments. Hydrol. Earth Syst. Sci. 2007, 11, 703–710. [Google Scholar] [CrossRef]
- Chapiot, V. Impact of spatial input data resolution on hydrological and erosion modeling: Recommendations from a global assessment. Phys. Chem. Earth 2014, 67–69, 23–35. [Google Scholar] [CrossRef]







| Data | Sources | Description | |
|---|---|---|---|
| Daily climate data (1977–2004) | C1 | Iranian Ministry of Energy database; local observation data based on ground level measurement [32] | Variables used are daily precipitation, maximum and minimum temperature |
| C2 | Iranian Meteorological Organization database; local observation data based on ground level measurement (http://www.irimo.ir/eng/index.php) | ||
| C3 | Modeling grid cell centroids data obtained from GFDL-ESM2M (Geophysical Fluid Dynamics Laboratory of national oceanic and atmospheric administration—Earth System Model) General Circulation Model (GCM) climate model with 0.5° × 0.5° resolution—Global level [33] | ||
| C4 | Merged from selected stations in C1 and C2 based on their performance in discharge simulation—Details illustrated in Section 3.1 and Figure 2 | ||
| Landuse | L1 | United States Geological Survey (USGS) Global Land Cover Characterization (GLCC) database [34] with 90m resolution for year 1997 | Classification according to Figure 2e and Table 2 |
| L2 | Created from Indian Remote Sensing-Linear P6 (IRS-P6) satellite with Linear Imaging and Self Scanning (LISS-IV) sensor, IRS-P5 satellite with panchromatic cameras, Enhanced Thematic Mapper+2001 (ETM+2001) Landsat, and 3300 field sampling points [35] with 90m resolution for year 2009_ENREF_34 | Classification according to Figure 2f and Table 2 | |
| Land Use Categories | L1 (%) | L2 (%) |
|---|---|---|
| All forest types | 25.8 | 0.2 |
| Grassland | 18.3 | 20.5 |
| Crop land | 19.2 | 22.4 |
| Irrigated crop land | 23.1 | 23.5 |
| Barren and sparsely vegetated | 0.0 | 0.5 |
| Urban residential medium density | 8.8 | 0.1 |
| Shrub land | 1.4 | 32.7 |
| Savanna | 2.0 | 0.1 |
| Water bodies | 1.4 | 0.0 |
| Parameter | Definition | Initial Values |
|---|---|---|
| r_CN2.mgt | SCS (Soil Conservation Service) runoff curve number for moisture condition II | Spatially variable |
| r_SOL_AWC.sol | Soil available water storage capacity (mm H2O/mm soil) | Spatially variable |
| v_ESCO.hru | Soil evaporation compensation factor | 0.95 |
| r_OV_N.hru | Manning’s n value for overland flow | Spatially variable |
| v_ALPHA_BF.gw | Base flow alpha factor (days) | 0.048 |
| v_GW_DELAY.gw | Groundwater delay time (days) | 31 |
| v_GW_REVAP.gw | Capillary flow from groundwater into root zone | 0.02 |
| r_REVAPMN.gw | Threshold depth of water in the shallow aquifer (mm) | 750 |
| v_GWQMN.gw | Threshold depth of water in the shallow aquifer required for return flow to occur (mm) | 1000 |
| Configuration | Calibration Period 1988–2004 | Validation Period 1980–1987 | ||||
|---|---|---|---|---|---|---|
| NS | p-factor | r-factor | NS | p-factor | r-factor | |
| C1L1 (Class1) | 0.60 | 0.68 | 1.19 | 0.61 | 0.59 | 1.32 |
| C2L1 (Class2) | 0.51 | 0.54 | 1.23 | 0.50 | 0.52 | 1.39 |
| C3L1 (Class3) | −3.5 | 0.41 | 1.77 | −0.5 | 0.25 | 1.05 |
| C4L1 (Class2) | 0.49 | 0.64 | 1.12 | 0.51 | 0.58 | 1.36 |
| C1L2 (Class1) | 0.62 | 0.71 | 1.37 | 0.60 | 0.67 | 1.50 |
| C2L2 (Class2) | 0.46 | 0.54 | 1.47 | 0.48 | 0.50 | 1.27 |
| C3L2 (Class3) | −1.69 | 0.37 | 0.60 | −1.75 | 0.38 | 1.32 |
| C4L2 (Class2) | 0.51 | 0.65 | 1.15 | 0.53 | 0.60 | 1.27 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamali, B.; Abbaspour, K.C.; Yang, H. Assessing the Uncertainty of Multiple Input Datasets in the Prediction of Water Resource Components. Water 2017, 9, 709. https://doi.org/10.3390/w9090709
Kamali B, Abbaspour KC, Yang H. Assessing the Uncertainty of Multiple Input Datasets in the Prediction of Water Resource Components. Water. 2017; 9(9):709. https://doi.org/10.3390/w9090709
Chicago/Turabian StyleKamali, Bahareh, Karim C. Abbaspour, and Hong Yang. 2017. "Assessing the Uncertainty of Multiple Input Datasets in the Prediction of Water Resource Components" Water 9, no. 9: 709. https://doi.org/10.3390/w9090709
APA StyleKamali, B., Abbaspour, K. C., & Yang, H. (2017). Assessing the Uncertainty of Multiple Input Datasets in the Prediction of Water Resource Components. Water, 9(9), 709. https://doi.org/10.3390/w9090709





