Sustainable Restoration of Degraded Farm Land by the Sheet-Pipe System
Abstract
:1. Introduction
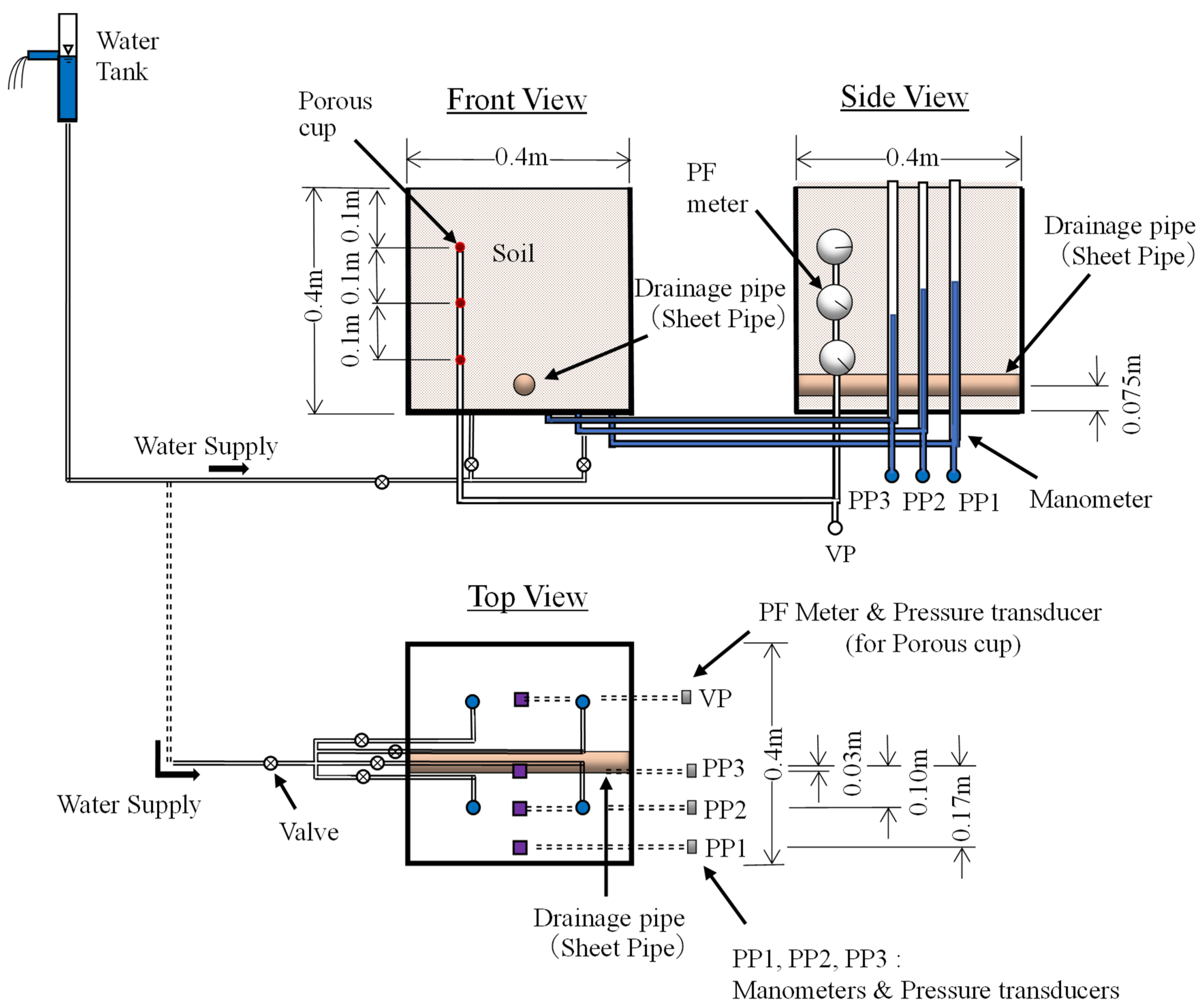
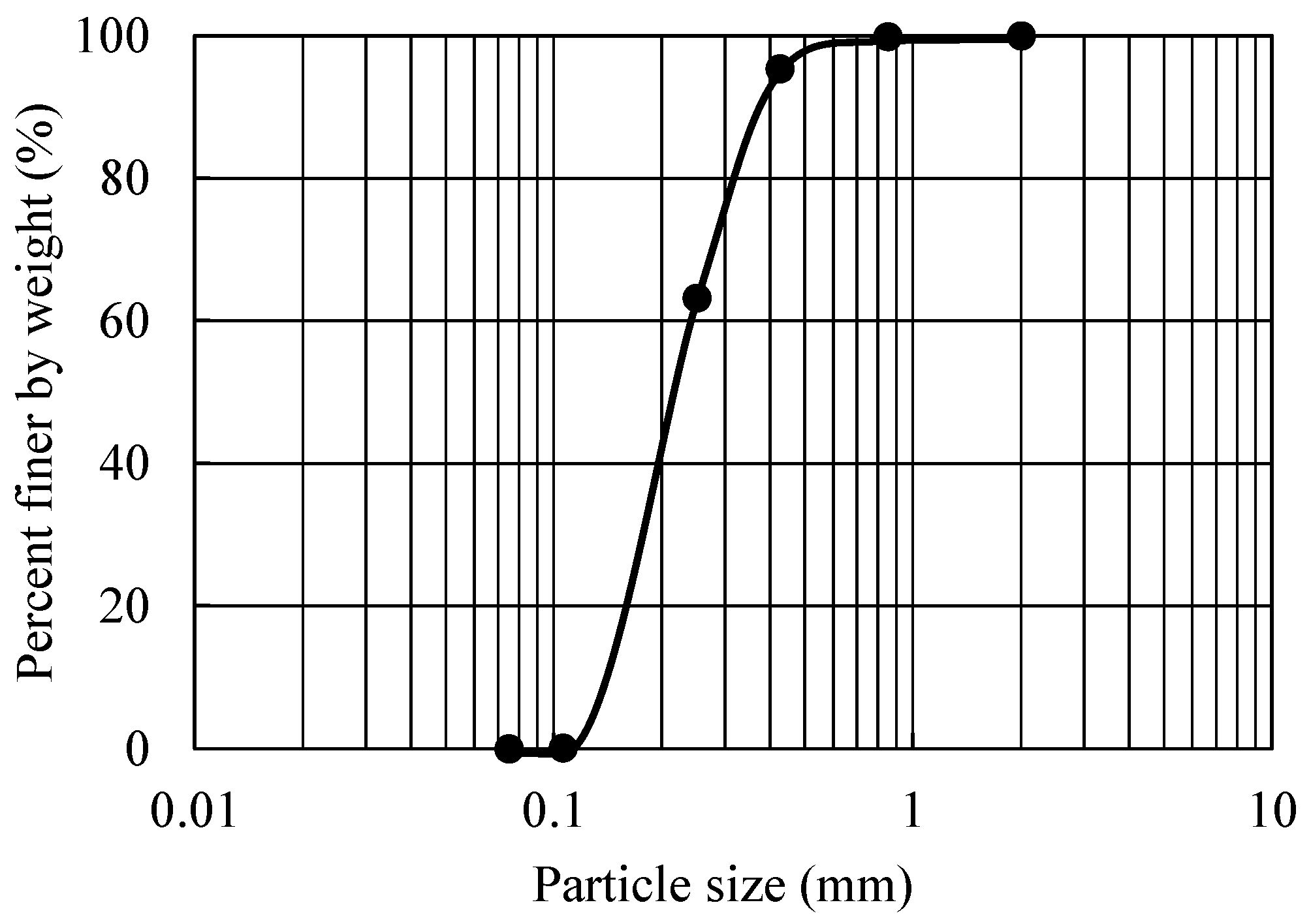
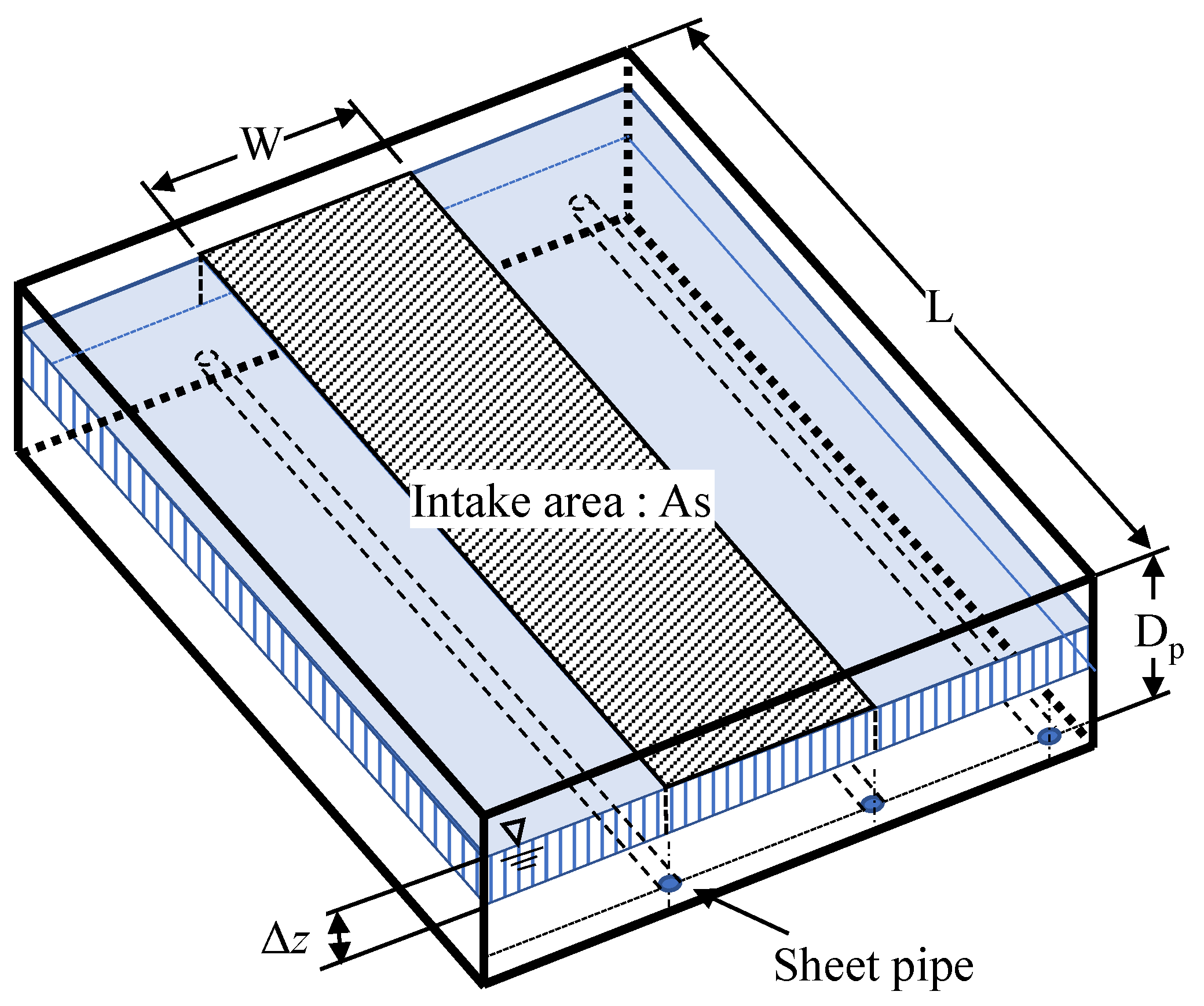
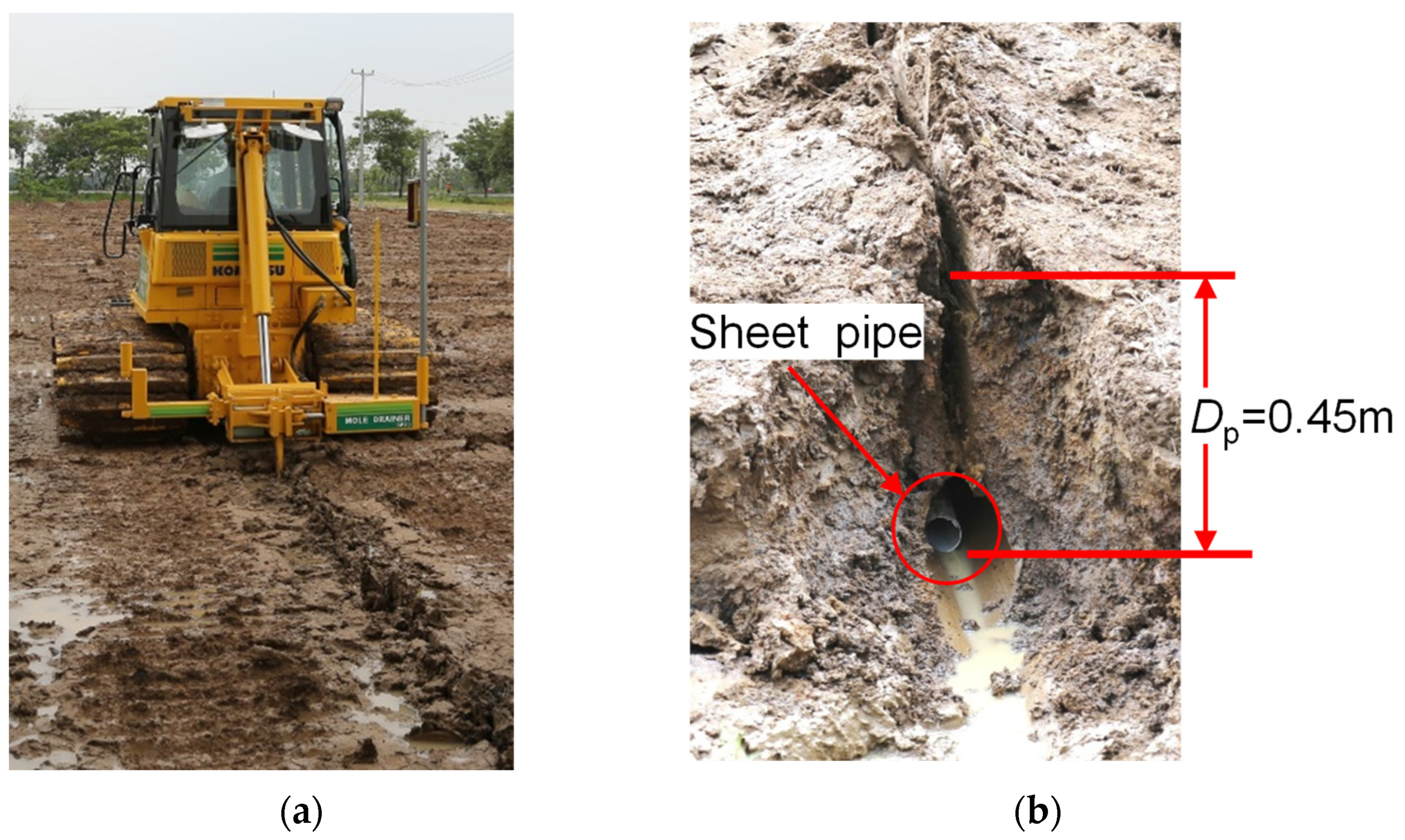
2. Materials and Methods
3. Results and Discussions
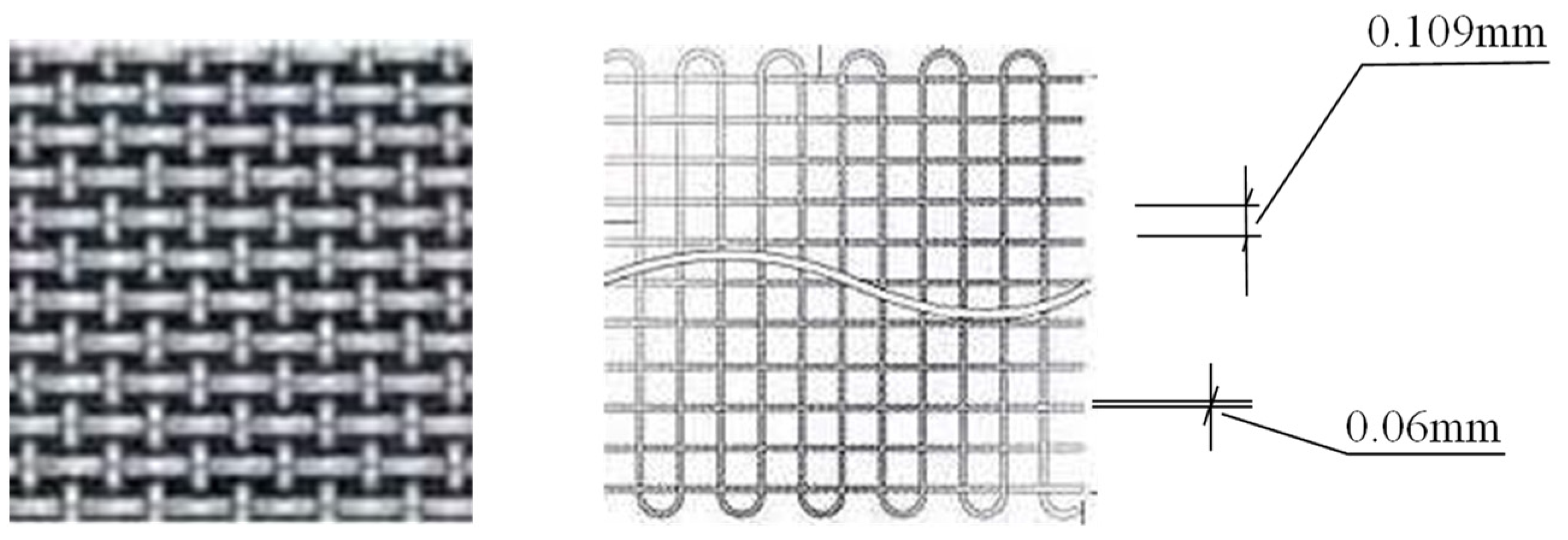
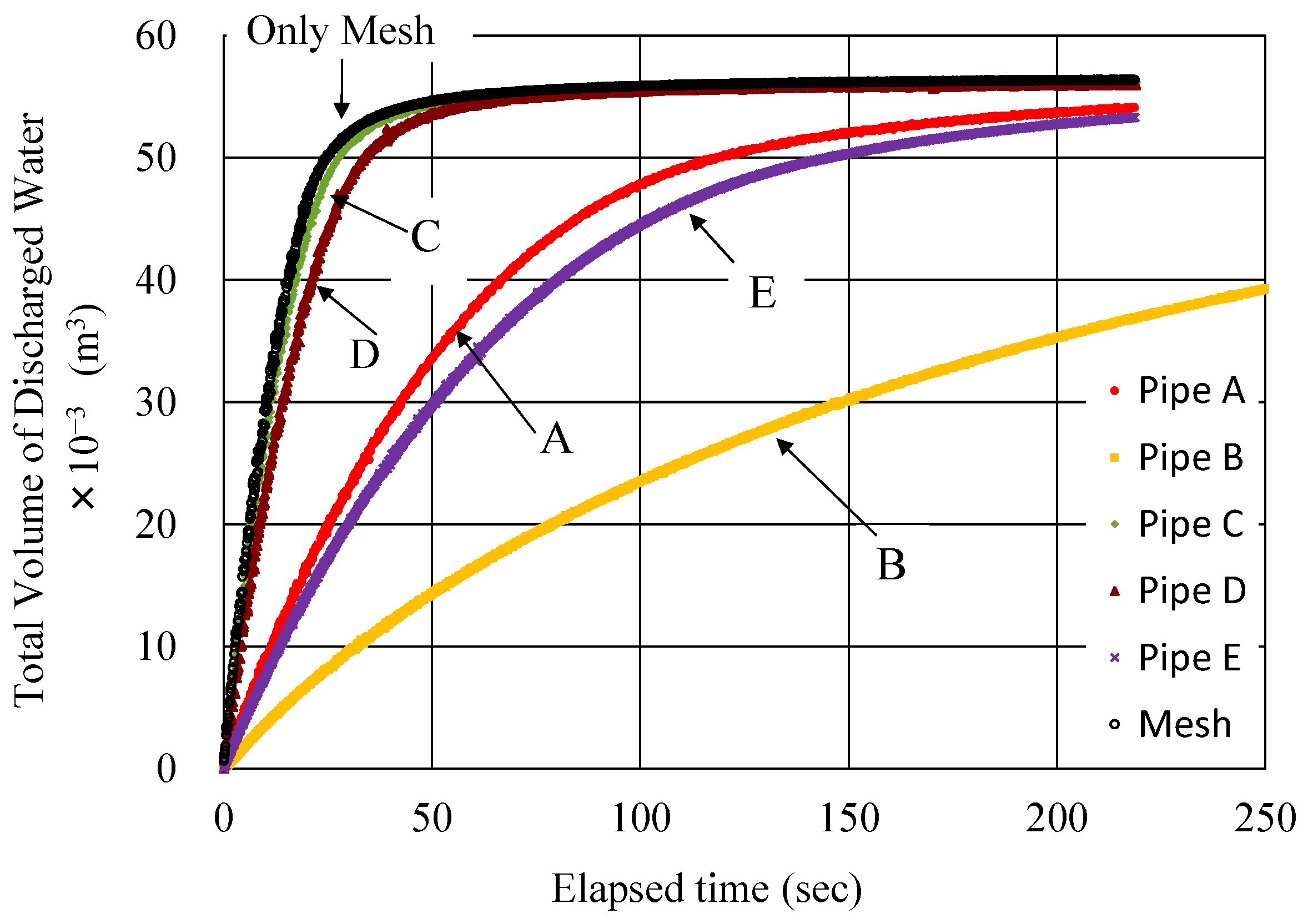
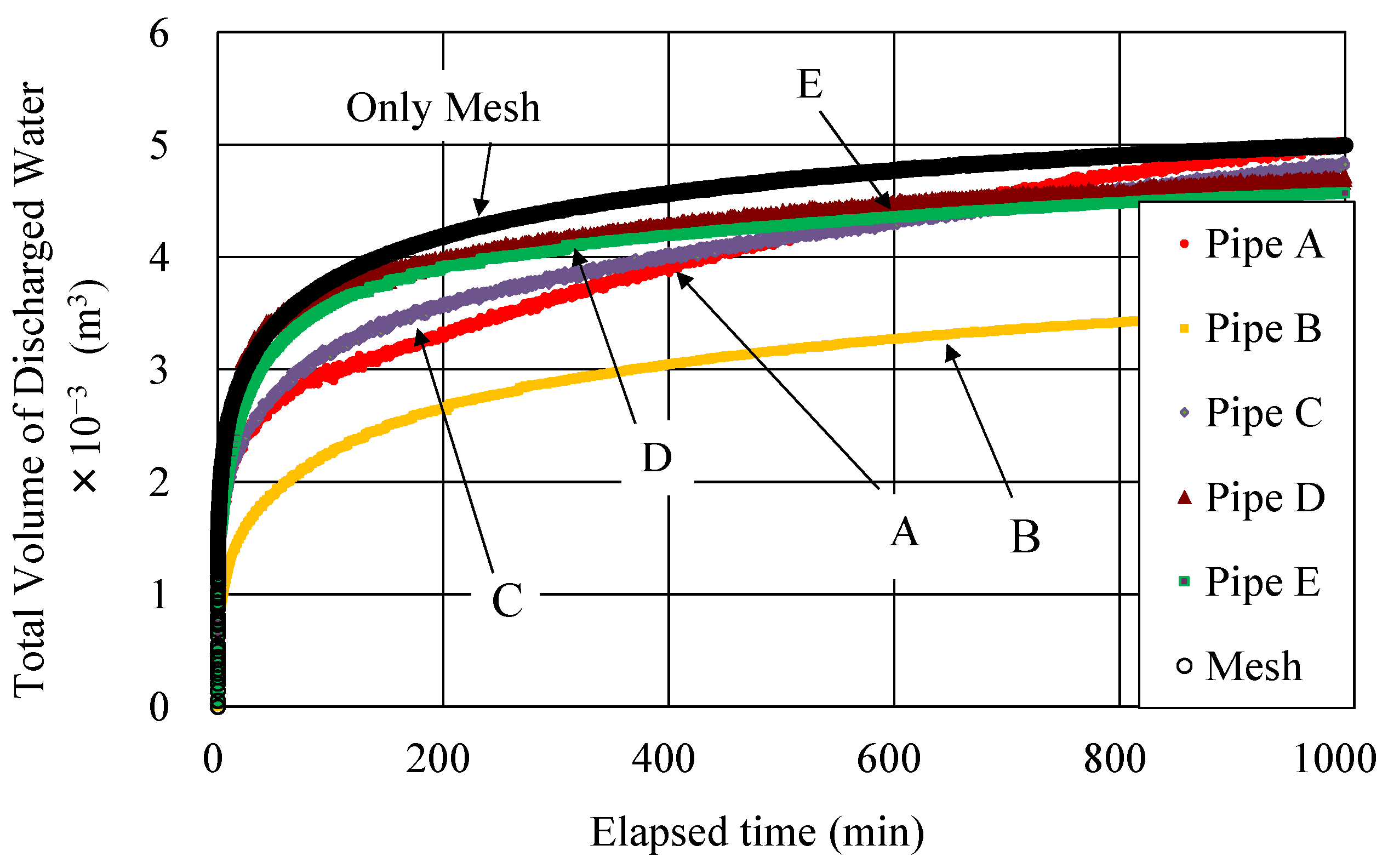
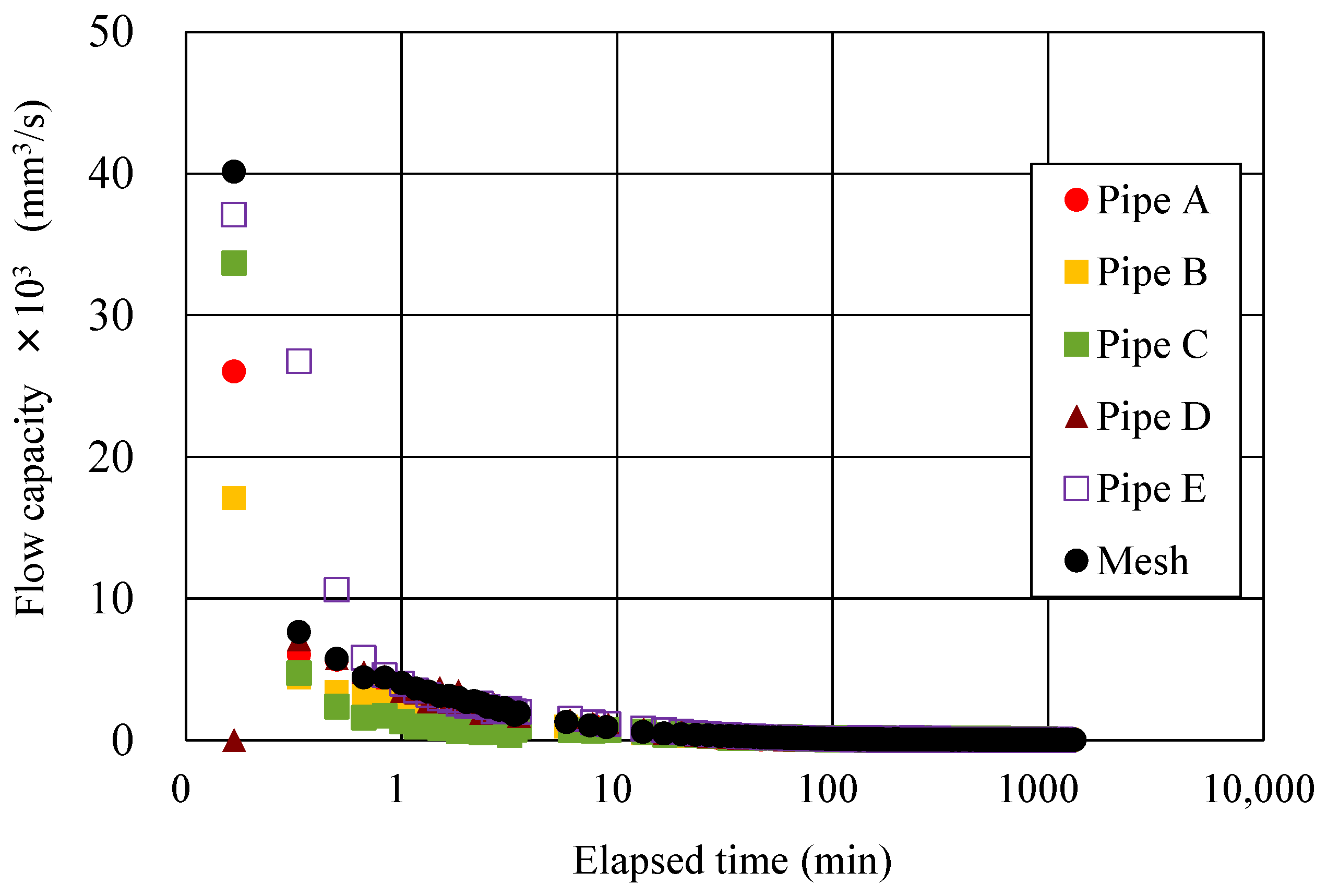
3.1. Flow Capacity of the Sheet Pipe
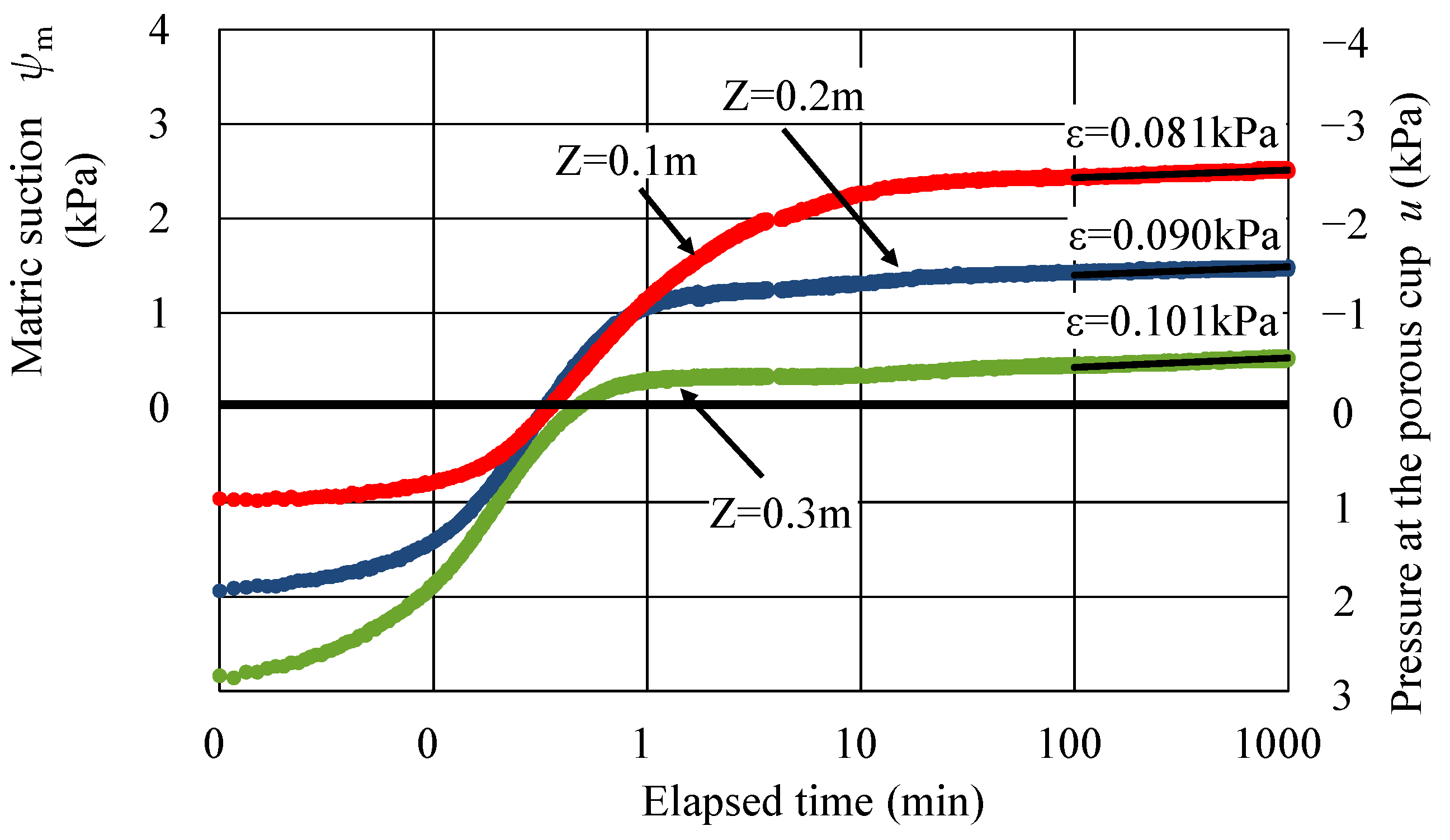
3.2. Effects of Drainage by the Sheet Pipe on the Water Head, Matric Suction, and Storage Coefficient
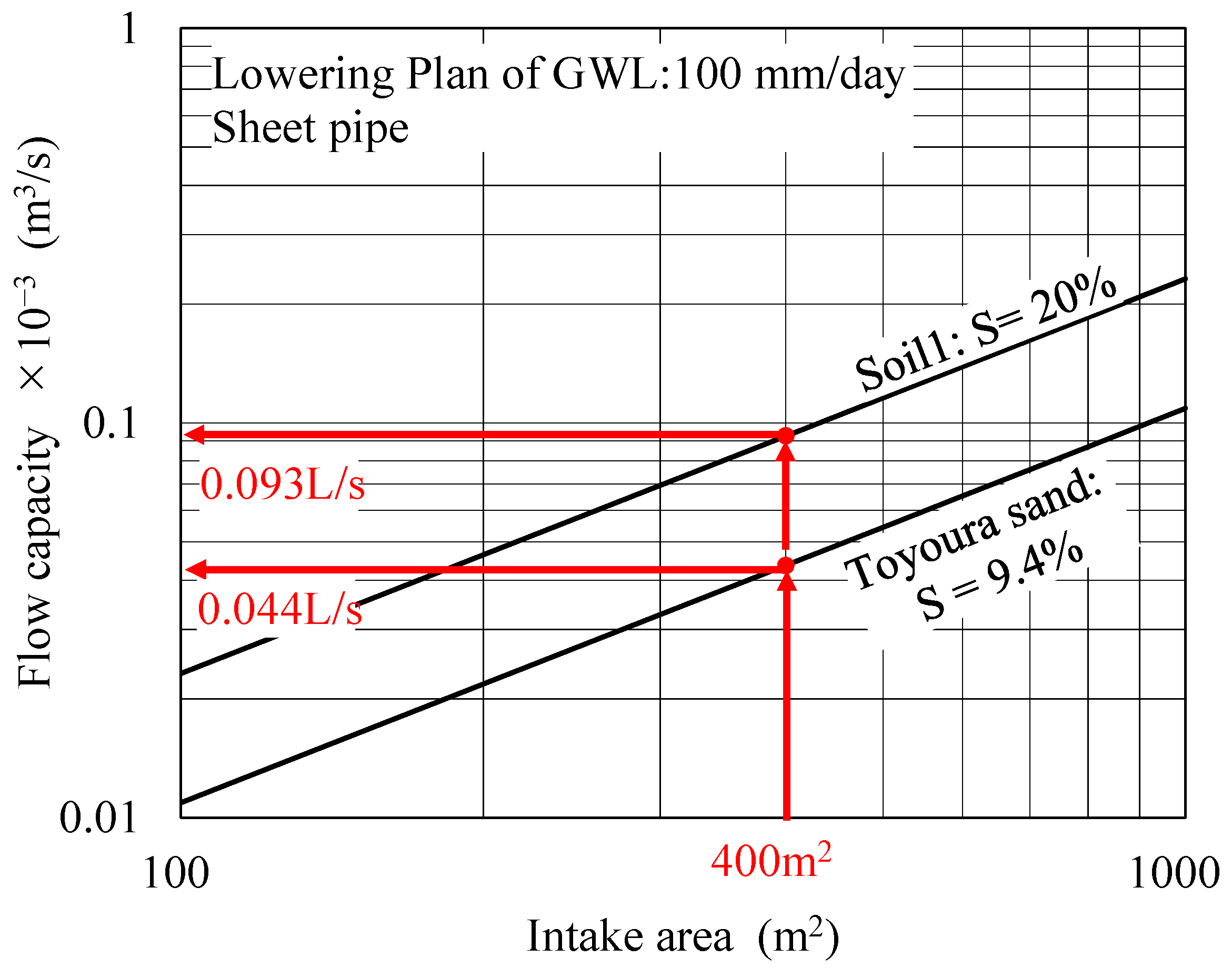
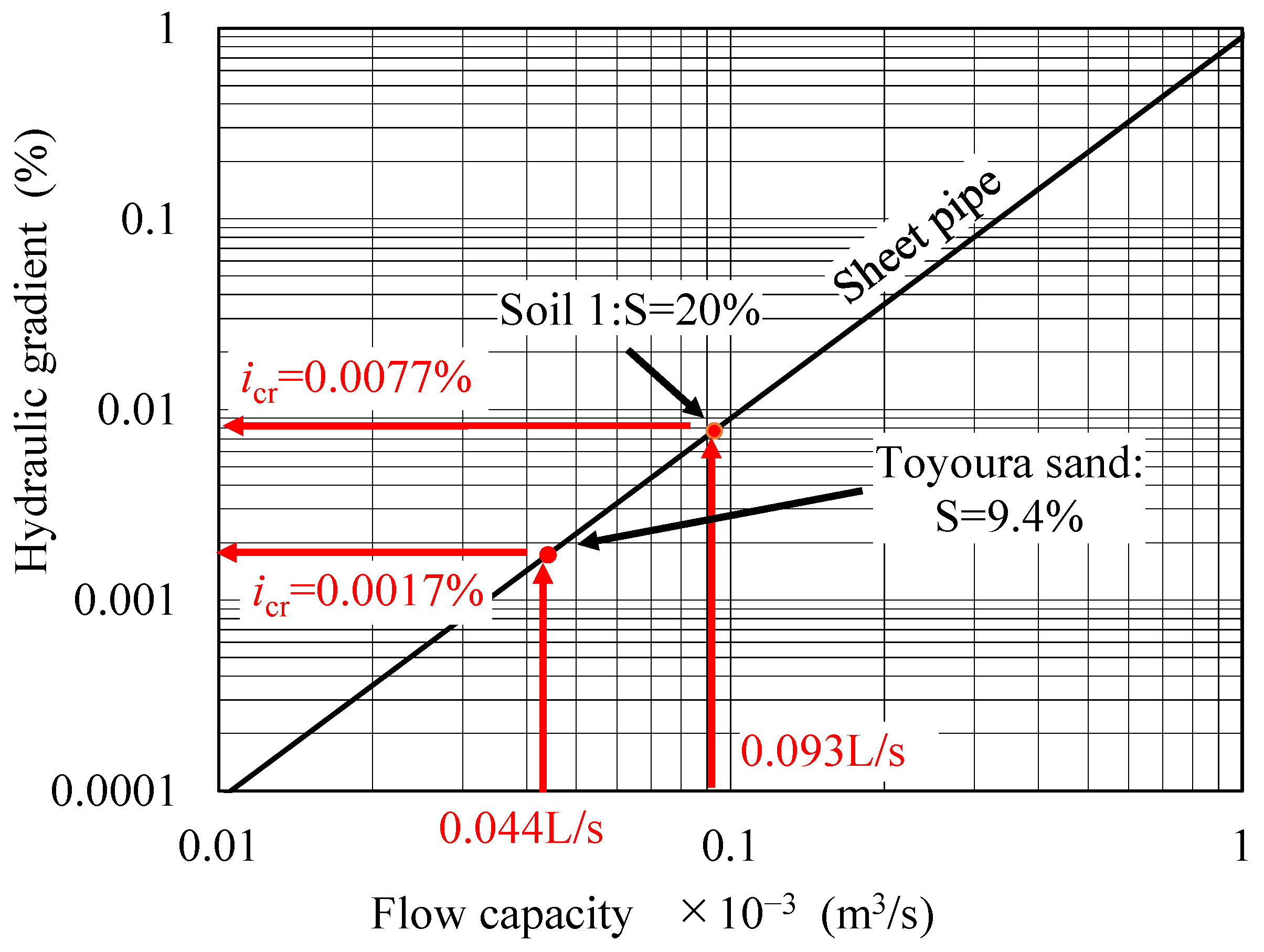
3.3. Drainage Capacity by the Sheet Pipe
3.3.1. Maximum Drainage Capacity through the Horizontally Installed Sheet Pipe
3.3.2. Limitations and Constraints
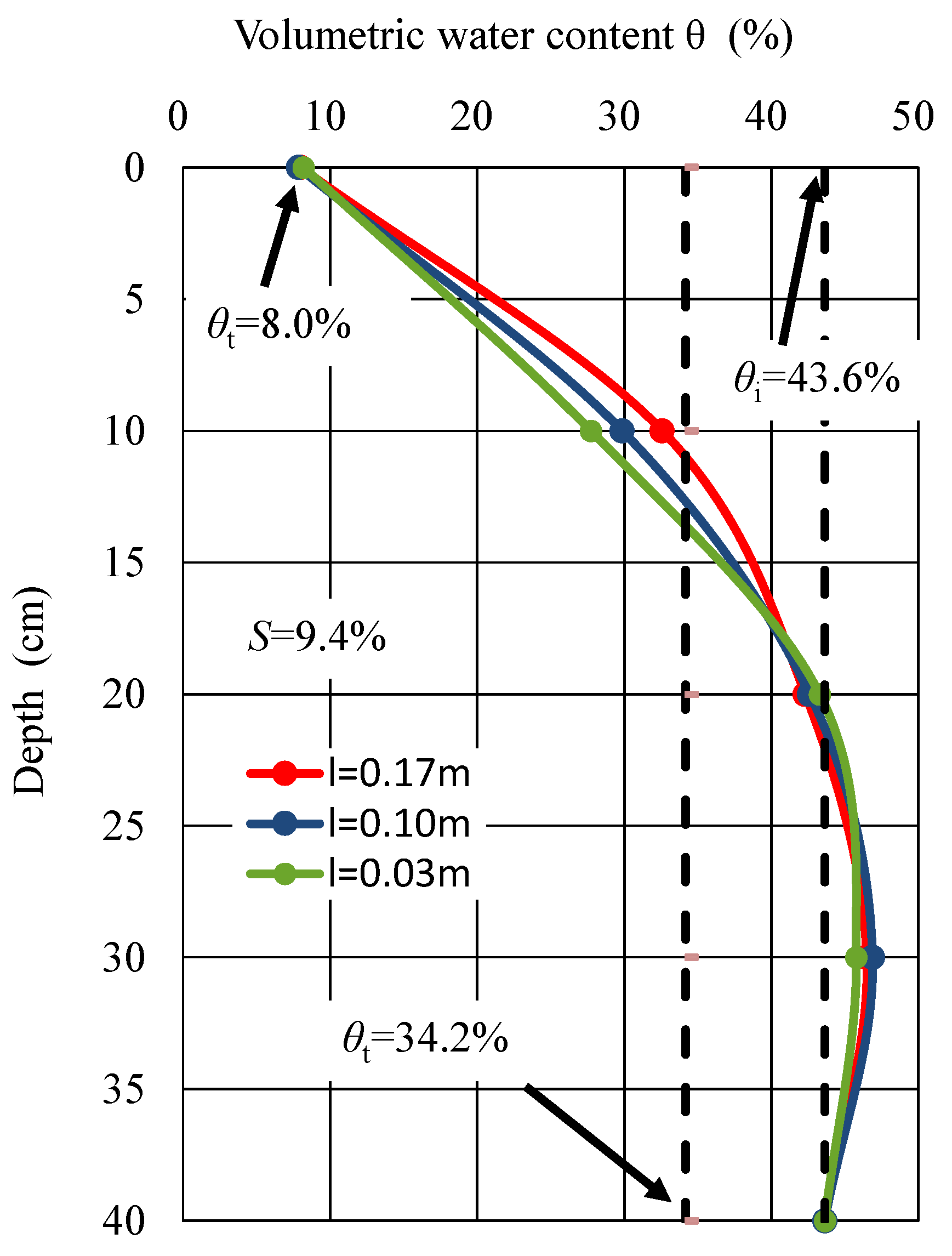
3.4. A Case Study on the Drainage by Using the Sheet-Pipe System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vineis, P.; Chan, Q.; Khan, A. Climate change impacts on water salinity and health. J. Epidemiol. Glob. Health 2011, 1, 5–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ullah, A.; Bano, A.; Khan, N. Climate change and salinity effects on crops and chemical communication between plants and plant growth-promoting microorganisms under stress. Front. Sustain. Food Syst. 2021, 5, 1–16. [Google Scholar] [CrossRef]
- Kang, N.; Kim, S.; Kim, Y.; Noh, H.; Hong, S.J.; Kim, H.S. Urban drainage system improvement for climate change adaptation. Water 2016, 8, 268. [Google Scholar] [CrossRef] [Green Version]
- Fukuda, T.; Shinogi, Y. Drainage mechanism of sheet pipe underdrainage and desalination effect. Jpn. Soc. Irrig. Drain. Rural. Eng. 2015, 83, 326–327. (In Japanese) [Google Scholar]
- Hillel, D. 8 Groundwater Drainage. In Soil and Water; Academic Press: New York, NY, USA, 1971; pp. 167–181. [Google Scholar]
- Setiawan, B.I.; Arif, C.; Saptomo, S.K.; Matsuda, H.; Tamura, K.; Inoue, Y. Water Flow in Soils Installed with Sheet-Pipe Model Drains; PAWEES (International Society of Paddy and Water Environment Engineering): Nara, Japan, 2018; pp. 743–748. [Google Scholar]
- Sugiyama, M.; Tsuda, Y. Construction method on the cross culvert by sheet pipe and the condition after construction. JSIDRE J. 1990, 58, 159–167. (In Japanese) [Google Scholar]
- Soe, Y.M.; Shinogi, Y.; Taniguchi, T. Impacts of perforated sheet pipe installation on some paddy soil properties. Paddy Water Environ. 2019, 17, 151–164. [Google Scholar] [CrossRef]
- Sasmita, P.; Agustiani, N.; Margaret, S.; Yusup, A.M.; Tamura, K. The effect of sheet-pipe technology application on soil properties, rice growth, yield and prospect to increase planting index. In Proceedings of the 1st International Conference on Sustainable Tropical Land Management, Virtual Conference, 16–18 September 2020; Volume 648, pp. 1–9. [Google Scholar]
- Arif, C.; Setiawan, B.I.; Saptomo, S.K.; Matsuda, H.; Tamura, K.; Inoue, Y.; Hikmah, Z.M.; Nugroho, N.; Agustiani, N. Water use efficiency and productivity in paddy field under subsurface drainage technology with sheet-pipe system. In Proceedings of the 3rd World Irrigation Forum (WIF3), Bali, Indonesia, 1–7 September 2019; pp. 1–10. [Google Scholar]
- Setiawan, B.I.; Saptomo, S.K.; Arif, C.; Matsuda, H.; Tamura, K.; Inoue, Y. Automatic subsurface irrigation and drainage using sheet-pipe typed model drain. In Proceedings of the 3rd World Irrigation Forum (WIF3), Bali, Indonesia, 1–7 September 2019; pp. 1–11. [Google Scholar]
- Arif, C.; Setiawan, B.I.; Saptomo, S.K.; Matsuda, H.; Tamura, K.; Inoue, Y.; Hikmah, Z.M.; Nugroho, N.; Agustiani, N.; Suwarno, W.B. Performances of sheet-pipe typed subsurface drainage on land and water productivity of paddy fields in Indonesia. Water 2021, 13, 48. [Google Scholar] [CrossRef]
- Agriculture Victoria. Available online: https://agriculture.vic.gov.au/livestock-and-animals/dairy/managing-wet-soils/types-of-subsurface-drainage-systems#h2-1 (accessed on 18 September 2021).
- Matsuda, H.; Tamura, K.; Setiawan, B.I.; Saptomo, S.K. Effects of drainage by the sheet pipe on the suction and volume water content of subsurface layer. In Proceedings of the XVII European Conference on Soil Mechanics and Geotechnical Engineering, Reykjavik, Iceland, 1–6 September 2019; pp. 1–9. [Google Scholar]
- Hillel, D. Introduction to Environmental Soil Physics; Elsevier Academic Press: Cambridge, MA, USA, 2004; p. 327. [Google Scholar]
- Verdugo, R.; Ishihara, K. The steady state of sandy soils. Soils Found. 1996, 36, 81–91. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Jin, Y.; Ye, B. A try to give a unified description of Toyoura sand. Soils Found. 2010, 50, 679–693. [Google Scholar] [CrossRef] [Green Version]
- Koseki, J.; Yoshida, T.; Sato, T. Liquefaction properties of Toyoura sand in cyclic tortional shear tests under low confining stress. Soils Found. 2005, 45, 103–113. [Google Scholar] [CrossRef] [Green Version]
- Kato, S.; Ishihara, K.; Towhata, I. Undrained shear characteristics of saturated sand under anisotropic consolidation. Soils Found. 2001, 41, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Hillel, D. Environmental Soil Physics; Academic Press: Cambridge, MA, USA, 1998; p. 485. [Google Scholar]
- Zhang, C.; Lu, N. Unitary definition of matric suction. J. Geotech. Geoenviron. Eng. ASCE 2019, 145, 1. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, K.; Feng, W.Q.; Borana, L.; Yin, J.H. Influence of matric suction on nonlinear time-dependent compression behavior of a granular fill material. Acta Geotech. 2020, 15, 615–633. [Google Scholar] [CrossRef]
- Mogami, T. Seepage, 3rd ed.; Kajima Institute Publishing Co., Ltd.: Tokyo, Japan, 1979; p. 19. (In Japanese) [Google Scholar]
- Kikuoka, T. Handbook on Irrigation, Drainage and Reclamation Engineering; Maruzen Publishing: Tokyo, Japan, 1979; p. 790. (In Japanese) [Google Scholar]
- Suetsugu, Y.; Yamanaka, H. Technical Reports of Shin-Etsu Sheet Pipe; Shin-Etsu Polymer Co. Ltd.: Saitama, Japan, 2003. (In Japanese) [Google Scholar]
- Vlotman, W.F.; Smedema, L.K.; Rycroft, D.W. 11 Design of pipe drainage systems. In Modern Land Drainage; CRC Press: London, UK, 2020; pp. 195–225. [Google Scholar]
- Raadsma, S. 7 Current Draining Practices in Flat Areas of Humid Regions in Europe. In Drainage for Agriculture; Dinaure, R.C., Davis, M.E., Eds.; American Society of Agronomy, Inc.: Madison, WI, USA, 1974; p. 132. [Google Scholar]











| ρs (g/cm3) | 2.673 |
| emax | 0.991 |
| emin | 0.630 |
| k (m/s) Dr = 60% | 2.246 × 10−4 |
| k (m/s) Dr = 70% | 1.700 × 10−4 |
| k (m/s) Dr = 80% | 1.629 × 10−4 |
| Drainage Pipe | Diameter (mm) | Drainage Hole Size (mm) | Thickness (mm) | Length (mm) |
|---|---|---|---|---|
| A (Sheet pipe) | 50.5 | φ2 | 1.0 | 400.0 |
| B | 60.0 | φ7 | 4.1 | 400.0 |
| C | 59.6 | 8 × 1 | 5.0 | 400.0 |
| D | 60.4 | - | - | 400.0 |
| E | 54.0 | φ7 | 2.0 | 400.0 |
| Time (min) | Coefficient of Drainage Capacity | ||||
|---|---|---|---|---|---|
| Pipe A | Pipe B | Pipe C | Pipe D | Pipe E | |
| 200 | 0.79 | 0.63 | 0.85 | 0.95 | 0.93 |
| 300 | 0.83 | 0.65 | 0.87 | 0.94 | 0.92 |
| 400 | 0.86 | 0.67 | 0.88 | 0.94 | 0.92 |
| 500 | 0.89 | 0.68 | 0.89 | 0.93 | 0.91 |
| 600 | 0.92 | 0.69 | 0.91 | 0.93 | 0.91 |
| 700 | 0.94 | 0.69 | 0.92 | 0.93 | 0.91 |
| 800 | 0.97 | 0.7 | 0.93 | 0.93 | 0.91 |
| 900 | 0.98 | 0.7 | 0.95 | 0.94 | 0.92 |
| 1000 | 1 | 0.71 | 0.97 | 0.94 | 0.92 |
| Sample | S (%) | L (m) | W (m) | D (mm) | Δz (mm/d) | Q (×10−3) (m3/s) | i (%) | Qmax (×10−3) (m3/s) | Δzmax (mm/d) |
|---|---|---|---|---|---|---|---|---|---|
| Toyoura sand | 9.4 | 100.0 | 4.0 | 50.0 | 100.0 | 0.044 | 0.017 | 0.237 | 543.4 |
| Soil1 | 20.0 | 100.0 | 4.0 | 50.0 | 100.0 | 0.093 | 0.077 | 0.237 | 255.4 |
| Sample | Toyoura Sand | ||
|---|---|---|---|
| h (height of GWL at the center above pipe) m | 0.30 | 0.20 | 0.10 |
| ΔZ = q (lowing rate of GWL) m/d | 0.10 | 0.10 | 0.10 |
| W (drain spacing) m | 19.90 | 15.76 | 10.79 |
| Bore Hole | No.1 | No.2 | No.3 | No.4 | No.5 |
|---|---|---|---|---|---|
| Clay(%) <0.005 mm | 69.10 | 80.75 | 67.06 | 61.82 | 57.77 |
| Silt(%) <0.075 mm | 29.76 | 19.25 | 29.72 | 36.02 | 39.43 |
| Fine sand(%) <0.420 m | 1.14 | 0.00 | 3.00 | 2.16 | 2.12 |
| w (%) | 29.85 | 37.45 | 36.14 | 39.52 | 34.37 |
| Gs | 2.540 | 2.535 | 2.544 | 2.531 | 2.493 |
| PI | 32.77 | 45.37 | 44.18 | 32.97 | 37.80 |
| Void ratio | 0.76 | 0.96 | 0.93 | 1.01 | 0.87 |
| k (m/s) | 3.75 × 10−8 | 1.98 × 10−7 | 1.47 × 10−7 | 5.9 × 10−9 | 3.09 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamura, K.; Matsuda, H.; Setiawan, B.I.; Saptomo, S.K. Sustainable Restoration of Degraded Farm Land by the Sheet-Pipe System. Land 2021, 10, 1328. https://doi.org/10.3390/land10121328
Tamura K, Matsuda H, Setiawan BI, Saptomo SK. Sustainable Restoration of Degraded Farm Land by the Sheet-Pipe System. Land. 2021; 10(12):1328. https://doi.org/10.3390/land10121328
Chicago/Turabian StyleTamura, Koremasa, Hiroshi Matsuda, Budi Indra Setiawan, and Satyanto Krido Saptomo. 2021. "Sustainable Restoration of Degraded Farm Land by the Sheet-Pipe System" Land 10, no. 12: 1328. https://doi.org/10.3390/land10121328
APA StyleTamura, K., Matsuda, H., Setiawan, B. I., & Saptomo, S. K. (2021). Sustainable Restoration of Degraded Farm Land by the Sheet-Pipe System. Land, 10(12), 1328. https://doi.org/10.3390/land10121328







