Spatial Interactions in Business and Housing Location Models
Abstract
:1. Introduction
2. Location of Business and Real Estate—Determinants and Decision Processes
2.1. Theories on Firms’ Location
2.2. Theories on Real Estate Location
3. Spatial Issues in the Revision of Business and Housing Location Theories
4. Spatial Methods to Verify the Spatial Mechanisms
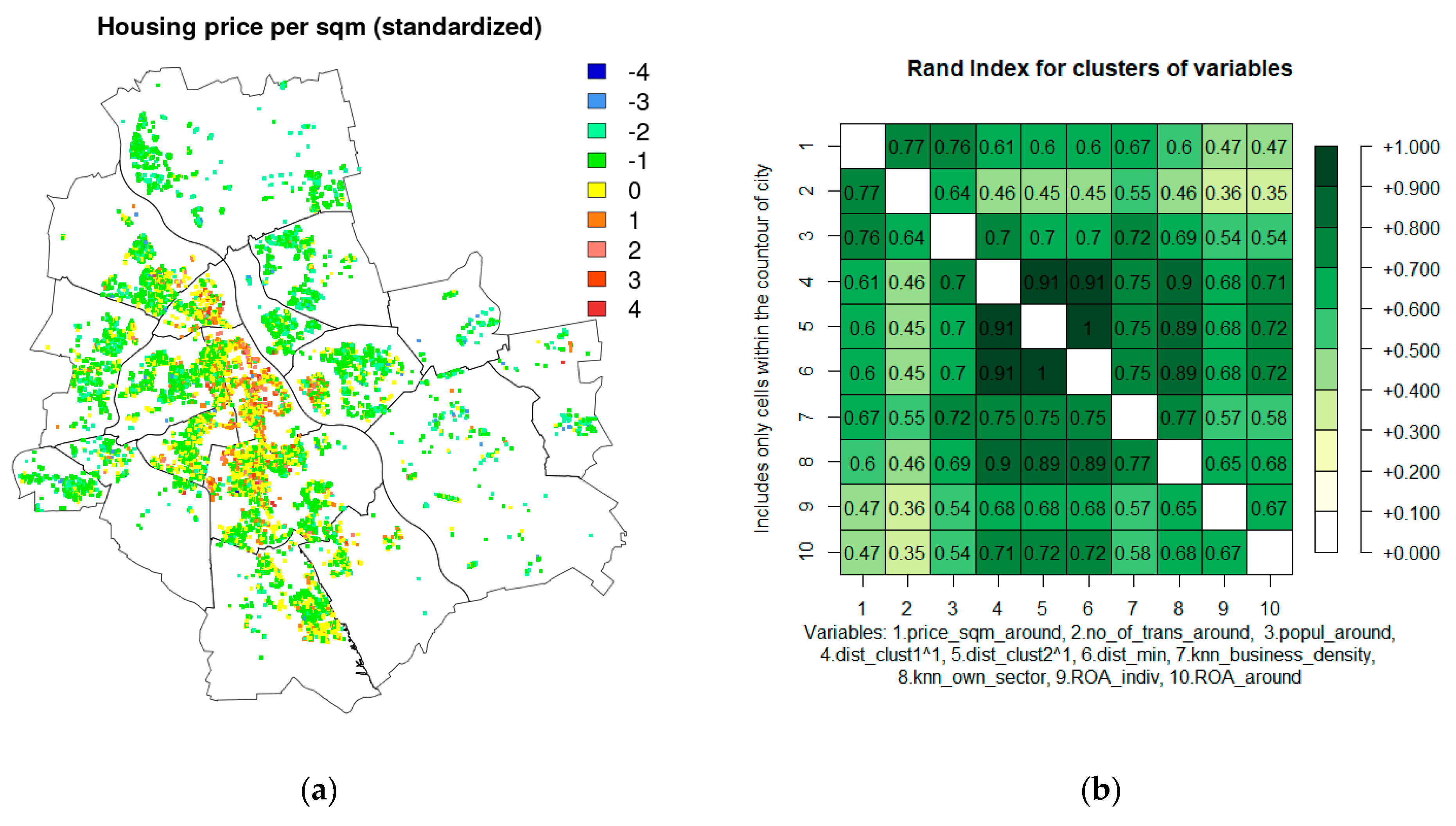
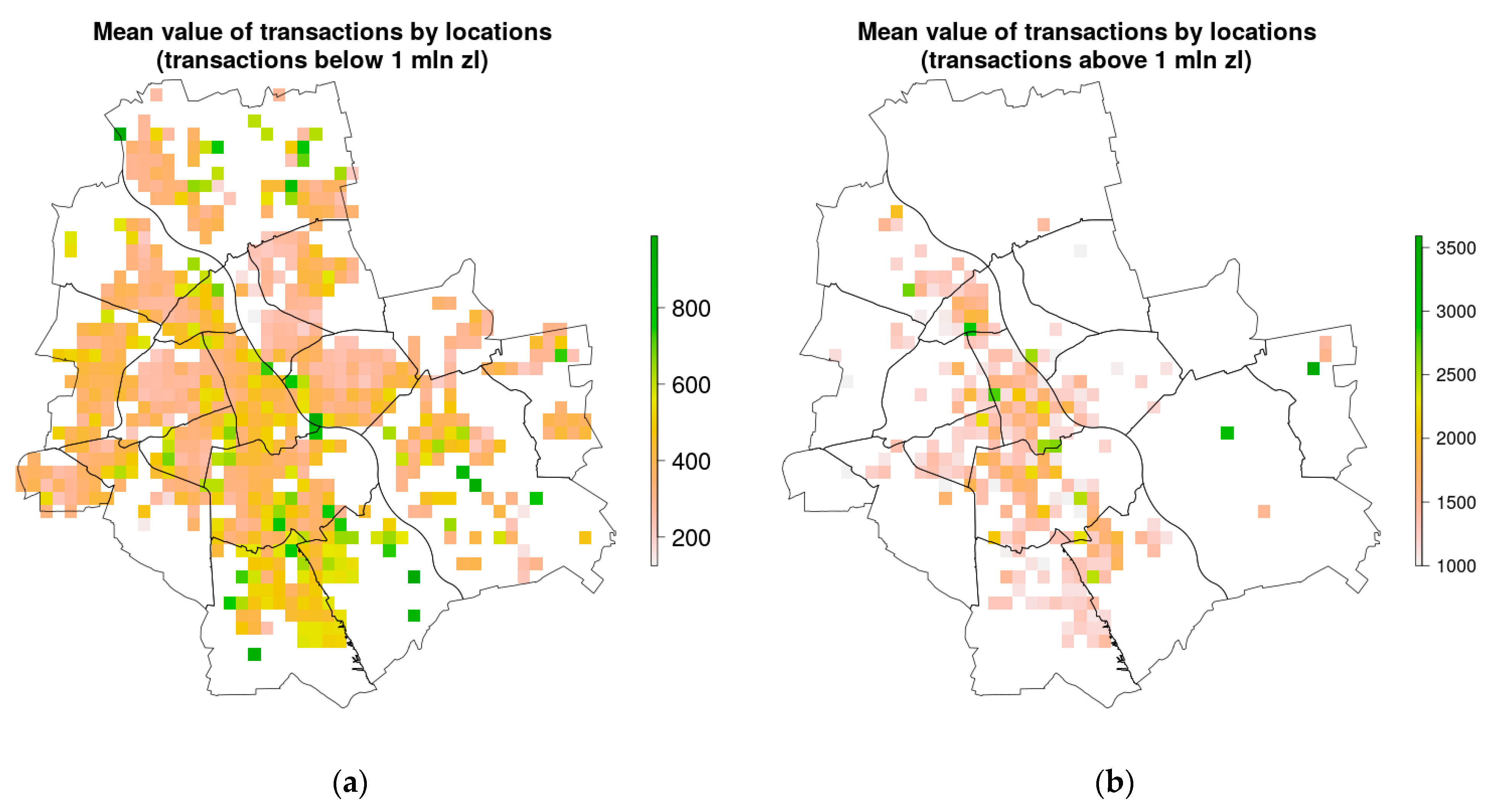
4.1. Spatial Variables Included in the Modelling
4.2. Data Used in Modelling
4.3. Choice of Econometric Methods
+ βl ∙ population + βm ∙ distances.to.cores + βn ∙ sectoral.dummies + ε
5. Interpretation of Results
5.1. Interpretation of Spatial Phenomena
5.2. Interpretation in the Light of Location Theories
5.3. Discussion of the Results
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- 1.
- Technical details of estimation in R
- 2.
- Rand Index as a measure of dependence of spatial point-patterns

- 3.
- Agglomeration measure based on the entropy of tessellated point-pattern
- 4.
- Econometric methods in verification of location choice
- 5.
- Hedonic models for housing valuation
- 6.
- Links between the business location and its profitability
Appendix B
| VARIABLES | Min | Q1 | Median | Mean | Q3 | Max |
|---|---|---|---|---|---|---|
| lat | 52.104 | 52.196 | 52.227 | 52.221 | 52.239 | 52.363 |
| lon | 20.856 | 20.985 | 21.007 | 21.011 | 21.031 | 21.254 |
| ROA_indiv | −29.950 | −4.120 | 1.040 | 1.320 | 7.690 | 29.990 |
| ROA_around | −27.730 | 0.032 | 1.006 | 1.338 | 2.592 | 28.210 |
| knn_business_density | 1.000 | 23.000 | 60.000 | 130.473 | 201.000 | 888.000 |
| knn_BusinessServices | 0.000 | 4.000 | 13.000 | 29.948 | 45.000 | 234.000 |
| knn_Wholesale | 0.000 | 3.000 | 9.000 | 17.031 | 24.000 | 104.000 |
| knn_own_sector | 1.000 | 2.000 | 7.000 | 18.037 | 21.000 | 234.000 |
| popul_around | 0.000 | 8.000 | 19.000 | 18.212 | 26.000 | 58.000 |
| price_sqm_around | 2528.845 | 7709.940 | 8621.766 | 8707.044 | 9543.100 | 20,208.349 |
| no_of_trans_around | 0.000 | 3.000 | 30.000 | 53.285 | 87.000 | 526.000 |
| dist_clust1^1 | 0.147 | 4.714 | 5.986 | 6.503 | 8.015 | 20.607 |
| dist_clust2^1 | 0.086 | 1.461 | 4.073 | 4.598 | 6.771 | 18.291 |
| sec_Bank_Insur_FinServ | 0.000 | 0.000 | 0.000 | 0.046 | 0.000 | 1.000 |
| sec_Biotech_and_LifeScien | 0.000 | 0.000 | 0.000 | 0.006 | 0.000 | 1.000 |
| sec_BusinessServ | 0.000 | 0.000 | 0.000 | 0.212 | 0.000 | 1.000 |
| sec_Chemic_Petr_Rubber_Plast | 0.000 | 0.000 | 0.000 | 0.011 | 0.000 | 1.000 |
| sec_Communicat | 0.000 | 0.000 | 0.000 | 0.010 | 0.000 | 1.000 |
| sec_CompHard | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 1.000 |
| sec_CompSoft | 0.000 | 0.000 | 0.000 | 0.042 | 0.000 | 1.000 |
| sec_Constr | 0.000 | 0.000 | 0.000 | 0.112 | 0.000 | 1.000 |
| sec_Food_Tobacco_Manuf | 0.000 | 0.000 | 0.000 | 0.010 | 0.000 | 1.000 |
| sec_Industr_Electric_Electro | 0.000 | 0.000 | 0.000 | 0.014 | 0.000 | 1.000 |
| sec_InformServ | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 1.000 |
| sec_Leather_Stone_Clay_Glass | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 1.000 |
| sec_Media_Broadcast | 0.000 | 0.000 | 0.000 | 0.026 | 0.000 | 1.000 |
| sec_Metals_MetalProd | 0.000 | 0.000 | 0.000 | 0.007 | 0.000 | 1.000 |
| sec_MiningExtr | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 1.000 |
| sec_Misc_Manuf | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 1.000 |
| sec_Print_Publish | 0.000 | 0.000 | 0.000 | 0.018 | 0.000 | 1.000 |
| sec_PropertyServ | 0.000 | 0.000 | 0.000 | 0.110 | 0.000 | 1.000 |
| sec_Publ_Adm_Edu_Health_SocServ | 0.000 | 0.000 | 0.000 | 0.046 | 0.000 | 1.000 |
| sec_Retail | 0.000 | 0.000 | 0.000 | 0.046 | 0.000 | 1.000 |
| sec_Textiles_Cloth | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 1.000 |
| sec_Transp_Manuf | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 1.000 |
| sec_Transp_Freight_Storage | 0.000 | 0.000 | 0.000 | 0.025 | 0.000 | 1.000 |
| sec_Travel_Pers_Leisure | 0.000 | 0.000 | 0.000 | 0.051 | 0.000 | 1.000 |
| sec_Utilities | 0.000 | 0.000 | 0.000 | 0.019 | 0.000 | 1.000 |
| sec_Waste_Manag_Treat | 0.000 | 0.000 | 0.000 | 0.005 | 0.000 | 1.000 |
| sec_Wholesale | 0.000 | 0.000 | 0.000 | 0.158 | 0.000 | 1.000 |
| sec_Wood_Furnit_Paper_Manuf | 0.000 | 0.000 | 0.000 | 0.006 | 0.000 | 1.000 |
References
- Thünen, J.V. Der isolierte Staat. Beziehung auf Landwirtschaft und Nationalökonomie; Perthes: Hamburg, Germany, 1826. [Google Scholar]
- Weber, A.; Friedrich, C.J. Alfred Weber’s Theory of the Location of Industries; University of Chicago Press: Chicago, IL, USA, 1929. [Google Scholar]
- Lösch, A. The Spatial Organization of the Economy; Encyclopædia Britannica: London, UK, 1940. [Google Scholar]
- Moses, L.N. Location and the theory of production. Q. J. Econ. 1958, 72, 259–272. [Google Scholar] [CrossRef]
- Hotelling, H. Stability in Competition. Econ. J. 1929, 39, 41–57. [Google Scholar] [CrossRef]
- Salop, S.C. Monopolistic Competititon with Outside Goods. Bell J. Econ. 1979, 10, 141–156. [Google Scholar] [CrossRef]
- Webber, M.J. Sub-optimal behaviour and the concept of maximum profits in location theory. Aust. Geogr. Stud. 1969, 7, 1–8. [Google Scholar] [CrossRef]
- Cocco, L.; Deidda, M.; Marchesi, M.; Pigliaru, F. Insularity and economies of density: Analysing the efficiency of a logistic network using an econometric simulation-based approach. Reg. Stud. 2018, 53, 900–911. [Google Scholar] [CrossRef]
- Pred, A. Behaviour and location: Foundations for a geographic and dynamic location theory, part 1. Lund Stud. Geogr. 1967, 27, 128. [Google Scholar]
- Claus, R.J.; Claus, K.E. Behavioural location theory: A review and discussion of Pred’s dynamic location model. Aust. Geogr. 1971, 11, 522–530. [Google Scholar] [CrossRef]
- Karlson, S.H. Modeling location and production: An application to US fully-integrated steel plants. Rev. Econ. Stat. 1983, 65, 41–50. [Google Scholar] [CrossRef]
- Krugman, P. Geography and Trade; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Ottaviano, G.I. ‘New’new economic geography: Firm heterogeneity and agglomeration economies. J. Econ. Geogr. 2010, 11, 231–240. [Google Scholar] [CrossRef]
- Boschma, R. Evolutionary economic geography and its implications for regional innovation policy. Pap. Evol. Econ. Geogr. 2009, 9, 1–33. [Google Scholar]
- Gong, H.; Hassink, R. Co-evolution in contemporary economic geography: Towards a theoretical framework. Reg. Stud. 2018, 53, 1344–1355. [Google Scholar] [CrossRef]
- Fitjar, R.D.; Gjelsvik, M. Why do firms collaborate with local universities? Reg. Stud. 2018, 52, 1525–1536. [Google Scholar] [CrossRef]
- Alonso, W. Location and Land Use: Toward a General Theory of Land Rent; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Levine, J. Rethinking accessibility and jobs-housing balance. J. Am. Plan. Assoc. 1998, 64, 133. [Google Scholar] [CrossRef]
- Straszhem, M. The theory of urban residential location. In Handbook of Regional and Urban Economics; Elsevier: Amsterdam, The Netherlands, 1987; Volume 2, pp. 717–757. [Google Scholar]
- Smith, N. Toward a theory of gentrification a back to the city movement by capital, not people. J. Am. Plan. Assoc. 1979, 45, 538–548. [Google Scholar] [CrossRef]
- Diappi, L.; Bolchi, P. Smith’s rent gap theory and local real estate dynamics: A multi-agent model. Computers. Environ. Urban Syst. 2008, 32, 6–18. [Google Scholar] [CrossRef]
- Wheaton, W.C. Income and urban residence: An analysis of consumer demand for location. Am. Econ. Rev. 1977, 67, 620–631. [Google Scholar]
- DiPasquale, D.; Wheaton, W.C. The markets for real estate assets and space: A conceptual framework. Real Estate Econ. 1992, 20, 181–198. [Google Scholar] [CrossRef]
- DeSalvo, J.S. Teaching the DiPasquale-Wheaton Model. J. Real Estate Pract. Educ. 2017, 20, 1–25. [Google Scholar] [CrossRef]
- Bravo, M.; Briceño, L.; Cominetti, R.; Cortés, C.E.; Martínez, F. An integrated behavioral model of the land-use and transport systems with network congestion and location externalities. Transp. Res. Part B Methodol. 2010, 44, 584–596. [Google Scholar] [CrossRef]
- Pangallo, M.; Nadal, J.P.; Vignes, A. Residential income segregation: A behavioral model of the housing market. J. Econ. Behav. Organ. 2019, 159, 15–35. [Google Scholar] [CrossRef] [Green Version]
- Kyriakopoulou, E.; Xepapadeas, A. Spatial location decisions under environmental policy and housing externalities. Environ. Econ. Policy Stud. 2011, 13, 195. [Google Scholar] [CrossRef]
- Partridge, M.D.; Rickman, D.S.; Ali, K.; Olfert, M.R. Agglomeration spillovers and wage and housing cost gradients across the urban hierarchy. J. Int. Econ. 2009, 78, 126–140. [Google Scholar] [CrossRef] [Green Version]
- Glaeser, E.L. Cities, Agglomeration, and Spatial Equilibrium; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Suedekum, J. Agglomeration and regional costs of living. J. Reg. Sci. 2006, 46, 529–543. [Google Scholar] [CrossRef]
- Hanushek, E.; Yilmaz, K. The complementarity of Tiebout and Alonso. J. Hous. Econ. 2007, 16, 243–261. [Google Scholar] [CrossRef]
- Papageorgiou, Y.Y. Externality diffusion. Syst. Urban 1982, 4, 17–39. [Google Scholar]
- Werczberger, E. Endogenous spatial externalities in residential location theory. In Regional Science; Springer: Berlin/Heidelberg, Germany, 1991; pp. 79–96. [Google Scholar]
- Niu, F.; Liu, W. Modeling urban housing price: The perspective of household activity demand. J. Geogr. Sci. 2017, 27, 619–630. Available online: https://www.researchgate.net/publication/316551331_Modeling_urban_housing_price_The_perspective_of_household_activity_demand (accessed on 15 November 2021). [CrossRef] [Green Version]
- Kauko, T. What makes a location attractive for the housing consumer? Preliminary findings from metropolitan Helsinki and Randstad Holland using the analytical hierarchy process. J. Hous. Built Environ. 2006, 21, 159–176. [Google Scholar] [CrossRef]
- Borgoni, R.; Michelangeli, A.; Pontarollo, N. The value of culture to urban housing markets. Reg. Stud. 2018, 52, 1672–1683. [Google Scholar] [CrossRef]
- Ala-Mantila, S.; Heinonen, J.; Junnila, S.; Saarsalmi, P. Spatial nature of urban well-being. Reg. Stud. 2018, 52, 959–973. [Google Scholar] [CrossRef]
- Morrison, P.S.; Weckroth, M. Human values, subjective well-being and the metropolitan region. Reg. Stud. 2018, 52, 325–337. [Google Scholar] [CrossRef]
- Tiebout, C.M. Location theory, empirical evidence, and economic evolution. Pap. Reg. Sci. 1957, 3, 74–86. [Google Scholar] [CrossRef]
- Tiebout, C.M. A pure theory of local expenditures. J. Political Econ. 1956, 64, 416–424. [Google Scholar] [CrossRef]
- Tabuchi, T. Urban agglomeration and dispersion: A synthesis of Alonso and Krugman. J. Urban Econ. 1998, 44, 333–351. [Google Scholar] [CrossRef] [Green Version]
- Van der Panne, G. Agglomeration externalities: Marshall versus Jacobs. J. Evol. Econ. 2004, 14, 593–604. [Google Scholar] [CrossRef]
- Daskalopoulou, I.; Liargovas, P. Regional determinants of manufacturing start-ups in Greece: Evidence on the effect of agglomeration economies. Appl. Econ. Lett. 2010, 17, 1841–1844. [Google Scholar] [CrossRef]
- Mion, G. Spatial externalities and empirical analysis: The case of Italy. J. Urban Econ. 2004, 56, 97–118. [Google Scholar] [CrossRef]
- Guevara-Rosero, G.C.; Riou, S.; Autant-Bernard, C. Agglomeration externalities in Ecuador: Do urbanisation and tertiarisation matter? Reg. Stud. 2018, 53, 706–719. [Google Scholar] [CrossRef]
- de Matteis, P.; Pietrovito, F.; Pozzolo, A.F. Local context and exports: An analysis with a matched sample of firm–province data. Reg. Stud. 2019, 53, 550–561. [Google Scholar] [CrossRef]
- Hervas-Oliver, J.L.; Belussi, F. Cluster Advantage and Firm Performance: A Shift into the Future! In Agglomeration and Firm Performance; Springer: Cham, Switzerland, 2018; pp. 1–7. [Google Scholar]
- Porter, M.E. Clusters and the New Economics of Competition; Harvard Business Review: Boston, MA, USA, 1998; Volume 76, pp. 77–90. [Google Scholar]
- McCann, P. Rethinking the economics of location and agglomeration. Urban Stud. 1995, 32, 563–577. [Google Scholar] [CrossRef]
- Cainelli, G.; Giannini, V.; Iacobucci, D. Agglomeration, networking and the Great Recession. Reg. Stud. 2018, 53, 951–962. [Google Scholar] [CrossRef]
- Yang, T.; Pan, H.; Hewings, G.; Jin, Y. Understanding urban sub-centers with heterogeneity in agglomeration economies—Where do emerging commercial establishments locate? Cities 2019, 86, 25–36. [Google Scholar] [CrossRef]
- Boussauw, K.; Sansen, J.; van Meeteren, M.; Meijers, E.; Louw, E.; Storme, T.; Derudder, B.; Witlox, F. Planning for agglomeration economies in a polycentric region: Envisioning an efficient metropolitan core area in Flanders. Eur. J. Spat. Dev. 2018, 2018, 1–26. [Google Scholar] [CrossRef]
- White, M.J. A model of residential location choice and commuting by men and women workers. J. Reg. Sci. 1977, 17, 41–52. [Google Scholar] [CrossRef]
- Guo, J.Y.; Bhat, C.R. Operationalising the concept of neighborhood: Application to residential location choice analysis. J. Transp. Geogr. 2007, 15, 31–45. [Google Scholar] [CrossRef] [Green Version]
- McFadden, D. Modeling the choice of residential location. Transp. Res. Rec. 1978, 673, 72–77. [Google Scholar]
- Kwon, Y. Rent-Commuting Cost Function Versus Rent-Distance Function. J. Reg. Sci. 2002, 42, 773–791. [Google Scholar] [CrossRef]
- Gutiérrez-i-Puigarnau, E.; Mulalic, I.; van Ommeren, J.N. Do rich households live farther away from their workplaces? J. Econ. Geogr. 2014, 16, 177–201. [Google Scholar] [CrossRef] [Green Version]
- Berechman, J.; Small, K.A. Modeling land use and transportation: An interpretive review for growth areas. Environ. Plan. A 1988, 20, 1285–1309. [Google Scholar] [CrossRef] [Green Version]
- Heldt, B.; Gade, K.; Heinrichs, D. Determination of Attributes Reflecting Household Preferences in Location Choice Models. Transp. Res. Procedia 2016, 19, 119–134. [Google Scholar] [CrossRef] [Green Version]
- Wong, S.C.; Ho, H.W. A combined model of housing location and traffic equilibrium problems in a continuous transportation system. In Transportation and Traffic Theory. Flow, Dynamics and Human Interaction, Proceedings of the 16th International Symposium on Transportation and Traffic Theory, College Park, MD, USA, 19–21 July 2005; Elsevier: New York, NY, USA, 2005; pp. 761–779. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46 (Suppl. 1), 234–240. [Google Scholar] [CrossRef]
- Papageorgiou, G.J. Spatial externalities I: Theory. Ann. Assoc. Am. Geogr. 1978, 68, 465–476. [Google Scholar] [CrossRef]
- Papageorgiou, G.J. Spatial externalities II: Applications. Ann. Assoc. Am. Geogr. 1978, 68, 477–492. [Google Scholar] [CrossRef]
- Papageorgiou, Y.Y.; Smith, T.R. Agglomeration as local instability of spatially uniform steady-states. Econom. J. Econom. Soc. 1983, 51, 1109–1119. [Google Scholar] [CrossRef]
- Döring, T.; Schnellenbach, J. What do we know about geographical knowledge spillovers and regional growth?: A survey of the literature. Reg. Stud. 2006, 40, 375–395. [Google Scholar] [CrossRef] [Green Version]
- Fujita, M.; Ogawa, H. Multiple equilibria and structural transition of non-monocentric urban configurations. Reg. Sci. Urban Econ. 1982, 12, 161–196. [Google Scholar] [CrossRef]
- Vasanen, A. Functional polycentricity: Examining metropolitan spatial structure through the connectivity of urban sub-centres. Urban Stud. 2012, 49, 3627–3644. [Google Scholar] [CrossRef]
- Mussa, A.; Nwaogu, U.G.; Pozo, S. Immigration and housing: A spatial econometric analysis. J. Hous. Econ. 2017, 35, 13–25. [Google Scholar] [CrossRef]
- Montero, J.M.; Mínguez, R.; Fernández-Avilés, G. Housing price prediction: Parametric versus semi-parametric spatial hedonic models. J. Geogr. Syst. 2018, 20, 27–55. [Google Scholar] [CrossRef]
- Golledge, R.G.; Stimson, R. Spatial Behavior: A Geographic Perspective; Guilford Press: New York, NY, USA, 1997. [Google Scholar]
- Overmars, K.P.; de Groot, W.; Huigen, M. Comparing Inductive and Deductive Modeling of Land Use Decisions: Principles, a Model and an Illustration from the Philippines. Hum. Ecol. 2007, 35, 439–445. [Google Scholar] [CrossRef] [Green Version]
- Shmueli, G. To explain or to predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Comber, A.; Brunsdon, C.; Charlton, M.; Dong, G.; Harris, R.; Lu, B.; Lu, Y.; Murakami, D.; Nakaya, T.; Wang, Y.; et al. The GWR route map: A guide to the informed application of Geographically Weighted Regression. arXiv 2020, arXiv:2004.06070. [Google Scholar]
- Hill, R. Hedonic Price Indexes for Housing; OECD Statistics Working Papers, No. 2011/01; OECD Publishing: Paris, France, 2011. [Google Scholar] [CrossRef]
- Kopczewska, K. Entropy as a measure of agglomeration, In Handbook on Entropy, Complexity, and Spatial Dynamics: The Rebirth of Theory? Reggiani, A., Schintler, L., Czamanski, D., Patuelli, R., Eds.; Edward Elgar: Cheltenham, UK, 2021. [Google Scholar]
- Lews, R. Redundancy as an index of change in point pattern analysis. Geogr. Anal. 1979, 11, 374–388. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Helbich, M.; Griffith, D.A. Spatially varying coefficient models in real estate: Eigenvector spatial filtering and alternative approaches. Comput. Environ. Urban Syst. 2016, 57, 1–11. [Google Scholar] [CrossRef]
- Osland, L. An application of spatial econometrics in relation to hedonic house price modeling. J. Real Estate Res. 2010, 32, 289–320. [Google Scholar] [CrossRef]
- Chrostek, K.; Kopczewska, K. Spatial Prediction Models for Real Estate Market Analysis. Ekonomia 2013, 35, 25–43. [Google Scholar]
- Bhat, C.R.; Paleti, R.; Singh, P. A Spatial Multivariate Count Model for Firm Location Decisions. J. Reg. Sci. 2014, 54, 462–502. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, K. Spatial dependence and heterogeneity in the location processes of new high-tech firms in Nanjing, China. Pap. Reg. Sci. 2015, 96, 519–535. [Google Scholar] [CrossRef]
- Sirmans, G.S.; Macpherson, D.A.; Zietz, E.N. The composition of hedonic pricing models. J. Real Estate Lit. 2005, 13, 3–46. [Google Scholar] [CrossRef]
- Kohlhase, J.E.; Ju, X. Firm location in a polycentric city: The effects of taxes and agglomeration economies on location decisions. Environ. Plan. C Gov. Policy 2007, 25, 671–691. [Google Scholar] [CrossRef] [Green Version]
- Mori, T. Monocentric versus polycentric models in urban economics. New Palgrave Dict. Econ. 2016, 1–4. [Google Scholar]
- Barrios Garcia, J.A.; Rodriguez Hernandez, J.E. Housing and urban location decisions in Spain: An econometric analysis with unobserved heterogeneity. Urban Stud. 2007, 44, 1657–1676. [Google Scholar] [CrossRef]
- Kaklauskas, A.; Zavadskas, E.K.; Banaitis, A.; Šatkauskas, G. Defining the utility and market value of a real estate: A multiple criteria approach. Int. J. Strateg. Prop. Manag. 2007, 11, 107–120. [Google Scholar] [CrossRef]
- Arentze, T.; Timmermans, H. Modeling agglomeration forces in urban dynamics: A multi-agent system approach. Int. J. Urban Sci. 2003, 7, 1–13. [Google Scholar] [CrossRef]
- Selim, H. Determinants of house prices in Turkey: Hedonic regression versus artificial neural network. Expert Syst. Appl. 2009, 36, 2843–2852. [Google Scholar] [CrossRef]
- Morano, P.; Tajani, F.; Locurcio, M. Land use, economic welfare and property values: An analysis of the interdependencies of the real-estate market with zonal and socio-economic variables in the municipalities of Apulia region (Italy). Int. J. Agric. Environ. Inf. Syst. 2015, 6, 16–39. [Google Scholar] [CrossRef]
- Pavlov, A.D. Space-varying regression coefficients: A semi-parametric approach applied to real estate markets. Real Estate Econ. 2000, 28, 249–283. [Google Scholar] [CrossRef]
- Bagnoli, C.; Smith, H. The theory of fuzz logic and its application to real estate valuation. J. Real Estate Res. 1998, 16, 169–200. [Google Scholar] [CrossRef]
- Özsoy, O.; Şahin, H. Housing price determinants in Istanbul, Turkey: An application of the classification and regression tree model. Int. J. Hous. Mark. Anal. 2009, 2, 167–178. [Google Scholar] [CrossRef]
- Poulhes, M. From Latin Quarter to Montmartre: Investigating Parisian Real Estate Prices. Ann. Econ. Stat. 2018, 130, 39–68. [Google Scholar] [CrossRef]
- Fingleton, B. Housing supply, housing demand, and affordability. Urban Stud. 2008, 45, 1545–1563. [Google Scholar] [CrossRef]
- Dachis, B.; Duranton, G.; Turner, M.A. The effects of land transfer taxes on real estate markets: Evidence from a natural experiment in Toronto. J. Econ. Geogr. 2011, 12, 327–354. [Google Scholar] [CrossRef] [Green Version]
- Arrazola, M.; de Hevia, J.; Romero-Jordán, D.; Sanz-Sanz, J.F. Long-run Supply and Demand Elasticities in the Spanish Housing Market. J. Real Estate Res. 2015, 37, 371–404. [Google Scholar] [CrossRef]
- Saiz, A. The geographic determinants of housing supply. Q. J. Econ. 2010, 125, 1253–1296. [Google Scholar] [CrossRef] [Green Version]
- Meen, G.; Nygaard, C. Local housing supply and the impact of history and geography. Urban Stud. 2011, 48, 3107–3124. [Google Scholar] [CrossRef]
- Portnov, B.A.; Schwartz, M. On the relativity of urban location. Reg. Stud. 2008, 42, 605–615. [Google Scholar] [CrossRef]
- Braguinsky, S.; Ohyama, A.; Okazaki, T.; Syverson, C. Acquisitions, productivity, and profitability: Evidence from the Japanese cotton spinning industry. Am. Econ. Rev. 2015, 105, 2086–2119. [Google Scholar] [CrossRef] [Green Version]
- Addison, J.T. The determinants of firm performance: Unions, works councils, and employee involvement/high-performance work practices. Scott. J. Political Econ. 2005, 52, 406–450. [Google Scholar] [CrossRef] [Green Version]
- Jo, Y.; Lee, C.Y. Technological capability, agglomeration economies and firm location choice. Reg. Stud. 2014, 48, 1337–1352. [Google Scholar] [CrossRef]
- El-Sayed Ebaid, I. The impact of capital-structure choice on firm performance: Empirical evidence from Egypt. J. Risk Financ. 2009, 10, 477–487. [Google Scholar] [CrossRef]
- SME Survey. 2014. Available online: https://www.smesurvey.co.za/reports/SME%20Survey%20summary%202014.pdf (accessed on 15 November 2021).
- Stavropoulos, S.; Skuras, D. Firm profitability and agglomeration economies: An elusive relationship. Tijdschr. Voor Econ. En Soc. Geogr. 2016, 107, 66–80. [Google Scholar] [CrossRef]
- Holl, A. Start-ups and re-locations: Manufacturing plant location in Portugal. Pap. Reg. Sci. 2004, 83, 649–668. [Google Scholar]
- Anderstig, C.; Mattsson, L.G. An integrated model of residential and employment location in a metropolitan region. Pap. Reg. Sci. 1991, 70, 167–184. [Google Scholar] [CrossRef]
- Anderstig, C.; Mattsson, L.G. Modelling land-use and transport interaction: Policy analyses using the IMREL model. In Network Infrastructure and the Urban Environment; Springer: Berlin/Heidelberg, Germany, 1998; pp. 308–328. [Google Scholar]
- Boyce, D.; Mattsson, L.G. Modeling residential location choice in relation to housing location and road tolls on congested urban highway networks. Transp. Res. Part B Methodol. 1999, 33, 581–591. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopczewska, K.; Kopyt, M.; Ćwiakowski, P. Spatial Interactions in Business and Housing Location Models. Land 2021, 10, 1348. https://doi.org/10.3390/land10121348
Kopczewska K, Kopyt M, Ćwiakowski P. Spatial Interactions in Business and Housing Location Models. Land. 2021; 10(12):1348. https://doi.org/10.3390/land10121348
Chicago/Turabian StyleKopczewska, Katarzyna, Mateusz Kopyt, and Piotr Ćwiakowski. 2021. "Spatial Interactions in Business and Housing Location Models" Land 10, no. 12: 1348. https://doi.org/10.3390/land10121348
APA StyleKopczewska, K., Kopyt, M., & Ćwiakowski, P. (2021). Spatial Interactions in Business and Housing Location Models. Land, 10(12), 1348. https://doi.org/10.3390/land10121348






