Assessing the Impacts of Rural Development Plan Measures on the Sustainability of Agricultural Holdings Using a PMP Model

Abstract

Rural Development Plan (RDP) measures support farmers in improving the sustainability of their agricultural holdings. The implementation of these policies has economic, social, and environmental impacts, which are monitored either ex-ante, ongoing, or ex-post, as required from the European Commission impact assessment guidelines. In this frame, this paper aims to assess the impacts of RDP measures on the sustainability of agricultural holdings. For this reason, a positive mathematical programming (PMP) model was developed and implemented in combination with a set of economic, social, and environmental indicators. The model was used to assess the ex-post impacts of the measure titled ‘Modernization of agricultural holdings’ of the Greek RDP 2007–2013. This research was conducted on a sample of 219 agricultural holdings in a region of northern Greece. The impacts were measured through the changes of the crop plan in the agricultural land. The results show that the measure has positive economic impacts, negative social impacts, and negative impacts on most of the environmental indicators. The results also underline the significant role of the impact assessment process in supporting policymakers in understanding the impacts of their policies.

1. Introduction

Nowadays, there are many agricultural policies, rural development plans, and concrete measures that help farmers improve the sustainability of their agricultural holdings. The European Union (EU) introduced the concept of impact assessment to assess the impact of these policies. According to the European Commission, impact assessment (IA) [1] is defined as “a set of logical steps to be followed in the preparation of policy proposals”. Indeed, the European Commission, in 2009, drew up IA guidelines to highlight the importance of the impact assessment process. These guidelines emphasize the importance of impact assessment as an essential tool to ensure that policies are prepared based on transparent, comprehensive, and balanced procedures, define the various quality standards, and provide basic instructions to the impact assessment process [1]. In recent years, many impact assessment studies have been conducted at the European, national, and regional levels. In these studies, a plethora of impact assessment tools and processes for impact assessment have been developed [2].

Additionally, there are many studies in the literature regarding the sustainability of agricultural holdings that have tried to assess the impacts of the main agricultural policies of the EU [3,4,5,6]. In these studies, many authors do not use the term “sustainability”; often, sustainability is associated with the term “sustainable development” with regard to agricultural holdings. As agricultural holdings are the basic economic unit of the primary sector, the concept of sustainability or sustainable development of this sector is based on them [7]. One of the most commonly used definitions of sustainable development and, thus, sustainability, is the one given in the Brundtland report [8], which defines sustainable development as “development that meets the needs of the present without compromising the ability of future generations to meet their own needs” [9]. Economists occasionally use the definition given by Robert Solow [10], who argued that what is needed to maintain sustainability is “generalized capacity to create well-being”, while stressing that this ability does not have to consist of “any particular thing or natural resource” since resources, at least to some extent, are interchangeable or substitutable. The sustainable development principles are summarized in the triptych of the balanced development of economy, society, and environment [11]. Additionally, the Common Agricultural Policy (CAP) of the EU combines social, economic, and environmental aspects for achieving the sustainability of the agricultural sector [12]. In terms of sustainability measurement, indicators are presented as the most appropriate choice for many international organizations [13,14,15].

As regards the methodologies used for measuring sustainability, mathematical programming models are a widespread methodology for assessing any kind of impact. Lotze-Campen [16] argued that modeling methods “help to structure scientific thinking, emphasizing the most relevant processes, analyzing significant compromises between conflicting objectives, determining scenarios and, to some extent, making predictions of possible future developments”. Mathematical programming models are related to the farmers’ decision-making process in relation to sustainability issues [17,18,19,20,21,22]. Our literature review highlights a wide variety of mathematical programming models that have been applied for assessing the impacts of agricultural and environmental policies and measuring sustainability issues [23,24,25,26,27]. The approach of positive mathematical programming has been used in various cases for assessing the impacts of policies at national, regional, and farm levels. Indeed, several European research projects such as CAPRI, SEAMLESS, and EUROTOOLS have developed models based on the positive mathematical programming method because of its ability to reproduce the results of the existent crop plan. This is another advantage of the method, which gives the farmers the opportunity to have a progressive reaction to policy changes.

The objective of this study is to assess the economic, social, and environmental impacts of Rural Development Plan measures on the sustainability of agricultural holdings. For this reason, a positive mathematical programming (PMP) model was developed and implemented. The model was used to assess the impacts of a specific Rural Development Plan measure ex-post through suggested changes in the crop plan of the farmers’ agricultural land. From the changes in agricultural land, the economic, environmental, and social impacts were measured with a set of 11 indicators. The study was conducted in the region of Central Macedonia in Greece. A specific measure entitled “Modernization of agricultural holdings”, belonging to the Greek RDP 2007–2013, was used to select the sample of farmers and the average farm. This study provides a future path for policymakers to understand the impacts of their policies and to plan according to their best policy options.

In the next section, the Rural Development Plans are presented, the methodology approach, which includes positive mathematical programming, follows and the constraints and indicators used for the PMP model are analyzed. The sample, data, area of the study and the results are provided in the Section 3. Finally, Section 4 concludes.

2. Materials and Methods

2.1. Rural Development Plan (RDP)

The Greek Rural Development Plan (RDP) 2007–2013 belongs to the second pillar of the Common Agricultural Policy (CAP) and includes various measures distributed in four main axes. The Rural Development Plan measures are aimed at supporting farmers in modernizing their farms and becoming more competitive while protecting the environment by helping them improve the sustainability of agricultural holdings [28]. Regulation (EC) 1698/2005 of the European Agricultural Fund for Rural Development (EAFRD) defined the country’s priorities for the period 2007–2013. The Greek RDP 2007–2013 focused on three main axes [28], assisted by the fourth horizontal axis entitled “LEADER”:

• Improving the competitiveness of agriculture and forestry.
• Improving the environment and countryside.
• Improving the quality of life in rural areas and diversification in the rural economy.

The measure that was chosen in this study for assessing its impacts was Measure 121—“Modernization of agricultural holdings” of the Greek RDP. This measure is the main measure for improving the sustainability of agricultural holdings, as evidenced by the main aims of the measure, which are [28]:

• modernizing of agricultural holdings; and
• improving their overall performance through better use of production factors, including the introduction of new technologies and innovation.

The selection of Measure 121 for this study was based on substantial reasons. Originally, this measure was one of the most popular measures among farmers in Greece, as it had the highest participation rate. According to the final list of beneficiaries, the number of approved plans of this measure was 5490 for the period 2007–2013. Most beneficiaries in Greece originated from the region of Central Macedonia, with 1934 beneficiaries in total (35.2%). One more reason is that the official data of the Directorate-General for Regional Rural Economy and Veterinary of the Region of Central Macedonia was accessible by the researchers. Equally important in the measure choice was the previous implementation of the measure in the 2000–2006 programming period and its future implementation in the 2014–2020 programming period. This fact shows the importance of the measure for both the EU and the farmers [28].

2.2. Impact Assessment (IA) Tools

In recent years, the rapid and widespread increase of impact assessment as a method for evaluating policies has been reflected by the rapid growth of the number of tools, methods, and procedures that assist the process. However, in many cases, the results of the impact assessment processes arising from various tools are not fully satisfactory [29]. Studies such as Nilsson et al. [30] found that the tools used in IA processes tend not to be advanced tools such as complex computer models. Most of the IA processes use very simple tools, such as checklists with specific lists of possible impacts. This is due to the fact that public servants or policymakers care more about easy results than using advanced tools. In the literature, a number of studies analyzing impact assessment tools have recorded the tools used by the researchers to assess the impact of policies, especially agricultural and environmental policies [2,18,31,32,33,34,35,36]. According to these studies, one of the most important IA tool categories is mathematical programming models. The use of mathematical programming models and especially linear programming models in impact assessment processes for agriculture has presented some weaknesses. One is the failure to represent in the results the cultivations that participate in the existent crop plan. This weakness is considered significant, especially in cases where mathematical programming is used as a policy analysis tool since the results do not reflect reality. The reasons why this may happen may be the lack of data, incorrect analysis of the objective function or the constraints, and the choice of unreal assumptions for the model. Incorrect analysis of the constraints is one of the causes of the above problem, particularly when there is a lack of data for the preparation of the linear programming matrix. For this purpose, we searched the literature for a methodology that leads to optimum crop plans, taking into account the existent crop plan.

Many mathematical programming approaches have been developed to address this kind of problem [37]. Howitt [38] proposed a different perspective of mathematical programming, using more flexible requirements than traditional linear constraints. This approach, named positive mathematical programming, uses the existent crop plan of the farm to create automatic calibration models of agricultural production and resource use, according to microeconomic theory [38]. Heckelei and Wolff [39] argue that the approach of the PMP is used to calibrate the model and ensure accurate reproduction of the existent crop plan without using additional calibration constraints. Thus, one advantage of the method is that it achieves the accurate calibration of linear programming models even when there is a lack of data for the selection of the constraints. Another advantage is that the PMP process is a general and fully automated process, which means that it can be easily adapted and used for different regions and types of farming without any additional data. On the other hand, a major weakness of the method is that it cannot include crops that do not participate in the existent crop plan. This excludes possible alternative crops from the optimal crop plan. For these reasons, positive mathematical programming was chosen in this study for the impact assessment (economic, social, and environmental) of the Rural Development Plan measures on the sustainability of agricultural holdings.

The literature review revealed that PMP had been used in similar studies. However, a series of variations of PMP in bioeconomic analysis has been developed and used [39,40,41]. These variations are designed to overcome the limitations of the standard PMP approach and improve the predictive ability of the models by using additional available data. In their study, Fragoso et al. [42] evaluate the calibration and prediction capacity of a supply response PMP for the Alentejo region. Two different variations of PMP were used by Kanellopoulos et al. [43] in order to evaluate the prediction performance of a general bioeconomic farm model. One other bioeconomic model for farm-level analysis has been developed by Janssen et al. [44] and Louhichi et al. [22]. This model is used to simulate the behavior of the farmer as well as his future decisions. The use of this PMP model was also confirmed by a large number of applications in the literature ([22]; Louhichi et al., 2008, 2009; Kanellopoulos et al., 2009; Majewski et al., 2009; Mouratiadou et al., 2010; Traoré et al., 2009). The application of the EU Water Framework Directive has also led to an increasing number of analyses with different mathematical programming techniques [23,45,46,47,48], including PMP models [48]. Solazzo, Donati, and Arfini [49] used positive mathematical programming to assess the different schemes of regionalization and greening implementation according to both the preliminary proposals presented to the Trilogue and the CAP Reform. Cortignani and Dono [50] assessed the impact of greening using a hybrid model calibrated using positive mathematical programming.

2.3. The Positive Mathematical Programming (PMP) Model

According to Kanellopoulos et al. [51], the positive mathematical programming model is a linear programming model “which maximizes the total gross margin of an average farm of a certain farm type, subject to a set of resource and policy constraints”.

$$\underset{x\in \left[0\dots +\infty \right)}{\max }\left\{z=r\prime x-c\prime x\right\}$$

(1)

s.t. Ax ≤ b[π],
x ≥ 0

where

• z is the objective value;
• x is the n × 1 vector of production activities;
• r is the n × 1 vector of activity revenues;
• c is the n × 1 vector of variable costs;
• A is the m × n matrix of the technical coefficients;
• b is the m × 1 vector of the upper bounds of the resources and the policy constraints;
• π is the m × 1 vector of the shadow prices of the resources and the policy constraints.

Positive mathematical programming is described by Heckelei [39] as a two-step approach. The first step is an extension of the linear model by adding a set of calibrated constraints that match the simulated crop levels in the existent crop plan. According to Kanellopoulos et al. [51], a small perturbation ε is allowed to ensure that all binding resource constraints of the model described in Equation (1) are still binding in the model described below:

$$\underset{x\in \left[0\dots +\infty \right)}{\max }\left\{z=r\prime x-c\prime x\right\}$$

(2)

$$\begin{array}{c}s.t.Ax\le \mathrm{b}\left[\mathsf{\pi }\right],\\ \mathrm{x} \le {\mathrm{x}}^0 + \mathsf{\epsilon }\left[\mathsf{\lambda }\right]\\ \mathrm{x} \ge 0\end{array}$$

where

• x⁰ is the n × 1 vector of observed activity levels;
• ε is the n × 1 vector of small positive numbers; and
• λ is the n × 1 vector of dual values of the calibration constraints.

In the solution of Model (2), the preferred crops (with high average gross margin) are bound by the calibrated constraints, while nonpreferred crops (with low average gross margin) are bound by policy and other constraints [51]. The calibrated constraints on the nonpreferred crops are not binding, and, therefore, the shadow prices are equal to 0.

In the second step of the PMP, the calibrated constraints of the model described in Equation (2) are disregarded even though the shadow prices are used to estimate the parameters of the next quadratic cost function (Equation (3)). Thus, the model calibrates to the data of the existent crop plan [51]. For this reason, we can use different functional forms with the required properties. According to Heckelei [39], a quadratic cost function is used in most studies related to PMP. This is used, according to [51], for simplicity reasons and because there are no strong arguments for using a different functional form.

$$C=d\prime x+0.5x\prime Qx$$

(3)

where

• d is the n × 1 vector of the parameter associated with the linear term, and
• Q is a symmetrical (n × n) positive semi-definite matrix of parameters associated with the quadratic terms.

The general structure of the calibrated model is:

$$\begin{array}{c}\underset{x\in \left[0\dots +\infty \right)}{\max }\left\{z=r\prime x-d\prime x-0.5x\prime Qx\right\}\\ s.t.Ax\le \mathrm{b}\left[\mathsf{\pi }\right],\\ \mathrm{x} \ge 0\end{array}$$

To ensure accurate calibration, the parameters of the cost function should be determined to satisfy the first-order conditions of the quadratic optimization model [51]:

C + λ = d + Qx⁰

Assuming that d = c, Q is a diagonal matrix with diagonal elements that are defined as follows:

q = λ/χ⁰

where “/” means the right division element (element-wise division). Each element of Vector l is divided by the corresponding element of vector χ⁰ (where q is the n × 1 vector of the diagonal elements of the Q matrix); we can estimate a set of parameters of the quadratic cost function that will ensure exact calibration at the base year.

2.4. Constraints and Indicators

The constraints used in our model concern total land, irrigated and nonirrigated agricultural land, CAP constraints for each crop, market constraints, constraints for labor hours, variable capital and fertilizers use, and, finally, historical and other constraints.

As mentioned in the introduction section, indicators are essential instruments for the measurement of sustainability. The indicators linked to surveys and questionnaires are an essential part of the sustainability assessment and implementation process because they reflect the perceptions of farmers. Over the last few decades, there has been much effort from organizations [13,14,15] and researchers to suggest sustainability indicators [52,53,54]. Bell and Morse [55] reviewed the value of indicators and analyzed whether it is possible to measure the immeasurable. They proposed to include a holistic approach rather than focusing only on quantitative indicators. Moreover, the choice of indicators should be determined by local conditions and the needs and priorities of the local people. In our case, many of the sustainability indicators were not available due to a lack of data. Previous studies in the region have suggested a set of indicators that can be measured on the farm level and include the three dimensions of sustainability [18,24,56]. The economic, social, and environmental indicators that were selected from these studies have been tested in practice and reflect a balance between ideal sustainability indicators and the limitations due to the availability of data. In this study, we have examined 11 indicators (economic, environmental, and social). The economic indicators are gross revenue and gross margin. The social indicators are labor use, annual work units, and seasonality. Finally, six environmental indicators were examined, and these are crop diversity, soil coverage, water use, nitrogen use, and electrical and thermal power derived from biomass [57]. The selected indicators are presented in the

Table 1. Selected indicators.

	Indicators	Units
Economic	Gross Revenue	€
	Gross Margin	€
Social	Labor Use	Hours
	Annual Work Units	AWUs
	Seasonality	hours/month
Environmental	Crop Diversity	Number of crops cultivated
	Soil Coverage	%
	Water Use	m3
	Nitrogen Use	Kg
	Electrical Power	MWh
	Thermal power	MWh

below.

3. Results

3.1. Sample, Data, and Study Area

The region of Central Macedonia in Greece was selected as the study area. The sample of the study consisted of 219 agricultural holdings, beneficiaries of Measure 121. For the collection of the technical and economic data of agricultural holdings, a survey was conducted with the use of a detailed questionnaire. The agricultural land for the region of Central Macedonia includes wheat (hard and soft; the main cultivation of the region), cotton, rice, tree crops such as peach, cherry, and olive trees. The existent crop plan of the average farm is presented in Figure 1. This crop plan is the result of the average farm from the farmers who are beneficiaries of Measure 121. All the calculations, suggestions, and results of this research refer to this average farm.

From Figure 1, we can conclude that the highest participation in the crop plan comes from hard wheat, with 27.79%. The cultivations of rice and cotton follow with 16.72% and 10.80%, respectively. Maize participates in the crop plan with 8.97% and alfalfa with 7.29%. The participation rates of cherry (5.45%), barley (5.15%), and soft wheat (5.03%) are quite similar. Sugar beets (2.45%), vetch (2.33%), peach (2.05%), olives trees (1.84%), and sunflower (1.46%) have a lower participation rate in the crop plan. Finally, a share of around 1% or below comes from tomatoes (0.92%), apples (0.85%), potatoes (0.55%), and kiwis (0.34%).

3.2. Agricultural Land Change

The implementation of the PMP model suggests changes in the agricultural land of the average farm. These agricultural land changes propose a new crop plan that is optimum for the average farm to the farmers.

Table 2. Comparison of the existent and optimal crop plan with the method of the PMP model.

	Existent	PMP Model
		Values	% Deviation
Gross margin (€)	15,699	16,398	4.5
Fertilizers use (kg)	6791	6801	0.1
Labor use (hours)	2715	2613	−3.8
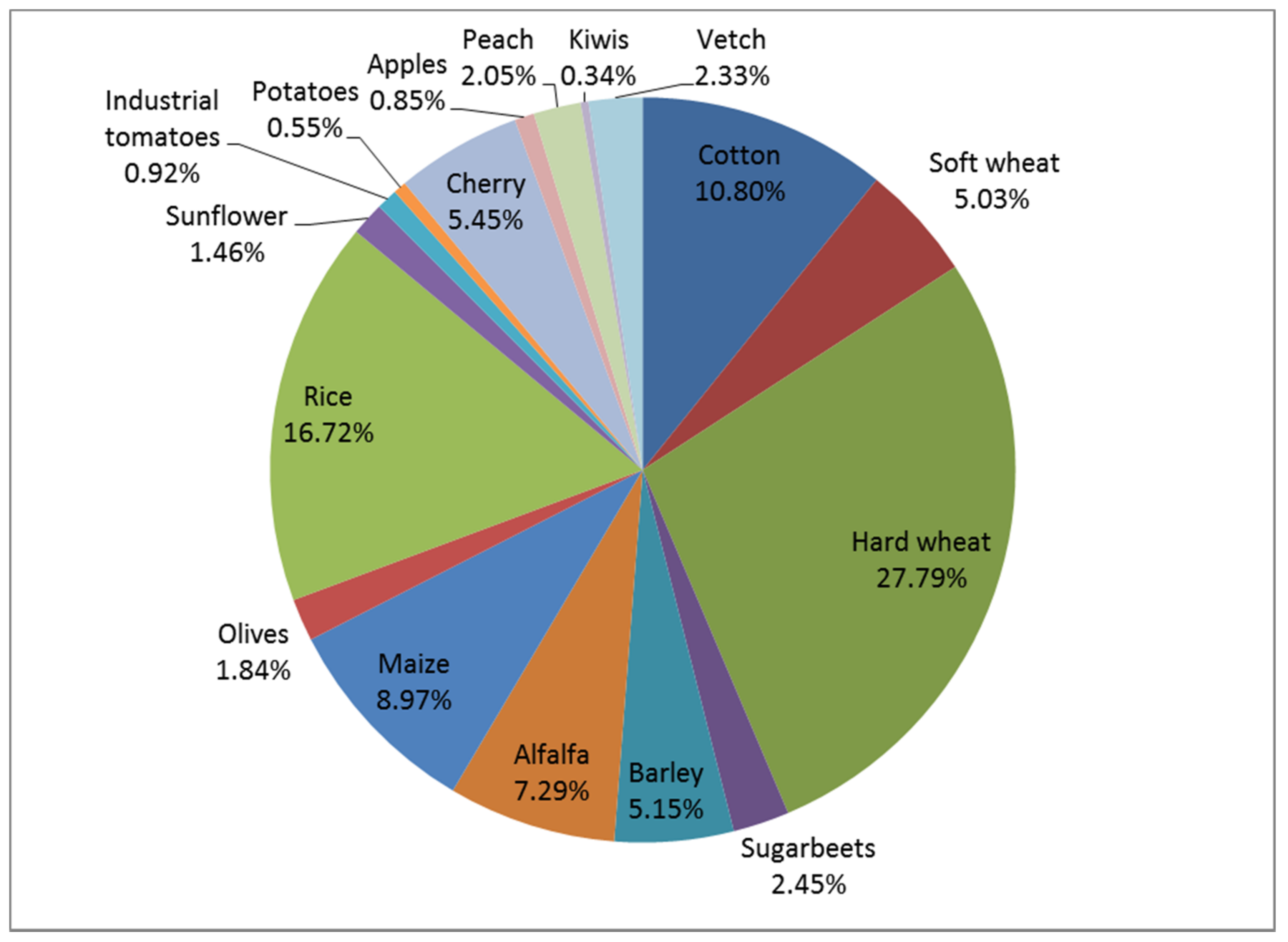
Cotton	10.80	4.00	−62.9
Soft wheat	5.03	4.96	−1.5
Hard wheat	27.79	32.48	16.9
Sugarbeets	2.45	0.00	−100.0
Barley	5.15	6.12	18.7
Alfalfa	7.29	8.74	20.0
Maize	8.97	10.76	19.9
Olive	1.84	1.93	4.7
Rice	16.72	16.55	−1.0
Sunflower	1.46	1.45	−0.4
Tomatoes	0.92	0.92	−0.2
Potatoes	0.55	0.67	20.8
Cherries	5.45	5.72	4.9
Apples	0.85	0.90	5.4
Peaches	2.05	2.15	4.8
Kiwis	0.34	0.36	4.9
Vetch	2.33	2.30	−1.3
Total	100.0	100.0

presents the suggested changes in the crop plan. The main objective of the PMP model is to maximize the gross margin. In fact, this objective was achieved. The gross margin increased by 4.5%, from EUR 15,699 to EUR 16,398. Additionally, we can see an increase in fertilizer use from 6791 to 6801 kg. On the other hand, labor use was reduced from 2715 to 2613 h (−3.8%). In detail, the abandonment of the sugar beets is proposed in the new crop plan. A decrease in the cultivated area of six crops (cotton, soft wheat, rice, sunflower, tomatoes, and vetch) can also be observed. Specifically, cotton is decreased by 62.9%, from 10.80 to 4 ha. Additionally, soft wheat cultivation is decreased from 5.03 to 4.96 ha, i.e., a decrease of −1.5%. The agricultural land of rice is reduced by 1%, from 16.72 to 16.55 ha. Crops such as sunflower and tomato, with a decrease of 0.4% and 0.2%, respectively, have lower decrease percentages. Finally, vetch cultivation has a reduction of 1.3%, i.e., from 2.33 to 2.30 ha. To all other crops, an increase is observed. The agricultural land of hard wheat is increased by 16.9%, from 27.79 to 32.48 ha. Barley (5.15 ha) increased to 6.12 ha, i.e., by 18.7%. The agricultural land of alfalfa is increased by 20%, from 7.29 to 8.74 ha. A similar growth rate is also proposed in the agricultural land of maize (19.9%), from 8.97 to 10.76 ha. The agricultural land of olive is increased by 4.7%, from 1.84 to 1.93 ha. A higher increase is shown for potatoes (20.8%, from 0.55 to 0.67 ha). The agricultural land of cherry and kiwi have similar increase rates of 4.9%; cherry cultivation is increased from 5.45 to 5.72 ha and kiwi from 0.34 to 0.36 ha. Peach cultivation is increased by 4.8%. Finally, apple cultivation is increased from 0.85 to 0.90 ha, i.e., 5.4%.

In the next section, the results of the 11 indicators (economic, social, and environmental) are presented after the application of the PMP model.

3.3. Economic Indicators

Table 3. Comparison of economic indicators

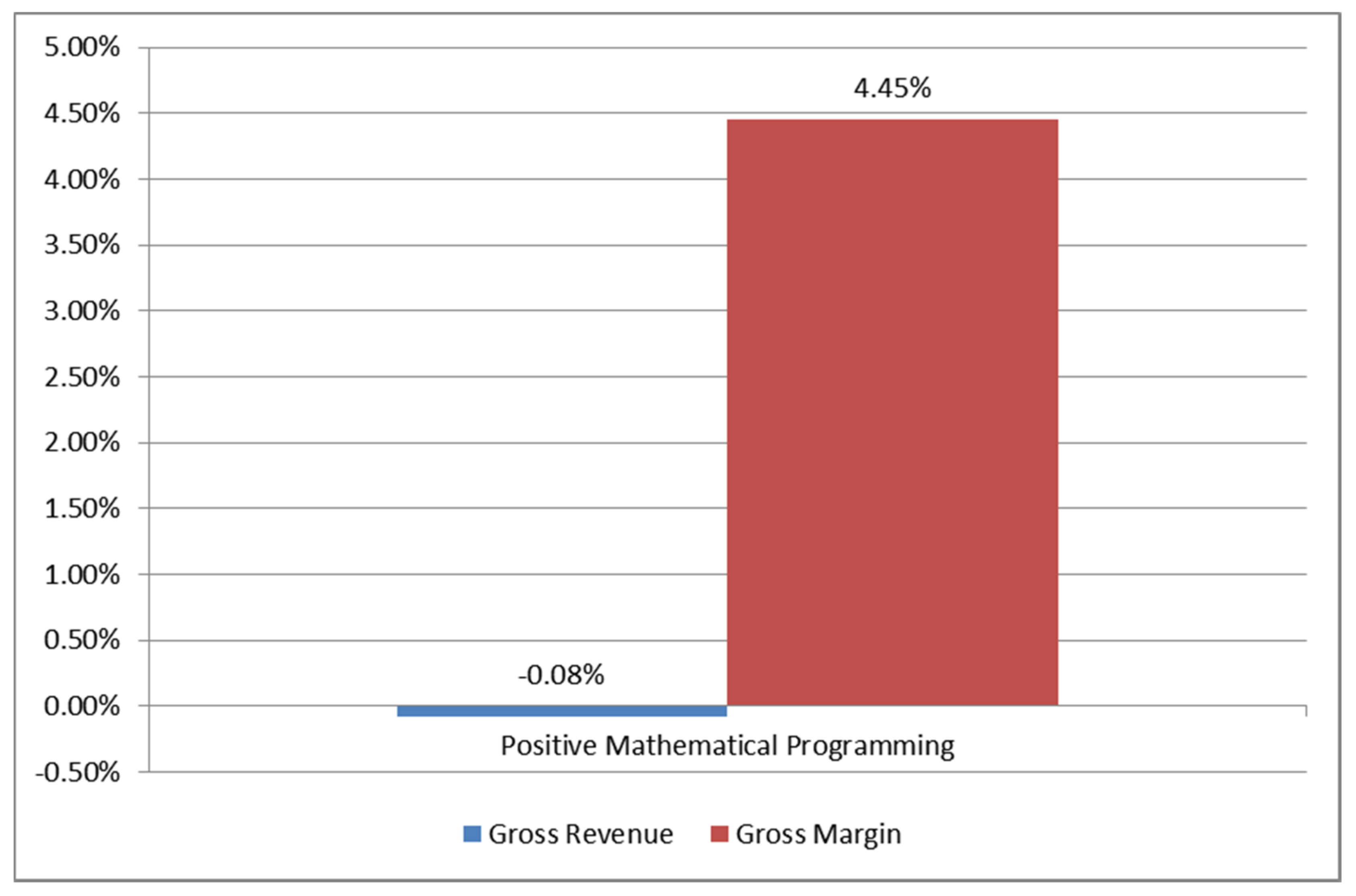
	Gross Revenue (€)	Gross Margin (€)
Existent	29,499.16	15,698.75
PMP model	29,474.66	16,398.07
Deviation	−0.08%	4.45%

shows the changes in the two economic indicators of gross revenue and gross margin. In the existent crop plan, farm income is equal to EUR 29,499.16, while in the optimum farm plan achieved by the PMP model, this is equal to EUR 29,474.66. As regards gross margin, in the existent crop plan, this is EUR 15,698.75, while in the optimum plan, this is increased to EUR 16,398.07.

The Figure 2 below shows the deviation for these two economic indicators (gross revenue and gross margin). Although there is a small reduction in gross revenue by −0.08%, gross margin is increased by 4.45%. This is due to the agricultural land crop changes. The proposed production plan includes crops with a lower variable cost, which leads to an increase in the gross margin.

3.4. Social Indicators

Table 4. Comparison of social indicators.

	Labor Use (h)	Annual Work Units (AWUs)	Seasonality (h/Month)
Existent	2714.98	1.55	226.25
PMP model	2612.72	1.49	217.73
Deviation	−3.77%	−3.77%	−3.77%

shows the changes in the three social indicators of labor use, annual work units (AWUs), and seasonality after PMP model implementation. Labor use in the existent crop plan is 2714.98 h, and, in the optimum crop plan, it is reduced by −3.77%. AWUs in the existent crop plan are 1.55, while in the new crop plan, they are 1.49. Finally, seasonality in the existent crop plan is 226.25 h/month, while this decreases by −3.77% in the new crop plan. We observe that the deviation in the selected social indicators is common for the three indicators. This is due to the fact that the social indicators are affected by the working hours, which are reduced in the proposed crop plan.

3.5. Environmental Indicators

The following

Table 5. Comparison of environmental indicators.

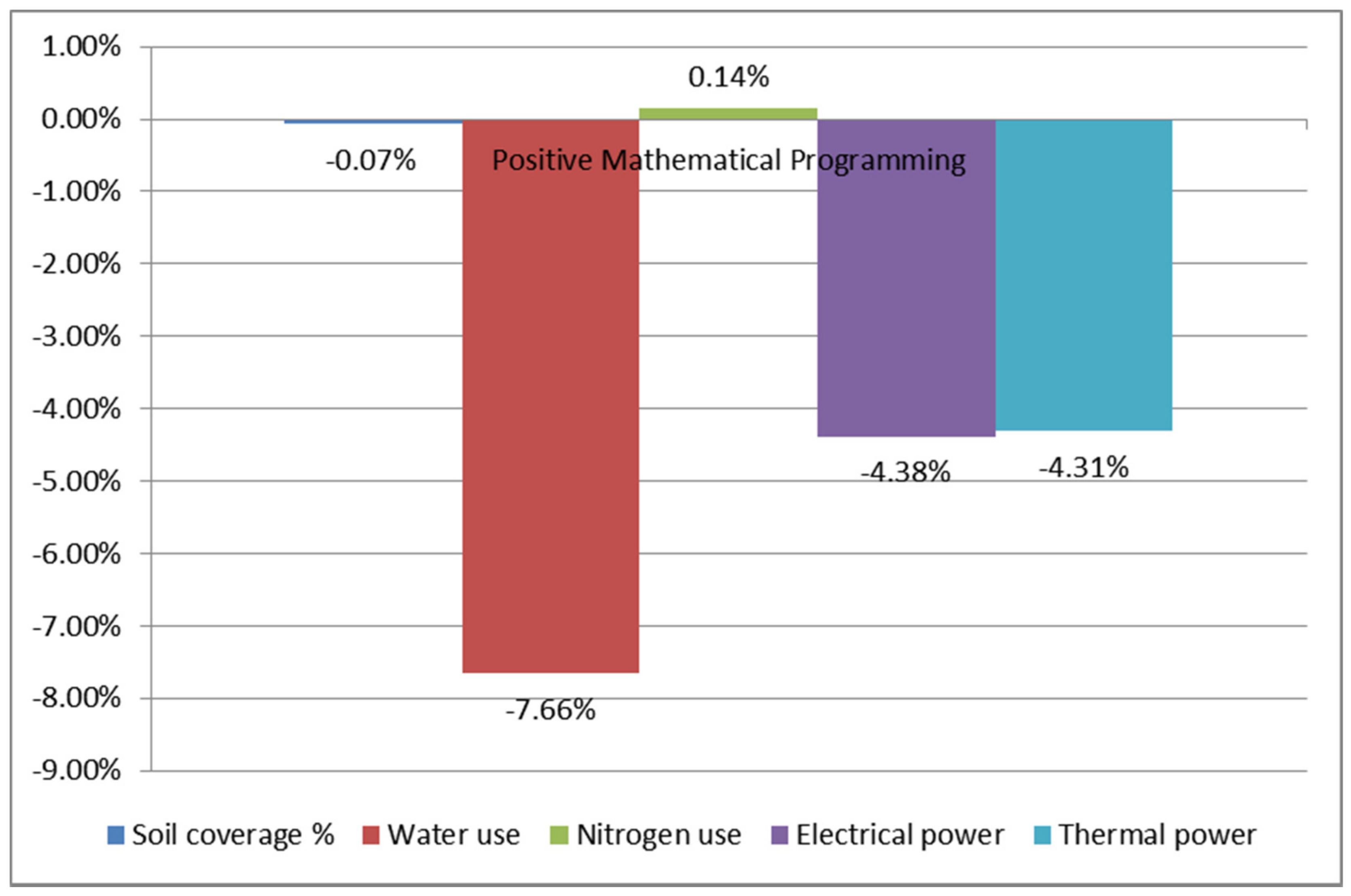
	Crop Diversity (Number of Crops Cultivated)	Soil Coverage (%)	Water Use (m3)	Nitrogen Use (kg)	Electrical Power (MWh)	Thermal Power (MWh)
Existent	17	74.84	38,435	6791.31	21.46	97.04
PMP model	16	74.79	35,491	6800.83	20.52	92.85
Deviation	−1	−0.07%	−7.66%	0.14%	−4.38%	−4.31%

shows the changes for the six environmental indicators of crop diversity, soil coverage, water use, nitrogen use, and electrical and thermal power when applying the PMP model. Crop diversity in the existent crop plan is 17, while in the optimum plan, it is 16. In the existent crop plan, soil coverage is equal to 74.84%, while in the optimum plan, it is 74.79%. Water use in the existent crop plan is equal to 38,435 m³, and this is reduced to 35,491 m³ when implementing the PMP model. Moreover, nitrogen use in the existent crop plan equals 6791.31 kg, which increases to 6800.83 kg in the optimum plan. Electrical power is equal to 21.46 MWh in the existent crop plan, and the PMP model gives 20.52 MWh. Finally, thermal power is equal to 97.04 MWh in the existent crop plan, and it is reduced to 92.85 MWh in the PMP model.

The Figure 3 below shows the changes in the environmental indicators of soil coverage, water use, nitrogen use, electrical power, and thermal power after the implementation of the PMP model. Specifically, soil coverage shows a −0.07% decrease and water use a −7.66% decrease. On the other hand, there is an increase in nitrogen use by 0.14%. Electrical power is reduced by −4.38%, while the reduction in thermal power is −4.31%.

4. Conclusions

In this study, an attempt was made to assess the impacts of Rural Development Plan measures on the sustainability of agricultural holdings. For this reason, a PMP model was developed and implemented, aiming at the optimization of the crop plan of the average farm of the sample of agricultural holdings that participated in the RDP measure under study. Eleven economic, social, and environmental indicators were estimated for both the existent and optimum plans.

From the results of the implementation of the PMP model, a number of useful conclusions were derived. The PMP model achieved an increase in the gross margin, which is considered the main goal of farmers. As regards the participation of the crops in the crop plan, the PMP model managed to reorganize the crop plan without abandoning the agricultural land for a large number of existent crops. This is one of the main advantages of using the PMP method since it uses the existent crop plan of the average farm to create the automatic calibration models. We can also draw the conclusion that the PMP model will incorporate dynamic elements into the objective function because it introduces changes in several variables (e.g., costs, prices, subsidies) and calculates them automatically by introducing the appropriate commands. For this reason, PMP can be easily adapted and used for different regions and types of farms without the requirement of additional data since the process is general and fully automated.

As mentioned above, 11 sustainability indicators were used for the assessment of the economic, social, and environmental impacts of Measure 121—“Modernization of agricultural holdings”. These indicators were calculated based on the existent crop plan, and they were compared with the results for the suggested changes in the agricultural land and the average farm crop plan. The first economic indicator examined was gross revenue, which remained stable after PMP model implementation. Regarding the ratio of gross margin, the result of gross revenue after deducting variable costs, the results show that it is increased compared to the existent crop plan. The social indicators used were labor use, the annual work units, and seasonality. Labor use and annual work units are decreased compared to the existent crop plan, and, finally, the seasonality of labor use also decreases in the optimal crop plan. The six environmental indicators used were crop diversity, soil coverage, water use, nitrogen use, electrical power, and thermal power derived from crop residues. Crop diversity in the existent crop plan consists of 17 crops, while in the optimal plan, there are 16 crops, which confirms that the PMP model reorganizes the existing crops without significant changes to the crop plan. Soil coverage in the existent crop plan and the optimal crop plan is similar, with very small deviations. The ratio of water use is reduced in the optimal crop plan. On the other hand, the ratio of nitrogen use is increased after the application of the PMP model. Electrical power and thermal power are reduced after the application of the PMP model.

The results show that the optimum farm plan of the average holding presents positive economic impacts, negative social impacts, and negative impacts in most of the environmental indicators. These results are in accordance with the results of previous studies in the region of Central Macedonia. Manos et al. [18,58] found that the economic, environmental, and social impacts of RDP measures vary between the prefectures of the region and are dependent on the crop plan of each prefecture. Additionally, Aggelopoulos and Arabatzis [59] argued that the impacts are dependent on the characteristics of each geographical region and the type of agricultural production. Finally, we can conclude that the impact assessment process has a significant role in supporting policymakers in understanding the impacts of their policies and designing their future policies.

Despite the use of the PMP model for assessing the impacts of RDP measures on the sustainability of agricultural holdings, future work on implementing different tools for the impact assessment of RDP measures and a comparison of their results should be made. Finally, the main limitation of this research is the lack of data for a number of indicators. These indicators could reflect a more integrated presentation of the sustainability of the agricultural holdings concept.