1. Introduction
Soil moisture lies at the heart of a number of societally relevant phenomena, ranging from ecosystem health and agricultural productivity to the frequency of hydrometeorological extremes like floods and droughts. However, it is also an inherently complicated field to understand and predict. Its behavior is governed not only by atmospheric drivers like precipitation and temperature, but also by overlying vegetation and the soil’s own properties (i.e., texture and porosity). As a result, many have approached the problem of predicting soil moisture with the notion that one must have considerable information about each of these factors. A number of studies have thus employed the soil water balance equation to explore the potential predictability of soil moisture based on stochastic rainfall inputs drawn from pre-determined distributions [
1,
2,
3,
4,
5,
6,
7]. However, this approach must necessarily rely on a number of assumptions to represent the many controlling factors that act on soil moisture. Parameterizations of the soil’s dry-down characteristics, the depth of the active layer, the rate at which plants remove water from the soil, the amount of precipitation interception by vegetation, and a host of others must be estimated for such a model to function properly.
To their credit, these highly detailed models are firmly rooted in physical theory and perform reasonably well when their parameters are carefully tuned for specific sites [
1,
2,
3,
4,
5,
6,
7]. However, as with any model, there are unavoidable downsides to this approach. The observations on which each parameterization is based are often lacking at sufficiently fine spatial resolution, and the process of tuning those parameters for a specific location can be a tedious, imprecise process. These complex models are also often constrained to periods wherein the moisture can be considered in steady-state for numerical tractability—that is, during the well-defined and somewhat homogeneous wet and dry seasons [
2,
5]. To predict the evolution of soil moisture at a larger, less restrictive scale, a more scalable approach may be necessary.
One alternative to relying on these sorts of numerical models is to develop simpler empirical models built solely on direct measurements of soil moisture and temperature, avoiding the need for numerous parameterizations to characterize each site and maintaining validity year-round. In other words, we might seek to understand and predict soil moisture by using the field itself as a predictor. The empirical model studied here, Linear Inverse Modeling (LIM), is also a dynamical model in that it is based on a specified equation of motion [
8]. The specified equation, however, is assumed to be simple enough that all of the relevant parameters can be estimated from measured data. We make the assumption that the dynamical system can be approximated by a linear, multivariate process driven by stochastic forcing. This approach has several advantages. Firstly, the assumption can be verified a posteriori. Next, estimates of forecast error accompany the forecasts. Further, since the linear operator estimated by LIM need not be orthogonal, exponential decay of forecast skill may be preceded by a temporary period of exceptionally skillful forecasts, depending on the initial conditions (ICs). ICs leading to these skillful forecasts can be identified in advance, leading to “forecasts of opportunity” [
9,
10,
11].
There are, of course, disadvantages to this approach, even if the dynamical assumptions are valid. Direct observations of soil moisture are prone to their own shortcomings, chief among them being the length of each record currently available. In-ground measurements of soil moisture and temperature have only been reliably collected for a handful of years now [
12,
13,
14], which limits the range of internal variability that is been captured and can hamper the verification of new models against independent data. Note, however, that the issue of verification period hampers any soil moisture model; numerous studies have been forced to rely on 1–2 years of data or less to validate their own more detailed soil models and explore spatiotemporal trends in the field [
3,
6,
12,
15]. Beyond issues surrounding record length, soil observations must also undergo some level of quality control, but the approach used for that can vary across observational networks [
14,
16] and, returning to the issue of temporal longevity, must be sustained for a number of years to ensure consistently reliable data.
It appears that a two-pronged approach to soil moisture forecasting, one that uses the extensive physical justifications of numerical models and one using the physical reality embodied in an empirical-dynamical model based on in situ observations, would be desirable. Such an approach is too extensive to be contained in a single article. Detailed descriptions of numerical hydrological models are found elsewhere; it is the purpose of this particular study to examine the predictive properties of the other prong, LIM.
This work builds on a long history of studies that have employed LIMs for probabilistic forecasting and diagnosis of global climate models (GCMs). The roots of this approach date back a few decades to when it was proposed [
17], with strong foundations in principal oscillation pattern analysis [
18,
19]. LIM extracts dynamical information about a system from its observed statistics [
8,
20,
21], a fundamentally different approach than deriving such from the governing equations of the field instead. In LIM, the system is subdivided into two components—a slowly evolving portion that is linearly dependent on the field itself, and a more rapidly varying component whose timescale of evolution is sufficiently shorter so as to be described as unresolved stochasticity. The main assumption behind LIM is thus one of dynamical linearity, which is often used in empirical and numerical models alike. Despite the variety of assumptions that underlie this approach, LIM has been shown to have demonstrable skill in predicting tropical sea surface temperature anomalies [
8,
20,
21,
22,
23] as well as in predicting atmospheric phenomena and the skill of such forecasts on subseasonal scales [
9,
10,
24].
Here, we apply the same methodology to investigate the predictability of soil moisture, using soil moisture itself and soil temperature at specified depth as predictors. It should be noted that the prediction information in other variables, such as vegetation cover, are assumed to be implicitly taken into account by using the statistics of temperature and soil moisture in the development of the prediction model. Though not discussed at length, precipitation itself is considered in the model as stochastic forcing rather than a predictand; the predictable signal in soil moisture due to precipitation is integrated into the soil temperature and soil moisture itself, yielding results that are strongly consistent with a probabilistic description of moisture. As further justification for confining our predictors to soil temperature and moisture alone, we present a test of whether the information contained in these predictors is sufficient, allowing our forecasting model to be as parsimonious as possible.
The treatment of rainfall as a stochastic process is not necessarily unique to the model proposed here, but the proposed modeling approach is structured so as to avoid assumptions regarding the distribution of precipitation frequency and amount that are often included in other soil moisture models [
2,
4,
5,
6].
Using variables (temperature and moisture) internal to the subsurface as predictors, we perform LIM forecasts and compare the average observed skill of these forecasts with LIM’s predicted skill. We further show how LIM may be employed to identify ICs for forecasts of opportunity, and provide a benchmark for the skill that could be expected in soil moisture forecasts. This estimate can then be used in the future to diagnose errors in comprehensive numerical hydrological models like those discussed above. Identical diagnostic procedures to the ones established here can be applied to numerical model output as well, with differences and similarities to these observational results used to inform improvements to those models as in previous studies [
25,
26]. Establishing a baseline predictability estimate from observations alone represents a key first step towards this goal and others.
We choose as our first subject California soil temperature and moisture in an attempt to isolate the internal predictability of these fields from the effects of atmospheric forcing on daily timescales. The soil moisture in California varies with a wet season, with the majority of precipitation occurring from late fall to late spring, and a dry season from late spring to late fall. We have now reached a point where, at least in this region, there exists a number of observing stations with a sufficiently long record of quality-controlled data (5+ years) so as to reasonably capture a range of climate variability. The northern half of the state is of particular interest not only for its economic productivity and high level of instrumentation [
27,
28], but also for its vulnerability to extremes. California suffered an intense multi-year drought from 2012 to 2015—the worst the state has seen in centuries—with the strongest impacts concentrated near the Sierra Nevada region [
29,
30]. That dry period was soon followed by a historic water year that ultimately led to the Oroville dam crisis in 2017 [
31]. Soil moisture anomaly forecasting has the potential to improve our understanding and the predictability of both drought and flood phenomena such as these.
There is one important contrast between this study and previous applications of LIM: the time series used here are point measurements rather than the spatially averaged values studied in, for example, the analysis of sea surface temperature presented by [
8]. Thus, analysis of satellite products of temperature and moisture, which represent characteristics of finite areas, would be more consistent with previous applications of LIM than this study. Further, it may be easier to use LIM applied to satellite products rather than to point measurements to derive physical parameterizations for use in numerical models, since these models represent physical variables as averages over a finite grid size. In fact, the difficult problem of how to develop numerical parameterizations from point measurements is as well-known as the difficulty in deriving predictions at a single location from gridded model results.
Nevertheless, there are compelling reasons to analyze point measurements. First, time series of satellite measurements of soil moisture are often too short to apply LIM, and even when they are long enough, specific depth information and/or corresponding temperatures are unavailable in these data sets. Further, although soil moisture estimations from the Gravity Recovery and Climate Experiment (GRACE) can extend below the surface layer (0–5 cm) [
32], other satellite retrievals (e.g., Soil Moisture Active Passive satellite: SMAP, [
33]; and Soil Moisture and Ocean Salinity satellite: SMOS, [
34]) are confined to the upper 5 cm. Most importantly, operational hydrologists at the American National Weather Service and the water management community in California use station data to monitor drought and for flash flood guidance and require products such as those we investigate here.
Apart from the intrinsic value of better understanding and predicting soil moisture in California, part of the impetus behind this work lies with recent efforts from the National Oceanic and Atmospheric Administration (NOAA) to move towards probabilistic forecasts, outlined in their Forecasting a Continuum of Environmental Threats (FACETs) program [
35]. Though FACETs has primarily focused on severe weather in the past [
35], there is now a concerted effort to expand into other phenomena and to longer timescales. The forecasting of soil moisture with inherent probabilistic-based skill estimates fits well under this expanding umbrella: it varies on timescales of weeks to months, interacts strongly with other hazards such as floods and droughts, and has potential importance for stakeholders such as reservoir operators and farmers.
The following section describes the process of creating a LIM and subsequent forecasts, as well as a brief description of the data used for this study. In
Section 3, we investigate the ability of LIM to describe the field via a stochastic linear equation, and assess the resulting predictability of soil moisture relative to a first order autoregressive (AR1) model. We show skillful forecasts of daily values on the order of 1–2 weeks. As will be seen, that predictability window is longer for ICs satisfying criteria for “forecasts of opportunity”.
Section 4 concludes the study with a summary of the key findings, a discussion of their implications, and suggestions for using these results both to diagnose numerical models and to extend analysis of empirical models.
2. Data and Methods
2.1. Soil Data
The empirical model we build is based on data from 10 land stations, located primarily in northern California. We draw from two soil networks to maximize coverage in the region: the NOAA Hydrometeorological Testbed (HMT), where five stations are used from the Russian River Valley, and the United States Climate Reference Network (CRN) as provided by the National Soil Moisture Network, which yields five additional stations (see
Figure 1 for the locations of each station and
Table 1 for their names and aliases). We also include an observing station in Santa Barbara even though it does not fall in the typically defined region of “northern” California as a means to increase data availability. We will see later that this is also a strategic choice for increasing predictability in the model. Both networks have undergone rigorous levels of quality control [
16,
36,
37], and though they use different instruments, their behavior is found to be consistent enough to warrant their combination here.
To maintain consistency between networks, all soil observations were taken at a depth of 10 cm for the period 23 May 2012 to 31 December 2017. Hourly data from the HMT network were averaged to the daily scale so as to match the temporal resolution of the CRN data. The average annual cycles in soil moisture and temperature were then calculated for each of the 10 stations independently and removed linearly from the relevant time series to isolate soil anomalies, which better capture the moisture/temperature variations than the full field itself.
Though our primary interest is in the predictability of soil moisture, soil temperature is used in addition to describe the field evolution. That is, the model we build here is based on a combination of both metrics rather than on soil moisture alone to lend additional predictive capacity. However, since these two characteristics vary with different magnitudes, we make use of their z-scores for the remainder of this analysis to allow similar contributions from each to the empirical model.
Combining soil temperature and moisture in one form or another is not a unique feature of this study; soil temperature has in fact often been used as a means of deriving soil moisture. The novelty here is that we use the moisture to remove redundant information in soil temperature, which is found to improve the predictability of the moisture field itself. A linear regression is thus carried out to isolate only the temperature residual, removing the portion of the field that is already explained by soil moisture. Thus, greater weight is given to the independent information that is found in soil temperature rather than double-counting the variability common to both soil properties. The matrix of daily, anomalous, soil temperature residuals is then combined with soil moisture to build a linear inverse model as described below.
The period of 23 May 2012–31 December 2017 was long enough to allow data denial experiments for some exploration of prediction skill. However, the entire period was employed for diagnosing skillful ICs and for hindcast experiments to measure potential predictability.
2.2. Linear Inverse Modeling: Background
We outline here the key steps used in creating the soil model, but refer the reader to previous studies for a more detailed description of LIM and the theory behind it (e.g., [
8,
17,
20,
21], and to
Appendix A for more information on the application of it here. To apply LIM, we assume that the system is linear with the relevant dynamics separated on the basis of time scales; one dynamic component—the predictable part—must occur on timescales slow enough relative the rest of the field, which varies on timescales fast enough that it can be described as unresolved stochasticity. This allows the system to be reasonably well approximated by a stochastic differential equation of the form:
where
i is the time series of soil temperature or moisture at each station
i, and
Lij is the linear operator describing the predictability of conditions at station
i stemming from knowledge of conditions at stations
j. The matrix
S contains the coefficients for the vector of white noise forcing,
, with the individual components of white noise subscripted
α. The second term on the right-hand side of Equation (1) is described in terms of the noise covariance matrix,
Q:
For simplicity, we assume in the following that
Q is independent of
, though this may not be the case everywhere. After all, there is evidence that soil moisture may affect phenomena such as precipitation [
38], which are assumed to be included in the stochastic forcing. In any case, the procedure we outline here results from deriving the best linear predictions of
in the mean squared sense [
18].
Given these assumptions, the matrices
L and
Q describe the dynamics of the system and its evolution. Their values can be determined by starting with the appropriate Fokker-Plank Equation (FPE) associated with Equation (1):
where
describes the conditional probability of finding a value at a certain time,
(
t), given the initial condition
(0). This is also called the forecast probability. When the temporal derivative on the left-hand side of Equation (3) is set to zero, the resulting stationary FPE is satisfied by the stationary probability
. Taking the moments of these FPEs allows estimation of the lagged covariance matrix
given lag
and the contemporaneous covariance matrix
, which can be combined to form the Green function
as follows:
This matrix is called the Green function because for systems governed by Equation (1) it is equivalent to exp(L) and, when operated on an initial condition (0), provides the vector () at which the forecast probability is maximized. That is, given Equation (1) with constant L and Q, is Gaussian centered on , making the most likely forecast at lead time given initial condition . For long lead times, the forecast probability converges to the centered stationary probability .
Details of how the eigenstructure of
can be used to estimate matrices
L and
Q are given in
Appendix A. These matrices are important in diagnosing the dynamical system generating the measured field
, and we shall consider them in detail for the system analyzed here in
Section 3.4. For now, we turn our attention to the use of LIM for forecasting.
2.3. Linear Inverse Modeling: Forecasts
For many measured quantities, the estimate of the stationary probability distribution
given by the histogram of measurements is in fact not Gaussian. We shall see that this is true for soil moisture in which case the forecast probabilities are not Gaussian, either. Nevertheless, it can be shown that the best linear forecast of
in the mean square sense [
18] is in fact still given by
, with
estimated as in Equation (4).
However, using Equation (4) to estimate the Green function at every lead time for which a forecast is desired is neither more nor less than forecasting by multiple linear regression. We require more than such forecasts; we require an estimation of how good the approximation in Equation (1) is to the true dynamics of the system and a prioi estimates of the expected forecast error.
Appendix A provides a method for estimating
Green functions at other leads
estimated from the original matrix
. If Equation (1) is valid, then
is theoretically independent of
(the tau test: [
8,
17];
Appendix A). In practice, issues such as undersampling, Nyquist problems that arise when
is roughly half the period of an oscillation internal to the system [
39], and omission of relevant variables can all cause failure of the tau test, even when Equation (1) is valid. Nevertheless, the better the tau test is passed (with “better” being defined by the user), the better Equation (1) is as an approximation to the real system.
In this study, we shall apply the tau test and also estimate the expected forecast error by considering the theoretically expected mean-square forecast error using Green functions
:
In Equation (5), angle brackets indicate an average over ICs
or verifications
Note that if
is strongly dependent on
, then so is
, indicating that the tau test fails. In the remainder of
Section 2, we shall assume that the tau test is passed and drop the argument
from our notation of the estimated Green function, henceforth denoted as
.
2.4. Linear Inverse Modeling: Forecasts of Opportunity
Clearly, not all forecasts have equal skill. We note from the last section that in this particular model, the only entity varying from forecast to forecast is the initial condition. Thus, since knowing when soils are likely to be anomalously wet or dry could be linked to increased predictability for floods or droughts, we would like to identify a class of ICs for which forecasts may be expected in advance to be unusually skillful. To look for these “forecasts of opportunity”, we first ask a different question: what initial condition leads to the forecast at lead
with the largest amplitude? This initial condition, or “optimal structure” (defined below), has been explored by many authors [
8,
40,
41,
42,
43,
44] as a mechanism for growth, called “optimal growth,” in geophysical systems. A brief description of optimal growth is provided here while a more detailed discussion is provided in
Appendix B.
Optimal growth occurs when the eigenvectors of a linear system (i.e., their modes) are not orthogonal. The modes of
L in Equation (1) all correspond to eigenvalues with negative real parts. Without forcing, then, the time series coefficients of these modes decay exponentially. However, because the imaginary parts of the eigenvalues are generally nonzero, and modes themselves are not orthogonal, the amplitude of the system as a whole can temporarily grow even without forcing. To illustrate, consider a system with three modes corresponding to a purely decaying eigenvalue and to a complex conjugate pair, as illustrated in
Figure 2. The complex conjugate pair of modes is basically the same physical mode, but requires two degrees of freedom to describe it. In
Figure 2a, the vector A represents the length of the complex mode and vector B represents the purely decaying mode, orthogonal to A. After some time, A has rotated and decayed to A’, and B has decayed to B’ (
Figure 2b). The vector sum A’ + B’ now has a smaller magnitude than the initial condition A + B. Now consider
Figure 2c, showing the same complex mode A, but another purely decaying mode C, which is the same length as B but is
not orthogonal to A. After some time, C has decayed to C’ having the same length and decay time as B’, and A has decayed to A’ as before (
Figure 2d). However, the magnitude of A’ + C’ is now larger than that of the initial condition A + C. Of course, without forcing, the modes will continue to decay and so this growth is only temporary.
In our model, the only forcing is stochastic. Thus, any
predictable growth in the system is of this non-normal type. The optimal structure is then the initial condition consisting of the optimal combination of modes leading to the maximum amount of growth. As discussed in
Appendix B, the optimal structure
1 for a forecast at lead
is the leading eigenvector of
, and the variance of the forecast field
is amplified over the variance of
by a factor given by the corresponding eigenvalue
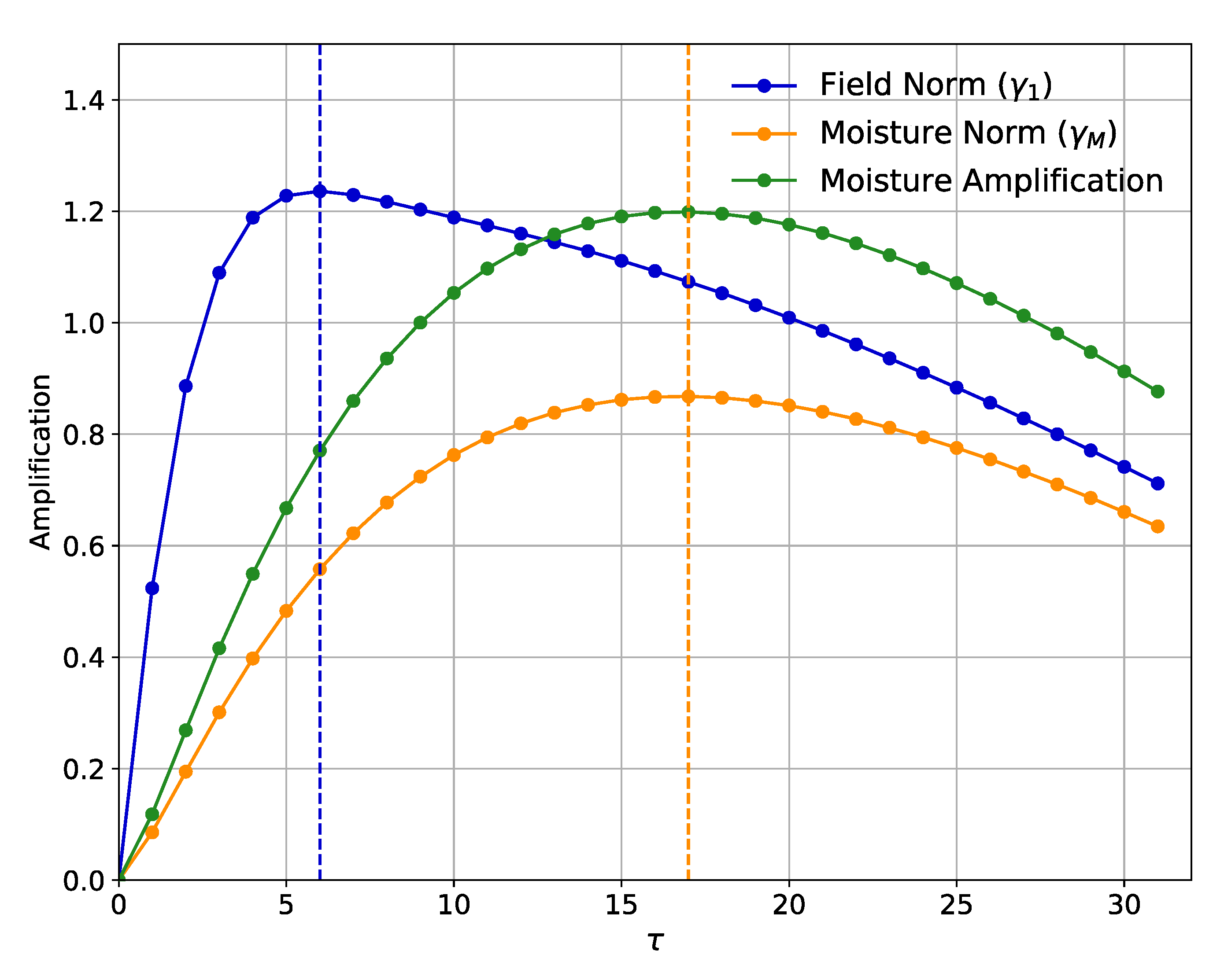
. Typically, a graph of
vs.
has a maximum at lead time
peak; this curve is thus called the Maximum Amplification Curve.
Having estimated an optimal structure, which we normalize to unity, it is possible to generate a histogram of projections of the observed field onto the structure of
. In previous studies involving LIM forecasts (e.g., [
9,
10,
11] it has been shown that forecasts based on ICs with strong positive or negative projections onto
1 are also the most skillful. Recalling that each vector in the timeseries is a candidate initial condition, we shall show that ICs in the upper tercile of the histogram of |
(
t)| are indeed more skillful than other forecasts; forecasts based on this class of ICs are therefore called “forecasts of opportunity in the field norm,” consistent with previous work cited here.
In this study, we are less interested in forecasts of the combined soil temperature and soil moisture field than in forecasts of the soil moisture by itself. We do, however, wish to take advantage of whatever additional predictability soil temperature can give forecasts of moisture. It is possible to find an optimal structure which maximizes the growth of moisture alone, regardless of how soil temperature evolves, by employing a “moisture norm” N that excludes forecasts of temperature from estimation of the optimal structure. That is, we use a procedure identical to that discussed above with the modification that the optimal structure in the moisture norm is the leading eigenvector M of , corresponding to leading eigenvalue . As with the field norm, forecasts of opportunity in the moisture norm are based on ICs with relatively strong values of |(t)|.
4. Conclusions and Discussion
Accurate forecasts of soil moisture have the potential to advance the forecasting of floods and flash droughts, and could offer tangible benefits for reservoir and agricultural operations. However, prior attempts to craft these predictions have been hampered by a reliance on imprecise model data, unsatisfying parameterizations of soil and vegetation properties, and/or the necessity of careful site-specific model calibration. Here, we test the predictability of soil moisture using an approach new to the field of terrestrial hydrologic forecasting, linear inverse modeling, which has been used for a number of years in oceanic and atmospheric topics [
8,
20,
21,
22,
23].
The application of LIM in this context is shown to maintain skill in soil moisture hindcasts for lead times of 1–2 weeks when built on observations of soil temperature and moisture across a network of 10 stations in California. That skill can be extended by utilizing a critical piece of information produced by the model: the optimal structure. This is the set of ICs at each station that would lead to the maximum amount of growth in soil anomalies, and when projected onto the observed ICs can give an estimate of how good the forecast will be at the time of its creation. We thus follow in the footsteps of previous studies [
9,
10,
11] to identify forecasts of opportunity; if the magnitude of that projection is in the upper tercile of all those observed, the forecast is expected to have higher than average skill. Indeed, this approach extends the length of time for which forecast skill can be maintained in an MSE sense, ranging from 8–20 days between stations. Those ICs that fall into this upper tercile offer additional avenues for further exploration to better understand which synoptic conditions tend to create these opportunities and their potential for acting as early warnings of highly anomalous soil moisture conditions.
The timescale of predictability found here when using only direct, in-ground measurements of soil temperature and moisture align well with previous predictability studies. [
13], using a soil water balance model and observed forcings (i.e., precipitation, evapotranspiration, etc.), found that soil moisture could be skillfully forecast to a one-week lead time in Switzerland. They also note that incorporating additional information, such as snow melt or seasonal forecasts of relevant moisture forcing, could double that predictability time scale. Incorporating additional environmental variables in this manner may thus improve the predictability estimated by LIM, but we have chosen to focus here on establishing a baseline for the internal predictability of the system without including atmospheric forcing as a predictor.
There are additional opportunities to refine and improve the model introduced here, as well. In the course of assessing the underlying soil temperature and moisture data used to build this LIM, it was found that while soil temperature residuals are roughly Gaussian, soil moisture as a whole is in fact strongly non-Gaussian (not shown). The model created here may thus benefit from accounting for the non-Gaussian nature of moisture itself, potentially through considering combinations of additive and multiplicative noise. This does, however, complicate the model and its implementation and is thus reserved for future analysis.
The results presented above thus represent only the first step in improving our predictions of soil moisture evolution in California. There are a number of features in this model that deserve to be explored more fully. Why do certain stations play a larger role than others in determining the growth of the field? Why do some grow more strongly than others after days? Which environmental factors are the driving forces behind the slow and fast growth components of the model? Additional considerations expand beyond just this region and model—does this type of analysis perform similarly well in other California regions, such as the Sierra Nevada range? Can we expand to different states, and what are the scale limitations on data inclusion in a single application of LIM? Additionally, perhaps most importantly, how can these forecasts be most usefully employed to benefit stakeholders in the region?
As in any modeling study, the above results are limited by a number of factors. The length of each station’s soil record has regrettably hampered some of our efforts to understand soil moisture in the region, and in particular limits model validation efforts. Quality can also be an issue. For this reason, we have been selective (at least to the extent possible in the face of limited data) in which observations are used and rely only on well quality-controlled data. Future studies may benefit by assessing the sensitivity of results when incorporating remotely sensed or modeled data.
By construction, LIM also simplifies the driving forces behind soil moisture growth and decay into two single matrices,
L and
Q; there is not a quick and easy way to determine when rainfall, soil properties, or plant function are the primary culprit for altering soil conditions. That said, there does exist the potential to diagnose the stochastic forcing,
Q, through temporally higher resolution observations and/or model output [
45]. Though these are all critical things to consider and a number of tasks remain to be accomplished, we reserve such for future work in the interest of first introducing an innovative method for producing realistic estimates of soil conditions on multi-week timescales.
We suggest that the performance of LIM shown here is a strong argument for further exploring its use in the context of soil moisture predictability. One particularly interesting avenue for future exploration pertains to the ability of numerical models to capture similar features of predictability as those shown here. We hope these initial observational results will inspire researchers to assess soil moisture evolution in numerical models, including NOAA’s National Water Model [
46]. By applying the same LIM approach to model output as we did to observations, one has the opportunity to investigate how well the model captures realistic soil moisture growth, at least at a series of point-based measurements. Because of the increased spatial coverage and length of model-derived data, one can also investigate the effects of increasing spatiotemporal resolution on soil moisture predictability in this manner.
Soil moisture forecasting, particularly in the western United States, is a topic likely to continue growing in importance as climate variability increases and the threat of more frequent/intense hydrometeorological extremes looms larger in the coming decades [
47,
48]. In the face of these changes, LIM is uniquely situated to aid the development of simple and adaptable approaches to understanding soil moisture anomaly growth using observations and/or model output in these critical regions.