A Joint Bayesian Optimization for the Classification of Fine Spatial Resolution Remotely Sensed Imagery Using Object-Based Convolutional Neural Networks

Abstract

In recent years, deep learning-based image classification has become widespread, especially in remote sensing applications, due to its automatic and strong feature extraction capability. However, as deep learning methods operate on rectangular-shaped image patches, they cannot accurately extract objects’ boundaries, especially in complex urban settings. As a result, combining deep learning and object-based image analysis (OBIA) has become a new avenue in remote sensing studies. This paper presents a novel approach for combining convolutional neural networks (CNN) with OBIA based on joint optimization of segmentation parameters and deep feature extraction. A Bayesian technique was used to find the best parameters for the multiresolution segmentation (MRS) algorithm while the CNN model learns the image features at different layers, achieving joint optimization. The proposed classification model achieved the best accuracy, with 0.96 OA, 0.95 Kappa, and 0.96 mIoU in the training area and 0.97 OA, 0.96 Kappa, and 0.97 mIoU in the test area, outperforming several benchmark methods including Patch CNN, Center OCNN, Random OCNN, and Decision Fusion. The analysis of CNN variants within the proposed classification workflow showed that the HybridSN model achieved the best results compared to 2D and 3D CNNs. The 3D CNN layers and combining 3D and 2D CNN layers (HybridSN) yielded slightly better accuracies than the 2D CNN layers regarding geometric fidelity, object boundary extraction, and separation of adjacent objects. The Bayesian optimization could find comparable optimal MRS parameters for the training and test areas, with excellent quality measured by AFI (0.046, −0.037) and QR (0.945, 0.932). In the proposed model, higher accuracies could be obtained with larger patch sizes (e.g., 9 × 9 compared to 3 × 3). Moreover, the proposed model is computationally efficient, with the longest training being fewer than 25 s considering all the subprocesses and a single training epoch. As a result, the proposed model can be used for urban and environmental applications that rely on VHR satellite images and require information about land use.

1. Introduction

As a source of understanding of socio-economic functions or activities in complex urban areas, land-use/land-cover information is critical for effective urban planning and management, government policymaking, biodiversity protection, and population activity monitoring [1,2,3]. Urban land-use maps are also commonly used in simulations of urban growth and road transportation models [4]. In environmental applications, urban land-use information is critical for understanding the dynamic interactions between environmental changes and human activities [4]. Modern techniques, such as remote sensing, have opened up new avenues for extracting detailed information on urban land use [5]. Remote sensors capture highly complex and heterogeneous urban features that include the contrast of anthropogenic urban and semi-natural surfaces. The same urban land-use types (e.g., buildings) are frequently distinguished by distinct physical properties or land-cover materials (e.g., made of different roof tiles), and different land-use categories may exhibit the same or similar reflectance spectra and textures (e.g., asphalt roads and parking lots) [6].

Urban land-use information is presented as patterns or high-level semantic functions in satellite images [7]. Some low-level ground features are frequently shared by various land-use categories. As a result, classifying satellite images into different land-use classes is regarded as a difficult task. A large number of previous studies have presented methods for classifying urban land use [4,8,9,10,11,12]. The methods are mostly based on accurately representing spatial patterns or structures in remote sensing data.

Pixels, objects, patches, and scenes are the four types of spatial unit representation used in urban land-use classification methods. Pixel-level methods are solely based on spectral information. They can classify land cover, but their use in urban settings is limited. These methods induce uncertainty and “salt-and-pepper” effects in classification results, especially in high-spectral-heterogeneity regions [13]. Spatial and textural information can be extracted through moving kernel windows [14]. The problem with this method is that it requires the predefinition of arbitrary image structures, whereas actual objects in the real world may be irregularly shaped [15]. As a result, object-level methods are preferable to moving kernel windows because they allow image objects to be defined spatially in the real world [16]. Objects are created by segmenting image pixels based on spectral, spatial, and contextual information. Object-based methods make use of both within-object (spectral, texture, and shape) and between-object (connectivity, contiguity, distances) information. Due to the inability to use low-level features in semantic feature representation, methods that use only within-object information tend to overlook semantic functions or spatial configurations. As a result, other researchers have used both within-object and between-object information to address the issues raised [3]. Land-use units, such as cadastral fields or street blocks, are used to group objects based on their spatial context (derived using spatial metrics). The issue with these methods is that the land-use units may be inaccessible in some areas. Another difficulty is describing and characterizing the spatial context as a set of rules. Complex structures or patterns can be recognized and distinguished by human experts. Rule-based methods, on the other hand, are incapable of learning effective high-level features. As a result, methods capable of learning land-use semantics via high-level feature representations are currently being used in land-use mapping from remote sensing data. The most common approach to achieving that is deep learning. However, recent studies showed that combining OBIA with deep learning achieves the best classification accuracy, with consistent semantic results [17,18,19,20,21].

The main objective of this study is to develop a novel object-based convolutional neural network (OCNN) model for extracting land use and land cover from fine spatial resolution satellite imagery using a joint Bayesian optimization approach for learning the best segmentation parameters and classifying the image data employing deep learning methods. The following sub-objectives are addressed to achieve the main objective:

• Establish an image segmentation using the multiresolution segmentation (MRS) technique to help classification tasks by providing additional spatial and contextual features.
• Construct a CNN model to extract low- and high-level features.
• Employing joint Bayesian optimization to find the best segmentation parameters and updating the CNN’s network weights by transfer learning.
• Apply decision-level fusion based on best segmentation output, using Gaussian filtering to further improve the quality of classification results.

The organization of this paper is as follows: in Section 2, the related works are reviewed and discussed. Section 3 presents the study area, datasets, and adapted methodologies. Section 4 presents the results from this research and discussions. Section 5 summarizes the research’s conclusions and potential directions for future work.

2. Related Work

Object-based and deep learning methods have been considered the dominant paradigm for remote sensing image classification over the last decade [22]. OBIA methods require manual selection of object attributes, which is subjective. On the other hand, deep learning methods, due to their hierarchical abstract nature, lack capturing of the precise outline of different objects at the pixel level. As a result, there are several ways to integrate them for land-use and land-cover classification which are discussed in previous works. They can be categorized into the following techniques.

2.1. Deep Learning Based on Object-Level Features

Pixels are the fundamental spatial unit representation in many remote sensing applications. However, many recent studies have found that OBIA methods perform better due to the additional spatial and contextual features generated by segmenting the image data into several homogeneous regions [23]. The features extracted at the object level can be used to perform classification tasks using classical statistical methods, machine learning, and deep learning methods. The issue with these methods is that the OBIA features are represented as tabular data. Deep learning methods were previously thought to be ineffective for tabular data [24]. Nonetheless, several recent studies have attempted to optimize deep learning performance for tabular data [25,26,27]. However, the problem with integrating deep learning with object-level features represented as tabular data is that (1) OBIA features are extracted manually, many of which may be irrelevant to the classification task at hand, (2) under- and over-segmentation have a significant impact on the features calculated, and (3) the spatial characteristics of image pixels are not effectively represented in the classification model. It is also difficult to hand-craft abstract features (edges, textures) that may be useful for classifying image data using these methods.

Nevertheless, this integration approach could outperform classical machine learning methods. For example, in a study by [9] Jozdani et al. (2019), such models performed better than other traditional machine methods in terms of the classification of urban land cover in the United States. Such integrated models also achieved accurate results for road detection in orthophotos [28] and weed species identification and detection in a challenging grassland environment [29]. A large number of spectral, spatial, and contextual features can be extracted from segmented objects; some may not be relevant to the classification task. In this case, CNNs with one-dimensional (1D) kernels were used to fine-tune the feature before the application of the final classification [30]. The approach with features fine-tuned by the CNN outperformed the other feature-selection approaches, i.e., the Random Forest feature-importance ranking and recursive feature elimination.

2.2. Feature-Level Fusion

OBIA provides features at the image object level which can be computed manually after image segmentation is performed. On the other hand, deep learning models enable the extraction of deep abstract features from images automatically. Feature fusion can be performed to make use of both OBIA-based features and deep features, which may help to improve the classification results. This approach is often implemented as a two-branch computational network which contains a processing chain to perform segmentation and OBIA feature extraction and a network to learn deep and abstract features from the data. After combining the two feature sets, a classifier such as tree-based models or Support Vector Machines (SVM) is used to obtain class labels for the image pixels [21,31]. Li et al. [32] developed a novel hybrid model called (OSVM-OCNN) used for the classification of crops. Their model combines a shallow-structured (OBIA-SVM) model and a deep-structured (OBIA-CNN) model. The developed OSVM-OCNN effectively extracts low-level and high-level information within image objects. They suggest that the developed approach is an efficient tool to overcome the challenges of remote sensing-based crop classification methods. Sutha et al. [33] combined SVM and CNN to perform the classification of high-resolution remote sensing images, aiming to improve classification accuracy. Hong et al. [34] used the common multiscale segmentation algorithm to extract multiscale low-level image features and a CNN to obtain deep features from the low-level features at each scale, respectively. An approach to extract tree plantations from very-high-resolution remote sensing images was proposed by Tang et al. [35]. They used an integrated OBIA-CNN framework to achieve that. They performed image segmentation to obtain OBIA features and a fine-tuned CNN to obtain deep features. To reduce the computation time of the model, they conducted feature selection based on the Gini index. The tea objects were then classified by a Random Forest (RF). The basic problem of this integration method is heavy computation [36]. Other problems associated with this integration method include duplication in some features extracted by OBIA and CNN such as shape, texture, and color.

2.3. Decision-Level Fusion

Decision-level fusion techniques are also known as post-deep learning classification refinement [37]. In these methods, a deep learning model is used to establish a classification map of the study area first. The results are then refined by majority voting based on segmentation. Each object contains several pixels with class labels predicted at the pixel or patch level by a deep learning model. Finally, each object is assigned a single label depending on the most frequently occurring class labels within that object. Zhao et al. [21] presented an integrated OBIA and deep learning model to precisely classify three images representing urban scenes: Vaihingen (Germany), Beijing (China), and Pavia (Italy). Their results indicated that the integrated OBIA-deep learning model has the ability to identify and extract different types of buildings such as residential and commercial buildings with an accuracy over 90%. Abdi et al. [38] proposed a method to refine a classification map produced by a CNN using image segmentation. They showed a significant improvement in classification accuracy over other traditional classifiers. Liu et al. [37] developed a new approach to optimize land-cover mapping, they used a post-classification technique based on the segmentation resulting from OBIA classification to refine the result of image classification based on a CNN algorithm by labeling each image object according to the dominant land cover type of its pixels. Their method outperformed traditional classification methods such as OBIA-Random Forest (RF) and OBIA-Support Vector Machine (SVM). Robson et al. [39] applied a combination of OBIA and CNN to identify rock glaciers in mountainous landscapes. Timilsina et al. [40] studied urban tree cover changes and their relationship with socioeconomic variables. In their approach, OBIA was used to refine and improve the tree heatmap obtained by a CNN. In addition, He et al. [41] incorporated multiresolution segmentation into the classification layer of U-net and DenseNet architectures for land-cover classification. They also used a voting method to optimize the classification results. While studies have highlighted the significance of decision-level fusion techniques, this method does not fully utilize the OBIA method, as no features are used for classification. More recently, Bengoufa et al. [42] used such an approach for rocky shoreline extraction from Pleiades satellite images.

2.4. Deep Learning with Context Patches

Traditional deep learning models (for example, CNN) operate on rectangular image patches of a fixed size (e.g., 24 × 24). While these methods outperform traditional pixel-based methods and OBIA alone, they are ineffective at accurately extracting object boundaries. As a result, several studies have proposed using context patches created by object centers, random point (s) within image objects, object skeletons [43], or, more recently, region-based voting methods. The idea behind these new methods is to use image objects generated by a segmentation algorithm to create image patches from which a deep learning model can extract features and then perform classification. According to studies, such methods can more accurately classify data at object boundaries. Furthermore, such methods have a lower computational cost than traditional rectangular patch-based methods. The segmentation step, on the other hand, has a notable effect on the accuracy of the preceding methods. Objects delineated from remote sensing imagery vary widely in size in most cases, resulting in large object representations failing to capture small ground objects (e.g., urban trees, small buildings, bridges on the water). Martins et al. [43] tested integration between CNN and multiscale object-based methods for image classification at regional level and heterogeneous landscapes. For extracting convolutional positions, they used a skeleton-based algorithm for CNN predictions. The method on their newly developed datasets, i.e., IowaNet, presented a classification accuracy of 87.2%, which is considered better than other methods such as fixed-input (OCNN) and patch-based CNN, which achieved accuracies of 81.6% and 82%, respectively. Misclassification was detected in some classes, such as shadow versus lake or road versus buildings. The main limitations of the (multi-OCNN) approach are that it is affected by the number of image bands (i.e., aerial photos) and the quality of segmentation. Li et al. [18] proposed a Scale Sequence Object-based Convolutional Neural Network (SS-OCNN) that classifies images at the object level. These segmented objects were subsequently classified using a CNN model integrated with an automatically generated scale sequence of input patch sizes. This scale sequence can effectively fuse the features learned at different scales by progressively transforming the information extracted at small scales to larger scales. Experimental results revealed that the SS-OCNN consistently achieved the most accurate classification results. Lv et al. [17] developed a model based on the improved object-based convolutional neural network (IOCNN) used to classify very-high-resolution imagery sources with convolutional position sampling and zone-division techniques. This model is able to classify objects that have irregular shapes. The final result indicated that the IOCNN model is considerably more accurate than state-of-the-art models. The IOCNN model achieved classification accuracies 91.65% and 93.49% on two different images.

2.5. Deep Learning with Filtered Patches

There are several ways to transform or filter the information contained in image patches before passing them to a deep learning model. These can be based on summary statistics or even utilizing ancillary data (image segments). The motivation behind this process is to achieve heterogeneous image patches. Pan et al. [44] proposed an object-based heterogeneous filter integrated into a CNN to overcome the limitations of jagged errors at boundaries and the expansion/shrinkage of land-cover areas originating from CNN-based models. More recently, Wang et al. [45] proposed adaptive patch sampling to map the object primitives into image patches along with the object primitive axes. The methods based on image patch filtering or image object filtering aim to improve the model’s ability to classify the precise edge of ground objects correctly with some filtering methods that can be applied to image patches or image objects. While some studies have reported improvement in classification accuracy using this method, the challenge remains to best map image objects into image patches.

Research gap and aim of this research: There have been no assessment studies that compare the effectiveness of each of the methods listed above. Nevertheless, different streams of study are being pursued to improve the performance of each method. To that end, this study develops a novel classification technique based on decision-level fusion, to resolve the fundamental issue with methods in this category, namely, that the “segmentation step is independent of feature extraction and classification”. For accurate image classification, the proposed model learns the best segmentation parameters and high-level features jointly.

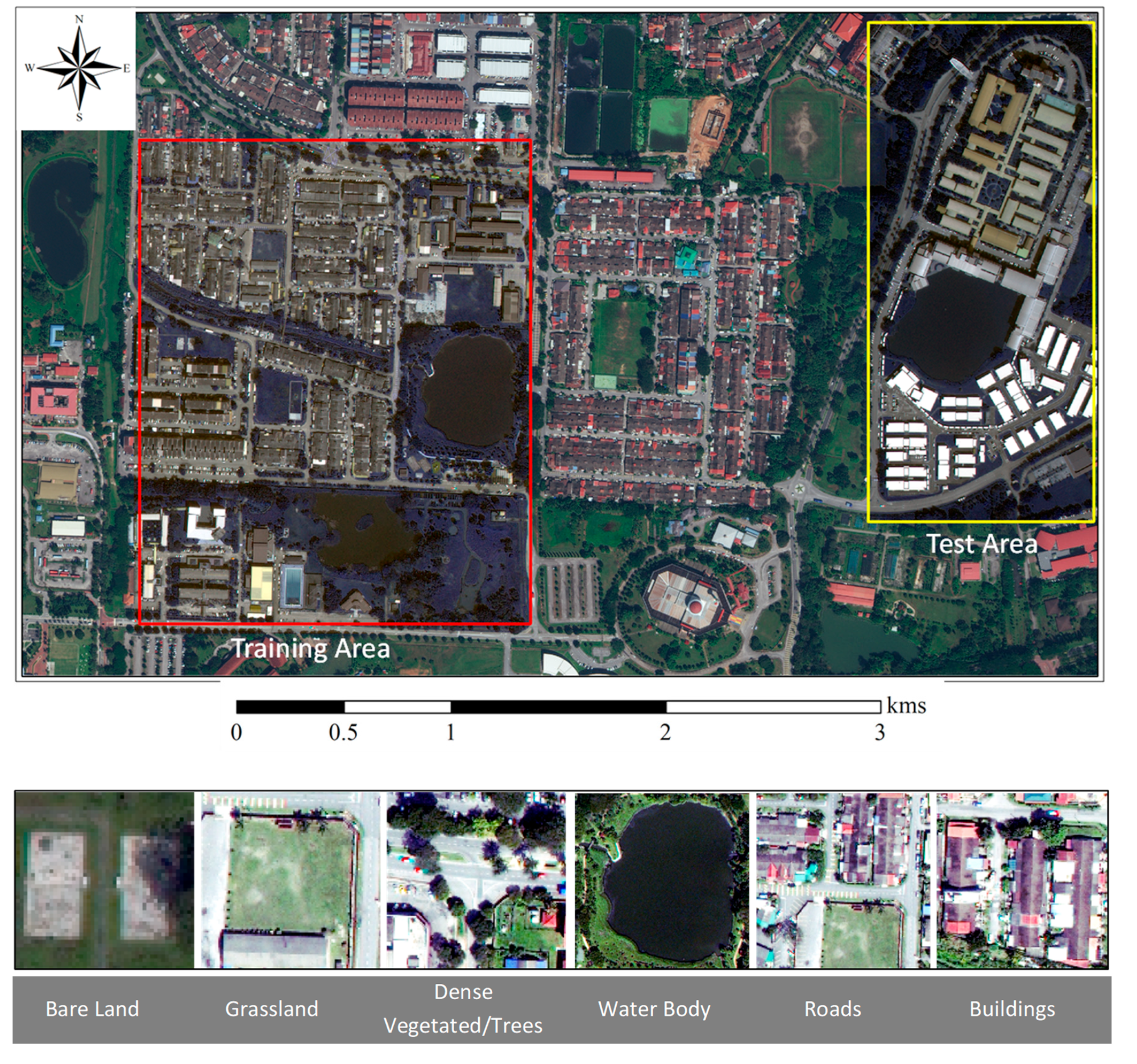
3. Study Area and Dataset

The Worldview-3 satellite image data used in this study were obtained over the Universiti Putra Malaysia (UPM) campus in Selangor, Malaysia (3°0′8.0181” N, 101°43′1.2172” E). The data were taken in November of 2014 by the Digital Globe. The spatial resolution of Worldview-3 image data is 0.31 m for the panchromatic band and 1.24 m for the multispectral bands. The dataset includes eight spectral bands with radiometric resolutions of 11 bits each: coastal, yellow, green, blue, red, red edge, near-infrared1 (NIR1), and near-infrared2 (NIR2).

Figure 1 depicts the training and test areas selected from the image of the study area. There are various types of land cover in the area, including bare lands, grasslands, water bodies, roads, buildings, and dense vegetation/trees. Roads and buildings are the most dominant land-cover classes in the area. Figure 1 depicts some examples of these land-cover types within the study area. The ground-truth data were obtained in the form of land-use and land-cover map in shapefile file format. The Department of Survey and Mapping Malaysia (JUPEM) prepared the data in 2015. Figure 2 depicts the ground-truth data for the training and test areas. In the area, there are six land-cover types: bare land, grassland, road, building, dense vegetation/trees, and water bodies.

Table 1. Training and test data class distribution (i.e., number of pixels and area percentage) in the ground-truth dataset.

Land-Cover Class	Pixels		Percentage
	Training Area	Test Area	Training Area	Test Area
Buildings	275,441	144,260	26.10%	23.90%
Roads	288,816	191,106	27.36%	31.66%
Grassland	168,018	87,707	15.92%	14.53%
Dense Vegetation/Trees	215,104	111,872	20.38%	18.53%
Water Body	85,762	54,183	8.13%	8.98%
Bare Land	22,284	14,469	2.11%	2.40%
SUM	1,055,425	603,597	100.00%	100.00%

shows the training and test data class distribution (i.e., number of pixels and area percentage) in the ground-truth dataset.

4. Methodology

4.1. Data Preprocessing

The WV-3 image data were subjected to standard preprocessing steps such as radiometric calibration, and atmospheric and geometric corrections [46]. To correct errors caused by sensors or the satellite, radiometric correction is required. This study used the quick atmospheric correction module available in Exelis Visual Information Solutions (ENVI) for atmospheric calibration (Boulder, CO, USA). Atmospheric correction converts image pixel values to surface reflectance to compensate for atmospheric degradation. Geometric distortions in the image include the rotation of the earth during image capture and the curvature of the earth, which can be corrected with geometric correction. To perform the geometric correction, 13 ground control points (GCPs) were collected from Google Earth imagery at clear positions (road intersections, building corners) and used to geo-reference the image’s geographic location. The geometric correction’s precision was 0.6 pixels (root mean square error). The data were projected to the Universal Transverse Mercator World Geodetic System 84 datum.

4.2. Image Segmentation

Image segmentation aims at generating image objects that can be used to help classification tasks by providing additional spatial and contextual features. This process is a key component of OBIA. There are several segmentation algorithms applied in remote sensing including multiresolution segmentation (MRS) [47], mean shift [48,49], watershed methods [50,51], and simple linear iterative clustering (SLIC) [52]. However, MRS (first proposed by Baatz in 2000) [53] is the most common approach used for fine spatial resolution image segmentation [54]. Thus, it was used for the OBIA process in this study.

MRS is a bottom-up multi-scale segmentation that generates the objects using an iterative algorithm, which minimizes the average heterogeneity of image objects weighted by the size. It has three critical parameters that need to be set to control the growth of the generated objects: scale, shape, and compactness. The scale and shape parameters are defined as the maximum allowed heterogeneity and textural homogeneity in the resultant image segments. Likewise, the last parameter is used to optimize segments relating to their compactness, aiming for relatively compact segments [55,56]. The scale parameter controls the size of the generated image objects. For a certain scale value, the size of the image object is larger for homogeneous data, whereas the size of the image object is smaller for heterogeneous data. The relationship between color and shape criteria influences by the shape parameter value. The color standard can be adjusted and set by selecting a suitable value for shape criteria. The compactness of an image object can be defined by the product of the width and the length over pixels numbers.

The algorithm starts from individual pixels and then groups these pixels until the predefined parameters are satisfied or a stopping criterion is reached [57]. The merging cost function integrates spectral and shapes heterogeneity, as shown in Equation (1).

$${f=w \times h}_{color}+\left(1-w\right){ \times h}_{shape}$$

(1)

where $w$ belongs to weight for spectral heterogeneity with the interval 0–1, and $h_{shape}$ and $h_{color}$ refer to shape and color parameters, respectively.

MRS parameters are determined experimentally based on the approach of trial-and-error [58]. However, the three parameters of the algorithm have a significant impact on the quality of output segmentation results. As a result, it is critical to find the optimal or suboptimal values for these parameters with a systematic approach to ensure improved classification results.

4.3. Object-Based Convolutional Neural Networks (OCNN)

As discussed in Section 2, there are several ways to combine deep learning with OBIA. The focus of this research is the method of decision-level fusion, which first develops a classification map by a deep learning model and then applies a refinement process (majority voting) based on image segmentation.

4.3.1. The Backbone Convolutional Neural Network (CNN)

A CNN is a deep learning model based on a multilayer perceptron that performs convolutional and pooling operations on image patches. It was developed for image processing with the use of local connections and weight sharing [59]. CNNs, as opposed to dense feedforward networks, reduce the risk of overfitting and training time. These advantages are increased with multidimensional images. A typical CNN is made up of several layers, such as convolutional, pooling, and fully connected. Each layer is fed by small image patches that scan over the entire image to capture different feature attributes at local and global scales. Convolutional layers apply filters to images to extract low- and high-level features. A feature map is formed by the features retrieved from the image by convolutional layers. To increase nonlinearity, a nonlinear activation function (e.g., sigmoid, hyperbolic tangent, rectified linear units) is used outside the convolutional layer [60]. Feature maps are generalized inside the CNN framework by pooling layers until high-level features are produced [61]. The statistics of features inside certain regions are aggregated by pooling layers, resulting in the output feature map. The fully connected layers transform feature maps into image feature vectors that may be classified using Softmax or any other classifier. Figure 3 illustrates the CNN architecture used in this study.

4.3.2. The Proposed OCNN Framework (OCNN-JO)

Figure 4 shows the proposed object-based CNN that is based on joint optimization of image segmentation and learning deep features from very-high-resolution satellite imagery. The model consists of two main stages, which are: (1) training a CNN on processed image patches, and (2) employing joint Bayesian optimization to find the best segmentation parameters and updating the CNN’s network weights by transfer learning.

After establishing image data and ground-truth pairs, image patches extracted from the raw image are processed in four steps: balancing class samples, dividing the data into training, validation, and test sets, encoding class labels, and normalizing the image data into a standard value range. In remote sensing, data with imbalanced classes are a prevalent issue [62]. They affect the classification algorithm in that it correctly predicts classes that make up the majority while misclassifying classes that make up the minority. This study used random oversampling to balance the amount of data within various classes in the dataset because deep learning methods need rather large training datasets. By choosing random samples from the class dataset with replacement, the approach increases the number of data in a minority class. The samples are then split into three groups: training (70%), validation (15%), and test (15%), which are used to train, validate, and test the models, respectively. The target data are then encoded after that. The image data are finally normalized using the min–max technique.

A CNN classification model is trained based on patch-based samples. Image segmentation is utilized in decision-fusion approaches to refine the classification results produced by the CNN with majority voting. However, the choice of segmentation parameters has a major impact on the outcome. While optimizing segmentation parameters alone may result in accurate segmentation, not sharing knowledge between segmentation and feature learning can have a major influence on classification performance. As a result, a Bayesian optimization strategy was employed in this study to jointly optimize the image segmentation process and train the CNN model for image classification.

The Bayesian optimization workflow used in this study is depicted in Figure 1. The approach begins by taking the pretrained CNN and updating the network’s weights via transfer learning. The MRS, on the other hand, segments the input image using the initial segmentation parameters scale = 100, shape = 0.1, and compactness = 0.5. To obtain the classification map, a majority voting method is applied to the CNN predictions based on image segmentation. A Gaussian filter with a 7 × 7 kernel is additionally used to smooth and reduce the noise in the results. Finally, the classification accuracy is assessed at the pixel level using the mean intersection over union (mIoU) metric.

The entire procedure, from transfer learning to accuracy measurement, is regarded as an objective function for Bayesian optimization. Consequently, it is anticipated that the Bayesian optimization will identify the best segmentation parameters that result in the best feature learning and classification. After transfer learning, the optimum segmentation parameters and a trained CNN are used to create the study area’s final classification map.

• Bayesian Optimization

Optimization methods such as grid and random search are often used with objective functions f(x) that are cheap to evaluate. However, with expensive objective functions, it is important to minimize the number of samples drawn from the black box function. Bayesian optimization is an approach that best suits this kind of problem. It attempts to find the global optimum in a minimum number of iterations. Bayesian optimization incorporates prior belief about f and updates the prior with samples drawn from f to obtain a posterior that better approximates f. The model used for approximating the objective function is called a surrogate model. Bayesian optimization also uses an acquisition function that directs sampling to areas where an improvement over the current best observation is likely.

Bayesian optimization works based on the following steps: (1) selecting a surrogate model for defining the prior of the objective function, (2) obtaining the posterior using the Bayes rule based on the function evaluations, (3) using an acquisition function to decide the next sample point, and (4) adding newly sampled data to the set of observations and repeating the process from step 2 till convergence or budget elapses. For the complete mathematical foundation of Bayesian optimization, readers are referred to [63,64,65].

Gaussian processes (GPs) are used as a surrogate model for Bayesian optimization and incorporate prior beliefs about the objective function. They are iteratively updated to capture the objective function’s posterior probability distribution. A GP is parametrized by a mean function, μ, and covariance or kernel function, k. Ref. [66] recommended the use of the ARD Matérn kernel [67] because the squared exponential kernel is unrealistically smooth for practical optimization problems.

An acquisition function is used to propose new $x$ combinations in the domain space to evaluate with $f\left(x\right)$ by making use of the GP posterior probability distribution. Even though there are many acquisition functions, expected improvement (EI) [68] is the most commonly used [65]. EI helps to choose the next query sample as the one which has the highest EI over the current $max f\left(x^{+}\right)$, where $x^{+}={\mathrm{argmax}}_{{\mathrm{x}}_{\mathrm{i}}\in {\mathrm{x}}_{1:\mathrm{t}}}\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}\right)$and ${\mathrm{x}}_{\mathrm{i}}$is the location queried at $i\mathrm{th}$ time step.

In this acquisition function, $\mathrm{t}+1^{\mathrm{th} }$query point, ${\mathrm{x}}_{\mathrm{t}+1}$, is selected according to the Equation (2).

$$x_{t+1}=argmi{n}_{x}E\left(\parallel h_{t+1}(x\right)-f\left(x^{*}\right)\parallel \left|D_t)\right.$$

(2)

where $f$ is the actual ground-truth function, ${\mathrm{h}}_{\mathrm{t}+1}$is the posterior mean of the surrogate at $\mathrm{t}+1^{\mathrm{th} }$timestep, ${\mathrm{D}}_{\mathrm{t}}$is the training data, and ${\mathrm{x}}^{*}$ is the actual position where $f$ takes the maximum value.

An objective function to minimize: our objective function, f(x), takes a parameter combination, x, from the domain space, and applies a series of data processing steps to obtain the accuracy of classification results by the means of mIoU. Those steps include transfer learning, image segmentation, majority voting, and Gaussian filtering, which are described below.

The Python programming language was used to implement the Bayesian optimization. This study used the Bayesian optimization implementation of GPyOpt (http://sheffieldml.github.io/GPyOpt/) (accessed on 15 September 2022).

GPyOpt is a Bayesian optimization library based on GPy (https://sheffieldml.github.io/GPy/) (accessed on 15 September 2022). This contains the parameter space of each MRS parameter, of which the Bayesian optimization routine has to identify the optimal parameter combination. The scale ranged from 25 to 5000, shape from 0 to 0.9, and compactness from 0 to 1.

• Transfer Learning

In the proposed classification framework, optimal parameters of MRS algorithm cannot be effectively determined independently. There should be a knowledge-sharing mechanism between the classification and segmentation to achieve the best possible optimization. Transfer learning was employed to produce classification maps based on given MRS parameters. The aim of the transfer learning was to reduce the computational burden as, if the original classification model was used, each optimization iteration would have taken a much longer time. Transfer learning also aimed to effectively exploit learned weights with large samples to produce classification maps with small samples in new situations.

• Majority Voting

Deep learning classification results are improved further by the majority voting of class categories by pixels in each object segmented by MRS. Each pixel in the deep learning classification map contains a class label predicted by the model. Calculating the most common class occurring within the objects yields a single class label for each image object. In the final classification map, each pixel in the object takes the new class label of the object it contains.

• Gaussian Filtering

The Gaussian filter is a non-uniform, low-pass filter often used to blur images or reduce noise in images. It is a 2D convolution operator; however, different kernels can be used, such as bell-shaped, based on the application type. In this study, the Gaussian filter was applied with 7 × 7 kernel size to the input images to smooth out the noise.

• Training Strategy

CNNs, like other deep learning models, are trained using backpropagation and stochastic gradient descent (SGD), which is based on differentiation or chain rules. Concerning the model’s parameters, SGD efficiently minimizes a differentiable objective function (e.g., categorical cross-entropy). Several enhancements and new optimization strategies for training CNNs have recently been proposed. The adaptive moment estimation (Adam) method was employed in this study, which is an optimization method that computes adaptive learning rates for each parameter of a network model. Adam’s technical details can be found in the original paper [69]. It was used in this study to minimize categorical cross-entropy loss (Equation (1)). The weights are all initialized with a zero-mean Gaussian distribution with a standard deviation of 0.01, whereas the biases are initialized with a constant of 1. The learning rate is initially set at 0.001, and the learning rate policy is sigmoidal decay. The models are trained for 500 iterations before being terminated. If no improvement in validation accuracy is observed after 15 iterations, the training process is immediately halted, as shown in Equation (3).

$$loss\left(\widehat{y}, y\right)=-\frac{1}{m}{\displaystyle \sum }_{i=1}^m{y}^{\left(i\right)}log{\widehat{y}}^{\left(i\right)}+(1-y^{\left(i\right)}log(1-{\widehat{y}}^{\left(i\right)}))$$

(3)

4.4. Benchmark Methods

Patch-based CNN, Center-Point OCNN, region majority voting OCNN (RMA-OCNN), and Decision-Fusion OCNN were used as benchmarks to assess the effectiveness of the proposed classification model, OCNN-JO. To ensure a fair comparison, the underlying CNN in each approach was identical in terms of network parameters and hyperparameters. The methods that use image segments were implemented based on the same segmented objects acquired from MRS. Descriptions and parameter settings of these benchmarks are detailed as follows:

• Patch CNN: This model is based on densely overlapping patches with the size of a 9 × 9 set experimentally. The number of convolutional layers and their corresponding number of filters are also set experimentally to 2 and 64, respectively.
• Center-Point OCNN: In contrast to pixel-wise CNN, this model uses image segmentation to extract patches at the objects’ centers. The segmentation parameter scale, shape, and compactness were set experimentally to 4500, 0.15, and 0.1, respectively.
• RMV-OCNN: This model works principally as the CPOCNN; however, it randomly generates N convolutional positions within each image segment and trains the CNN. The same segmentation parameters are chosen for this model. The network’s architecture and hyperparameters are also identical to the CPOCNN.
• Decision-Fusion OCNN: This model generates predictions for each image pixel within image segments by using the PCNN and subsequently fuses them with a majority voting strategy to achieve the final classification results.

4.5. Accuracy Assessment

4.5.1. Classification Accuracy Assessment

This study uses three common classification accuracy assessment methods, namely, overall accuracy ($\mathrm{OA}$), Kappa coefficient ($\mathrm{K}$), and mean intersection over union ($\mathrm{mIoU}$). $\mathrm{OA}$ and $\mathrm{K}$ are notably two accuracy measures used in traditional remote sensing studies. These measures can be computed at pixel or object level. This study uses them at the pixel level due to the nature of the validation data prepared for this research. OA refers to the specific value of the total number of all correct classifications and that of samplings and reflects the degree of correctness of all categories in the classification results of images (Equation (4)). The Kappa coefficient refers to an assessment index to judge the extent of coincidence between two images and ranges from 0 to 1. It indicates how much the classification method selected is better than the method where the single pixel is randomly assigned to any category (Equation (5)). On the other hand, $\mathrm{mIoU}$ (also known as the Jaccard index) is reported occasionally in semantic segmentation applications as well as classification problems [70]. $\mathrm{mIoU}$ can be calculated based on pixels or bounding boxes. It is the ratio of intersection between the reference and classified samples with the union of the two groups. The former method is well-suited for classification applications, while the latter is preferable for instant segmentation or object-detection tasks. In this study, $\mathrm{mIoU}$ is applied directly to pixels over the classified image as a whole. It uses the true positive (TP), false positive (FP), and false negative (FN) classes at the pixel level (Equation (6)).

$$\mathrm{OA}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{ii}}}{{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{ij}}}$$

(4)

$$\mathrm{K}=\frac{\mathrm{N}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{ii}}-{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}+}{\mathrm{m}}_{+\mathrm{i}}}{{\mathrm{N}}^2-{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}+}{\mathrm{m}}_{+\mathrm{i}}}$$

(5)

$$\mathrm{mIoU}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}+\mathrm{FN}}$$

(6)

where ${\mathrm{m}}_{\mathrm{ij}}$represents the total number of pixels that are assigned to Class $\mathrm{j}$ from those subordinate to Class $\mathrm{i}$ in the research region and $\mathrm{n}$ represents the total number of classes. $\mathrm{N}$ represents the total number of samples, and ${\mathrm{m}}_{+\mathrm{i}}$ and ${\mathrm{m}}_{\mathrm{i}+}$ are, respectively, sums of rows and lines in the confusion matrix.

4.5.2. Segmentation Quality Assessment

The quality of image segmentation can be measured with some reference data based on comparing segmented objects and their actual objects in the reference data. The quality of segmentation degrades due to anomalies such as under-segmentation or over-segmentation. These values can be formulated by metrics such as area of fit ($\mathrm{AFI}$) or quality rate ($\mathrm{QR}$), which can be calculated using the reference object area (${\mathrm{A}}_{\mathrm{r}}$) and the object area obtained as a result of segmentation (${\mathrm{A}}_{\mathrm{s}}$) [37,71]. In optimal segmentation, $\mathrm{AFI}$ is expected to be 0 and the $\mathrm{QR}$ value is expected to be 1. Quality metrics were calculated using the following equations:

$$\mathrm{AFI}=\frac{{\mathrm{A}}_{\mathrm{r}}-{\mathrm{A}}_{\mathrm{s}}}{{\mathrm{A}}_{\mathrm{r}}}$$

(7)

$$\mathrm{QR}=1-\frac{{\mathrm{A}}_{\mathrm{r}}\cap {\mathrm{A}}_{\mathrm{s}}}{{\mathrm{A}}_{\mathrm{r}}\cup {\mathrm{A}}_{\mathrm{s}}}$$

(8)

5. Results and Discussions

5.1. Segmentation Results

Segmentation is a major processing step in object-based deep learning classification methods and its parameters can have a significant impact on segmentation results and, ultimately, the classification results. Setting segmentation parameters by experience can achieve reasonable results, but it can only be performed independently from feature learning, which as a result may impact the final classification results as no knowledge is shared between the two segmentation and feature extraction tasks. In this study, segmentation parameters were optimized by the proposed Bayesian optimization workflow discussed in Section 3. Figure 5 shows the segmentation results for the training and test areas with the optimal parameters. For the training areas, the optimization procedure found the following best parameters, i.e., scale, shape, and compactness. For the test area, the best segmentation parameters were for scale, shape, and compactness, respectively.

Table 2. Search space, initial values, and best values of MRS segmentation parameters for the training and test areas.

Parameter	Search Space	Initial Value	Best Value (Training Area)	Best Value (Test Area)
Scale	Integer [25, 5000]	100	4705	4617
Shape	Real [10−2, 100]	0.5	0.2	0.14
Compactness	Real [10−2, 100]	0.5	0.1	0.1

illustrates the search space, initial values, and best values of MRS segmentation parameters for the training and test areas.

Table 3. Segmentation quality metrics for the training and test area datasets.

Dataset	AFI	QR
Training Area	0.046	0.945
Test Area	−0.037	0.932

presents the quality metrics for the segmentation results. The training area was segmented with AFI and QR of 0.046 and 0.945 m, respectively. The metrics for the test area were −0.037 AFI and 0.932 QR. The results indicate good segmentation for both areas.

The three MRS parameters were optimized based on search spaces experimentally set up in this research. For the scale parameter, the low bound and high bound were determined as 25 and 5000, respectively. For the shape and compactness, the search space of the real values between 0.01 and 1 was used in the optimization process. The initial values of the parameters were decided randomly. The best values were then determined by the proposed Bayesian optimization method for both training and test areas. The best scales were 4705 and 4617 for the training and test areas, respectively. The best shape and compactness values were 0.2 and 0.1 for the training area and 0.14 and 0.1 for the test area. The best parameter values found for the training area are very close to those found for the test area. In both areas, higher scale value, and lower shape and compactness, are preferred.

5.2. The Results of the Proposed Model

The proposed classification workflow experimented with three CNN models, namely, 2D CNN, 3D CNN, and HybridSN. A visual comparison of these methods as classification maps is presented in Figure 6 and Figure 7 for the training and test areas, respectively.

Table 4. Classification assessment of different CNN methods used with the proposed model for the training and test areas.

	Training Area			Test Area
Class	2D CNN	3D CNN	HybridSN	2D CNN	3D CNN	HybridSN
Buildings	0.94	0.94	0.97	0.95	0.96	0.97
Roads	0.98	0.96	0.94	0.98	0.98	0.98
Grass Land	0.93	0.93	0.95	0.93	0.91	0.94
Dense Vegetation/Trees	0.93	0.96	0.94	0.9	0.91	0.95
Water Body	0.98	0.97	0.98	0.98	0.98	0.99
Bare Land	0.88	0.92	0.98	0.93	0.95	0.98
OA	0.94	0.95	0.96	0.94	0.95	0.97
Kappa	0.92	0.94	0.95	0.93	0.94	0.96
mIoU	0.94	0.95	0.96	0.94	0.95	0.97

presents the classification accuracies obtained for the three methods in the training and test areas including the overall accuracies (OA, Kappa, mIoU) as well as per-class accuracies. Generally, the three applied methods produced accurate boundary information and the smoothest visual results. In addition, the semantic contents of buildings and linearly shaped features (roads) were identified with high geometric fidelity and accuracy compared to the ground-truth data. The 3D CNN layers and combining 3D and 2D CNN layers (HybridSN) yielded slightly better accuracies than the 2D CNN layers. The ability of CNN models with higher kernel dimensions improved the boundary extraction of the image objects, which helped in obtaining better geometric fidelity and classification accuracies. The results also highlight that the CNNs with higher kernel dimensions help in extracting better contextual features by combing the spectral and spatial information of the image data for feature extraction.

In terms of classification accuracy, the HybridSN model achieved the best accuracies in both the training and test areas. In the training area, the HybridSN model achieved 0.96 OA and mIoU and 0.95 Kappa. Slightly better accuracies (0.97 OA and mIoU and 0.96 Kappa) were obtained for this model in the test area due to the less-complex urban features (buildings and roads) compared to the features of the training area. The 3D CNN performed better than the 2D CNN based on the overall accuracy metrics in both the training and test areas. Looking at the per-class accuracies, the results indicate that water bodies were extracted most accurately due to their significant spectral variation compared to other classes. Buildings and roads were also extracted with higher accuracies than dense vegetation and bare lands by the three models due to their accurate geometric representations by the optimized segmentation. As the classes, i.e., buildings and roads are the dominant classes in the training and test areas, the Bayesian optimization could better identify the boundaries of these objects with the optimal segmentation parameters obtained. A generic accuracy metric (mIoU) was used to optimize the segmentation parameters in this study. However, for specific applications, e.g., vegetation studies, a modified accuracy metric (average vegetation class accuracy) can be used to improve the process of segmentation, which may acquire better accuracies for the required application.

Figure 8 illustrates convergence plots showing the progress of Bayesian optimization of MRS parameters with 2D CNN, 3D CNN, and HybridSN models. The results indicate that the 2D CNN requires the least number of iterations (19) to stabilize during optimization, while the 3D CNN and HybridSN required larger numbers of iterations (24 and 25, respectively). On the other hand, Figure 9 presents the convergence plots visualizing the progress of optimization. It depicts the accuracy (mIoU) of classification after n calls of Bayesian optimization.

5.3. Performance Comparison with Benchmark Models

The proposed model’s performance was assessed based on the comparison with existing benchmark approaches involving the pixel-wise Patch CNN, Center OCNN, Random OCNN, and Decision Fusion. The base CNN and network hyperparameters for the object-based methods were the same. The same training data were employed to train the benchmark models and measure their validation performance.

Figure 10 and Figure 11 show the classification maps obtained for the training and test areas using different classification models. The result of Patch CNN contains a “salt-and-pepper effect” more than the other methods because it processes the image data at the pixel level. This method also misclassified buildings as roads more than the other methods, indicating that object-level features help to separate these two classes more effectively than using pixel-level features. In object-based methods, salt-and-pepper noise is significantly decreased due to image segmentation and the use of majority voting for classification. However, over-segmentation and using small scales may also lead to classification results with salt-and-pepper noise. As a result, segmentation optimization can help to keep this type of noise to a minimum. Both Center OCNN and Random OCNN produced classification maps with less speckle noise, especially within building objects due to the fact of using majority voting for obtaining the objects’ class labels. However, the former method is more accurate in separating adjacent buildings. The Decision-Fusion method obtained results with less noise; however, it has worse smoothness in the boundaries of buildings and roads, especially for complex objects. The proposed model combines the advantages of low salt-and-pepper noise, accurate separation of adjacent buildings, and accurate boundary identification.

The accuracy of classification maps was measured by OA, Kappa, and mIoU at the pixel level.

Table 5. Overall accuracy and per-class accuracies of the proposed and benchmark classification methods based on samples from the training area.

Class	Patch CNN	Center OCNN	Random OCNN	Decision Fusion	Proposed
Buildings	0.85	0.96	0.85	0.84	0.97
Roads	0.85	0.87	0.83	0.83	0.94
Grass Land	0.91	0.95	0.94	0.8	0.95
Dense Vegetation/Trees	0.93	0.93	0.94	0.84	0.94
Water Body	0.96	0.98	0.98	0.93	0.98
Bare Land	0.93	0.98	0.98	0.89	0.98
OA	0.89	0.93	0.9	0.89	0.96
Kappa	0.86	0.91	0.87	0.88	0.95
mIoU	0.89	0.93	0.9	0.89	0.96

and

Table 6. Overall accuracy and per-class accuracies of the proposed and benchmark classification methods based on samples from the test area.

Class	Patch CNN	Center OCNN	Random OCNN	Decision Fusion	Proposed
Buildings	0.9	0.96	0.96	0.92	0.97
Roads	0.91	0.93	0.94	0.89	0.98
Grass Land	0.89	0.94	0.89	0.9	0.94
Dense Vegetation/Trees	0.96	0.96	0.93	0.94	0.95
Water Body	0.99	0.97	0.98	0.98	0.99
Bare Land	0.97	0.98	0.98	0.95	0.98
OA	0.93	0.95	0.94	0.93	0.97
Kappa	0.91	0.94	0.9	0.92	0.96
mIoU	0.93	0.95	0.93	0.93	0.97

summarize the measured accuracies for different methods in training and testing areas. The Patch CNN achieved the worst accuracy of 0.89 OA and Kappa and 0.86 mIoU in the training area and slightly better accuracy in the test area of 0.93 OA and Kappa and 0.91 mIoU. The Decision-Fusion method performed almost the same as the Patch CNN. The methods that rely on context patches show that the Center OCNN achieved better classification accuracy than the Random OCNN in both the training and test areas. For example, based on mIoU, the Center OCNN achieved 0.93 compared to 0.90 for the Random OCNN in the training area. In the test area, the two methods achieved 0.95 and 0.93 mIoU, respectively. The proposed method, on the other hand, achieved the best accuracy compared to other methods. In the training area, it achieved 0.96 OA, 0.95 Kappa, and 0.96 mIoU. In the test area, the accuracies were slightly better at 0.97 OA, 0.96 Kappa, and 0.97 mIoU.

5.4. Sensitivity Analysis

5.4.1. Sensitivity Analysis of the Segmentation Parameters

The segmentation process played a vital role in the proposed classification model and its parameters (shape, scale, and compactness), which have a significant effect on the classification accuracy. In this study, the segmentation parameters were optimized using the proposed joint Bayesian optimization approach. However, it is important to investigate how each parameter impacts the segmentation quality and ultimately the classification accuracy. Figure 12 presents the classification accuracy measured by mIoU based on different segmentation parameter values sampled by the Bayesian optimization method as expected improvement regions. As the optimization was performed jointly with the feature extraction, the results were presented for different base CNN models, namely, 2D CNN, 3D CNN, and HybridSN. With all three models, the results indicate that generally lower shape and compactness values yield better segmentation quality and classification accuracy. However, no systematic pattern was observed for the scale parameter. After n calls, the Bayesian optimization directed the search for regions of lower shape and compactness (<0.5). For the scale parameter, the optimal values ranged from 1000 to 5000 with no specific optimal region in between. The results highlight that as the area contains objects of different sizes, the optimal scale could be a small or large value. On the other hand, as the area is mostly covered by buildings of regular geometry (rectangular, square), lower values of shape and compactness achieved the best segmentation and classification accuracy in the area.

5.4.2. The Effect of Patch Size

The process of sensitivity analysis was conducted to investigate the effect of patch size on the accuracy (mIoU) of the proposed model with different base CNN models. The patch sizes varied from 3 × 3 to 9 × 9, with a step size of 2.

Table 7. Accuracy assessment based on mIoU of the proposed classification under different CNN models using patch sizes from 3 × 3 to 9 × 9.

Patch Size	mIoU
	2D CNN	3D CNN	HybridSN
3	0.93	0.94	0.95
5	0.93	0.94	0.95
7	0.94	0.95	0.96
9	0.94	0.95	0.97

presents the accuracies obtained from this experiment. It can be seen that a larger patch size increases the accuracy of the models for all the base CNNs [72,73]. The smallest patch size (3 × 3) yielded accuracies of 0.93, 0.94, and 0.95 for the models, i.e., 2D CNN, 3D CNN, and HybridSN, respectively. Higher accuracies were obtained with larger patch sizes and the largest patch size (9 × 9) achieved accuracies as high as 0.94, 0.95, and 0.97 for the mentioned CNN models, respectively.

5.4.3. Computational Efficiency

The proposed models were evaluated and compared with benchmark approaches in terms of the computational efficiency, as shown in Table 1. All analysis were conducted using the libraries (Keras and Tensorflow) within the Python environment (e.g., python 3.7) and a computer laptop with Radeon Graphics (2.90 GHz), 16.0 GB of memory, AMD Ryzen 7 4800H processor, and a 64-bit Windows 11 operating system. The networks’ training was performed on the CPU. In each method, the processing times of different processing stages were calculated including data preparation/preprocessing, image segmentation, model training, and post-processing. As shown in

Table 8. The computational efficiency of the proposed and benchmark classification models including their subprocesses.

Model	Base CNN	Segmentation (s)	Data Preparation and Preprocessing (s)	Training Time (s/epoch)	Post-Processing Time (s)	Total (s)
Patch CNN	2D CNN	-	5.3	2.27	0	7.57
Center OCNN	2D CNN	2	17.66	0.001	2	21.661
Random OCNN	2D CNN	2	15.61	0.003	3	20.613
Decision Fusion	2D CNN	2	5.3	2.27	3	12.57
Proposed	2D CNN	2	5.3	2.27	5	10.57
Proposed	3D CNN	2	5.5	11.13	5	23.63
Proposed	HybridSN	2	5.5	12.14	5	24.64
Bayesian Optimization (per iteration)	-	-	-	13	-	13

, the image segmentation with its optimal parameters required only 2 s to obtain the image segments from the processed images. For the data preparation and preprocessing, all the methods except the Center OCNN and Random OCNN methods required 5.3 s. This processing stage required a longer time for the Center OCNN and Random OCNN as they required additional processing of extracting segments’ centers or random points within image segments, respectively. They took about 17.66 and 15.61 s, respectively. Regarding the training time for the base CNN models, the 2D CNN in Patch CNN, Decision Fusion, and the proposed method, their training required 2.27 s. The Center OCNN and Random OCNN took much less time to train, 0.001 and 0.003 s, respectively, due to the lower number of training image patches. On the other hand, the proposed method with the 3D CNN and HybridSN required the longest time to train, 11.13 and 12.14 s, respectively. Adding the time required for all the subprocesses, the total time required for each method shows that the Patch CNN (7.57 s), followed by the proposed method with 2D CNN (10.57 s), and the Decision Fusion (12.57 s) had the lowest time. The Center OCNN and Random OCNN had total processing times of 21.661 and 20.613 s, respectively. The proposed methods with 3D CNN and HybridSN had the longest time of 23.63 and 24.64 s, respectively. Much more efficient implementation of the data preprocessing and post-processing can reduce the processing time of the methods that required a longer time.

5.5. Discussion

Very-high-resolution (VHR) satellite images contain complex and heterogeneous objects which require efficient feature extraction and classification models to convert them into meaningful thematic maps. Precise characterization of image objects is critical for robust representation of spatial contexts. In addition, appropriate feature extraction methods and the way image patches are extracted from image objects also play a significant role in producing accurate thematic maps from VHR images.

This study presents a joint optimization of image segmentation and deep feature learning for the classification of VHR satellite images. Previous methods applied segmentation optimization independently from deep learning feature extraction, which lacks knowledge sharing between the two tasks. Using image segmentation and deep learning sequentially or combining them in post-processing can overcome several issues of pixel-level classification such as “salt-and-pepper” noise, smoothness of object boundary, and separation of adjacent buildings. However, joint optimization of segmentation and feature extraction can even further improve upon the traditional methods [74]. The proposed method is different from those presented in previous works in multiple aspects: (1) jointly optimizing the extraction of image objects and feature learning, (2) utilizing hybrid CNN models to extract hierarchical features which combine 2D and 3D convolutional operations, and (3) using transfer leaning to achieve efficient integration of segmentation and deep feature extraction.

In sequential methods, the errors are propagated from one task to another. For example, poor segmentation will result in less-accurate classification because the latter task is based on the output of the former task. In this case, optimizing the segmentation is highly needed [73]. The problem with optimizing segmentation independently from feature extraction is that most deep learning methods utilize image segments as a spatial unit for extracting image patches and ultimately learning the image features. Considering segmentation, a separate step may lead to an optimized solution for specific integration workflows and not a general optimal solution. With joint optimization, this issue can be overcome, and the optimal segmentation will always be obtained regardless of the integration workflow. In the methods that use post-processing to combine segmentation and classification predictions, poor segmentation continues to have a significant impact on the final classification. Not sharing the knowledge between the two tasks results in learning fewer effective features. Figure 13 shows the improved land-cover extraction depending on the proposed OCNN method compared to some traditional methods.

The pixel-based CNN algorithm that depends on image patches often weakens the boundary information of the land use, somewhat like the Gabor filter or morphological methods. In these methods, blurred boundaries occur between the classified objects, with a loss of useful land features. This problem can be overcome with object-based CNNs. Object-based deep learning classification demonstrates a strong ability for classifying complex land uses through deep feature representation and maintaining the fine spatial details of image objects [45,75]. Accurate segmentation is very important for learning effective spatial features that can easily distinguish different land-use classes, especially for methods that are based on context patches which are extracted based on the object center or random points within objects. The way these objects are created decides the image patches that are used for feature extraction by the deep learning models. In optimal segmentation, there is a need to ensure that small objects are segmented but also to prevent large objects from being over-segmented. Furthermore, the parameters of the MRS algorithm can be used to control the boundary of image objects through shape and compactness.

However, object-based CNNs require innovative use of appropriate functional units and convolutional processes based on image segmentation. The methods Center OCNN and Random OCNN share the same problem. The center point or the generated random points may exist near the boundary of the object due to the complexity of the object’s outline shape. This will lead to some undesirable deep features that might be involved and thus severely affect classification. In Random OCNN, the effect of this problem can be decreased by using several random points and taking the majority voting among the class labels predicted at those random points. Nevertheless, the computation efficiency of the model can be significantly increased. Some studies have attempted to overcome this and related issues by using the appropriate distribution of voting points within image objects with geometry conditions or advanced analysis of convolutional processes.

In this study, some parameters have been selected experimentally such as patch size. These parameters are related to image segmentation in object-based deep learning classification. Therefore, it is significant to be optimized jointly with the segmentation parameters. This can be investigated in future research either by our proposed Bayesian optimization approach or any other suitable optimization methods.

6. Conclusions

In remote sensing imagery, urban land-use information is illustrated as high-level semantic functions or geospatial patterns. As a result, urban land-use/land-cover extraction from remotely sensed sources requires methods with the efficient capability of spectral, spatial, and contextual feature learning. In recent years, deep learning methods such as CNN have shown great success in feature extraction from remotely sensed images. However, there is a problem with these methods for the accurate extraction of object boundary information due to the use of rectangularly shaped image patches. OBIA is another image classification paradigm that is widely used to extract features from remotely sensed data and perform land-use classification at the object level. In addition, several new research works combined the two methods into a single approach, commonly known as object-based CNN. The major advantage of such an integrated approach is to effectively learn image features while accurately characterizing the boundary of objects through image segmentation.

This research aimed to use a Bayesian optimization technique to jointly optimize MRS segmentation parameters and learn the weights of the CNN network for land-cover classification in urban areas from VHR satellite images. The classification workflow also included the application of a decision-level fusion based on the best segmentation output and the use of Gaussian filtering to further improve the quality of classification results. In addition, several CNN variations including 2D CNN, 3D CNN, and HybridSN were investigated to show how the proposed workflow is affected by these base feature extraction methods. To investigate the performance of the proposed classification model, a comparison with several recently developed benchmark models was considered. The validation of the proposed model was based on two subsets (training and test) taken from a Worldview-3 satellite image over UPM campus located in Selangor province, Malaysia (101°43′1.2172” E, 3°0′8.0181” N). In both areas, buildings and roads were the dominant land-cover classes. The quality of segmentation was measured by AFI and QR while the classification accuracy was measured by OA, Kappa, and mIoU.

The major findings of the research are as follows:

• Bayesian optimization could find comparable optimal MRS parameters for the training and testing areas with excellent quality measured by AFI (0.046, −0.037) and QR (0.945, 0.932). The best scales were 4705 and 4617 for the training and test areas, respectively. The best shape and compactness values were 0.2 and 0.1 for the training area and 0.14 and 0.1 for the test area.
• For the proposed classification workflow, the HybridSN model achieved the best results compared to 2D and 3D CNNs. In the training area, the HybridSN model achieved 0.96 OA and mIoU and 0.95 Kappa. Slightly better accuracies (0.97 OA and mIoU and 0.96 Kappa) were obtained for this model in the test area. The 3D CNN layers and combining 3D and 2D CNN layers (HybridSN) yielded slightly better accuracies than the 2D CNN layers regarding geometric fidelity, object boundary extraction, and separation of adjacent objects.
• A comparison of the proposed model with several benchmark methods showed that the proposed model achieved the highest accuracy, reaching 0.96 OA, 0.95 Kappa, and 0.96 mIoU in the training area and 0.97 OA, 0.96 Kappa, and 0.97 mIoU in the test area.
• Sensitivity analysis on patch size used for CNN showed that higher accuracies could be obtained with larger patch sizes and the largest patch size (9 × 9) achieved accuracies as high as 0.94 for 2D CNN, 0.95 for 3D CNN, and 0.97 for HybridSN.
• The computational efficiency assessment of the presented model and the implemented benchmark methods showed that all the methods could be trained on a normal computer with no GPU in a relatively short time (<25 s for the most complex model).

According to the results listed above, the proposed classification model can serve as an efficient tool for extracting land-cover information from VHR satellite imagery. In addition, the proposed model can be used for a wide range of urban and environmental applications that are based on remote sensing data or use land-cover products as a data layer. However, further improvements can be made to jointly optimize patch size and other network-related parameters with the MRS parameters and feature extraction models.