Superpixel-Based Long-Range Dependent Network for High-Resolution Remote-Sensing Image Classification

Abstract

Data-driven deep neural networks have demonstrated their superiority in high-resolution remote-sensing image (HRSI) classification based on superpixel-based objects. Currently, most HRSI classification methods that combine deep learning and superpixel object segmentation use multiple scales of stacking to satisfy the contextual semantic-information extraction of one analyzed object. However, this approach does not consider the long-distance dependencies between objects, which not only weakens the representation of feature information but also increases computational redundancy. To solve this problem, a superpixel-based long-range dependent network is proposed for HRSI classification. First, a superpixel segmentation algorithm is used to segment HRSI into homogeneous analysis objects as input. Secondly, a multi-channel deep convolutional neural network is proposed for the feature mapping of the analysis objects. Finally, we design a long-range dependent framework based on a long short-term memory (LSTM) network for obtaining contextual relationships and outputting classes of analysis objects. Additionally, we define the semantic range and investigate how it affects classification accuracy. A test is conducted by using two HRSI with overall accuracy (0.79, 0.76) and kappa coefficients ($\kappa$) (0.92, 0.89). Both qualitative and quantitative comparisons are adopted to test the proposed method’s efficacy. Findings concluded that the proposed method is competitive and consistently superior to the benchmark comparison method.

1. Introduction

Remote-sensing images are generally ground images taken by sensing equipment mounted on an air or space vehicle [1,2]. The spatial resolution of the images has increased steadily as remote-sensing sensors have advanced. These images greatly benefit a wide range of fields, including urban spatial planning, land surveying, environmental monitoring, etc. [3,4]. However, remote-sensing images with high spatial resolution usually contain complex ground targets and objects of different scales [5,6,7]. They have scale dependency, which further presents a challenge to HRSI classification. According to classification strategies, they can be classified into pixel-based and object-based classification methods [8].

The pixel-based classification methods usually determine the category to which each pixel belongs based on the grayscale information of image elements [9]. Depending on the level of automation, they can be categorized into supervised and unsupervised classifications. Unsupervised methods include the iterative self-organizing analysis algorithm [10], K-means [11,12], and fuzzy clustering [13]. Zhang et al. [14] proposed a K-means-based framework to extract effective feature-learning representations for remote-sensing image classification. Common methods for supervised classification include the maximum likelihood method [15], multilayer perceptron [16], SVM [17] and random forest classifier [18]. Dong et al. [19] combined conditional random fields, SVM and random forests to propose a method based on multi-model fusion for high-resolution remote-sensing applications. Though the aforementioned pixel-based classification approaches are more appropriate for high-spectral resolution remote-sensing images with a greater number of wavebands, it is still a challenge for these methods to capture the long-range contextual relationship between pixels.

Further, with the development of deep learning, semantic segmentation has been successfully applied in HRSI classification, such as in fully connected network [20], U-Net [21], DeepLab [22]. These methods are the data-driven approach to learning high-level features of pixels and establish contextual relationships between pixels, which compensate for the limitations of pixel classification based on manual features. Theoretically, these methods can fit all the pixel features to be classified. However, these methods rely heavily on the richness of the training data. For HRSI, the detailed information (texture features, geometric features and spatial features) is much richer due to the richness [23]. These pixel-based classification methods are prone to the “pretzel phenomenon” and generate misclassification. To solve these problems, many research works have been carried out to reduce the pretzel effect by increasing the network depth, redesigning the network structure and adding Markov random fields for post-processing [24].

Compared with the pixel-oriented approach, the object-oriented method is mostly applied for HRSI classification [25]. They apply the strategy of segmentation and then classification for HRSI classification, which compensates for the pretzel effect caused by pixel-based classification methods. Kim et al. [26] analyzed the role of texture, scale and objects in image classification of high-resolution aerial images, and the results showed that the object-based multi-scale classification algorithm had the highest accuracy. Ma et al. [27] analyzed the factors affecting the accuracy of object-oriented classification, and found that the optimal segmentation scale was related to the image spatial resolution and the study area, and that random forests performed better in object-based classification. Zheng et al. [28] proposed an object-oriented Markov random field model. Specifically, this method built the weighted-region neighborhood graph based on region size and edge information as feature information, and then achieved semantic segmentation by probabilistic inference from random fields. However, the above object-based approaches still hardly meet the accuracy needs of HRSI classification, despite these methods improving the classification accuracy.

Currently, many studies use object-based segmentation integrating a deep neural network approach for HRSI classification. These methods avoid complex artificially designed features and improve the classification accuracy. Hong et al. [29] proposed a depth feature-based remote-sensing image classification method using multi-scale object analysis and a convolutional neural network (CNN) model. Zhou et al. [30] proposed a fine-grained functional-area classification method based on segmented objects and convolutional neural networks, and combined frequency statistics methods to identify the functional classes of basic units. Although the above object-based classification methods can obtain higher accuracy using deep learning networks, they fail to determine segmentation scale due to the network output size, which can easily cause over-segmentation or under-segmentation problems.

Superpixel segmentation, which situates neighboring pixels into uniformly distributed irregular pixel blocks, has been successfully applied to HRSI classification. Lv et al. [31] proposed a deep-learning method based on CNN and energy-driven sampling for HRSI classification. Li et al. [32] adopted a deep neural network method for objects’ standardized segmentation for HRSI classification. These superpixel-based methods can effectively delineate and map the features of high spatial resolution images. However, these methods only perform feature extraction at multiple scales, which not only increases the information redundancy, but also increases the non-separability between features. Figure 1 shows the current deep neural network approach using superpixels, $s_1$, $s_2$, $...$, $s_i$ scales are sampled and these data are simultaneously used as the input to feature extraction for this superpixel block classification. This approach only obtains a category, while not obtaining the long-range dependencies of superpixel blocks.

Although some progress has been made in deep learning for HRSI classification based on superpixel segmentation, it is still worth exploring. The main problems faced are as follows. (1) Semantic scale. HRSI usually contains features at different scales, and using images of fixed scale range as input will increase the burden of heterogeneous feature representation of superpixel objects at different scales by the network. (2) Long-distance dependence. The superpixel objects only contain pixels with homogeneity in a smaller range, and they fail to determine the class to which the object belongs using only one superpixel object because of the homospectral and heterospectral, and the long-distance dependency between surrounding objects.

To tackle the above problems, this paper proposes a long-distance dependent deep neural network structure for HRSI classification. The main contributions are: (1) For semantic scaling, we propose a multiple-channel all-inclusive shared deep neural network considering the multiple scales between different superpixel objects. A larger range of superpixel objects is used as input, and each object is used as a feature extraction unit, which enhances the feature contribution of each segmented object to feature classification. (2) For long-distance dependence, we design a deep neural network with long-range dependencies. A mesh of contextual correspondences between input objects is established, and contextual dependencies between surrounding distant objects are incrementally enhanced, while the class of each superpixel object is determined.

2. Method

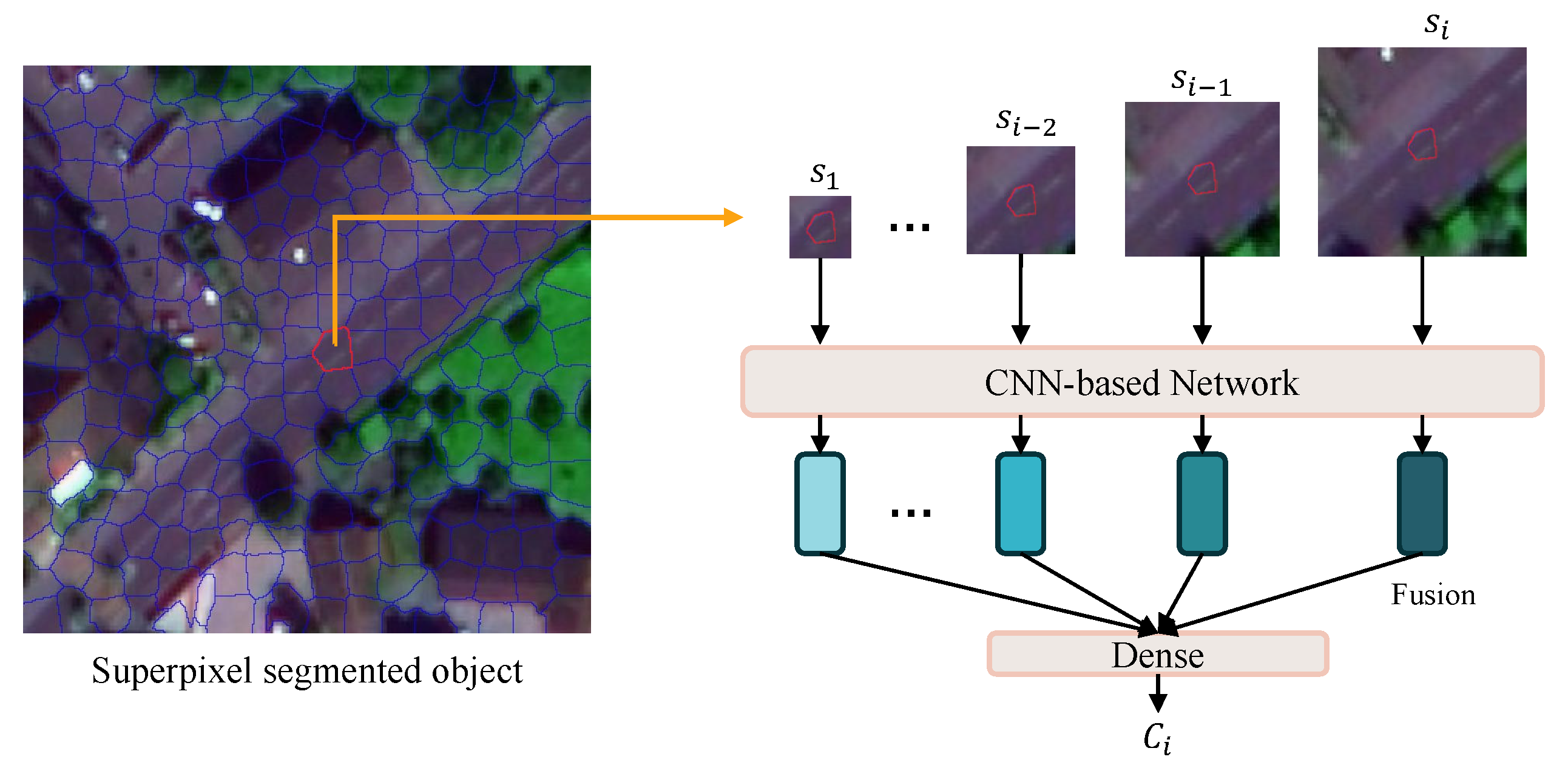
2.1. Methodological Framework

Figure 2 illustrates the technical flowchart of HRSI classification based on a long-range dependent deep neural network, and the process is divided into three main parts: (1) Superpixel segmentation. Superpixel segmentation is performed by simple linear iterative clustering (SLIC) on HRSI to obtain superpixel segmentation objects. The centroid of objects is defined as the center of the cropped patches to generate the data as the network input. (2) Model training and classification. A deep neural network with long-range dependencies is designed. It can extract the contextual relationships between objects for the category output as well as the features of the input data and their long-range dependencies. We divide the objects into training and test data, which are used for the training and prediction of the model, respectively. (3) Classification accuracy analysis and semantic range selection. For HRSI, the trained model’s prediction accuracy is examined. The feedback-designed network structure is utilized to determine the semantic range of the network’s input superpixel objects (the number of input objects) based on accuracy analysis.

2.2. Superpixel Segmentation

Simple linear iterative clustering (SLIC) is a superpixel segmentation algorithm. First, the color space of the image is transformed into CIELab, and the initial clustering centers are obtained by sampling on S pixels apart. To produce superpixels of approximately the same size, the distance of the clustering points is set to $S=\sqrt{\frac{N}{k}}$, where k is the desired number of superpixel sizes. The clustering centers need to be moved to the lowest gradient in the $3\times 3$ domain. The specific computational steps are followings.

(1)

The seed points (clustering centers) are initialized according to the set number of superpixels, and the seed points are distributed evenly within the image. Suppose the image has a total of N pixel points, pre-segmented into k superpixels of the same size; then, the size of each superpixel is $\frac{N}{k}$, and the distance (step) of adjacent seed points is approximated as $S=\sqrt{\frac{N}{k}}$.

(2)

The seed points are reselected in the $n\times n$ neighborhood, the gradient values of all pixel points in that neighborhood are calculated, and the seed points are moved to the place with the smallest gradient in that neighborhood.

(3)

Each pixel point is assigned class labels within the neighborhood around each seed point. The search range is limited to $2S\times 2S$, which can accelerate the convergence of the algorithm. The desired superpixel size is $S\times S$, and the search range is $2S\times 2S$.

(4)

Distance metric. The distance metric includes color and spatial distance. For each searched pixel point, they are calculated as the distance to that seed point. The distance is calculated as follows.

$$\begin{array}{cc}\hfill d_c& =\sqrt{{\left(l_j-l_i\right)}^2+{\left(a_j-a_i\right)}^2+{\left(b_j-b_i\right)}^2}\hfill \\ \hfill d_s& =\sqrt{{\left(x_j-x_i\right)}^2+{\left(y_j-y_i\right)}^2}\hfill \\ \hfill D^{\prime }& =\sqrt{{\left(\frac{d_c}{N_c}\right)}^2+{\left(\frac{d_s}{N_s}\right)}^2}\hfill \end{array}$$

(1)

where $d_c$ represents the color distance, $d_s$ represents the spatial distance, and $N_s$ is the maximum spatial distance within a class, defined as $N_s=S=\sqrt{\frac{N}{k}}$, which is applicable to each cluster. The maximum color distance $N_c$ varies both with pictures and with clusters, so we take a fixed constant m instead. The final distance metric $D^{\prime }$ is as follows.

$$D^{\prime }=\sqrt{{\left(\frac{d_c}{m}\right)}^2+{\left(\frac{d_s}{S}\right)}^2}$$

(2)

Since each pixel point is searched by multiple seed points, each pixel point is given a distance from the surrounding seed points, and the seed point corresponding to the minimum value is taken as the clustering center of that pixel point.

(5)

Iterative optimization. The above steps are iterated continuously until the error converges.

Given the limitations of CNN, the input data must be rectangular image patches. Although objects have homogeneous regions, they are irregularly polymorphic in size. To unify the structure of the input data, we crop patches containing superpixel objects as input. First, the position of the centroid of the irregular graph of each superpixel partition object is calculated. Second, the image blocks are cropped at equidistant positions above and below the center of mass according to the size of the cropped image blocks. The detailed formula for calculating the centroid of the irregular image is as follows.

$$(\overline{x},\overline{y})=\left(\frac{{\sum }_{i=1}^n{A}_i{\overline{x}}_i}{{\sum }_{i=1}^n{A}_i},\frac{{\sum }_{i=1}^n{A}_i{\overline{y}}_i}{{\sum }_{i=1}^n{A}_i}\right)$$

(3)

where x and y are the position coordinates of each pixel within the superpixel object and A is the number of pixels of the irregular graph. Figure 3 depicts the flowchart of cropping.

2.3. Long-Range Dependent Network

Figure 4 depicts the framework of a deep neural network with long-range dependencies. The network has two components: feature extraction based on a multichannel CNN and long-distance dependent mapping based on LSTM. The feature-extraction structure of the multichannel-based CNN takes superpixel objects as input, and the network structure of each of their channels is the same. Weight sharing is used to reduce the number of parameters in the training phase. The network is first operated by a convolution and activation function, and then output to Stage-1, Stage-2, Stage-3 and Stage-4 for feature extraction, respectively. Feature reuse is performed between each stage, i.e., the input and output of each stage are summed as the final output. Each stage is composed of CNN, activation function, normalization, and pooling layers. The size of the convolution kernel is set to $3\times 3$, and the step size of the convolution operation is designed to be $2\times 2$ to reduce the size of the feature map in Stage-2 and Stage-4, respectively. Finally, $2\times 2$ pooling is used to reduce the size of the feature map to 1/8 of the original size, and reshape it to $1\times 1/8$ as the input of the LSTM. The detailed parameters of the feature-extraction structure of the multichannel-based CNN are shown in

Table 1. Network structure parameters.

Layer	Operation	Feature Map	Size	Kernel Size	Stride	Activate
Input	-	-	$32\times 32$	-	-
	2× CNN	64	$32\times 32$	3 × 3	$1\times 1$	ReLU
Stage-1	2× CNN	128	$32\times 32$	3 × 3	$1\times 1$	ReLU
Stage-1	Max Pooling	128	$32\times 32$	3 × 3	$1\times 1$	ReLU
Stage-2	2× CNN	256	$32\times 32$	3 × 3	$1\times 1$	ReLU
Stage-2	Max Pooling	256	$16\times 16$	3 × 3	$2\times 2$	ReLU
Stage-3	2× CNN	512	$16\times 16$	3 × 3	$1\times 1$	ReLU
Stage-3	Max Pooling	512	$16\times 16$	3 × 3	$2\times 2$	ReLU
Stage-4	2× CNN	512	$16\times 16$	3 × 3	$1\times 1$	ReLU
Stage-4	Max Pooling	512	$8\times 8$	3 × 3	$2\times 2$	ReLU
FCN	FC	-	256	-	-	-

.

LSTM is used in the long-distance dependent mapping structure to handle long-distance relationships in the sequence of segmented objects, remembering the contextual information between each superpixel-segmented object feature information. The LSTM “gate” mechanism is designed as a way to allow information to be selected for passage. It consists of an oblivion gate, an input gate, and an output gate, which determines which information needs to be discarded from the cell state and which new information can be stored in the state as the final output. Suppose the input $i_{t-1}$ of the previous layer and the sequence data $i_t$ to be input in this layer; the output is obtained by an activation function. The output values range from [0, 1] from the forgetting gate, which indicates the probability that the information state of the previous layer is forgotten, with 1 being completely retained and 0 being completely discarded.

$$o_t=\sigma \left(W_f·\left. [i_{t-1},x_t\right]+b_f\right)$$

(4)

The input gate contains two parts, each consisting of two activation functions, and the outputs are $i_t$, $i_t^{\prime }$, where $i_t^{\prime }$ are taken in the interval [0, 1], indicating the degree to which the information in $i_t^{\prime }$ is retained. $i_t\times i_t^{\prime }$ denotes the new information that is retained in this layer, and the new information can be updated to the cell state $i_t^{\prime }$ in this layer.

$$i_t=\sigma \left(W_f·\left. [\begin{array}{cc}{i}_{t-1},\hfill & x_t\hfill \end{array}\right]+b_i\right)$$

(5)

$$i_t^{\prime }=tanh\left(W_c·\left. [i_{t-1},x_t\right]+b_c\right)$$

(6)

$$C_t=f_t\ast i_{t-1}+i_t\ast i_t$$

(7)

$$o_t=\sigma \left(W_o\left. [h_{t-1},x_t\right]+b_o\right)$$

(8)

$$h_t=\left(o_t\ast tanh\left(C_t\right)\right.$$

(9)

The output gate is used to control the amount of information being filtered in this layer. An activation function is first used to obtain a $o_t$ with values in the interval [0, 1], followed by multiplying the cell state with $o_t$ after processing it through another activation function, which is the output $h_t$ of this layer.

3. Data and Parameter Settings

3.1. Data

WHDLD [33] is a densely labeled dataset which can be used for remote-sensing image retrieval and pixel-based tasks such as remote-sensing classification. We use the pixels of each image with the following five category labels, namely, buildings, roads, bare soil, vegetation and water.

Zurich Summer dataset [34] is a densely labeled dataset of high-resolution remote-sensing image classification which can be used for the semantic segmentation of remote-sensing images. We choose the image file (named mediumresidential) with four category labels, namely, building, road, woodland and vegetation, for training.

Figure 5 shows the two test HRSI used in the experiment. Both images consist of four multispectral bands (including red, green, blue and near infrared). The two images were acquired by two different sensors with rich coverage of feature classes. Therefore, it is suitable to test the generalization ability of our proposed method for classification.

Figure 5a is a Gaofen-2 image (GF) with a resolution of 1 m and a size of 1200 × 1120, located in Wuhan, China. Figure 5c is a QuickBird satellite image (QB) with the location of a Zurich suburb, resolution of 0.61 m and size of 1100 × 1320. Figure 5b,d represent the data used for training and testing. The main feature classes covered on QB are buildings, roads, vegetation, woodland and water. Since these features constitute different proportions of the whole image, the same number of samples cannot be selected for training according to each category. Therefore, the training data is selected based on the proportion of each category in the whole image. In QB, the proportion of buildings is high, and the proportion of water bodies and woodland is low. The proportion of the training sample for each feature in the whole training sample should be selected to be similar to the proportion on the original image. Similarly, in the GF, the samples are selected according to the same strategy.

3.2. Parameter Settings

The accuracy of classification is significantly influenced by the settings of the superpixel-segmentation parameters. Pixels within superpixel-segmented objects act as homogeneous classes; therefore, it is necessary to experiment with the superpixel parameters of the images. Increasing the number of superpixel objects can increase the homogeneity of pixels within each object, which obviously requires a long time for image classification. Therefore, a balance between the number of objects and the tightness is needed to reduce the number of segmented objects while ensuring the homogeneity of each segmented object. Due to the limitation of the deep neural network, it must be ensured that the cropped image patches contain the segmented superpixel objects. Therefore, this requires increasing the tightness to ensure that each superpixel object has approximately the same shape.

Figure 6 shows the partial segmentation effect of the two images with different segmentation parameters. The number of segmented superpixels is determined according to the size of the two images, and the tightness parameter is set to 1–60 for comparison. Figure 6a–e show the segmentation results for tightness of 1, 15, 30, 45, and 60. For GF, the tightness coverage parameter is set between 15–30 to obtain a better segmentation effect. This is due to GF covering complex features with more mixed pixels, and the reduced tightness can ensure the heterogeneity of each segmented object. For QB, the covered features are mainly artificial buildings with distinct geometries, and increasing the tightness can obviously obtain a higher homogeneity of segmented objects. The results show that the tightness parameter of QB image when set between 30–45 is more suitable.

3.2.1. Semantic-Range Selection

The choice of semantic range is the basis for establishing the superpixel distant dependencies. A circle with different radius sizes is defined as the semantic range, i.e., superpixel objects contained within the circle as the input to the network. Figure 7 shows the superpixel inputs to the network for classification contained in circles of different radii. Theoretically, the smallest semantic range should include one superpixel object. The maximum semantic range should be smaller than the size of the remote-sensing image. A larger semantic range can obtain the superpixel-object long-range dependency. However, a larger number of inputs will inevitably increase the difficulty of training and the complexity of computation. Therefore, choosing the appropriate semantic range is very important for remote-sensing image classification. In Section 4.2, we analyze in detail the effect of semantic range on classification accuracy for selecting the appropriate semantic range.

3.2.2. Model-Training Parameters Setting

Different semantic ranges correspond to the number of inputs; therefore, a network model with multiple channels is required to be designed for feature extraction and the classification of superpixel objects. The network parameters for each channel are the same as in Table 1. The parameters are shared between multiple channels during the training and prediction phases, which can reduce the number of parameters of the model and improve computational efficiency. The model is implemented by the Pytorch library and all the experiments are implemented on DUAL-RTX 2070-O8G-EVO. The optimization model of the network is used with Adam and the learning rate, epoch time and batch size were set to 0.0001, 4000 and 32.

4. Experiment and Analysis

In this section, we first perform a qualitative and quantitative comparison with competitive methods (OBIA-SVM, Superpixel-DCNN and DeepLab v3 [35]) on two test images to validate the performance of our proposed method. OBIA-SVM is implemented using the eCognition Developer 9.0. In GF and QB, the optimal scale, shape and compactness obtained by human visual judgment are set to the parameters of 60, 0.6, 0.8 and 60, 0.85, 0.9, respectively. For Superpixel-DCNN and the proposed, they both use SLIC for superpixel segmentation. Superpixel-DCNN uses the network structure in

Table 2. A confusion matrix. TP is the number of correctly classification $C_1$ pixels. FN is the number of undetected $C_1$ pixels. FP is the number of incorrectly extracted $C_1$ pixels. TN is the number of correctly rejected $C_2$ pixels.

		Reference Data
		${\mathbf{C}}_{\mathbf{1}}$	${\mathbf{C}}_{\mathbf{2}}$
Classified data	$C_1$	TP	FP
	$C_2$	FN	TN

, for comparison. DeepLab v3 follows the parameter settings of [35] for training and testing on the dataset.

The classification accuracy of each category in the image, overall accuracy (OA) and statistical Kappa ($\kappa$) coefficients are used as evaluation metrics. Taking the binary classification as an example, the detailed calculation is given below.

$$OA=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{T}}$$

(10)

where T is the total number of pixels in the accuracy assessment.

$$\kappa =\frac{\mathrm{T}(\mathrm{TP}+\mathrm{TN})-\sum }{{\mathrm{T}}^2-\sum }$$

(11)

where ∑ is the chance accuracy represented by (TP + FP)(TP + FN) + (FN + TN)(FP + TN).

4.1. Classification Results

Classification results.The quantitative comparison results of our proposed method and competitive methods on two images are provided in

Table 3. Classification results on GF.

Method	Building	Road	Bare Ground	Vegetation	Water
	Accuracy					OA	$\mathit{\kappa }$
OBIA-SVM	$0.65\pm 0.16$	$0.55\pm 0.18$	$0.52\pm 0.07$	$0.39\pm 0.24$	$0.63\pm 0.06$	$0.57$	$0.51$
Superpixel-DCNN	$0.64\pm 0.17$	$0.66\pm 0.17$	$0.62\pm 0.06$	$0.64\pm 0.21$	$0.69\pm 0.07$	$0.65$	$0.62$
Deeplab V3	$0.61\pm 0.15$	$0.72\pm 0.10$	$0.66\pm 0.08$	$0.74\pm 0.05$	$0.75\pm 0.08$	$0.70$	$0.68$
Proposed	$0.75\pm 0.09$	$0.78\pm 0.18$	$0.75\pm 0.04$	$0.80\pm 0.19$	$0.85\pm 0.07$	$0.79$	$0.76$

. For GF, the proposed method obtains the highest classification accuracy with OA of 0.79 and $\kappa$ of 0.76. The OA and $\kappa$ for OBIA-SVM, Superpixel-DCNN and DeepLab v3 are (0.57, 0.51), (0.65, 0.62), and (0.70, 0.68), respectively. For each category of classification accuracy, the effectiveness of the proposal is further demonstrated. The accuracy of buildings, roads, vegetation, water, and bare soil increased by 0.15, 0.41, 1.05 and 0.34 compared to OBIA-SVM, with especially vegetation and water increasing more significantly. The accuracy of road increased dramatically by 0.15 in comparison to Superpixel-DCNN, and the accuracy of buildings, vegetation, water, and bare soil increased by 0.17, 0.25, and 0.23, respectively. The proposal increased considerably by 0.22 for buildings and slightly by 0.08, 0.08, 0.13 and 0.13 for roads, vegetation, water, and bare soil as compared to DeepLab v3.

The proposal obtained the highest classification accuracy on QB with OA and $\kappa$ higher than GF, as shown in

Table 4. Classification results on QB.

Method	Building	Road	Woodland	Vegetation	Water
	Accuracy					OA	$\mathit{\kappa }$
OBIA-SVM	$0.63\pm 0.07$	$0.66\pm 0.14$	$0.61\pm 0.06$	$0.46\pm 0.21$	$0.88\pm 0.05$	$0.62$	$0.61$
Superpixel-DCNN	$0.71\pm 0.06$	$0.74\pm 0.13$	$0.70\pm 0.05$	$0.72\pm 0.24$	$0.83\pm 0.08$	$0.73$	$0.73$
Deeplab v3	$0.75\pm 0.06$	$0.75\pm 0.11$	$0.73\pm 0.08$	$0.71\pm 0.26$	$0.87\pm 0.06$	$0.77$	$0.74$
Proposed	$0.91\pm 0.03$	$0.90\pm 0.13$	$0.89\pm 0.07$	$0.93\pm 0.15$	$0.94\pm 0.06$	$0.92$	$0.89$

. On QB, the OA of the proposed method is 0.92 and $\kappa$ is 0.89. The OA and $\kappa$ of the proposed method increased by (0.48, 0.62), (0.26, 0.21) and (0.19, 0.20), respectively, in comparison to OBIA-SVM, Superpixel-DCNN, and DeepLab v3. The overall performance ranking of classification accuracy is OBIA-SVM < Superpixel-DCNN < DeepLab V3 < the proposed method. The classification performance of each category on QB proved the effectiveness. The accuracy of each category was much higher than OBIA-SVM, at 0.91, 0.90, 0.89, 0.93, and 0.94, respectively. The proposal improved more considerably than Superpixel-DCNN for roads and water, by 0.20 and 0.13, respectively. However, for buildings and vegetation, their classification accuracy increased less. For buildings, roads, woodland, vegetation and water, the accuracy increased by 0.21, 0.20, 0.30 and 0.08 relative to DeepLab v3, respectively.

Discussion and analysis. The proposed method had a higher classification performance than OBIA-SVM, Superpixel-DCNN and DeepLab v3 on two images. OBIA-SVM method used the strategy of object-based segmentation before classification for remote-sensing image. However, it was limited by the selection of segmentation parameters and the feature representation of the examined objects, which resulted in classification outcomes which were noticeably inferior to those of other approaches, as shown in Figure 8 and Figure 9. The influence of the SVM features allowed confusing each category, despite the fact that OBIA-SVM could obtain fine boundaries on specific feature categories, such as buildings and roads. For example, roads on QB were misclassified as buildings, with water bodies misclassified into vegetation. Superpixel-DCNN classified each segmented object using a deep neural network after applying a superpixel-segmentation approach to obtain a precise boundary. Compared to OBIA-SVM, Superpixel-DCNN was more accurate in classifying objects. Since Superpixel-DCNN only performed feature extraction on a segmented object, lacking contextual information between objects, it achieved lower classification accuracy obtained on the water in GF and roads in QB. This was owing to the large scale of these objects, the difficulty of characterizing the linear properties of roads using only one segmentation object, and the lack of information transmission between upper and lower objects in Superpixel-DCNN. DeepLab v3 was an end-to-end classification method based on deep neural networks, which was a semantic segmentation algorithm. However, DeepLab v3 had lower classification accuracy than our proposed method in the classification of small samples. This is a result of the DeepLab v3 algorithm’s ability to classify each individual pixel and need for a wide range of training data. Deeplab v3 provided a lower classification accuracy due to the homospectral and heterospectral on high-resolution remote-sensing images.

The superpixel-based proposal broadened the semantic range of the data input and could identify long-distance semantic relationships between numerous segmented objects, which enabled our proposed method to correctly classify large-scale features such as water in GF and roads in QB. Additionally, objects were input into CNN and LSTM networks, which not only gathered high-level features of objects, but also increased the effectiveness of classification.

Finally, the speed of classification is also important. Since the comparison methods OBIA-SVM, Superpixel-DCNN and the proposed method all used a segmentation first and then classification strategy, the time of the optimal segmentation parameters was difficult to quantify. For a fair comparison, we tested the processing speed (sec/sample) of the classification models on the test images. All evaluations were based on an Intel(R) i7-7700 CPU and a DUAL-RTX 2070-O8G-EVO.

Table 5. Time complexity comparisons on GF and QB. The unit is second (s).

	OBIA-SVM	Superpixel-DCNN	DeepLab v3	Proposed	Superpixel-DCNN	DeepLab v3	Proposed
Backend	CPU				GPU
GF	$10.27$	$15.25$	$9.46$	$12.85$	$4.64$	$3.15$	$4.06$
QB	$10.59$	$15.77$	$10.19$	$13.25$	$4.91$	$3.53$	$4.62$

compared the estimated time complexity of the different methods. Although Superpixel-DCNN, DeepLab v3 and the proposed method spent more time on the CPU, the compatibility with the GPU made these methods the fastest in processing speed.

4.2. The Effect of Semantic Range on Classification Accuracy

The semantic range was quantified as the number of input segmentation objects. Superpixel segmentation objects were introduced in Section 3.2, and they were encircled by various-sized circles. The number of input objects (N) was chosen as 9, 12, 16, 20, 25, and 36 for measuring the classification performance to investigate the impact of various semantic ranges on classification accuracy. The overall classification maps for GF and QB with various semantic ranges are displayed in Figure 10. The classification maps for roads and water bodies in GF exhibited discontinuity, or misclassification, at smaller semantic ranges. With no essential change in classification accuracy, plane buildings and vegetation display extremely good color continuity. On GF, bare soil had mixed classifications with buildings and an overall linear and plane shape. Bare soil exhibited an increase in correct classification on GF as the semantic range widens. For QB, the classification map exhibited a similar phenomenon to GF. The QB contained a large number of homogeneous regions such as vegetation, water, and textures on QB. They displayed less complexity while maintaining excellent classification accuracy at a constrained semantic range. Since roads and buildings were linear types on QB, the classification map showed the same class color constancy as the semantic range expands. On QB, woodland was plane and point-like, and the classification differed dramatically from the maps for smaller semantic ranges.

Figure 11 depicted the accuracy of each category in the two test images. Overall, as the semantic range widens, the classification accuracy of each category tended to steadily increase, with various categories showing different patterns in classification accuracy. The overall results were similar to conclusions obtained above. As the semantic range widens, the classification accuracy for roads and water in GF increased from 0.38 to a maximum value of 0.79, with a more significant growth between 9 and 16. For buildings and vegetation, their classification accuracy increased insignificantly. For bare soil, the classification accuracy trend was between linear features (roads, water) and plane features (buildings, vegetation). Both the roads in QB and GF followed the same pattern, whereby the classification accuracy increased as the semantic range raised, peaking at values between 20 and 25. While most of the buildings in QB exhibited a linear type, its classification accuracy was significantly affected by the semantic range. Since the accuracy change curves for vegetation and water were nearly constant, it was possible to classify these objects accurately within a limited semantic range. The classification accuracy for vegetation on QB reached its highest level in the semantic range of 16–25.

Result analysis. Objects with linear shapes are subject to larger semantic range images. This might be because there were not as many objects with the linear category within a certain semantic range, which caused a lack of long-distance dependencies between the obtained objects and misclassification. We designed the semantic range with plane circular-selection segmentation objects as input, which had a major impact on why the classification progress of faceted objects was less impacted by the semantic range. Strong dependencies between plane segmentation objects allowed the network to construct a heterogeneous representation between them. Additionally, the homogeneity of plane objects was more influenced than that of the semantic range, as was the case for vegetation and water with high homogeneity in QB. Contrarily, since distinct buildings in GF were impacted by mixed image elements, they were heterogeneous and required a wider semantic range for classification.

4.3. Ablation Studies for Network Configuration

An ablation study of the long-range dependency network was conducted to evaluate the efficiency of joining various network operations to assist in the design of classification networks. A multichannel convolutional network and an LSTM constituted the classification network, whose primary function was to identify the long-distance dependencies among the segmented input objects. Consequently, the multichannel convolutional network serves as the foundational network (MCCB). To evaluate the performance of the classification, MCCB and LSTM networks were combined, either with or without configured longitudinal connections (NL, YL). Additionally, we contrasted the impact of various LSTM layer counts (l = 3, l = 4, l = 5) on the dependencies between the input objects. The detailed network combinations and classification results were shown in

Table 6. Ablation study classification results on GF and QB.

Data	Object	MCCB	MCCB + NL	MCCB + YL	MCCB + YL (l = 3)	MCCB + YL (l = 4)	MCCB + YL (l = 5)
	Building	$0.46\pm 0.06$	$0.54\pm 0.08$	$0.75\pm 0.08$	$0.74\pm 0.07$	$0.73\pm 0.08$	0.76 ± 0.03
	Road	$0.41\pm 0.06$	$0.53\pm 0.01$	0.78 ± 0.06	$0.71\pm 0.08$	$0.75\pm 0.06$	$0.75\pm 0.07$
GF	Bare ground	$0.56\pm 0.07$	$0.67\pm 0.03$	$0.77\pm 0.05$	$0.70\pm 0.06$	$0.77\pm 0.07$	0.79 ± 0.06
	Vegetation	$0.62\pm 0.04$	$0.61\pm 0.01$	0.79 ± 0.07	$0.77\pm 0.07$	$0.76\pm 0.08$	$0.73\pm 0.07$
	Water	$0.68\pm 0.07$	$0.68\pm 0.00$	0.83 ± 0.06	$0.78\pm 0.04$	$0.71\pm 0.08$	$0.77\pm 0.06$
	Building	$0.59\pm 0.07$	$0.60\pm 0.06$	$0.91\pm 0.04$	0.92 ± 0.03	$0.87\pm 0.07$	$0.82\pm 0.03$
	Road	$0.57\pm 0.05$	$0.64\pm 0.06$	0.89 ± 0.07	$0.87\pm 0.03$	$0.81\pm 0.07$	$0.88\pm 0.07$
QB	Woodland	$0.54\pm 0.08$	$0.60\pm 0.02$	0.92 ± 0.05	$0.84\pm 0.06$	$0.82\pm 0.05$	$0.87\pm 0.04$
	Vegetation	$0.63\pm 0.03$	$0.66\pm 0.04$	0.93 ± 0.06	$0.85\pm 0.08$	$0.84\pm 0.05$	$0.86\pm 0.01$
	Water	$0.69\pm 0.04$	$0.70\pm 0.01$	0.94 ± 0.05	$0.90\pm 0.06$	$0.89\pm 0.06$	$0.89\pm 0.02$

. The networks for each combination allowed the random training variables (epoch time, learning rate, batch size) to be deterministic. The effectiveness of the configured networks was evaluated using the classification accuracy of each category on the evaluation test images.

The experimental results showed that MCCB performed significantly worse than MCCB+NL, MCCB+YL, MCCB + YL (l = 3), MCCB + YL (l = 4) and MCCB + YL (l = 5) for classification on all features. Despite the fact that the input objects in MCCB shared the same parameters, they lacked the contextual relationship between the objects, which led to a lower level of classification accuracy. The classification performance of MCCB + NL was slightly higher than that of MCCB overall. This was because MCCB+NL merely expanded the underlying network by a laterally connected LSTM and did not perform information dependency extraction between the input objects. Therefore, the overall classification performance was lower than that of MCCB + YL.

MCCB + YL (l = 3), MCCB + YL (l = 4) and MCCB + YL (l = 5) established long-range dependencies for the input objects and had higher classification accuracy on the whole. From the classification results of MCCB + YL (l = 4) and MCCB + YL (l = 5), increasing the number of layers of the network did not significantly increase the classification accuracy. This indicated that the LSTM’s layer number had less of an impact on classification accuracy. The accuracy affecting the classification of features was mainly dominated by the longitudinally connected LSTM.

5. Conclusions

In this paper, a long-range-dependent deep neural network is constructed for high-resolution remote-sensing image classification. A weight-sharing multi-channel feature-extraction network was proposed to alleviate the network’s training burden. An LSTM-based mesh mapping network was developed to obtain the long-range dependencies between the input objects. The experimental findings demonstrate that the proposed long-range dependency network structure can obtain contextual relationships between the input objects. The proposed network provides a heterogeneous representation for segmented objects obtaining high classification accuracy. It was tested using two high-resolution remote-sensing images, and their OA and $\kappa$ are 0.79, 0.76 and 0.92, 0.89, respectively. In addition, we defined the concept of semantic range and explored the effects of different semantic ranges for different categories. The results show that linear features and non-homogeneous plane objects require a larger semantic range. This opens up additional solutions for the joint use of superpixel segmentation and deep neural networks.