Impacts of Urban Spatial Development Patterns on Carbon Emissions: Evidence from Chinese Cities
Abstract
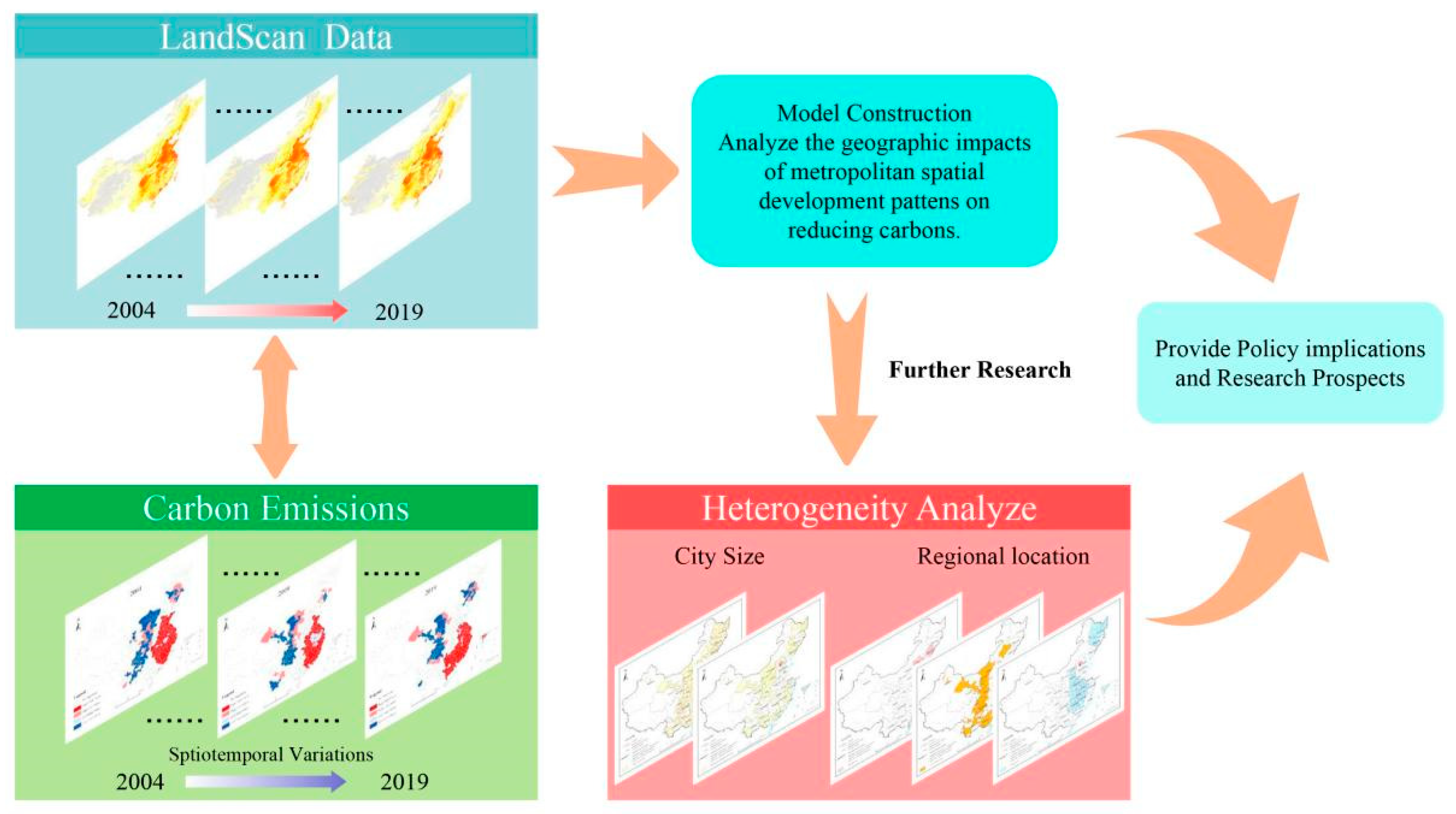
:1. Introduction
2. Methodology and Data
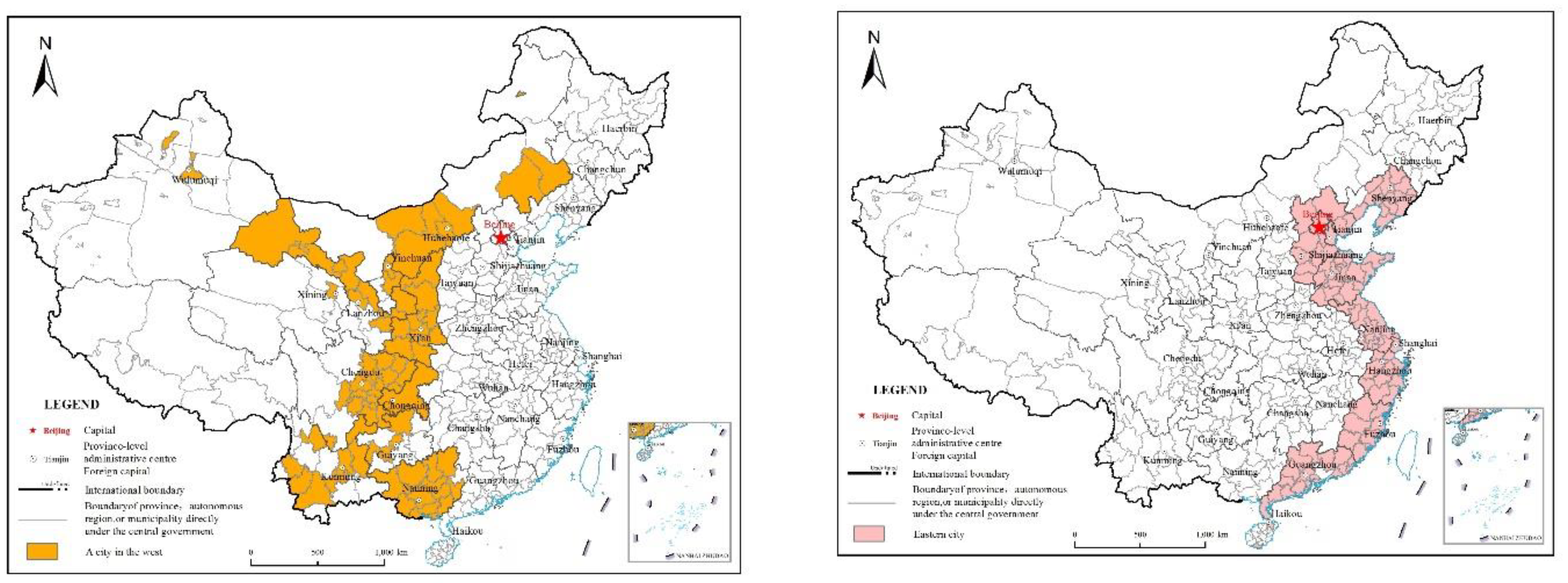
2.1. Study Area
2.2. Variables
2.2.1. Dependent Variable
2.2.2. Independent Variable
2.2.3. Control Variables
2.3. Data
2.4. Models
2.4.1. Spatial Weight Matrix Setting
2.4.2. Spatial Econometric Model
3. Results and Discussion
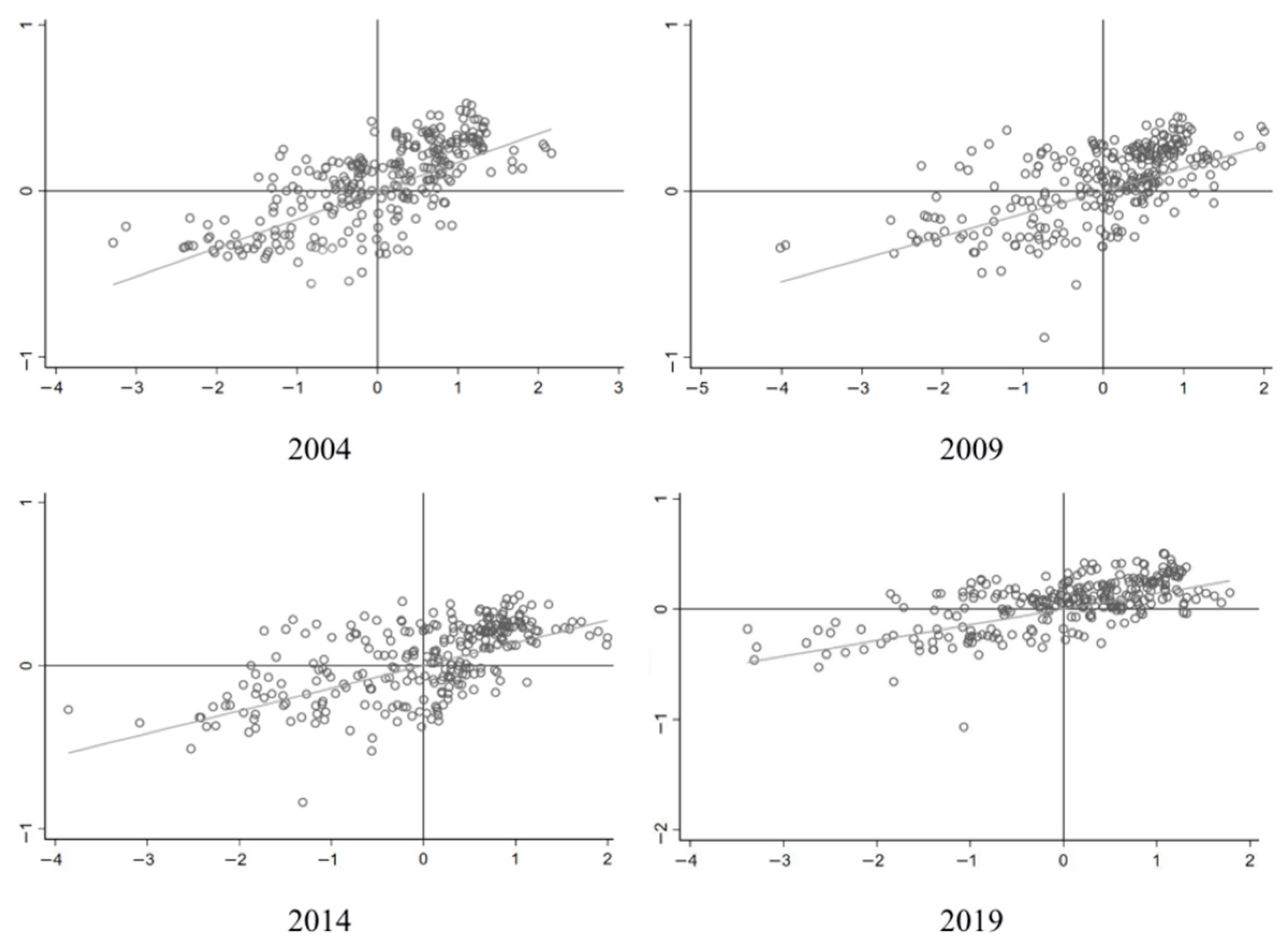
3.1. Results of Spatial Econometric Model
3.1.1. Benchmark Regression
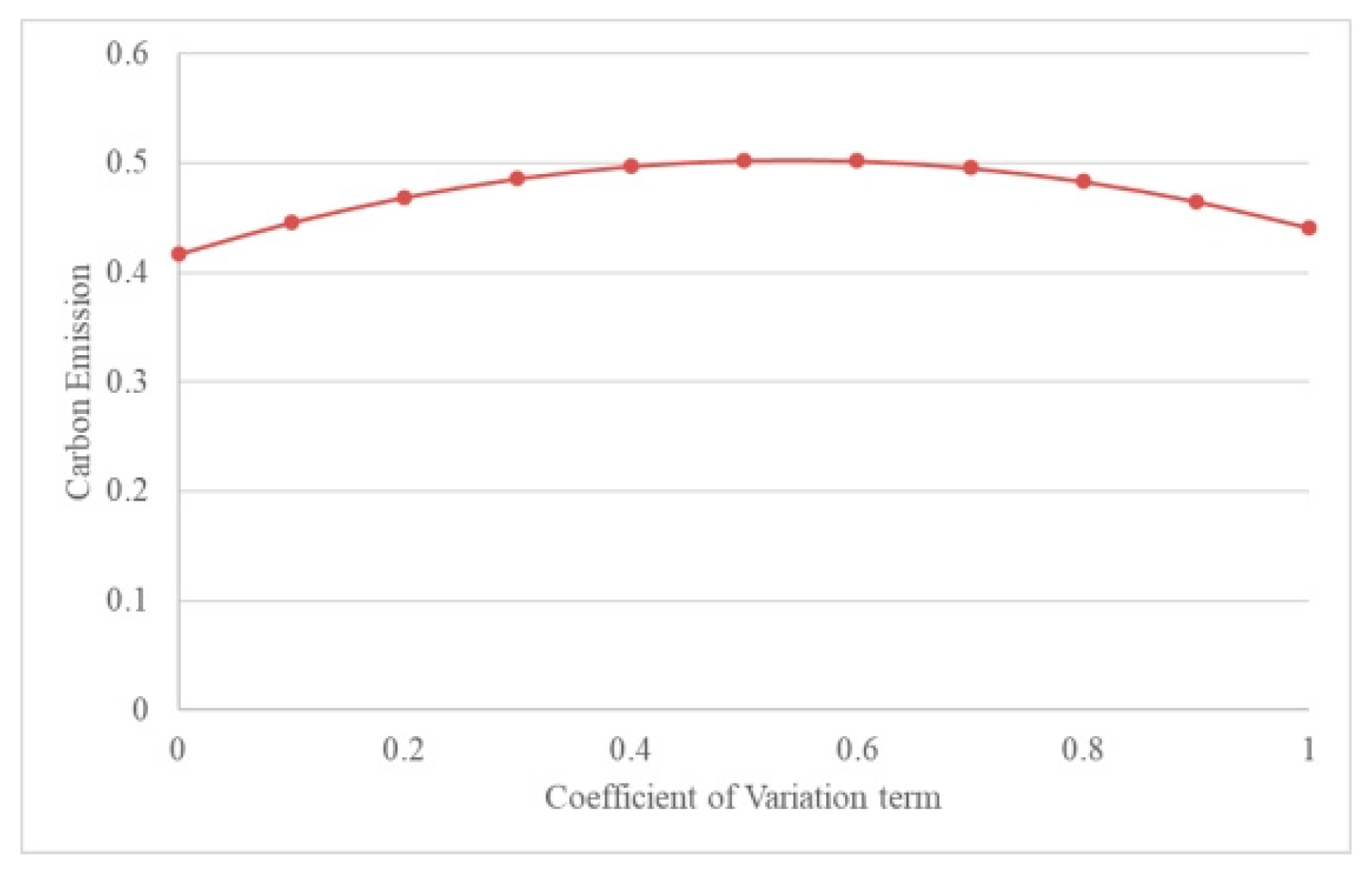
3.1.2. The Decomposition Analysis
3.2. Robustness Checks
3.2.1. Changing the Dependent Variable
3.2.2. Changing the Spatial Weight Matrix
3.2.3. Changing the Parameter Estimation Method
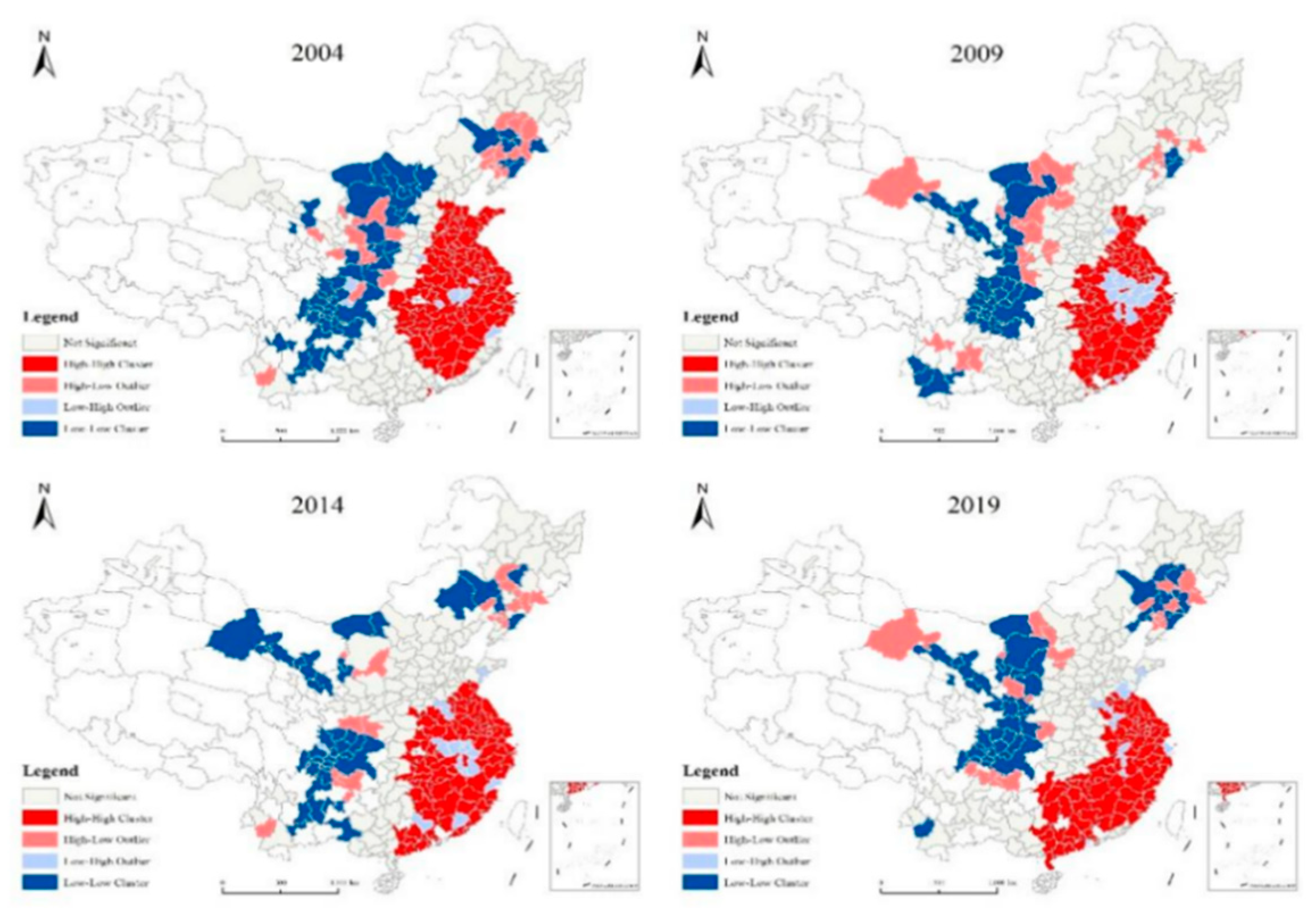
3.3. Heterogeneity Analysis
3.3.1. City Size Heterogeneity
3.3.2. Regional Location Heterogeneity
3.4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, B.; Sun, L.; Qin, L. Optimization of China’s provincial carbon emission transfer structure under the dual constraints of economic development and emission reduction goals. Environ. Sci. Pollut. Res. 2022, 83, 110–120. [Google Scholar] [CrossRef] [PubMed]
- Jalil, A.; Mahmud, S.F. Environment Kuznets curve for CO2 emissions: A cointegration analysis for China. Energy Policy 2009, 37, 5167–5172. [Google Scholar] [CrossRef] [Green Version]
- Daskalakis, G. Temporal restrictions on emissions trading and the implications for the carbon futures market: Lessons from the EU emissions trading scheme. Energy Policy 2020, 115, 88–91. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Derudder, B. Dynamics in the polycentric development of Chinese cities, 2001–2016. Urban Geogr. 2020, 56, 272–292. [Google Scholar] [CrossRef]
- Cortinovis, N.; Vanort, F.G. Between spilling over and boiling down: Network-mediated spillovers, absorptive capacity and productivity in European regions. J. Econ. Geogr. 2019, 19, 1233–1260. [Google Scholar] [CrossRef] [Green Version]
- Burger, M.; Meijers, E. Form follows function? Linking morphological and functional Polycentricity. Urban Stud. 2012, 49, 1127–1149. [Google Scholar] [CrossRef]
- Veneri, P.; Burgalassi, D. Questioning polycentric development and its effects. Issues of definition and measurement for the Italian NUTS-2 regions. Eur. Plan. Stud. 2012, 20, 1017–1037. [Google Scholar] [CrossRef] [Green Version]
- Peris, A.; Meijers, E.; Ham, M. The evolution of the system of cities literature since 1995: Schools of thought and their interaction. Netw. Spat. Econ. 2019, 18, 533–554. [Google Scholar] [CrossRef] [Green Version]
- Münter, A.; Volgmann, K. Polycentric regions: Proposals for a new typology and terminology. Urban Stud. 2020, 37, 1983–1997. [Google Scholar] [CrossRef]
- Zeng, C.; Zhou, Y.; Wang, S.; Yan, F.; Zhao, Q. Population spatialization in China based on night-time imagery and land use data. Int. J. Remote Sens. 2011, 32, 9599–9620. [Google Scholar] [CrossRef]
- Zhuo, L.; Ichinose, T.; Zheng, J.; Chen, J.; Shi, P.J.; Li, X. Modelling the population density of China at the pixel level based on DMSP/OLS non-radiance-calibrated night-time light images. Int. J. Remote Sens. 2009, 30, 1003–1018. [Google Scholar] [CrossRef]
- Gaughan, A.E.; Stevens, F.R.; Huang, Z.; Nieves, J.J.; Sorichetta, A.; Lai, S.; Ye, X.; Linard, C.; Hornby, G.M.; Hay, S.I.; et al. Spatiotemporal patterns of population in mainland China, 1990 to 2010. Sci. Data 2016, 3, 160005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, A.; Mertes, C.M.; Tatem, A.J.; Tan, B.; Sulla-Menashe, D.; Graves, S.J.; Patel, N.N.; Horton, J.A.; Gaughan, A.E.; Rollo, J.T. A new urban landscape in East–Southeast Asia, 2000–2010. Environ. Res. Lett. 2015, 10, 034002. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Qin, M. Urban spatial structure and regional economic efficiency--and the model choice of China’s urbanization development path. Manag. World 2017, 1, 51–64. [Google Scholar] [CrossRef]
- Gilles, D.; Matthew, A. Urban form and driving: Evidence from US cities. J. Urban Econ. 2018, 108, 170–191. [Google Scholar] [CrossRef]
- Thinh, N.X.; Arlt, G.; Heber, B.; Hennersdorf, J.; Lehmann, I. Evaluation of urban land-use structures with a view to sustainable development. Environ. Impact Assess. Rev. 2002, 22, 475–492. [Google Scholar] [CrossRef]
- Ye, C.; Sun, C.; Chen, L. New evidence for the impact of financial agglomeration on urbanization from a spatial econometrics analysis. J. Clean. Prod. 2018, 200, 65–73. [Google Scholar] [CrossRef]
- Lu, S.; Shi, C.; Yang, X. Impacts of Built Environment on Urban Vitality: Regression Analyses of Beijing and Chengdu, China. Int. J. Environ. Res. Public Health 2019, 16, 4592. [Google Scholar] [CrossRef] [Green Version]
- Edward, L.; Glaeser, T. Chapter 56—Sprawl and Urban Growth. Handb. Reg. Urban Econ. 2004, 4, 2481–2527. [Google Scholar] [CrossRef]
- Cheng, K.; Li, J. Empirical evidence of compact cities and sustainable development in China. Financ. Econ. Res. 2007, 10, 73–82,106. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y. Financial structure, industrial structure upgrading and economic growth—A perspective of technological progress based on different characteristics. Econ. 2022, 2, 118–128. [Google Scholar] [CrossRef]
- Hamidi, S.; Zandiatashbar, A. Does urban form matter for innovation productivity? A national multi-level study of the association between neighbourhood innovation capacity and urban sprawl. Urban Stud. 2019, 56, 1576–1594. [Google Scholar] [CrossRef]
- Kim, J.; Brownstone, D. The impact of residential density on vehicle usage and fuel consumption. Acad. Press 2009, 65, 95–98. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Jia, B. Sustainable urban form for Chinese compact cities: Challenges of a rapid urbanized economy. Habitat Int. 2007, 32, 28–40. [Google Scholar] [CrossRef]
- Yang, L.; Li, Z. Technology advance and the carbon dioxide emission in China—Empirical research based on the rebound effect. Energy Policy 2017, 101, 150–161. [Google Scholar] [CrossRef]
- Shao, S.; Zhao, K.; Dou, J. Energy saving and emission reduction effects of economic agglomeration:theory and Chinese experience. Manag. World 2019, 35, 36–60,226. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, D. Interactive effects of economic agglomeration and environmental pollution and spatial spillover. China Ind. Econ. 2014, 6, 70–82. [Google Scholar] [CrossRef]
- Roca, J.; Alcántara, V. Energy intensity, CO2 emissions and the environmental Kuznets curve. The Spanish case. Energy Policy 2001, 29, 553–556. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, B.; Liu, T. Empirical analysis on the factors influencing national and regional carbon intensity in China. Renew. Sustain. Energy Rev. 2016, 55, 34–42. [Google Scholar] [CrossRef]
- Poumanyvong, P.; Kaneko, S. Does urbanization lead to less energy use and lower CO2 emissions? A cross-country analysis. Ecol. Econ. 2010, 70, 434–444. [Google Scholar] [CrossRef]
- Martínez-Zarzoso, I.; Maruotti, A. The impact of urbanization on CO2 emissions: Evidence from developing countries. Ecol. Econ. 2011, 70, 1344–1353. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Sun, Y.X.; Wang, X.J. Research on the impact of global scientific and technological innovation on carbon productivity and countermeasures. China Popul. Resour. Environ. 2019, 29, 30–40. [Google Scholar]
- Sher, V.K.; Wing, I.S. Accounting for quality: Issues with modeling the impact of R&D on economic growth and carbon emissions in developing economies. Energy Econ. 2008, 30, 2771–2784. [Google Scholar] [CrossRef]
- Kerui, D.; Li, P. Do green technology innovations contribute to carbon dioxide emission reduction? Empirical evidence from patent data. Technol. Forecast. Soc. Change 2019, 146, 297–303. [Google Scholar] [CrossRef]
- Beck, N.; Katz, J.N. What To Do (and Not to Do) with Time-Series Cross-Section Data. Am. Political Sci. Rev. 1995, 89, 634–647. [Google Scholar] [CrossRef]
- Guo, J.H.; Li, B.Y. Evolutionary game analysis of duopoly’s remanufacturing entry decision. Syst. Eng. Theory Pract. 2013, 33, 370–377. [Google Scholar]
- Christophers, B. Mind the rent gap: Blackstone, housing investment and the reordering of urban rent surfaces. Urban Stud. 2022, 59, 698–716. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Chen, X.; Yan, J. An empirical study on population density, industrial agglomeration and carbon emissions in Chinese provinces-based on the perspective of agglomeration economy, congestion effect and spatial effect. Nankai Econ. Res. 2019, 2, 207–225. [Google Scholar] [CrossRef]
- Tang, L.; Hu, Z.; Su, J.; Xiao, P. Threshold characteristics and regional differences in the impact of urbanization on domestic carbon emissions. J. Manag. 2015, 12, 291–298. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X. How did urban polycentricity and dispersion affect economic productivity? A case study of 306 Chinese cities. Landsc. Urban Plan. 2018, 173, 51–59. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, J. Urban cluster polycentricity and green development efficiency--an analysis of the spatial layout of urbanization based on heterogeneity. China Popul. -Resour. Environ. 2022, 32, 107–117. [Google Scholar] [CrossRef]
- Han, F.; Xie, R.; Iu, Y.; Fang, J.; Liu, Y. The effects of urban agglomeration economies on carbon emissions: Evidence from Chinese cities. J. Clean. Prod. 2018, 172, 1096–1110. [Google Scholar] [CrossRef]
- Azka, A.; Waqar, A.; Hazrat, Y.; Akbar, M. Financial Development, Institutional Quality, and the Influence of Various Environmental Factors on Carbon Dioxide Emissions: Exploring the Nexus in China. Front. Environ. Sci. 2022, 9, 121–130. [Google Scholar] [CrossRef]
- Desmet, K.; Gomes, J.; Ortuño, I. The geography of linguistic diversity and the provision of public goods. J. Dev. Econ. 2020, 143, 102384. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, C.; Hong, J.; Nian, M. Natural conditions, administrative hierarchy and urban development in China. Manag. World 2015, 1, 41–50. [Google Scholar] [CrossRef]
- Ren, X.S.; Liu, Y.J.; Zhao, G.H. Impact of economic agglomeration on carbon emission intensity and transmission mechanism. China Popul.-Resour. Environ. 2020, 30, 95–106. [Google Scholar]
- Hansen, B.E. Threshold Effects in Non-Dynamic Panels: Estimation, Testing and Inference. J. Econom. 1999, 93, 345–368. [Google Scholar] [CrossRef] [Green Version]
- Walker, H.W.; Antonio, M. Agglomeration: A long-run panel data approach. J. Urban Econ. 2017, 99, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Giovanni, M.; Marianna, M. The Impact of the European Emission Trading Scheme on Multiple Measures of Economic Performance. Environ. Resour. Econ. 2018, 71, 551–582. [Google Scholar] [CrossRef]
- Baptist, S.; Teal, F. Technology and Productivity in African Manufacturing Firms. World Dev. 2014, 64, 713–725. [Google Scholar] [CrossRef]
- Lee, J. The contribution of foreign direct investment to clean energy use, carbon emissions and economic growth. Energy Policy 2013, 55, 483–489. [Google Scholar] [CrossRef]
- Ye, J.Y.; Wu, L.W. Social capital and the wage level of migrant workers—Resource measurement and causal identification. Economics 2014, 13, 1303–1322. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, J.; Long, Y. Outside the ivory tower: Visualizing university students’ top transit-trip destinations and popular corridors. Reg. Stud. 2016, 3, 202–206. [Google Scholar] [CrossRef]
- Rouse, P.; Wodenitscharow, K. Equity and Health Inequalities: Should DCEA be Considered for Decision Making in the United Kingdom? Value Health 2022, 25, S86. [Google Scholar] [CrossRef]
- Park, J. International and Intersectoral R&D Spillovers in the OECD and East Asian Economies. Econ. Inq. 2004, 42, 739–757. [Google Scholar] [CrossRef]
- Yang, J.; Yu, Z.; Ding, W. Interpolation methods for missing data in sample surveys. Math. Stat. Manag. 2008, 5, 821–832. [Google Scholar] [CrossRef]
- Liu, Z.; Yau, C. A propensity score adjustment method for longitudinal time series models under nonignorable nonresponse. Stat. Pap. 2021, 18, 317–342. [Google Scholar] [CrossRef]
- Lu, G.; Copas, J.B. Missing at Random, Likelihood Ignorability and Model Completeness. Ann. Stat. 2004, 32, 754–765. [Google Scholar] [CrossRef] [Green Version]
- Shao, S.; Fan, M.; Yang, L. Economic restructuring, green technological progress and low-carbon transformational development in China-an empirical examination based on the perspective of overall technological frontier and spatial spillover effects. Manag. World 2022, 38, 46–69+4-10. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Ingmar, R. A Generalized Spatial Two-Stage Least Squares Procedure for Estimating a Spatial Autoregressive Model with Autoregressive Disturbances. J. Real Estate Financ. Econ. 1998, 17, 99–121. [Google Scholar] [CrossRef]
- Yu, B. Can agglomeration of productive service industries improve manufacturing productivity? An analysis based on industry, regional and city heterogeneity perspectives. Nankai Econ. Res. 2017, 2, 112–132. [Google Scholar] [CrossRef]
- Sharif, H.M. Panel estimation for CO2 emissions, energy consumption, economic growth, trade openness and urbanization of newly industrialized countries. Energy Policy 2011, 39, 6991–6999. [Google Scholar] [CrossRef]
- Meijers, E. Summing small cities does not make a large city: Polycentric urban regions and the provision of cultural, leisure and sports amenities. Urban Stud. 2018, 45, 2323–2342. [Google Scholar] [CrossRef]
- Haider, H.; Hewage, K.; Umer, A.; Ruparathna, R. Sustainability Assessment Framework for Small-sized Urban Neighbourhoods: An Application of Fuzzy Synthetic Evaluation. Sustain. Cities Soc. 2017, 12, 21–32. [Google Scholar] [CrossRef]



| Variable | Definition | Computation Method | Data Source |
|---|---|---|---|
| lnCE | Carbon emission | Measurement of liquefied petroleum, natural gas, and community-wide electricity consumption at the city level | The World Bank World Development Indicators (WDI). http://data.worldbank.org/indicator (Accessed on 10 November 2022). China Electricity Yearbook China Energy Statistics Yearbook |
| lnCOV | Variation term | Extracted from LandScan Data using ArcGis 10.2 | LandScan Global Population Database https://landscan.ornl.gov/ (Accessed on 10 November 2022) |
| lnIA | Innovation ability | Number of patent applications | China Urban Statistical Yearbook https:/stats.gov.cn/tjsj/ndsj/ (Accessed on 10 November 2022) |
| lnFI | Foreign investment | Total actual foreign capital used in the year/nominal GDP | China Urban Statistical Yearbook |
| lnWAGE | Wage level | Urban active workers income | China Urban Statistical Yearbook |
| lnHC | Human capital | Number of general undergraduates and above/city’s resident population | China Urban Statistical Yearbook China Statistical Yearbook |
| lnFDL | Financial development level | Financial institutions year-end deposit and loan balances | China Financial Yearbook |
| lnHOS | Hospital beds | Hospital beds per 10,000 | China Urban Statistical Yearbook |
| (1) | (2) | |
|---|---|---|
| Variables | Static SDM | Dynamic SDM |
| lnCEt-1 | −0.342 *** | |
| (−4.013) | ||
| lnCOA | 0.318 *** | 0.374 * |
| (4.871) | (1.891) | |
| lnCOA2 | −0.294 ** | −0.116 ** |
| (−2.014) | (−2.043) | |
| W.lnCOA | −0.412 | 0.348 * |
| (−0.005) | (1.857) | |
| W.lnCOA2 | −0.436** | −0.296 *** |
| (−2.118) | (−3.995) | |
| lnIA | −0.041 *** | 0.020 *** |
| (−14.354) | (3.018) | |
| lnFI | −0.084 *** | −0.015 *** |
| (−3.985) | (−4.251) | |
| lnWAGE | 0.096 *** | 0.091 *** |
| (13.517) | (12.704) | |
| lnHC | 0.010 | −0.004 |
| (0.000) | (−0.261) | |
| lnFDL | 0.006 | −0.024 |
| (0.403) | (−0.389) | |
| lnHOS | 0.097 *** | −0.033 ** |
| (13.539) | (−2.231) | |
| Time fixed effect | YES | |
| Regional fixed effect | YES | |
| Log L | 126.978 | 107.856 |
| N | 4448 | 4448 |
| R2 | 0.609 | 0.574 |
| Hausman | 123.62 | |
| (0.013) | ||
| Short-Term Effect | Long-Term Effect | |||
|---|---|---|---|---|
| Direct Effect | Indirect Effect | Direct Effect | Indirect Effect | |
| InCOA | 0.354 *** | −0.115 *** | 0.052 | 0.337 * |
| (3.897) | (−3.882) | (1.026) | (1.889) | |
| InCOA2 | −0.268 | 0.214 | −0.137 *** | 0.235 *** |
| (−0.034) | (0.548) | (−3.987) | (4.218) | |
| Variables | Change the Dependent Variable | Change the Spatial Weight Matrix | GS2SLS |
|---|---|---|---|
| L.lnCOAt-1 | 0.418 *** | ||
| (3.579) | |||
| L.lnCOA2t-1 | −0.175 ** | ||
| (−2.364) | |||
| lnCOA | −0.021 * | 0.031 * | |
| (−1.852) | (1.783) | ||
| lnCOA2 | −0.179 *** | −0.268 ** | |
| (−3.974) | (−2.339) | ||
| W.lnCOA | 0.049 ** | 0.084 ** | |
| (2.512) | (2.071) | ||
| W.lnCOA2 | −0.157 ** | 0.108 ** | |
| (−2.413) | (2.015) | ||
| L.W.lnCOAt-1 | 0.146 *** | ||
| (3.759) | |||
| L.W.lnCOA2t-1 | 0.237 *** | ||
| (4.598) | |||
| Control variables | YES | ||
| Time fixed effect | YES | ||
| Regional fixed effect | YES | ||
| Cragg–Donald Wald F | 243.579 | ||
| Kleibergen–Paap rk Wald F | 253.791 | ||
| N | 4448 | 4448 | 4448 |
| Variables | Larger Cities | Small and Medium-Sized Cities |
|---|---|---|
| lnCOA | 0.146 ** | −0.307 * |
| (2.413) | (−1.846) | |
| lnCOA2 | −0.121 * | −0.235 |
| (−1.903) | (−0.697) | |
| W.lnCOA | 0.185 *** | 0.348 * |
| (3.986) | (1.857) | |
| W.lnCOA2 | 0.213 ** | 0.107 |
| (2.476) | (1.083) | |
| Control variables | YES | |
| Time fixed effect | YES | |
| Regional fixed effect | YES | |
| Log L | 701.00 | 735.61 |
| N | 1840 | 2608 |
| R2 | 0.462 | 0.773 |
| Variables | Eastern Region | Central Region | Western Region |
|---|---|---|---|
| lnCOA | 0.214 * | 0.223 ** | −0.361 *** |
| (1.869) | (2.305) | (−3.978) | |
| lnCOA2 | −0.325 ** | −0.351 | 0.348 |
| (−2.436) | (-0.023) | (0.299) | |
| W.lnCOA | 0.371 ** | 0.348 * | 0.014 |
| (2.397) | (1.857) | (1.015) | |
| W.lnCOA2 | 0.193 ** | 0.237 | 0.097 |
| (2.308) | (1.095) | (0.078) | |
| Control variables | YES | ||
| Time fixed effect | YES | ||
| Regional fixed effect | YES | ||
| Log L | 377.65 | 426.52 | 507.71 |
| N | 1584 | 1600 | 1264 |
| R2 | 0.438 | 0.180 | 0.394 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, X.; Zhang, S. Impacts of Urban Spatial Development Patterns on Carbon Emissions: Evidence from Chinese Cities. Land 2022, 11, 2031. https://doi.org/10.3390/land11112031
Li X, Wang X, Zhang S. Impacts of Urban Spatial Development Patterns on Carbon Emissions: Evidence from Chinese Cities. Land. 2022; 11(11):2031. https://doi.org/10.3390/land11112031
Chicago/Turabian StyleLi, Xuanting, Xiaohong Wang, and Shaopeng Zhang. 2022. "Impacts of Urban Spatial Development Patterns on Carbon Emissions: Evidence from Chinese Cities" Land 11, no. 11: 2031. https://doi.org/10.3390/land11112031




