Comparison of Random Forest and Kriging Models for Soil Organic Carbon Mapping in the Himalayan Region of Kashmir
Abstract
1. Introduction
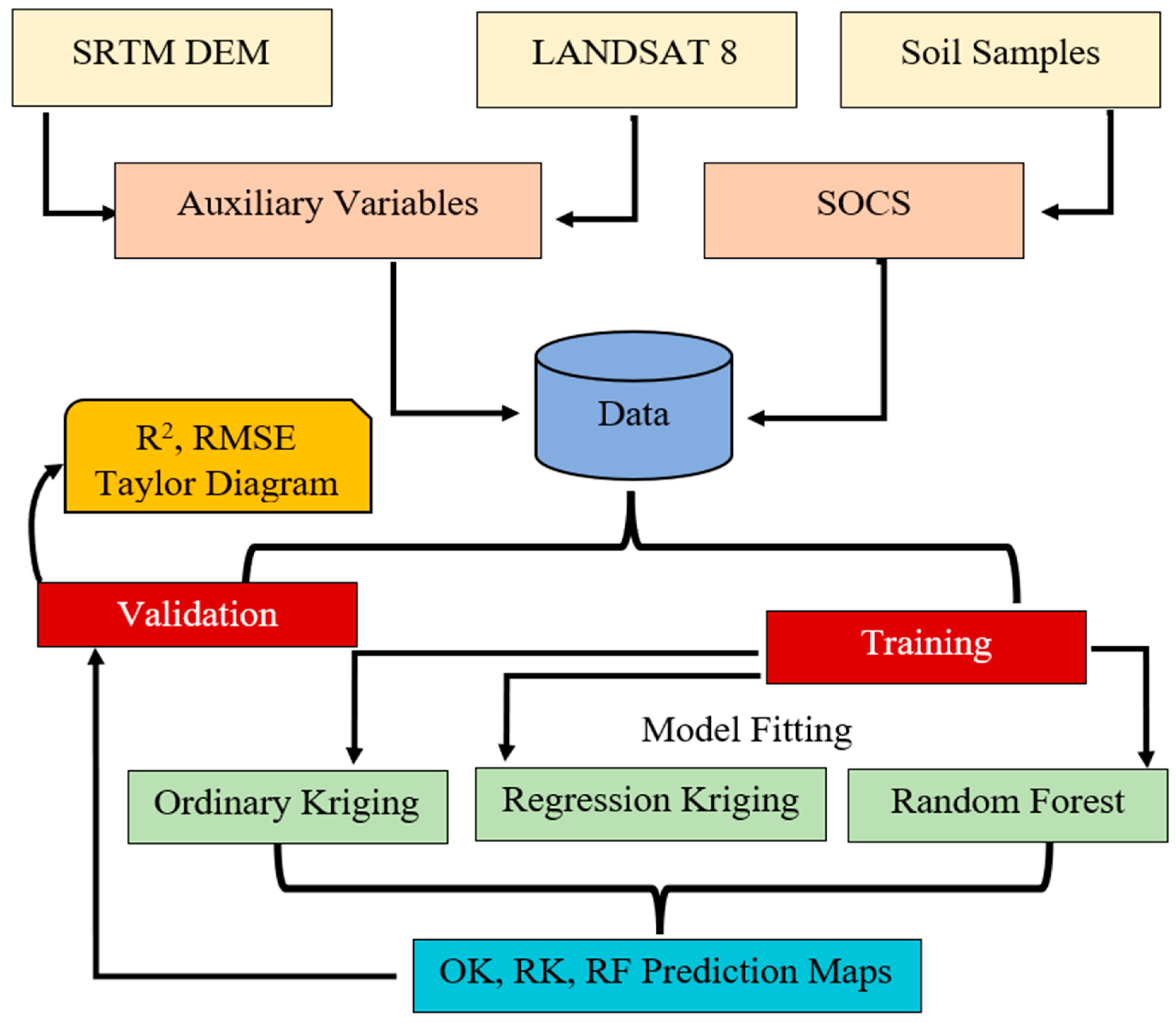
2. Materials and Methods
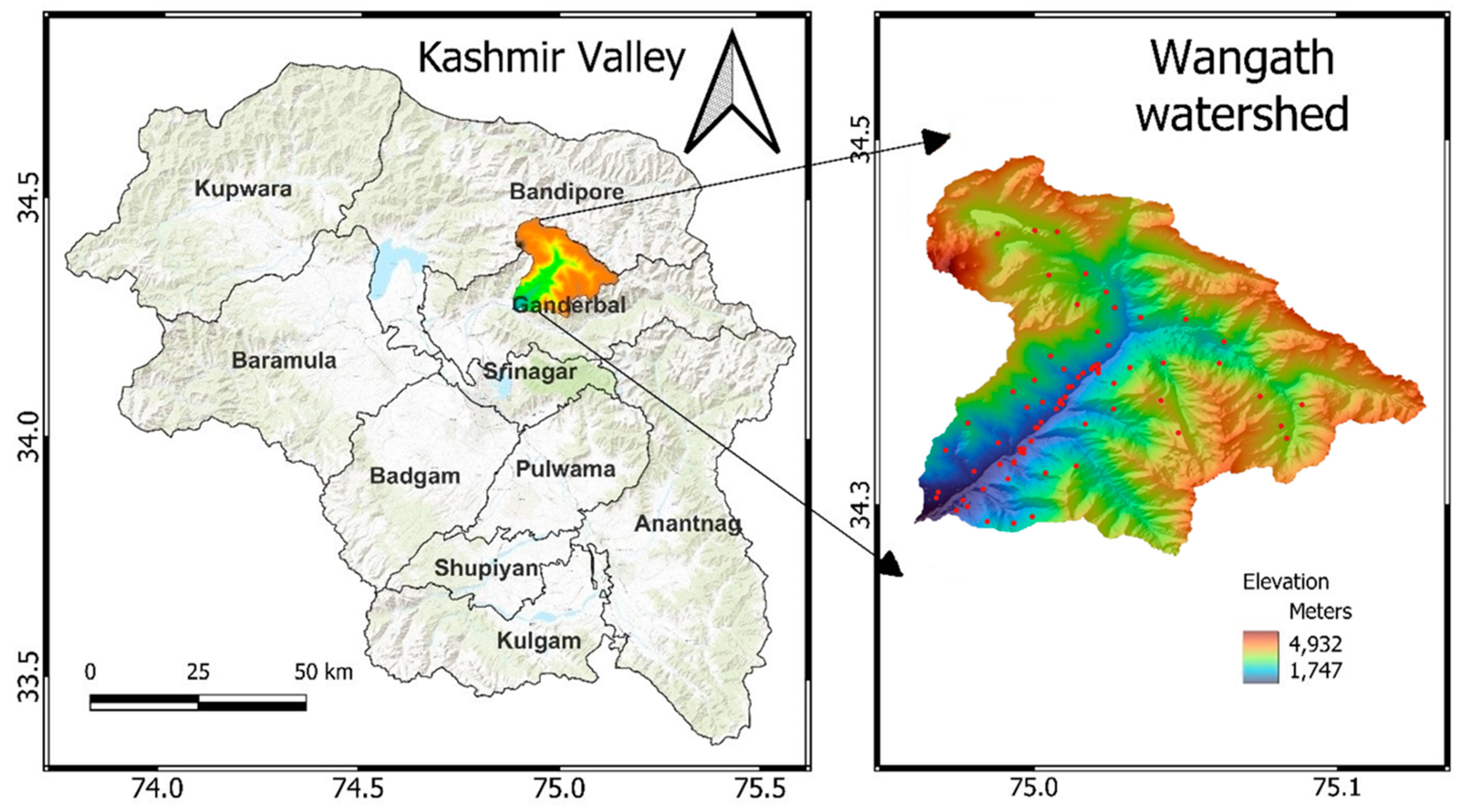
2.1. Study Area
2.2. Soil Sampling and Analysis
2.3. SOC Stock Estimation
2.4. Auxiliary Covariates
2.5. Geostatistical and Machine Learning Techniques
2.5.1. Ordinary Kriging
2.5.2. Regression Kriging
2.5.3. Random Forest
2.6. Model Validation
3. Results and Discussion
3.1. Statistical Analysis of SOC Stocks
3.2. Correlation of SOCS with Environmental Variables
3.3. Spatial Distribution of SOCS
3.3.1. Ordinary Kriging
3.3.2. Regression Kriging
3.3.3. Random Forest
3.4. Model Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hussain, S.; Sharma, V.; Arya, V.M.; Sharma, K.R.; Rao, C.S. Total organic and inorganic carbon in soils under different land use/land cover systems in the foothill Himalayas. Catena 2019, 182, 104104. [Google Scholar] [CrossRef]
- Li, L.; Lu, J.; Wang, S.; Ma, Y.; Wei, Q.; Li, X.; Ren, T. Methods for estimating leaf nitrogen concentration of winter oilseed rape (Brassica napus L.) using in situ leaf spectroscopy. Ind. Crop. Prod. 2016, 91, 194–204. [Google Scholar] [CrossRef]
- Antonangelo, J.A.; Sun, X.; Zhang, H. The roles of co-composted biochar (COMBI) in improving soil quality, crop productivity, and toxic metal amelioration. J. Environ. Manag. 2021, 277, 111443. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Rossi, L.; Zotarelli, L.; Gao, B.; Shahid, M.A.; Sarkhosh, A. Biochar improves soil physical characteristics and strengthens root architecture in Muscadine grape (Vitis rotundifolia L.). Chem. Biol. Technol. Agric. 2021, 8, 7. [Google Scholar] [CrossRef]
- Mandal, U.K. Spectral Color Indices Based Geospatial Modeling of Soil Organic Matter in Chitwan District, Nepal. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 43–48. [Google Scholar] [CrossRef]
- Bangroo, S.A.; Najar, G.R.; Rasool, A. Effect of altitude and aspect on soil organic carbon and nitrogen stocks in the Himalayan Mawer Forest Range. Catena 2017, 158, 63–68. [Google Scholar] [CrossRef]
- Petermann, E.; Meyer, H.; Nussbaum, M.; Bossew, P. Mapping the geogenic radon potential for Germany by machine learning. Sci. Total Environ. 2021, 754, 142291. [Google Scholar] [CrossRef]
- Swiderski, B.; Osowski, S.; Kruk, M.; Barhoumi, W. Aggregation of classifiers ensemble using local discriminatory power and quantiles. Expert Syst. Appl. 2016, 46, 316–323. [Google Scholar] [CrossRef]
- Bashir, O.; Ali, T.; Baba, Z.A.; Rather, G.H.; Bangroo, S.A.; Mukhtar, S.D.; Naik, N.; Mohiuddin, R.; Bharati, V.; Bhat, R.A. Soil Organic Matter and Its Impact on Soil Properties and Nutrient Status. In Microbiota and Biofertilizers; Springer: Berlin/Heidelberg, Germany, 2021; Volume 2, pp. 129–159. [Google Scholar]
- Batjes, N.H. Total carbon and nitrogen in the soils of the world. Eur. J. Soil Sci. 1996, 47, 151–163. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Zhang, C.; Tang, Y.; Xu, X.; Kiely, G. Towards spatial geochemical modelling: Use of geographically weighted regression for mapping soil organic carbon contents in Ireland. Appl. Geochem. 2011, 26, 1239–1248. [Google Scholar] [CrossRef]
- Ma, S.; Qiao, Y.P.; Wang, L.J.; Zhang, J.C. Terrain gradient variations in ecosystem services of different vegetation types in mountainous regions: Vegetation resource conservation and sustainable development. For. Ecol. Manag. 2021, 482, 118856. [Google Scholar] [CrossRef]
- Lagacherie, P.; McBratney, A.B. Spatial soil information systems and spatial soil inference systems: Perspectives for digital soil mapping. Dev. Soil Sci. 2006, 31, 3–22. [Google Scholar]
- Reza, S.K.; Nayak, D.C.; Chattopadhyay, T.; Mukhopadhyay, S.; Singh, S.K. Srinivasan, R. Spatial distribution of soil physical properties of alluvial soils: A geostatistical approach. Arch. Agron. Soil Sci. 2016, 62, 972–981. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, P.; Yin, A.; Yang, X.; Zhang, M.; Gao, C. Prediction of soil organic carbon in an intensively managed reclamation zone of eastern China: A comparison of multiple linear regressions and the random forest model. Sci. Total Environ. 2017, 592, 704–713. [Google Scholar] [CrossRef]
- Pham, T.G.; Kappas, M.; Van Huynh, C.; Nguyen, L.H.K. Application of ordinary kriging and regression kriging method for soil properties mapping in hilly region of Central Vietnam. ISPRS Int. J. Geo-Inf. 2019, 8, 147. [Google Scholar] [CrossRef]
- Duffera, M.; White, J.G.; Weisz, R. Spatial variability of Southeastern US Coastal Plain soil physical properties: Implications for site-specific management. Geoderma 2007, 137, 327–339. [Google Scholar] [CrossRef]
- Fathololoumi, S.; Vaezi, A.R.; Alavipanah, S.K.; Ghorbani, A.; Saurette, D.; Biswas, A. Effect of multi-temporal satellite images on soil moisture prediction using a digital soil mapping approach. Geoderma 2021, 385, 114901. [Google Scholar] [CrossRef]
- Keerthan, K.; Shubha, T.G.; Sushma, S.A. Random forest algorithm for soil fertility prediction and grading using machine learning. Int. J. Innov. Technol. Explor. Eng. 2019, 9, 1301–1304. [Google Scholar]
- Heuvelink, G.B.M.; Webster, R. Modelling soil variation: Past, present, and future. Geoderma 2001, 100, 269–301. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Barthold, F.; Blank, B.; Kögel-Knabner, I. Digital mapping of soil organic matter stocks using Random Forest modeling in a semi-arid steppe ecosystem. Plant Soil 2011, 340, 7–24. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping soil organic matter contents at field level with Cubist, Random Forest and kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lützow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Ließ, M.; Garcia-Franco, N.; et al. Soil organic carbon storage as a key function of soils-A review of drivers and indicators at various scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Yang, Z.; Di, L.; Yu, G.; Chen, Z. Vegetation condition indices for crop vegetation condition monitoring. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 3534–3537. [Google Scholar]
- Huang, H.; Chen, Y.; Clinton, N.; Wang, J.; Wang, X.; Liu, C.; Gong, P.; Yang, J.; Bai, Y.; Zheng, Y.; et al. Mapping major land cover dynamics in Beijing using all Landsat images in Google Earth Engine. Remote Sens. Environ. 2017, 202, 166–176. [Google Scholar] [CrossRef]
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.E.; Peterson, G.A. Soil attribute prediction using terrain analysis. Soil Sci. Soc. Am. J. 1993, 57, 443–452. [Google Scholar] [CrossRef]
- Baltensweiler, A.; Walthert, L.; Hanewinkel, M.; Zimmermann, S.; Nussbaum, M. Machine learning based soil maps for a wide range of soil properties for the forested area of Switzerland. Geoderma Reg. 2021, 27, e00437. [Google Scholar] [CrossRef]
- Wang, S.; Huang, M.; Shao, X.; Mickler, R.A.; Li, K.; Ji, J. Vertical distribution of soil organic carbon in China. Environ Manag. 2004, 33, S200–S209. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q. Magnetic properties of two soil profiles from Yan’an, Shaanxi Province and their implications for paleorainfall reconstruction. Sci. China Earth Sci. 2014, 57, 719–728. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C., Jr. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma 2015, 239, 68–83. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Dash, P.; Sazib, N. TauDEM 5.3: Guide to Using the TauDEM Command Line Functions. 2015. Available online: https://hydrology.usu.edu/taudem/taudem5/TauDEM53CommandLineGuide.pdf (accessed on 13 July 2021).
- Tahir, M.; Imam, E.; Hussain, T. Evaluation of land use/land cover changes in Mekelle City, Ethiopia using Remote Sensing and GIS. Comput Ecol Softw. 2013, 3, 9. [Google Scholar]
- Nelson, D.W.; Sommers, L. Total carbon, organic carbon, and organic matter. Method. Soil Anal. Part 2 Chem. Microbiol. Prop. 1983, 9, 539–579. [Google Scholar]
- Blake, G.R.; Hartge, K.H. Bulk Density. In Methods of Soil Analysis, Part I Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; ASA-SSSA: Madison, WI, USA, 1986; pp. 363–375. [Google Scholar] [CrossRef]
- Penman, J.; Gytarsky, M.; Hiraishi, T.; Krug, T.; Kruger, D.; Pipatti, R.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K.; et al. Good Practice Guidance for Land Use, Land Use Change and Forestry; Institute for Global Environmental Strategies: Hayama, Japan, 2003. [Google Scholar]
- Khan, N.M.; Rastoskuev, V.V.; Sato, Y.; Shiozawa, S. Assessment of hydro saline land degradation by using a simple approach of remote sensing indicators. Agric. Water Manag. 2005, 77, 96–109. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Liu, W.T. Kogan, F.N. Monitoring regional drought using the Vegetation Condition Index. Int. J. Remote Sens. 1996, 17, 2761–2782. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with erts. NASA Spec. Publ. 1974, 351, 309–317. [Google Scholar]
- Mathieu, R.; Pouget, M.; Cervelle, B.; Escadafal, R. Relationships between Satellite-Based Radiometric Indices Simulated Using Laboratory Reflectance Data and Typic Soil Color of an Arid Environment. Remote. Sens. Environ. 1998, 66, 17–28. [Google Scholar] [CrossRef]
- Pearson, R.L.; Miller, L.D. Remote Mapping of Standing Crop Biomass for Estimation of the Productivity of the Short-Grass Prairie. In Proceedings of the Eighth International Symposium on Remote Sensing of Environment, Pawnee National Grasslands, Colorado, Ann Arbor, MI, USA, 2–6 October 1972; pp. 357–1381. [Google Scholar]
- Amro, F.A. Using Remote Sensing data to identify iron deposits in central western Libya. In Proceedings of the International Conference on Emerging Trends in Computer and Image Processing (ICETCIP 2011), Bangkok, Thailand, 23–24 December 2011. [Google Scholar]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Prodanovic, D.; Stanic, M.; Milivojevic, V.; SimiC, Z.; ArsiC, M. DEM-Based GIS Algorithms for Automatic Creation of Hydrological Models Data. J. Serb. Soc. Comput. Mech. 2009, 3, 64–85. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. (Eds.) Terrain analysis: Principles and applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Jenness, J. Topographic Position Index (tpi_jen.avx) extension for ArcView 3.x, v. 1.2. Jenness Enterprises. 2006. Available online: http://www.jennessent.com/arcview/tpi.htm (accessed on 13 July 2021).
- Boehner, J.; Koethe, R.; Conrad, O.; Gross, J.; Ringeler, A.; Selige, T. Soil Regionalisation by Means of Terrain Analysis and Process Parameterisation. In Soil Classification 2001; European Soil Bureau, Research Report No. 7, EUR 20398 EN; Micheli, E., Nachtergaele, F., Montanarella, L., Eds.; Office for Official Publications of the European Communities: Luxembourg, 2002; pp. 213–222. [Google Scholar]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Erskine, R.H.; Green, T.R.; Ramirez, J.A.; MacDonald, L.H. Comparison of grid-based algorithms for computing upslope contributing area. Water Resour. Res. 2006, 42, W09416. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the revised universal soil loss equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Moore, I.D.; Burch, G.J. Modelling Erosion and Deposition: Topographic Effects. Trans. ASAE 1986, 29, 1624–1630. [Google Scholar] [CrossRef]
- Moore, I.D.; Turner, A.K.; Wilson, J.P.; Jenson, S.K.; Band, L.E. GIS and land-surface-subsurface process modelling. In Environmental Modelling with GIS; Goodchild, M.F., Parks, B.O., Steyaert, L.T., Eds.; CRC Press: Boca Raton, FL, USA, 1993; pp. 213–230. [Google Scholar]
- Bai, T.; Tahmasebi, P. Accelerating geostatistical modeling using geostatistics-informed machine Learning. Comput Geosci. 2021, 146, 104663. [Google Scholar] [CrossRef]
- Das, S. Extreme rainfall estimation at ungauged locations: Information that needs to be included in low-lying monsoon climate regions like Bangladesh. J. Hydrol. 2021, 601, 126616. [Google Scholar] [CrossRef]
- Brunello, A.; Urgolo, A.; Pittino, F.; Montvay, A.; Montanari, A. Virtual Sensing and Sensors Selection for Efficient Temperature Monitoring in Indoor Environments. Sensors 2021, 21, 2728. [Google Scholar] [CrossRef]
- Cambardella, C.A.; Moorman, T.B.; Parkin, T.B.; Karlen, D.L.; Novak, J.M.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Heung, B.; Bulmer, C.E.; Schmidt, M.G. Predictive soil parent material mapping at a regional-scale: A random forest approach. Geoderma 2014, 214, 141–154. [Google Scholar] [CrossRef]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water feature extraction and change detection using multitemporal Landsat imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. 2020. Available online: https://www.R-project.org/ (accessed on 15 March 2021).
- Denton, O.A.; Aduramigba-Modupe, V.O.; Ojo, A.O.; Adeoyolanu, O.D.; Are, K.S.; Adelana, A.O.; Oke, A.O. Assessment of spatial variability and mapping of soil properties for sustainable agricultural production using geographic information system techniques (GIS). Cogent Food Agric. 2017, 3, 1279366. [Google Scholar] [CrossRef]
- Wan, Y.; Lin, E.; Xiong, W.; Guo, L. Modeling the impact of climate change on soil organic carbon stock in upland soils in the 21st century in China. Agric. Ecosyst. Environ. 2011, 141, 23–31. [Google Scholar] [CrossRef]
- Liu, S.; An, N.; Yang, J.; Dong, S.; Wang, C.; Yin, Y. Prediction of soil organic matter variability associated with different land use types in mountainous landscape in southwestern Yunnan province, China. Catena 2015, 133, 137–144. [Google Scholar] [CrossRef]
- McNicol, G.; Bulmer, C.; D’Amore, D.; Sanborn, P.; Saunders, S.; Giesbrecht, I.J.; Arriola, S.G.; Bidlack, A.; Butman, D.; Buma, B. Large, climate-sensitive soil carbon stocks mapped with pedology-informed machine learning in the North Pacific coastal temperate rainforest. Environ. Res. Lett. 2019, 14, 014004. [Google Scholar] [CrossRef]
- Kumar, S.; Lal, R. Mapping the organic carbon stocks of surface soils using local spatial interpolator. J. Environ. Monit. 2011, 13, 3128–3135. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Guo, Z.; Ullah, S.; Melagraki, G.; Afantitis, A.; Lynch, I. Nanotechnology and artificial intelligence to enable sustainable and precision agriculture. Nat. Plants 2021, 7, 864–876. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Zhu, Z.; Montzka, C.; Chai, L.; Liu, S.; Ge, Y.; Liu, J.; Lu, Z.; He, X.; Zheng, J.; et al. Inter-comparison of several soil moisture downscaling methods over the Qinghai-Tibet Plateau, China. J. Hydrol. 2020, 592, 125616. [Google Scholar] [CrossRef]
- Gasmi, A.; Gomez, C.; Chehbouni, A.; Dhiba, D.; El Gharous, M. Using PRISMA Hyperspectral Satellite Imagery and GIS Approaches for Soil Fertility Mapping (FertiMap) in Northern Morocco. Remote Sens. 2022, 14, 4080. [Google Scholar] [CrossRef]
- Gomez, C.; Rossel, R.A.V.; McBratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and field vis-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar] [CrossRef]
- Sekulic, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolic, M.; Bajat, B. Random Forest Spatial Interpolation. Remote. Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.C.; Brus, D.J.; Heuvelink, G.B.M. Sampling design optimization for soil mapping with random forest. Geoderma 2019, 355, 113913. [Google Scholar] [CrossRef]




| Sources | Variables | Description | References |
|---|---|---|---|
| LANDSAT 8 (OLI and TIRS) | BI | Brightness index BI = ((R2 + G2 + B2)/3)0.5 | Khan et al., 2005 [37] |
| GI | Greenness index GI = 2G – R − B/2G + R + B | Gitelson et al., 1996 [38] | |
| WI/NDMI | Wetness index/Normalized difference moisture index WI = (NIR − SWIR1)/(NIR + SWIR1) | Gao 1996 [39] | |
| VCI | Vegetation condition index VCI = ((NDVI − NDVImin)/(NDVImax − NDVImin)) × 100 | Liu and Kogan 1996 [40] | |
| NDVI | Normalized difference vegetation index NDVI = (NIR − Red)/(NIR + Red) | Rouse et al., 1974 [41] | |
| SI | Saturation index SI = (R − B)/(R + B) | Mathieu et al., 1998 [42] | |
| HI | Hue index HI = atan (2R − G − B)/[30.5 (G − B)] | ||
| CI | Coloration index CI = R − G/R + G | ||
| RI | Redness index RI = R2/(B × G3) | ||
| RVI | Ratio vegetation index RVI = NIR/Red | Pearson and Miller 1972 [43] | |
| CLI | Clay index (clay mineral ratio) CI= SWIR1/SWIR2 | Amro and Alasta 2011 [44] | |
| PVI | Perpendicular vegetation index (NIR – aR − b)/(1 + a2)1/2 | Richardson and Wiegand 1977 [45] | |
| SAVI | Soil-adjusted vegetation index SAVI = (NIR − R) (1 + L)/(NIR + R + L) | Huete 1988 [46] | |
| SRTM DEM | Slope | Steepness | Prodanovis et al., 2009 [47] |
| Elevation | Distance above sea level | ||
| Aspect | Direction that the slope faces | ||
| PC | Profile curvature | Wilson and Gallant 2000 [48] | |
| PLC | Plan curvature | ||
| MC | Mean curvature | ||
| FD | Flow direction | ||
| TPI | Topographic position index | Jenness 2006 [49] | |
| SWA | SAGA wetness index | Boehner et al., 2002 [50] | |
| CTI | Compound topographic index | Moore et al., 1991 [51] | |
| TUL | Total upslope length | Erskine et al., 2006 [52] | |
| LUL | Longest upslope length | ||
| CA | Contributing area | Moore and Wilson 1992 [53] | |
| TCI | Transport capacity index/Sediment transport index | Moore and Burch 1986 [54] | |
| SPI | Stream power index | Moore et al., 1993 [55] |
| Soil Parameter | Mean | Min | Max | 95% C.I. | S.D. | CV (%) | MDR |
|---|---|---|---|---|---|---|---|
| SOCS (Mg/ha) | 26.48 | 1.12 | 70.60 | 23.09–29.80 | 15.51 | 33.81 | 62.09 |
| Land Use | SOCS (Mg/ha) | |
|---|---|---|
| Horticulture | Mean | 46.26 |
| 95% C.I. | 26.69–62.83 | |
| Maize | Mean | 13.12 |
| 95% C.I. | 4.80–21.45 | |
| Forest | Mean | 30.23 |
| 95% C.I. | 26.83–33.60 | |
| Wasteland | Mean | 5.48 |
| 95% C.I. | 2.84–8.12 | |
| Paddy | Mean | 33.01 |
| 95% C.I. | 23.12–42.90 | |
| Soil Property | Auxiliary Variables | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BI | GI | WI | VCI | NDVI | SI | HI | CI | RI | RVI | |
| SOCS | −0.42 ** | 0.17 | 0.41 ** | 0.32 ** | 0.30** | −0.37 ** | 0.23 * | −0.42 ** | 0.14 | 0.31 ** |
| Soil Property | Auxiliary Variables | |||||||||
| CLI | PVI | SAVI | Slope | Elevation | Aspect | PLC | PC | CTI | MC | |
| SOCS | 0.27 * | −0.01 | 0.30 ** | 0.03 | −0.19 | 0.16 | 0.09 | −0.12 | −0.16 | 0.12 |
| Soil Property | Auxiliary Variables | |||||||||
| FD | TPI | SWI | TUL | LUL | CA | TCI | SPI | |||
| SOCS | −0.19 * | −0.10 | −0.16 | −0.06 | −0.09 | −0.06 | −0.16 | −0.22 * | ||
| Type | Model Fit | Range (m) | Sill | Nugget | Psill | Nugget:Sill Ratio | Spatial Dependence |
|---|---|---|---|---|---|---|---|
| Ordinary Kriging | Gau | 2241.0 | 2.82 | 1.80 | 1.02 | 53 | Moderate |
| Regression Kriging | Sph | 350.34 | 2.144 | 0.89 | 1.254 | 41.0 | Moderate |
| Soil Property | Transformation | Evaluation Parameters | Digital Soil Mapping Algorithms | ||
|---|---|---|---|---|---|
| Ordinary Kriging | Regression Kriging | Random Forest | |||
| SOCS (Mg/ha) | Sqrt | RMSE | 15.60 | 17.73 | 8.21 |
| R2 | 0.53 | 0.29 | 0.90 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farooq, I.; Bangroo, S.A.; Bashir, O.; Shah, T.I.; Malik, A.A.; Iqbal, A.M.; Mahdi, S.S.; Wani, O.A.; Nazir, N.; Biswas, A. Comparison of Random Forest and Kriging Models for Soil Organic Carbon Mapping in the Himalayan Region of Kashmir. Land 2022, 11, 2180. https://doi.org/10.3390/land11122180
Farooq I, Bangroo SA, Bashir O, Shah TI, Malik AA, Iqbal AM, Mahdi SS, Wani OA, Nazir N, Biswas A. Comparison of Random Forest and Kriging Models for Soil Organic Carbon Mapping in the Himalayan Region of Kashmir. Land. 2022; 11(12):2180. https://doi.org/10.3390/land11122180
Chicago/Turabian StyleFarooq, Iqra, Shabir Ahmed Bangroo, Owais Bashir, Tajamul Islam Shah, Ajaz A. Malik, Asif M. Iqbal, Syed Sheraz Mahdi, Owais Ali Wani, Nageena Nazir, and Asim Biswas. 2022. "Comparison of Random Forest and Kriging Models for Soil Organic Carbon Mapping in the Himalayan Region of Kashmir" Land 11, no. 12: 2180. https://doi.org/10.3390/land11122180
APA StyleFarooq, I., Bangroo, S. A., Bashir, O., Shah, T. I., Malik, A. A., Iqbal, A. M., Mahdi, S. S., Wani, O. A., Nazir, N., & Biswas, A. (2022). Comparison of Random Forest and Kriging Models for Soil Organic Carbon Mapping in the Himalayan Region of Kashmir. Land, 11(12), 2180. https://doi.org/10.3390/land11122180







