Assessment of Physical Vulnerability and Uncertainties for Debris Flow Hazard: A Review concerning Climate Change
Abstract
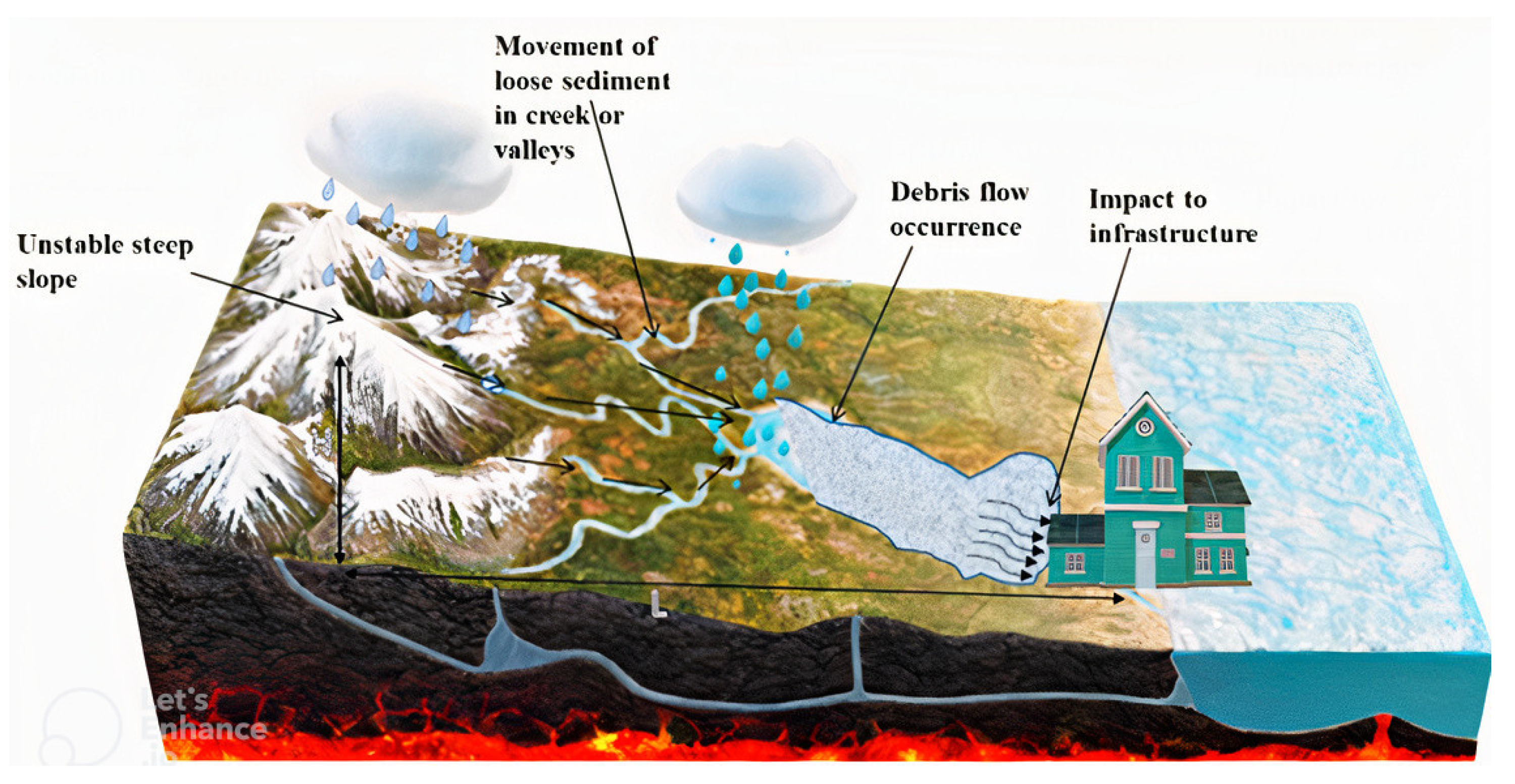
:1. Introduction
2. Debris Flow and Its Consequences
3. Overview of Physical Vulnerability Approaches
3.1. Empirical Methods
3.2. Analytical Methods
| S. No. | Reference | Event/Location/Number of Structures Affected | Process Intensity | Damage Value/Classification | Remark |
|---|---|---|---|---|---|
| 1 | Zanchetta et al., 2004 [59] | 6 May 1998/Italy/25 buildings | 35 kPa, l = 900–2000 m | Reconstruction value (€)/complete, heavy, and moderate | Vulnerability Matrix |
| 2 | Hu et al., 2012 [60] | 7 August 2010/China/16 buildings | p = 0–110 kPa, Q = 1485 , volume = 2.2 million | Municipality value/complete (18 < p < 110 kPa), heavy, (8 < p < 50 kPa), moderate, (6 < p < 35 kPa), slight, (p ≤ 8 kPa), and very slight) | Vulnerability matrix |
| 3 | Jakob et al., 2012 [61] | 68 well-documented date/20 buildings | for slight damage to destruction | Insurance value/some sedimentation (I) < 25% of an insured loss, some structural damage (II) = 25–50% insured loss, major structural damage (III) > 75% insured loss, destruction (IV) = 100% loss | Vulnerability matrix |
| 4 | Winter et al., 2013 [62] | 17 countries’ data/20 roads | volume = 10–10,000 m3 | Limited, serious, and destroyed | Vulnerability matrix with fragility curve |
| 5 | Kang and Kim 2016 [63] | August 2011/South Korea/25 buildings | v = 3–14.9 m/s, d = 0–6 m, p = 0–35 kPa Q = 15.6–759.3 | Property value/complete damage For non-RC building (p > 30 kPa) For RC building (p > 35 kPa)/NA | Vulnerability Curve For RC building , , |
| 6 | Fuchs et al. 2007 [55] | 16 August 1997/Austria/16 buildings | h = 0–3 m | Reconstruction value (1600–140,000€)/NA | Vulnerability curves V = 0.11 h2–0.02 h, for h < 2.5 m and r2 = 0.865 |
| 7 | Haugen and Kaynia 2008 [64] | 6 May 1998/Italy/6 buildings | x = 0.015–0.127 m p = 0.1–1.15 MN | Insurance value/complete (0.45 < p <1.15 MN), extensive (0.34 < p < 0.81 MN), moderate (0.15 < p < 0.40), and slight (0.1 < p < 0.15) | Vulnerability model |
| 8 | Akbas et al., 2009 [49] | 13 July 2008/Italy/20 buildings | h = 0.30–3 m | reconstruction value (€ 2000 to € 290,000)/damage factor (0–1) | Vulnerability curves V = 0.17 h2–0.03 h, r2 = 0.995 |
| 9 | Papathoma-Köhle et al., 2012 [52] | August 1987/Italy/51 buildings | h = 0–4 m | Degree of loss based on photographic documentation and repair cost from the municipality (approx. 8.5 million €)/NA | Physical vulnerability curve |
| 10 | Quan Luna et al., 2011, 2014 [65,66] | 13 July 2008/Italy/30 buildings | h = 0–4 m m2s p = 0–40 kPa | Reconstruction value (€)/damage index (0.35 to 0.66) | Vulnerability curve 5.32 m2s |
| 11 | Totschnig and Fuchs 2013 [28] | 16 August 2005/Austria/193 buildings | h = 0–4 m IR = 0–0.60 | Property value (€)/damage ratio (0–1) | Vulnerability model (Log logistic) |
| 12 | Ciurean et al., 2017 [67] | 1998/Italy/41 building (1–3 floors) | Iobs = 0.1 hdpt | Municipality value (€)/damage ratio DR = DC/MV = 0.15–0.90 | Vulnerability model |
| 13 | Shen et al., 2018 [68] | 14 August 2010/China 390 buildings | h = 0–3.5 m m/s p = 0–35 kPa | Reconstruction value (€)/degree of loss (0.25–0.85) | Vulnerability curve |
| 14 | Yan et al., 2020 [69] | September 2010/China/2 bridge pier | v = 1–12 m/s h = 0–6 m Rb = 0.1–0.80 m | Insurance value (€)/4 damage classes (0.2–1) | Physical vulnerability curve (Damage class 3) |
| 15 | Kappes et al., 2012 [70] | Well-documented debris flow data/65 buildings | Building surrounding, building, and human-related characteristics, | N/A | Indicator based vulnerability |
| 16 | Godfrey et al., 2015 [54] | 2004,2005/Romania/60 buildings | h = 0–3 m d = 0–5 m | Municipality report (€)/damage factor (0-1) | Specific vulnerability curve |
| 17 | Du et al., 2015 [15] | 19 September 1982/El Salvador/58 buildings | p = 4.5–14 kPa | Susceptibility factor Sstr = 0.1–0.8 for reinforced-to-brick masonry structure | Vulnerability model |
| 18 | Dadfar et al., 2018 [71] | Arbitrary data/pipeline | D/t = 36, 64, 78, and 96. PGD width = 10, 20, 30 m | NA/Tensile rupture, local buckling, and premature cross-sectional failure | Novel vulnerability function repair rate = P.(E) * vALD* (repair rate) ALD |
| 19 | Wu and Li, 2019 and Mustaffa et al., 2021 [29,72] | Debris flow data from China, Malaysia/pipeline | Exposed width = 10–40 m = 15°–90° width of the corrosion pit = 0.3–2 m. p = 42.6 to 600 kPa | Shear failure observed due to impact of stone/NA | A multivariate regression equation for corrosion parameters of the pipeline |
| 20 | Thouret et al., [53] | 2004/Venezuela/15 buildings | Building type, Number of floors, age of construction | Reconstruction value (€)/damage was assessed using 3 × 3 DEM file of the study area | Physical vulnerability maps for city block, and residential building |
3.3. Qualitative Methods (Vulnerability Matrix)
3.4. Quantitative Method (Vulnerability Curve)
3.5. Semi-Quantitative Methods (Vulnerability Indicator)
3.6. Combination of Approaches
4. Uncertainties in Vulnerability Analysis
Uncertainty Quantification Techniques
5. Recent Advancements in Vulnerability Assessment
- Development of the advanced vulnerability function to assess the vulnerability quantitatively by correlating intensity along the (X-axis) with the building’s state of damage (Y-axis).
- Bahler et al., 2001 [106] initiated the "Pragmatic approach" based on the past existing data, local experience of the practitioner, expert judgment, and regional representative of the population for risk estimation of natural hazards. Furthermore, Swiss federal offices for civil protection and the environment developed an e-learning platform using a pragmatic approach. This software provides the calculation tools for simplified risk analysis in Switzerland and abroad.
- Recently, the MOVE vulnerability assessment framework has been developed by the FP7 MOVE Project engineers to address the vulnerability in a multidimensional view with respect to space and time.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| h | Depositional height (m) |
| v | Maximum flow velocity (m/s) |
| Impact Pressure (kPa) | |
| l | Runout distances (m) |
| Q | Discharge (m3/s) |
| Vulnerability of structure | |
| I | Process intensity |
| IDF | Average impact index |
| IR | Relative intensity |
| Iobs | Observed intensity |
| a,b,c | Intensity parameter (cm) a lowest value, b highest value, c (in between a and b) |
| ℇ | Quantity belongs to mention subset |
| R | Resilience of structure |
| Rb | Boulder radius (m) |
| Impact angle (°) | |
| Maximum von mises stresses in MPa | |
| D/t | Diameter to thickness ratio |
| Embedment depth to diameter ratio | |
| vALD | Occurrence rate of ALD along the pipeline route |
| q | Uniformly distributed load (kN/m2) |
| D | Diameter of pipeline |
| S | Susceptibility |
| Soil resistance (kN/m2) | |
| Weight of indicator | |
| Indicator | |
| Score of indicators | |
| P.(E) | Probability of occurrence |
| T | Thickness of pipe (mm) |
| t | Depth of corrosion pit (m) |
| Abbreviations | |
| ALD | Active layer detachment |
| BN | Bayesian network |
| DPM | Damage probability matrices |
| DR | Damage ratio |
| DC | Damage cost |
| FOSM | First-order second moment |
| GFLD | Global fatal landslide database |
| GIS | Geoinformatics system |
| GVC | Generic vulnerability curve |
| LIFE | Large deformation finite element |
| MOVE | Methods for improvement of vulnerability assessment in Europe |
| MV | Municipality value |
| PVI | Physical vulnerability index |
| PR | Private residential |
| RCC | Reinforced concrete |
| RVI | Relative vulnerability index |
| SVC | Specific vulnerability curve |
References
- Jakob, M. Chapter 14—Landslides in a changing climate. In Hazards and Disasters Series; Davies, T., Rosser, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 505–579. ISBN 978-0-12-818464-6. [Google Scholar]
- Santi, P.M.; Hewitt, K.; VanDine, D.F.; Cruz, E.B. Debris-Flow Impact, Vulnerability, and Response. Nat. Hazards 2011, 56, 371–402. [Google Scholar] [CrossRef]
- Dilley, M. Natural Disaster Hotspots: A Global Risk Analysis; World Bank Publications: Herndon, VA, USA, 2005; Volume 5, ISBN 0821359304. [Google Scholar]
- Petley, D. Global Patterns of Loss of Life from Landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global Fatal Landslide Occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Dowling, C.A.; Santi, P.M. Debris Flows and Their Toll on Human Life: A Global Analysis of Debris-Flow Fatalities from 1950 to 2011. Nat. Hazards 2014, 71, 203–227. [Google Scholar] [CrossRef]
- Ahmad, A.; Sutanto, M.H.; Harahap, I.S.H.; Al-Bared, M.A.M.; Khan, M.A. Feasibility of Demolished Concrete and Scraped Tires in Peat Stabilization—A Review on the Sustainable Approach in Stabilization. In Proceedings of the 2020 2nd International Sustainability and Resilience Conference: Technology and Innovation in Building Designs, Sakheer, Bahrain, 11–12 November 2020. [Google Scholar] [CrossRef]
- Lee, S.G.; Winter, M.G. The Effects of Debris Flow in the Republic of Korea and Some Issues for Successful Risk Reduction. Eng. Geol. 2019, 251, 172. [Google Scholar] [CrossRef]
- Reports, U.S. Geological Survey, USGS Science for Changing World. 2018. Available online: htpps://www.usgs.gov/faqs/how-many-deaths-result-each-year (accessed on 25 July 2022).
- Thouret, J.C.; Antoine, S.; Magill, C.; Ollier, C. Lahars and Debris Flows: Characteristics and Impacts. Earth-Sci. Rev. 2020, 201, 103003. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Crema, S.; Marchi, L.; Marra, F.; Guzzetti, F.; Borga, M. Impact of Uncertainty in Rainfall Estimation on the Identification of Rainfall Thresholds for Debris Flow Occurrence. Geomorphology 2014, 221, 286–297. [Google Scholar] [CrossRef]
- Hakro, M.R.; Harahap, I.S.H. Flume Experiments for Investigation of Rainfall-Induced Slope Failure. Int. J. Eng. Res. Afr. 2015, 16, 49–56. [Google Scholar] [CrossRef]
- Ibrahim, M.B.; Mustaffa, Z.; Balogun, A.L.; Hamonangan Harahap, I.S.; Ali Khan, M. Advanced Data Mining Techniques for Landslide Susceptibility Mapping. Geomat. Nat. Hazards Risk 2021, 12, 2430–2461. [Google Scholar] [CrossRef]
- Cannon, S.H.; Gartner, J.E.; Rupert, M.G.; Michael, J.A.; Rea, A.H.; Parrett, C. Predicting the Probability and Volume of Postwildfire Debris Flows in the Intermountain Western United States. Bull. Geol. Soc. Am. 2010, 122, 127–144. [Google Scholar] [CrossRef]
- Du, J.; Yin, K.; Lacasse, S.; Nadim, F. Quantitative Vulnerability Estimation of Structures for Individual Landslide: Application to the Metropolitan Area of San Salvador, El Salvador. J. Softw. Eng. 2015, 9, 1251–1264. [Google Scholar]
- Shanmugam, G.; Alderton, D.; Elias, S.A. (Eds.) Deep-Water Processes and Deposits; Academic Press: Oxford, UK, 2021; pp. 965–1009. ISBN 978-0-08-102909-1. [Google Scholar]
- Khan, M.A.; Mustaffa, Z.; Balogun, A.L.B.; Al-Bared, M.A.M.; Ahmad, A. Role of the Rheological Parameters in Debris Flow Modelling. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1092, 012041. [Google Scholar] [CrossRef]
- Iverson, R.M. The Debris-Flow Rheology Myth. Int. Conf. Debris-Flow Hazards Mitig. Mech. Predict. Assess. Proc. 2003, 1, 303–314. [Google Scholar]
- Iverson, R.M.; Reid, M.E.; Lahusen, R.G. Debris-Flow Mobilisation. Annu. Rev. Earth Planet Sci. 1997, 25, 85–138. [Google Scholar] [CrossRef]
- Jakob, M. Debrisow hazard analysis. In Debris-Flow Hazards and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Varnes, J.; Cruden, M. Chapter 3—Landslide types and process. In Landslides: Investigation and Mitigation; Transportation Research Boar: Washington, DC, USA, 1996. [Google Scholar]
- Lee, E.M. Landslide Risk Assessment: The Challenge of Estimating the Probability of Landsliding. Q. J. Eng. Geol. Hydrogeol. 2009, 42, 445–458. [Google Scholar] [CrossRef]
- Gartner, J.E.; Jakob, M. Debris-Flow Risk Assessment and Mitigation Design for Pipelines in British Columbia, Canada. In Proceedings of the 7th International Conference on Debris-Flow Hazards Mitigation, Golden, CO, USA, 10–13 June 2019; pp. 677–684. [Google Scholar]
- Michael-Leiba, M.; Baynes, F.; Scott, G.; Granger, K. Quantitative Landslide Risk Assessment of Cairns, Australia. In Landslide Hazard and Risk; Glade, T., Anderson, M.G., Crozier, M.J., Eds.; Wiley: London, UK, 2005; pp. 621–642. [Google Scholar]
- Birkmann, J.; Cardona, O.D.; Carreño, M.L.; Barbat, A.H.; Pelling, M.; Schneiderbauer, S.; Kienberger, S.; Keiler, M.; Alexander, D.; Zeil, P.; et al. Framing Vulnerability, Risk and Societal Responses: The MOVE Framework. Nat. Hazards 2013, 67, 193–211. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Kouris, L.A.; Panagopoulos, G.; Kappos, A.J.; Nigro, E.; Rossetto, T.; Lloyd, T.O.; Stathopoulos, T. Structural Vulnerability Assessment under Natural Hazards: A Review. In COST ACTION C26: Urban Habitat Constructions under Catastrophic Events—Proceedings of the Final Conference; Taylor & Francis Group: London, UK, 2010; pp. 711–723. ISBN 978-0-415-60685-1. [Google Scholar]
- Papathoma-Köhle, M.; Gems, B.; Sturm, M.; Fuchs, S. Matrices, Curves and Indicators: A Review of Approaches to Assess Physical Vulnerability to Debris Flows. Earth-Sci. Rev. 2017, 171, 272–288. [Google Scholar] [CrossRef]
- Totschnig, R.; Fuchs, S. Mountain Torrents: Quantifying Vulnerability and Assessing Uncertainties. Eng. Geol. 2013, 155, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Li, J. Finite Element Analysis on Mechanical Behavior of Semi-Exposed Pipeline Subjected to Debris Flows. Eng. Fail. Anal. 2019, 105, 781–797. [Google Scholar] [CrossRef]
- Pierson, T.C.; Costa, J.E.; Vancouver, W. A rheologic classification of subaerial sediment-water flows. In Debris Flow/Avalanches: Process, Recognition, and Mitigation; Geological Society of America: Boulder, CO, USA, 1987; Volume 7, pp. 1–12. [Google Scholar]
- Hürlimann, M.; Coviello, V.; Bel, C.; Guo, X.; Berti, M.; Graf, C.; Hübl, J.; Miyata, S.; Smith, J.B.; Yin, H.Y. Debris-Flow Monitoring and Warning: Review and Examples. Earth-Sci. Rev. 2019, 199. [Google Scholar] [CrossRef]
- Pierson, T.C. Important Process in High Country Gully Erosion. J. Tussock Grassl. Mt. Lands Inst. 1980, 3–14. [Google Scholar]
- Amaral, G.; Bushee, J.; Cordani, U.G.; Kawashita, K.; Reynolds, J.H.; Almeida, F.F.M.; de Almeida, F.F.M.; Hasui, Y.; de Brito Neves, B.B.; Fuck, R.A.; et al. A Review of the Classifcation of Landslide of the Flow Type. J. Petrol. 2013, 369, 1689–1699. [Google Scholar] [CrossRef]
- Castelli, F.; Freni, G.; Lentini, V.; Fichera, A. Modelling of a Debris Flow Event in the Enna Area for Hazard Assessment. Procedia Eng. 2017, 175, 287–292. [Google Scholar] [CrossRef]
- Innes, J.L. Debris Flows. Prog. Phys. Geogr. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Wells, W. Debris Flows/Avalanches. Geol. Soc. Am. 1987, 7, 105–114. [Google Scholar]
- Petrović, N. Climate Change and Landslide Hazard. Annu. Disaster Risk Sci. 2018, 1, 3–18. [Google Scholar]
- Tohari, A. Study of rainfall-induced landslide: A review. IOP Conf. Ser.: Earth Environ. Sci. 2018, 118, 012036. [Google Scholar] [CrossRef]
- Turner, K.A.; Schuster, R.L. Landslides Investigation and Mitigation Report by NRC United State; Transportation Research Board: Washington, DC, USA, 2022. [Google Scholar]
- Reid, M.E.; Iverson, R.M.; Logan, M.; Lahusen, R.G.; Godt, J.W.; Griswold, J.P. Entrainment of Bed Sediment by Debris Flows: Results from Large-Scale Experiments. Ital. J. Eng. Geol. Environ. 2011, 367–374. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Yao, C.; Li, Y. Debris-Flow Impact on Piers with Different Cross-Sectional Shapes. J. Hydraul. Eng. 2020, 146, 04019045. [Google Scholar] [CrossRef]
- Eu, S.; Im, S.; Kim, D. Development of Debris Flow Impact Force Models Based on Flume Experiments for Design Criteria of Soil Erosion Control Dam. Adv. Civ. Eng. 2019, 2019, 3567374. [Google Scholar] [CrossRef]
- Schuster, R.L.; Salcedo, D.A.; Valenzuela, L. Overview of Catastrophic Landslides of South America in the Twentieth Century. Rev. Eng. Geol. 2002, 15, 1–34. [Google Scholar]
- Papathoma-Köhle, M.; Kappes, M.; Keiler, M.; Glade, T. Physical Vulnerability Assessment for Alpine Hazards: State of the Art and Future Needs. Nat. Hazadrs 2011, 58, 645–657. [Google Scholar] [CrossRef]
- Fuchs, S.; Ornetsmüller, C.; Totschnig, R. Spatial Scan Statistics in Vulnerability Assessment: An Application to Mountain Hazards. Nat. Hazards 2012, 64, 2129–2151. [Google Scholar] [CrossRef] [Green Version]
- Yiğit, A.; Lav, M.A.; Gedikli, A. Vulnerability of Natural Gas Pipelines under Earthquake Effects. J. Pipeline Syst. Eng. Pract. 2018, 9, 1–14. [Google Scholar] [CrossRef]
- Leone, F.; Asté, J.-P.; Velasquez, E. Contribution Des Constats d’endommagement Au Développement d’une Méthodologie d’évaluation de La Vulnérabilité Appliquée Aux Phénomènes de Mouvements de Terrain (Contribution of Damaging Reports to the Development of an Appraisal Methodology of Vulnerabil. Bull. L’Assoc. Géogr. Fr. 1995, 72, 350–371. [Google Scholar] [CrossRef]
- Huggel, C.; Allen, S.; Deline, P.; Fischer, L.; Noetzli, J.; Ravanel, L. Ice Thawing, Mountains Falling—Are Alpine Rock Slope Failures Increasing? Geol. Today 2012, 28, 98–104. [Google Scholar] [CrossRef]
- Akbas, S.O.; Blahut, J.; Sterlacchini, S. Critical assessment of existing physical vulnerability estimation approaches for debris flows. Proc. Landslide Process. Geomorphol. Mapp. Dyn. Model. 2009, 67, 229–233. [Google Scholar]
- Zhang, S.; Zhang, L.; Li, X.; Xu, Q. Physical Vulnerability Models for Assessing Building Damage by Debris Flows. Eng. Geol. 2018, 247, 145–158. [Google Scholar] [CrossRef]
- Birkmann, J. Chapter 2—Indicators and Criteria for Measuring Vulnerability: Theoretical Bases and Requirements. In Measuring Vulnerability to Natural Hazards: Towards Disaster Resilient Societies, 2nd ed.; United Nation University Press: Tokyo, Japan, 2013; pp. 55–77. [Google Scholar]
- Papathoma-Köhle, M.; Keiler, M.; Totschnig, R.; Glade, T. Improvement of Vulnerability Curves Using Data from Extreme Events: Debris Flow Event in South Tyrol. Nat. Hazards 2012, 64, 2083–2105. [Google Scholar] [CrossRef]
- Thouret, J.C.; Ettinger, S.; Guitton, M.; Santoni, O.; Magill, C.; Martelli, K.; Zuccaro, G.; Revilla, V.; Charca, J.A.; Arguedas, A. Assessing Physical Vulnerability in Large Cities Exposed to Flash Floods and Debris Flows: The Case of Arequipa (Peru). Nat. Hazards 2014, 73, 1771–1815. [Google Scholar] [CrossRef]
- Godfrey, A.; Ciurean, R.L.; Van Westen, C.J.; Kingma, N.C.; Glade, T. Assessing Vulnerability of Buildings to Hydro-Meteorological Hazards Using an Expert Based Approach–An Application in Nehoiu Valley, Romania. Int. J. Disaster Risk Reduct. 2015, 13, 229–241. [Google Scholar] [CrossRef]
- Fuchs, S.; Heiss, K.; Hübl, J. Towards an Empirical Vulnerability Function for Use in Debris Flow Risk Assessment. Nat. Hazards Earth Syst. Sci. 2007, 7, 495–506. [Google Scholar] [CrossRef] [Green Version]
- Rossetto, T.; Ioannou, I.; Grant, D.; Maqsood, T. Guidelines for the Empirical Vulnerability Assessment. GEM Tech. Rep. 2014, 8, 140. [Google Scholar]
- Westen, C.J.V. Vulnerability Role in Disaster Management (Report). In CHARIM. 2020, pp. 1–8. Available online: www.charim.net (accessed on 25 February 2022).
- FEMA Hazus Flood Model User Guidance. Hazus User Guidance & Technical Manuals. U.S. Department of Homeland Security. 2018; p. 263. Available online: www.fema.gov (accessed on 20 April 2022).
- Zanchetta, G.; Sulpizio, R.; Pareschi, M.T.; Leoni, F.M.; Santacroce, R. Characteristics of 5–6 May 1998 Volcaniclastic Debris Flows in the Sarno Area (Campania, Southern Italy): Relationships to Structural Damage and Hazard Zonation. J. Volcanol. Geotherm. Res. 2004, 133, 377–393. [Google Scholar] [CrossRef]
- Hu, K.H.; Cui, P.; Zhang, J.Q. Characteristics of Damage to Buildings by Debris Flows on 7 August 2010 in Zhouqu, Western China. Nat. Hazards Earth Syst. Sci. 2012, 12, 2209–2217. [Google Scholar] [CrossRef]
- Jakob, M.; Stein, D.; Ulmi, M. Vulnerability of Buildings to Debris Flow Impact. Nat. Hazards 2012, 60, 241–261. [Google Scholar] [CrossRef]
- Winter, M.; Smith, J.; Fotopoulou, S.; Pitilakis, K.; Mavrouli, O.; Corominas, J.; Agyroudis, S. The Physical Vulnerability of Roads to Debris Flow. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; pp. 307–313. [Google Scholar]
- Kang, H.; Kim, Y. The Physical Vulnerability of Different Types of Building Structure to Debris Flow Events. Nat. Hazards 2016, 80, 1475–1493. [Google Scholar] [CrossRef]
- Haugen, E.D.; Kaynia, A.M. Vulnerability of Structures Impacted by Debris Flow. In Landslides and Engineered Slopes; Taylor & Francis: London, UK, 2008; pp. 381–387. [Google Scholar]
- Quan Luna, B.; Blahut, J.; Van Westen, C.J.; Sterlacchini, S.; Van Asch, T.W.J.; Akbas, S.O. The Application of Numerical Debris Flow Modelling for the Generation of Physical Vulnerability Curves. Nat. Hazards Earth Syst. Sci. 2011, 11, 2047–2060. [Google Scholar] [CrossRef] [Green Version]
- Quan Luna, B.; Blahut, J.; Camera, C.; van Westen, C.; Apuani, T.; Jetten, V.; Sterlacchini, S. Physically Based Dynamic Run-out Modelling for Quantitative Debris Flow Risk Assessment: A Case Study in Tresenda, Northern Italy. Environ. Earth Sci. 2014, 72, 645–661. [Google Scholar] [CrossRef]
- Ciurean, R.L.; Hussin, H.; van Westen, C.J.; Jaboyedoff, M.; Nicolet, P.; Chen, L.; Frigerio, S.; Glade, T. Multi-Scale Debris Flow Vulnerability Assessment and Direct Loss Estimation of Buildings in the Eastern Italian Alps. Nat. Hazards 2017, 85, 929–957. [Google Scholar] [CrossRef] [Green Version]
- Shen, P.; Zhang, L.; Chen, H.; Fan, R. EDDA 2.0: Integrated Simulation of Debris Flow Initiation and Dynamics Considering Two Initiation Mechanisms. Geosci. Model Dev. 2018, 11, 2841–2856. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.; He, S.; Deng, Y.; Liu, W.; Wang, D.; Shen, F. A Reliability-Based Approach for the Impact Vulnerability Assessment of Bridge Piers Subjected to Debris Flows. Eng. Geol. 2020, 269, 105567. [Google Scholar] [CrossRef]
- Kappes, M.S.; Papathoma-Koehle, M.; Keiler, M. Assessing Physical Vulnerability for Multi-Hazards Using an Indicator-Based Methodology. Appl. Geogr. 2012, 32, 577–590. [Google Scholar] [CrossRef]
- Dadfar, B.; El Naggar, M.H.; Nastev, M. Vulnerability of Buried Energy Pipelines Subject to Earthquake-Triggered Transverse Landslides in Permafrost Thawing Slopes. J. Pipeline Syst. Eng. Pract. 2018, 9, 1–12. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Al-Bared, M.A.M.; Habeeb, N.; Khan, M.A. Examining the Effect of Debris Flow on Oil and Gas Pipelines Using Numerical Analysis. Glob. J. Earth Sci. Eng. 2022, 9, 74–87. [Google Scholar] [CrossRef]
- Leone, F.; Asté, J.P.; Leroi, E. Vulnerability Assessment of Elements Exposed to Mass-Movement: Working toward a Better Risk Perception. In Landslides, Glissements de Terrain; Senneset, K., Ed.; Balkema: Rotterdam, The Netherlands, 1996; pp. 263–270. [Google Scholar]
- Leone, F.; Asté, J.-P.; Leroi, E. L’évaluation de La Vulnérabilité Aux Mouvements de Terrains: Pour Une Meilleure Quantification Du Risque/The Evaluation of Vulnerability to Mass Movements: Towards a Better Quantification of Landslide Risks. Rev. Géogr. Alp. 1997, 84, 35–46. [Google Scholar] [CrossRef]
- Ouyang, C.; Wang, Z.; An, H.; Liu, X.; Wang, D. An Example of a Hazard and Risk Assessment for Debris Flows—A Case Study of Niwan Gully, Wudu, China. Eng. Geol. 2019, 263, 105351. [Google Scholar] [CrossRef]
- Delannay, R.; Valance, A.; Mangeney, A.; Roche, O.; Richard, P. Granular and Particle-Laden Flows: From Laboratory Experiments to Field Observations. J. Phys. D Appl. Phys. 2017, 50, 053001. [Google Scholar] [CrossRef]
- Han, Z.; Su, B.; Li, Y.; Wang, W.; Wang, W.; Huang, J.; Chen, G. Numerical Simulation of Debris-Flow Behavior Based on the SPH Method Incorporating the Herschel-Bulkley-Papanastasiou Rheology Model. Eng. Geol. 2019, 255, 26–36. [Google Scholar] [CrossRef]
- Shimizu, H.A.; Koyaguchi, T.; Suzuki, Y.J. A Numerical Shallow-Water Model for Gravity Currents for a Wide Range of Density Differences. Prog. Earth Planet. Sci. 2017, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Zhang, L.M.; Chen, H.X.; Shen, P. Simulating Debris Fl Ow Mobility in Urban Settings. Eng. Geol. 2016, 214, 67–78. [Google Scholar] [CrossRef]
- Christen, M.; Kowalski, J.; Bartelt, P. RAMMS: Numerical Simulation of Dense Snow Avalanches in Three-Dimensional Terrain. Cold Reg. Sci. Technol. 2010, 63, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Gregoretti, C.; Degetto, M.; Boreggio, M. GIS-Based Cell Model for Simulating Debris Flow Runout on a Fan. J. Hydrol. 2016, 534, 326–340. [Google Scholar] [CrossRef]
- Azmeri, A.; Isa, A.H. An Analysis of Physical Vulnerability to Flash Floods in the Small Mountainous Watershed of Aceh Besar Regency, Aceh Province, Indonesia. Jàmbá: J. Disaster Risk Stud. 2018, 10, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuchs, S.; Keiler, M.; Ortlepp, R.; Schinke, R.; Papathoma-Köhle, M. Recent Advances in Vulnerability Assessment for the Built Environment Exposed to Torrential Hazards: Challenges and the Way Forward. J. Hydrol. 2019, 575, 587–595. [Google Scholar] [CrossRef]
- Karagiorgos, K.; Heiser, M.; Thaler, T.; Hübl, J.; Fuchs, S. Micro-Sized Enterprises: Vulnerability to Flash Floods. Nat. Hazards 2016, 84, 1091–1107. [Google Scholar] [CrossRef] [Green Version]
- Ronold, B.K.O.; Bjerager, P. Model Uncertainty Representation in Geotechnical Reliability Analyses. J. Geotech. Eng. 1992, 118, 363–376. [Google Scholar] [CrossRef]
- Papathoma-Köhle, M.; Schlögl, M.; Fuchs, S. Vulnerability Indicators for Natural Hazards: An Innovative Selection and Weighting Approach. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ettinger, S.; Mounaud, L.; Magill, C.; Yao-Lafourcade, A.F.; Thouret, J.C.; Manville, V.; Negulescu, C.; Zuccaro, G.; De Gregorio, D.; Nardone, S.; et al. Building Vulnerability to Hydro-Geomorphic Hazards: Estimating Damage Probability from Qualitative Vulnerability Assessment Using Logistic Regression. J. Hydrol. 2016, 541, 563–581. [Google Scholar] [CrossRef]
- Eidsvig, U.M.K.; Papathoma-Köhle, M.; Du, J.; Glade, T.; Vangelsten, B.V. Quantification of Model Uncertainty in Debris Flow Vulnerability Assessment. Eng. Geol. 2014, 181, 15–26. [Google Scholar] [CrossRef]
- Ciurean, R.L.; Schröter, D.; Glade, T. Conceptual Frameworks of Vulnerability Assessments for Natural Disasters Reduction; InTech: Saitama-shi, Japan, 2013. [Google Scholar]
- Uzielli, M.; Nadim, F.; Lacasse, S.; Kaynia, A.M. A Conceptual Framework for Quantitative Estimation of Physical Vulnerability to Landslides. Eng. Geol. 2008, 102, 251–256. [Google Scholar] [CrossRef]
- Kaynia, A.M.; Papathoma-Köhle, M.; Neuhäuser, B.; Ratzinger, K.; Wenzel, H.; Medina-Cetina, Z. Probabilistic Assessment of Vulnerability to Landslide: Application to the Village of Lichtenstein, Baden-Württemberg, Germany. Eng. Geol. 2008, 101, 33–48. [Google Scholar] [CrossRef]
- Uzielli, M.; Lacasse, S.; Nadim, F. Probabilistic Risk Estimation for Geohazards: A Simulation Approach. In Proceedings of the International Symposium on Geotechnical Safety and Risk; CRC Press: Boca Raton, FL, USA, 2009; pp. 355–362. [Google Scholar]
- Gong, W.; Gupta, H.V.; Yang, D.; Sricharan, K.; Hero, A.O. Estimating Epistemic and Aleatory Uncertainties during Hydrologic Modeling: An Information Theoretic Approach. Water Resour. Res. 2013, 49, 2253–2273. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Nadim, F.; Huang, H.; Uzielli, M.; Lacasse, S. Quantitative Vulnerability Estimation for Scenario-Based Landslide Hazards. Landslides 2010, 7, 125–134. [Google Scholar] [CrossRef]
- Liang, W.; Zhuang, D.; Jiang, D.; Pan, J.; Ren, H. Assessment of Debris Flow Hazards Using a Bayesian Network. Geomorphology 2012, 171–172, 94–100. [Google Scholar] [CrossRef]
- Reckhow, K.H. Water Quality Prediction and Probability Network Models. Can. J. Fish. Aquat. Sci. 1999, 56, 1150–1158. [Google Scholar] [CrossRef]
- Uzielli, M. Risk and Vulnerability for Geohazards—Probabilistic Estimation of Regional Vulnerability to Landslides. In Proceedings of the 13th Panamerican Conference on Soil Mechanics and Geotechnical Engineering at Margarita, Porlamar, Venezuela, 16–20 July 2007. [Google Scholar]
- Papadopoulos, C.E.; Yeung, H. Uncertainty Estimation and Monte Carlo Simulation Method. Flow Meas. Instrum. 2001, 12, 291–298. [Google Scholar] [CrossRef]
- Khalaj, S.; BahooToroody, F.; Mahdi Abaei, M.; BahooToroody, A.; De Carlo, F.; Abbassi, R. A Methodology for Uncertainty Analysis of Landslides Triggered by an Earthquake. Comput. Geotech. 2020, 117, 103262. [Google Scholar] [CrossRef]
- Christian, J.T. Geotechnical Engineering Reliability: How Well Do We Know What We Are Doing? J. Geotech. Geoenvironmental Eng. 2004, 130, 985–1003. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, W.H.; Zhang, L.M.; Huang, H.W. Characterising Geotechnical Model Uncertainty by Hybrid Markov Chain Monte Carlo Simulation. Comput. Geotech. 2012, 43, 26–36. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, Y.P.; Sun, H.; Xie, W.; Wu, G. Predicting the Occurrence of Channelized Debris Flow by an Integrated Cascading Model: A Case Study of a Small Debris Flow-Prone Catchment in Zhejiang Province, China. Geomorphology 2018, 308, 78–90. [Google Scholar] [CrossRef]
- Fuchs, S.; Thaler, T. Vulnerability and Resilience to Natural Hazards; Cambridge University Press: Cambridge, UK, 2018; ISBN 1107154898. [Google Scholar]
- Fuchs, S.; Keiler, M.; Zischg, A. A Spatiotemporal Multi-Hazard Exposure Assessment Based on Property Data. Nat. Hazards Earth Syst. Sci. 2015, 15, 2127–2142. [Google Scholar] [CrossRef] [Green Version]
- Röthlisberger, V.; Zischg, A.P.; Keiler, M. A Comparison of Building Value Models for Flood Risk Analysis. Nat. Hazards Earth Syst. Sci. 2018, 18, 2431–2453. [Google Scholar] [CrossRef] [Green Version]
- Bähler, F.; Wegmann, M.; Merz, H. Pragmatischer Ansatz Zur Risikobeurteilung von Naturgefahren. Wasser Energ. Luft 2001, 93, 193–196. [Google Scholar]
- Totschnig, R.; Sedlacek, W.; Fuchs, S. A Quantitative Vulnerability Function for Fluvial Sediment Transport. Nat. Hazards 2011, 58, 681–703. [Google Scholar] [CrossRef]









| Approaches | Advantages | Limitation |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
| Reference | Quantification Techniques | Characteristics |
|---|---|---|
|
| |
|
| |
|
|
|
|
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.A.; Mustaffa, Z.; Harahap, I.S.H.; Ibrahim, M.B.; Al-Atroush, M.E. Assessment of Physical Vulnerability and Uncertainties for Debris Flow Hazard: A Review concerning Climate Change. Land 2022, 11, 2240. https://doi.org/10.3390/land11122240
Khan MA, Mustaffa Z, Harahap ISH, Ibrahim MB, Al-Atroush ME. Assessment of Physical Vulnerability and Uncertainties for Debris Flow Hazard: A Review concerning Climate Change. Land. 2022; 11(12):2240. https://doi.org/10.3390/land11122240
Chicago/Turabian StyleKhan, Mudassir Ali, Zahiraniza Mustaffa, Indra Sati Hamonangan Harahap, Muhammad Bello Ibrahim, and Mohamed Ezzat Al-Atroush. 2022. "Assessment of Physical Vulnerability and Uncertainties for Debris Flow Hazard: A Review concerning Climate Change" Land 11, no. 12: 2240. https://doi.org/10.3390/land11122240
APA StyleKhan, M. A., Mustaffa, Z., Harahap, I. S. H., Ibrahim, M. B., & Al-Atroush, M. E. (2022). Assessment of Physical Vulnerability and Uncertainties for Debris Flow Hazard: A Review concerning Climate Change. Land, 11(12), 2240. https://doi.org/10.3390/land11122240






