Competition between Export Cities in China: Evolution and Influencing Factors
Abstract
:1. Introduction
1.1. Literature Review: Competition between Export Countries
1.2. Hypothesis and Framework: Competition between Export Cities
- The ESI is used to represent the export competition between cities, and the evolution of the ESIs from all cities and regions is analyzed to form an overall understanding of the competitive relationships among cities.
- The panel Granger causality test model is used to analyze the relationship between export competitive relationships and Gross Domestic Product (GDP).
- The relationship between export competitive relationships and geographical distance is explored through scatter plot fitting.
- The mechanism of the evolution of export competitive relationships between cities is explored by using the nonlinear least square (NLS) method, based on the gravity model.
2. Materials and Methods
2.1. Methodology
2.1.1. ESI and Average Export Similarity Index (AESI)
2.1.2. Panel Unit Root Tests
2.1.3. Panel Cointegration Tests
2.1.4. Panel Granger Causality Test
2.1.5. Gravity Model
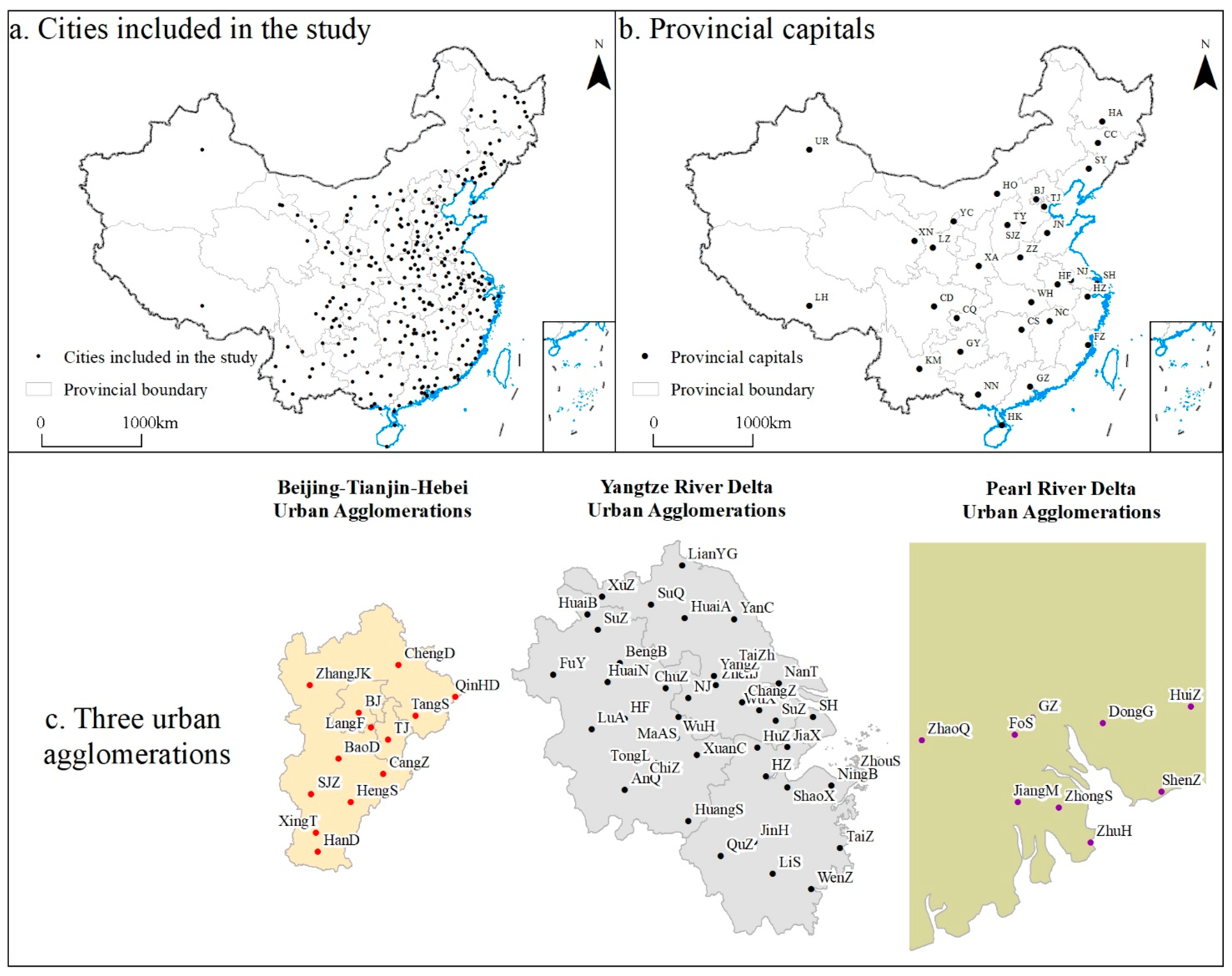
2.2. Data and Study Area
2.2.1. Data
- The export data of each city came from the customs database of China (service trade data are not included). According to the enterprise codes, the export situation of enterprises in the same cities were summarized and used as the original export data of those cities. In addition, the customs database includes a large span of data collection years, resulting in multiple versions (HS1996, HS2002, HS2007, HS2012, and HS2017). Although the differences between the versions are not significant from a macro viewpoint, each version has a certain degree of fine-tuning compared with its previous version, so they need to be recoded systematically. According to the comparison table of the commodity codes issued by the United Nations Trade Database (https://unstats.un.org/unsd/trade/classifications/correspondence-tables.asp (accessed on 1 June 2021)), we uniformly adjusted the 8-digit commodity codes of every year of the customs data to the HS1996 version with 6-digit codes, so that the export similarity between the different years could be comparatively measured. However, because of the large amount of data in the customs database, there were extremely large calculation tasks when determining the ESI between different cities in different years. Therefore, we used PyCharm to calculate the ESIs programmatically.
- In addition to the data processing of the customs database, the GDP for each city in this study was taken from the cities’ statistical yearbooks and the provincial statistical yearbooks. Data that were difficult to obtain for some regions and years were based on the National Economic and Social Development Statistical Bulletin and local yearbooks.
2.2.2. Study Area
3. Results and Discussion
3.1. Spatiotemporal Evolution of the ESI
3.1.1. Overall Analysis
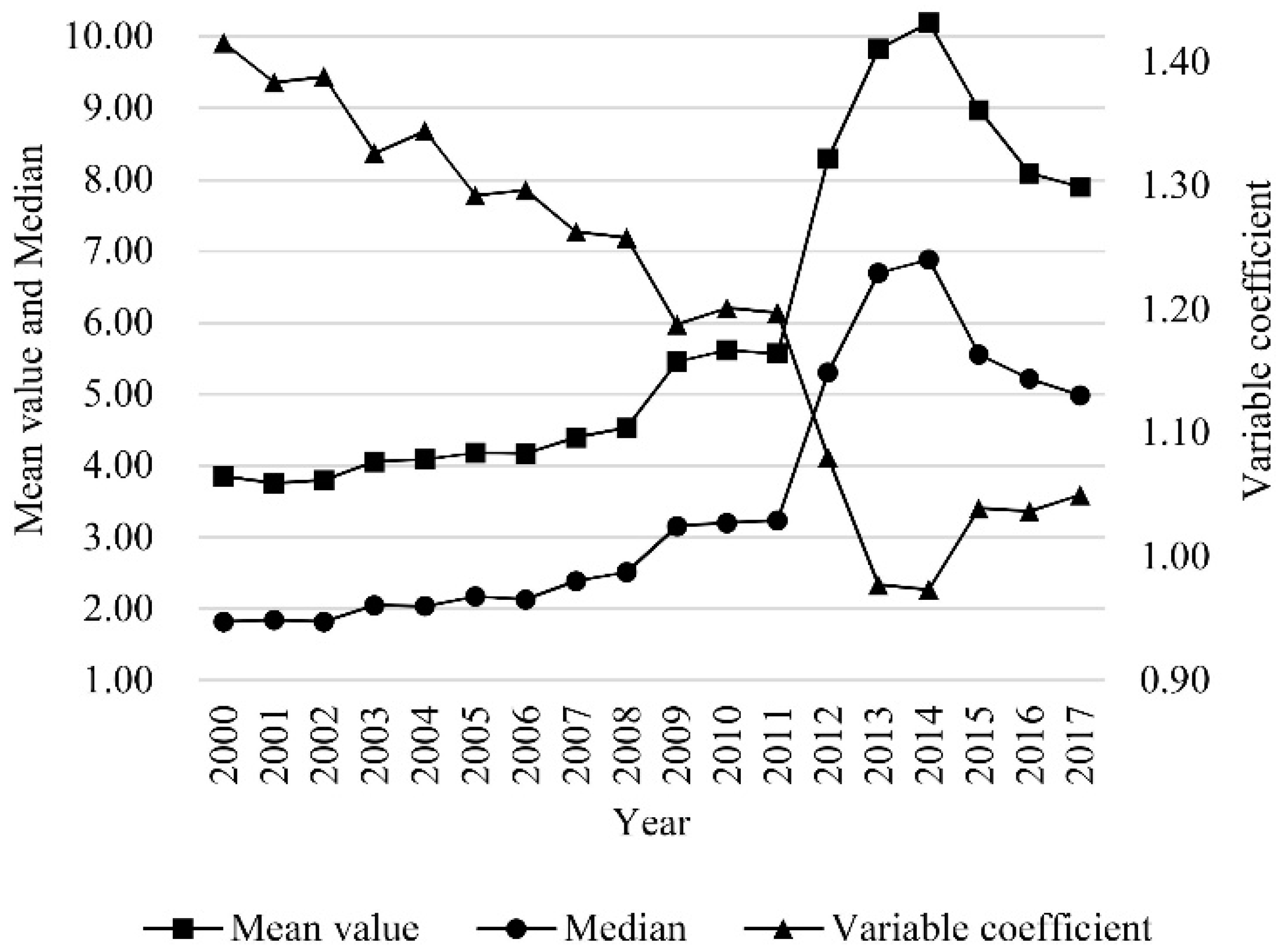
- From 2000 to 2011, the similarities among Chinese cities’ exports in the global market is relatively low. The mean values are always below six and the median also fluctuates at a low level. Especially between 2000 and 2008, these two indicators are in the low ranges of three to five and one to three, respectively.
- From 2011 to 2014, the similarity of exports between cities in the global market increases significantly. Compared with 2011, the mean and median in 2014 increased by 82.94% and 112.65%, respectively, indicating that during this period, the competition between different cities increased significantly and the complementarity weakened.
- From 2014 to 2017, the similarity of exports between cities in the global market declined. In 2017, the mean and median ESIs were 7.90 and 5.22, respectively, which are 22.47% and 24.24% lower than the 2014 peak.
3.1.2. Regional Analysis
Evolution of the ESI Network Structure among the Provincial Capitals
The ESI Network Structure Evolution among the BTH, YRD, and PRD
3.2. The Relationship between AESI and GDP
3.2.1. Correlation between AESI and GDP
3.2.2. Causal Analysis of AESI and GDP
All Cities
Regional Analysis
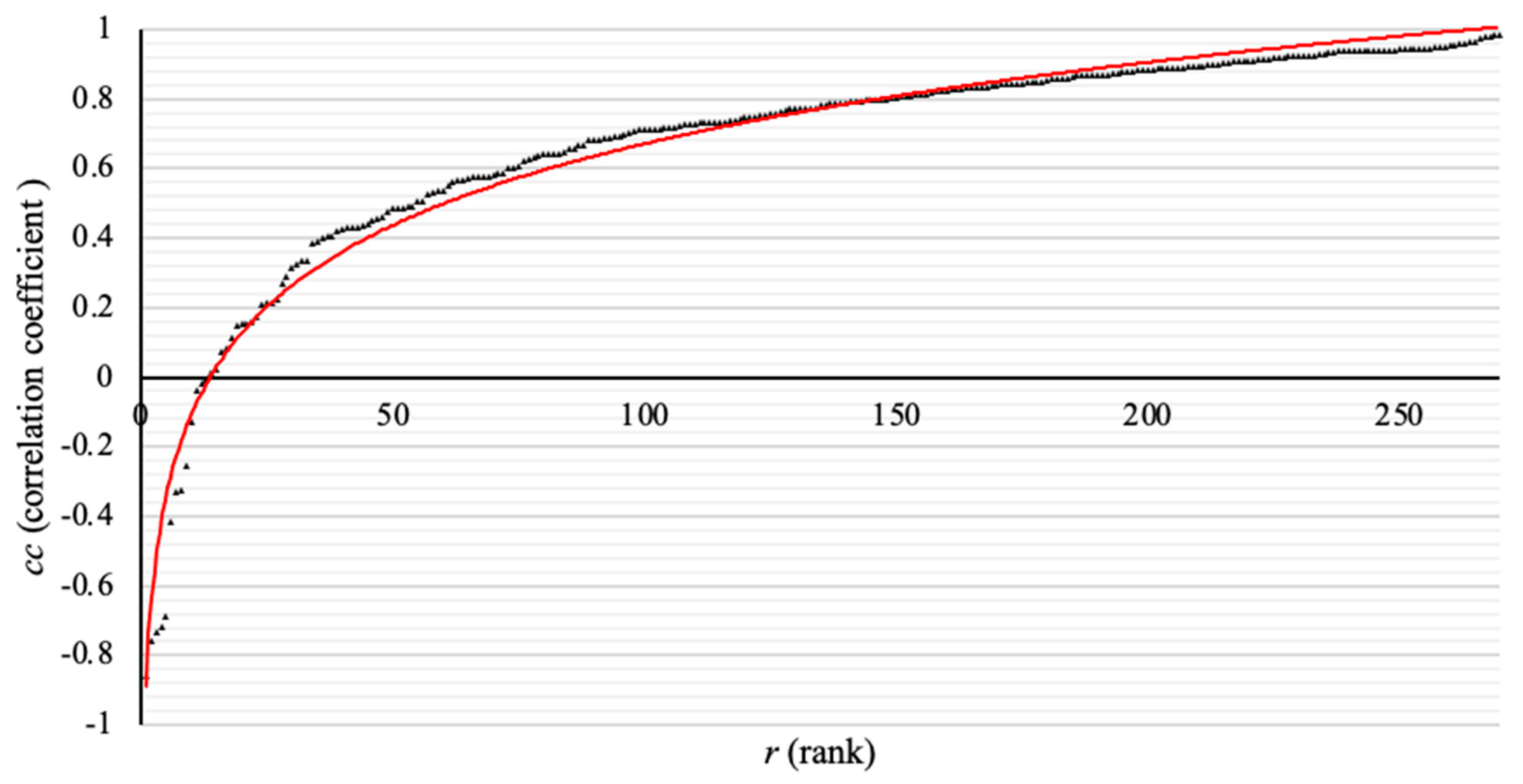
3.2.3. Relationship between ESI and Distance
All Cities
Regional Analysis
3.2.4. Gravity Model: Relation between the ESI, GDP, and Distance
- The GDP is the Granger cause of the export competitive pressure that cities face.
- The greater the distance between two cities, the less the competition between them.
4. Conclusions
- From a national perspective, the intensity of the competition among cities in the global market first increased and then decreased from 2000 to 2017. Competition relationship change reflects the evolution and development of Chinese cities regarding industry and economic structure. Cities in different regions have different competition relationships in export trade, indicating that the export structure and basic characteristics of cities are related to their geographical location. Provincial capitals, as regional economic centers, have high levels of industrialization and urbanization and their industrial layout and export structure are relatively close. PRD, as the pioneer area of China’s reform and opening up, had its economy grow dramatically, accompanied by the introduction of foreign capital and the development of local industrialization [49,50]. Therefore, local foreign trade processing products in the PRD tend to be similar in category and the competition between them in the global market is more significant than for BTH and YRD.
- The GDP of each city was highly correlated with the AESI. Overall, the economic growth of cities and the pressure of export competition from other cities was related via cause and effect. However, at the regional level, the empirical results were more likely to support the GDP as the Granger cause of the AESI; that is, a city’s economic growth will intensify the export competition pressure that it faces. Confirmation of such a causal relationship lays a foundation for the use of the gravity model in this study.
- The evolution of the urban export structure in China is related to geographical proximity, to some extent. The ESI shows a trend of decreasing with increasing geographical distance. The proximity of a geographical location means there are similar development conditions [51], a higher possibility of economic factor spillover, a higher probability of export product convergence, and a more evident competitive relationship in the market.
- The relationships among the ESI, the GDP, and geographical distance can be incorporated well into the gravity model. If the economic aggregate of the two cities is larger and the geographical distance is smaller, then the export similarity of the two cities will be higher, and the competition in the global market will be more obvious. However, the impact of GDP and distance on ESI varies in different regions. For example, in BTH, the influence of distance on the competition between cities is more obvious than that of YRD and PRD. The success of empirical research using the gravity model reflects two basic characteristics of Chinese cities in developing export trading. First, economic growth provides the capital, technology, and human resources for increasing the variety of export products and upgrading the export structure. However, the path and direction of the export trade development tend to converge, resulting in an increased ESI and progressively fierce competition for global markets. Second, the ESI has obvious geographical proximity characteristics. This rule makes a high ESI more likely to occur in cities that are geographically adjacent, and competition in the global market is more obvious.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The BTH urban agglomerations include the cities of Beijing and Tianjin as well as Hebei Province, with a total of 13 cities. According to the “Outline of the Regional Integration Development Plan of the Yangtze River Delta” (http://www.gov.cn/zhengce/2019-12/01/content_5457442.htm (accessed on 14 March 2021)), the YRD urban agglomerations include Jiangsu Province, Zhejiang Province, Anhui Province, and the city of Shanghai. Because of a data defect, Bozhou City in Anhui Province is not included in the analysis. With reference to the latest plan for the Guangdong–Hong Kong–Macao Greater Bay Area (http://www.gov.cn/zhengce/2019-02/18/content_5366593.htm#1 (accessed on 15 March 2021)) released in recent years, this study takes the cities of Guangzhou, Shenzhen, Zhuhai, Foshan, Huizhou, Dongguan, Zhongshan, Jiangmen, and Zhaoqing as the PRD urban agglomerations. |
| 2 | Because there are 270 cities in total, the ESI has 269 + 268 + … + 1 = 36,315 values. The mean is the average of 36,315 ESIs; the median is the median value of 36,315 ESIs. |
| 3 | Data source: Statistical Yearbook of Changzhi City. |
| 4 | Data source: China Regional Economic Statistics Yearbook. |
| 5 | Data source: Statistical Bulletin of Jinchang National Economic and Social Development. |
| 6 | Data source: Yinchuan Yearbook. |
References
- Zhang, C.; Xingchen, J.I.; Finance, S.O. The evolution and logic of forward-looking monetary policy. Chin. Rew. Financ. Stud. 2017, 9, 33–42. [Google Scholar]
- He, Y.; Bai, X. The Trade competitiveness and similarities of the urban agglomerations in the middle reaches of the Yangtze River. Contemp. Econ. Manag. 2017, 39, 51–56. [Google Scholar]
- Bao, J.; Gao, S.; Ge, J. Dynamic land use and its policy in response to environmental and social-economic changes in China: A case study of the Jiangsu coast (1750–2015). Land Use Policy 2019, 82, 169–180. [Google Scholar] [CrossRef]
- Chen, F.; Yu, M.; Zhu, F.; Shen, C.; Zhang, S.; Yang, Y. Rethinking rural transformation caused by comprehensive land consolidation: Insight from program of whole village restructuring in Jiangsu province, China. Sustainability 2018, 10, 2029. [Google Scholar] [CrossRef] [Green Version]
- Crespo, N.; Simoes, N.; Moreira, S. Bringing geography into the analysis of trade competition. Appl. Econ. Lett. 2019, 26, 948–953. [Google Scholar] [CrossRef]
- Molendowski, E.; Polan, W. Poland in the single European market-changes in the similarity of import and export structures in comparison with the EU-10 countries in 2004–2017. Int. J. Manag. Econ. 2020, 56, 20–30. [Google Scholar]
- Kreinin, M.E.; Plummer, M.G. Regional groupings, discrimination, and erosion of preferences: Effects of EU enlargement on the Mediterranean Basin. J. Int. Trade Econ. Dev. 2007, 16, 213–230. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X. A study on the comparative advantage and growth potential of agricultural trade between China and EU. Res. Agric. Mod. 2015, 36, 521–527. [Google Scholar]
- Wang, P.-Z.; Liu, X.-J. Comparative analysis of Export Similarity Index between China and EU. In Proceedings of the 2015 International Conference on Management Science and Management Innovation, Guilin, China, 15–16 August 2015; Advances in Economics, Business and Management Research 62015; Wang, M., Ed.; Atlantis Press: Dordrecht, The Netherlands, 2015; pp. 222–227. [Google Scholar]
- Dean, J.M.; Fung, K.C. Measuring vertical specialization: The case of China. Rev. Int. Econ. 2011, 19, 609–625. [Google Scholar] [CrossRef]
- Schott, P.K. The relative sophistication of Chinese exports. Econ. Policy 2008, 23, 5–49. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, S.J. What Accounts for the Rising Sophistication of China’s Exports? University of Chicago Press: Chicago, IL, USA, 2010. [Google Scholar]
- Moreira, M.M. Fear of China: Is there a future for manufacturing in Latin America? World Dev. 2007, 35, 355–376. [Google Scholar] [CrossRef] [Green Version]
- Caselli, F.G. China’s rise, asymmetric trade shocks and exchange rate regimes. Rev. Int. Econ. 2019, 27, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Xu, B. The sophistication of exports: Is China special? China Econ. Rev. 2010, 21, 482–493. [Google Scholar] [CrossRef]
- Athukorala, P.-C. Post-crisis export performance: The Indonesian experience in regional perspective. Bull. Indones. Econ. Stud. 2006, 42, 177–211. [Google Scholar] [CrossRef]
- Finger, J.M.; Kreinin, M.E. A measure of export similarity’ and its possible uses. Econ. J. 1979, 89, 905–912. [Google Scholar] [CrossRef]
- Liu, C.L.; Xu, J.Q.; Zhang, H. Competitiveness or complementarity? A dynamic network analysis of international agri-trade along the belt and road. Appl. Spat. Anal. Policy 2020, 13, 349–374. [Google Scholar] [CrossRef]
- Nguyen, T.N.A.; Pham, T.H.H.; Vallee, T. Similarity in trade structure: Evidence from ASEAN+3. J. Int. Trade Econ. Dev. 2017, 26, 1000–1024. [Google Scholar] [CrossRef]
- Lu, S.; Dickerson, K. The United States-Korea free trade agreement (KORUS) and its impacts on China’s textile and apparel exports to the United States. Cloth Text Res. J. 2012, 30, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Rondinella, S.; Agostino, M.; Demaria, F.; Drogue, S. Similarity and competition in the agri-food trade among European Mediterranean countries. Int. Trade J. 2019, 33, 444–468. [Google Scholar] [CrossRef]
- Adewuyi, A.O.; Awodumi, O.B. Biomass energy consumption, economic growth and carbon emissions: Fresh evidence from West Africa using a simultaneous equation model. Energy 2017, 119, 453–471. [Google Scholar] [CrossRef]
- Chaiboonsri, C.; Sriboonjit, J.; Sriwichailamphan, T.; Chaitip, P.; Sriboonchitta, S. A panel cointegration analysis: An application to international tourism demand of Thailand. Ann. Univ. Petrosani Econ. 2010, 10, 69–86. [Google Scholar]
- Srivastava, S.; Talwar, S. Decrypting the dependency relationship between the triad of foreign direct investment, economic growth and human development. J. Dev. Areas 2020, 54, 1–14. [Google Scholar] [CrossRef]
- Wongsrida, S.; Chaitip, P. Effect of macro factor volatility on the returns of financial sector in Southeast Asian stock markets. Chin. Bus. Rev. 2014, 13, 28–33. [Google Scholar]
- Levin, A.; Lin, C.-F.; Chu, C.-S.J. Unit root tests in panel data: Asymptotic and finite-sample properties. J. Econom. 2002, 108, 1–24. [Google Scholar] [CrossRef]
- Kao, C. Spurious regression and residual-based tests for cointegration in panel data when the cross-section and time-series dimensions are comparable. Economet. J. 1997, 90, 1–44. [Google Scholar] [CrossRef]
- Pedroni, P. Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxf. Bull. Econ. Stats. 1999, 61, 653–670. [Google Scholar] [CrossRef]
- Westerlund, J. Testing for error correction in panel data. Oxf. Bull. Econ. Stats. 2010, 69, 709–748. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Liu, Y. Panel Granger Test on urban land expansion and fiscal revenue growth in China’s prefecture-level cities. Acta Geogr. Sinica 2013, 68, 1595–1606. [Google Scholar]
- Lu, Y.-D.; Li, D. Trade structure, division economy and the welfare effect of regional service trade liberalization. Int. Econ. Trade Res. 2012, 5, 15–34. [Google Scholar]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Dumitrescu, E.-I.; Hurlin, C. Testing for Granger non-causality in heterogeneous panels. Econ. Model. 2012, 29, 1450–1460. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. The Bayesian information criterion. Ann. Statist. 1978, 6, 461–464. [Google Scholar]
- Hannan, E.J.; Quinn, B.G. The determination of the order of an autoregression. J. R. Stat. Soc. B. 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Melitz, J.; Toubal, F. Somatic distance, trust and trade. Rev. Int. Econ. 2019, 27, 786–802. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.W.; Zhang, M. High-speed rail impacts on travel times, accessibility, and economic productivity: A benchmarking analysis in city-cluster regions of China. J. Transp. Geogr. 2018, 73, 25–40. [Google Scholar] [CrossRef]
- Fratianni, M.; Marchionne, F. Trade costs and economic development. Econ. Geogr. 2012, 88, 137–163. [Google Scholar] [CrossRef]
- Shaopai, L.; Jipeng, T.; Lin, L. A case study of Shanghai Disneyland on spatial structure forecast for proposed scenic spot market: Modification and its application of gravity model. Acta Geogr. Sinica 2016, 71, 304–321. [Google Scholar]
- Tang, F.; Zhou, X.; Wang, L.; Zhang, Y.; Fu, M.; Zhang, P. Linking ecosystem service and MSPA to construct landscape ecological network of the Huaiyang Section of the Grand Canal. Land 2021, 10, 919. [Google Scholar] [CrossRef]
- Surya, B.; Ahmad, D.N.A.; Sakti, H.H.; Sahban, H. Land use change, spatial interaction, and sustainable development in the metropolitan urban areas, South Sulawesi Province, Indonesia. Land 2020, 9, 95. [Google Scholar] [CrossRef] [Green Version]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Rastvortseva, S.N. Innovative path of the regional economy’s departure from the previous path-dependent development trajectory. Ekon. Reg. 2020, 16, 28–42. [Google Scholar] [CrossRef]
- Ravselj, D.; Aristovnik, A. The impact of private research and development expenditures and tax incentives on sustainable corporate growth in selected OECD countries. Sustainability 2018, 10, 2304. [Google Scholar] [CrossRef] [Green Version]
- Mehrara, M.; Seijani, S.; Karsalari, A.R. Determinants of high-tech export in developing countries based on Bayesian model averaging. Zb. Rad. Ekon. Fak. Rije. 2017, 35, 199–215. [Google Scholar]
- Pham, C.S.; Ulubasoglu, M.A. The role of endowments, technology and size in international trade: New evidence from product-level data. J. Int. Trade Econ. Dev. 2016, 25, 913–937. [Google Scholar] [CrossRef]
- Boylan, B.M.; McBeath, J.; Wang, B. US–China relations: Nationalism, the trade war, and COVID-19. Fudan. J. Hum. Soc. Sci. 2021, 14, 23–40. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Y.; Xu, Q.; Li, S. The new process of urbanization in the Pearl River Delta. Geogr. Res. 2019, 38, 45–63. [Google Scholar]
- Xun, L.I.; Xin Zheng, D. Spatial aggregation and location selection of FDI base on empirical analysis Zhujiangl river delta of China. Sci. Geogra. Sinica 2007, 27, 636–641. [Google Scholar]
- Sheng, G. Multiple correlation effect of regional economic growth and its empirical test. Economist 2018, 4, 34–41. [Google Scholar]
- Wang, S.; Gao, S.; Wang, Y. Spatial structure of the urban agglomeration based on space of flows: The study of the Pearl river Delta. Geogr. Res. 2019, 38, 1849–1861. [Google Scholar]
- Wang, C.; Cao, Y.; Chen, G. Study on urban network of Yangtze River Delta region based on producer services. Geogr. Res. 2014, 33, 323–335. [Google Scholar]
- Jung-Dong, P.; Kyong-Hui, K. Comparison of competitiveness by export item of Incheon and Busan in China. Korean-Chin. Soc. Sci. Stud. 2010, 8, 31–56. [Google Scholar]




| Region | Criterion | Statistics | Optimal Lag Length | HA: GDP Is not the Granger Cause of AESI | Optimal Lag Length | HB: AESI Is Not the Granger Cause of GDP |
|---|---|---|---|---|---|---|
| all cities | AIC | W-bar | 3 | 13.3684 | 3 | 6.5296 |
| Z-bar | 69.5531 *** | 23.6775 *** | ||||
| Z-bar Tilde | 21.1994 *** | 4.8518 *** | ||||
| BIC | W-bar | 3 | 13.3684 | 1 | 1.56622 | |
| Z-bar | 69.5531 *** | 6.5323 *** | ||||
| Z-bar Tilde | 21.1994 *** | 2.9908 *** | ||||
| HQIC | W-bar | 3 | 13.3684 | 3 | 6.5296 | |
| Z-bar | 69.5531 *** | 23.6775 *** | ||||
| Z-bar Tilde | 21.1994 *** | 4.8518 *** | ||||
| provincial capitals | AIC | W-bar | 3 | 10.0982 | 3 | 6.4667 |
| Z-bar | 16.1344 *** | 7.8799 *** | ||||
| Z-bar Tilde | 5.8643 *** | 2.2536 ** | ||||
| BIC | W-bar | 3 | 10.0982 | 1 | 1.3879 | |
| Z-bar | 16.1344 *** | 1.5272 | ||||
| Z-bar Tilde | 5.8643 *** | 0.5946 | ||||
| HQIC | W-bar | 3 | 10.0982 | 3 | 6.4667 | |
| Z-bar | 16.1344 *** | 7.8799 *** | ||||
| Z-bar Tilde | 5.8643 *** | 2.2536 ** | ||||
| BTH | AIC | W-bar | 3 | 6.2438 | 3 | 3.3452 |
| Z-bar | 4.7747 *** | 0.5081 | ||||
| Z-bar Tilde | 0.9147 | −0.6057 | ||||
| BIC | W-bar | 3 | 6.2438 | 1 | 1.1876 | |
| Z-bar | 4.7747 *** | 0.4783 | ||||
| Z-bar Tilde | 0.9147 | −0.0225 | ||||
| HQIC | W-bar | 3 | 6.2438 | 3 | 3.3452 | |
| Z-bar | 4.7747 *** | 0.5081 | ||||
| Z-bar Tilde | 0.9147 | −0.6057 | ||||
| YRD | AIC | W-bar | 3 | 15.7630 | 3 | 7.7811 |
| Z-bar | 32.9539 *** | 12.3446 *** | ||||
| Z-bar Tilde | 13.0591 ** | 4.0444 *** | ||||
| BIC | W-bar | 3 | 15.7630 | 3 | 7.7811 | |
| Z-bar | 32.9539 *** | 12.3446 *** | ||||
| Z-bar Tilde | 13.0591 ** | 4.0444 *** | ||||
| HQIC | W-bar | 3 | 15.7630 | 3 | 7.7811 | |
| Z-bar | 32.9539 *** | 12.3446 *** | ||||
| Z-bar Tilde | 13.0591 ** | 4.0444 *** | ||||
| PRD | AIC | W-bar | 3 | 4.0850 | 2 | 2.3188 |
| Z-bar | 1.3288 | 0.4782 | ||||
| Z-bar Tilde | −0.1811 | −0.2197 | ||||
| BIC | W-bar | 1 | 1.2150 | 1 | 0.5300 | |
| Z-bar | 0.4560 | −0.9970 | ||||
| Z-bar Tilde | 0.0225 | −1.0100 | ||||
| HQIC | W-bar | 3 | 4.0850 | 2 | 2.3188 | |
| Z-bar | 1.3288 | 0.4782 | ||||
| Z-bar Tilde | −0.1811 | −0.2197 |
| Statistics | All Cities | Regional Level | |||
|---|---|---|---|---|---|
| ProvinceCapital | BTH | YRD | PRD | ||
| 0.0073 *** (0.0002) | 1.5555 *** (0.1905) | 0.1749 *** (0.0623) | 0.0904 *** (0.0071) | 29.226 *** (5.7968) | |
| 0.2630 *** (0.0007) | 0.1161 *** (0.0029) | 0.1718 *** (0.0088) | 0.1911 *** (0.0020) | 0.0343 *** (0.0051) | |
| 0.2556 *** (0.0014) | 0.2296 *** (0.0079) | 0.3298 *** (0.0264) | 0.2112 *** (0.0057) | 0.2224 *** (0.0170) | |
| 0.53 | 0.81 | 0.76 | 0.84 | 0.95 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, E.; Chen, Y.; Hu, G.; Lu, M. Competition between Export Cities in China: Evolution and Influencing Factors. Land 2022, 11, 201. https://doi.org/10.3390/land11020201
Li E, Chen Y, Hu G, Lu M. Competition between Export Cities in China: Evolution and Influencing Factors. Land. 2022; 11(2):201. https://doi.org/10.3390/land11020201
Chicago/Turabian StyleLi, Enkang, Yu Chen, Guojian Hu, and Mengqiu Lu. 2022. "Competition between Export Cities in China: Evolution and Influencing Factors" Land 11, no. 2: 201. https://doi.org/10.3390/land11020201
APA StyleLi, E., Chen, Y., Hu, G., & Lu, M. (2022). Competition between Export Cities in China: Evolution and Influencing Factors. Land, 11(2), 201. https://doi.org/10.3390/land11020201





