Carbon Emission Intensity Characteristics and Spatial Spillover Effects in Counties in Northeast China: Based on a Spatial Econometric Model
Abstract
:1. Introduction
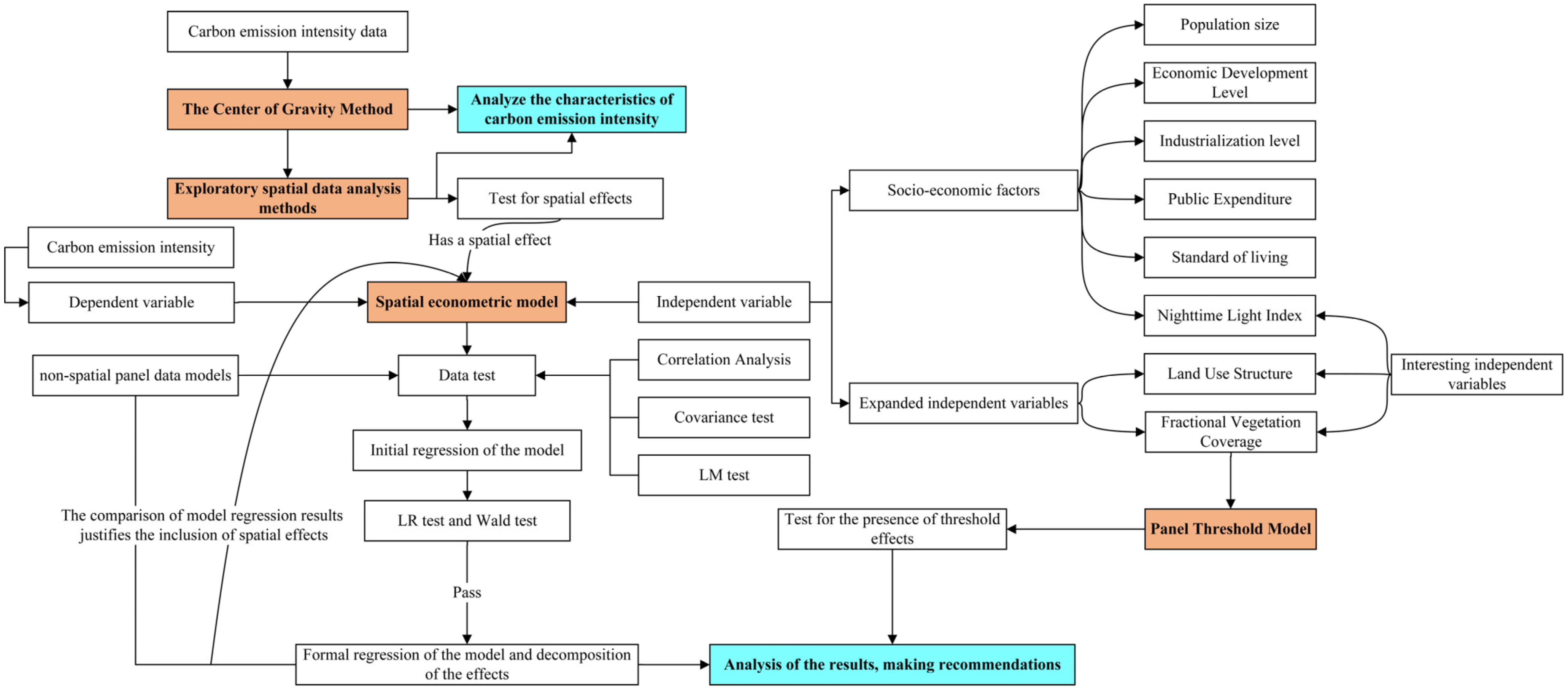
2. Materials and Methods
2.1. Study Area
2.2. Variable Selection and Data Source
2.2.1. Variable Selection
2.2.2. Data Source
2.3. Research Methodology
2.3.1. Exploratory Spatial Data Analysis Methods
2.3.2. The Center of Gravity Method
2.3.3. Spatial Econometric Model
2.3.4. Panel Threshold Model
3. Results
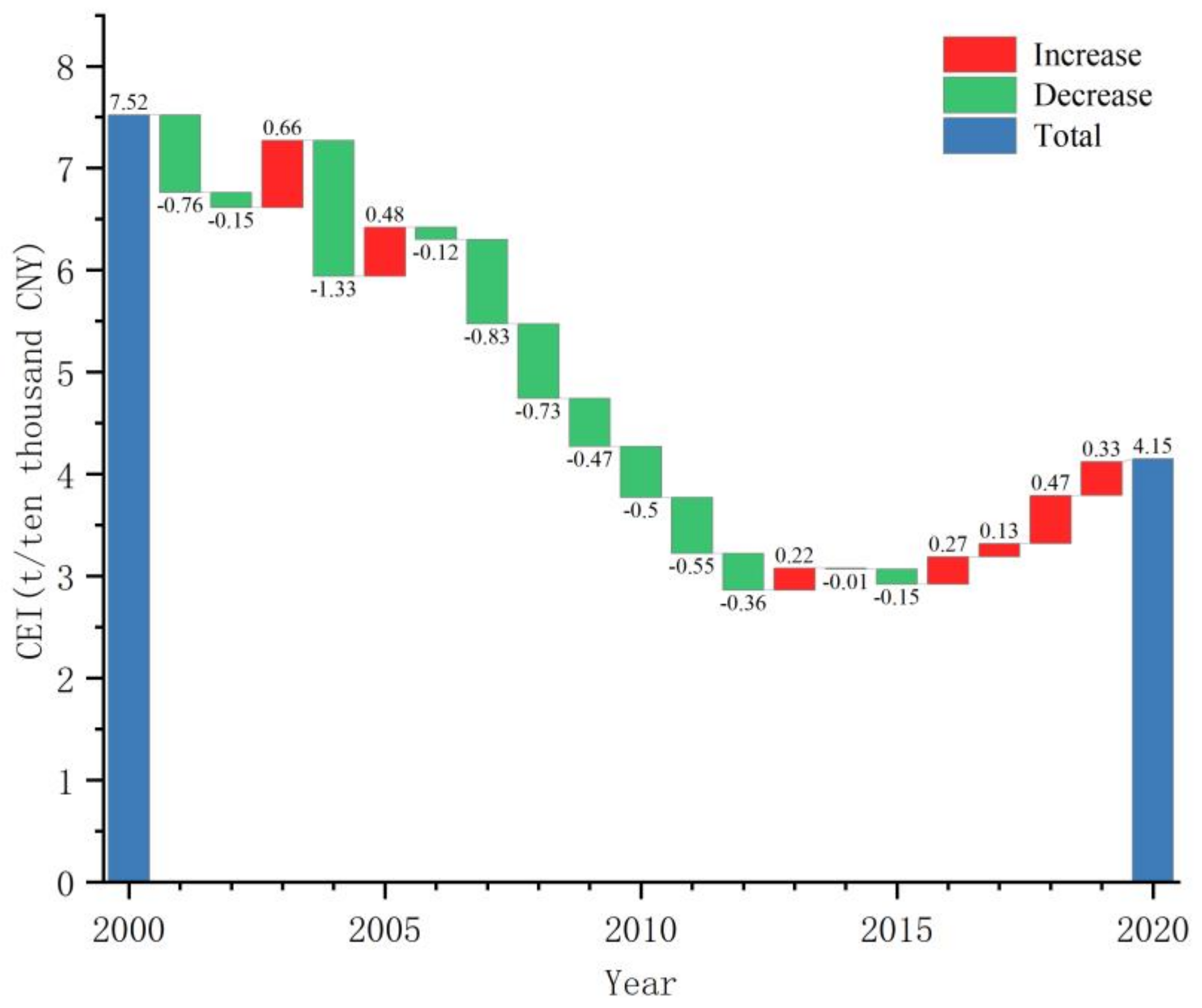
3.1. The Overall State of Carbon Emission Intensity in Northeast China’s Counties
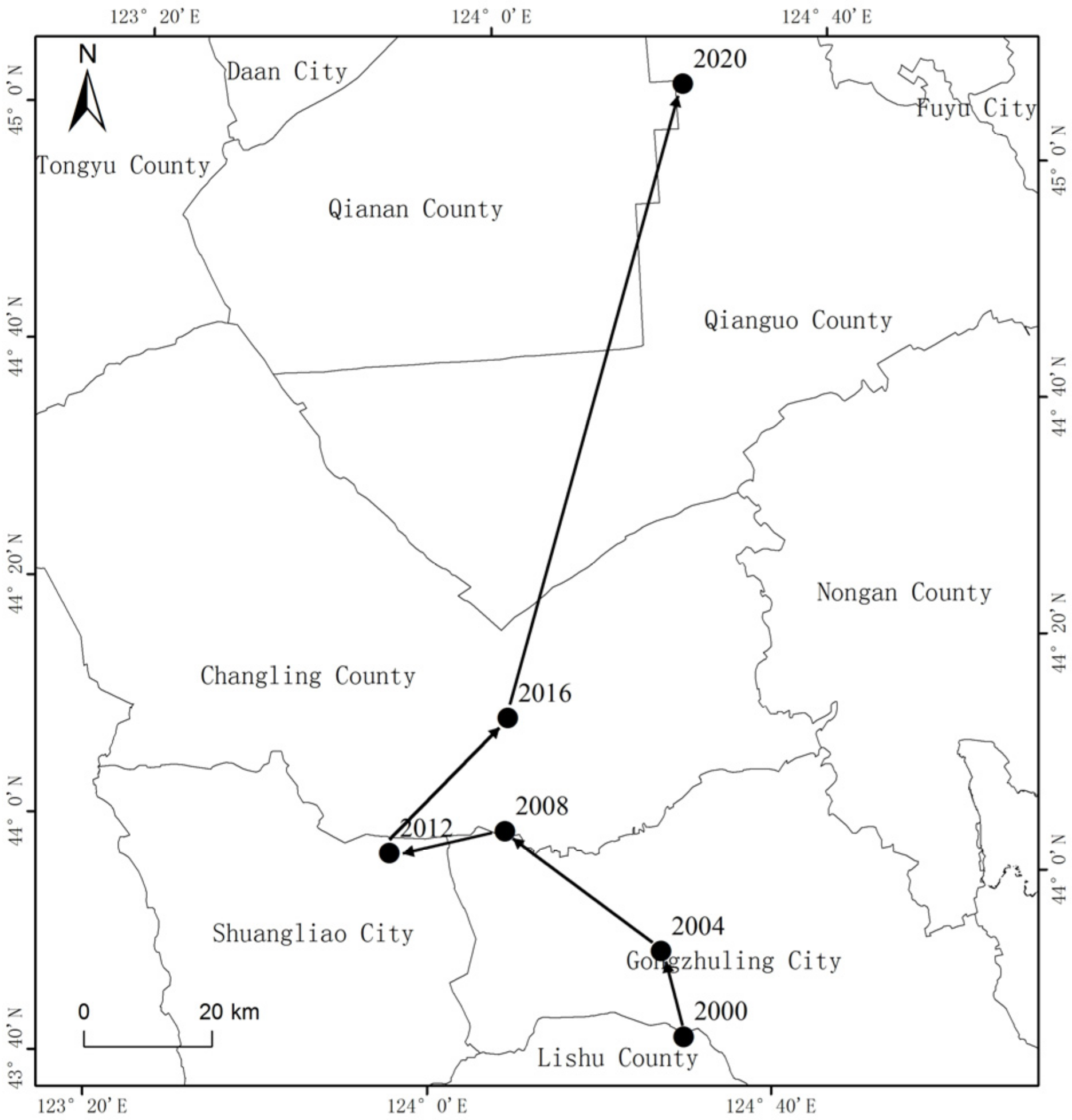
3.2. Analysis of the Carbon Emission Intensity Center of Gravity Shift in Northeast China’s Counties
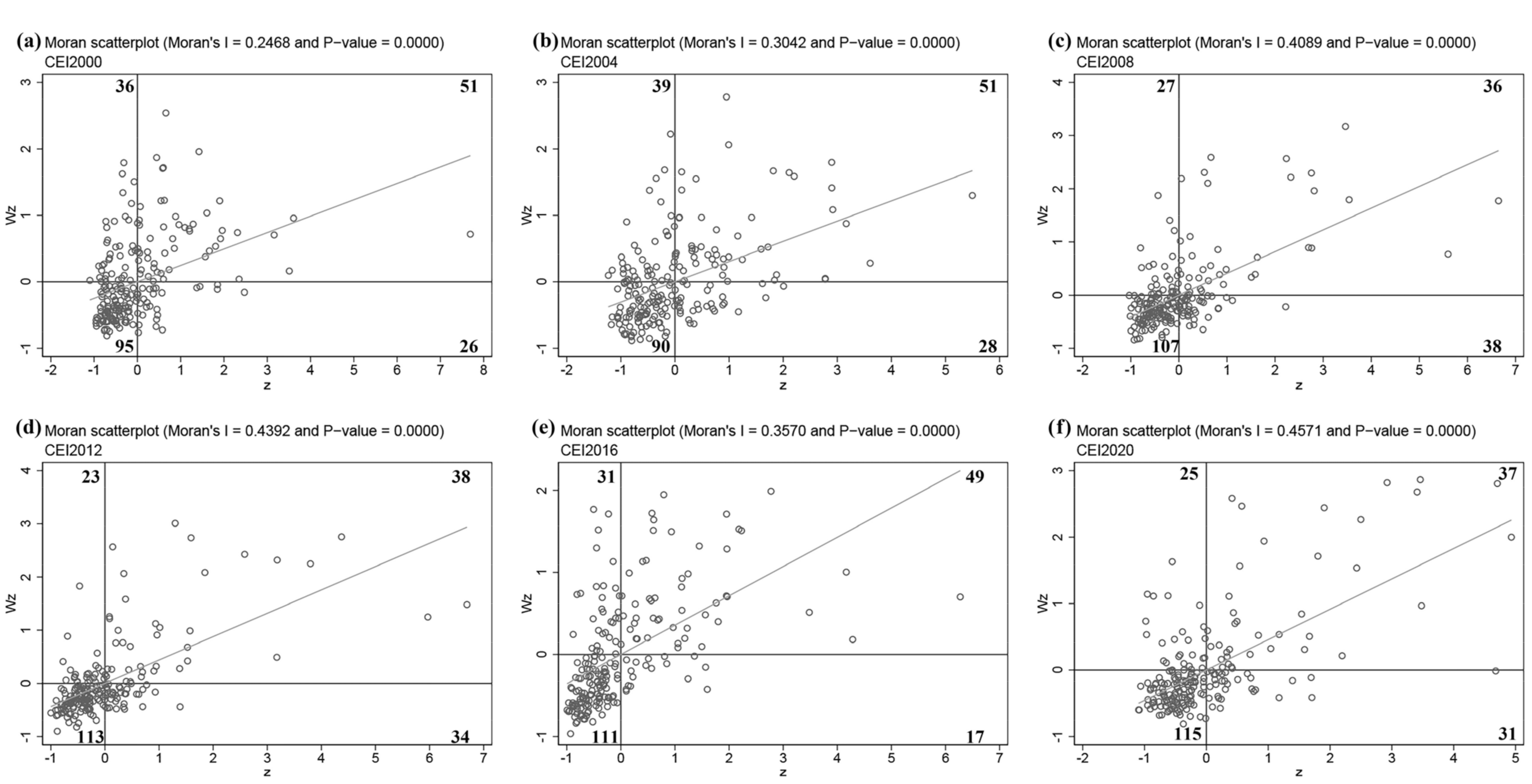
3.3. Carbon Emission Intensity in Northeast China: A Spatial Correlation Study
3.4. A Study into the Spatial Spillover Effect of Carbon Emission Intensity in Northeast China
4. Discussion
4.1. Comparative Analysis of the Results
4.2. Policy Implications
- (1)
- Attaching great importance to the spatial correlation of carbon emission intensity and spatial spillover effects, creating carbon-cutting policies tailored to the needs of each location. As a carbon reduction community, to jointly accomplish the “double carbon” goal, all regions should work together to design carbon reduction policies and embrace a collaborative governance model of integrated planning, resource and information sharing, and industrial integration and development. Locations where carbon emission intensity is relatively high, and agglomeration occurs would drive the carbon emission intensity of their surrounding areas to increase as well. This necessitates an increase in public finance spending, the gradual reduction of coal-based high-consumption, high-emission development methods, industrial transformation and upgrading, and the maintenance of a high-quality level of economic development. Lower carbon-intensity regions should continue to use their spatial spillover effects to encourage nearby regions to pursue low-carbon green growth.
- (2)
- Determine the major directions for designing carbon reduction programs by grasping the dominant factors of high carbon emission intensity. The role of population size and level of economic development in curbing carbon emission intensity is highly valued. The population decrease in the northeast is alarming, and governments should take proactive measures to address it. They should improve social security policies and address employment issues, as well as change the industrial structure, elevate the status of tertiary industry in economic development, and capitalize on the “Belt and Road” development opportunity to resuscitate Northeast China’s traditional industrial bases.
- (3)
- Insist in land and space use regulation system. Keep the present arable land acreage and quality constant. Limit the conversion of arable land to construction land, keep the overall amount of construction land under control, and keep the total amount of construction land steady or decreasing.
- (4)
- Continue to focus on afforestation and urban greening to maintain a high level of vegetation cover and stabilize vegetation’s ability to sequester and reduce carbon. Greening activities should be prioritized in counties with poor vegetation cover, such as Tumen City and Yushu City. Northeast China should continue to excavate the potential of forest carbon sinks and engage in carbon market activities.
4.3. Uncertainties and Prospects
5. Conclusions
- (1)
- Since 2000, the carbon emission intensity in the Northeast has increased after first declining, and the growth rate of carbon emission intensity in the western and northern regions of Northeast China is higher than the average level in Northeast China. Carbon emission intensity has a spatial correlation in northeast China. Since 2000, the spatial aggregation of carbon emission intensity has improved.
- (2)
- The results of the spatial econometric model show that in the counties of Northeast China, population size, economic development level, public expenditure, and fractional vegetation cover have a suppressive effect on carbon emission intensity. When the vegetation cover exceeds its threshold value, it can have a larger inhibitory influence on carbon emission intensity. The level of industrialization, living standard, land use structure dominated by arable land and construction land, and urbanization level all promote the increase of carbon emission intensity. The population size and level of economic development are significant driving forces among them.
- (3)
- Northeast China’s carbon emission intensity has a positive spatial spillover effect. Through the feedback mechanism, the increase in population size, the rise in economic development level, the level of industrialization as well as the improvement of living standard, the land use structure dominated by arable land and construction land, and the increase in urbanization level in the region will increase the carbon emission intensity in the surrounding areas. An increase in public expenditures leads to a decrease in carbon emission intensity in the surrounding area. The change in vegetation cover in this area does not affect the surrounding areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bronselaer, B.; Zanna, L. Heat and carbon coupling reveals ocean warming due to circulation changes. Nature 2020, 584, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Qi, S.Z.; Tan, X.J. Decomposition and prediction of China’s carbon emission intensity towards carbon neutrality: From perspectives of national, regional and sectoral level. Sci Total Environ. 2022, 825, 14. [Google Scholar] [CrossRef] [PubMed]
- Dong, F.; Yu, B.L.; Hadachin, T.; Dai, Y.J.; Wang, Y.; Zhang, S.N.; Long, R.Y. Drivers of carbon emission intensity change in China. Resour. Conserv. Recycl. 2018, 129, 187–201. [Google Scholar] [CrossRef]
- Lv, T.; Hu, H.; Zhang, X.M.; Xie, H.L.; Wang, L.; Fu, S.F. Spatial spillover effects of urbanization on carbon emissions in the Yangtze River Delta urban agglomeration, China. Environ. Sci. Pollut. Res. 2022, 29, 33920–33934. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Y. Spatial effects of carbon emission intensity and regional development in China. Environ. Sci. Pollut. Res. 2021, 28, 14131–14143. [Google Scholar] [CrossRef]
- Zeyang, C.; Jingang, Y.; Jian, S. An analysis of regional carbon intensity space—Time evolution and its influence factors in China. Sci. Technol. Manag. Res. 2017, 37, 260–266. [Google Scholar]
- Wang, S.; Huang, Y.; Zhou, Y. Spatial spillover effect and driving forces of carbon emission intensity at the city level in China. J. Geogr. Sci. 2019, 29, 231–252. [Google Scholar] [CrossRef] [Green Version]
- Song, M.; Wu, J.; Song, M.; Zhang, L.; Zhu, Y. Spatiotemporal regularity and spillover effects of carbon emission intensity in China’s Bohai Economic Rim. Sci. Total Environ. 2020, 740, 140184. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C.; Matsumura, W. Changes in the GHG emission intensity in EU-15: Lessons from a decomposition analysis. Energy 2010, 35, 3315–3322. [Google Scholar] [CrossRef]
- Pang, J.X.; Li, H.J.; Lu, C.P.; Lu, C.Y.; Chen, X.P. Regional differences and dynamic evolution of carbon emission intensity of agriculture production in China. Int. J. Environ. Res. Public Health 2020, 17, 7541. [Google Scholar] [CrossRef]
- Yu, S.W.; Hu, X.; Fan, J.L.; Cheng, J.H. Convergence of carbon emissions intensity across Chinese industrial sectors. J. Clean. Prod. 2018, 194, 179–192. [Google Scholar] [CrossRef]
- Yu, J.H.; Yu, Y.; Jiang, T.Y. Structural factors influencing energy carbon emissions in China’s service industry: An input-output perspective. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y.; Zhang, R.; He, B. The carbon emission reduction effect of tourism economy and its formation mechanism: An empirical study of China’s 92 tourism-dependent cities. Int. J. Environ. Res. Public Health 2022, 19, 1824. [Google Scholar] [CrossRef] [PubMed]
- Xianzhao, L.; Zhangchun, G.; Yong, Z.; Dongshui, Z.; Jinning, X.; Yan, S.; Zhiqiang, W. Spatial dependence pattern of carbon emission intensity in China’s provinces and spatial heterogeneity of its influencing factors. Sci. Geogr. Sin. 2018, 38, 681–690. [Google Scholar]
- Zheng, Y.M.; Lv, Q.; Wang, Y.D. Economic development, technological progress, and provincial carbon emissions intensity: Empirical research based on the threshold panel model. Appl. Econ. 2021, 54, 3495–3504. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Xu, Y.R.; Liu, C.Z.; Fang, Z.Q.; Guo, J.Y. Spatial effects of technological progress and financial support on China’s provincial carbon emissions. Int. J. Environ. Res. Public Health 2019, 16, 1743. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wu, L. Analysis of Hubei province industry’s carbon emissions based on the LMDI. In Proceedings of the 2nd International Conference on Renewable Energy and Environmental Technology (REET), Dalian, China, 19–20 August 2014; pp. 1865–1868. [Google Scholar]
- Li, W.; Sun, W.; Li, G.M.; Jin, B.H.; Wu, W.; Cui, P.F.; Zhao, G.H. Transmission mechanism between energy prices and carbon emissions using geographically weighted regression. Energy Policy 2018, 115, 434–442. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, P.F. Differentiation research of CO2 emissions from energy consumption and their influencing mechanism on the industrial enterprises above designated size in Chinese industrial cities: Based on geographical detector method. Nat. Hazards 2020, 102, 645–658. [Google Scholar] [CrossRef] [Green Version]
- Li, S.P.; Wang, Q.; Meng, Y. Analysis on the status and influencing factors of industrial carbon emissions in Northeast China. In Proceedings of the 3rd International Conference on Energy, Environment and Sustainable Development (EESD 2013), Shanghai, China, 12–13 November 2013; pp. 866–869. [Google Scholar]
- Gong, W.-F.; Fan, Z.-Y.; Wang, C.-H.; Wang, L.-P.; Li, W.-W. Spatial spillover effect of carbon emissions and its influencing factors in the Yellow River basin. Sustainability 2022, 14, 3608. [Google Scholar] [CrossRef]
- Qin, J.C.; Tao, H.; Zhan, M.J.; Munir, Q.; Brindha, K.; Mu, G.J. Scenario analysis of carbon emissions in the energy base, Xinjiang autonomous region, China. Sustainability 2019, 11, 4220. [Google Scholar] [CrossRef] [Green Version]
- Huibin, M.; Shaojian, W. Spatio-temporal evolution and spatial effect mechanism of carbon emission at county level in the Yellow River basin. Sci. Geogr. Sin. 2021, 41, 1324–1335. [Google Scholar]
- Heting, B.; Mingguo, M.; Ran, Y.; Kangning, L.; Chuhan, J. Evaluation of urban expansion in Chongqing city based on the nighttime light data. Remote Sens. Technol. Appl. 2019, 34, 216–224. [Google Scholar]
- Lin, Q.W.; Zhang, L.; Qiu, B.K.; Zhao, Y.; Wei, C. Spatiotemporal analysis of land use patterns on carbon emissions in China. Land 2021, 10, 141. [Google Scholar] [CrossRef]
- Liu, X.Y.; Duan, Z.Y.; Shan, Y.L.; Duan, H.Y.; Wang, S.; Song, J.N.; Wang, X.E. Low-carbon developments in Northeast China: Evidence from cities. Appl. Energy 2019, 236, 1019–1033. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.Y. Revitalizing old industrial base of Northeast China: Process, policy and challenge. Chin. Geogr. Sci. 2008, 18, 109–118. [Google Scholar] [CrossRef]
- Liu, S.B. Energy consumption and structural reformation in Chinese northeast old industrial base. In Proceedings of the International Conference on Renewable Energy and Environmental Technology (REET 2013), Jilin, China, 21–22 September 2013; pp. 4281–4284. [Google Scholar]
- Wei, X.D.; Wang, S.N.; Wang, Y.K. Spatial and temporal change of fractional vegetation cover in North-western China from 2000 to 2010. Geol. J. 2018, 53, 427–434. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Gao, M.; Cheng, S.; Hou, W.; Song, M.; Liu, X.; Liu, Y.; Shan, Y. County-level CO2 emissions and sequestration in China during 1997–2017. Sci. Data 2020, 7, 391. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Lixian, Z.; Zhehao, R.; Bin, C.; Peng, G.; Haohuan, F.; Bing, X. A Prolonged Artificial Nighttime-Light Dataset of China (1984–2020); National Tibetan Plateau Data Center: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Anselin, L. Interactive techniques and exploratory spatial data analysis. Geogr. Inf. Syst. Princ. Tech. Manag. Appl. 1999, 47, 415–421. [Google Scholar] [CrossRef]
- Quah, D. The global economy’s shifting centre of gravity. Glob. Policy 2011, 2, 3–9. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Effects of population and affluence on CO2 emissions. Proc. Natl. Acad. Sci. USA 1997, 94, 175–179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.; Du, L. Assessment framework of provincial carbon emission peak prediction in China: An empirical analysis of Hebei province. Pol. J. Environ. Stud. 2019, 28, 3753–3765. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Belotti, F.; Hughes, G.; Mortari, A.P. Spatial panel-data models using Stata. Stata J. 2017, 17, 139–180. [Google Scholar] [CrossRef] [Green Version]
- Repkine, A.; Min, D. Foreign-funded enterprises and pollution halo hypothesis: A spatial econometric analysis of thirty Chinese regions. Sustainability 2020, 12, 5048. [Google Scholar] [CrossRef]
- James, L.; Robert, K.P. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wenmeng, Y.; Tingting, Z.; Dajun, S. County-level spatial pattern and influencing factors evolution of carbon emission intensity in China: A random forest model analysis. China Environ. Sci. 2022, 1–10. Available online: https://kns.cnki.net/kcms/detail/11.2201.X.20220219.1311.002.html (accessed on 3 March 2022).
- Anselin, L.; Bera, A.K.; Florax, R.; Yoon, M.J. Simple diagnostic tests for spatial dependence. Reg. Sci. Urban Econ. 1996, 26, 77–104. [Google Scholar] [CrossRef]
- Wang, Q.Y. Fixed-effect panel threshold model using Stata. Stata J. 2015, 15, 121–134. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Cao, T.; Sun, T. Analysis on the variation rule and influencing factors of energy consumption carbon emission intensity in China’s urbanization construction. J. Clean. Prod. 2019, 238, 117958. [Google Scholar] [CrossRef]
- Zhao, R.Q.; Huang, X.J.; Liu, Y.; Zhong, T.Y.; Ding, M.L.; Chuai, X.W. Carbon emission of regional land use and its decomposition analysis: Case study of Nanjing city, China. Chin. Geogr. Sci. 2015, 25, 198–212. [Google Scholar] [CrossRef]

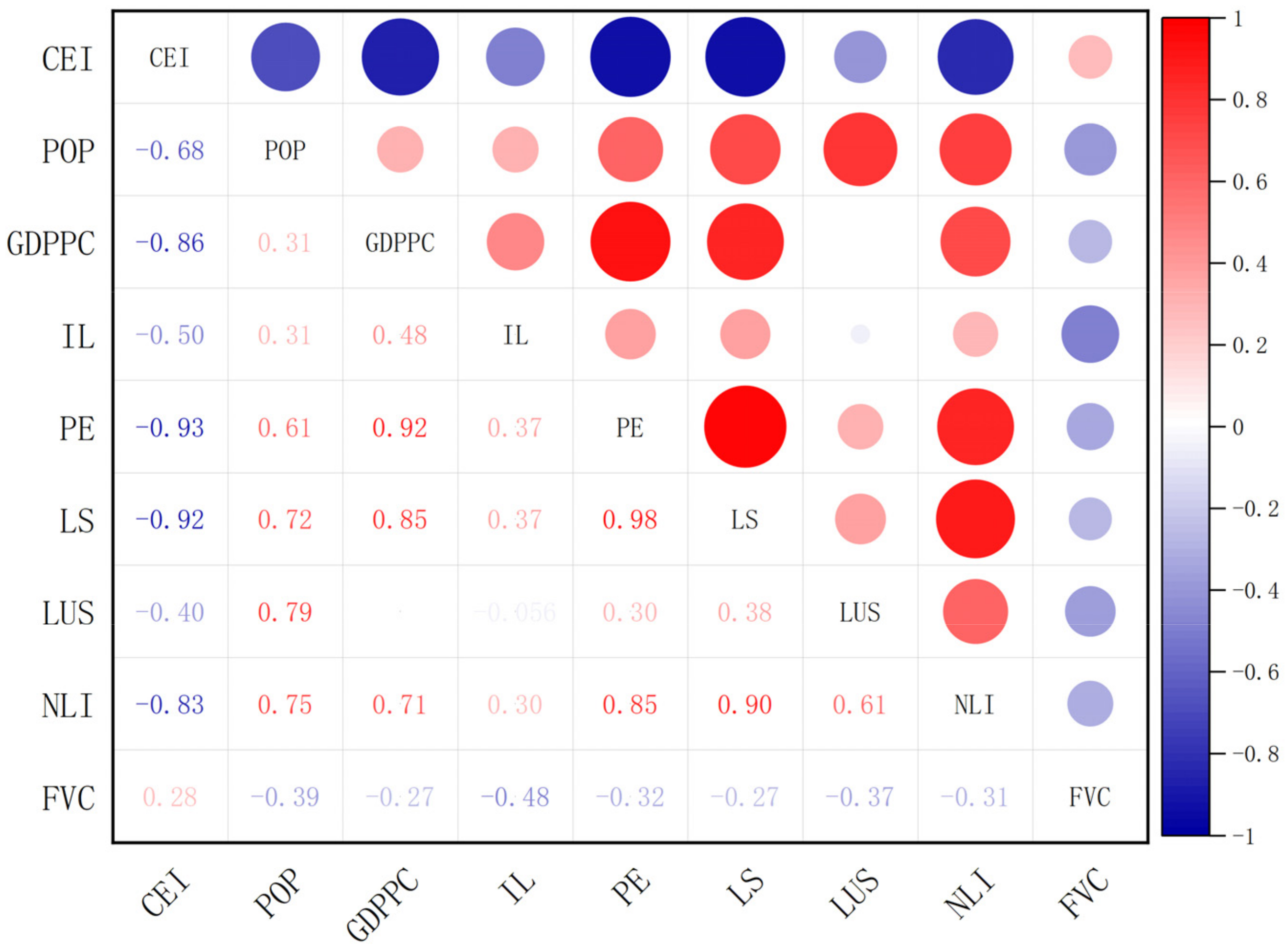
| Variable | Abbreviation | Name | Definition | Number of Observations |
|---|---|---|---|---|
| Dependent variable | CEI | Carbon emission intensity | CO2 emissions/GDP (t/ten thousand CNY) | 4368 |
| Independent variables | POP | Population size | Population (ten thousand people) | 4368 |
| GDPPC | Economic Development Level | GDP/Population (ten thousand CNY/per person) | 4368 | |
| IL | Industrialization level | Value added by the secondary industry/GDP | 4368 | |
| PE | Public Expenditure | Expenditures from the general public budget of local governments (ten thousand CNY) | 4368 | |
| LS | Standard of living | Savings account balance for residents (ten thousand CNY) | 4368 | |
| LUS | Land Use Structure | Percentage of cropland and construction land | 4368 | |
| NLI | Nighttime Light Index | The product of average light intensity and light area ratio | 4368 | |
| FVC | Fractional Vegetation Coverage | Percentage of vegetation area | 4368 |
| Year | I | Z | P |
|---|---|---|---|
| 2000 | 0.2468 *** | 5.9271 | 0.0000 |
| 2001 | 0.2936 *** | 6.7896 | 0.0000 |
| 2002 | 0.3018 *** | 7.0066 | 0.0000 |
| 2003 | 0.2334 *** | 5.7486 | 0.0000 |
| 2004 | 0.3042 *** | 7.0568 | 0.0000 |
| 2005 | 0.3298 *** | 7.7291 | 0.0000 |
| 2006 | 0.3597 *** | 8.4308 | 0.0000 |
| 2007 | 0.3698 *** | 8.7736 | 0.0000 |
| 2008 | 0.4089 *** | 9.6735 | 0.0000 |
| 2009 | 0.4258 *** | 10.0442 | 0.0000 |
| 2010 | 0.4586 *** | 10.8632 | 0.0000 |
| 2011 | 0.4489 *** | 10.7745 | 0.0000 |
| 2012 | 0.4392 *** | 10.4601 | 0.0000 |
| 2013 | 0.3869 *** | 9.1200 | 0.0000 |
| 2014 | 0.3844 *** | 9.0599 | 0.0000 |
| 2015 | 0.4238 *** | 9.9571 | 0.0000 |
| 2016 | 0.357 *** | 8.3554 | 0.0000 |
| 2017 | 0.4218 *** | 9.7992 | 0.0000 |
| 2018 | 0.4786 *** | 11.0602 | 0.0000 |
| 2019 | 0.4363 *** | 10.1479 | 0.0000 |
| 2020 | 0.4571 *** | 10.6199 | 0.0000 |
| Pooled OLS | Spatial Fixed Effects | Time-Period Fixed Effects | Spatial and Time- Period Fixed Effect | |
|---|---|---|---|---|
| ln (POP) | −0.4247 *** | −0.8335 *** | −0.4246 *** | −0.8449 *** |
| (0.0167) | (0.0178) | (0.0195) | (0.0159) | |
| ln (GDPPC) | −0.6870 *** | −0.8636 *** | −0.6623 *** | −0.8987 *** |
| (0.0162) | (0.0083) | (0.0165) | (0.0079) | |
| ln (IL) | −0.0184 | 0.0154 ** | 0.0102 | 0.0673 *** |
| (0.0146) | (0.0071) | (0.0156) | (0.0068) | |
| ln (PE) | 0.0218 * | 0.0496 *** | 0.0415 ** | −0.0632 *** |
| (0.0131) | (0.0071) | (0.0183) | (0.0078) | |
| ln (LS) | 0.0838 *** | 0.1399 *** | 0.0603 *** | 0.0839 *** |
| (0.0129) | (0.0067) | (0.0144) | (0.0075) | |
| ln (LUS) | −0.2016 *** | 0.1092 ** | −0.1926 *** | 0.2166 *** |
| (0.0100) | (0.0349) | (0.0105) | (0.0309) | |
| ln (NLI) | 0.1421 *** | 0.1749 *** | 0.1406 *** | 0.1668 *** |
| (0.0062) | (0.0031) | (0.0068) | (0.0032) | |
| ln (FVC) | −0.3295 *** | −0.0574 *** | −0.2865 *** | 0.0010 |
| (0.0267) | (0.0155) | (0.0277) | (0.0139) | |
| constant | 0.9209 *** | 2.2196 *** | 1.0599 *** | 4.5484 *** |
| (0.1173) | (0.1089) | (0.1470) | (0.1392) | |
| Adjusted. R2 | 0.596 | 0.958 | 0.603 | 0.969 |
| No. Obs. | 4368 | 4368 | 4368 | 4368 |
| LM Spatial Lag | 1080.5710 *** | 159.0936 *** | 41.2029 *** | 58.0721 *** |
| Robust LM Spatial Lag | 30.0360 *** | 3.3772 * | 13.0061 *** | 8.9961 *** |
| LM Spatial Error | 1552.9960 *** | 348.8960 *** | 327.2038 *** | 373.7763 *** |
| Robust LM Spatial Error | 502.4610 *** | 193.1796 *** | 299.0071 *** | 324.7002 *** |
| Variables | Spatial Durbin Model Estimation | Variables | Spatial Durbin Model Lag Estimation |
|---|---|---|---|
| ln (POP) | −0.925 *** | W × ln (POP) | 0.729 *** |
| (−81.346) | (28.381) | ||
| ln (GDPPC) | −0.962 *** | W × ln (GDPPC) | 0.709 *** |
| (−154.686) | (45.343) | ||
| ln (IL) | 0.027 *** | W × ln (IL) | 0.030 *** |
| (5.267) | (3.431) | ||
| ln (PE) | −0.054 *** | W × ln (PE) | −0.005 |
| (−9.318) | (−0.452) | ||
| ln (LS) | 0.042 *** | W × ln (LS) | 0.037 *** |
| (7.707) | (3.738) | ||
| ln (LUS) | 0.123 *** | W × ln (LUS) | −0.006 |
| (4.213) | (−0.145) | ||
| ln (NLI) | 0.124 *** | W × ln (NLI) | −0.053 *** |
| (39.352) | (−11.672) | ||
| ln (FVC) | −0.044 *** | W × ln (FVC) | 0.047 ** |
| (−2.753) | (2.143) | ||
| 0.681 *** | 0.007 *** | ||
| (53.109) | (45.220) | ||
| LR test spatial lag | 2105.50 *** | Wald test spatial lag | 1044.54 *** |
| LR test spatial error | 396.86 *** | Wald test spatial error | 100.00 *** |
| Variables | Direct | Indirect | Total |
|---|---|---|---|
| ln (POP) | −0.904 *** | 0.288 *** | −0.616 *** |
| (−70.904) | (4.759) | (−9.141) | |
| ln (GDPPC) | −0.951 *** | 0.154 *** | −0.797 *** |
| (−171.981) | (5.614) | (−27.191) | |
| ln (IL) | 0.038 *** | 0.143 *** | 0.181 *** |
| (6.685) | (5.512) | (6.418) | |
| ln (PE) | −0.062 *** | −0.121 *** | −0.183 *** |
| (−9.517) | (−3.639) | (−5.111) | |
| ln (LS) | 0.054 *** | 0.188 *** | 0.243 *** |
| (7.827) | (6.987) | (7.911) | |
| ln (LUS) | 0.142 *** | 0.236 *** | 0.378 *** |
| (5.309) | (2.631) | (4.093) | |
| ln (NLI) | 0.131 *** | 0.093 *** | 0.224 *** |
| (44.274) | (10.449) | (24.266) | |
| ln (FVC) | −0.042 *** | 0.056 | 0.014 |
| (−3.086) | (1.329) | (0.325) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Li, S.; Cao, X.; Li, Y. Carbon Emission Intensity Characteristics and Spatial Spillover Effects in Counties in Northeast China: Based on a Spatial Econometric Model. Land 2022, 11, 753. https://doi.org/10.3390/land11050753
Gao Z, Li S, Cao X, Li Y. Carbon Emission Intensity Characteristics and Spatial Spillover Effects in Counties in Northeast China: Based on a Spatial Econometric Model. Land. 2022; 11(5):753. https://doi.org/10.3390/land11050753
Chicago/Turabian StyleGao, Zhenjun, Shujie Li, Xiufeng Cao, and Yuefen Li. 2022. "Carbon Emission Intensity Characteristics and Spatial Spillover Effects in Counties in Northeast China: Based on a Spatial Econometric Model" Land 11, no. 5: 753. https://doi.org/10.3390/land11050753
APA StyleGao, Z., Li, S., Cao, X., & Li, Y. (2022). Carbon Emission Intensity Characteristics and Spatial Spillover Effects in Counties in Northeast China: Based on a Spatial Econometric Model. Land, 11(5), 753. https://doi.org/10.3390/land11050753






