Towards Carbon Neutrality: The Innovation Efficiency of China’s Forestry Green Technology and Its Spatial Spillover Effects
Abstract
:1. Introduction
2. Literature Review
3. Methods and Data
3.1. Methods
3.1.1. Super-Efficiency SBM-DEA Model
3.1.2. Spatial Econometric Model
- Global indicators of spatial association
- Local indicators of spatial association
- SDM
3.2. Data
3.2.1. Data Description
3.2.2. Evaluation Indicators
3.2.3. Influencing Factors on FGTIEs
- SS: Previous studies have demonstrated that the level of employees’ social security affects technological innovation behaviour [26]. Innovative behaviour is often accompanied by some risk. With the improvement of social security, the willingness of forestry practitioners to bear risks rises, and social security can meaningfully reduce forestry practitioners’ fear of innovation risks. Therefore, social security can advance and motivate forestry practitioners’ potential and motivation for technological innovation, thus enhancing FGTIEs. In this paper, SS is measured by the average annual wage of workers in the forestry system in each province.
- HC: Human capital as an innovative subject is a carrier of knowledge and technology that can induce innovative behaviour by matching the path of technological structures and upgrading and developing innovative ecological solutions. HC is capable of allocating resources and guiding the concentration of other input factors in forestry to improve and innovate production technology and promote the diffusion of new knowledge and technological approaches to advance the overall optimisation of forestry development. Previous studies have found that the level of HC is determined by labourers’ education, and the higher the education level is, the greater the contributions to innovation are. This study measures HC as the number of forestry station workers in each province with an education level of short-cycle courses or above.
- GS: The special nature of the forestry industry is that it is basic, ecological and related to public welfare. Since the forestry industry is highly influenced by natural factors and carries a high degree of risk, the government often tries to adjust the forestry industry’s development through the provision of financial subsidies. Existing studies have reached two different conclusions regarding the government’s financial support. The first research view is that government financial subsidies can promote forestry innovation behaviour, as such subsidies not only encourage forestry technological innovation research and development (R&D) at a lower cost, but more importantly, these subsidies can also increase the motivation for technological innovation R&D [27]. Another research view is that government financial subsidies reduce innovation behaviour. The forestry industry will alter the demand for innovation in forestry production after receiving GS, instead reducing investment in technological innovation, as the innovation generates the same income [28]. In this study, GS is measured by the total state investment in forestry.
- IS: The adjustment of industrial structures can improve the quality of economic growth and is also an important means of improving the ecological environment [29]. Green technology innovation is a technology-intensive activity, and industrial restructuring and upgrades promote the vitality of industrial innovation and enhance the development of green technology innovation in regional industries. Promoting the transformation and upgrading of the forestry industry and accelerating the cultivation of technological innovation as the core of the new advantages of competitive forestry development can effectively promote the improvement of FGTIE. This study measures IS as the ratio of tertiary provincial forestry sector outputs to GDP.
- FS: Different forestry scales have different effects on the absorption of national innovation support policies. First, larger-scale forestry indicates that the province has advantages in human, financial, technological and managerial resources for forestry development [30], which can effectively supplement the innovative capital of other productive and functional activities to optimise production efficiency. Second, a larger forestry industry indicates that it has a well-established market, standardised trading criteria and a sound credit system, which can increase the industry’s ability to bear the risks of technological innovation. This study measures FS using the ratio of forestry employees to the total number of employees.
- EDL: The current investment return cycle of China’s forestry industry is lengthy, with the characteristics of a low return rate in the early stage; thus, FGTIE requires considerable capital and scientific economic development support. Provinces with high levels of economic development can establish innovative policy support for forestry development through financial support, preferential policies, technical guidance and talent introduction. Highly developed provinces generate more opportunities to offer cooperation with social capital and use the funds provided for technological R&D to provide the impetus for FGTIE upgrades. This study uses provincial GDP to measure EDL.
- FDI: There are two hypotheses regarding the impact of FDI; the ‘pollution haven hypothesis’ and the ‘pollution halo hypothesis’ [31,32]. FDI is highly permeable and practical and is capable of effectively addressing the comprehensive technology, capital and knowledge reserve challenges that arise in the development of China’s forestry industry. In contrast, although FDI provides motivations, tools and opportunities for technological innovation in China’s forestry industry, a high probability remains that contemporary products are pollution-intensive and resource-consuming, and thus are likely to become a ‘pollution haven’ for other countries [33]. This study measures FDI as the amount of actual foreign investment in each province.
- UL: The process of urbanisation is one of both continuous industrial and population concentration and rapid social development, as well as the generation of massive energy consumption and high concentrations of carbon emissions. The urbanisation process is characterised by the continuous improvement of urban infrastructure and individual living standards. The level of urbanisation is an important indicator of economic development [34]. Urbanisation indirectly affects innovation through forestry production methods, technology circulation and trade development. UL is measured in this study by the ratio of year-end urban population to year-end total population.
- EPS: The impact of environmental policy stringency on GTIE has been controversial, and there are two prevailing views. One view is ‘following costs’ [35], which argues that environmental policies lead to increased production costs and lower profits, which can reduce organisations’ innovative behaviour. Another view is that appropriate or more stringent environmental policies can better motivate organisations to improve productivity through technological innovation, referring to the ‘innovation compensation’ caused by environmental policies (also known as the ‘Porter hypothesis’). Our study produces evidence on the effect of environmental policies on the impact of different provinces’ FGTIE. The EPS measure is calculated as the ratio of the amount of national investment in controlling environmental pollution to GDP. Table 3 presents the descriptive statistics of the above factors.
4. Results
4.1. Spatiotemporal Dynamics
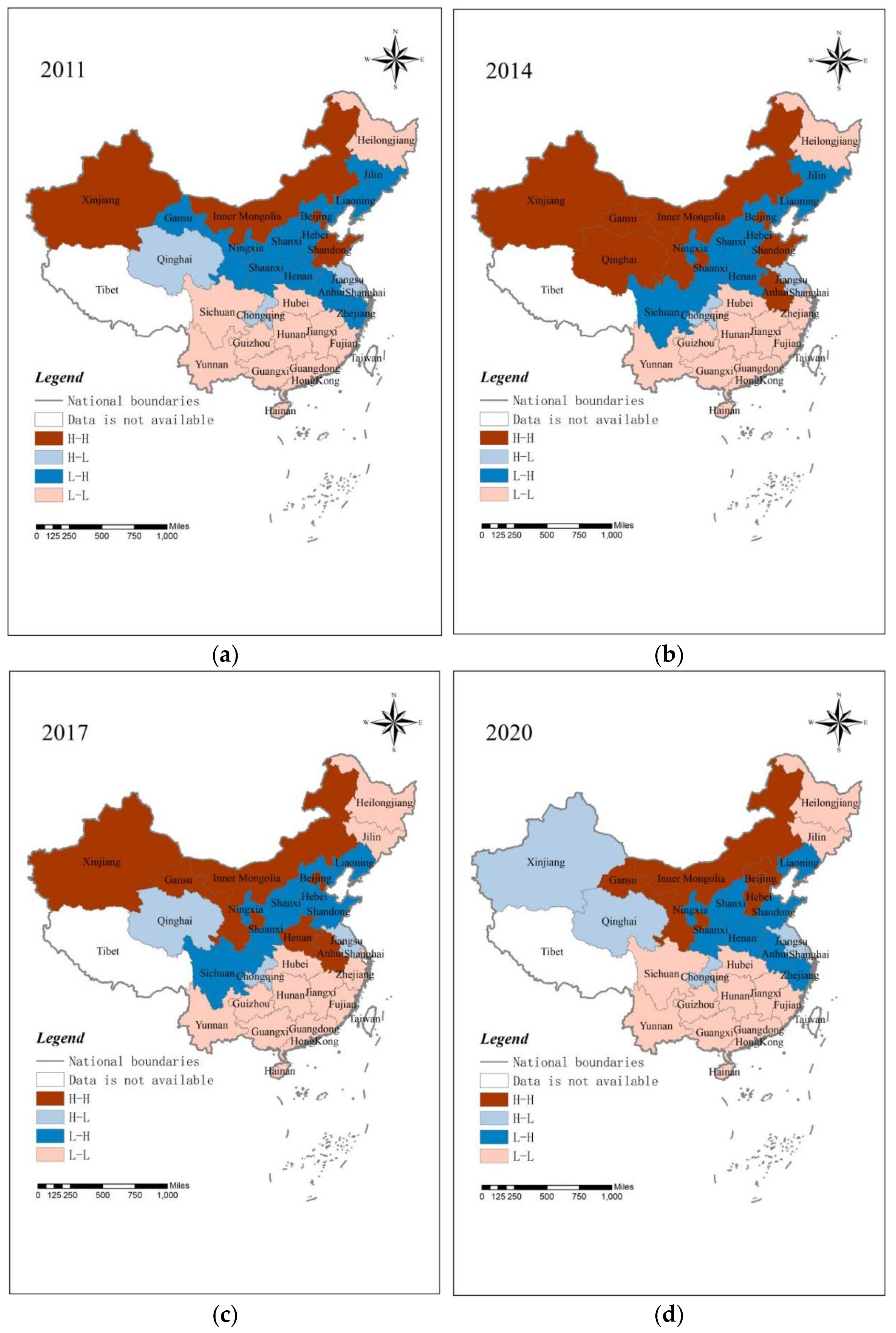
4.2. Spatial Correlations
4.2.1. Global Spatial Correlations
4.2.2. Local Spatial Correlations
4.3. Analysis of Influencing Factors
4.3.1. Identification of Influencing Factors
4.3.2. Robustness Test
5. Conclusions and Policy Implications
5.1. Conclusions
- (1)
- In terms of spatiotemporal dynamics, China’s FGTIE has obvious spatial distribution differences and geographical imbalance, taking Sichuan–Shaanxi–Henan–Shandong as the boundary, and revealing a north–south polarisation pattern and overall spatial distribution characteristics of ‘high north and low south’. The provinces to the north of this boundary are primarily higher- and high-efficiency provinces, whereas the provinces to the south of the boundary are mostly medium- and low-efficiency provinces. From the perspective of time development, the FGTIE in the southwestern provinces is relatively stable, while that in the central and southeastern provinces are highly variable, and the overall development has the characteristics of concerted development.
- (2)
- In terms of spatial correlation, the FGTIE in China is not randomly distributed in space but exhibits significant spatial correlation, and the intensity of the spatial correlation demonstrates a ‘W’-shaped trend of ‘decline–rise–decline’, indicating that the characteristics of the global spatial pattern of FGTIE have not yet formed a steady state. However, a stable spatial aggregation relationship is evident among provinces.
- (3)
- FGTIE has a significant spatial spillover effect. Increased SS, FDI and EPS will advance local FGTIE, and neighbouring provinces’ FGTIE increase through positive spillover effects. EDL will restrict local FGTIE increases and suppress neighbouring provinces’ FGTIE increases through negative spillover effects. FS has no significant effect on local FGTIE increases, but will suppress neighbouring provinces’ FGTIE increases through negative spillover effects. UL will promote local FGTIE increase but has no spillover effect on neighbouring provinces’ FGTIE. GS and IS will suppress local FGTIE enhancements, with no spillover effect on neighbouring provinces.
5.2. Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anhui | 0.28681 | 0.31999 | 0.53328 | 0.62964 | 1.01511 | 1.06569 | 0.63455 | 0.56960 | 0.45085 | 0.34729 |
| Beijing | 1.11041 | 1.18311 | 1.21517 | 1.16818 | 1.15855 | 1.06797 | 1.41716 | 1.66109 | 1.64992 | 1.72036 |
| Fujian | 0.31567 | 0.26330 | 0.33831 | 0.26769 | 0.40387 | 0.40003 | 0.38229 | 0.42795 | 0.40062 | 0.39796 |
| Gansu | 0.47108 | 0.61483 | 0.64744 | 0.74693 | 1.01959 | 1.01224 | 0.66819 | 1.01182 | 1.10817 | 0.67128 |
| Guangdong | 0.22269 | 0.26901 | 0.25419 | 0.30093 | 0.41748 | 0.43739 | 0.49725 | 0.39475 | 0.38823 | 0.41318 |
| Guangxi | 0.12598 | 0.11886 | 0.14979 | 0.22610 | 0.18854 | 0.14376 | 0.11507 | 0.13163 | 0.30659 | 0.14462 |
| Guizhou | 0.32328 | 0.47547 | 0.30822 | 0.39053 | 0.48196 | 1.19193 | 0.57260 | 1.11199 | 0.48512 | 0.28679 |
| Hainan | 0.45083 | 1.14176 | 1.01110 | 0.34902 | 1.01399 | 1.02583 | 0.30589 | 0.47774 | 0.57097 | 0.27063 |
| Hebei | 0.39461 | 0.41488 | 0.36993 | 0.46331 | 0.50641 | 0.72012 | 0.59143 | 1.02084 | 1.09262 | 1.06621 |
| Henan | 0.51347 | 0.55419 | 0.55308 | 0.59228 | 0.62611 | 0.48084 | 0.63824 | 0.72663 | 0.65103 | 0.63143 |
| Heilongjiang | 0.37990 | 0.41394 | 0.39339 | 0.44761 | 0.45439 | 0.39028 | 0.39534 | 0.35151 | 0.39606 | 0.21253 |
| Hubei | 0.34870 | 0.37143 | 0.39812 | 0.41670 | 0.46265 | 0.45202 | 0.46266 | 0.42607 | 0.52408 | 0.38518 |
| Hunan | 0.30357 | 0.35212 | 0.41416 | 0.46642 | 0.44008 | 0.36344 | 0.33373 | 0.32297 | 0.41309 | 0.43116 |
| Jilin | 0.21688 | 0.20708 | 0.33937 | 0.31534 | 0.28849 | 0.32641 | 0.33753 | 0.35954 | 0.28429 | 0.29279 |
| Jiangsu | 1.13737 | 1.13136 | 1.14138 | 1.14082 | 1.12667 | 1.12099 | 1.12491 | 1.14315 | 1.14500 | 1.14391 |
| Jiangxi | 0.14086 | 0.22188 | 0.22155 | 0.19607 | 0.27219 | 0.27821 | 0.28518 | 0.34766 | 0.31238 | 0.34040 |
| Liaoning | 0.41519 | 0.41325 | 0.39410 | 0.46524 | 0.39442 | 0.38403 | 0.33095 | 0.37125 | 0.45221 | 0.39529 |
| Inner Mongolia | 1.15521 | 1.13760 | 1.15701 | 1.12512 | 1.10829 | 1.07201 | 1.09442 | 1.07569 | 1.05354 | 1.05008 |
| Ningxia | 0.35711 | 0.36481 | 0.40995 | 0.37360 | 0.37513 | 0.39356 | 0.47904 | 0.53400 | 0.59987 | 0.48821 |
| Qinghai | 1.19865 | 1.13802 | 1.09112 | 1.14088 | 1.08826 | 1.25363 | 1.25344 | 1.26791 | 1.25024 | 1.25716 |
| Shandong | 0.62511 | 0.63127 | 0.68528 | 1.00513 | 1.04159 | 1.02402 | 0.59804 | 0.56740 | 1.02131 | 0.59015 |
| Shanxi | 0.37812 | 0.56651 | 0.48840 | 0.46249 | 0.43481 | 0.53160 | 0.53172 | 0.61739 | 0.87944 | 0.46076 |
| Shaanxi | 0.40860 | 0.42325 | 0.44870 | 0.54025 | 0.49999 | 0.42122 | 0.44068 | 0.42509 | 0.56170 | 0.41161 |
| Shanghai | 1.04796 | 1.02221 | 1.02733 | 0.14460 | 0.28443 | 0.31210 | 0.38683 | 0.53303 | 1.31309 | 1.49219 |
| Sichuan | 0.35643 | 0.36518 | 0.35143 | 0.42335 | 0.53969 | 0.60788 | 0.45635 | 0.40569 | 0.46592 | 0.45013 |
| Tianjin | 1.39128 | 1.43114 | 1.28899 | 1.49944 | 1.40778 | 1.53590 | 1.63096 | 1.54385 | 1.58813 | 1.49361 |
| Xinjiang | 1.16806 | 1.19954 | 1.16011 | 1.11680 | 1.25797 | 1.12750 | 1.15471 | 1.12102 | 1.09167 | 1.05826 |
| Yunnan | 0.32455 | 0.38376 | 0.35339 | 0.43366 | 0.61815 | 0.35434 | 0.36945 | 0.36415 | 0.39503 | 0.34876 |
| Zhejiang | 0.26357 | 0.28923 | 0.31452 | 0.30254 | 0.43064 | 0.39598 | 0.41747 | 0.47615 | 0.32597 | 0.40997 |
| Chongqing | 0.57058 | 0.55912 | 0.48219 | 1.16080 | 1.14384 | 1.14496 | 1.06606 | 1.04143 | 1.03596 | 1.02411 |
References
- Panja, P. Deforestation, Carbon dioxide increase in the atmosphere and global warming: A modelling study. Int. J. Simul. Model. 2019, 27, 209–219. [Google Scholar] [CrossRef]
- Xu, G.; Dong, H.; Xu, Z. China can reach carbon neutrality before 2050 by improving economic development quality. Energy 2022, 243, 123087. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Ciais, P.; Peylin, P.; Huang, Y.; Sitch, S.; Wang, T. The carbon balance of terrestrial ecosystems in China. Nature 2009, 458, 1009–1013. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L. Research on the Connotation and Implementation Path of Innovation-Driven Development Strategy. Am. J. Ind. Bus. Manag. 2022, 12, 145–152. [Google Scholar] [CrossRef]
- Zhang, Y.; Kant, S.; Long, H. Collective Action Dilemma after China’s Forest Tenure Reform: Operationalizing Forest Devolution in a Rapidly Changing Society. Land 2020, 9, 58. [Google Scholar] [CrossRef] [Green Version]
- Wade, C.M.; Baker, J.S.; Latta, G.; Ohrel, S.B. Evaluating potential sources of aggregation bias with a structural optimization model of the U.S. forest sector. J. Forest Econ. 2019, 34, 337–366. [Google Scholar] [CrossRef]
- Magnus, K.; Anna, W. Using an optimization model to evaluate the economic benefits of industrial symbiosis in the forest industry. J. Clean. Prod. 2008, 16, 1536–1544. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Guo, H.R.; Li, S.Q. Analysis on green technology efficiency and influencing factor in mining enterprises. Inno. Min. Res. Dev. 2022, 42, 187–192. [Google Scholar] [CrossRef]
- Wang, H.G.; Yang, T.T. Research on green technology innovation efficiency and its influencing factors of biomass power generation enterprises: Test based on Bootstrap-DEA method. Sci. Tech. Manag. Res. 2021, 41, 191–198. [Google Scholar]
- Shen, N.; Zhou, J.J. A study on China’s green innovation efficiency evaluation and functional mechanism based on hybrid DEA and SEM model. J. Ind. Eng. Manag. 2018, 32, 46–53. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, L.J. Research on proactive technological innovation efficiency evaluation of industrial enterprises: Analysis based on improved three stage SBM-DEA model. J. Stat. Inf. 2020, 35, 50–61. [Google Scholar]
- Luo, L.W.; Liang, S.R. Green technology innovation efficiency and factor decomposition of China’s industrial enterprises. China Popul. Resour. Environ. 2016, 26, 149–157. [Google Scholar] [CrossRef]
- Huang, W.H.; Wang, M.D. Measurement of green technology innovation efficiency of manufacturing industry in Yangtze River Economic Belt. Stat. Decis. 2021, 37, 61–63. [Google Scholar] [CrossRef]
- He, Y.J.; Cai, D.Y.; Wang, S.T. Efficiency and influencing factors of industrial green technology innovation in Yangtze River Delta—In view of the government behavior. J. Jiangsu Univ. Sci. Tech. 2021, 21, 82–96. [Google Scholar] [CrossRef]
- Cheng, Q.W.; He, X.X.; Li, B.S. Green technology innovation efficiency and its influencing factors: Empirical study based on 35 industries in China. J. Cent.-South Univ. 2020, 26, 97–107. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.Q. Research on the cities’green technology innovation efficiency and its dynamic mechanism in the Yangtze River Economic Belt. J. Chongqing Univ. 2021, 27, 50–64. [Google Scholar] [CrossRef]
- Yao, C.; Liang, L. Super-efficiency DEA in the presence of infeasibility: One model approach. Eur. J. Oper. Res. 2011, 213, 359–360. [Google Scholar]
- Tone, K.A. Slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Qu, Y.; Zhao, W.; Guan, M.; Ping, Z. Evolution and Optimization of Territorial-Space Structure Based on Regional Function Orientation. Land 2022, 11, 505. Available online: https://www.mdpi.com/2073-445X/11/4/505/pdf (accessed on 15 June 2022). [CrossRef]
- Wang, Z.B.; Liang, L.W.; Wang, X.J. Spatio-temporal evolution patterns and influencing factors of PM2.5 in Chinese urban agglomerations. Acta Geogr. Sin. 2019, 74, 2614–2630. [Google Scholar]
- Nathaniel, B.; Skrede, G.K.; Kyle, B. Space Is More than Geography: Using Spatial Econometrics in the Study of Political Economy. Int. Stud. Q. 2006, 50, 27–44. [Google Scholar] [CrossRef]
- Kimberly, J.R.; Evanisko, M.J. Organizational innovation: The influence of individual, organizational, and contextual factors on hospital adoption of technological and administrative innovations. Acad. Manag. J. 1981, 24, 689–713. [Google Scholar] [CrossRef]
- Liu, T.; Li, J.X. Temporal-spatial differentiation of forestry green total factor productivity in china and its influencing factors. World For. Res. 2020, 33, 56–61. [Google Scholar]
- Nikolay, N.; Stanislava, K.; Iveta, H.; Mariana, S.; Petar, A.; Blanka, G. Economic efficiency of forest enterprises—empirical study based on data envelopment analysis. Forests 2021, 12, 462. [Google Scholar] [CrossRef]
- Broadberry, S.; Gupta, B. The early modern great divergence: Wages, prices and economic development in Europe and Asia. Econ. Hist. Rev. 2006, 59, 2–31. [Google Scholar] [CrossRef] [Green Version]
- Guellec, D.; Potterie, B. The impact of public R&D expenditure on business R&D. Econ. Innov. New Technol. 2003, 12, 225–243. [Google Scholar] [CrossRef]
- Clausen, T.H. Do subsidies have positive impacts on R&D and innovation activities at the firm level? Struct. Chang. Econ. Dyn. 2009, 20, 239–253. [Google Scholar] [CrossRef]
- Oosterhaven, J.; Broersma, L. Sector structure and cluster economies: A Regional labour productivity. Reg. Stud. 2007, 41, 631–659. [Google Scholar] [CrossRef]
- Meulenaere, K.D.; Winne, S.D.; Marescaux, E. The Role of Firm Size and Knowledge Intensity in the Performance Effects of Collective Turnover. J. Manag. 2021, 47, 993–1023. [Google Scholar] [CrossRef]
- Keller, W.; Levinson, A. Pollution abatement costs and foreign direct investment inflow to U.S. states. Rev. Econ. Stat. 2002, 84, 691–703. [Google Scholar] [CrossRef]
- Antweiler, C.B.; Taylor, M. Is free trade good for the environment? Am. Econ. Rev. 2001, 4, 877–908. [Google Scholar] [CrossRef] [Green Version]
- Roger, M.F.; Fragkiskos, F.; Carmen, S.; Soo, H.L. Does foreign direct investment promote institutional development in Africa? Int. Bus. Rev. 2021, 30, 101835. [Google Scholar] [CrossRef]
- Bai, X.; Chen, J.; Shi, P. Landscape Urbanization and Economic Growth in China: Positive Feedbacks and Sustainability Dilemmas. Environ. Sci. Technol. 2012, 46, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhu, Z.; Fan, Y. The impact of environmental regulation on the coordinated development of environment and economy in China. Nat. Hazard 2018, 91, 473–489. [Google Scholar] [CrossRef]
- Chen, X.Y.; Shao, S.; Tian, Z.H.; Xie, Z.; Yin, P. Impacts of air pollution and its spatial spillover effect on public health based on China’s big data sample. J. Clean. Prod. 2017, 142, 915–925. [Google Scholar] [CrossRef]
- Dong, Z.Q.; Wang, H. Local-neighborhood effect of green technology of environmental regulation. China Ind. Econ. 2019, 100–118. [Google Scholar] [CrossRef]

| Variable | Name | Meaning |
|---|---|---|
| Inputs | Forestry capital | The number of forestry innovation funds invested by the Chinese government. |
| Forestry labour | The number of forestry science and technology-related employees. | |
| Forestry resources | The proportion of provincial forest cover. | |
| Forestry energy consumption. | ||
| Outputs | Good outputs | The number of forestry-related patents. |
| New forested area in the province. | ||
| Rate of forest pest and rodent control. | ||
| Bad outputs | Sulphur dioxide emissions from the forestry industry by province. | |
| NOx emissions from forestry industry by province. | ||
| Soot emissions from forestry industry by province. |
| Name | Meaning |
|---|---|
| SS | The average annual wage of unit workers in the forestry system in each province. |
| HC | The number of forestry station workers in each province with an education level of short-cycle courses or above. |
| GS | Total state investment in forestry. |
| IS | The ratio of tertiary provincial forestry sector output to GDP. |
| FS | The ratio of forestry employees to the total number of employees. |
| EDL | Provincial GDP. |
| FDI | The amount of actual foreign direct investment in each province. |
| UL | The ratio of year-end urban population to year-end total population. |
| EPS | The ratio of the amount of national investment in controlling environmental pollution to GDP. |
| Name | Mean | Std. | Maximum | Minimum |
|---|---|---|---|---|
| FGTIE | 0.646 | 0.382 | 0.115 | 1.720 |
| SS | 57,000 | 32,000 | 14,000 | 210,000 |
| HC | 2404.317 | 1377.170 | 11.000 | 7249 |
| GS | 1,400,000 | 1,600,000 | 53,000 | 11,000,000 |
| IS | 0.157 | 0.109 | 0.001 | 0.613 |
| FS | 0.002 | 0.003 | 0.000 | 0.017 |
| EDL | 26,000 | 21,000 | 1670.440 | 110,000 |
| FDI | 5,300,000 | 5,200,000 | 813.873 | 23,000,000 |
| UL | 58.184 | 12.062 | 34.9600 | 89.600 |
| EPS | 1.410 | 0.785 | 0.299 | 4.466 |
| Year | Moran’ I | z-Value | p-Value | Year | Moran’ I | z-Value | p-Value |
|---|---|---|---|---|---|---|---|
| 2011 | 0.045 | 2.284 | 0.011 | 2016 | 0.029 | 1.778 | 0.038 |
| 2012 | 0.020 | 1.556 | 0.060 | 2017 | 0.082 | 3.379 | 0.000 |
| 2013 | 0.036 | 2.004 | 0.023 | 2018 | 0.096 | 3.730 | 0.000 |
| 2014 | 0.071 | 2.994 | 0.001 | 2019 | 0.124 | 4.511 | 0.000 |
| 2015 | 0.032 | 1.871 | 0.031 | 2020 | 0.080 | 3.271 | 0.001 |
| Variables | Value | p-Value |
|---|---|---|
| LM_Spatial lag | 189.583 | 0.0000 |
| Robust LM_Spatial lag | 14.795 | 0.0000 |
| LM_Spatial error | 211.880 | 0.0000 |
| Robust LM_Spatial error | 37.093 | 0.0000 |
| LR_Spatial lag | 25.950 | 0.0021 |
| Wald_Spatial lag | 36.500 | 0.0000 |
| LR_Spatial error | 23.910 | 0.0044 |
| Wald_Spatial error | 34.710 | 0.0001 |
| Hausman | 67.190 | 0.0000 |
| Direct Effect | Indirect Effect | Total Effect | ||||
|---|---|---|---|---|---|---|
| Coef. | t-Value | Coef. | t-Value | Coef. | t-Value | |
| SS | 0.000 *** | 3.03 | 0.000 *** | 2.74 | 0.000 *** | 3.14 |
| HC | 0.000 | −0.24 | 0.000 | 0.13 | 0.000 | 0.10 |
| GS | −0.000 * | −1.91 | 0.000 | 0.68 | 0.000 | 0.35 |
| IS | −0.294 * | −1.66 | 0.548 | 0.47 | 0.255 | 0.21 |
| FS | 11.200 | 1.36 | −142.765 *** | −3.20 | −131.569 *** | −3.08 |
| EDL | −0.000 *** | −4.32 | −0.000 *** | −3.63 | −0.000 *** | −3.94 |
| FDI | 0.000 *** | 5.07 | 0.000 * | 1.76 | 0.000 ** | 2.38 |
| UL | 0.006 *** | 2.98 | 0.002 | 0.15 | 0.008 | 0.72 |
| EPS | 0.102 *** | 4.18 | 0.540 *** | 3.71 | 0.641 *** | 4.34 |
| Direct Effect | Indirect Effect | Total Effect | ||||
|---|---|---|---|---|---|---|
| Coef. | t-Value | Coef. | t-Value | Coef. | t-Value | |
| Robustness test 1 | ||||||
| SS | 0.000 ** | 2.39 | 0.000 * | 1.67 | 0.000 ** | 2.44 |
| HC | 0.000 | −0.81 | 0.000 | −1.01 | 0.000 | −1.06 |
| GS | 0.000 | −1.60 | 0.000 | 1.26 | 0.000 | 0.71 |
| IS | −0.349 * | −1.84 | 0.631 | 1.14 | 0.282 | 0.46 |
| FS | 21.481 ** | 2.58 | −71.660 *** | −3.06 | −50.179 ** | −2.29 |
| EDL | −0.000 *** | −3.56 | −0.000 *** | −3.88 | −0.000 *** | −4.27 |
| FDI | 0.000 *** | 4.66 | 0.000 ** | 2.06 | 0.000 *** | 2.93 |
| UL | 0.005 ** | 2.37 | −0.008 | −1.23 | −0.003 | −0.45 |
| EPS | 0.114 *** | 4.81 | 0.321 *** | 3.63 | 0.434 *** | 4.64 |
| Robustness test 2 | ||||||
| SS | 0.000 *** | 2.85 | 0.000 ** | 2.32 | 0.000 *** | 2.74 |
| HC | 0.000 | −0.43 | 0.000 | −0.26 | 0.000 | −0.29 |
| GS | −0.000 * | −1.67 | 0.000 | 0.84 | 0.000 | 0.54 |
| IS | −0.285 | −1.58 | 0.452 | 0.38 | 0.167 | 0.14 |
| FS | 12.830 | 1.54 | −142.234 *** | −3.18 | −129.401 *** | −3.02 |
| EDL | −0.000 *** | −4.10 | −0.000 *** | −3.59 | −0.000 *** | −3.87 |
| FDI | 0.000 *** | 4.91 | 0.000 * | 1.92 | 0.000 ** | 2.48 |
| UL | 0.006 *** | 2.70 | −0.003 | −0.30 | 0.002 | 0.18 |
| EPS | 0.107 *** | 4.37 | 0.548 *** | 3.61 | 0.655 *** | 4.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, H.; Yang, C. Towards Carbon Neutrality: The Innovation Efficiency of China’s Forestry Green Technology and Its Spatial Spillover Effects. Land 2022, 11, 1081. https://doi.org/10.3390/land11071081
Shang H, Yang C. Towards Carbon Neutrality: The Innovation Efficiency of China’s Forestry Green Technology and Its Spatial Spillover Effects. Land. 2022; 11(7):1081. https://doi.org/10.3390/land11071081
Chicago/Turabian StyleShang, Hangbiao, and Chuwei Yang. 2022. "Towards Carbon Neutrality: The Innovation Efficiency of China’s Forestry Green Technology and Its Spatial Spillover Effects" Land 11, no. 7: 1081. https://doi.org/10.3390/land11071081





