A Research on Cohesion Hyperspectral Detection Model of Fine-Grained Sediments in Beichuan Debris Flow, Sichuan Province, China
Abstract
:1. Introduction
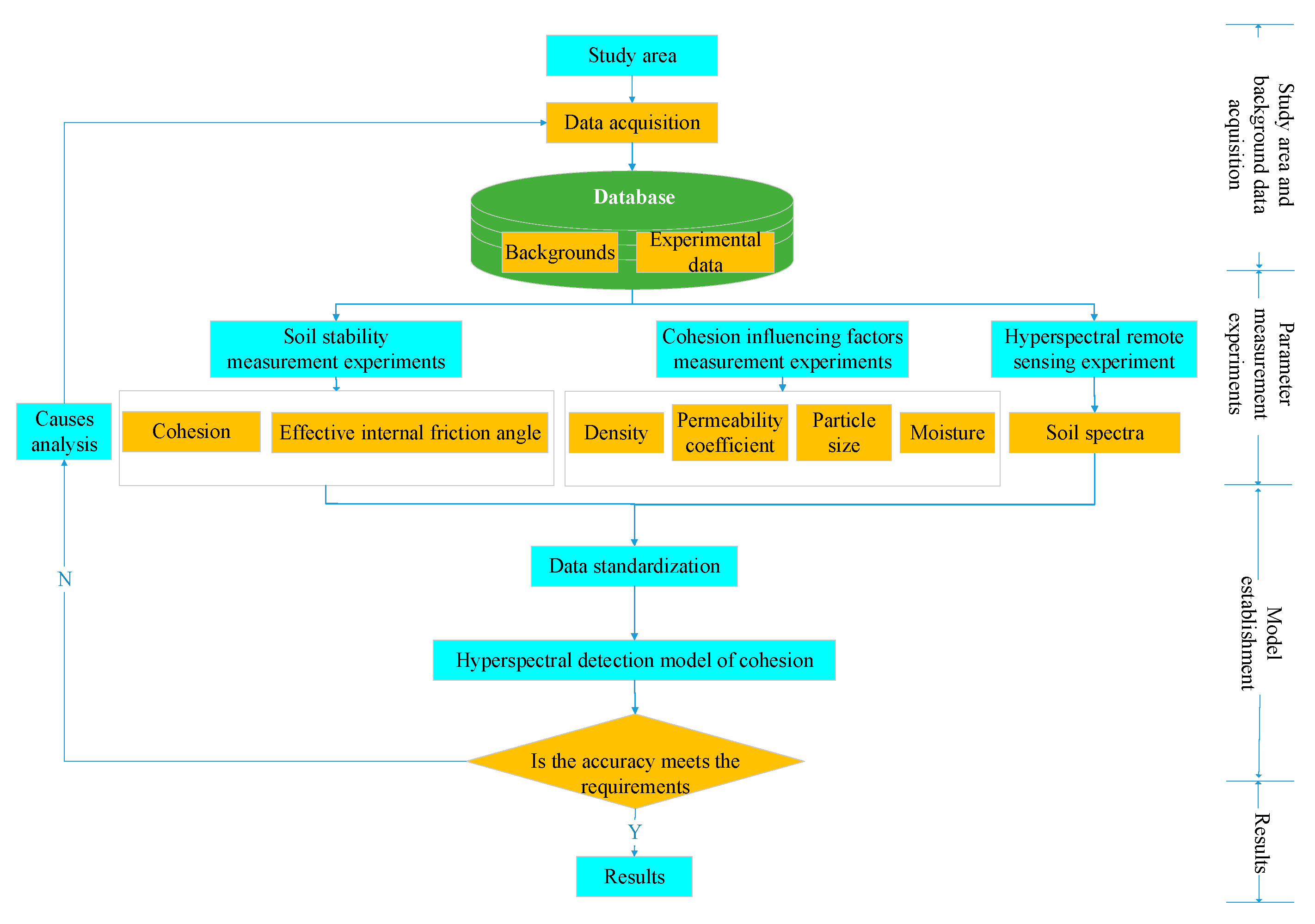
2. Materials and Methods
2.1. Study Area
2.2. Methods
2.3. Data Acquisition and Processing
3. Results and Analysis
3.1. Cohesion Influencing Factors
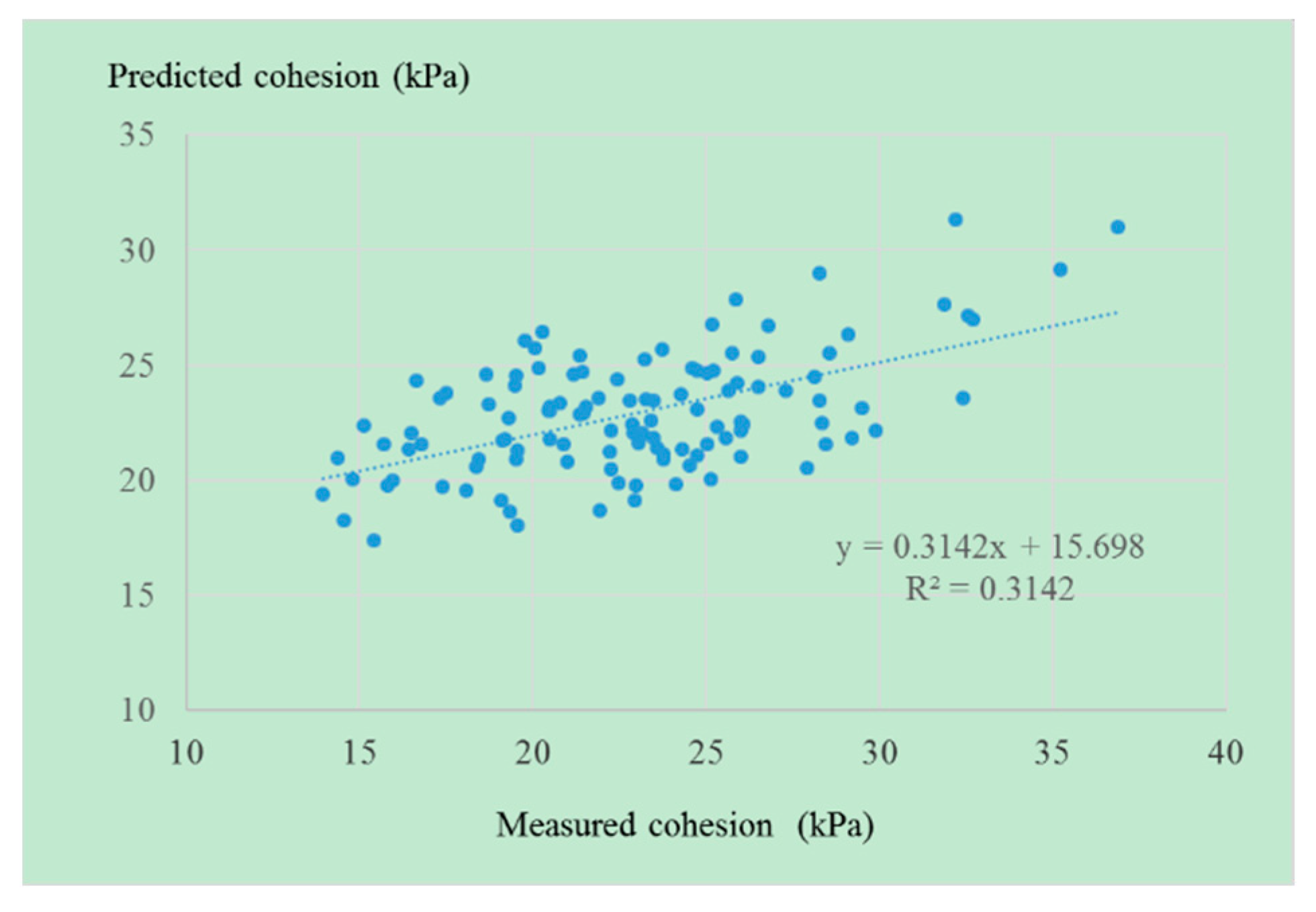
3.2. Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, P.; Wei, Y.; Wang, Q.; Xie, J.; Chen, Y.; Li, Z.; Zhou, H. A research on landslides automatic extraction model based on the improved Mask R-CNN. ISPRS Int. J. Geo-Inf. 2021, 10, 168. [Google Scholar] [CrossRef]
- Xiao, J. The Emergency Management Department of China Announced the National Top Ten Disasters in 2019 [ER/OL]. 2020. Available online: https://society.people.com.cn/n1/2020/0112/c1008-31544517.html (accessed on 2 January 2022).
- Tang, C.; Liang, J. Study on characteristics of 9.24 rainstorm and debris flow in Beichuan, Wenchuan earthquake area. J. Eng. Geol. 2008, 16, 751–758. [Google Scholar]
- Wu, Q.; Xu, L.; Zhou, K.; Liu, Z. Starting analysis of loose sediments of gully debris flow. J. Nat. Disasters 2015, 24, 89–97. [Google Scholar]
- Miao, Q.; Yang, D.; Yang, H.; Li, Z. Establishing a rainfall threshold for flash flood warnings in China’s mountainous areas based on a distributed hydrological model. J. Hydrol. 2016, 541, 371–386. [Google Scholar] [CrossRef]
- Xie, J.; Wang, M.; Liu, K.; Coulthard, T.J. Modeling sediment movement and channel response to rainfall variability after a major earthquake. Geomorphology 2018, 320, 18–32. [Google Scholar] [CrossRef]
- Ma, M. Stability analysis of high slope of accumulation at the outlet of pressure flood discharge and sediment discharge tunnel of Jiudianxia Water Control Project. Water Conserv. Plan. Des. 2019, 4, 64–67. [Google Scholar]
- Tang, M.; Xu, Q.; Li, J.; Luo, J.; Kuang, Y. An experimental study of the failure mechanism of shallow landslides after earthquake triggered by rainfall. Hydrogeol. Eng. Geol. 2016, 43, 128–135. [Google Scholar]
- Hürlimann, M.; Coviello, V.; Bel, C.; Guo, X.; Berti, M.; Graf, C.; Hübl, J.; Miyata, S.; Smith, J.B.; Yin, H. Debris-flow monitoring and warning: Review and examples. Earth-Sci. Rev. 2019, 199, 102981. [Google Scholar] [CrossRef]
- Langat, P.K.; Kumar, L.; Koech, R. Monitoring river channel dynamics using remote sensing and GIS techniques. Geomorphology 2019, 325, 92–102. [Google Scholar] [CrossRef]
- AfiqHarun, M.; Aminuddin, A.; Mohammadpour, G.; WengChan, N. Stable channel analysis with sediment transport for rivers in Malaysia: A case study of the Muda, Kurau, and Langat rivers. Int. J. Sediment Res. 2020, 35, 455–466. [Google Scholar] [CrossRef]
- Wang, Q.; Wei, Y.; Chen, Y.; Lin, Q. Hyperspectral soil dispersion model for the source region of the Zhouqu debris flow, Gansu, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 876–883. [Google Scholar] [CrossRef]
- Hu, W.; Scaringi, G.; Xu, Q.; Pei, Z.; van Asch, T.W.J.; Hicher, P. Sensitivity of the initiation and runout of flow slides in loose granular sediments to the content of small particles-An insight from flume tests. Eng. Geol. 2017, 231, 34–44. [Google Scholar] [CrossRef]
- Fan, R.L.; Zhang, L.M.; Wang, H.J.; Fan, X.M. Evolution of debris flow activities in Gaojiagou Ravine during 2008-2016 after the Wenchuan earthquake. Eng. Geol. 2018, 235, 1–10. [Google Scholar] [CrossRef]
- Khezri, N.; Mohamad, H.; HajiHassani, M.; Fatahi, B. The stability of shallow circular tunnels in soil considering variations in cohesion with depth. Tunn. Undergr. Space Technol. 2015, 49, 230–240. [Google Scholar] [CrossRef]
- Sun, J.; Hong, B.; Li, J. Sensitivity analysis on stability of embankment slope based on cohesion and friction angle. J. Resour. Archit. Eng. 2013, 11, 99–104. [Google Scholar]
- Zhang, K.; Li, M.; Yang, B. Research on effect of water content and dry density on shear strength of remolded loess. J. Anhui Univ. Sci. Technol. (Nat. Sci.) 2016, 36, 74–79. [Google Scholar]
- Zhou, C.; Cheng, Y.; Wang, Y.; Wang, Q.; Fu, M. Study on influencing factors of shear strength parameters of compacted loess. J. Disaster Prev. Mitig. Eng. 2018, 38, 258–264. [Google Scholar]
- Yan, M. The Effect of Water Content on Apparent Cohesion of Sand and Its Engineering Application. Master’s Thesis, Chang’an University, Xi’an, China, 2018. [Google Scholar]
- Tian, W.; Tong, F.; Liu, C.; Zhao, Y. Shear strength model of red soil considering influence of saturation and its application. Water Resour. Power 2018, 36, 124–127. [Google Scholar]
- Song, Y.; Xu, X.; Yang, S.; Gao, M. Influence of water content on shear strength of granite residual soil in Huangdao area. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2019, 38, 33–40. [Google Scholar]
- Dong, S.; Wang, H.; Li, J.; Ma, F.; Bai, X. Effects of water content and compaction degree on mechanical characteristics of compacted silty soil. J. Guangxi Univ. (Nat. Sci. Ed.) 2020, 45, 978–985. [Google Scholar]
- Wang, C.; Sun, Z.; Bian, H.; Lu, X.; Qiu, X. Significance analysis of factors affecting the cohesion of silty clay. J. Shandong Agric. Univ. (Nat. Sci. Ed.) 2020, 51, 646–650. [Google Scholar]
- Tang, C.; Borden, R.H.; Gabr, M.A. Model applicability for prediction of residual soil apparent cohesion. Transp. Geotech. 2019, 19, 44–53. [Google Scholar] [CrossRef]
- Kim, Y.; Satyanaga, A.; Rahardjo, H.; Park, H.; Sham, A.W.L. Estimation of effective cohesion using artificial neural networks based on index soil properties: A Singapore case. Eng. Geol. 2021, 289, 106163. [Google Scholar] [CrossRef]
- Saygin, S.D.; Arı, F.; Temiz, Ç.; Arslan, S.; Ünal, M.A.; Erpul, G. Analysis of soil cohesion by fluidized bed methodology using integrable differential pressure sensors for a wide range of soil textures. Comput. Electron. Agric. 2021, 191, 106525. [Google Scholar] [CrossRef]
- DZ/T 02161-2014; Geological and Mineral Industry Standard of the People’s Republic of China: Code for Investigation of Landslide, Collapse and Debris Flow Disasters 1:50,000. China Standards Press: Beijing, China, 2015.
- GB/T 36197-2018; National Standard of the People’s Republic of China: Technical Guide for Soil Sampling of Soil Quality. China National Standardization Administration Committee: Beijing, China, 2018.
- SL237-1999; National Standard of the People’s Republic of China: Geotechnical Test Code. China Water Resources and Hydropower Press: Beijing, China, 1999.
- Wang, Q.; Xie, J.; Yang, J.; Liu, P.; Chang, D.; Xu, W. Research on permeability coefficient of fine sediments in debris-flow gullies, southwestern China. Soil Syst. 2022, 6, 29. [Google Scholar] [CrossRef]
- GB/T 30319-2013; National Standard of the People’s Republic of China: Basic Provisions for Basic Geographic Information Database. China National Standardization Administration Committee: Beijing, China, 2013.
- Sun, X.; Wang, D. Analysis of cohesion value of soil. Liaoning Build. Mater. 2010, 3, 39–42. [Google Scholar]
- Chen, T.; Wang, Y.; Pu, X. The application of Fourier transform in the noise smoothing of weak Raman spectrum. J. Yunnan Univ. 2005, 27, 509–513. [Google Scholar]
- Wu, B.; Wang, X.; Zhang, L. Iterative abstraction of endmember based on total least square for mixture pixel decomposition. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 457–461. [Google Scholar]
- Liu, Y. Study on test method of permeability coefficient of cohesion less coarse-grained soil in hydraulic engineering. Shanxi Water Conserv. 2020, 12, 211–213. [Google Scholar]




| Cohesion | Effective Internal Friction Angle | Permeability Coefficient | Density | Moisture | Particle Size | |
|---|---|---|---|---|---|---|
| Cohesion | 1 | −0.664 ** | −0.557 ** | 0.356 ** | 0.316 ** | 0.076 |
| Effective Internal Friction Angle | −0.664 ** | 1 | 0.323 ** | −0.08 | −0.127 | −0.053 |
| Permeability Coefficient | −0.557 ** | 0.323 ** | 1 | −0.459 ** | −0.428 ** | 0.002 |
| Density | 0.356 ** | −0.08 | −0.459 ** | 1 | 0.796 ** | 0.131 |
| Moisture | 0.316 ** | −0.127 | −0.428 ** | 0.796 ** | 1 | 0.068 |
| Particle Size | 0.076 | −0.053 | 0.002 | 0.131 | 0.068 | 1 |
| Coefficient | Standard Error | p-Value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|
| Intercept | 22.7045 | 0.3616 | 0.0000 | 21.9880 | 23.4210 |
| 750 nm | 10.3582 | 2.0827 | 0.0000 | 6.2312 | 14.4853 |
| 1578 nm | −37.3150 | 11.0193 | 0.0010 | −59.1506 | −15.4795 |
| 1835 nm | 42.5733 | 11.6960 | 0.0004 | 19.3968 | 65.7498 |
| 2301 nm | −30.3357 | 8.4139 | 0.0005 | −47.0085 | −13.6629 |
| 2305 nm | 56.1503 | 11.5549 | 0.0000 | 33.2535 | 79.0471 |
| 2309 nm | −40.4223 | 8.2513 | 0.0000 | −56.7728 | −24.0719 |
| Cohesion | Effective Internal Friction Angle | Permeability Coefficient | Density | Moisture | Particle Size | 750 nm | 1578 nm | 1835 nm | 2301 nm | 2305 nm | 2309 nm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cohesion | 1 | −0.664 ** | −0.557 ** | 0.356 ** | 0.316 ** | 0.076 | 0.222 * | 0.162 | 0.154 | 0.145 | 0.155 | 0.142 |
| Effective Internal Friction Angle | −0.664 ** | 1 | 0.323 ** | −0.08 | −0.127 | −0.053 | −0.348 ** | −0.318 ** | −0.314 ** | −0.311 ** | −0.319 ** | −0.307 ** |
| Permeability Coefficient | −0.557 ** | 0.323 ** | 1 | −0.459 ** | −0.428 ** | 0.002 | −0.217 * | −0.162 | −0.152 | −0.152 | −0.157 | −0.145 |
| Density | 0.356 ** | −0.08 | −0.459 ** | 1 | 0.796 ** | 0.131 | −0.152 | −0.286 ** | −0.307 ** | −0.302 ** | −0.300 ** | −0.302 ** |
| Moisture | 0.316 ** | −0.127 | −0.428 ** | 0.796 ** | 1 | 0.068 | −0.159 | −0.293 ** | −0.311 ** | −0.305 ** | −0.303 ** | −0.306 ** |
| Particle Size | 0.076 | −0.053 | 0.002 | 0.131 | 0.068 | 1 | −0.078 | −0.091 | −0.089 | −0.092 | −0.093 | −0.090 |
| 750 nm | 0.222 * | −0.348 ** | −0.217 * | −0.152 | −0.159 | −0.078 | 1 | 0.965 ** | 0.954 ** | 0.957 ** | 0.959 ** | 0.958 ** |
| 1578 nm | 0.162 | −0.318 ** | −0.162 | −0.286 ** | −0.293 ** | −0.091 | 0.965 ** | 1 | 0.998 ** | 0.995 ** | 0.996 ** | 0.994 ** |
| 1835 nm | 0.154 | −0.314 ** | −0.152 | −0.307** | −0.311 ** | −0.089 | 0.954 ** | 0.998 ** | 1 | 0.996 ** | 0.996 ** | 0.996 ** |
| 2301 nm | 0.145 | −0.311 ** | −0.152 | −0.302 ** | −0.305 ** | −0.092 | 0.957 ** | 0.995 ** | 0.996 ** | 1 | 0.999 ** | 0.998 ** |
| 2305 nm | 0.155 | −0.319 ** | −0.157 | −0.300 ** | −0.303 ** | −0.093 | 0.959 ** | 0.996 ** | 0.996 ** | 0.999 ** | 1 | 0.999 ** |
| 2309 nm | 0.142 | −0.307 ** | −0.145 | −0.302 ** | −0.306 ** | −0.090 | 0.958 ** | 0.994 ** | 0.996 ** | 0.998 ** | 0.999 ** | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Xie, J.; Yang, J.; Liu, P.; Chang, D.; Xu, W. A Research on Cohesion Hyperspectral Detection Model of Fine-Grained Sediments in Beichuan Debris Flow, Sichuan Province, China. Land 2022, 11, 1609. https://doi.org/10.3390/land11091609
Wang Q, Xie J, Yang J, Liu P, Chang D, Xu W. A Research on Cohesion Hyperspectral Detection Model of Fine-Grained Sediments in Beichuan Debris Flow, Sichuan Province, China. Land. 2022; 11(9):1609. https://doi.org/10.3390/land11091609
Chicago/Turabian StyleWang, Qinjun, Jingjing Xie, Jingyi Yang, Peng Liu, Dingkun Chang, and Wentao Xu. 2022. "A Research on Cohesion Hyperspectral Detection Model of Fine-Grained Sediments in Beichuan Debris Flow, Sichuan Province, China" Land 11, no. 9: 1609. https://doi.org/10.3390/land11091609
APA StyleWang, Q., Xie, J., Yang, J., Liu, P., Chang, D., & Xu, W. (2022). A Research on Cohesion Hyperspectral Detection Model of Fine-Grained Sediments in Beichuan Debris Flow, Sichuan Province, China. Land, 11(9), 1609. https://doi.org/10.3390/land11091609







