Analysis of China’s Embodied Ecological Footprint and Its Flows among Economic Sectors per Unit of Currency Production
Abstract
1. Introduction
- (1)
- This study builds an embodied EF accounting framework with an EE-IO model, which can clarify the relationship between production-based and consumption-based EF. Further tracking the content of the embodied EF in the final product provides a basis for dividing ecological and environmental protection responsibilities from the perspective of consumption, comparing ecological impact from the perspective of EF production flow and consumption flow.
- (2)
- This study provides a new perspective for subsequent research on various types of hidden pollution problems, especially the hidden pollution transfer paths among economic sectors. In this study, it is possible to track the flow of footprints among sectors (industries) and provide a basis for locating the source of embodied EFs. In addition, it provides a reference for optimizing efficient ecological production.
- (3)
- The analysis of the key footprint transfer paths among sectors (industries) helps locate the source of important EFs and provides a reference for ecological compensation among the sectors. This content provides a reference for implementing better policy strategies, optimizing or restraining key EF transfer paths, and promoting eco-green development among industries. This study provides a reference for the industrial green development of China.
2. Data and Method
2.1. Data Source
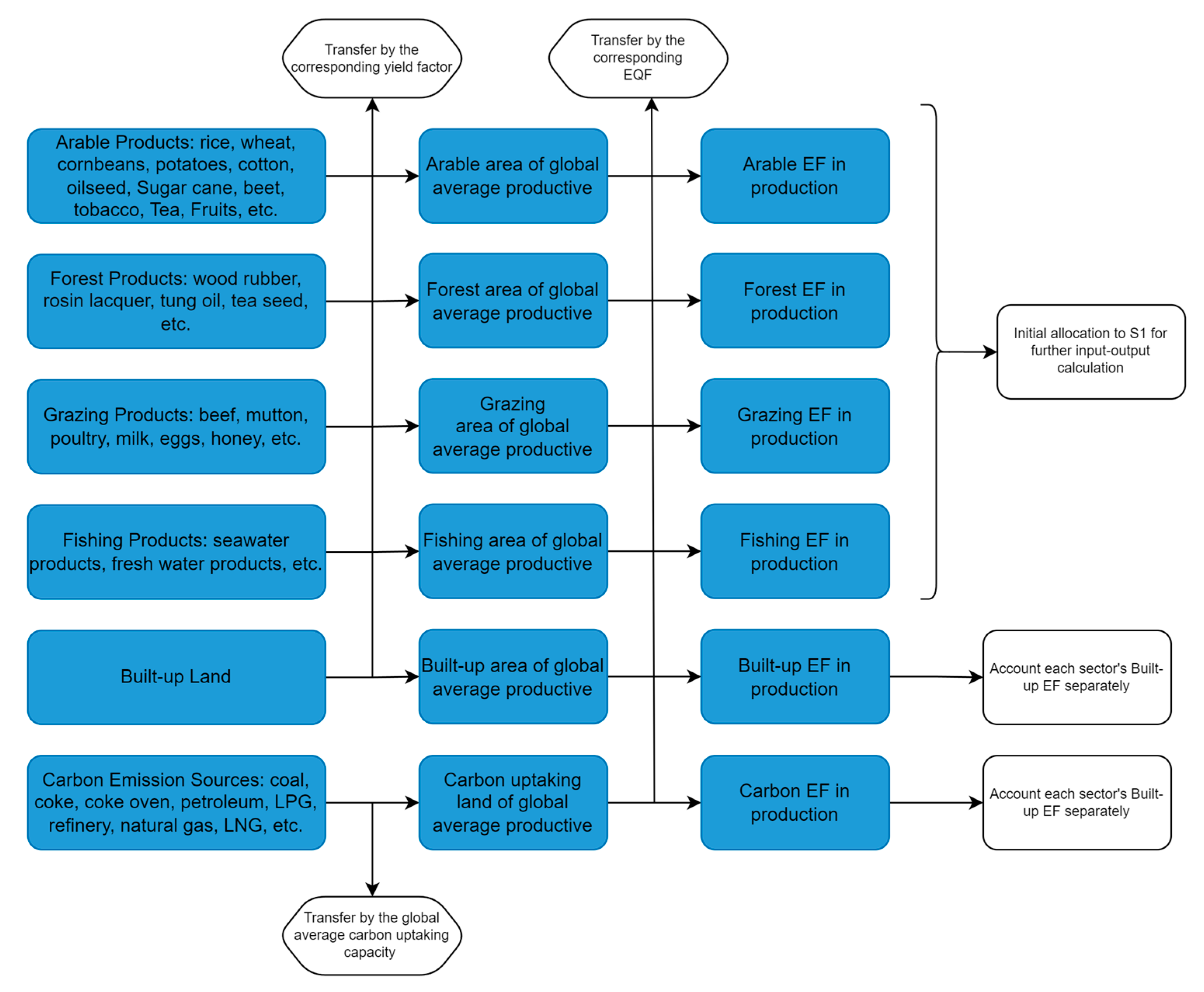
2.2. Ecological Footprint Accounting and Its Production Intensity
2.3. Ecological Footprint Extended Input–Output Tables
2.4. Total EFPI Flows between Any Two Sectors
2.5. Decomposition of Sector EFPI
3. Results and Analysis
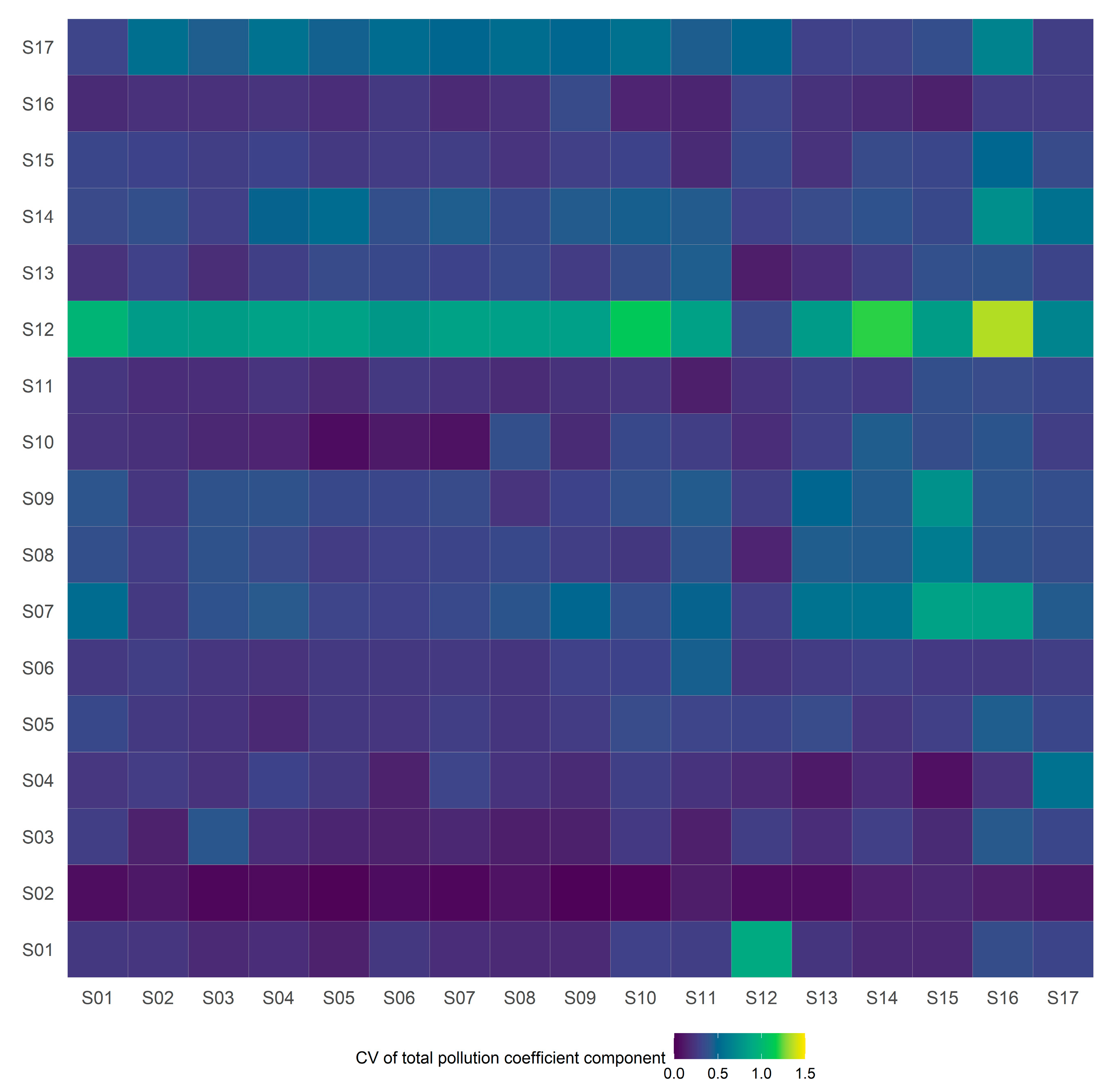
3.1. Analysis of the Total Pollution Coefficient Component
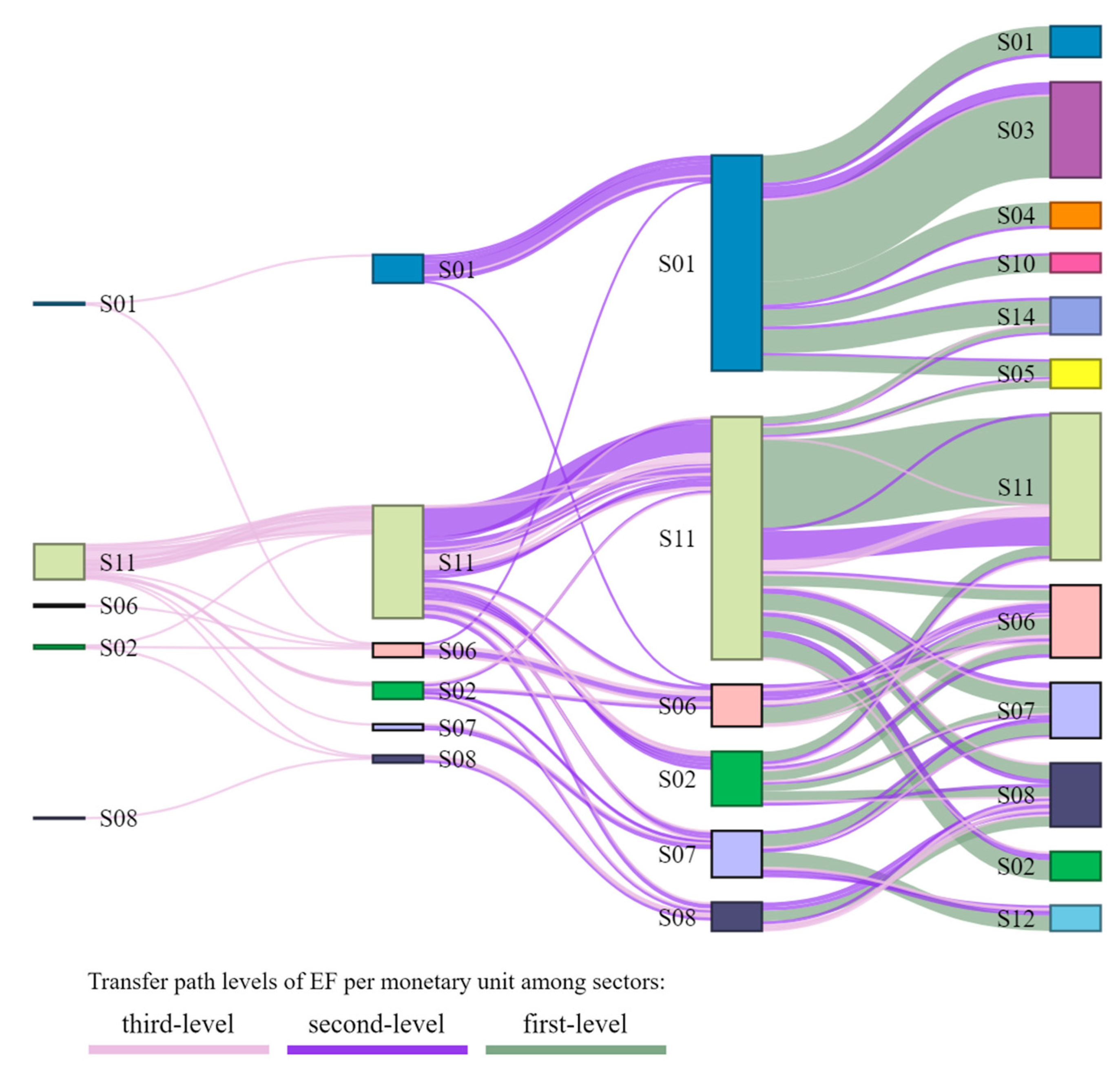
3.2. Analysis of the Net Embodied EFPI Component Transfer among Sectors
3.3. Analysis of the Change in EFPI Component Transfer Paths
4. Discussion
4.1. GFN EF and IOA Accounting EF
4.2. EF, Production, and Consumption
4.3. Three Aspects of Embodied EF
5. Conclusions and Policy Implications
5.1. Conclusions
- (1)
- Decomposition of the TPC and DPC with IOA could be used to track the embodied EF flows and transfer path. The decomposition model and procedures of the IOA may also be applied to track other types of environmental pollution, e.g., water footprint, carbon emissions, land use, and PM2.5.
- (2)
- China’s 2005, 2010, and 2015 TPCCs showed a downward trend overall due to the faster economic speed. The main embodied transfer flows of EFPI were S1→S12, S7→S15, and S7→S16. High TPCC values from the supply side involved S1, S2, S6, and S11. S12 varied greatly, illustrating the case of a larger EFPI input. The transfer links in the chord diagrams showed that the overall inflow-outflow structures of net embodied TPCC remained almost unchanged, with main export sectors being S1, S11; main import sectors, S3–S5, S9, S10, S12, and S14–S17; and sectors with partial imports and exports of net embodied EFPI being S2, S6–S8, and S13.
- (3)
- The transfer EFPIs of critical transfer paths showed a downward trend in the study years. There was a large number of self-transferred EFPIs, and their value was relatively high, concentrated in sectors S6, S8, S11, and S1. The receiving end sectors became increasingly concentrated, while the input sectors experienced little change. These critical transfer paths highlighted the EF key governance and ecological compensation path.
- (4)
- Based on the result analysis and discussion, policy implications, including reducing the EFPI on both the supply and demand sides, optimizing ecological tax, and implementing ecological compensation among economic sectors, were ultimately recommended.
5.2. Policy Implications
5.3. Limitations of the Study
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Sector ID | Sector Name | Sub Sector ID of | Sector Name |
|---|---|---|---|
| S1 | Agriculture | SS1 | Agriculture, forestry, animal husbandry, and fishery |
| S2 | Mining products | SS2 | Mining and washing of coal |
| SS3 | Extraction of petroleum and natural Gas | ||
| SS4 | Mining and processing of metal ores | ||
| SS5 | Mining and processing of nonmetal and other ores | ||
| S3 | Food and tobacco | SS6 | Foods and tobacco |
| S4 | Textiles, clothing, shoes, and leather-down products | SS7 | Textile |
| SS8 | Textile and apparel shoes and hats leather down and its products | ||
| S5 | Woodworking, furniture, paper, and crafts supplies | SS9 | Wood products and furniture |
| SS10 | Papermaking, printing, cultural, educational, and sporting goods | ||
| S6 | Refining, coking, and chemical products | SS11 | Petroleum, coking products, and nuclear fuel processed products |
| SS12 | chemical product | ||
| S7 | Non-metallic mineral products | SS13 | Non-metallic mineral products |
| S8 | Metal industries | SS14 | Metal smelting and rolling products |
| SS15 | made from metal | ||
| S9 | Equipment of Machinery, transportation, and electronics | SS16 | General equipment Special equipment |
| SS17 | Transportation equipment | ||
| SS18 | Electrical machinery and equipment | ||
| SS19 | Communication equipment, computers, and other electronic equipment | ||
| SS20 | Instrumentation, | ||
| S10 | Other various manufacturing products | SS21 | Repair services for other manufactured products, scrap, metal products, machinery, and equipment |
| S11 | Electricity, heat, gas, and water | SS22 | Production and supply of electricity and heat |
| SS23 | Gas production and supply | ||
| SS24 | Water production and supply | ||
| S12 | Construction industry | SS25 | building |
| S13 | Wholesale, retail, transportation, warehousing, and post | SS26 | Wholesale and retail |
| SS27 | Transportation, storage, and post | ||
| SS28 | Accommodation and dining | ||
| S14 | Information industry | SS29 | Information transmission, software, and information technology services |
| S15 | Finance and real estate | SS30 | financial |
| SS31 | real estate | ||
| SS32 | Rental and business services | ||
| S16 | Scientific research and technical services | SS33 | Scientific research and technical services |
| S17 | Other public services | SS34 | Water conservancy, environment, and public facilities management |
| SS35 | Resident services, repairs, and other services | ||
| SS36 | education | ||
| SS37 | Health and social work | ||
| SS38 | Culture, sports, and entertainment | ||
| SS39 | Public management, social security, and social organization |
| 2005 | 2010 | 2015 | ||||||
|---|---|---|---|---|---|---|---|---|
| Input Sector | Output Sector | Value (gha) | Input Sector | Output Sector | Value (gha) | Input Sector | Output Sector | Value (gha) |
| S1 | S3 | 1.45 | S1 | S3 | 1.01 | S1 | S3 | 0.72 |
| S1 | S14 | 0.86 | S1 | S14 | 0.60 | S1 | S4 | 0.39 |
| S1 | S4 | 0.73 | S1 | S4 | 0.49 | S11 | S8 | 0.37 |
| S11 | S7 | 0.71 | S11 | S7 | 0.45 | S11 | S7 | 0.30 |
| S11 | S8 | 0.63 | S11 | S8 | 0.44 | S11 | S10 | 0.24 |
| S11 | S6 | 0.51 | S11 | S6 | 0.32 | S1 | S5 | 0.24 |
| S11 | S9 | 0.49 | S11 | S9 | 0.32 | S11 | S12 | 0.22 |
| S11 | S12 | 0.46 | S1 | S5 | 0.31 | S11 | S6 | 0.22 |
| S11 | S5 | 0.45 | S11 | S5 | 0.31 | S11 | S9 | 0.20 |
| S1 | S10 | 0.43 | S11 | S12 | 0.29 | S11 | S5 | 0.19 |
| S1 | S5 | 0.42 | S1 | S10 | 0.27 | S11 | S2 | 0.16 |
| S11 | S2 | 0.42 | S11 | S2 | 0.23 | S1 | S10 | 0.15 |
| S1 | S12 | 0.42 | S11 | S4 | 0.23 | S6 | S10 | 0.13 |
| S11 | S4 | 0.36 | S11 | S10 | 0.19 | S11 | S4 | 0.13 |
| S11 | S16 | 0.34 | S11 | S14 | 0.18 | S6 | S5 | 0.13 |
| S11 | S17 | 0.32 | S11 | S16 | 0.17 | S6 | S7 | 0.12 |
| S11 | S14 | 0.32 | S11 | S17 | 0.17 | S11 | S16 | 0.12 |
| S11 | S10 | 0.31 | S7 | S12 | 0.16 | S2 | S7 | 0.10 |
| S7 | S12 | 0.27 | S6 | S5 | 0.16 | S2 | S8 | 0.10 |
| S6 | S5 | 0.24 | S11 | S3 | 0.16 | S6 | S12 | 0.10 |
| S11 | S3 | 0.24 | S2 | S8 | 0.14 | S1 | S6 | 0.10 |
| S11 | S13 | 0.22 | S6 | S4 | 0.14 | S6 | S4 | 0.10 |
| S11 | S15 | 0.22 | S2 | S7 | 0.13 | S6 | S9 | 0.10 |
| S6 | S4 | 0.21 | S6 | S7 | 0.13 | S8 | S9 | 0.09 |
| S6 | S9 | 0.20 | S11 | S13 | 0.13 | S1 | S13 | 0.09 |
| S8 | S9 | 0.20 | S6 | S9 | 0.13 | S7 | S12 | 0.09 |
| S1 | S16 | 0.19 | S8 | S9 | 0.13 | S11 | S17 | 0.09 |
| S6 | S7 | 0.19 | S6 | S12 | 0.11 | S1 | S12 | 0.09 |
| S1 | S17 | 0.18 | S6 | S17 | 0.11 | S6 | S16 | 0.09 |
| S6 | S17 | 0.18 | S1 | S16 | 0.11 | S1 | S7 | 0.09 |
| 2005 | 2010 | 2015 | |||
|---|---|---|---|---|---|
| Tax-Paying Sectors | Benefit Sectors | Tax-Paying Sectors | Benefit Sectors | Tax-Paying Sectors | Benefit Sectors |
| S3 (14.06%), S4 (10.99%), S5 (9.31%), S7 (5.36%), S8 (1.57%), S9 (8.84%), S10 (8.56%), S12 (12.37%), S14 (11.10%), S15 (4.18%), S16 (7.04%), S17 (6.62%) | S1 (−40.19%), S2 (−2.54%), S6 (−9.80%), S11 (−46.07%), S13 (−1.40%) | S3 (15.17%), S4 (11.33%), S5 (9.71%), S7 (6.91%), S8 (3.77%), S9 (8.59%), S10 (7.46%), S12(10.90%), S14(11.22%), S15 (3.28%), S16 (5.28%), S17 (6.38%) | S1 (−38.11%), S2 (−4.80%), S6 (−6.05%) S11 (−50.11%), S13 (−0.92%) | S3 (14.54%), S4 (11.03%), S5 (10.18%), S7 (6.96%), S8 (3.30%), S9 (9.10%), S10 (8.20%), S12 (10.57%), S14 (11.10%), S15 (3.55%), S16 (5.91%), S17 (5.58%) | S1 (−39.14%), S2 (−7.64%), S6 (−9.24%) S11 (−42.98%), S13 (−0.99%) |
References
- Folke, C.; Biggs, R.; Norström, A.V.; Reyers, B.; Rockström, J. Social-Ecological Resilience and Biosphere-Based Sustainability Science. ES 2016, 21, art41. [Google Scholar] [CrossRef]
- Liu, C.; Li, W.; Xu, J.; Zhou, H.; Li, C.; Wang, W. Global Trends and Characteristics of Ecological Security Research in the Early 21st Century: A Literature Review and Bibliometric Analysis. Ecol. Indic. 2022, 137, 108734. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, H.; Li, W.; Du, H.; Huang, H.; Wu, Y.; Liu, S. Research on Provincial Carbon Quota Allocation under the Background of Carbon Neutralization. Energy Rep. 2022, 8, 903–915. [Google Scholar] [CrossRef]
- Steffen, W.; Richardson, K.; Rockström, J.; Cornell, S.E.; Fetzer, I.; Bennett, E.M.; Biggs, R.; Carpenter, S.R.; de Vries, W.; de Wit, C.A.; et al. Planetary Boundaries: Guiding Human Development on a Changing Planet. Science 2015, 347, 1259855. [Google Scholar] [CrossRef]
- Wackernagel, M.; Hanscom, L.; Jayasinghe, P.; Lin, D.; Murthy, A.; Neill, E.; Raven, P. The Importance of Resource Security for Poverty Eradication. Nat. Sustain. 2021, 4, 731–738. [Google Scholar] [CrossRef]
- Lei, H.; Fang, L.; Qian, Z.; Xu, C.; Deng, M.; Liu, X. The Quantitative Analysis of Ecological Compensation Responsibility in Watershed. Energy Procedia 2012, 16, 1324–1331. [Google Scholar] [CrossRef][Green Version]
- Lenzen, M.; Murray, J.; Sack, F.; Wiedmann, T. Shared Producer and Consumer Responsibility—Theory and Practice. Ecol. Econ. 2007, 61, 27–42. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Boquera, L.; Chàfer, M.; Vérez, D. Embodied Energy and Embodied Carbon of Structural Building Materials: Worldwide Progress and Barriers through Literature Map Analysis. Energy Build. 2021, 231, 110612. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, W.; Fan, J.; Yu, J.; Zhao, H. Transfers of Embodied PM2.5 Emissions from and to the North China Region Based on a Multiregional Input-Output Model. Environ. Pollut. 2018, 235, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Infante-Amate, J.; Aguilera, E.; Palmeri, F.; Guzmán, G.; Soto, D.; García-Ruiz, R.; de Molina, M.G. Land Embodied in Spain’s Biomass Trade and Consumption (1900–2008): Historical Changes, Drivers and Impacts. Land Use Policy 2018, 78, 493–502. [Google Scholar] [CrossRef]
- Borucke, M.; Moore, D.; Cranston, G.; Gracey, K.; Iha, K.; Larson, J.; Lazarus, E.; Morales, J.C.; Wackernagel, M.; Galli, A. Accounting for Demand and Supply of the Biosphere’s Regenerative Capacity: The National Footprint Accounts’ Underlying Methodology and Framework. Ecol. Indic. 2013, 24, 518–533. [Google Scholar] [CrossRef]
- Rees, W.E. Ecological Footprints and Appropriated Carrying Capacity: What Urban Economics Leaves Out. Environ. Urban. 1992, 4, 121–130. [Google Scholar] [CrossRef]
- Wackernagel, M.; Onisto, L.; Bello, P.; Callejas Linares, A.; Susana López Falfán, I.; Méndez García, J.; Isabel Suárez Guerrero, A.; Guadalupe Suárez Guerrero, M. National Natural Capital Accounting with the Ecological Footprint Concept. Ecol. Econ. 1999, 29, 375–390. [Google Scholar] [CrossRef]
- Musikavong, C.; Gheewala, S.H. Assessing Ecological Footprints of Products from the Rubber Industry and Palm Oil Mills in Thailand. J. Clean. Prod. 2017, 142, 1148–1157. [Google Scholar] [CrossRef]
- Murakami, S.; Takasu, T.; Islam, K.; Yamasue, E.; Adachi, T. Ecological Footprint and Total Material Requirement as Environmental Indicators of Mining Activities: Case Studies of Copper Mines. Environ. Sustain. Indic. 2020, 8, 100082. [Google Scholar] [CrossRef]
- Galli, A. On the Rationale and Policy Usefulness of Ecological Footprint Accounting: The Case of Morocco. Environ. Sci. Policy 2015, 48, 210–224. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, H. Ecological Deficit Tax: A Tax Design and Simulation of Compensation for Ecosystem Service Value Based on Ecological Footprint in China. J. Clean. Prod. 2019, 230, 1128–1137. [Google Scholar] [CrossRef]
- Wei, Y.; Song, B.; Wang, Y. Designing Cross-Region Ecological Compensation Scheme by Integrating Habitat Maintenance Services Production and Consumption—A Case Study of Jing-Jin-Ji Region. J. Environ. Manag. 2022, 311, 114820. [Google Scholar] [CrossRef]
- Rudolph, A.; Figge, L. Determinants of Ecological Footprints: What Is the Role of Globalization? Ecol. Indic. 2017, 81, 348–361. [Google Scholar] [CrossRef]
- Ulucak, R.; Lin, D. Persistence of Policy Shocks to Ecological Footprint of the USA. Ecol. Indic. 2017, 80, 337–343. [Google Scholar] [CrossRef]
- Baabou, W.; Grunewald, N.; Ouellet-Plamondon, C.; Gressot, M.; Galli, A. The Ecological Footprint of Mediterranean Cities: Awareness Creation and Policy Implications. Environ. Sci. Policy 2017, 69, 94–104. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, T.; Zhang, H.; Pan, T.; Ni, X.; Grydehøj, A.; Zhang, J. Factors Influencing the Ecological Security of Island Cities: A Neighborhood-Scale Study of Zhoushan Island, China. Sustain. Cities Soc. 2020, 55, 102029. [Google Scholar] [CrossRef]
- Ahmed, Z.; Asghar, M.M.; Malik, M.N.; Nawaz, K. Moving towards a Sustainable Environment: The Dynamic Linkage between Natural Resources, Human Capital, Urbanization, Economic Growth, and Ecological Footprint in China. Resour. Policy 2020, 67, 101677. [Google Scholar] [CrossRef]
- Marrero, M.; Puerto, M.; Rivero-Camacho, C.; Freire-Guerrero, A.; Solís-Guzmán, J. Assessing the Economic Impact and Ecological Footprint of Construction and Demolition Waste during the Urbanization of Rural Land. Resour. Conserv. Recycl. 2017, 117, 160–174. [Google Scholar] [CrossRef]
- Udemba, E.N. A Sustainable Study of Economic Growth and Development amidst Ecological Footprint: New Insight from Nigerian Perspective. Sci. Total Environ. 2020, 732, 139270. [Google Scholar] [CrossRef] [PubMed]
- Duro, J.A.; Teixidó-Figueras, J. Ecological Footprint Inequality across Countries: The Role of Environment Intensity, Income and Interaction Effects. Ecol. Econ. 2013, 93, 34–41. [Google Scholar] [CrossRef]
- Szigeti, C.; Toth, G.; Szabo, D.R. Decoupling—Shifts in Ecological Footprint Intensity of Nations in the Last Decade. Ecol. Indic. 2017, 72, 111–117. [Google Scholar] [CrossRef]
- Kissinger, M.; Fix, J.; Rees, W.E. Wood and Non-Wood Pulp Production: Comparative Ecological Footprinting on the Canadian Prairies. Ecol. Econ. 2007, 62, 552–558. [Google Scholar] [CrossRef]
- Cerutti, A.K.; Bagliani, M.; Beccaro, G.L.; Bounous, G. Application of Ecological Footprint Analysis on Nectarine Production: Methodological Issues and Results from a Case Study in Italy. J. Clean. Prod. 2010, 18, 771–776. [Google Scholar] [CrossRef]
- Herva, M.; García-Diéguez, C.; Franco-Uría, A.; Roca, E. New Insights on Ecological Footprinting as Environmental Indicator for Production Processes. Ecol. Indic. 2012, 16, 84–90. [Google Scholar] [CrossRef]
- de Alvarenga, R.A.F.; da Silva Júnior, V.P.; Soares, S.R. Comparison of the Ecological Footprint and a Life Cycle Impact Assessment Method for a Case Study on Brazilian Broiler Feed Production. J. Clean. Prod. 2012, 28, 25–32. [Google Scholar] [CrossRef]
- Wu, D.; Liu, J. Multi-Regional Input-Output (MRIO) Study of the Provincial Ecological Footprints and Domestic Embodied Footprints Traded among China’s 30 Provinces. Sustainability 2016, 8, 1345. [Google Scholar] [CrossRef]
- Wiedmann, T. A First Empirical Comparison of Energy Footprints Embodied in Trade—MRIO versus PLUM. Ecol. Econ. 2009, 68, 1975–1990. [Google Scholar] [CrossRef]
- Galli, A.; Weinzettel, J.; Cranston, G.; Ercin, E. A Footprint Family Extended MRIO Model to Support Europe’s Transition to a One Planet Economy. Sci. Total Environ. 2013, 461–462, 813–818. [Google Scholar] [CrossRef] [PubMed]
- Peters, G.P. Opportunities and Challenges for Environmental MRIO Modelling: Illustrations with the GTAP Database. In Proceedings of the 16th International Input-Output Conference of the International Input-Output Association (IIOA), Istanbul, Turkey, 2–6 July 2007; pp. 1–26. [Google Scholar]
- Fang, D.; Chen, B. Inequality of Air Pollution and Carbon Emission Embodied in Inter-Regional Transport. Energy Procedia 2019, 158, 3833–3839. [Google Scholar] [CrossRef]
- Lan, J.; Malik, A.; Lenzen, M.; McBain, D.; Kanemoto, K. A Structural Decomposition Analysis of Global Energy Footprints. Appl. Energy 2016, 163, 436–451. [Google Scholar] [CrossRef]
- Zheng, H.; Xu, L. Production and Consumption-Based Primary PM2.5 Emissions: Empirical Analysis from China’s Interprovincial Trade. Resour. Conserv. Recycl. 2020, 155, 104661. [Google Scholar] [CrossRef]
- Hubacek, K.; Giljum, S. Applying Physical InputÁ/Output Analysis to Estimate Land Appropriation (Ecological Footprints) of International Trade Activities. Ecol. Econ. 2003, 44, 137–151. [Google Scholar] [CrossRef]
- Wiedmann, T.; Minx, J.; Barrett, J.; Wackernagel, M. Allocating Ecological Footprints to Final Consumption Categories with Input–Output Analysis. Ecol. Econ. 2006, 56, 28–48. [Google Scholar] [CrossRef]
- Turner, K.; Lenzen, M.; Wiedmann, T.; Barrett, J. Examining the Global Environmental Impact of Regional Consumption Activities—Part 1: A Technical Note on Combining Input–Output and Ecological Footprint Analysis. Ecol. Econ. 2007, 62, 37–44. [Google Scholar] [CrossRef]
- Zhou, X.; Imura, H. How Does Consumer Behavior Influence Regional Ecological Footprints? An Empirical Analysis for Chinese Regions Based on the Multi-Region Input–Output Model. Ecol. Econ. 2011, 71, 171–179. [Google Scholar] [CrossRef]
- Carballo Penela, A.; Sebastián Villasante, C. Applying Physical Input–Output Tables of Energy to Estimate the Energy Ecological Footprint (EEF) of Galicia (NW Spain). Energy Policy 2008, 36, 1148–1163. [Google Scholar] [CrossRef]
- Weinzettel, J.; Steen-Olsen, K.; Hertwich, E.G.; Borucke, M.; Galli, A. Ecological Footprint of Nations: Comparison of Process Analysis, and Standard and Hybrid Multiregional Input–Output Analysis. Ecol. Econ. 2014, 101, 115–126. [Google Scholar] [CrossRef]
- Marti, L.; Puertas, R. Analysis of the Efficiency of African Countries through Their Ecological Footprint and Biocapacity. Sci. Total Environ. 2020, 722, 137504. [Google Scholar] [CrossRef]
- Ding, Z.; Yao, S. Theory and Valuation of Cross-Regional Ecological Compensation for Cultivated Land: A Case Study of Shanxi Province, China. Ecol. Indic. 2022, 136, 108609. [Google Scholar] [CrossRef]
- Cao, Y.; Dallimer, M.; Stringer, L.C.; Bai, Z.; Siu, Y.L. Land Expropriation Compensation among Multiple Stakeholders in a Mining Area: Explaining “Skeleton House” Compensation. Land Use Policy 2018, 74, 97–110. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. Available online: https://www.fao.org/ (accessed on 16 August 2022).
- GFN National Footprint and Biocapacity Accounts Public Data Package. Available online: https://www.footprintnetwork.org/licenses/public-data-package-free/ (accessed on 16 August 2022).
- IPCC 2006 IPCC Guidelines for National Greenhouse Gas Inventories. Available online: https://www.ipcc.ch/report/2006-ipcc-guidelines-for-national-greenhouse-gas-inventories/ (accessed on 16 August 2022).
- Salman, M.; Long, X.; Dauda, L.; Mensah, C.; Muhammad, S. Different Impacts of Export and Import on Carbon Emissions across 7 ASEAN Countries: A Panel Quantile Regression Approach. Sci. Total Environ. 2019, 686, 1019–1029. [Google Scholar] [CrossRef]
- Abid, M.; Sakrafi, H.; Gheraia, Z.; Abdelli, H. Does Renewable Energy Consumption Affect Ecological Footprints in Saudi Arabia? A Bootstrap Causality Test. Renew. Energy 2022, 189, 813–821. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, R.; Li, L. The Impact of Renewable Energy on Decoupling Economic Growth from Ecological Footprint—An Empirical Analysis of 166 Countries. J. Clean. Prod. 2022, 354, 131706. [Google Scholar] [CrossRef]
- Gassner, A.; Lederer, J.; Kanitschar, G.; Ossberger, M.; Fellner, J. Extended Ecological Footprint for Different Modes of Urban Public Transport: The Case of Vienna, Austria. Land Use Policy 2018, 72, 85–99. [Google Scholar] [CrossRef]
- Tong, J.; Yue, T.; Xue, J. Carbon Taxes and a Guidance-Oriented Green Finance Approach in China: Path to Carbon Peak. J. Clean. Prod. 2022, 367, 133050. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Li, Y.; Tian, Y.; Li, X.; Zhang, X.; Mol, A.P.J.; Sonnenfeld, D.A.; Liu, J.; Ping, Z.; et al. Neglected Environmental Health Impacts of China’s Supply-Side Structural Reform. Environ. Int. 2018, 115, 97–103. [Google Scholar] [CrossRef] [PubMed]






| Intermediate Use | Final Use | Total Output | ||
| Sector | j:1,2,…,n | |||
| Intermediate supply | i:1,2,…,n | Z | F | X |
| Value added | V | |||
| Total input | X’ | |||
| Environmental extended matrix | k:1.2.m | P |
| Abbreviation | Meaning |
|---|---|
| EF | ecological footprint |
| EFPI | ecological footprint production intensity |
| DPC | direct pollution coefficient |
| TPC | total pollution coefficient |
| TPCC | total pollution coefficient component |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Wu, G.; Yang, H. Analysis of China’s Embodied Ecological Footprint and Its Flows among Economic Sectors per Unit of Currency Production. Land 2023, 12, 41. https://doi.org/10.3390/land12010041
Wu D, Wu G, Yang H. Analysis of China’s Embodied Ecological Footprint and Its Flows among Economic Sectors per Unit of Currency Production. Land. 2023; 12(1):41. https://doi.org/10.3390/land12010041
Chicago/Turabian StyleWu, Decun, Guangzhu Wu, and He Yang. 2023. "Analysis of China’s Embodied Ecological Footprint and Its Flows among Economic Sectors per Unit of Currency Production" Land 12, no. 1: 41. https://doi.org/10.3390/land12010041
APA StyleWu, D., Wu, G., & Yang, H. (2023). Analysis of China’s Embodied Ecological Footprint and Its Flows among Economic Sectors per Unit of Currency Production. Land, 12(1), 41. https://doi.org/10.3390/land12010041





