GIS-Based RUSLE Reservoir Sedimentation Estimates: Temporally Variable C-Factors, Sediment Delivery Ratio, and Adjustment for Stream Channel and Bank Sediment Sources
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Sites
2.1.1. General Description
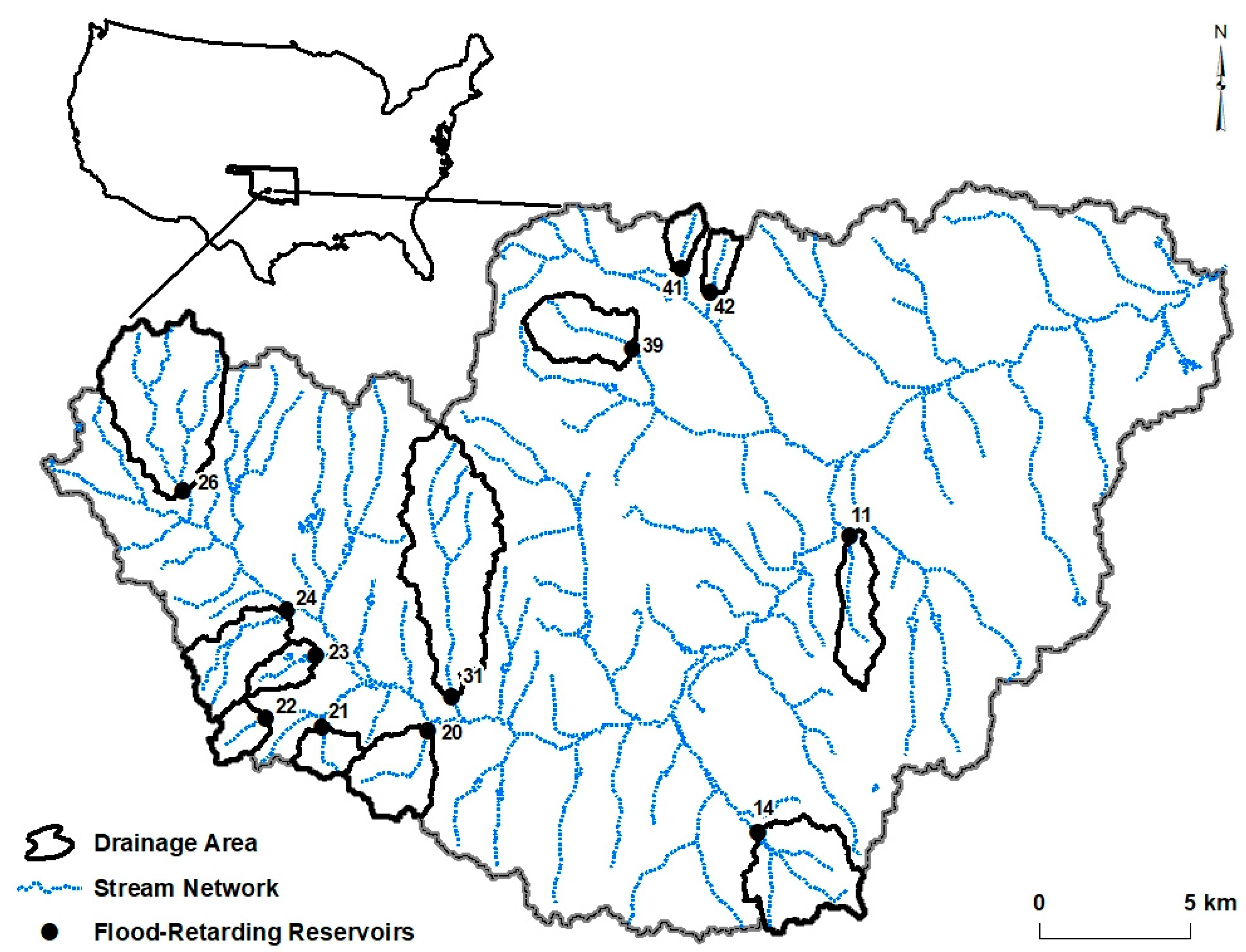
2.1.2. Watershed and Stream Geomorphic and Topographic Variables
2.1.3. Stream Corridor Variables
| % Watershed Area under Land Cover Type | Bathymetric Information | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Watershed/ Reservoir ID | * Date Construction Completed (dd/mm/yr) | WA (km2) | Crop | Grass | Tree/Shrub | Subdominant Land Cover ID | Survey Date | Impoundment Period (yr) | Sediment Volume (m3) |
| 11 | 6 November 1973 | 4.9 | 10 | 73 | 15 | Grass | 24/05/2012 | 39.0 | 36,991 |
| 14 | 14 April 1978 | 10.8 | 5 | 75 | 16 | Grass | 15/05/2012 | 34.1 | 146,856 |
| 20 | 27 October 1982 | 6.7 | 2 | 60 | 33 | Tree/Shrub | 22/05/2012 | 29.6 | 115,906 |
| 21 | DD May 1970 | 2.8 | 3 | 80 | 11 | Grass | 22/05/2012 | 42.1 | 37,485 |
| 22 | 8 April 1977 | 2.9 | 15 | 69 | 13 | Grass | 18/05/2012 | 35.1 | 96,917 |
| 23 | 27 July 1971 | 2.5 | 34 | 59 | 2 | Crop | 17/05/2012 | 40.8 | 24,155 |
| 24 | 8 November 1976 | 7.0 | 43 | 46 | 6 | Crop | 17/05/2012 | 35.5 | 72,256 |
| 26 | DD December 1971 | 18.0 | 42 | 50 | 2 | Crop | 16/05/2012 | 40.4 | 439,581 |
| 31 | 14 September 1978 | 19.2 | 14 | 60 | 21 | Crop | 23/05/2012 | 33.7 | 308,015 |
| 39 | 26 June 1978 | 6.3 | 1 | 56 | 35 | Tree/Shrub | 24/05/2012 | 33.9 | 69,174 |
| 41 | DD October 1969 | 2.0 | 2 | 44 | 44 | Tree/Shrub | 14/05/2012 | 42.5 | 36,868 |
| 42 | DD October 1969 | 1.9 | 4 | 66 | 24 | Tree/Shrub | 25/05/2012 | 42.6 | 27,867 |
2.1.4. Within-Channel Variables
2.2. GIS-Based RUSLE/SEDIMENTATION
2.2.1. RUSLE Model Description
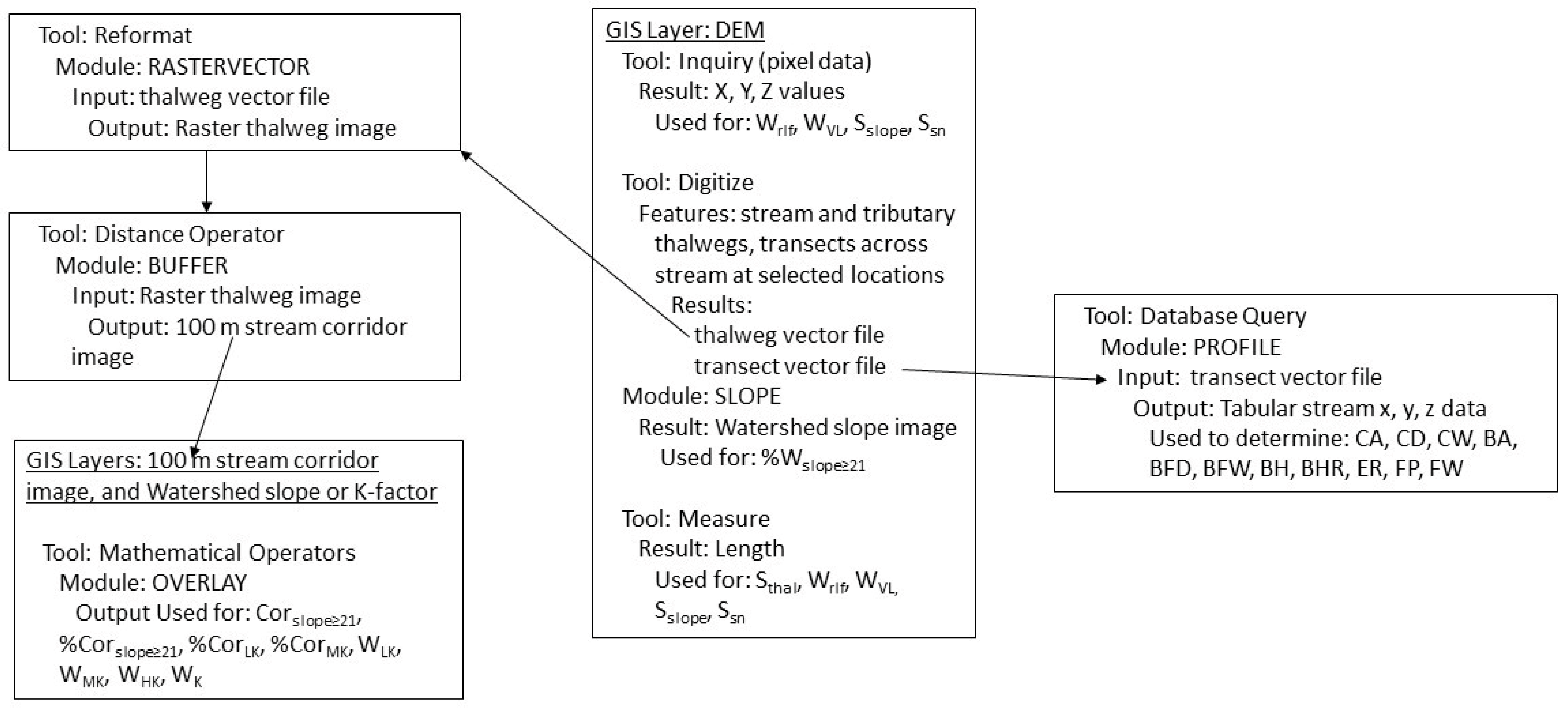
2.2.2. GIS-Based RUSLE Module

2.2.3. GIS-Based RUSLE Inputs
2.2.4. SDR Models
| SDR Models | ||||
|---|---|---|---|---|
| Watershed ID | Equation (2) | Equation (3) | Equation (4) | Equation (5) |
| 11 | 0.254 | 0.474 | 0.257 | 0.387 |
| 14 | 0.260 | 0.435 | 0.213 | 0.351 |
| 20 | 0.248 | 0.458 | 0.238 | 0.372 |
| 21 | 0.372 | 0.504 | 0.293 | 0.415 |
| 22 | 0.364 | 0.503 | 0.291 | 0.414 |
| 23 | 0.268 | 0.511 | 0.302 | 0.421 |
| 24 | 0.229 | 0.456 | 0.236 | 0.37 |
| 26 | 0.103 | 0.411 | 0.188 | 0.329 |
| 31 | 0.179 | 0.408 | 0.186 | 0.327 |
| 39 | 0.255 | 0.461 | 0.242 | 0.375 |
| 41 | 0.321 | 0.524 | 0.318 | 0.433 |
| 42 | 0.395 | 0.527 | 0.322 | 0.436 |
2.3. Normalized GIS-Based RUSLE Reservoir Sedimentation Estimates
2.4. Stream Bank Sediment Contributions
2.4.1. First-Order Adjustment
2.4.2. Statistical Linkages between NDRes and Watershed, Stream, Stream Corridor, and Within-Channel Variables
2.5. Statistical Analysis
3. Results and Discussion
3.1. Variability in RUSLE C- and K-Factors
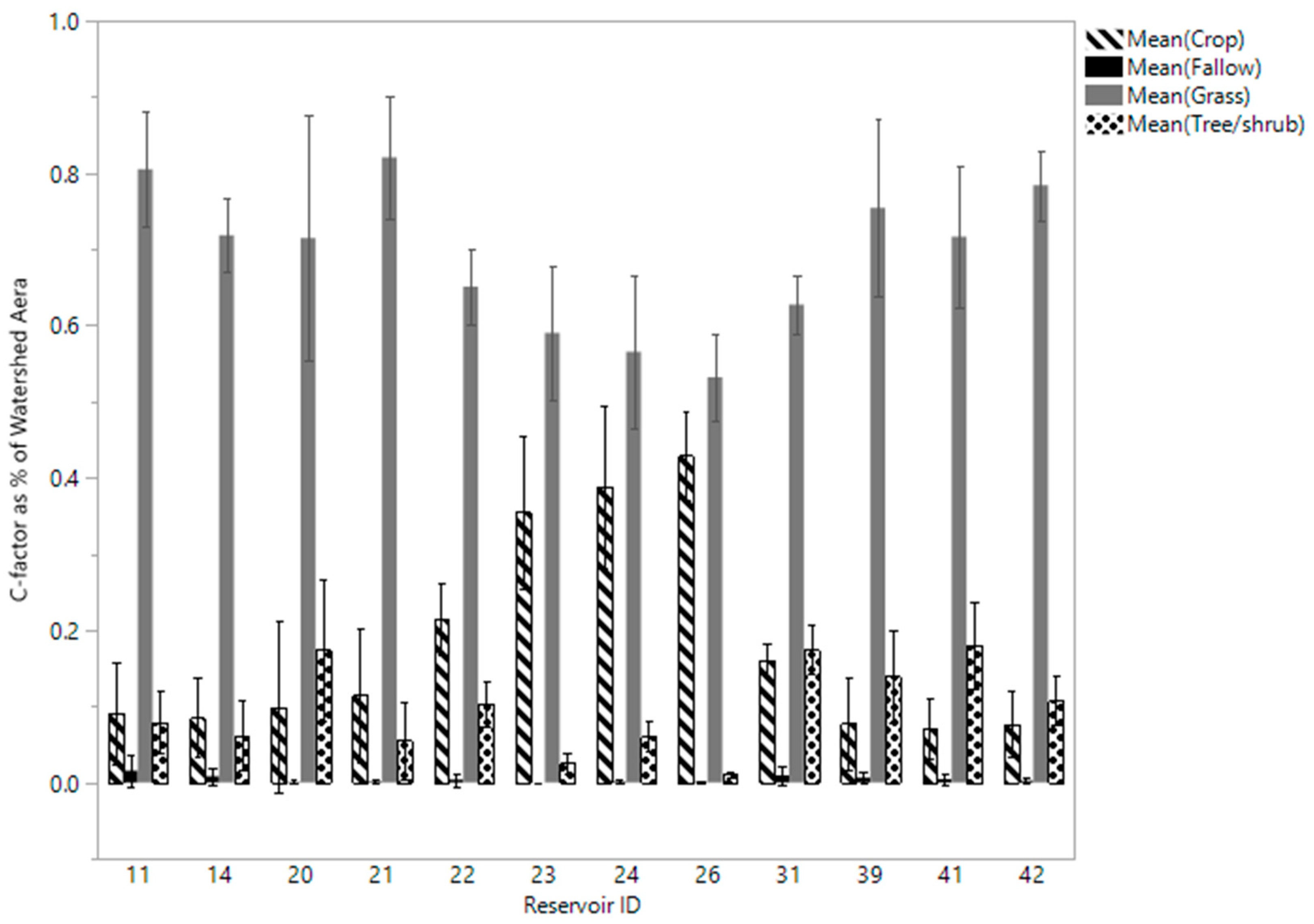
3.1.1. C-Factors (Land Cover)
| Image Year | |||||
|---|---|---|---|---|---|
| Cover Type | 1981 | 1985 | 1989 | 1994 | 1997 |
| Crop | 0.471 | 0.414 | 0.179 | 0.394 | 0.445 |
| Fallow | -- | 0.002 | 0.005 | -- | -- |
| Grass | 0.488 | 0.544 | 0.752 | 0.594 | 0.537 |
| Tree/Shrub | 0.064 | 0.064 | 0.088 | 0.035 | 0.042 |
3.1.2. K-Factors
3.2. Initial Reservoir Sedimentation Analysis
3.3. Effects of Land Cover (C-factor) Date on Sedimentation Estimates
3.3.1. Date Effects Pooled over All Watersheds
3.3.2. Date Effects within Watershed Subdominant Land Cover Group
| Date | All | Crop | Grass | Tree/Shrub |
|---|---|---|---|---|
| 1981 | 0.438 | 0.510 | 0.481 | 0.323 ab |
| 1985 | 0.545 | 0.618 | 0.422 | 0.593 a |
| 1989 | 0.499 | 0.843 | 0.462 | 0.193 b |
| 1994 | 0.454 | 0.565 | 0.401 | 0.395 ab |
| 1997 | 0.595 | 0.738 | 0.667 | 0.369 ab |
3.4. Comparison of Averaged Estimated and Measured Reservoir Sedimentation
3.4.1. Between Subdominant Land Cover Groups
| Watershed Land Cover | * NDResT Least Square Mean |
|---|---|
| Crop | 0.655 a |
| Grass | 0.489 b |
| Tree/shrub | 0.374 b |

3.4.2. Between Reservoirs within Subdominant Land Cover Group
3.4.3. Across All Watersheds
| Watershed/Reservoir ID | Watershed Land Cover Group | * NDResT | NDRes Mean (%) | NDRes_adj Mean (%) |
|---|---|---|---|---|
| 24 | Crop | 0.763 a | −56.0 | −4.3 abc |
| 11 | Grass | 0.726 b | −50.0 | 8.7 a |
| 26 | Crop | 0.681 ab | −61.6 | −16.6 abcd |
| 23 | Crop | 0.679 abc | −53.4 | 1.4 ab |
| 22 | Grass | 0.589 abcd | −62.8 | −19.2 abcd |
| 41 | Tree/shrub | 0.476 abcde | −76.5 | −49.0 bcde |
| 39 | Tree/shrub | 0.417 bcde | −82.3 | −61.5 cde |
| 31 | Crop | 0.387 cde | −82.7 | −62.5 cde |
| 42 | Tree/shrub | 0.383 cde | −83.8 | −64.8 de |
| 21 | Grass | 0.370 de | −84.6 | −66.6 de |
| 14 | Grass | 0.269 e | −88.9 | −75.9 e |
| 20 | Tree/shrub | 0.222 e | −89.1 | −76.3 e |
3.5. Stream Bank Contributions—First-Order Adjustment
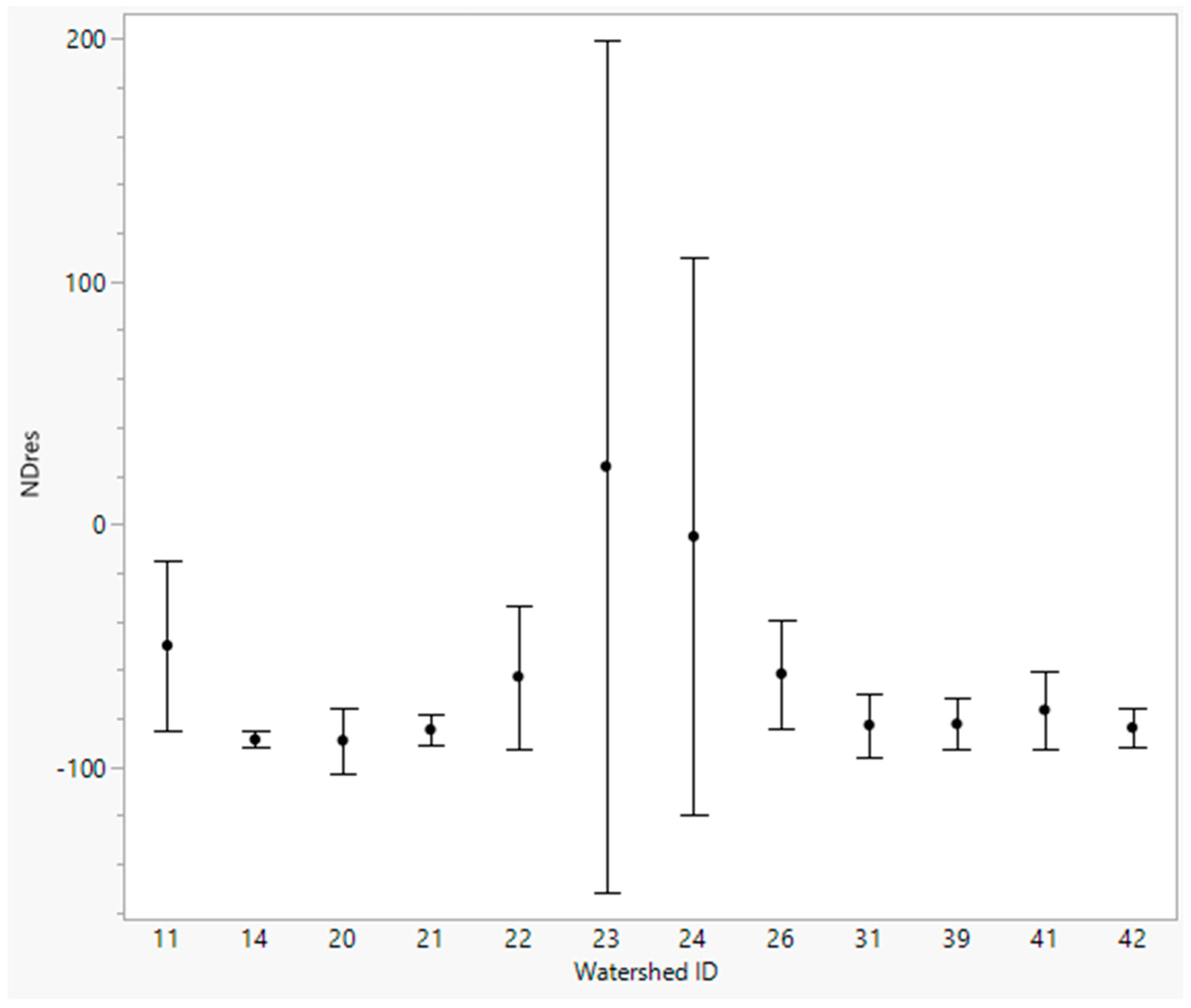
3.6. Watershed, Stream, Stream Corridor, and Within-Channel Variables
3.6.1. Watershed and Stream Variables
| Watershed Variables * | Stream Variables | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Broad Group ID | WA (km2) | Wrlf (m) | %Wslope≥21 | Wvl | %WLK | %WMK | %WHK | WK | Sthal (m) | Sslope (m m−1) | Ssn |
| 1 | 7.1 | 51.0 | 1.7 | 5101 | 19 b | 66 a | 13 a | 0.33 a | 6078 | 0.011 | 1.21 |
| 2 | 7.1 | 51.5 | 1.0 | 3753 | 74 a | 19 b | 3 b | 0.21 b | 4124 | 0.015 | 1.09 |
3.6.2. Stream Corridor Variables
3.6.3. Within-Channel Variables
| Group ID | ICK * | ICSa | ICSi | %ICLK | %ICMK | %ICHK | ICPI |
|---|---|---|---|---|---|---|---|
| 1 | 0.33 a | 40.8 b | 37.2 a | 21.6 b | 78.2 a | 0.14 | 10.9 |
| 2 | 0.23 b | 59.6 a | 23.1 b | 73.9 a | 25.1 b | 0.09 | 7.6 |
3.7. Sediment Delivery Ratios (SDRs)
3.8. Watershed, Stream, Stream Corridor, and Within-Channel Variables as Predictors of NDRes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | Meaning |
| %CorHK | Percentage of the 100 m stream corridor area having high K-factor soils |
| %CorLK | Percentage of the 100 m stream corridor area having low K-factor soils |
| %CorMK | Percentage of the 100 m stream corridor area having moderate K-factor soils |
| %Corslope≥21 | Percentage of the 100 m stream corridor area having slopes ≥ 21° |
| %ICHK | Weighted percentage of high K-factor soils composing the stream bank and channel |
| %ICLK | Weighted percentage of low K-factor soils composing the stream bank and channel |
| %ICMK | Weighted percentage of moderate K-factor soils composing the stream bank and channel |
| %ICWK | Weighted average K-factor of the stream bank and stream channel soils |
| %Wslope>21 | Percentage of the WA having slopes ≥ 21° |
| ANOVA | Analysis of Variance |
| BA | Bank angle (deg) |
| BFD | Bank full depth (m) |
| BFW | Bank full width (m) |
| BFW:BFD | Ratio of BFW to BFD |
| BH | Bank height (m) |
| BHR | Bank height ratio |
| BSTEM | Bank Stability and Toe Erosion Model |
| CA | Stream channel area (m2) |
| CD | Stream channel depth (m) |
| CW | Stream channel width (m) |
| CW:CD | Ratio of CW to CD |
| Corslope≥21 | Actual area of the 100 m stream corridor having slopes ≥ 21° (m2) |
| Corslope≥21:Wvl | Area within the 100 m stream corridor having slopes ≥ 21° per m of Wvl (m2 m−1) |
| DEM | Digital elevation model |
| ER | Entrenchment ratio |
| EUROSEM | European Soil Erosion Model |
| FP | Flood plain |
| FWA | Flood way area |
| GIS | Geographical information system |
| IC | Within-channel |
| ICPI | Weighted average plasticity index of the stream bank and stream channel soils |
| ICSa | Weighted average sand fraction of the stream bank and stream channel soils |
| ICSi | Weighted average silt fraction of the stream bank and stream channel soils |
| LWREW | Little Washita River Experimental Watershed |
| NDRes | Normalized difference between estimated and measured sedimentation |
| NDRes_adj | NDRes adjusted to account for stream channel/bank sediment contributions |
| NDResT | Johnson Su transformation of NDRes |
| RMSE | Root mean square error |
| RUSLE | Revised Universal Soil Loss Equation |
| RUSLE2 | RUSLE version 2 |
| SDR | Sediment delivery ratio |
| SE | Total soil erosion |
| SY | Sediment yield |
| Sslope | Stream slope (m m−1) |
| Ssn | Stream sinuosity |
| Sthal | Stream thalweg length (m) |
| USLE | Universal soil loss equation |
| USDA-NRCS | United States Department of Agriculture-Natural Resources Conservation Service |
| WEPP | Water Erosion Prediction Project |
| WRB | Washita River Basin |
| WA | Watershed drainage area (km2) |
| WHK | Percentage of watershed drainage area in high K-factor soils |
| WLK | Percentage of watershed drainage area in low K-factor soils |
| WK | Area-weighted watershed K-factor |
| WMK | Percentage of watershed drainage area in moderate K-factor soils |
| Wrlf | Watershed relief (m) |
| Wvl | Watershed valley length (m) |
References
- Moriasi, D.N.; Steiner, J.L.; Duke, S.E.; Starks, P.J.; Verser, A.J. Reservoir sedimentation rates in the Little Washita River experimental watershed: Measurement and controlling factors. J. Amer. Water Resour. Assoc. 2018, 54, 1011–1023. [Google Scholar] [CrossRef]
- Hanson, G.J.; Caldwell, L.; Lobrecht, M.; McCook, D.; Hunt, S.L.; Temple, D. A look at the engineering challenges of the USDA Small Watershed Program. Centennial Edition Trans. ASABE 2007, 50, 1677–1682. [Google Scholar] [CrossRef]
- Hunt, S.L.; Hanson, G.L.; Temple, D.M.; Caldwell, L. The importance of the USDA Small Watershed Program to the rural United States. Water Resour. IMPACT 2011, 13, 9–11. [Google Scholar]
- Allen, P.B.; Naney, J.W. Hydrology of the Little Washita River Watershed, Oklahoma; United States Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1991; ARS-90.
- Bennett, S.J.; Dunbar, J.A.; Rhoton, F.E.; Allen, P.M.; Bigham, J.M.; Davidson, G.R.; Wren, D.G. Assessing sedimentation issues within aging flood-control reservoirs. Rev. Engin. Geol. 2013, 21, 25–44. [Google Scholar]
- Ketchem, A.J.; Mathew, P.E.; Lyons, P.E.; Evans, R. Reservoir Sediment Impacts on the Rehabilitation of NRCS-Assisted Flood Control Dams in Virginia; ASABE Paper No. 1900198; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2019; 3p. [Google Scholar]
- Zhang, X.C.J.; Zhang, G.H.; Wei, X.; Guan, Y.H. Evaluation of cesium-137 conversion models and parameter sensitivity for erosion estimation. J. Environ. Qual. 2015, 44, 789–802. [Google Scholar] [CrossRef]
- The Small Watershed Rehabilitation Amendments of 2000. Available online: https://www.congress.gov/bill/106th-congress/house-bill/728 (accessed on 7 August 2023).
- Laflen, J.M.; Elliot, W.J.; Flanagan, D.C.; Meyer, C.R.; Nearing, M.A. WEPP-predicting water erosion using a process-based model. J. Soil Water Conserv. 1997, 52, 96–102. [Google Scholar]
- Morgan, R.P.C.; Quinton, J.N.; Smith, R.E.; Govers, G.; Poesen, J.W.A.; Auerswald, K.; Chisci, G.; Torri, D.; Styczen, M.E. The European Soil Erosion Model (EUROSEM): A dynamic approach for predicting sediment transport from fields and small catchments. Earth Surf. Proc. Landforms J. Brit. Geomorph. Group 1998, 23, 527–544. [Google Scholar] [CrossRef]
- Kinnell, P.I. Sediment delivery ratios: A misaligned approach to determining sediment delivery from hillslopes. Hydrolog. Proc. 2004, 18, 3191–3194. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Soil Loss Equation (RUSLE); Agriculture Handbook No. 703; United States Department of Agriculture: Washington, DC, USA, 1997; 404p.
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; U.S. Department of Agriculture, Handbook No. 537; United States Department of Agriculture: Washington, DC, USA, 1978.
- Shi, Z.H.; Cai, C.F.; Ding, S.W.; Wang, T.W.; Chow, T.L. Soil conservation planning at the small watershed level using RUSLE with GIS: A case study in the Three Gorges area of China. Catena 2004, 55, 33–48. [Google Scholar] [CrossRef]
- Chen, H.; El Garouani, A.; Lewis, L.A. Modelling soil erosion and deposition within a Mediterranean mountainous environment utilizing remote sensing and GIS–Wadi Tlata, Morocco. Geograph. Helvet. 2008, 63, 36–47. [Google Scholar] [CrossRef]
- Anees, M.T.; Abdullah, K.; Nawawi, M.N.M.; Norulaini, N.A.N.; Syakir, M.I.; Omar, A.K.M. Soil erosion analysis by RUSLE and sediment yield models using remote sensing and GIS in Kelantan state, Peninsular Malaysia. Soil Res. 2018, 56, 356–372. [Google Scholar] [CrossRef]
- Kumar, A.; Devi, M.; Deshmukh, B. Integrated Remote Sensing and Geographic Information System Based RUSLE Modelling for Estimation of Soil Loss in Western Himalaya, India. Water Resour. Manag. 2014, 28, 3307–3317. [Google Scholar] [CrossRef]
- Kouli, M.; Soupios, P.; Vallianatos, F. Soil erosion prediction using the Revised Universal Soil Loss Equation (RUSLE) in a GIS framework, Chania, Northwestern Crete, Greece. Environ. Geol. 2009, 57, 483–497. [Google Scholar] [CrossRef]
- Boomer, K.B.; Weller, D.E.; Jordan, T.E. Empirical models based on the Universal Soil Loss Equation fail to predict sediment discharges from Chesapeake catchments. J. Environ. Qual. 2008, 37, 79–89. [Google Scholar] [CrossRef]
- Moges, M.M.; Abay, D.; Engidayehu, H. Investigating reservoir sedimentation and its implications to watershed sediment yield: The case of two small dams in data-scarce upper Blue Nile basin, Ethiopia. Lakes and Reser. 2018, 23, 217–229. [Google Scholar] [CrossRef]
- Kaffas, K.; Pisinaras, V.; Al Sayah, M.J.; Santopietro, S.; Righetti, M. A USLE-based model with modified LS-factor combined with sediment delivery module for Alpine basins. Catena 2021, 207, 105655. [Google Scholar] [CrossRef]
- Bufalini, M.; Materazzi, M.; Martinello, C.; Rotigliano, E.; Pambianchi, G.; Tromboni, M.; Paniccia, M. Soil erosion and deposition rate inside an artificial reservoir in central Italy: Bathymetry versus RUSLE and morphometry. Land 2022, 11, 1924. [Google Scholar] [CrossRef]
- Trimble, S.W. Contribution of stream channel erosion to sediment yield from an urbanizing watershed. Science 1997, 278, 1442–1444. [Google Scholar] [CrossRef]
- Prosser, I.P.; Rutherford, I.D.; Olley, J.M.; Young, W.J.; Wallbrink, P.J.; Moran, C.J. Large-scale patterns of erosion and sediment transport in river networks, with examples from Australia. Mar. Freshw. Res. 2001, 52, 81–99. [Google Scholar] [CrossRef]
- Basher, L.; Douglas, G.; Elliott, S.; Hughes, A.; Jones, H.; McIvor, I.; Page, M.; Rosser, B.; Tait, A. Impacts of Climate Change on Erosion and Erosion Control Methods–A Critical Review. Final Report MPI Technical Paper No: 2012/45, 2012. Available online: https://www.mpi.govt.nz/document-vault/4074 (accessed on 8 March 2023).
- Simon, A.; Rinaldi, M. Disturbance, stream incision, and channel evolution: The roles of excess transport capacity and boundary materials in controlling channel response. Geomorphology 2006, 79, 361–383. [Google Scholar] [CrossRef]
- Wilson, C.G.; Kuhnle, R.A.; Bosch, D.D.; Steiner, J.L.; Starks, P.J.; Tomer, M.D.; Wilson, G.V. Quantifying relative contributions from sediment sources in Conservation Effects Assessment Project watersheds. J. Soil Water Conser. 2008, 63, 523–532. [Google Scholar] [CrossRef]
- Simon, A.; Klimetz, L. Relative magnitudes and sources of sediment in benchmark watersheds of the Conservation Effects Assessment Project. J. Soil Water Conser. 2008, 63, 504–522. [Google Scholar] [CrossRef]
- Benavidez, R.; Jackson, B.; Maxell, D.; Norton, K. A review of the (Revised) Universal Soil Loss Equation ((R)USLE): With a view to increasing it global applicability and improving soil loss estimates. Hydrol. Earth Sys. Sci. 2018, 22, 6059–6086. [Google Scholar] [CrossRef]
- Oklahoma Climatological Survey. Available online: http://climate.ok.gov/index.php/climate/climate_normals_by_county/local_data (accessed on 7 August 2023).
- Rosgen, D.L. A classification of natural rivers. Catena 1994, 22, 169–199. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Site Assessment and Investigation. Part 654 Stream Restoration Design, Chapter 3, National Engineering Handbook; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2007. Available online: https://directives.sc.egov.usda.gov/viewerFS.aspx?hid=21433 (accessed on 31 March 2023).
- United States Department of Agriculture-Agricultural Research Service, Watershed Physical Processes Research: Oxford, MS. Available online: https://www.ars.usda.gov/Research/docs.htm?docid=5044 (accessed on 30 March 2023).
- Rosgen, D.L. A practical method of computing streambank erosion rate. In Proceedings of the Seventh Interagency Sedimentation Conference, Reno, NV, USA, 25–29 March 2001; Volume 2, pp. 9–15. [Google Scholar]
- United States Department of Agriculture-Natural Resources Conservation Service. Web Soil Survey. Available online: https://websoilsurvey.sc.egov.usda.gov/app/ (accessed on 22 September 2023).
- United States Department of Agriculture-Natural Resources Research Serivice. Geospatial Data Gateway. Available online: https://gdg.sc.egov.usda.gov/ (accessed on 22 September 2023).
- Starks, P.J.; Steiner, J.L.; Stern, A.J. Upper Washita River experimental watersheds: Land cover data sets (1974–2007) for two southwestern Oklahoma agricultural watersheds. J. Environ. Qual. 2014, 43, 310–1318. [Google Scholar] [CrossRef]
- United States Department of Agriculture-Natural Resources Conservation Service. Available online: https://efotg.sc.egov.usda.gov/references/Agency/OK/RUSLE_Chap4_C_Factors.pdf (accessed on 23 March 2023).
- Garbrecht, J.D. Effects of climate variations and soil conservation on sedimentation of a west-central Oklahoma reservoir. J. Hydrol. Eng. 2011, 16, 899–906. [Google Scholar] [CrossRef]
- Maner, S.B. Factors affecting sediment delivery ratios in the Red Hills physiographic area. Trans. Amer. Geophys. Union 1958, 39, 669–675. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Sediment sources, yields, and delivery ratios. In National Engineering Handbook; Section 3; Sedimentation; United States Department of Agriculture: Washington, DC, USA, 1972. [Google Scholar]
- Boyce, R.C. Sediment routing with sediment delivery ratios. In Present and Pospective Technology for Predicting Sediment Yields and Sources; Publication ARS-S-40; United States Department of Agriculture: Washington, DC, USA, 1975; pp. 61–65. [Google Scholar]
- Vanoni, V.A. Sedimentation Engineering; American Society of Civil Engineers: Reston, VA, USA, 2006. [Google Scholar]
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef]
- Schumm, A.A. Patterns of alluvial rivers. Ann. Rev. Earth and Planet. Sci. 1985, 13, 5–27. [Google Scholar] [CrossRef]
- New Mexico State University. Available online: https://jornada.nmsu.edu/files/geomorp_terms.pdf (accessed on 24 April 2023).
- United States Department of Agriculture. Rosgen Stream Classification Technique Supplemental Materials. Technical Supplement 3, Part 654, National Engineering Handbook. Available online: https://directives.sc.egov.usda.gov/rollupviewer.aspx?hid=17092 (accessed on 25 April 2023).
| NDRes (%) | ||||||
|---|---|---|---|---|---|---|
| SDR | n-Size | Mean * | Std. Dev. | CV | Min | Max |
| Equation (2) | 60 | −40.2 ab | 104.9 | 261.1 | −96.9 | 548.2 |
| Equation (3) | 60 | −61.9 b | 66.6 | 107.6 | −97.8 | 332.8 |
| Equation (4) | 60 | −45.6 ab | 94.6 | 207.5 | −96.9 | 518.7 |
| Equation (5) | 60 | −54.9 ab | 78.3 | 142.5 | −97.4 | 412.6 |
| K-Factors as a Decimal% of Watershed Area | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WS ID | 0 (Water Area) | 0.02 | 0.1 | 0.15 | 0.2 | 0.24 | 0.28 | 0.32 | 0.37 | 0.43 | 0.49 | WK |
| Low Erosivity | Moderate Erosivity | High | ||||||||||
| 11 | 0.0089 | 0.155 | 0 | 0.233 | 0.288 | 0 | 0 | 0.008 | 0.077 | 0.116 | 0.115 | 0.23 |
| 14 | 0.125 | 0.014 | 0 | 0.242 | 0.619 | 0 | 0 | 0 | 0 | 0 | 0 | 0.16 |
| 20 | 0.012 | 0.02 | 0.104 | 0.214 | 0.353 | 0 | 0.156 | 0 | 0.052 | 0.077 | 0.012 | 0.22 |
| 21 | 0.008 | 0.064 | 0.131 | 0.2 | 0.314 | 0 | 0.203 | 0 | 0.059 | 0 | 0.021 | 0.20 |
| 22 | 0.04 | 0 | 0.044 | 0 | 0.098 | 0 | 0.061 | 0 | 0.417 | 0.182 | 0.158 | 0.35 |
| 23 | 0.028 | 0 | 0.0001 | 0.015 | 0.078 | 0 | 0.205 | 0 | 0.493 | 0.137 | 0.044 | 0.34 |
| 24 | 0.022 | 0 | 0 | 0 | 0.011 | 0.011 | 0.154 | 0 | 0.599 | 0.113 | 0.089 | 0.36 |
| 26 | 0.028 | 0 | 0 | 0 | 0.0005 | 0.001 | 0 | 0 | 0.743 | 0 | 0.228 | 0.39 |
| 31 | 0.027 | 0.001 | 0.01 | 0.002 | 0.093 | 0.088 | 0.222 | 0 | 0.394 | 0.02 | 0.143 | 0.33 |
| 39 | 0.022 | 0.032 | 0 | 0.035 | 0.653 | 0.113 | 0.145 | 0 | 0 | 0 | 0 | 0.20 |
| 41 | 0.025 | 0 | 0 | 0.333 | 0.642 | 0 | 0 | 0 | 0 | 0 | 0 | 0.18 |
| 42 | 0.029 | 0 | 0 | 0.013 | 0.91 | 0 | 0 | 0 | 0.024 | 0.007 | 0.017 | 0.20 |
| Watershed Land Cover Group | ||||
|---|---|---|---|---|
| Statistic | Crop | Grass | Tree/Shrub | All |
| Maximum (%) | 332.8 | 8.9 | −56.1 | 332.8 |
| Minimum (%) | −97.5 | −93.4 | −97.8 | −97.8 |
| Mean (%) | −31.4 | −71.7 | −82.9 | −62.0 |
| Std. Dev. (%) | 106.5 | 27.0 | 12.2 | 66.6 |
| N-size | 20 | 20 | 20 | 60 |
| Crop | Grass | Tree/Shrub | |||
|---|---|---|---|---|---|
| Watershed ID | NDResT * | Watershed ID | NDResT | Watershed ID | NDResT |
| 24 | 0.809 a | 11 | 0.726 a | 41 | 0.476 |
| 23 | 0.743 a | 22 | 0.589 ab | 39 | 0.417 |
| 26 | 0.681 a | 21 | 0.370 bc | 42 | 0.383 |
| 31 | 0.387 b | 14 | 0.269 c | 20 | 0.222 |
| Watershed/Reservoir ID | Watershed Subdominant Land Cover Group | * NDResT |
|---|---|---|
| 24 | Crop | 0.809 a |
| 23 | Crop | 0.743 ab |
| 11 | Grass | 0.726 ab |
| 26 | Crop | 0.681 abc |
| 22 | Grass | 0.589 abcd |
| 41 | Tree/shrub | 0.476 bcde |
| 39 | Tree/shrub | 0.417 cde |
| 31 | Crop | 0.387 de |
| 42 | Tree/shrub | 0.383 de |
| 21 | Grass | 0.370 de |
| 14 | Grass | 0.269 e |
| 20 | Tree/shrub | 0.222 e |
| Soil K-Factor * | Topographic * | ||||
|---|---|---|---|---|---|
| Group ID | %CorLK | %CorMK | %CorHK | %Corslope>21 | Corslope>21:Wvl (m2 m−1) |
| 1 | 19.8 b | 71.9 a | 8.3 a | 7.7 | 15.4 a |
| 2 | 67.4 a | 31.6 b | 1.0 b | 13.8 | 5.2 b |
| Within-Channel Variables * | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group ID | BFD (m) | BFW (m) | BFW:BFD | BA (deg) | BH (m) | BHR | ER | CD (m) | CW (m) | CW: CD | CA (m2) | FWA_ %WA |
| 1 | 0.65 | 15.3 | 43.2 | 17.9 | 3.0 | 5.8 a | 2.1 | 3.6 | 36.1 | 18.0 | 91.3 | 3.7 |
| 2 | 0.57 | 15.6 | 38.8 | 12.7 | 2.0 | 3.5 b | 4.5 | 2.4 | 38.8 | 36.0 | 70.0 | 2.7 |
| # Model Variables | Variables Used | RMSE (%) | R2 | Adjusted R2 | p-Value |
|---|---|---|---|---|---|
| 1 | LNWSK | 11.7 | 0.436 | --- | 0.0194 |
| NDRes = (117.3 × LNWSK) − 103.6 | |||||
| 2 | SHASHER, FWA_%WA | 7.8 | 0.775 | 0.724 | 0.0012 |
| NDRes = (−31.0 × SHASHER) + (7.1 × FWA_%WA) − 79.4 | |||||
| 3 | LNBFD, FWA_%WA,%ICK | 6.2 | 0.871 | 0.822 | 0.0006 |
| NDRes = (243.7 × %ICK) + (7.0 × FWA_%WA) − (30.7 × LNBFD) − 145.7 | |||||
| 4 | LNWK,LNWvl, LNCorslope≥21:Wvl, SHASHER | 3.4 | 0.967 | 0.948 | <0.0001 |
| NDRes = (62.5 × LNWK) − (64.8 × SHASHER) − (82.2 × LNCorslope≥21:Wvl) − (46.2) − 8.8 | |||||
| 5 | LNWA, LNWSK, LNWvl, LNCorslope≥21:Wvl, SHASHER | 1.9 | 0.991 | 0.984 | <0.0001 |
| NDRes = (41.1 × LNWA) + (86.5 × LNWK) - (107.7 × LNWvl) − (124.1 × LNCorslope≥21:Wvl) − (91.1 × SHASHER) | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starks, P.J.; Moriasi, D.N.; Fortuna, A.-M. GIS-Based RUSLE Reservoir Sedimentation Estimates: Temporally Variable C-Factors, Sediment Delivery Ratio, and Adjustment for Stream Channel and Bank Sediment Sources. Land 2023, 12, 1913. https://doi.org/10.3390/land12101913
Starks PJ, Moriasi DN, Fortuna A-M. GIS-Based RUSLE Reservoir Sedimentation Estimates: Temporally Variable C-Factors, Sediment Delivery Ratio, and Adjustment for Stream Channel and Bank Sediment Sources. Land. 2023; 12(10):1913. https://doi.org/10.3390/land12101913
Chicago/Turabian StyleStarks, Patrick J., Daniel N. Moriasi, and Ann-Marie Fortuna. 2023. "GIS-Based RUSLE Reservoir Sedimentation Estimates: Temporally Variable C-Factors, Sediment Delivery Ratio, and Adjustment for Stream Channel and Bank Sediment Sources" Land 12, no. 10: 1913. https://doi.org/10.3390/land12101913
APA StyleStarks, P. J., Moriasi, D. N., & Fortuna, A.-M. (2023). GIS-Based RUSLE Reservoir Sedimentation Estimates: Temporally Variable C-Factors, Sediment Delivery Ratio, and Adjustment for Stream Channel and Bank Sediment Sources. Land, 12(10), 1913. https://doi.org/10.3390/land12101913





